Keywords

17.1 Introduction

A pedestrian exerts dynamic forces on the structure he walks on. When the structure is a footbridge and if the bridge is flexible and have one or more natural frequencies in the proximity of the dynamic forces generated by the pedestrian, resonance of the bridge structure may occur. This may lead to serviceability problems and probably the most well-known bridge that has experienced excessive vibrations is The Millennium Bridge in London [1].

This paper deals with load models for pedestrians with particular focus on the vertical action. Some years ago, these models were deterministic, for example the load models suggested in [2,3,4] and the calculation of walking loads were quite simple too. However, one drawback was that the load models did not account for the variability in walking forces imposed the bridge by different pedestrians (exchange the pedestrian and you have another set of parameters for pedestrian step frequency, step length and dynamic load factors being input parameters for your calculation of pedestrian forces). Variability in these parameters is known to exist [5,6,7,8].

It is considered useful to employ a load model that accounts for the stochastic nature of these parameters. Load models that embrace the uncertain input are employed in the studies of this paper. A load model that handles these parameters as random variables is already developed [9] but a somewhat simpler variant of that model is introduced and examined in this paper.

The outputs of both load models are quantiles of structural vibrations (more specifically quantiles for the vertical peak bridge accelerations occurring at bridge midspan), hence properties that describe bridge responses in a probabilistic sense. They are brought about by numerically simulating the action of a pedestrian crossing the bridge and by computing the resulting bridge vibrations. Repetitions of pedestrian crossings (established by Monte Carlo simulations) ensure that a cumulative distribution function for bridges vibration levels are established from which quantiles of interest are sampled.

This strategy is employed for both load models allowing direct comparison between estimates of acceleration quantiles of footbridge response.

The difference between the two load models is the level of detail in which they model the nature of walking. In one model the spreading of energy around the harmonic loads in the force spectrum observed in [10] is accounted for. This is not the case in the other load model. Nevertheless, it is introduced here as it has other advantages. The models are described in Sect. 17.2.

Section 17.3 outlines the methodology in more detail, covering a description of the artificial footbridges used for the investigations being pin-supported single-span footbridges. Section 17.4 presents the results in terms of acceleration quantiles of bridge vibrations obtained for the two load models and Sect. 17.5 provides conclusions and discusses the results.

17.2 Modelling of Walking Loads

As mentioned two different walking load models will be considered for the studies of this paper. They will be denoted load model I and II.

Common for both are that the vertical modal load, Q(t), acting on the structure (on the footbridge and generated by the pedestrian) can be calculated using Eq. (17.1):

$$ Q(t)=\varPhi (t)F(t) $$
(17.1)

where F(t) is the vertical load at the point of action of the pedestrian when moving across the bridge.

The definition of Ф(t) will be presented later in this paper as it will be common for both load models.

Hence, initially, focus is on the way in which F(t) is modelled in load model I and II, respectively.

17.2.1 Load Model I

This load model is the model introduced in [9]. The time-domain load model is believed to capture and model effects of the nature of walking not encompassed in time-domain load models proposed prior to the introduction of load model I.

The mathematical expression for F(t) is seen in Eqs. (17.2, 17.3, and 17.4):

$$ F(t)=\sum_{i=1}^5{F}_i(t)+\sum_{i=1}^5{F}_i^S(t) $$
(17.2)
$$ {F}_i(t)={W\alpha}_i\sum_{{\overline{f}}_j=i-0.25}^{i+0.25}{\overline{\alpha}}_i\left({\overline{f}}_j\right)\cos \left(2\pi {\overline{f}}_j{f}_st+\theta \left({\overline{f}}_j\right)\right) $$
(17.3)
$$ {F}_i^S(t)={W\alpha}_i^S\sum_{{\overline{f}}_j^S=i-0.75}^{i-0.25}{\overline{\alpha}}_i^S\left({\overline{f}}_j^S\right)\cos \left(2\pi {\overline{f}}_j^S{f}_st+\theta \left({\overline{f}}_j^S\right)\right) $$
(17.4)

It is beyond the scope of this paper to define all parameters appearing in the load model. However, here it is useful to know that W represents the static weight of the pedestrian, and that f s represents the step frequency. Also that five main load harmonics (introduced in Eq. (17.3) with associated dynamic load factors, α i), and five subharmonics (introduced in Eq. (17.4) with associated dynamic load factors, \( {\alpha}_i^S \)) constitute the basis of the load model. The presence of subharmonics is due to the fact that “the fundamental period of the force time history is equal to the time required to make two successive steps, rather than one”, [9]. Many of the other parameters in the model ensures that it accounts for the fact that energy is spreading around the main harmonics and subharmonics in the force spectrum. Reference is made to [9] for definition of the parameters not defined in this paper. Overall, the model has the advantage that it models the fact that the locomotion of a pedestrian is not fully period and that load energy leaks at the load harmonics in the force spectrum. In total 400 harmonics are used to calculate the load F(t), following the line of procedure outlined in [9].

17.2.2 Load Model II

A simpler variant of load model I (denoted load model II) is one in which the leaking of load energy at harmonics is not accounted for. By disregarding this effect, the load model can be described by Eqs. (17.5, 17.6, and 17.7).

$$ F(t)=\sum_{i=1}^5{F}_i(t)+\sum_{i=1}^5{F}_i^S(t) $$
(17.5)
$$ {F}_i(t)=W{\alpha}_i\cos \left(2\pi i{f}_st+{\varphi}_i\right) $$
(17.6)
$$ {F}_i^S(t)=W{\alpha}_i^S\cos \left(\pi \left(2i-1\right){f}_st+{\varphi}_{i+5}\right) $$
(17.7)

The load model introduced here, in line with load model I, consists of five main load harmonics (introduced in Eq. (17.6) with associated dynamic load factors, α i), and five subharmonics (introduced in Eq. (17.7) with associated dynamic load factors, \( {\alpha}_i^S \)). The main load harmonics excite the supporting structure at the step frequency f s and integer multiples hereof. The subharmonics excite at half of the step frequency and at 1.5f s, 2.5f s etc. A frequency domain representation of this load model would show 10 spikes separated by 0.5f s along the frequency axis. This would also be the case for load model I, but in that load model energy would also exist between the spikes.

The model to some extent mimics the type of time domain load models suggested prior to the introduction of model 1, such as models suggested in [2,3,4] – which are models assuming fully periodic action. However, load model II respects that there are subharmonic load components exciting the supporting structure at frequencies between the frequencies of the main load harmonics.

There are other features of the model that differ from the load models introduced prior to the time of introduction of load model I. Firstly, five main load harmonic are considered whereas some earlier load models considered fewer main load harmonics. In this paper, five main harmonics are considered for the sake of allowing meaningful comparisons to be made between structural responses calculated using load model I and load model II. Secondly, for the calculations of this paper, the walking parameters are modelled as random variables in load model II, as they are in load model I.

17.2.3 Common for Both Load Models

The mode shape function, Ф(t), need to be defined and regardless of the model assumed for F(t) is can be determined using Eq. (17.8):

$$ \varPhi (t)=\sin \left(\pi vt/L\right) $$
(17.8)

as this represents the mode shape function for a pin-supported single-span footbridge with a length of L between the supports.

In the equation, v represents the walking velocity of the pedestrian. Common for load models I and II is that it is determined using Eq. (17.9):

$$ v={f}_s{l}_s $$
(17.9)

In this equation, l s represents the step length of the pedestrian and f s represents step frequency of the pedestrian. These parameters are modelled as random variables. The way in which this is done is described later in this section.

Returning to the load models there are other parameters that need to be defined prior to calculations.

Focusing on the dynamic load factors of the modelled action, and starting with the dynamic load factor associated with the first main harmonic, α 1, it is modelled as a random variable with a mean value, μ, and a standard variation, σ, according to Eq. (17.10).

$$ \mu =-0.2649{f}_S^3+1.3206{f}_S^2-1.7597{f}_S+0.7613;\sigma =0.16\mu $$
(17.10)

The relationship is due to work in [7]. A Gaussian distribution is assumed.

This is also the assumption for the other main harmonic load factors, α i(i = 2, 3, 4, 5), and the assumed mean values (μ) and standard deviations (σ) for these parameters are listed in Table 17.1.

Table 17.1 Mean values and standard deviations [7, 9]
Full size table

The subharmonic load factors \( {\alpha}_i^S \) are derived from the main harmonic load factor, α 1, in the way described in [9].

A premise for load model I is that the pedestrian weight, W, is modelled as a deterministic property. Also, and as already mentioned, the step length and step frequency are modelled as random variables, and as independent random variables. Hence, these assumptions will also be made for load model II.

The assumptions made for both models are presented in Table 17.2.

Table 17.2 Mean values and standard deviations
Full size table

In both load models the phases, θ and φ, are modelled by a uniform distribution in the range [−π, π].

17.3 Methodology

Above two load models have been outlined. The methodology is to employ both load models for calculating selected statistical properties associated with the vertical acceleration response of different footbridges. For the investigations is it chosen to consider pin-supported single-span footbridges. Instead of examining solely a single bridge, the responses of three different bridges are investigated.

Table 17.3 lists the modal properties assumed for the bridges considered in this paper. The natural frequency is denoted f 1, the damping ratio is denoted ζ 1, and the modal mass is denoted m 1. These properties define the modal properties of the first vertical bending mode of the bridges. The assumed bridge length, L, is also shown in the table.

Table 17.3 Modal properties of bridges and bridge lengths
Full size table

The motivation for choosing a bridge with a frequency of 1.875 Hz (bridge A) for investigation is that its natural frequency is close to the mean value of the assumed probability density function for the step frequency (1.87 Hz). Hence, it is a bridge, which is likely to be excited by the first main load harmonic. Bridge C is also likely to be excited but by the second subharmonic as this is at 1.5 times 1.87 Hz (approximately 2.80 Hz). Furthermore, it is of interest to investigate a bridge with a frequency in between the frequencies of bridge A and C. For this bridge, denoted B, a natural frequency of 2.35 Hz is assumed.

It is mentioned that the bridge modal masses and bridge lengths are set such that they increase as the bridge frequency decreases which it considered a realistic feature.

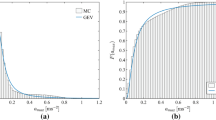
Based on the assumptions outlined above it is possible to numerically simulate load time histories for a pedestrian crossing the bridges using Newmark time-integration methods and Monte Carlo simulations allowing for repeating pedestrians crossings. For each simulated crossing of the bridge its vertical motion is computed and from this the vertical peak acceleration occurring at bridge midspan is tracked being a bridge feature relevant in the context of serviceability-limit-state evaluation.

In this way probability distribution functions for bridge peak accelerations are established for the three bridges and from these, the acceleration quantiles a 95, a 90 and a 75 are extracted where the subscripts define the quantile. For example, the quantile a 95 is the acceleration level exceeded in 5% of the pedestrian crossings.

For each bridge 100.000 simulations were conducted.

17.4 Results

This section is concerned with presentation of results in terms of acceleration quantiles derived from calculations.

For the presentation of results it is considered useful to introduce the ratio r x defined in Eq. (17.11).

$$ {r}_x=\frac{a_x^{\mathrm{I}}}{a_x^{\mathrm{I}\mathrm{I}}} $$
(17.11)

In Eq. (17.11), a represents the peak acceleration, and the superscript (I or II) represents the load model assumed for the calculations. The subscript x represents the quantile of peak acceleration.

Hence, for example, r 95 defines the ratio between the acceleration quantile a 95 computed employing load model I, and the corresponding value computed employing load model II. Introduction of the ratio eases identifying which load model delivers the highest bridge response and at the same time is provides information about the size of the difference.

A value of r x higher than unity indicates that load model I (accounting for the leaking of energy at harmonics) provides higher estimates of bridge acceleration response than load model II (not accounting for leaking of energy).

Table 17.4 presents results for a 95 and for the ratio r 95 obtained for the three bridges (A, B, and C).

Table 17.4 Acceleration quantile a 95 and ratio r 95 for the three bridges
Full size table

First item to notice is that bridge A vibrates the most (if evaluated based on a 95). This is not surprising as this bridge is likely to be excited by the first main load harmonic. The energy in this load harmonic is significantly higher than the energy in the subharmonic exciting bridge C. For bridge A both load models (I and II) provide estimates of a 95 which are almost identical - the value of r 95 being close to 1. As the value is below 1, load model II provides the highest estimate of a 95. This is consistent with the modelling feature of load model I where load energy is modelled to leak around the load harmonic in the force spectrum.

A similar tendency is seen for bridge C, however, here the value of r 95 is somewhat lower (r 95 = 0.82). Hence, the overestimation of a 95 involved with employing load model II (not modelling the leaking of energy) is more pronounced for this bridge.

For bridge B, load model II is seen to underestimate the value of a 95 and by a factor of 1.26. That load model I provides the highest estimate of a 95 is explained by the spreading of load energy around the harmonics modelled in load model I – a spreading of energy that enters into the frequency region between the harmonics where bridge B is located for many pedestrian crossings of the bridge.

It can be seen that (for load model 1) the value of a 95 for bridge B is higher than the corresponding value computed for bridge C. This is believed to be a result of the fact that although the second subharmonic excites at a frequency close to the natural frequency of bridge C, the first main load harmonic will, for some pedestrian crossings, cause resonance of bridge B. This excitation is much higher than that of the second subharmonic, and hence the resulting effect will be a balance between likelihood of occurrence and size of excitation.

In order to widen the basis for discussion, Table 17.5 presents results for ratios r 95, r 90 and r 75 obtained for the three bridges (A, B, and C).

Table 17.5 Ratio r 95, r 90 and r 75 for the three bridges
Full size table

The ratios r 95 are those already presented in Table 17.4 but it is useful to align these with values computed for r 90 and r 75.

It can be seen that for the higher quantiles of bridge response (represented by r 95 and r 90), the tendency is the same, namely that for bridge A and bridge C, load model II overestimates the acceleration quantiles but for bridge B it underestimates the acceleration quantiles. For bridge A and bridge C, the overestimation changes to an underestimation of the acceleration quantile a 75. In a serviceability-limit-state evaluation perspective it is most likely the higher bridge acceleration quantiles that are of interest.

Overall, the difference between the estimates of computed acceleration quantiles are within about 35%. If the bridge frequency is very close to the expected mean value of the probability density function for the step frequency of pedestrians (as the case for bridge A), the difference between estimates obtained using load model I and load model II is quite limited.

17.5 Conclusion and Discussion

In the paper two load models were examined with focus on their difference in predicting acceleration quantiles of bridge responses to single-person pedestrian traffic on single-span pin-supported footbridges. One model accounted for leaking of load energy around the load harmonics. The other model did not.

The results showed estimates of acceleration quantiles that differed up to 35%, however for some scenarios and acceleration quantiles, the difference in estimates was much smaller.

Generally, it seems most logical to employ the load model that best captures the nature of the pedestrian forces, which would be the load model that accounts for the leaking of load energy around the load harmonics in the force spectrum. However, the alternative load model introduced in this paper (not accounting for the leaking of energy) may be a useful alternative in that it does capture the nature of walking that suggests that subharmonic load components excite the supporting structure at frequencies between the excitation frequencies of the main load harmonics. For instance, it estimates acceleration quantiles of a bridge with a natural frequency likely to be present in the region where a subharmonic would be present fairly accurately. This would not be accomplished by a fully periodic load model only accounting for load effects associated with the main harmonics.

Overall, the choice of load model is a trade-off between required accuracy in prediction, complexity of the nature of the mechanism to the modelled, other influencing uncertainties, programming and simulation time. That there are other influencing uncertainties associated with estimating acceleration quantiles for serviceability-limit-state evaluations are discussed in, for instance [8].

The benefits of the load model introduced in this paper (not accounting for the leaking of energy) is that it is simpler to program than the load model accounting for leaking of energy. Additionally that the simulations run about 40 times faster than the model accounting for spreading of energy at load harmonics. However, it would be useful to conduct a more compressive study of its limitations.