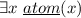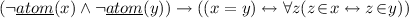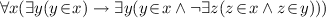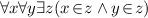Mathematical Foundation of Cognitive Computing Based Artificial Intelligence

Abstract

Today Cognitive computing and Artificial Intelligence (AI) face the same challenges namely, simulate human thought processes and mimic the way human brain works. The main difference between Cognitive computing and AI is: (i) AI models various functions of human intelligence, where computer is one of the modelling means though often the most important one, i.e. intelligence is in the focus while (ii) Cognitive computing models human thought processes and simulates the hypothetical way human brain works as computation.

Our aim is to develop a theoretically and methodologically well-founded theory of AI together with a unified computational theory, which will provide specific tools and methods for Cognitive computing.

To achieve our goal we follow a methodology triangle, consisting of a conceptual-philosophical, a system theoretical and a logical-mathematical component. Computing will play a fundamental role in both system-theoretical and logical-mathematical methodological components.

Hereby we concentrate on the development of the logical-mathematical foundation in detail by the use of category theory, which provides an excellent frame for defining all notions necessary for developing a universal theory for computing, specification, cognitive reasoning, information, knowledge and their various combinations. Foundation theory is by the use of the so-called constitutions, the mathematical basis for the cognitive computation. Logical foundation will be developed as a special constitution and cognitive computing processes are defined by using situations, infons and information. The main properties are discussed with some examples.

1 Introduction

1.1 Artificial Intelligence Today

What is meant by artificial intelligence? So far not a single conceptual apparatus has been formed, nor there is a single conceptual justification and a single scientifically based methodology. Besides, there has not yet been developed a generally accepted philosophical foundation in the form of such epistemology and ontology, which would consider and respond to the challenges that arise during the development of the field of artificial intelligence (AI).

The High-Level Expert Group on AI of the European Commission dealing with the definition of AI provides the following definition for AI [1] as a scientific discipline: AI includes several approaches and techniques, such as machine learning (of which deep learning and reinforcement learning are specific examples), machine reasoning (which includes planning, scheduling, knowledge representation and reasoning, search, and optimization), and robotics (which includes control, perception, sensors and actuators, as well as the integration of all other techniques into cyber-physical systems).

Today, modern dictionary definitions focus on AI since it is a field that applies computer science and how machines can imitate human intelligence (human-like rather than becoming human). The English Oxford Living Dictionary [31] gives this definition: The theory and development of computer systems able to perform tasks normally requiring human intelligence, such as visual perception, speech recognition, decision-making, and translation between languages.

At the same time The Encyclopedia Britannica defines artificial intelligence as it the ability of a digital computer or computer-controlled robot to perform tasks commonly associated with intelligent beings. The term is frequently applied to the project of developing systems endowed with the intellectual processes characteristic of humans, such as the ability to reason, discover meaning, generalize, or learn from past experience [32].

The term artificial intelligence is frequently applied to systems endowed with the intellectual processes characteristic of humans, such as the ability to make decisions, to solve problems, to understand texts, to recognize pictures, to learn from an actual activity and a past experience, etc. There are different technologies that get ranked as artificial intelligence and there are different types of AI.

The current wave of AI innovation focuses on several real-life applications of artificial intelligence that often start with words such as smart, intelligent, predictive and, indeed, cognitive, depending on the exact application and vendor. One major issue is that artificial intelligence is indeed a broad concept and reality, covering many technologies and realities that lead to misunderstandings about what it exactly means. Some people are actually speaking about machine learning when they talk about AI. The most advertised AI tools by Google, Facebook etc. are mainly or only machine learning and, mostly, deep learning related. This is why the wide public thinks that all new AI applications are carried out only with this type of machine learning. However, neither machine learning, nor deep learning are synonyms for AI. They are only one of the many areas of AI research. Moreover, deep learning is a technology of the 1980’s while trained with more data, 1970’s neural networks with hidden layers gave better results; and then it was renamed as deep learning and was hyped as such.

Today, AI is a conglomerate of techniques, technologies and of various research and development directions. Machine learning and especially deep learning are the most common methods. However, deep learning technology, from the application point of view has been close to its limit. Artificial intelligence urgently needs to be promoted to a new stage, and to achieve breakthroughs in the development of an appropriate underlying theory.

1.2 Cognitive Computing

As AI applications became more and more widespread, a new name, Cognitive computers appeared. This actually is a renaming that has not brought much new to the content of AI. Cognitive computing is a term really, that has been popularized by IBM mainly to describe the current wave of artificial intelligence with a twist of purpose, adaptiveness, self-learning, contextuality and human interaction. The latter, the human one is the key here and without a doubt, also easier to digest than all those AI-related science fiction scenarios.

Note that thanks to science fiction, many people think of artificial intelligence as a computer or robot thinking like a person, including self-awareness and independent will. Instead, what we call cognitive computing uses the ideas behind neuroscience and psychology to augment human reasoning with better pattern matching while determining the optimal information a person needs to make decisions.

However, if we peel off the marketing catches from the notion of Cognitive computing used by IBM then we get back AI with one important difference. Namely, Cognitive computing emphasizes the augmentation of human intelligence instead of mimicking it. This is why it is claimed that IBM’s Watson is armed with perception and understanding that is refined and expanded with every interaction. Moreover, it should be appropriate for supporting the solution of problems that encompass enormous amounts of information and discernment.

Cognitive computing is primarily a marketing term indicating a computing service that is able to understand, reason and learn from the data it is supplied with. In essence, it is the application of machine learning and artificial intelligence to data processing. IBM is the flag bearer for cognitive computing. Presumably, it wanted a term that differentiated its Watson cloud based service from the ocean of other such services. IBM has its own definition of cognitive computing, cited below [8]:

Cognitive computing refers to next-generation information systems that understand, reason, learn, and interact. These systems do this by continually building knowledge and learning, understanding natural language, and reasoning and interacting more naturally with human beings than traditional programmable systems.

IBM’s volatile, often science-fiction-like allegations have provoked serious criticism (see e.g. Schank [23]) . Independently from IBM’s way Cognitive computing has its history, see for a brief state of the art Gutierrez-Garcia and López-Neri [15]. The notion of Cognitive computing appeared in Schank [22], where natural language understanding and knowledge structures were in the focus. e structures were in the focus.

Valiant [25] defined cognitive computing as a discipline that links together neurobiology, cognitive psychology and artificial intelligence. Brasil et al. [6] state that cognitive computing is a collection of emerging technologies inspired by the biological processing of information in the nervous system, human reasoning, decision making, and natural selection.

Today, Cognitive computing refers to the ability of automated systems to handle conscious, critical, logical, attentive, reasoning modes of thought. Semantic computing facilitates and automates the cognitive processes involved in defining, modelling, translating, transforming, and querying the deep meanings of words, phrases, and concepts. This claim is very similar to that of AI.

Therefore, Cognitive computing faces the same challenges that AI does. Cognitive computing aims to simulate human thought processes and mimic the way human brain works, addressing complex situations are characterized by ambiguity and uncertainty. AI aims to perform operations analogous to learning and decision making in humans. Intelligent personal assistants can recognize voice commands and queries, respond with information, or take desired actions quickly, efficiently, and effectively.

Today the main difference between Cognitive computing and AI is the following:

• 1. AI aims to model various functions of human intelligence with different levels of detail and abstraction, where computer is one of the modelling means but very often the most important one, i.e. intelligence is in the focus while,

• 2. Cognitive computing aims to model human thought processes and simulate the hypothetical way the human brain works, i.e. computing is in the focus.

The fundamental shortcoming of the two areas is that neither has a uniform system of concepts, theoretical and methodological foundations. Instead, both consist of a conglomerate of technologies and methods. For example, Cognitive computing would also need a unified computational theory that should be developed with specific tools and methods that support the modelling of the main features of cognizing and thinking processes. However, such theory does not exist as yet, though there had been some attempts, see e.g. Amir [3].

At the same time there is a complex approach to provide a theoretical framework for cognitive computing together with some advances in the study of cognitive computing theories and methodologies in cognitive informatics, soft computing, and computational intelligence, see Wang [27] and [28]. This approach provides conceptual and behavioural models of cognitive computing. It also introduces mathematical tools such as inference algebra and denotational mathematics to deal with the design and implementation of cognitive computing systems.

Note Wang [27] defines Cognitive computing as the conglomerate of more intelligent technologies beyond imperative and autonomic computing, which embodies major natural intelligence behaviours of the brain such as thinking, inference, learning, and perceptions.

However, it is important to emphasize that the formal modelling of the cognitive processes aims to mimic the fundamental mechanisms of the brain. This approach develops a model for the brain architecture called Layered Reference Model of the Brain (LRMB), see Wang [26]. This model formally and rigorously explains the functional mechanisms and cognitive processes of the natural intelligence. A comprehensive and coherent set of mental processes and their relationships is identified in LRMB, that encompasses 37 cognitive processes at six layers known as the sensation, memory, perception, action, meta cognitive, and higher cognitive layers from the bottom-up. The modelling tools are computers. Therefore this approach leads to the area where the processes of human intelligence are to be modelled by the use of computers. This is the area of computational mind. Computationalism is the main way of seeing the cognitive processes. Computationalism is a family of theories about the mechanisms of cognition. The main relevant evidence for testing computational theories comes from neuroscience, though psychology and AI are relevant, too. Computationalism comes in many versions, which continue to guide competing research programs in philosophy of mind as well as psychology and neuroscience. Computation theoretic approach is grounded in the idea that the mind, in many ways works like a digital computer; the mind is parsing internal representations (symbols) in algorithmic ways.

In order to appropriately use the notion of computing it is important to clarify its nature. Computation is an ambiguous concept and computer scientists, philosophers and cognitive scientists who use the concept can contest some claim using it and do not realise they are not actually in disagreement with each other, even though it looks as if they were. For a deep and detailed analysis of the notion of computing we refer to Fresco [10].

Moreover, instead of going into detail review of the main approaches to the computation theory of mind we refer to some good works that represent the current state of the art in this area, such as Ivancevic [17], Milkowski [20] and Piccinini [21].

1.3 What We Offer

Our aim is to develop a theoretically and methodologically well founded theory of AI, where this abbreviation means Amplifier for Intelligence. This AI will be able to act as genuine problem-solving companion understanding and responding to complex problem situations. This AI system will be able to act either as a partner system for cooperative functioning with a human agent or as an autonomous cognitive system for a well-defined problem area. As to become a cooperative partner for human agents, the system has to function very similarly to humans. e.g., it should be able to communicate and understand natural language, reason in a compatible way, learn from its experience, etc. AI will be able to cognize the environment and itself including the co-operative partner. Namely, this AI will be able to self-reflection.

The cognizing activity may run on a wide scale from learning objects, events till discovering various tendencies and regularities. This expected activity would realise the data $\rightarrow$ information $\rightarrow$ knowledge transformation and processing at different computation levels. Special attention will be devoted to the knowledge change and management that results during the data $\rightarrow$ information $\rightarrow$ knowledge transformation and processing.

The long-term vision is to develop a theoretically well-founded, coherent, integrated theory, technology and design methodology for a new computation paradigm – the so-called COgnitive Intelligence co-Operating System (COIOS). COIOS supports Collaborative Intelligence, where humans and AI systems are joining their abilities. Therefore, in our case AI will be a symbiosis rather, instead of a replacement.

Unlike traditional computers within the von Neumann paradigm, COIOS-systems will be able to interpret and gain novel insights from data, solve problems and make decisions without explicit algorithmic instructions from humans. Instead of being programmed to perform pre-defined tasks, they will act as genuine problem-solving companions able to understand and respond to complex problem situations. Unlike data-centric processing of the traditional computers COIOS analyses data and processes information in a cognitive way and deals with knowledge in a goal-oriented way. Essentially this processing targets the reduction of the uncertainty of a problem situation of ignorance.

According to the proposed vision COIOS-systems take problem situations with various uncertainties as their input, and they resolve or decrease these uncertainties via cognitive reasoning, without relying on predefined problem-solving algorithms known in advance. Bearing this in mind COIOS will realise a reasoning-based, uncertainty-driven, upper-level computation.

To achieve our goal we follow a methodology triangle which consists of a conceptual-philosophical, a system theoretical and a logical-mathematical component. In the proposed approach computing will also play a fundamental role in both system-theoretic and logical-mathematical methodological components. The conceptual-philosophical component provides a formal epistemology with cognizing agents and ontology characterising the world to be cognized. Formal epistemology deals with data analysis, information extraction and knowledge acquisition with respect to an actual problem situation and the active cognizing agent. System-theoretic component provides the main principles for the organisation of cognizing processes, which are controlled by directed thinking. Directed thinking is goal-oriented and connected with a cognizing agent’s problem solving activity.

It will be developed by the use of category theory, which provides an excellent frame for defining all notions necessary for elaborating a universal theory for computing, specification, cognitive reasoning, information, knowledge and there various combinations. The foundation theory is provided by the use of so-called constitutions, which form the mathematical basis for cognitive computation. The logical foundation will be developed as a special constitution.

Two constructive versions of set theory will be provided:

• 1. $clFSA$ theory of finite sets with atoms and classes,

• 2. $cclFSA$ theory of finite sets with atoms, classes and co-classes.

It is shortly described how $clFSA$ permits to describe the entire traditional computation theory including e.g. program semantics, computation power of various programming languages, various programming paradigms like instructional, declarative programming and program specification. It is shown how $cclFSA$ can support the description of the programs that use metadata called information and knowledge in a strong mathematical frame.

It is shown how various specific approaches such as granular programming or probabilistic programming can be represented in the proposed approach.

In a general setting, the mathematical theory provides an important method to extend a given theory according to specific needs. This method is the inductive and co-inductive extension in constitutions.

By the use of the proposed mathematical tools it is shown how cognitive reasoning can be handled in the proposed logical-mathematical framework. The main specificities of cognitive reasoning for cognitive computing are connected with the possibility to handle

• 1. The dynamic nature of the reasoning-based cognitive computation processes. The dynamic characterisation of the cognitive computation processes will be based on the representation of a cognitive reasoning process as a motion from ignorance to knowledge.

• 2. Spatial strategies, which permit to combine data driven statistical and cognitive data processing with the logic based modification calculi.

• 3. The semantic or contentual aspects of reasoning, whereas traditional instructional and declarative programming articulate statements inferentially, according only to their shape, without regard to reference. A referential reasoning is proposed, which is based on a special dual (semantic-syntactic) approach, which uses a set of axioms, which entirely and uniquely describes the semantic structure. The latter is considered as a model of our initial knowledge about the subject domain.

• 4. Indeterminacy and temporal contradictions of the cognitive computation processes in contrast to correctness of traditional instructional and declarative programs. A special formal approach can be provided to deal with the logical contradictions.

• 5. It provides a scientifically well-founded general approach that possesses methods and tools for modelling, designing and generating information processing responsible for the formation of cognitive processes of artificial cognitive systems. The proposed approach, at the same time, provides an innovative logical foundation for the entire area of cognitive reasoning and it provides support for cognitive system development at the following three levels of abstraction: conceptual, formal, and realisational levels.

Cognitive computing processes will be defined using situations, infons and information. However, the well-known constructions of situations, infons and information (see e.g. Barwise [5] or Devlin [9]) are used in a modified way, which will be formalised by the use of the proposed methods of extension. Here Cognition Kernel will be one of the main constructs, which generalises (i) the information theory and the corresponding data analysis together with a referential reasoning system, and (ii) the multilevel organisation of situation related information and knowledge management processes. Thus Cognitive Kernel will provide an adequate framework to handle the data $\rightarrow$ information $\rightarrow$ knowledge transformation and processing. Cognitive computing is defined by the use of Cognition Kernel.

2 The Mathematical Foundation

Considering the formalism used in the present paper we first of all assume that the reader is familiar with the basics of set theory and with a basic course on mathematical logic. Moreover, reading Sect. 2 also requires familiarity with a basic course in category theory. However, the reader not familiar with the latter can avoid Sect. 2 and can read the paper as a constructive specification theory based on the theory of finite sets which uses a special first order language as a specification language.

2.1 Constitution Theory

The basic foundational construct is the so-called constitution theory, which provides a logical and category theoretical frame for the development of the cognitive computation theory within the framework of the proposed approach. The first order logic provides the operative tool-set for the constitution theory. Compact constitutions form an important class, which provides the foundation for (i) descriptive theory to describe and investigate various aspects of costructivity necessary for any type of computations, (ii) specification theory to provide a framework for specifying computational objects.

Definition 1

A pre-constitution $\mathbb {P}$ is a pair (${ Uni }$,${ Cons }$) where

• 1. ${ Uni }$ is a category.

• 2. $Cons$ is a subcategory of $Uni$ such that $Ob Cons =Ob Uni$.

• 3. For any diagram

  

  where $c\in Mor Cons$ there exists its colimit

  

  such that $c'$ also belongs to $Mor Cons$. This property is called hierarchy persistence property of the pre-constitution $\mathbb {P}$.

Example 1

Let $First$ denote the category of all first order theories and theory morphisms between them. A morphism $Th_1\rightarrow Th_2$ is called conservative iff it is a composition of a renaming map and of a conservative extension in the original sense. Let $FCons$ denote the subcategory of $First$ generated by the class of all conservative theory morphisms. It is an easy exercise using Craig interpolation theorem to prove that the pair $( First , FCons )$ is a pre-constitution, further on be denoted as $\mathbb {FOL}$.

Example 2

The following logical systems satisfy the Craig interpolation property and hence their theories with the conservative extensions form a pre-constitution:

• classical first order logic;

• classical higher-order logic;

• $\omega$-logic;

• intuitionist first order logic;

• intuitionist type theory;

• classical temporal logic;

• intuitionist temporal logic.

Example 3

In Burstall, Goguen [7] introduced the notion of institution to give a categorical-theoretical approach to model theory. For an institution can be defined the interpolation property as well. It can easily prove that institutions with interpolation property form a pre-constitution.

Example 4

(For details see Gergely, Ury [12]) It is well-know that a Cartesian-closed category having a subobject classifier is called topos. A topos form a pre-constitution. Moreover if $Uni$ is an arbitrary finitely cocomplete category within which partial maps are representable then $( Uni , Mon ( Uni ))$ is a pre-constitution. Accordingly a famous theorem partial maps in topoi are representable. For details see Gergely, Ury [12]

Definition 2

A constitution $\mathfrak {L}$ on a pre-constitution $\mathbb {P}=( Uni$, $Cons )$ is a function $\mathfrak {L}$ from $Uni$ to the category $Mor ( Uni )$ such that:

• 1. if Th is an object of $Uni$ then $\mathfrak {L}(Th)$ is a conservative morphism over Th called the superstructure of Th;

• 2. if f is a morphism then $\pi _1(\mathfrak {L}(f))=f$;

• 3. for all $Th\in Obj ( Uni )$ the following diagram is a colimit with respect to $(\mathfrak {L}(Th),f)$ where:

  

Definition 3

Let $( Uni , Cons )$ be a pre-constitution. A constitution $\mathfrak {L}$ on it is said to be perfect for an object $Th\in Ob Uni$ iff there is a morphism $red_{Th}$ such that

$$\begin{aligned} (\mathfrak {L}(cod(\mathfrak {L}(Th)),red_{Th}) \end{aligned}$$

is a projection system, i.e. the diagram below commute:

where Sp(Th) and Sp(Sp(Th) is the codomain of $\mathfrak {L}(Th)$ and $\mathfrak {L}(\mathfrak {L}(Th))$, respectively. Sp(Th) is called the superstructure of Th.

Definition 4

A constitution $\mathfrak {L}$ on a pre-constitution $\mathbb {P}=( Uni , Cons )$ is compact iff for all object of $Th\in Ob Uni$ $\mathfrak {L}$ is perfect for Th.

Definition 5

Fix a pre-constitution $\mathbb {P}=( Uni , Cons )$. Let $C(\mathbb {P})$ be the following category:

• $Ob C(\mathbb {P}) \rightleftharpoons \lbrace \mathfrak {L}\mid \mathfrak {L}$ is a constitution on $\mathbb {P}\rbrace$

• $Mor (C(\mathbb {P})) \rightleftharpoons \lbrace F:\mathfrak {L}_1\rightarrow \mathfrak {L}_2\mid F: Obj ( Uni ) \rightarrow Mor ( Uni )$ such that $\mathfrak {L}_1(Th)\circ F(Th)=\mathfrak {L}_2(Th) \rbrace .$

The last condition in the definition of $Mor (C(\mathbb {P}))$ means that the following diagram commutes:

Theorem 1

Let $\mathbb {P}=( Uni , Cons )$ be a pre-constitution and let $\mathfrak {L}$ be a constitution on it. Let us suppose that $Uni$ has countable coproducts. There is a unique (up to natural isomorphism) constitution $\mathfrak {L}'$ and a morphism $F:\mathfrak {L}\rightarrow \mathfrak {L}'$ such that

• 1. $\mathfrak {L}'$ is compact;

• 2. for any $G:\mathfrak {L}\rightarrow \mathfrak {L}''$ with closed $\mathfrak {L}''$ there is a factorization through F; i.e. there is a (unique) H such that commutes in $C(\mathbb {P})$.

• 3. This $\mathfrak {L}'$ is denoted as $\mathfrak {L}^*$

2.2 FOL-Based Constitutions

In this subsection we define a compact constitution $\mathbb {Y}$ called fixed-point constitution. The superstructures of this constitution add least and greatest fixed-point to each monotone operators. From now we will work in the first-order pre-constitution $\mathbb {FOL}$. A constitution called FOL-based if it is a constitution on a full subcategory of $\mathbb {FOL}$. In the sequel we give some examples for such constitution usable in computing, AI and cognitive computing.

The well-know notion of transitive closure can be turned into a constitution.

Definition 6

Let $Th = (\sigma ,Ax)$ be a fixed first-order theory.

• 1. A first-order operator in Th is a triple $(\varPhi ,R,X)$ written as $\varPhi (R,X)$ where R is an X-type new relation symbol, $\varPhi$ is a $\sigma \cup \{ R \}$-type formula free variables of which belongs to X. The set of variables X is called the type of $\varPhi (R,X)$

• 2. $\varPhi (R,X)$ is called monotone iff for any new X-type relation symbols S

  $$\begin{aligned} Ax \vdash (\forall X\ R(X) \rightarrow S(X)) \rightarrow \forall X\ (\varPhi (R,X) \rightarrow \varPhi (S,X)) \end{aligned}$$

• 3. For any $\psi (X)$ let

  $$\begin{aligned} \tilde{\varPhi }(\psi )(X)\ \mathrm{be\ the\ formula}\ \varPhi (R,X)[\psi /R]. \end{aligned}$$

  It is clear that $\tilde{\varPhi }$ is a function of type $Form_\sigma (X) \rightarrow Form_\sigma (X)$

• 4. Let us denote $\varDelta _{Th}$ be denote the set of all monotone first-order operator in Th.

Let $\top _X$ and $\bot _X$ be denote the X-type truth and falsity, respectively. If a first-order operator $\varPhi (R,X)$ is monotone in Th then we got an infinite chain

$$\begin{aligned} \bot _X \rightarrow \tilde{\varPhi }(\bot _X) \rightarrow \tilde{\varPhi }(\tilde{\varPhi }(\bot _X)) ....... \tilde{\varPhi }(\tilde{\varPhi }(\top _X))\rightarrow \tilde{\varPhi }(\top _X) \rightarrow \top _X \end{aligned}$$

where each individual implication is provable in Th.

Definition 7

$Th = (\sigma ,Ax)$ be a fixed first-order theory and fix a set $\mathcal {F}$ of monotone first-order operators.

• 1. Let $\tilde{\varPhi } \in \mathcal {F}$ be an X-type monotone first-order operation. A formula $\psi (X)$ is called a left fixed-point of $\tilde{\varPhi }$ iff $Ax \vdash \tilde{\varPhi }(\psi ) \rightarrow \psi$ and called a right fixed-point of $\tilde{\varPhi }$ iff $Ax \vdash \psi \rightarrow \tilde{\varPhi }(\psi )$.

• 2. For any $\tilde{\varPhi } \in \mathcal {F}$ let add two new X-type relation symbols $\varPhi ^\mu$ and $\varPhi ^\nu$ together the following axioms:

  • (a) $\tilde{\varPhi }(\varPhi ^\mu ) \rightarrow \varPhi$ and $\varPhi \rightarrow \tilde{\varPhi }(\varPhi ^\mu )$

  • (b) for an arbitrary $\sigma$-type formula $\psi (X)$ : $(\psi \rightarrow \tilde{\varPhi }(\psi )) \rightarrow (\varPhi ^\nu \rightarrow \psi )$

  • (c) for an arbitrary $\sigma$-type formula $\psi (X)$ : $(\tilde{\varPhi }(\psi )\rightarrow \psi ) \rightarrow (\psi \rightarrow \varPhi ^\mu )$

  • (d) Let $Ind(\mathcal {F})$ denote this new set of axioms.

Theorem 2

Let $Th = (\sigma ,Ax)$ be a fixed first-order theory. For an arbitrary $\mathcal {F} \subset \varDelta _{Th}$ the axiom system $Ax \cup Ind(\mathcal {F})$ is conservative over Ax. It means that there is a constitution Ind on the pre-constitution $\mathbb {FOL}$ which renders each Th the conservative extension $Ax \cup Ind(\varDelta _{Th})$

Let us suppose that the restriction of first-order operations are categorical. It means that for all Th there is a $Th_\mathcal {F} \subset \varDelta _{Th}$ given in such a way that a theory morphism $Th^1 \rightarrow Th^2$ transfer $Th^1_\mathcal {F}$ into a subset of $Th^2_\mathcal {F}$. If so then there is a constitution $Ind_\mathcal {F}$ on the pre-constitution $\mathbb {FOL}$ which renders each Th the conservative extension $Th_{Ax}\,\cup \,Ind(Th_\mathcal {F})$. One of the most well-known example of such a restriction is as follows. For any $\sigma$ let us consider the positive existential formulas of the form $\psi (X,X^\prime )$ where $\psi$ free variables as stated and X is a copy of $X^\prime$. Any such formulas generate a monotone first-order operators as $\exists U R(U) \wedge \psi (U,X)$. For any Th let $\mathcal {TR}$ let denote the set of all monotone first-order operator defined in such a way. Let Tran be denote this constitution on the pre-constitution $\mathbb {FOL}$.

Theorem 3

Tran is a compact constitution on the pre-constitution $\mathbb {FOL}$.

2.3 Inductive and Coinductive Extensions in Constitutions

It is obvious that it is not enough to just add fixed-points to underlying theory. Let $Th = (\sigma ,Ax)$ be a first order theory. There are many situations when we need to add new types, functions and relations to the original similarity type $\sigma$. All these additional symbols we can collect into a new similarity type $\theta$. Of course the similarity type has not, but the axiom system Ax has to improve new axioms and axiom schemas. If these axioms are short to inductive and coinductive ones then we can formulate a theorem similar to Theorem 1.

In details. Let us fix a similarity type $\eta$. Let $\mathbb {FOL}(\eta )$ denote the pre-constituti-on containing only those theories $(\sigma ,Ax)$ where $\eta \subset \sigma$. Let $\zeta$ be a new similarity type and let Eq and $Eq^c$ be a set of quasi-equations and quasi-coequations, respectively based on the similarity type $\zeta + \eta$.

Theorem 4

Let $\eta , \zeta$ and $Eq, Eq^c$ as in above. There is a least (up to natural isomorphism) constitution denoted by $\mathbb {Y}(\eta ,\zeta ,Eq,Eq^c)$

• 1. $\mathbb {Y}(\eta ,\zeta ,Eq,Eq^c)$ is compact,

• 2. All superstructures satisfy $Eq + Eq^c$,

• 3. All monotone operators in each superstructures have least and greatest fixed points,

• 4. If $\mathfrak {L}$ is such a constitution on $\mathbb {FOL}(\eta )$ that satisfies the previous assumptions then there is a unique (up to natural isomorphism) morphism (up to natural isomorphism) $\mathbb {Y}(\eta ,\zeta ,Eq,Eq^c) \rightarrow \mathfrak {L}$.

For any $Th\in Obj \mathbb {FOL}(\eta )$ the superstructure of Th, i.e. the codomain of the morphism $\mathbb {Y}(\eta ,\zeta ,Eq,Eq^c)(Th)$ is called canonical d-inductive extension of Th (d for double because extension was constructed by using both equations and coequations. If $Eq^c$ is empty we simply say inductive extension or if we want to emphasize that $Eq^c$ is empty we say simple inductive extension. If $\mathfrak {L}$ is such a constitution that satisfies the first three assumption of the theorem then $\mathfrak {L}$ is also called d-inductive extension of the extension system $(\eta ,\zeta ,Eq,Eq^c)$.

In Subsect. 3.2 we demonstrate that for a large part of computing theory the simple inductive extensions are sufficient. Coequations need to speak about cognitive aspects of computation.

Remark 1

There is a clear definition of quasi-equations. Let $\sigma$ be an arbitrary similarity type. A $\sigma$-type formulas in the form $\tau _1=\tau _2$ where $\tau _i (i=1,2)$ are $\sigma$ terms are called equation. A formula in the form

$$\begin{aligned} \bigwedge _{j=1..n} e_j \rightarrow e \end{aligned}$$

where $e_j (j=1..n),e$ are $\sigma$-type equations is called a quasi-equation. If n = 0 then we get back the notion of equation. See Grätzer [14]. Unfortunately there is no such an elegant and easily usable definition for quasi-coequations.

One of the main advantages of the d-inductive extensions is, that there are universal ones. Let $\eta ,\zeta$ be fixed and let $\mathbb {EQ}_(\eta ,\zeta )$ denote the set of all $(\eta +\zeta )$-type equations. Let $d\nabla (\eta ,\zeta )$ be the category of all d-inductive extensions on $(\eta ,\zeta ,Eq,Eq^c)$ where $Eq,Eq^c\subset \mathbb {EQ}_(\eta ,\zeta )$. The morphisms are the natural transformations between the functors. Also let $\nabla (\eta ,\zeta )$ be the category of all simple inductive extensions on $(\eta ,\zeta ,Eq,\emptyset )$

Theorem 5

Let $\eta ,\zeta$ be arbitrary but fixed similarity types.

• Both $d\nabla (\eta ,\zeta )$ and $\nabla (\eta ,\zeta )$ are really categories;

• $d\nabla (\eta ,\zeta )$ has terminal objects. Any terminal object of $d\nabla (\eta ,\zeta )$ is called d-universal extension on $(\eta ,\zeta )$.

• $\nabla (\eta ,\zeta )$ has terminal objects. Any terminal object of $\nabla (\eta ,\zeta )$ is called simple universal extension or just universal extension on $(\eta ,\zeta )$.

2.4 Constitutional Set Theories

Two versions of set theory are provided by the modification of the von Neumann-Bernays-Gödel set theory. The modification augments the set theoretic operations with fixed points of monotone operators. Namely, the so obtained set theories are as follows:

• $cHF$ is a compact constitution where superstructures are the finite sets with atoms and classes augmented with least fixed points of positive existential operators (cl stands for classes),

• $clFSA$ is a compact constitution where superstructures are the finite sets with atoms and classes augmented with least fixed points of monotone operators (cl stands for classes),

• $cclFSA$ (ccl stands for classes and coclasses) a compact constitution where superstructures are the finite sets with atoms, classes and co-classes augmented with least and greatest fixed points of monotone operators.

It is shortly explained how $clFSA$ permits to describe the entire traditional computation theory including e.g. program semantics, computation power of various programming languages, various programming paradigms like instructional, declarative programming and program specification, see e.g. Ury, Gergely [24]. For a short description of how $clFSA$ looks like see 7.1. It is clear that for a fixed similarity type $\sigma$ and the axiom system Ax the new axioms of $clFSA (\sigma , Ax)$ depends only on $\sigma$. Let $cFSA_\sigma$ denote this set of axioms.

The unifying theories developed in [16] can build using $cHF$ instead of ZFC.

Note that the use of the above two set theories is useful because they are universal as can be seen in the following theorem.

Theorem 6

Let $\eta ,\zeta$ be arbitrary but fixed similarity types.

• $clFSA (\eta )$ is a simple universal extension on $(\eta ,\zeta )$

• $cclFSA (\eta )$ is a d-universal extension on $(\eta ,\zeta )$.

Remark 2

We emphasize that there was not any assumption “how large” is $\zeta$ or the set of equations. However we suppose that both of them are recursively enumerable then $clFSA (\eta )$ and $cclFSA (\eta )$ are also recursively enumerable.

3 Examples

3.1 Specifications as Constitutions

Given a pre-constitution $\mathbb {P}= ( Uni , Cons )$ we can think that a specification itself defines the object perfectly. Later on we shall see that the elements of $Ob( Uni )$ are generally a set of algebraic equations or formulas. However, in our definition the notion of a specification is in an abstract form without any fixed meaning. Whatever we can say about the specifications it is identical with the properties of the category $Uni$.

One of the most important properties of the specifications is that they can be interpreted by each other. In the case of algebraic and logical specification theories these interpretations turn out to be homomorphisms or theory presentations. However, in our definition the notion of interpretation is as abstract as those of the specifications. See in Maibaum [19].

Definition 8

Let $\mathbb {P}=( Uni , Cons )$ be a pre-constitution and let $\mathfrak {L}$ be a constitution on it. An L -refinement is a pair of morphisms (f, c) as shown below iff there are two morphisms $c',d'$ such that if

then c splits such that

• 1. the diagram below commutes:

  

• 2. and $(c',d')$ is a projection pair.

Theorem 7

Let $\mathbb {P}=( Uni , Cons )$ be a pre-constitution and let $\mathfrak {L}$ be a constitution on it. $\mathfrak {L}$-refinements are closed under composition iff $\mathfrak {L}$ is a compact constitution.

An abstract specification theory is developed by the use of category theory, which allows the characterization of specification languages and the provision of the necessary conditions to operate with specifications, e.g. to put them together or to refine or to modularize them. Here only shown the condition necessary for stepwise refinement of specifications is shown. A specification classical first order language which can be used as a specification one. As it can be seen this theory is appropriate to support formal specifications with a “constructive” definition theory. It is shown how the specification language Z can be developed in this set theoretical framework so that it becomes more transparent from semantical point of view and more useable due to the “constructive” fixed point theory. Moreover, we develop the constructive version of the specification theory by using logic programming ideas. First, logic programming is defined for the abstract specification theory and then logic programming is developed in the proposed set theoretic framework.

One of the desired properties of a specification theory is the correct handling of the hierarchical specification. In our frame any interpretation $c:P\rightarrow S$ can be considered as a hierarchical specification. Specification P contains the so called primitive specification part and by using c and S we add some extra to this primitive specification part. It is a natural assumption with respect to the hierarchical specifications that any interpretation of the primitive part can be extended to an interpretation of the entire hierarchical specification. It means that any $f:P\rightarrow P'$ can be extended to a commutative diagram below:

However, in most cases initial and terminal specifications do not exist at all. This is the reason why we restrict the hierarchical specifications to conservative ones. Definition 8 (1) axiomatizes the existence of the initial specification for conservative hierarchical specifications.

3.2 Computing Theory

3.2.1 Instructional Programs

Intuitively it is evident that the main problem in defining the IO-relation of a program is connected with the definition of program iteration. Since e.g. denotational semantics renders a relation to a program, the reflexive and transitive closure of this relation corresponds to iteration. We are interested in internalizing, thus we deal with the formulas defining the relations. Therefore the main question is whether the reflexive and transitive closure of an arbitrary formula is definable. It is an easy exercise to prove that using least fixed-points the denotation of the while programs can be defined. However, Hoare, Jifeng [16] shows that the correct definition of the denotation of recursive procedure calls requires the greatest fixed-points.

Programs operate on their data environments. If we are interested in the change caused by the execution of a program in its environment then the input-output semantics defined as a binary relation on data sequences, is suitable. A great variety of program properties are connected with the relational semantics, e.g. partial correctness, quasi-total correctness, pseudo-total correctness, etc. See e.g. Gergely, Ury [13].

3.2.2 Logic Programs

The traditional way of programming according to Wirth can be represented as programs = algorithms + data structures (see Wirth [29]). An important combination of traditional programming with the declarative one can take place in the case of data declaration. The latter means that data structure component of the Wirth’s characterization of programs should be given by declarative tools, i.e. by the use of logic. In this case programs = algorithm + logic + realisation, where logic may consists of functional and relational parts. The logic component allows to define abstract data types which by the use of realization define the constructive model over which the execution of algorithms, i.e. the computation takes place.

Logic programming takes place in models constructed according to the logic programs. We suppose that a similarity type $\delta$ given. Any logic program contains definitions of new relation symbols. The goal of a logic program, i.e. the question which one should be answered reflects these new relations, see e.g. Gergely, Szőts [11]. Let us fix a rich enough similarity type $\eta$ and a constructive interpretation $\mu :\delta \rightarrow cTerm_\eta$. We consider how we can define relations new with respect to $\mu$ by the use of logical program’s approach.

Since we aim to develop logic programming in $cclFSA$, so the constructivity should be defined with respect to this system axioms. Intuitive meaning of a constructive model is that any component of that is computable in $cclFSA$. To define the required notion of constructive model first we have to define an appropriate notion of model, and the notion of computability over this model.

If $\eta$ a given similarity type and Ax is an $\eta$-type set of formulas let $cFSA_\eta (Ax)$ denote the axioms of the superstructure $cclFSA (\eta ,Ax)$. If Ax is empty we simply write $cFSA_\eta$.

Definition 9

Let $\sigma$ be a fixed similarity type. A function $\mu :\sigma \rightarrow cTerm_\eta$ is called an interpretation of $\sigma$ in $cFSA_\eta$. An interpretation $\eta$ generates a $\sigma$-type model in a model $\mathbf {V}\!\in \!Mod(cFSA_\eta )$ iff the followings hold in $\mathbf {V}$:

• (a) for all $s\!\in \!sort(\sigma )$, $\eta (s)$ is a non-empty class in $\mathbf {V}$;

• (b) for all $\rho \!\in \!rel(\sigma )$, $\mu (\rho )$ is a subclass of $\top \{\mu (s_i)|i=1,\ldots ,n\}$, where $\rho :s_1,\ldots ,s_n$ is the arity of $\rho$;

• (c) for all $f\!\in \!fun(\sigma )$, $\mu (f)$ is a functional class of the form $\top \{\mu (s_i)|i=1,\ldots ,n\}\rightarrow \mu (s)$, where $f:s_1,\ldots ,s_n\rightarrow s$ is the arity of f.

We say that $\mu$ generates a $\sigma$-type model in $cFSA_\eta$ iff for all $\mathbf {V}\!\in \!Mod(cFSA_\eta )$ $\mu$ generates a $\sigma$-type model in $\mathbf {V}$. The $\sigma$-type model $\mathbf {A}$ generated by $\mu$ in $\mathbf {V}$ is denoted by $\mathbf {V}(\mu )$.

Proposition 1

Let $\mu$ be an interpretation. There is a class formula $IM? (\mu )$ which is valid in a model iff $\mu$ generates a model in that set-theory, i.e.

$$\begin{aligned} \mathbf {V}\models IM? (\mu )\text { iff }\mathbf {V}(\mu ) \text{ exists }. \end{aligned}$$

An interpretation $\mu :\sigma \rightarrow cTerm_\eta$ is said to be correct in V iff the model $\mathbf {V}(\mu )$ exists.

Let us see how to restrict the investigation of formulas to a given interpretation only.

Definition 10

Let $\mu :\sigma \rightarrow cTerm_\eta$ be fixed and let $\varphi \!\in \!cForm_\sigma$. Let us define the relativization $\varphi ^\mu$ of $\varphi$ along $\mu$ by induction on the complexity of $\varphi$ in the following way.

(A) First for any term $\tau \!\in \!Term_\sigma$ let us define a relation $R_\tau (x,y^\tau )$ (where $x=var(\tau )$ and $y^\tau$ is a new variable) which expresses the fact that $\tau (x)=y$:

• if $\tau =x$ is an s-sorted variable then $R_\tau (x,y^\tau )\leftrightharpoons x=y^\tau \wedge x\!\in \!\mu (s)$;

• if $\tau =f(x_1,\ldots ,x_n)$ and $f:s_1,\ldots ,s_n\rightarrow s$ then $R_\tau (x,y^\tau )\leftrightharpoons \bigwedge \{R_{\tau i}(x,y^{\tau i})|i\!\in \!n\}\wedge (y^{\tau 1},\ldots ,y^{\tau n},u^\tau )\!\in \!\mu (f)\wedge y^\tau \!\in \!\mu (s)$.

We remark that $R_\tau (x,y)$ implies that $y\!\in \!\mu ()s$ where $s=sort(\tau )$.

(B)

• if $\varphi =\rho (\tau _1,\ldots ,\tau _n)$ then

  $\rho ^\mu \leftrightharpoons \exists y^{\tau 1}\ldots \exists y^{\tau n}\bigwedge \{R_{\tau i}(x,y^{\tau i})|i\!\in \!n\}\wedge (y^{\tau 1},\ldots ,y^{\tau n})\!\in \!\mu (\rho )$

• if $\varphi =\lnot \psi$ then $\varphi ^\mu \leftrightharpoons \lnot (\psi ^\mu )$

• if $\varphi =\psi _1\vee \psi _2$ then $\varphi ^\mu \leftrightharpoons (\psi _1^{\ \mu })\vee (\psi _2^{\ \mu })$

• is $\varphi =\exists x\psi$ then $\varphi ^\mu \leftrightharpoons \exists x(x\!\in \!\mu (s)\wedge (\psi ^\mu ))$, where $s=sort(x)$

The following statement shows that relativization restricts the investigation of validity of formulas to the given interpretation.

Theorem 8

Let $\mu :\sigma \rightarrow cTerm_\eta$ be an interpretation and let $\mathbf {V}(\mu )$ be the model generated by $\mu$ in $\mathbf {V}$. Let $\varphi \!\in \!cForm_\sigma$ and let $k\!\in \!Val(\mathbf {V}(\mu ))$

$$\begin{aligned} \mathbf {V}(\mu )\models \varphi [k]\text { iff }\mathbf {V}\models \varphi ^\mu [k] \end{aligned}$$

Definition 11

Let $\mu _\sigma :\sigma \rightarrow cV$ be a fixed injection. $\mu _\sigma$ is called the canonical interpretation of $\sigma$ in ${\mathbf {cFSA}}_\eta$. Let $\varphi ^\sigma$ denote the relativization of $\varphi$ along $\mu _\sigma$.

Definition 12

Let $\mathbf {V}\models ^\sigma \varphi$ denote the fact that a closed formula is true in every interpretation of $\sigma$ in $\mathbf {V}$. If so we say that $\varphi$ is valid in V. Take $cFSA_\eta \models ^\sigma \varphi$ iff for all $\mathbf {V}\!\in \!Mod(cFSA_\eta )$, $\mathbf {V}\models ^\sigma \varphi$. If so we say that $\varphi$ is valid in ${\mathbf {cFSA}}_\sigma$.

Let us consider the main properties of this notion of validity. Let $\mu :\sigma \rightarrow cTerm_\eta$ be an arbitrary interpretation. Let $\mu =\mu _\sigma$ be a shorthand for the formula $\bigwedge \{\mu (l)=\mu _\sigma (l)|l\!\in \!\sigma \}$.

Theorem 9

Let us suppose that $\varphi$ is a closed $\sigma$-type formula. Let $\mathbf {V}$ be an arbitrary model of $cFSA_\eta$. Let $\mu :\sigma \rightarrow cTerm_\eta$ be an interpetation.

(A) Let us suppose that u generates a model in $\mathbf {V}$. The followings are equivalent:

• $\mathbf {V}(\mu )\models \varphi$;

• $\mathbf {V}\models \varphi ^\mu$;

• $Th(\mathbf {V})+ IM? (\mu _\sigma )+(\mu =\mu _\sigma )\models \varphi ^\sigma$.

(B) $\mathbf {V}\models ^\sigma \varphi$ iff $Th(\mathbf {V})+ IM? (\mu _\sigma )\models \varphi ^\sigma$

(C) $cFSA_\eta \models ^\sigma \varphi$ iff $cFSA_\eta + IM? (\mu _\sigma )\models \varphi ^\sigma$.

Now we define the computability in $cFSA_\eta$ by the use of the theory of programs developed for the programming language $P_\eta$. The necessary notions used bellow can be found in Appendix 1.

Definition 13

(A) Let C be a class in a model $\mathbf {V}$ of $cFSA_\eta$. C is called computable in V iff there is a program $p\!\in \!P_\eta$ such that

$$\begin{aligned} C=dom\ Den_{\mathbf {V}}\llbracket p\rrbracket \end{aligned}$$

(B) A class C is called enumerable in V iff there is a computable surjection $\omega \rightarrow C$.

(C) The class C is called p$\exists$ -definable in V iff there is a term

$$\begin{aligned} t\!\in \!cTerm\varSigma ^+(\eta ;\{D\}) \end{aligned}$$

such that $C=Yt$, i.e. C is the least fixed point of the equation $D=t(D)$.

Theorem 10

Let $\mathbf {V}$ be a model of $cFSA_\eta$, and suppose that the class $Atom\leftrightharpoons \{x|\underline{atom}(x)\}$ is enumerable in $\mathbf {V}$. The p$\exists$-definable, the enumerable and the computable classes are the same in $\mathbf {V}$.

We remark that the assumption of Theorem 5.9 in most cases is true, e.g. if Atom is finite or equivalent with $\omega$.

Theorem 11

If Atom is enumerable in $\mathbf {V}$ then AC holds in $\mathbf {V}$.

Definition 14

An interpretation $\mu :\rightarrow cTerm_\eta$ is called constructive in V iff for all $l\!\in \!\sigma$, $\mu (l)$ is computable in $\mathbf {V}$.

Example 5

Let $\sigma$ contain the following symbols:

• $0,1:\rightarrow d$

• $+,\times :d,d\rightarrow d$

Let interpret these symbols in the ‘usual’ way:

• $\mu (d)\leftrightharpoons \omega$

• $\mu (0)\leftrightharpoons 0$

• $\mu (1)\leftrightharpoons \{0\}$

• $\mu (+)\leftrightharpoons \lambda x,y.\ x+y$

• $\mu (\times )\leftrightharpoons \lambda x,y.\ x*y$

where + and * is the sum and product of natural numbers. It is clear that $\mu$ generates a model in $cFSA_\sigma$ and in any $\mathbf {V}$ it is constructive.

Example 6

From the point of view of functional programming it is a very interesting question whether a factor of a constructive model is constructive again. Consider the following simple example. Again let $\sigma$ be as in 5.12. Take the following interpretation:

• $\xi (d)\leftrightharpoons \omega \times \omega$

• $\xi (0)\leftrightharpoons (0,0)$

• $\xi (1)\leftrightharpoons (\{0\},0)$

• $\xi (+)\leftrightharpoons \lambda (a,b),(c,d)\,.\,(a+c,b+d)$

• $\xi (*)\leftrightharpoons \lambda (a,b),(c,d)\,.\,(ac+bd,ad+bc)$

Clearly $\xi$ is a correct interpretation in any model of $cFSA_\sigma$. Moreover, $\xi$ is clearly constructive.

Let us define the following equivalence on $\xi (d)$:

$$\begin{aligned} (a,b)\equiv (c,d)\text { iff }a+d=b+c \end{aligned}$$

One can check that equiv is a congruence relation on $\mathbf {V}(\xi )$. Clearly $\mathbf {V}(\xi )/\equiv$ is a model for integer numbers $(\underline{Z},0,1,+,*)$. It is a question whether $\mathbf {V}(\xi )/\equiv$ is constructive.

The following theorem gives an answer to this question.

Theorem 12

Let $\mu :\sigma \rightarrow cTerm_\eta$ be a constructive and correct interpretation of $\sigma$ in a model $\mathbf {V}$. Let us suppose that $\equiv$ is a decidable congruence relation on $\mathbf {V}(\eta )$, i.e. both $\equiv$ and its complement are computable in $\mathbf {V}$. Moreover, let us suppose that all the classes $\mu (s)\!\in \!sort\ \sigma$ are enumerable in $\mathbf {V}$. If so then $\mathbf {V}(\mu )/\equiv$ is constructive in $\mathbf {V}$.

Now we can turn to prove the existence of $\mu /\equiv$. Take

$$\begin{aligned} \mu /\equiv (s)\leftrightharpoons \{x|x\!\in \!\mu (s)\wedge \forall y(\ulcorner y\urcorner <\ulcorner x\urcorner \rightarrow \lnot y\equiv x)\} \end{aligned}$$

By using the computability of $\ulcorner \urcorner$ and the decidability of $\equiv$ the right hand side of this equation is a $p\exists$ term in $cFSA_\eta$. Hence $\mu /\equiv$ is well defined on $sort(\sigma )$. Take

• $$\mu /\equiv (\rho )\leftrightharpoons \{(x_1,\ldots ,x_n)|\exists y_1,\ldots ,\exists y_n\bigwedge x_i\equiv y_i\wedge \rho (y_1,\ldots ,y_n)\}$$
• $$\begin{aligned}&\mu /\equiv (f)\leftrightharpoons \nonumber \\&\quad \{(x_1,\ldots ,x_n,x)|\exists y_1,\ldots ,\exists y_n,\exists y\bigwedge x_i\equiv y_i\wedge x\equiv y\wedge f(y_1,\ldots ,y_n)=y\} \end{aligned}$$

  (1)

It is clear that $\mu /\equiv :\sigma \rightarrow cTerm_\eta$ is an interpretation. Since $\equiv$ is a congruence relation $\mu /\equiv$ is correct in $\mathbf {V}$. By using the enumerability of classes one can check that $\mu /\equiv$ is a computable relation.

Returning to the example it is easily provable that $\omega \times \omega$ is enumerable in $cFSA_\eta$ and of course $\equiv$ is decidable. It means that $\xi /\equiv$ exists and it is computable in any model of $cFSA_\eta$.

Definition 15

Let $\sigma$ be a similarity type. Let

$$\begin{aligned} \varGamma _\sigma \leftrightharpoons \{P_s|s\!\in \!sort\ \sigma \}\cup \{P_f|f\!\in \!func\ \sigma \}\cup \{P_\rho |\rho \!\in \!rel\ \sigma \} \end{aligned}$$

be a fixed set of class variables. Any function $\varPhi :\varGamma _\sigma \rightarrow cTerm\varSigma ^+(\eta ;\varGamma _\sigma )$ is called a presentation of $\sigma$ in $\mathbf {cFSA_\sigma }$. A presentation is correct in a model $\mathbf {V}$ of $cFSA_\sigma$ if the interpretation $Y\varPhi :\sigma \rightarrow cTerm_\eta$ is correct, i.e. if $\mathbf {V}(Y\varPhi )$ exists.

Theorem 13

Let us suppose that Atom is enumerable in $\mathbf {V}$. Let $\varPhi$ be a correct presentation of $\sigma$ in $\mathbf {V}$. $V(Y\varPhi )$ is a constructive model of $\sigma$ in $\mathbf {V}$.

It is clear that the models of $cFSA_\sigma$, within which Atom is enumerable, have significant properties. So we give the following definition:

Definition 16

A model $\mathbf {V}$ of $cFSA_\sigma$ is called textbiconstructive iff Atom is enumerable in $\mathbf {V}$.

Proposition 2

‘Atom is enumerable’ is definable in $cFSA_\eta$.

Proof

Let U(x, y) be a universal computable relation with respect to the computable classes. ‘Atom is enumerable’ is expressible with the following class formula:

$$\begin{aligned} \exists x(\{y|U(x,y)\}=Atom) \end{aligned}$$

$\square$

Theorem 14

‘Atom is enumerable’ is independent from $cFSA_\eta$.

Proof

Clearly $cFSA_\eta$ + ‘Atom is enumerable’ is a conservative extension of $cFSA_\eta$. Let A be an uncountable set and fix a standard model $\mathbf {V}$ in such a way that Atom in $\mathbf {V}$ is just A. One can check that

We note, that by the downward Lövenheim-Skolem theorem there is also a computable $\mathbf {V}$ within which Atom is not enumerable. $\square$

Theorem 15

(on the existence on constructive models). Let $\mathbf {V}$ be a constructive model of $cFSA_\eta$. In $\mathbf {V}$ the $p\exists$-definable and computable classes are the same and therefore any correct presentation $\varPhi :\sigma \rightarrow cTerm_\eta$ generates a constructive model $\mathbf {V}(Y\varPhi )$ of $\sigma$ in $\mathbf {V}$.

This theorem plays an important role in the forthcoming chapters.

Definition 17

Let $\eta _1\supset \eta$ and let $\mu :\eta _1\rightarrow cTerm_\eta$ be such a correct interpretation of $\eta _1$ in $cFSA_\eta$ that for all $\mathbf {V}\!\in \!Mod(cFSA_\sigma )$$\mathbf {V}(\mu )\!\upharpoonright _\eta =\mathbf {V}$. Moreover let $\mu$ be constructive. In this case $\mu$ is called a constructive extension of $cFSA_\eta$.

Theorem 16

Let $\eta _2\supset \eta _1\supset \eta _0$ and $\mu _{i+1}$ be a constructive extension of $cFSA_{\eta i}$ ($i=0,l$). $\mu _2$ is a constructive extension of $cFSA_{\eta 0}$.

Definition 18

Let R be a set of new relation symbols. A rule is of the form

$$\begin{aligned} \rho (\tau _1,\ldots ,\tau _2)\Leftarrow \varphi \end{aligned}$$

where $\tau _i\!\in \!Term_{\eta 1}$, $\varphi \!\in \!p\exists (0,\delta \cup R)$.

A logic program is a finite set of rules. A logic program u is called well-formed iff whenever u contains two rules of the form

$$\begin{aligned} \rho (\tau _1^{\ i},\ldots ,\tau _{ni}^{\ i})\Leftarrow \varphi _i\ (i=1,2) \end{aligned}$$

then $\rho _1=\rho _2(\in R)$ implies $n_1=n_2$ and $sort(\tau _j^{\ 1})=sort(\tau _j^{\ 2})\ (j=1,\ldots ,n_1)$. Let $LP_\delta (R)$ denote the set of all well-formed logic programs.

Let $S=sort\ \delta$. Let $S'$ be a copy of S with bijection $\iota$. Define an $S'$-sorted similarity type $\sigma _u$ for any $u\!\in \!LP_\eta (R)$. Take sort $\sigma _u\leftrightharpoons S'$. Define

$$\begin{aligned} rel\ \sigma _u\leftrightharpoons \{\rho \!\in \!R|\ \mathrm{there\ is\ a\ rule\ }\rho (\ldots )\Leftarrow \varphi \ \mathrm{\ in }u\}\cup rel\ \delta . \end{aligned}$$

The arity of $\rho$ is $\rho :\iota (s_1),\ldots ,\iota (s_n)$ and u contains a rule of the form

$$\begin{aligned} \rho (\tau _1,\ldots ,\tau _n)\Leftarrow \varphi \end{aligned}$$

and for all $i=1,\ldots ,n$$\iota _i=sort(\tau _i)$. Since u is well-formed, this definition of arity is correct. Let

$$\begin{aligned} func\ \sigma _u\leftrightharpoons func\ \delta . \end{aligned}$$

Let $X\leftrightharpoons (x_1,\ldots ,x_n)$. Let $X\!\in \!\varGamma$ be a shorthand for $\bigwedge \{x_i\!\in \!\varGamma _{si}|i\!\in \!n\}$, where $s_i$ is the sort of $x_i$. Let $\varphi [\varGamma ]$ denote the relativization of $\sigma$ along $\mu _{\sigma u}$.

Definition 19

Let $u\!\in \!LP(R)$ be a well–formed logic program. By using u we define a presentation $u\ \hat{}\$ in the following way:

• (a) Let $\rho \!\in \!rel\ \sigma _u$. Take

• (b)
• (c)

where $f:s'_{\ 1},\ldots ,s'_{\ n}\rightarrow s'.$

Proposition 3

Let u be a well–formed logic program. Then $u\ \hat{}\$ is a correct presentation with respect to $\mu$.

Definition 20

Any logic program u generates a set of axioms Ax(u) which is called the logic generated by the logic program u in the following way:

$$\begin{aligned} Ax(u)~\leftrightharpoons ~\{\varphi \rightarrow \rho (\tau _1,\ldots ,\tau _n)|\rho (\tau _1,\ldots ,\tau _n)\Leftarrow \varphi '\!\in \!u\}. \end{aligned}$$

Similarly, you can give another set of axioms which describes how $u\ \hat{}\$ was generated from the original sorts and functions. Let $Gen(u\ \hat{}\ )$ denote this fact. Namely if $\sigma \leftrightharpoons \sigma _u$ then take:

$$\begin{aligned} \begin{aligned} Gen(u\ \hat{}\ )~\leftrightharpoons ~&\{\mu _\sigma (s)\subset \mu (s)|s\!\in \!sort\ \delta \}\\ \cup&\{\mu _\sigma (f)\subset \mu (f)|f\!\in \!func\ \delta \}\\ \cup&\{\mu _\sigma (\rho )=\mu (\rho )\!\upharpoonright \mu _\sigma (s_1)\times \ldots \times \mu _\sigma (s_n)|\rho :s_1,\ldots ,s_n\!\in \!rel\ \delta \} \end{aligned} \end{aligned}$$

Theorem 17

Let u be a well-formed logic program and $\mathbf {V}\!\in \!Mod(cFSA_\eta )$ be a model. $\mathbf {V}(Yu\ \hat{}\ )$ is called the denotation of u and it is denoted by $Den_{\mathbf {V}}\llbracket u \rrbracket$. Clearly $Den_{\mathbf {V}}\llbracket u\rrbracket \!\in \!Mod_\sigma$. If $\mathbf {V}$ and $\mu :\delta \rightarrow cTerm_\eta$ are constructive then so is $Den_{\mathbf {V}}\llbracket u\rrbracket$.

Theorem 18

Let u be a well-formed logic program and fix a $\mathbf {V}\!\in \!Mod(cFSA_\eta )$. Take $\sigma \leftrightharpoons \sigma _u$. Let $\rho (\tau _1,\ldots ,\tau _k)$ be a positive ground atomic formula from $Form_\sigma$. Then

$$\begin{aligned} \begin{aligned}&Den_{\mathbf {V}}\llbracket u\rrbracket \models \rho (\tau _1,\ldots ,\tau _k)\text { iff}\\&Th(\mathbf {V})+ IM? (\mu _\sigma )+Gen(u)\vdash Ax(u)^\sigma \rightarrow \rho (\tau _1,\ldots ,\tau _n)^\sigma \end{aligned} \end{aligned}$$

To formalize the initial property of $Den_{\mathbf {V}}\llbracket u\rrbracket$ let us consider the following category $\mathbf {C}$. Let us fix a model $\mathbf {V}\!\in \!Mod(cFSA_\sigma )$. The objects of $\mathbf {C}$ are pairs $(\xi ,\iota )$ where $\xi :\sigma _u\rightarrow cTerm_\sigma$ and $\iota :\xi \!\upharpoonright func\ \sigma \rightarrow \mu$ is a morphism between two interpretations in $\mathbf {V}$. Moreover, we suppose that $\iota$ is an embedding.

The morphisms of $\mathbf {C}$ are the morphisms $\kappa :\xi _1\rightarrow \xi _2$ which commute with $\iota$’s:

This category is called the model category generated by u and denoted by $\mathbf {C}(u)$ .

Theorem 19

$Den_{\mathbf {V}}\llbracket u\rrbracket$ with the natural injection is the initial object in $\mathbf {C}(u)$.

We show that logic programming based on Horn-formulas is only a particular case of our definition. Indeed let $\delta$ be a similarity type such that rel $\delta$ is empty. Let $\underline{Herb}(0,\delta )$ be the minimal Herbrand model generated from $\delta$ in $cFSA_\eta$. Clearly, there is an interpretation $\varTheta :\delta \rightarrow cTerm_\eta$ which defines this model. Clearly $\varTheta$ is constructive in $cFSA_\eta$.

Definition 21

A well-formed logic program $u\!\in \!LP_\delta (R)$ is called a Horn-type logic program iff each rule $\rho (\tau _1,\ldots ,\tau _n)\Leftarrow \varphi$ belonging to u is Horn-type, i.e. $\varphi \rightarrow \rho (\tau _1,\ldots ,\tau _n)$ is a Horn-formula.

It is clear that the mathematical tools defined in Chaps. 5.1–5.3 fits well for Horn-type logic programs. By using Theorem 5.29 and the construction of $\varTheta$ we can give another version of initiality. Let $u\!\in \!LP_\varTheta (R)$ be a fixed Horn-type logic program. Take $\sigma \leftrightharpoons \sigma _u$. Let $\mathbf {V}$ be a fixed constructive model of $cFSA_\eta$.

Theorem 20

Let $\mathbf {C}$ be the category the objects of which are $\sigma$-type correct interpretations in a constructive model $\mathbf {V}$, and the morphisms of which are the interpretations between them. Then $\mathbf {V}(Yu\ \hat{}\ )$ is the initial object of $\mathbf {C}$.

Corollary 1

Let u be a well-formed Horn-type logic program. Let $\rho (\tau _1,\ldots ,\tau _n)$ be a positive ground atomic formula from $Form_\sigma$.

$$\begin{aligned} \begin{aligned}&cFSA_\eta \models \rho (\tau _1,\ldots ,\tau _n)\text { iff}\\&cFSA_\eta + IM? (\mu _\sigma )\vdash Ax(u)^\mu \rightarrow \rho (\tau _1,\ldots ,\tau _n)^\mu \end{aligned} \end{aligned}$$

Moreover, let $\mathbf {V}$ be a fixed model of $cFSA_\sigma$. Then

$$\begin{aligned} \begin{aligned}&\mathbf {V}(Yu\ \hat{}\ )\models \rho (\tau _1,\ldots ,\tau _n)\text { iff}\\&Th(\mathbf {V})+ IM? (\mu _\sigma )\vdash Ax(u)^\mu \rightarrow \rho (\tau _1,\ldots ,\tau _n)^\mu \end{aligned} \end{aligned}$$

By the use of a fixed point theory, which allows us to have solutions definable in $cFSA_\sigma$ we will be able to work with definable least fixed points. To achieve this we use the positive existential (or constructive) functionals over which the fixed point theory with the usual properties may be developed. Note that this functional class consists of only the functions considered as computable. By the use of this fixed point theory we get the traditional logic programming case. Let us suppose that $\eta '$ contains finitely many new constant symbols: $A_1,\ldots ,A_n$. Let us denote the formula

$$\begin{aligned} \bigwedge \{\underline{atom}(A_i)|i=1,\ldots ,n\}\wedge \forall x\underline{atom}(x)\rightarrow \bigvee \{x=A_i|i=1,\ldots ,n\} \end{aligned}$$

by $\underline{Const}$.

Theorem 21

$cFSA_\eta \ '+\underline{Const}$ has an initial term model $\mathbf {V}_i$.

Let $\mu$ be the same as in the previous example.

Theorem 22

Let u be a well-formed logic program. Let $\rho (\tau _1,\ldots ,\tau _n)$ be a positive ground atomic formula from $Form_\sigma$. Then

$$\begin{aligned} \begin{aligned}&\mathbf {V}_i(u)\models \rho (\tau _1,\ldots ,\tau _n)\text { iff}\\&cFSA_\eta + IM? (\mu _\sigma )+\underline{Const}\vdash Ax(u)^\mu \rightarrow \rho (\tau _1,\ldots ,\tau _n)^\mu \end{aligned} \end{aligned}$$

3.2.3 Other Programming Paradigm

The proposed theoretic frame is appropriate to describe and analyse various other approaches in programming. We mention here only the rough set theory, which was proposed as an approach to support intelligent data analysis and data mining. Approximation is the basic concept of rough set theory. Let us suppose that a set X should be described with the terms of attribute values from a given set A. Then according to the rough set theory two operations are defined assigning to every X two sets A*(X) and A*(X) called the A-lower and the A-upper approximation of X, respectively. Note that the A-lower approximation of a set is the union of all A-granules that are included in the set, whereas the A-upper approximation of a set is the union of all A-granules that have a nonempty intersection with the set. Rough set theory gives us one of the important backgrounds for that type of computing when the aim is to deal with inexact solutions of computational problems. Rough set theory plays an important role in granular computing. The basic ingredients of granular computing are granules such as subsets, classes, objects, clusters, and elements of a universe. These granules are composed of finer granules that are drawn together by distinguishability, similarity and functionality. Based on complexity, abstraction level and size, granules can be measured in different levels. A problem domain may exist at the highest and coarsest granule. Granules at the lowest level are composed of elements of the particular model that is used. Granulation is one of the key issues in granular computing for problem solving. See e.g. Akama et al. [2], Kumar et al. [18] and Yao [30]. Note that the two-sided approximation of the sets used by rough set theory can be provided by the fixed point equations. The approximation itself is realized by the smallest and largest fixed points. At the same time the granules to be used in the approximation will be given in the universe that will correspond to the actual problem domain.

4 Cognitive Computing

4.1 Motivations

Computing is the basic method for representing, model and investigate processes of human intelligence in the fields of Artificial Intelligence, Cognitive computing and Computational theory of mind. Thus, our goal is to develop a general computation theory that considers all the important aspects of this modelling. It is essential to handle the various levels of computation, from computation that uses purely syntactic digits to computation at the content level that among others interprets data, information and knowledge. Our further aim is to provide a theoretical framework, which will able to consider all the processes of the data $\rightarrow$ information $\rightarrow$ knowledge transformation and processing.

The theoretical framework - developed above - will permit to represent, model and investigate the main processes of cognizing under the control of direct thinking by the use of appropriately defined and constructed computing, which we call cognitive computing.

4.2 Basic Definitions

Let $Th=(\sigma ,Ax)$ be a fixed theory. Cognitive processes are defined by the use of situations, infons and information. The proposed extension will formalise the well-known constructions of situations and information. See Devlin [9] or Barwise [5]. Let $\iota$ be a new similarity type containing the followings.

• 1. A sort s for situations,

• 2. A sort b, i for basic infons and infons respectively,

• 3. A sort tv for truth values,

• 4. A functional symbol $\kappa : s,i \rightarrow tv$. $\kappa$ gives the truth value to an infon in a situation

• 5. A sort k for knowledge.

• 6. A function $\tau _i : k,s \rightarrow i$. $\tau$ is the query function which in a given situation produces an infon by the use of the actual knowledge.

Let us add an axiom stating that infons form the greatest set containing all the basic infons and if A is an infon and S is a situation then the triple $\kappa ,S,A$ is also an infon. Let $\mathcal {I}$ be the fixed-point equation describing this. According to Barwise [5] well-founded infons are the elements of the least fixed-points of the equation $\mathcal {I}$. Let $BC_\iota$ denote this set of axioms.

It is clear that $Th \rightarrow Th + BC_\iota$ form a constitution on $\mathbb {FOL}$. According to Theorem 1 there is a least compact constitution containing this constitution. Let $\mathbb {CB}$ denote this constitution. $\mathbb {CB}$ is the so-called cognitive base constitution (compact by definition).

4.3 Cognitive Processes

We recall the modification calculi from Anshakov, Gergely [4] see Chapters 10 and 18. To treat non-monotonity of reasoning process we need to

• 1. differentiate external and internal truth values

• 2. add a new type r for reasoning to clarify why we think that about the truth value of an infon in a given situation

• 3. have inference rules for handling records which can contain infons, information and/or knowledge (see Anshakov, Gergely [4] pp. 145–149).

Now we are ready to give a short description of what we mean by cognitive process. Again, fix a theory $Th=(\sigma ,Ax)$. Using the superstructure $SP_\mathbb {CB}(Th)$ a cognitive process

• 1. is a logic program in the sense of 3.2.2, its inner logic is the above stated modification calculus. This is able to extract infons, to generate new information and knowledge.

• 2. is also a process that can generate new processes, start, terminate and eliminate processes and can communicate with other processes.

• 3. can have a lot of query functions to interact with its environment.

• 4. can have a predefined goal.

Let $PC_\iota$ denote the axioms describing the aboves. Again we can define a closed constitution $\mathbb {CK}$ over $\mathbb {FOL}$ being the least compact-one containing the axiom systems $BC_\iota$ and $PC_\iota$.

Note that only those processes are called cognitive processes, which can generate, store and use new elements of the sort k, i.e. new information and knowledge elements.

Now we define the important notion Cognition Kernel as follows.

Definition 22

Cognitive Kernel is a compact constitution $\mathcal {C}$ on $\mathbb {FOL}$ together with an embedding (in functor category) of $\mathbb {CK}$ into itself.

5 Cognitive Computing

A goal-oriented organisation of cognitive processes form cognitive computing. The goal is usually related to the solution of a given problem situation, i.e. to the reduction of the uncertainty level of a problem situation.

The Cognitive computing theory will provide a mathematically well-defined classification of the possible types of computing and it will consider a special theory of realisation. The Cognitive computing theory allows the investigation and the determination of the theoretical limitations of the computing based modelling of intelligent processes. Thus in addition to the computational capabilities and limitations of different programming paradigms, the multi-layer cognitive computing can be explored and a framework can be developed that support the realization of the data $\rightarrow$ information $\rightarrow$ knowledge transition processes that use thought-driven cognitive processes. At the beginning generic and/or specific data analytical methods will provide infons from the data and then from the generated set of infons the corresponding information will be built. This information is used to decrease the uncertainty of the actual problem situation. The methods and information successfully used in the solution of the problem situation will form knowledge candidates. The latters will become knowledge only after a successful checking done by the use of the existing knowledge repository.

In this context, generalizations of the concept of Church- and Turing-computa-bility can be given and the computational possibilities and limitations of cognitive computing can be investigated. A multilayer theory of complexity can be defined to characterise the problem situations. It can be shown that cognitive processes necessary for the solution of problems of certain complexity will not be cognitive computable, but they will become so by a cognitive computing system with oraculum.

6 AI Based on Cognitive Computing

The proposed cognitive computing theory permits to design systems, which are able to lean on and interact naturally with users to extend the capability of humans and/or machines. So that humans would able to do more of what they could do on their own normally without cognitive computing support. A cognitive computing system will be able to respond to the environment in an autonomous regime too, without pre-programming. It can sense, learn, infer and interact. Cognitive computing systems can sense or perceive the environment and collect the data on the basis of needs and situations. They understand, interpret and analyse the context based on collected data and information, and they make decision based on reasoning and act accordingly. Various semantics and knowledge-driven cognitive data analysis methods can be represented and realised in a constructive way within the proposed Cognitive computing approach.

Cognitive computing theory provides a possibility for the use of computational approach to realise the understanding processes of natural language. Namely, this theory provides tools to interpret natural language texts in the various levels of cognitive computing.

The development of cognitive computing covers the basics of computing from language design to evaluator implementation with the aim of explaining existing systems at a deep enough level. This will help to adopt and use any of both, the languages and systems that are currently used in artificial intelligence and cognitive system area thus enabling the next generation of cognitive computing designers and implementers to use this as a foundation to build upon which. This is associated/augmented with a methodology that supports the selection of an appropriate specification method together with a constructive language that permits to describe the problem situation so that it prescribes the realization of the cognitive computing processes necessary for the solution of the actual problem situation.

Therefore, the proposed cognitive computing theory provides a constructive foundation of AI, where this abbreviation means Amplifier for Intelligence. This AI will be able to act as genuine problem-solving companion understanding and responding to complex problem situations. This AI system will be able to act either as a partner system for cooperative functioning with a human agent or as an autonomous cognitive system for a well-defined problem area. As to become a cooperative partner for human agents, the system has to function very similarly to humans. E.g., it should be able to communicate and understand natural language, reason in a compatible way, learn from its experience, etc. AI will be able to cognize the environment and itself including the co-operative partner.

7 Appendixes

1.1 7.1 Axiomatization of $clFSA$

In order to interpret program execution and different data and control structures, our theory of programming needs appropriate models to be obtained from a relation structure (models) of a given similarity type by building up the corresponding superstructure as we have seen so far. However, to use these superstructures in our theory of programming we have to introduce an appropriate formalism which allows to provide a theory (an axiomatization) the models of which are the structures in question and by the use of which, statements can be formulated and proved about these structures. According to our aim to develop a first order theory of programming the axiomatization of superstructures will be done in an appropriate first order language.

Superstructure construction is followed by a set–theoretic approach so the signature of the language has to contain at least:

• a unary relation symbol $\underline{atom}: d$

to distinguish the elements of the original relation structure from which the superstructure is built up. These elements may be considered as elementary data;

• the ‘element’ relation symbol $\in :d,d$

• and the constant symbol $0:\rightarrow d$

which reflects the empty set.

A similarity type $\sigma$ is called rich enough iff it contains the above symbols. We use $\notin$ for the negation of element relation.

The variable symbols of the language correspond to sets and atoms. Therefore, sets and their elements are of the same nature, if the latter ones are not atoms. In other words, we consider hereditary sets the elements of which are either atoms or hereditary sets etc. Though atoms have no elements they are not equivalent to the empty set. Therefore we have to be careful while providing the Axiom of Extensionality and defining some of the set-theoretic operations.

A relation symbol of $\sigma$ is called non set-theoretical iff it is not equal with either $\in$ or 0 or to $\underline{atom}$.

The system of axioms $FSA_\sigma$ axiomatizes the hereditarily finite sets with atoms. Why do we need atoms? As we know the Zermalo-Fraenkel axiomatization is powerful enough to make atoms unnecessary. Set theory, as formalized in ZFC, provides an elegant and powerful way to organize mathematics but it is too strong for the programming theory. The aim to build up an adequate axiom system for this theory dictates to develop a set theory weaker than ZFC, weak in the principles of set existence which they attempt to formalize e.g. by allowing atoms. The latters just have a programming interpretation as elementary data or, if you think about the relation structures as the object modelling computers where the programs run then atoms represent the registers where the data are stored. Atoms also break the finiteness which we intend to axiomatize since they may be infinitely many. We axiomatize the hereditarily finite sets with atoms by modifying the axiom system ZF as follows:

• $FSA_0$: Existential axiom of atoms:

  

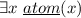
• $FSA_1$: Extensionality axiom:

  

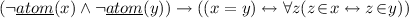
• $FSA_2$: Empty set axiom:

  

• $FSA_3$: Significance axiom of atoms:

  

This axiom together with $FSA_1$ declares that though atoms have no elements they differ from the empty set 0.

• $FSA_4$: Foundation axiom:

  

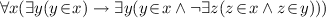
This axiom says that every non-empty set has a minimal element with respect to $\in$.

• $FSA_{5\sigma }$: Comprehension Scheme. For each $\sigma$-type formula $\varphi$:

  

The y asserted to exist is unique by Extensionality Axiom and it is denoted by

$$\begin{aligned} \{x|x\!\in \!z\wedge \varphi (x,y,w_1,\ldots ,w_n)\}\ \mathrm{or\ }\{x\!\in \!z|\varphi \}. \end{aligned}$$

Intuitively for a given formula $\varphi (x)$ there need not necessarily exist a set $\{x:\varphi (x)\}$ this collection may be too large to form a set. However, Comprehension Scheme says that if the collection is a subcollection of a given set then it does exist. The following axioms say that certain sets, which should exist, really do exist.

• $FSA_6$: Pairing axiom:

  

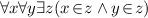
• $FSA_7$: Union axiom:

  

• $FSA_{8\sigma }$: Replacement scheme. For each $\sigma$-type formula $\varphi$:

  

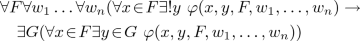
Intuitively (using also $FSA_{5\sigma }$) this axiom says that if H(x) is the unique y satisfying $\varphi (x,y,\ldots )$ then $\{H(x)|x\!\in \!F\}$ is a set.

• $FSA_9$: Finiteness axiom:

  

Definition 23

The set of axioms of the hereditarily finite sets with atoms is:

$$\begin{aligned} FSA_\sigma \leftrightharpoons \{FSA_i|i=0,1,2,3,4,6,7,9\}\cup \{FSA_{i\varphi }|i=5,8, \ \varphi \!\in \!Form_\sigma \}. \end{aligned}$$

If $R_1,\ldots ,R_k;f_1,\ldots ,f_n$ are new relation and function symbols respectively then $FSA_\sigma (R_1,\ldots ,R_k;f_1,\ldots ,f_n)$ stands for $FSA_{\sigma ^*}$ where $\sigma ^* = \sigma \cup (R_1,\ldots ,R_k;f_1,\ldots ,f_n)$.

The Finiteness Axiom implies the Axiom of Choice, i.e.:

Proposition 4

In $FSA_\sigma$ the following statements hold:

• (i) Each set can be well-ordered.

• (ii) There exists a choice function on sets.

Moreover, basically from the Finiteness Axiom, it follows that for any set there exists the power set, i.e. the Power Set Axiom is a consequence of $FSA_\sigma$.

Proposition 5

The axioms of $FSA_\sigma$ ensure that for any set there exists the power set:

$$\begin{aligned} FSA_\sigma \models \forall x(\lnot \underline{atom}(x)\rightarrow \exists y\forall z(z\!\in \!y\leftrightarrow z\subset x)). \end{aligned}$$

Therefore, the axiom system $FSA_\sigma$ is equivalent with the Zermalo-Fraenkel axiom system with the Axiom of Infinity and the Power Set Axiom deleted and Finiteness Axiom added.

Note that all the notions introduced in ZFC can be introduced in $FSA_\sigma$ as well. E.g. relation, domain, range, function, bijection, surjection, injection are such notions. The expressions that define these notions can also be used as a definition of new relation or function symbols. Adding these new symbols to the similarity type o and their definitions to $FSA_\sigma$, we obtain a conservative extention of $FSA_\sigma$.

Since in $FSA_\sigma$ all sets are finite, therefore the following preposition holds for ordinals:

Proposition 6

Each ordinal is finite in $FSA_\sigma$ and the usual addition and multiplication on ordinals are commutative.

Note that in set theory natural numbers are identified with finite ordinals. Namely, an ordinal $\alpha$ is a natural number if for all $\beta \le \alpha$ if $\beta \ne 0$ then $\beta$ is a successor of some $\gamma$. Again the Finiteness Axiom implies the following:

Proposition 7

The natural numbers, the ordinals (and the cardinals) are the same in $FSA_\sigma$.

A programming theory needs, among others, tools to handle infinite objects e.g. to represent infinite computation processes. Therefore, beyond finite sets as finite objects, we also have to be able to speak about infinite objects.

Different approaches provide different techniques for this aim, e.g. denotation approach to semantics makes the topological space complete. We introduce the notion of class to handle infinity. This notion is also important in ZFC axiom system, where e.g. the class of all ordinals On is often used. In the axiom system $FSA_\sigma$ the notion of class has a more important role, since the majority of the usual sets (namely, all infinite sets) cannot be identified with any set in $FSA_\sigma$.

Intuitively, a class is but a conglomerate of elements x which satisfy a given formula $\varphi (x)$. Since each $\sigma$-type model of $FSA_\sigma$ has constructive objects (atoms or finite sets) as elements a class is but a defined or specified conglomerate of these objects. Due to the significant role of classes in our further investigations they will frequently appear and we therefore have to precisely define what type of statements can be stated about classes. The definition is based on the followings. Having a given model a class does not consist of arbitrarily collected elements of the universe, but they may be collected only by the use of a given formula. Therefore, we extend the language such that it may contain statements about classes. Let us first fix an arbitrary set cV of the so called class variable. The intended meaning of a class variable in a model of $FSA_\sigma$ is a conglomerate of objects of the universe.

Let $\sigma$ be a rich similarity type. In order to handle classes we extend the $\sigma$-type classical first order language by adding class terms which provide definable conglomerate of objects of the universe of the models and the class formulas which allow to formulate statements about classes.

Definition 24.

• (a) The set of $\sigma$-type class terms (${\mathbf {cTerm}}_\sigma )$ consists of the terms in the form $\{x|\varphi \}$ where $x\!\in \!V$ and $\varphi \!\in \!cForm_\sigma$.

• (b) The set of $\sigma$-type class formulas (${\mathbf {cForm}}_\sigma$) is the minimal set satisfying the followings:

  • $Atom_\sigma \subset cForm_\sigma$;

  • if $x\!\in \!Term_\sigma$ and $C\!\in \!cV$ then $x\!\in \!C$ belongs to $cForm_\sigma$;

  • if $\varphi ,\psi$ are of $cForm_\sigma$ then $\lnot \varphi$ and $\varphi \wedge \psi$ also belong to $cForm_\sigma$;

  • if $\varphi$ is of $cForm_\sigma$, $x\!\in \!V$ then $\exists v\varphi$ also belong to $cForm_\sigma$.

Now let us see how the semantics of $cForm_\sigma$ can be defined. First of all, we extend the notion of valuation for class variables. A valuation of a class variable is a subset of the universe of the model under consideration.

Definition 25

Let $\mathbf {A}$ be an arbitrary but fixed $\sigma$-type model. A class valuation is a function k such that

• $dom(k)=C\cup cV$;

• $k(x)\!\in \!A$ for any $x\!\in \!V$;

• $k(x)\!\in \!Sb(A)$ for any class variable $x\!\in \!cV$.

As usual let $cVal_{\mathbf {A}}$ denote the family of all class valuations.

Having the valuation we can define the meaning of class terms and class formulas with respect to a given valuation in an arbitrary but fixed model.

Definition 26

Let a model $\mathbf {A}\!\in \!Mod_\sigma$ be given.

• (a) The meaning of a class term $t=\{x|\varphi \}$ in the model $\mathbf {A}$ with respect to k is the following family:

  $$\begin{aligned} t_{\mathbf {A}}\leftrightharpoons \{a|\mathbf {A}\models \varphi [k+(x,a)]\}. \end{aligned}$$

• (b) For any class formula $\varphi \!\in \!cForm_\sigma$ and valuation $k\!\in \!cVal_{\mathbf {A}}$ we define the validity $\varphi$ in $\mathbf {A}$ with respect to k (written as $\mathbf {A}\models \varphi [k]$) by induction on the complexity of $\varphi$:

  • if $\varphi \!\in \!Atom_\sigma$ then the validity is defined as in (i) and (ii) of 1.2.10;

  • if $\varphi \leftrightharpoons \tau \!\in \!C$ then $\mathbf {A}\models (\tau \!\in \!C)[k]$ iff $\tau _{\mathbf {A}}[k]$ is an element of k(C) ;

  • and (iv) are defined as in (iii) of 1.2.10 (i.e as usual).

In order to make the class valuation more transparent the $\sigma$-type models may be extended such that they will contain an entity which refers to classes.

Definition 27

A pair $\mathbf {V}=(\mathbf {A},\underline{Class})$ is called a class extention of $\mathbf {A}$ iff

• $\mathbf {A}$ is a $\sigma$-type model;

• $\underline{Class}\subset Sb(A)$;

• for any class term $t\!\in \!cTerm_\sigma$ and valuation $k\!\in \!cVal_{\mathbf {A}}$ we have $k(cV)\subset \underline{Class}$ implies $t_{\mathbf {A}}[k]\!\in \!\underline{Class}$.

Let $cMod_\sigma$ denote the family of all class extentions of $\sigma$-type models. If $\mathbf {V}\!\in \!cMod_\sigma$ then let $Val_{\mathbf {V}}$ denote those class valuations k for which $k(cV)\subset \underline{Class}$ holds.

Definition 28

Let $\mathbf {V}=(\mathbf {A},\underline{Class})$ be an arbitrary class extention belonging to $cMod_\sigma$. Let $\varphi \!\in \!cForm_\sigma$.

• (i) We say that $\varphi$ is valid in V with respect to a valuation k iff $k\!\in \!Val_{\mathbf {V}}$ and $\mathbf {V}\models \varphi [k]$.

• (ii) The class formula $\varphi$ is valid in $\mathbf {V}$ iff it is valid with respect to all $k\!\in \!Val_{\mathbf {V}}$ i.e.

  $$\begin{aligned} \mathbf {V}\models \varphi \text { iff for all }k\!\in \!Val_{\mathbf {V}},\mathbf {V}\models \varphi [k] \end{aligned}$$

• (iii) A class formula $\varphi$ is said to be valid in a $\sigma$-type model $\mathbf {A}$ iff for all class extention $\mathbf {V}= (\mathbf {A},\underline{Class})$ we have $\mathbf {V}\models \varphi$.

So we have defined the $\sigma$-type class language as a triple

$$\begin{aligned} CL_\sigma \leftrightharpoons (cForm_\sigma ,cMod_\sigma ,\models ) \end{aligned}$$

This language is really a two-sorted one. The first sort corresponds to sets and atoms and the second one to classes. However, quantification is allowed only for set variables.

A variable $x\!\in \!V\cup cV$ can also be considered as a shorthand for the class term $\{y|y\!\in \!x\}$ To have a clearer view of a variable let us see how the “element relation” $\in$ and the equality are defined for class terms.

• $\{x|\varphi \}\!\in \!\{y|\psi \}\leftrightharpoons \exists y(\forall x(x\!\in \!y\leftrightarrow \varphi )\wedge \psi )$;

• $\{x|\varphi \}=\{y|\psi \}\leftrightharpoons \forall x(\varphi \leftrightarrow \psi [x/y])$.

Depending on how we look at x as a variable or a=j a shorthand for $\{y|y\!\in \!x\}$ the class formulas $x\!\in \!y$ and $x\!\in \!C$ have different meanings. However, they are equivalent if we take the Extensionality Axiom ($FSA_1$).

Proposition 8

• (i) $FSA_1\models (x\!\in \!y)\leftrightarrow (\{z|z\!\in \!x\}\!\in \!{w|w\!\in \!y})$

• (ii) $FSA_1\models (x\!\in \!C)\leftrightarrow (\{z|z\!\in \!x\}\!\in \!\{w|w\!\in \!C\})$

Proof

We prove only the statement (i). Working in axiom system $\{FSA_1\}$ we have the following chain of semantic equivalences:

$$\begin{aligned} \{z|z\!\in \!x\}\!\in \!\{w|w\!\in \!y\}\equiv \exists u(\forall z(z\!\in \!x\leftrightarrow z\!\in \!u)\wedge u\!\in \!y)\equiv u(x=u\wedge u\!\in \!y)\equiv x\!\in \!y. \end{aligned}$$

$\square$

By using the above proposition we can define the following abbreviations:

• $C=D\leftrightharpoons \forall x(x\!\in \!C\leftrightarrow x\!\in \!D)$

• $C=y\leftrightarrow \forall x(x\!\in \!C\leftrightarrow x\!\in \!y)$

• $C\!\in \!x\leftrightharpoons \exists y(C=y\wedge y\!\in \!x)$

• $C\!\in \!D\leftrightharpoons \exists y(C=y\wedge y\!\in \!D)$

For the classical first order languages we have defined the simultaneous substitution of terms. This notion can be extended even to the class language. However, we have to make a careful distinction between substitution for variables and for class–terms. The only question is how substitute into a formula $x\!\in \!C$?

First let $\tau$ be a term belonging $Term_\sigma$. If so then take $(x\!\in \!C)[\tau /C]\leftrightharpoons x\!\in \!\tau$. Clearly $x\!\in \!\tau$ belongs to $cForm_\sigma$. In the case of class terms take $(x\!\in \!C)[\tau /C]\leftrightharpoons \varphi [x/y]$ where $\tau =\{y|\varphi \}$. This definition is comform with the fact that $x\!\in \!\{y|\varphi \}$ is just a shorthand for $\varphi [x/y]$. In the end if D is a class variable then take $(x\!\in \!C)[D/C]\leftrightharpoons x\!\in \!D$.

Without spelling out the whole definition we use the notation $\varphi [\tau _i/x_i]_i^{\ k}$ for the simultaneous substitution of terms $\tau _i$ for variables $x_i$, respectively.

Lemma 1

Let $\mathbf {V}\!\in \!cMod_\sigma$ and let $\varphi \!\in \!cForm_\sigma$ be arbitrary. Let us suppose that $var(\varphi )\cap cV=\{C_1,\ldots ,C_k\}$. Then for any class terms $\tau _1,\ldots ,\tau _n$ if $\mathbf {V}\models \varphi$ then $\mathbf {V}\models \varphi [\tau _i/C_i]_i^{\ k}$.

In order to handle classes axiomatically the axiom system $FSA_\sigma$ is to be appropriately extended. The extended axiom system denoted by $cFSA_\sigma$ consists of

• axioms which remain the same as they were in $FSA_\sigma$ dealing with sets only;

• axioms the scope of which is extended to classes;

• the extentions of the axiom schemas by allowing class formulas.

Namely, by extending the axiom system we get the following axiom system $cFSA_\sigma$ where variables $f , g , x , y , z , w, w_1 ,\ldots , w_n$ are from V and C, D are from cV.

• $FSA_0$ Existential axiom of atoms:

  

• $FSA_1$ Extensionality axiom:

  

• $FSA_2$ Empty set axiom:

  

• $FSA_3$ Significance axiom of atoms:

  

This axiom together with $FSA_1$ declares that though atoms have no elements they differ from the empty set 0.

• $FSA_4$ Foundation axiom:

  

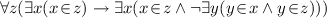
• $FSA_{5\sigma }$ Comprehension schema:

  

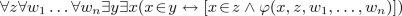
  $(\text {where }\varphi \!\in \!cForm_\sigma !)$

• $FSA_6$ Pairing axiom:

  

We remark that since classes have only sets as elements the Pairing Axiom is not extended to classes.

Before reformulating $FSA_7$ we remark that for any term t one can define its union by taking $\cup t=\{x|\exists y(x\!\in \!y\wedge y\!\in \!t)\}$. However, our original axiom states that if t is not proper then $\cup t$ is also not proper! Therefore, we have to use $FSA_7$ without any changes.

• $FSA_7$ Union axiom:

  

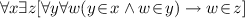
• $FSA_{8\sigma }$ Replacement scheme. For each $\sigma$-type formula $\varphi$:

  

  $(\text {where }\varphi \!\in \!cForm_\sigma )$

Similarly to the modification of the Comprehension schema we allow the use of class formulas in the scope of the Replecement schema as well.

• $FSA_9$ Finiteness axiom:

  

Now having the axiom system $cFSA_\sigma$ we clarify some notions. Let $\mathbf {V}=(\mathbf {A},\underline{Class})$ be an arbitrary class extention of $\mathbf {A}$.

• The elements of A are called objects.

• Let $a\!\in \!A$ be an object. If $\mathbf {V}\models \underline{atom}(x)[(a,x)]$ then a is said to be an $\underline{atom}$, otherwise it is a $\underline{set}$.

• The elements of $\underline{Class}$ are said to be classes.

• An object a and a class U are called equal iff $\mathbf {V}\models \forall y{(y\!\in \!x\leftrightarrow y\!\in \!C)} [(x,a)+(C,U)]$.

• A class $U\!\in \!\underline{Class}$ is called a proper class iff it is not equal to any object of $\mathbf {V}$. Namely U is a proper class if it satisfies the formula $\mathbf {V}\models \lnot \exists x(x=C)[(C,U)]$.

We redefine predicate ‘set’ by taking:

$$\begin{aligned} \underline{cset}(C)\leftrightharpoons \exists x(x=C\wedge \lnot \underline{atom}(x)). \end{aligned}$$

The $\lnot \underline{atom}(x)$ part of the conjunction is needed only when one substitutes a variable x for class-variable C:

$$\begin{aligned} \underline{cset}(C)[x/C]\equiv \exists y(y=x\wedge \lnot \underline{atom}(y)\equiv \lnot \underline{atom}(x)). \end{aligned}$$

Next we omit ‘c’ from the name of this redefined predicate because on sets the new and old meanings are the same.

The predicate ‘proper’ can be defined by taking:

$$\begin{aligned} \underline{proper}(C)\leftrightharpoons \lnot \exists x(x=C). \end{aligned}$$

According to the above defined predicates a class term $\tau$ is called relational or functional iff $Rel(\tau )$ or $Func(\tau )$ holds respectively.

The followings are two useful proper classes:

• $\underline{Universe}=\{x|x=x\}$;

• $\omega =\{x|Nat(x)\}$.