LAOS (Large Amplitude Oscillatory Shear) Applications for Semisolid Foods

Abstract

The rheological behavior of semisolid foods under large amplitude oscillatory shear (LAOS) can offer more detailed understanding of structural changes occurring during processing and consumption compared to traditional rheometry. This chapter focuses on a detailed description of LAOS measurements, including theory, testing method, data interpretation, and corrections. It also discusses LAOS application to food systems with different core structures ranging from dilute dispersions to gels, foams, emulsions, and soft elastic networks, along with a special emphasis on yogurt. Type of stress responses for different rheological behavior, Lissajous-Bowditch curves, and the resulting LAOS parameters (${G}_M^{\prime }$, ${G}_L^{\prime }$, ${\eta}_M^{\prime }$, ${\eta}_L^{\prime }$, e₃/e₁, ν₃/ν₁, S, and T) are used to understand the structural changes in all of these foods with special emphasis on high-fat, low-fat, and non-fat yogurt.

1 Nonlinear Rheology

1.1 LAOS (Large Amplitude Oscillatory Shear)

1.1.1 Theory

Small amplitude oscillatory shear (SAOS) tests have been one of the most commonly used rheological testing methods to study the linear viscoelastic properties of a wide range of soft materials and complex fluids (Bird et al. 1987; Hyun et al. 2011). SAOS measurements investigate the material’s response by observing the strain and frequency dependence of the storage modulus (G′, Pa) and loss modulus (G″, Pa) in the linear viscoelastic region (LVR) at small strains and provides information without significantly disturbing the three-dimensional structure of the materials (Duvarci et al. 2017b). However, most food materials are subjected to large, rapid deformations in most uses, including sensory evaluation during consumption, processing operations, transportation, and storage. Thus, nonlinear rheological properties may offer a more detailed understanding of food rheological behaviors under these real application conditions, which may not be obtainable through SAOS measurements. This fuller understanding of the system requires the evaluation of material nonlinearities through nonlinear test protocols that can provide full material characterization (Hyun et al. 2011).

A new fundamental theory of nonlinear viscoelastic behavior was developed by Ewoldt, McKinley, and their group (2007), which unraveled the progressive transition from linear to nonlinear viscoelastic rheological responses of complex fluids and soft solids. They developed sound rheological parameters to characterize viscoelastic behavior in the nonlinear viscoelastic region through the elegant use of Fourier transforms coupled with Chebyshev polynomials (Ewoldt et al. 2007; Hyun et al. 2011; Ewoldt 2013; Liu et al. 2014). A brief overview of this theory is presented below; for full details, the reader is encouraged to review the seminal paper by Ewoldt et al. (2008).

The linear viscoelastic properties of a material are traditionally measured at very low strain amplitudes (SAOS region) where G′ and G″ are constant as strain increases at a constant frequency. SAOS is a non-destructive test , and the stress response is a perfect sinusoidal wave when a small sinusoidal strain is applied (Fig. 1). After a critical strain value, G′ and G″ are no longer constant, and the material displays nonlinear viscoelastic behavior. The region where the nonlinear material response is probed by conducting oscillatory shear tests beyond the LVR is defined as the large amplitude oscillatory shear (LAOS) region. LAOS tests involve the systematic increase of the amplitude of the applied strain or stress at fixed frequencies (Hyun et al. 2011) and measuring the stress or strain response. The resulting material response is represented by Lissajous-Bowditch curves (see Sect. 1.1.2), which are intracycle stress versus strain plots typically normalized using the amplitude of stress and strain. The intracycle stress-strain plots can also be deconvoluted into viscous and elastic contributions. A rheological fingerprint of a material may be constructed by plotting Lissajous-Bowditch curves (or their elastic and viscous components) in the form of Pipkin diagrams, or an arrangement of the curves over a variety of frequencies and strains (Ewoldt et al. 2007).

Fig. 1

Lissajous-Bowditch curves for a frequency sweep measurement (at 0.1, 1, 10, and 100 rad/s) and at a constant strain of 1%. Blue lines in Lissajous-Bowditch plots are elastic planes of stress (τ(γ)); red lines are viscous planes of stress (τ(γ.)) (Läuger and Stettin 2010)

In the nonlinear viscoelastic region, the stress response is not sinusoidal and thus cannot be defined by a sinusoidal wave function . This non-sinusoidal stress response needs to be described by a different mathematical method, such as a Fourier series , which consists of an infinite sum of sine and cosine functions with progressively increasing frequencies (higher harmonics) where the transient data is transformed from the time domain to the frequency domain. The Fourier series can be decoupled into two different series that represent elastic (stress–strain behavior, Eq. 1) and viscous (stress–strain rate behavior, Eq. 2) behavior:

$$ \sigma \left(t;\omega, {\gamma}_0\right)={\gamma}_0\sum \limits_{n\ \mathrm{odd}}\left[{G}_n^{\prime}\left(\omega, {\gamma}_0\right)\sin n\omega t+{G}_n^{\prime \prime}\left(\omega, {\gamma}_0\right)\cos n\omega t\right] $$

(1)

$$ \sigma \left(t;\omega, {\dot{\gamma}}_0\right)=\dot{\gamma_0}\sum \limits_{n\ \mathrm{odd}}\left[{\eta}_n^{\prime \prime}\left(\omega, {\gamma}_0\right)\sin n\omega t+{\eta}_n^{\prime}\left(\omega, {\gamma}_0\right)\cos\ n\omega t\right] $$

(2)

where t represents time (s), ω is the imposed oscillation frequency (rad s^-1), γ₀ is the strain amplitude (unitless), n is number of odd harmonics, ${G}_n^{\prime }$ is elastic modulus of nth harmonic (Pa), ${G}_n^{\prime \prime }$ is viscous modulus of nth harmonic (Pa), ${\dot{\gamma}}_0$ is the resulting strain rate (s^-1), and ${\eta}_n^{\prime }$and ${\eta}_n^{\prime \prime }$ are dynamic viscosities of the nth harmonic (Pa.s) (Ewoldt et al. 2008).

In the LAOS region, as the stress response is non-sinusoidal, the storage modulus (G′, Pa) and the loss modulus (G″, Pa) lose their physical meanings and become a function of the strain amplitude as well as the applied frequency (G′(γ₀, ω)) and G″(γ₀, ω)) (Nam et al. 2010; Hyun et al. 2011). Ewoldt et al. (2008) deconvoluted the generic nonlinear, non-sinusoidal stress response into a superposition of an elastic stress σ^′(x) (Pa), where x = γ/γ₀ =  sin ωt, and viscous stress σ^′′(y) (Pa), where $y=y=\dot{\gamma}/{\dot{\gamma}}_0=\cos \omega t$. The sum of elastic and viscous contributions is expressed as the total periodic stress, σ(t) = σ^′(t) + σ^′′(t), and they are linked to the Fourier decomposition as indicated below:

$$ {\sigma}^{\prime}\equiv \frac{\sigma \left(\gamma, \dot{\gamma}\right)-\sigma \left(-\gamma, \dot{\gamma}\right)}{2}={\gamma}_0\sum \limits_{n\ \mathrm{odd}}{G}_n^{\prime}\left(\omega, {\gamma}_0\right)\sin n\omega t $$

(3)

$$ {\sigma}^{\prime \prime}\equiv \frac{\sigma \left(\gamma, \dot{\gamma}\right)-\sigma \left(\gamma, -\dot{\gamma}\right)}{2}={\gamma}_0\sum \limits_{n\ \mathrm{odd}}{G}_n^{\prime \prime}\left(\omega, {\gamma}_0\right)\cos n\omega t $$

(4)

Note that only odd harmonics are used to describe the rheological response of the sample (Läuger and Stettin 2010). Higher-order harmonics usually occur at larger amplitudes of strain; however, only odd harmonics are considered because they are caused by the rheological response of the fluid as a result of odd symmetry with respect to the directionality of shear strain or strain rate (Fig. 1). The presence of even harmonics might be due to wall slip, secondary flows, and fluid inertia and are less relevant (Graham 1995; Reimers and Dealy 1998; Yosick et al. 1998; Atalik and Keunings 2002).

The strain dependence of material properties is uniquely described using Chebyshev polynomials as follows:

$$ {\sigma}^{\prime }(x)={\gamma}_0\sum \limits_{n:\mathrm{odd}}{e}_n\left(\omega, {\gamma}_0\right){T}_n(x) $$

(5)

$$ {\sigma}^{\prime \prime }(y)={\dot{\gamma}}_0\sum \limits_{n:\mathrm{odd}}{v}_n\left(\omega, {\gamma}_0\right){T}_n(y) $$

(6)

where e_n and v_n are the nth-order Chebyshev coefficients and T_n(x) and T_n(y) are the nth-order Chebyshev polynomials for variables x and y, respectively. The first (T₁(x) = x), third (T₃ = 4x³ − 3x), and fifth (T₅ = 16x⁵ − 20x³ + 5x) Chebyshev polynomials are independent from each other due to their orthogonality. This is a key feature of the work: previous models used non-independent coefficients, meaning that their values changed if a different number of harmonics was used in the calculation. If a material showed a different number of harmonics above the noise level when run on multiple instruments, the coefficient values for each harmonic would change based on the number of harmonics used and the results would not be fundamental. Thus, Ewoldt et al. selected Chebyshev polynomials to remove this dependence, allowing different numbers of harmonics to be used in the calculation of the coefficients without impacting their values (Ewoldt et al. 2008).

Ewoldt et al. (2008) astutely recognized that e_n(ω, γ₀) represented the elastic Chebyshev coefficients and v_n(ω, γ₀) the viscous Chebyshev coefficients, and that these coefficients were related to the Fourier coefficients as follows:

$$e_n=G_n^{’}{\left(-1\right)}^{\left(n-1\right)/2}n:\mathrm{odd}$$

(7)

$$v_n=\frac{G_n^{’’}}{\omega }={\eta }_n^{’}n:\mathrm{odd}$$

(8)

The first-order Chebyshev and Fourier coefficients (e₁ and ${G}_1^{\prime }$, v₁ and ${G}_1^{\prime \prime }$) are a measure of the average elasticity and dissipated energy in a full sinusoidal strain cycle that includes both the contribution of deformation in the linear viscoelastic region and nonlinear viscoelastic region. When, e₃/e₁ ≪ 1 and v₃/v₁ ≪ 1, there is no contribution of nonlinearity and the material is in the linear viscoelastic region. Since the contribution of the fifth Chebyshev polynomial is very small, the third Chebyshev polynomial is used as a measure of nonlinearity. Therefore, the third-order Chebyshev coefficients (e₃ and v₃) may be used to interpret the deviations from linearity and evaluate the local nonlinear viscoelastic behavior of the material.

The total stress calculated by Ewoldt et al. (2008) is an improvement on the equation provided by Reimers and Dealy (1996), which is an expression of Fourier transform rheology in terms of amplitude and phase:

$$ \sigma ={\gamma}_0\sum \limits_{n:\mathrm{odd}}\mid {G}_n^{\ast}\mid \sin \left( n\omega t+{\delta}_n\right) $$

(9)

where $\left|{G}_n^{\ast}\right|=\sqrt{G{\prime}_n^2+G^{\prime }{\prime}_n^2}$ (Pa), γ₀ is strain amplitude (unitless), ${G}_n^{\ast }$ is complex modulus (Pa), ${G}_n^{\prime }$ is the nth harmonic elastic modulus (Pa), ${G}_n^{\prime \prime }$ is viscous modulus of nth harmonic (Pa), n is the number of odd harmonics (unitless), ω is the imposed oscillation frequency (rad/s), t is time (s), and δ_n is phase angle of the imperfect wave with respect to the input strain signal γ(t) = γ₀ sin ωt (rad). At ωt = 0, the third harmonic contribution is $\left|{G}_n^{\ast}\right|\sin \left({\delta}_3\right)$ and oscillates with a frequency of 3ω₁ for ωt > 0. The parameter δ₃ determines the initial value of the viscous and elastic third harmonic contributions and must range from 0 ≤ δ₃ ≤ 2π. Using these equations, Ewoldt et al. (2008) related the n = 3 Chebyshev coefficients and the third-order phase angle with the intracycle stiffening/softening and thickening/thinning behaviors as follows:

$$\begin{array}{c}>0\mathrm{f}\mathrm{o}\mathrm{r}\frac{\pi }{2}<{\delta }_3<3\pi /2,\mathrm{strain}\mathrm{stiffening}\\ e_3=-\mid G_3^{\ast }\mid cos{\delta }_3=0\mathrm{f}\mathrm{o}\mathrm{r}{\delta }_3=\pi /2,3\pi /2,\mathrm{linear}\mathrm{elastic}\\ <0\mathrm{f}\mathrm{o}\mathrm{r}-\pi /2<{\delta }_3<\pi /2,\mathrm{strain}\mathrm{softening}\end{array}$$

(10)

$$\begin{array}{c}>0\mathrm{f}\mathrm{o}\mathrm{r}0<{\delta }_3<\pi ,\mathrm{shear}\mathrm{thickening}\\ v_3=\frac{\left|G_3^{\ast }\right|}{\omega }sin{\delta }_3=0\mathrm{f}\mathrm{o}\mathrm{r}{\delta }_3=0,\pi ,\mathrm{linear}\mathrm{iscous}\\ <0\mathrm{f}\mathrm{o}\mathrm{r}\pi <{\delta }_3<2\pi ,\mathrm{shear}\mathrm{thinning}\end{array}$$

(11)

It is important to point out that the linear material functions G′ and G″ (equivalent to ${G}_1^{\prime }$ and ${G}_1^{\prime \prime }$) represent the average stress responses equivalent to the first-order Chebyshev coefficients e₁ and v₁, respectively. These moduli are commonly used to quantify the transition from SAOS to LAOS: the onset of nonlinear viscoelastic behavior is generally considered to occur when the deviation of G′is higher than 3% of its previous value. However, the magnitude of the third-order order elastic and viscous Chebyshev coefficients e₃ and v₃ can be used to indicate SAOS to LAOS transitions. Moreover, e₃ and v₃ can reveal the underlying cause(s) driving the nonlinear elastic and viscous intracycle stress response.

Note that these descriptions of strain- and shear-related behavior are derived from the decoupled elastic and viscous stress–strain curves, not the total stress–strain curve. Furthermore, these coefficients do not indicate the absolute or relative magnitude of elastic versus viscous behavior in a given sample; For example, it is possible for a viscoelastic solid with a low phase angle to exhibit shear-thinning or shear-thickening behavior according to its Chebyshev coefficients. A result like this would not indicate that the material is flowing during stress, merely that its viscous component is displaying shear-thinning behavior. Therefore, care must be taken when interpreting LAOS data, and a variety of parameters should be examined to provide an accurate description of material behaviors under LAOS.

1.1.2 Lissajous-Bowditch Curves

Lissajous-Bowditch curves consist of plots of the intracycle periodic stress normalized for stress amplitude, σ/σ₀(t; ω, γ₀), plotted against the strain data normalized for strain amplitude, γ/γ₀ (Ewoldt et al. 2008). These curves provide visual depictions of the characteristic transitions from the linear to the nonlinear viscoelastic region and the dramatic changes in the shape of the curve in the nonlinear viscoelastic region. Lissajous curves can also be decomposed into elastic and viscous components following the definitions in Equations 5 and 6.

To obtain the necessary data for these curves, strain sweep tests are conducted to obtain the linear viscoelastic region (SAOS region) followed by the transition from linear to the onset of nonlinear viscoelastic behavior (MAOS region) and finally the region of full nonlinear viscoelastic behavior (LAOS region). In the SAOS region, the Lissajous-Bowditch curves are elliptical regardless of frequency (Fig. 1). However, applied frequency can have a significant effect on the response of fluids and semisolids. A transition from more fluid-like to more solid-like flow behavior can be seen by a decrease in the enclosed area of τ(γ) and an increase in the enclosed area of $\tau \left(\dot{\gamma}\right)$ in Lissajous-Bowditch curves as frequency increases (Fig. 2).

Fig. 2

Elastic and viscous Lissajous-Bowditch curves of (a) a purely viscous liquid, (b) a purely elastic solid, (c) a viscoelastic liquid, and (d) a viscoelastic solid

LAOS measurements can be conducted using both strain-controlled and stress-controlled rheometers. Strain-controlled rheometers give inertia-free strain–frequency data. Stress-controlled rheometers can also be used for LAOS measurements if the torque inertia does not affect the sinusoidal shape of the applied strain (Bae et al. 2013). There is a third control mode known as direct strain oscillation (DSO) that uses a real-time position control and an electronically-commutated motor (EC motor). The desired sinusoidal strain input can be applied by direct control of the position (displacement) of the measuring system in each oscillation cycle as the motor applies torque. Thus, this control method is a hybrid of stress- and strain-controlled modes. It is important to note that differences in response can be observed between three different measurement modes. For example, the intracycle behavior of xanthan gum is shear-thickening for a sinusoidal strain input, but shear thinning for a sinusoidal stress input (Läuger and Stettin 2010). Because of these differences, caution is needed when comparing data collected using two different control modes.

Normalized intracycle stress data can be plotted versus both strain and strain rate. Stress versus strain plots provide elastic Lissajous-Bowditch curves; stress versus strain rate plots give viscous Lissajous-Bowditch curves. This pair of plots offers insights related to microstructural changes for a given imposed strain at a fixed frequency and temperature. A purely viscous fluid shows a perfect circle in the elastic plane and a straight line in the viscous plane (Fig. 2a) because purely viscous fluids dissipate all energy during deformation. A purely elastic solid stores all energy input, resulting in a straight line in the elastic plane and a perfect circle in the viscous plane (Fig. 2b). Hence, it can be said that the area of Lissajous-Bowditch curves in the stress–strain plane gives the energy lost during intracycle deformation and the area of the curves in the stress–strain rate plane is related to the stored energy during intracycle deformation. Because viscoelastic materials have elements of both viscous and elastic behavior, the Lissajous-Bowditch curves of these materials have elliptical shapes. Viscoelastic fluids show elliptically shaped Lissajous-Bowditch curves with a longer minor axis in the elastic plane and a shorter minor axis in the viscous plane (Fig. 2c). However, if the material is a viscoelastic solid, it shows a shorter minor axis and a longer minor axis in Lissajous-Bowditch curves in the elastic and viscous planes , respectively (Fig. 2d).

The new parameters defined by Ewoldt et al. (2008) lead to new and previously untapped insightful information on the nonlinear viscoelastic behavior of complex structured food materials. For example, the viscoelastic behaviors of tomato paste vary widely with the amplitude of an applied strain. At 0.01% strain, tomato paste is in the linear viscoelastic region and the elastic Lissajous-Bowditch curve has a narrow elliptical shape (Fig. 3a). As strain increases to 180%, the elliptical Lissajous-Bowditch curves become wider because the viscous forces rapidly increase in the nonlinear viscoelastic region and tomato paste starts to show highly fluid-like behavior. Furthermore, the elastic component of stress (σ^′) is no longer a pure sine wave due to the extent of nonlinear viscoelastic behavior, so the stress–strain curve becomes an odd orthogonal polynomial function (Fig. 3b).

Fig. 3

Lissajous-Bowditch curves of tomato paste at (a) 0.01% strain and (b) 180% strain at 1 rad/s and 25 °C

1.1.3 New Parameters for LAOS Testing

For further understanding and quantification of nonlinear elastic behavior, intracycle moduli at γ = 0 and γ = γ_o, defined as the minimum strain modulus (${G}_M^{\prime }$) and large strain modulus (${G}_L^{\prime }$), respectively, are used. In the linear viscoelastic region where e₃/e₁ ≪ 1, ${G}_M^{\prime }={G}_L^{\prime }={G}_1^{\prime }={G}^{\prime}\left(\omega \right)$. Note that when commercial rheometers report G′, they are effectively reporting ${G}_1^{\prime }$.

$$ {G}_M^{\prime}\equiv {\left.\frac{d\sigma}{d\gamma}\right|}_{\gamma =0}=\sum \limits_{n\ \mathrm{odd}}n{G}_n^{\prime }={e}_1-3{e}_3+\dots $$

(12)

$$ {G}_L^{\prime}\equiv {\left.\frac{\sigma }{\gamma}\right|}_{\gamma =\pm {\gamma}_0}=\sum \limits_{n\ \mathrm{odd}}{G}_n^{\prime }{\left(-1\right)}^{\frac{n-1}{2}}={e}_1+{e}_3+\dots $$

(13)

Similarly, for the interpretation of viscous nonlinearities, intracyle instantaneous viscosities, the minimum rate instantaneous viscosity (${\eta}_M^{\prime }$) and large rate instantaneous viscosity (${\eta}_L^{\prime }$) are obtained at strain rates of $\dot{\gamma}=0$ and $\dot{\gamma}={\dot{\gamma}}_o$, respectively. Like G′, in the linear viscoelastic region where ν₃/ν₁ ≪ 1, the following equations reduce to ${\eta}_L^{\prime }={\eta}_M^{\prime }={\eta}_1^{\prime }={\eta}^{\prime}\left(\omega \right)$. Also as for G′, when commercial rheometers report η^′, they are effectively reporting ${\eta}_1^{\prime }$.

$$ {\eta}_M^{\prime}\equiv {\left.\frac{d\sigma}{d\dot{\gamma}}\right|}_{\dot{\gamma}=0}=\frac{1}{\omega}\sum \limits_{n\ \mathrm{odd}}n{G}_n^{\prime \prime }{\left(-1\right)}^{\left(n-1\right)/2}={v}_1-3{v}_3+\dots $$

(14)

$$ {\eta}_L^{\prime}\equiv {\left.\frac{\sigma }{\dot{\gamma}}\right|}_{\dot{\gamma}={\dot{\pm \gamma}}_0}=\frac{1}{\omega}\sum \limits_{n\ \mathrm{odd}}{G}_n^{\prime \prime }={v}_1+{v}_3+\dots $$

(15)

These parameters are determined by plotting the stress response against strain (Fig. 4a) and strain rate (Fig. 4b), drawing tangent lines at zero strain or strain rate and secant lines at maximum strain or strain rate, and calculating the slope of each tangent line to determine the moduli and viscosity values (Ewoldt et al. 2008).

Fig. 4

Graphical descriptions and definitions of ${G}_M^{\prime }$ ${G}_L^{\prime }$ ${\eta}_M^{\prime }$ and ${\eta}_L^{\prime }$ determined from Lissajous-Bowditch curves in the nonlinear viscoelastic region. Data were collected for tomato paste at 200% strain and 0.5 rad/s

1.1.4 Dimensionless Characterization of Nonlinear Viscoelastic Behaviors

An alternative interpretation of ${G}_M^{\prime }$, ${G}_L^{\prime }$, ${\eta}_M^{\prime }$, and ${\eta}_L^{\prime }$ involves defining relations between them. If ${G}_L^{\prime }>{G}_M^{\prime }$ the response of the material is strain-stiffening. Hence, the strain-stiffening ratio S is defined as:

$$ S=\frac{G_L^{\prime }-{G}_M^{\prime }}{G_L^{\prime }}=\frac{4{e}_3+\dots }{e_1+{e}_3+\dots } $$

(16)

In the linear viscoelastic region, S = 0. It is positive when the material shows strain-stiffening behavior and negative when the material shows strain-softening behavior.

Similarly, the shear thickening ratio (T) is defined by Eq. 17. This ratio is greater than zero for intracycle shear-thickening, equal to zero in the linear viscoelastic region and less than zero for intracycle shear-thinning behavior.

$$ T=\frac{\eta_L^{\prime }-{\eta}_M^{\prime }}{\eta_L^{\prime }}=\frac{4{v}_3+\dots }{v_1+{v}_3+\dots } $$

(17)

Nonlinear viscoelastic responses for both the elastic and viscous components of stress may also be extracted using the Chebyshev coefficients. Negative and positive values for e₃/e₁ reflect strain-softening and strain-stiffening behavior, respectively, whereas negative values for v₃/v₁ correspond to shear-thinning and positive-values indicate shear thickening behavior (Ewoldt et al. 2008).

In summary, detailed structural information can be obtained from LAOS data by using three sets of parameters: (1) the Chebyshev coefficients (e₃ and v₃), (2) the derivatives of stress response with respect to strain and strain rate at zero and maximum intracycle strain values (${G}_M^{\prime }$${G}_L^{\prime }$${\eta}_M^{\prime }$ and ${\eta}_L^{\prime }$), and (3) the ratios of strain stiffening and shear thickening (S and T). These parameters (${G}_M^{\prime }$${G}_L^{\prime }$${\eta}_M^{\prime }$${\eta}_L^{\prime }$ e₃/e₁, v₃/v₁, S, and T) are referred to as LAOS parameters for the remainder of this chapter and can be used to interpret the intracycle behavior, providing insight into nonlinear viscoelastic behavior that cannot be obtained through SAOS measurements.

1.1.5 Frequency Considerations for LAOS Testing

The imposed frequency has an important impact on nonlinear viscoelastic rheological behavior. Since the energy delivered to the complex structure of food materials is carried out at different time periods, it may be advantageous to probe the material at different frequencies. The Lissajous-Bowditch curves enable the systematic evaluation of the evolution of intracycle rheological behavior at different strains and frequencies. Secondary loops have been observed in the stress–strain rate plane at progressively increasing frequency for many materials, such as molten polymers (Stadler et al. 2008), polystyrene solutions (Hoyle et al. 2014), polymer-clay suspensions (Hyun et al. 2012), tomato paste (Duvarci et al. 2017a), guar gum solutions (Szopinski and Luinstra 2016), egg white foams (Ptaszek et al. 2016), mashed potato paste (Joyner (Melito) and Meldrum 2016), and gluten-free dough samples (Yazar et al. 2017a). The mathematical interpretation of these loops has been offered by Ewoldt and McKinley (2010). Loops are formed in the viscous plot when the stress response has repeated values at a given strain rate (Fig. 5b). However, the elastic plot may not show these loops because the stress values at each strain value are unique (Fig. 5a). This behavior is related to a strong nonlinearity in elasticity and there should be a partial reversible structural change depending on the time scale of deformation which reoccur periodically. The origin of this distinctive behavior is aging and thixotropy and can be used to differentiate between structures of materials. Similarly, loops appearing in elastic stress versus strain plots but not viscous stress versus strain rate indicate strong nonlinear viscous behavior (Ewoldt and McKinley 2010).

Fig. 5

Secondary loops of tomato paste at a strain of 200%, a frequency of 0.5 rad/s, and 25 °C: (a) elastic plane, (b) viscous plane

2 Experimental Challenges during LAOS Measurements

2.1 Inertia Corrections

LAOS tests are prone to artifacts at high frequencies for low-viscosity samples due to large instrumental inertia contribution. The cyclic change in the motor shaft influences total torque at high frequencies. When the torque required to overcome the instrument inertia exceeds the torque required to deform the sample, the stress results become questionable and need correction (Franck 2006). Two types of inertia have been reported to be related to oscillatory shear tests. One type is instrumental inertia, which is related to the moving parts of the instrument, while the second type is sample inertia that occurs due to secondary flows, viscoelastic waves, and momentum diffusion. To obtain reliable data in oscillatory shear tests, test parameters should be set to minimize instrumental inertia or, if this is not possible, necessary corrections should be performed. To correct data for inertia, the first step is to identify whether the measurement is governed by instrument inertia. There are two parameters that need to be examined: raw phase and ratio of inertial torque to sample torque. Total torque applied by the rheometer leads to both acceleration of the moving parts of the rheometer and deformation of the sample (Läuger and Stettin 2016). The ratio of these two is given by:

$$ \frac{M_a}{M_s}=\frac{I\omega k}{\left|{\eta}^{\ast}\right|} $$

(18)

where M_a is acceleration torque (N.m), M_s is the torque delivered to the sample for deformation (N.m), I is the moment of inertia of the rheometer (kg.m²), ω is frequency of oscillation (rad/s), k is a geometry constant unique to the instrument geometry (1/m³ for parallel-plate geometries), and |η^∗| is magnitude of complex viscosity (Pa.s). When this ratio exceeds 0.2, instrumental inertia distorts the data (Merger and Wilhelm 2014), which then needs to either be discarded or corrected to eliminate inertia effects.

The second parameter to monitor instrumental inertia is the raw phase angle. It is defined as the angle between the total torque and the elastic component of torque during sample deformation (Fig. 6). If the raw phase angle exceeds 100 degrees, instrumental torque exceeds the torque required to deform the sample, and the data should be discarded or corrected.

Fig. 6

Vector representation of the raw phase angle (δ); M_o: total torque, M_e: elastic component of sample torque, M_v: viscous component of sample torque, M_a: acceleration torque, M_s: sample torque

The type of rheometer used can impact what inertial corrections are necessary. If the rheometer is a separate motor transducer type, the measurements are not affected by instrumental inertia friction (Franck 2006) because the torque-receiving elements in the rheometer remain immobile during the measurement, and the torque of the drive is not used for deforming the sample (Läuger and Stettin 2016). The measured torque at the transducer is controlled to a fixed position and its movements are very small. These small movements lead to small instrumental inertial effects. However, in combined motor-transducer design rheometers, the torque is not completely available for deforming the sample being tested; part of the total torque is needed for accelerating the moving parts of the instruments. This difference creates instrumental inertia effects. Hudson et al. (2017) provided an enhanced rheometer inertia correction procedure (ERIC) for combined motor-transducer rheometers, which builds on the procedure proposed by Franck (2006). Post-acquisition corrections on the data is carried out according to:

$$ {G}_m^{\prime }={G}_s^{\prime }-I{\omega}^2{k}_g $$

(19)

$$ {G}_m^{\prime \prime }={G}_s^{\prime \prime } $$

(20)

where ${G}_m^{\prime }$and ${G}_m^{\prime \prime }$ are material properties (Pa) and ${G}_s^{\prime }$ is a measured value (Pa). The measured value (${G}_s^{\prime }$, Pa) is proportional to the moment of the rheometer inertia (I, kg.m²), the square of the applied frequency (ω², rad²/s²), and the geometry constant (k_g if a parallel plate geometry is used, 1/m³). The measured loss modulus (${G}_s^{\prime \prime }$ Pa) does not need any correction since it is associated with the imaginary part of the measured sample .

2.2 Wall Slip

The presence of wall slip in LAOS tests results in nonlinear, non-sinusoidal stress waveforms. Because material responses under high oscillatory strains can also cause nonlinear, non-sinusoidal stress responses, wall slip can easily be conflated with true nonlinear viscoelastic material behaviors. In particular, application of high-frequency–strain combinations using smoth parallel plate geometries can cause significant slip. It is therefore important to determine if the distorted stress waveforms are due to nonlinearity or slip. The presence of even Chebyshev harmonics (e.g. n = 2, 4, 6…) and their corresponding coefficients are associated with slip since they are caused by broken shear symmetry (i.e. with responses that have not yet reached the time periodic state), similar to wall slip that inhibits steady-state. However, even harmonics are not always related to wall slip (Yoshimura and Prud’homme 1988; Macias-Rodriguez et al. 2018). The presence of slip can be evaluated by testing the same material using parallel plates at multiple gap heights but the same frequency and strain. If stress waveforms from both gaps are identical, this is an indication that slip does not occur and the nonlinearities and phase shifts are due to bulk fluid properties (Yoshimura and Prud’homme 1988). This approach was used to determine if observed nonlinearities in LAOS tests were caused by wall slip (Macias-Rodriguez et al. 2018). The lack of overlap of first harmonic viscoelastic moduli (${G}_1^{\prime }$ and ${G}_1^{\prime \prime }$) at different sample thicknesses (gap heights) was reported to be an indication of slip, internal fracture planes, or other non-ideal kinematics that derivate from homogeneous simple shear. To mitigate slip issues in oscillatory shear rheology, geometry modifications are commonly applied; for example, filter paper or sand paper can be attached to the surfaces of the plates to improve sample adhesion and minimize wall slip during measurements (Duvarci et al. 2017a, b; Yazar et al. 2016a, b, 2017a, b; Macias-Rodriguez et al. 2018).

3 LAOS Measurements and Interpretation for Different Food Systems

3.1 Applications of LAOS Principles to Characterize Food and Food Components

LAOS tests are able to offer more detailed understanding about the structural changes occurring in food systems during processing and consumption since food products are subjected to large deformations in these situations (Duvarci et al. 2017a). Many food materials have been studies using LAOS, including tomato paste (Duvarci et al. 2017a), mashed potato (Joyner (Melito) and Meldrum 2016), native starch in water (Klein et al. 2008), soy protein isolate-flax seed gum dispersions (Bi et al. 2013), gum extracted from Alyssum homolocarpum seed (Anvari et al. 2018), carragenan gels (Klein et al. 2008; Melito et al. 2013a), gelatin-alginate mixtures (Goudoulas and Germann 2017), whey protein-agar complexes (Rocha et al. 2014), agar with locust bean gum (Sousa and Goncalves 2015), crosslinked tapioca starch-polysaccharide systems (Fuongfuchat et al. 2012), tuna myofibrillar protein gels (Liu et al. 2014), waxy maize starch paste (Wang et al. 2012), waxy rice starch (Precha-Atsawanan et al. 2018), chewing gum (Martinetti et al. 2014), mayonnaise (Duvarci et al. 2017a), dark chocolate (van der Vaart et al. 2013), fish gelatin-gum arabic mixture in oil (Anvari and Joyner (Melito) 2018), water-in-oil emulsions (Shu et al. 2013); wheat dough (Lefebvre 2006; Yazar et al. 2016a, b), gluten-free doughs (Yazar et al. 2017a), cheddar, Mozarella, and American cheese (Melito et al. 2013b), fat crystal networks (Macias-Rodriguez et al. 2018), gluten (Ng et al. 2011), crude fractions of gliadin and glutenin (Yazar et al. 2017b), yeast biofilms (Brugnoni et al. 2014), and egg white protein foam with added apple pectin and xanthan gum (Ptaszek et al. 2016). Through these studies, much has been learned about the rheological behaviors of foods in the nonlinear viscoelastic region to supplement studies using SAOS measurements, and LAOS application and in-depth interpretation is rapidly progressing. These studies show that rich nonlinear viscoelastic behavior can be captured by LAOS analysis. Additionally, it is possible to determine the nonlinear viscoelastic behaviors of different food structures such as concentrated or dilute suspensions, emulsions, foams, gels, and soft elastic networks. It is also possible to distinguish structural changes in foods that arise due to different preparation methods, applied process parameters, and formulations. As examples of how LAOS can be used to interpret food behaviors, Sects. 3.2, 3.3, 3.4, and 3.5 discuss the current understanding of LAOS behaviors of common food systems and how those behaviors are related to the structure and texture of the food .

3.2 LAOS Behavior of Wheat Flour Dough

Dough rheology has been the focus of a large number of studies due to its unique viscoelastic behaviors. Wheat flour dough is reported to be in the linear viscoelastic region below strains of approximately 0.2% depending on the type of wheat (i.e. hard red winter or soft red winter) and becomes highly nonlinear beyond this strain level. Nonlinearity is related to the breakdown of the elastic gluten protein network. The gluten network is known to be held together by covalent disulfide bonds and secondary bonding interactions. The breakdown in the network occurs as a result of increasing mechanical energy as the amplitude of strain increases, overcoming the strength of both secondary bonding interactions and covalent bonds (Dus and Kokini 1990; Amemiya and Menjivar 1992). Nonlinearity of wheat flour dough has been studied by multiple groups (Hibberd and Parker 1979; Khatkar and Schofield 2002; Lefebvre 2006; Lefebvre 2009; Ng et al. 2006; Yazar et al. 2016a, b; Duvarci et al. 2017a). The presence and magnitude of higher-order harmonics in Fourier transformations of oscillatory stress response curves of dough leads to distinct nonlinear behavior on Lissajous-Bowditch curves (Lefebvre 2006). The nonlinear behavior of dough was attributed to the viscous component of dough, and the presence of starch and free water are responsible for the low linearity limit. A study on the LAOS behavior of dough at different stages of farinograph mixing showed that gluten network formation has a major effect on nonlinear viscoelastic behavior, especially on elastic modulus. These effects are related to the changes occurring in the protein fibrils in gluten network during farinograph mixing (Yazar et al. 2016a, b).

Plots of Lissajous-Bowditch curves at different strains and frequencies provide a comprehensive understanding of the structural evolution of dough with increasing strain and frequency. The elastic and viscous planes of normalized Lissajous-Bowditch curves of soft flour dough in the SAOS and LAOS region are given in Figs. 7 and 8. The curves are narrow ellipses in the elastic plane and circular in the viscous plane at low strains and frequencies, which indicate elastic-dominant rheological behavior.

Fig. 7

Elastic Lissajous-Bowditch curves of soft dough at 25 °C. All curves are plotted (σ(t)/σ_max) and (σ^′(t)/σ_max) vs. γ(t)/γ_o

Fig. 8

Viscous Lissajous-Bowditch curves of soft wheat flour dough at 25 °C. All curves are plotted (σ(t)/σ_max) and (σ^′′(t)/σ_max) vs. $\dot{\gamma}(t)/{\dot{\gamma}}_{\mathrm{max}}$

Because energy delivery from applied strain at higher frequencies is quite rapid, there is limited time for gluten filaments to recreate network junctions in the flow direction that are lost during stretching. An incomplete arrangement of chain orientation and alignment, and higher rate of network junction loss than the rate of creation results in less elastic and more viscous behavior. However, increased frequency does not necessarily promote increased nonlinear behavior of soft flour dough (Figs. 7 and 8). On the other hand, the emergence of higher-order harmonics at higher strains, denoting nonlinear behavior, profoundly affects the shape of the normalized Lissajous-Bowditch curves. There is greater area encompassed by the elastic plane curves, and their shape becomes distorted from that of an ellipse. Additionally, the major axis of the ellipses rotates either clockwise (strain-stiffening behavior) or counterclockwise (strain-softening behavior) at maximum strain. Similarly, clockwise and counterclockwise rotations of the major axes at maximum strain rate can be seen in the viscous plane for shear-thinning and shear-thickening behavior, respectively.

The third-order harmonic is the most significant of the higher-order harmonics, and can be used to calculate multiple nonlinear viscoelastic and LAOS parameters. The variation of ${G}_M^{\prime }$, ${G}_L^{\prime }$, and G′ with respect to strain is given in Fig. 9a for soft dough. ${G}_M^{\prime }={G}_L^{\prime }={G}_1^{\prime }$ in the linear viscoelastic region; all three of these values decreased at strains beyond the critical strain. At >10% strain, ${G}_M^{\prime }$, ${G}_L^{\prime }$, and G′ could be differentiated, indicating nonlinear viscoelastic behavior. G″, ${\eta}_M^{\prime }$, and ${\eta}_L^{\prime }$ showed a decreasing trend with strain rate, corresponding to shear-thinning behavior (Fig. 9b). The maximum strain rate was 2.07, 2.47 and 32 s⁻¹ when the frequency was 0.5, 1, and 15 rad/s, respectively. η^′, ${\eta}_M^{\prime }$, and ${\eta}_L^{\prime }$ had a decreasing trend , indicating shear-thinning behavior.

Fig. 9

Variation of (a) ${G}_M^{\prime }$, ${G}_L^{\prime }$, and G^′ with respect to strain, (b) ${\eta}_M^{\prime }$, ${\eta}_L^{\prime }$ and G^′′ with respect to strain rate. All data are for soft dough with measurement conducted at 0.5, 1, and 15 rad/s

The values of e₃, e₃/e₁, and S were approximately zero in the linear viscoelastic region, as expected. When the wheat flour dough samples were subjected to strains beyond the linear viscoelastic region, both soft and hard dough showed strain stiffening (e₃/e₁ > 0, S > 0), which may be associated with the stretching of the gluten network in the direction of flow. The presence of starch granules and free water also contribute to the reorganization of the dough structure. Although-shear-thinning behavior was indicated from the decrease in ${\eta}_M^{\prime }$, ${\eta}_L^{\prime }$ and G″ values (Fig. 9b), the ratio of viscous coefficients (ν₃/ν₁) showed intracycle shear-thickening behavior. Soft dough showed positive ν₃ values in the linear viscoelastic region followed by a decrease in ν₃ in the nonlinear viscoelastic region. Strain values had a shoulder at 6.9% strain for soft dough and 11% for hard dough, and a minimum value at about 113% for soft dough (Fig. 9a). These two peaks may be related with the two stages of dough structural reorganization reflected in the viscous component. Both doughs showed positive T values, an indication of intracycle shear thickening .

The LAOS behavior of gluten protein over a wide range of strain and frequencies in the nonlinear viscoelastic region offers additional interesting insights and shows major changes in both the elastic and viscous components’ stress responses. The Lissajous-Bowditch curves were much more elliptical, indicating a very strong elastic structure of gluten dough in nonlinear viscoelastic region. The clockwise rotation of the major axis of the stress–strain loop indicated a gradual intracycle softening of gluten dough, followed by an increase in stress that indicated intracycle strain stiffening (Fig. 7). Gluten dough maintained a considerable amount of its elasticity after experiencing larger deformations. LAOS behavior of gluten was further investigated by fractionating gluten into its main two fractions, gliadin and glutenin (Yazar et al. 2017b). Lissajous curves in the elastic analysis of both fractions showed that gliadin had broad ellipses with a rapid clockwise rotation in their major axes axis as strain increased, suggesting more fluid-like behavior and strain softening. Conversely, glutenin showed more elastic-dominant behavior: its Lissajous curves were narrower and the rate of clockwise rotation of the ellipse axes was considerably slower compared to gliadin, indicating a stiffer, more elastic structure that was more resistant to strain softening compared to gliadin. Glutenin also showed strain-softening behavior; however, the decay in elasticity with increasing strain and frequency for glutenin was notably slower than that of gliadin because the elliptic loops widen more slowly, and the rate of clockwise rotation of the elliptical axes is also slower compared to that for gliadin. These results ere due to the intermolecular disulfide bonds in glutenin that create a strong network compared to gliadin, in which there are no intermolecular disulfide covalent bonds to form a three-dimensional network .

3.3 LAOS Behavior of Yogurt Samples with Different Fat Levels

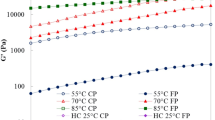
The effect of different levels of fat in yogurt samples obtained from the two commercial brands national brand and store brand were explored using LAOS tests at strain amplitudes of 0.01–1000% at a frequency of 1 rad/s. At the lowest applied strain (0.01%), all yogurt samples showed linear viscoelastic behavior that was not a function of applied strain. Deviation from linearity began as the strain amplitude reached 3–4%, and both G′ and G″ values started to decrease as the strain amplitude continued to increase up to 1000% (Fig. 10). A crossover point was observed for the national brand yogurt samples at ~20% strain, whereas a crossover in viscoelastic moduli occurred at ~30% strain for the store brand samples, suggesting a relatively stronger structure for the store brand yogurts . The crossover point was attributed to the breakdown of a gel-like structure and formation of aggregate spheres; the further decrease in the viscoelastic moduli can be attributed to further disruption of aggregate spheres. As strain increased, microstructural elements found in the yogurt, such as lipid droplets, whey protein-coated casein micelles, and microbial constituents in the serum, aligned themselves in the direction of flow and caused shear-thinning behavior (Van Marle et al. 1999).

Fig. 10

G′ and G′′ values for yogurt samples with different fat levels

The crossover of G′ and G″ occurred at almost the same strain for all national brand yogurts with different fat levels. Since fat globules act as a filler in yogurt structure (Lucey et al. 1998), low-fat store brand yogurt (2% fat) showed significantly lower G′ and G″ values compared to high-fat store brand yogurt (5% fat). However, the non-fat and high-fat store brand yogurts presented similar G′ and G″ values. These results suggested that fat replacers , such as hydrocolloids, gums, and starches, were added to the non-fat store brand yogurt to enhance the structure. On the other hand, the national brand yogurts with different fat levels all showed similar G′ and G″ values, suggesting a more precise adjustment in formulating the low-fat and non-fat yogurts to mimic the rheological behavior of the high-fat yogurt. Hydrocolloids and stabilizers are often used in the yogurt industry to increase consumer acceptance of yogurts by altering their rheological and textural characteristics (Mudgil et al. 2018).

An overall comparison of the strain sweep data for the two commercial yogurt brands revealed that national brand yogurts had higher G′ and G″ values than store brand yogurts. In the linear viscoelastic region, the national brand yogurts showed G′ values between 1500 and 2100 Pa, whereas G′ values of store brand yogurts ranged from 40 to 200 Pa. This result could be due to the differences in the raw material composition, homogenization (which impacts the size of fat globules), shear used to break the gel after fermentation, fermentation conditions, the pH reached during fermentation, the culture or other ingredients used, or some combination of these (Lee and Lucey 2010; Sfakianakis and Tzia 2014; Pascual et al. 2016). Although the G′ and G″ values of the national brand yogurts were found to be almost an order of magnitude higher compared to those of the store brand yogurts in the linear viscoelastic region, the structural network of the national brand yogurts deformed more quickly than those of the store brand yogurts . This difference in structural strength is likely due to the addition of pectin to the store brand yogurts but not the national brand yogurts. The addition of a high molecular weight polysaccharide with gel-forming ability appeared to delay significant deformation of the gel structure of the store brand yogurts, but was not able to enhance the elasticity of the structure and provide G′ and G″ values similar to those of the national brand yogurts .

SAOS tests showed perfect sinusoidal oscillatory stress responses as evidenced by the absence of higher harmonics (Fig. 11). At small strains (0.04%), the stress response was also small and was difficult to differentiate from equipment noise. As the strain amplitude increased above 0.4%, the equipment noise became insignificant compared to the stress response of the sample, and smooth, sinusoidal stress response curves appeared. As the strain amplitude further increased (>4%) deviation from a perfect sinusoidal response was observed, indicating the presence of higher-order harmonics and that the yogurt samples had entered the nonlinear viscoelastic region. The distortion of the stress response wave continued to increase with increasing strain, indicating increased nonlinear viscoelastic behavior.

Fig. 11

Raw stress responses of store brand yogurts with different fat levels at 1 rad/s in SAOS, MAOS, and LAOS regions

Comparison of the raw stress waves for the yogurt samples with different fat levels (Fig. 11) revealed that the characteristic stress waveforms for all yogurt types correlated with the information obtained through the strain sweep data. Increasing amplitude of strain resulted in a strong stress response for the non-fat yogurt compared to other samples and a lower response for the low-fat yogurt compared to high-fat yogurt. At the highest strain amplitude applied (1000%), the raw stress waves for the non-fat samples represented triangular-shaped sharper-edged trajectories at large strains, which is indicative of strain hardening according to the characteristic functions defined by Hyun et al. (2011). The waveforms obtained for low-fat store brand yogurt at high strains were more like the saw-tooth function which arises due to shear bands or wall slip.

The structural changes of materials can be observed by plotting stress data with respect to both strain and strain rate in three-dimensional plots. Because these plots can be used to visualize the stress response projections against the strain and strain rate simultaneously, the elastic and viscous components of a material’s intracycle nonlinear behavior can be analyzed synchronously. The stress–strain projection provides information about the elastic perspective of the material, while the stress–strain rate projection gives a viscous perspective. For all yogurt samples, as the amplitude of strain gradually increased, the elastic Lissajous curves showed wider elliptical trajectories (Fig. 12), indicating viscous-dominated intracycle nonlinear viscoelastic behavior . The magnitude of the stress amplitude was found to be higher for the national brand yogurts (250–320 Pa, Fig. 12a–c) compared to store brand yogurts (<80 Pa, Fig. 12d–f), which concurs with the strain sweep data (Fig. 10). In particular, the low-fat store brand yogurt had the lowest magnitude of elastic stress among all other yogurt samples over the entire strain range, indicating increased viscous-dominant behavior. Examining the stress–strain rate (viscous) projection, the ellipses for the national brand yogurts showed clockwise rotation with increased strain, which suggested intracycle shear-thinning behavior (Ewoldt et al. 2008). The viscous projections of store brand yogurts displayed clockwise rotation at lower strain values, indicating an onset of shear-thinning behavior at smaller strains for store brand yogurts compared to national brand yogurts.

Fig. 12

Three-dimensional un-normalized Lissajous-Bowditch curves of stress response (black), elastic component (green), and viscous component (blue) versus strain and strain rate for yogurt with different fat content and brand: (a) non-fat, (b) low-fat, and (c) high-fat national brand yogurt; (d) non-fat, (e) low-fat, and (f) high-fat store brand yogurt. Data were collected at 0.063%, 0.25%, 1.01%, 4.21%, 18%, 69%, 266%, and 1051% strain

Upon review of the normalized Lissajous curves, both viscous and elastic Lissajous curves for the store brand yogurts were found to be impacted by experimental noise at small strains, resulting in wavy structures (Fig. 13). The elastic Lissajous curves showed narrow elliptical trajectories at low strain amplitudes, an indication of linear viscoelastic behavior. As strain amplitude gradually increased, the ellipses widened, suggesting fluid-like viscoelastic nonlinear behavior for all yogurts. Distortion in the elliptical trajectories appeared at strain >4.21% for both the elastic and the viscous contributions. At the highest strain, the elastic Lissajous curves of the national brand yogurts, regardless of fat content, displayed rectangular trajectories, indicating both gel-like and reversible stick-slip flow-induced microstructure (Hyun et al. 2011). On the other hand, the ellipses in the viscous projection for all yogurt samples narrowed with increased strain, indicating more fluid-like behavior in the nonlinear viscoelastic region; this results was consistent with the elastic projections. The ellipses of the national brand yogurts in the viscous projection were narrower than those for the store brand yogurts at large strains, indicating that national brand yogurts had more fluid-like behavior. The stronger clockwise rotation observed for the national brand yogurts at the highest strain suggested a higher degree of intracycle shear thinning (Fig. 14). The viscous Lissajous curves of the national brand yogurts at the highest strain showed narrow ends and a slight thickening in the center. This is similar to loop behavior: the stress response has repeated values as the oscillation reaches the highest intracycle strain value and decreases. It indicated reversible structural change under these strain conditions. Additionally, elastic Lissajous curves for both store and national brand non-fat yogurts displayed narrower trajectories, while viscous Lissajous curves displayed wider ellipses at large strains compared those of to low-fat and high-fat samples, suggesting less viscous-dominant viscoelastic nonlinear behavior for non-fat yogurts.

Fig. 13

Elastic and viscous Lissajous-Bowditch curves for the store brand yogurts with different levels of fat at 1 rad/s; — σ/σ_o, — σ′/σ_o, — σ′′/σ_o

Fig. 14

(a) Elastic and (b) viscous Lissajous-Bowditch curves for national-brand yogurts with different levels of fat at 1 rad/s; —σ/σ_o, —σ′/σ_o, —σ′′/σ_o

The nonlinearities of the yogurt samples can also be observed via LAOS parameters. Figure 15 shows ${G}_L^{\prime }$, ${G}_M^{\prime }$, ${\eta}_L^{\prime }$, and ${\eta}_M^{\prime }$ of each sample in terms of oscillatory strain and strain rate, respectively. In the linear viscoelastic region, between 0.01% and 2% strain, ${G}_L^{\prime }$ and ${G}_M^{\prime }$ values of yogurt samples with different fat levels were similar for each brand, except for the low-fat store brand yogurt, which showed lower intracycle moduli values throughout the entire applied strain range. National brand yogurts had higher moduli values compared to store brand yogurts. As strain amplitude increased, ${G}_L^{\prime }$ values became higher than ${G}_M^{\prime }$ values for all yogurt samples from both brands, indicating intracycle strain-stiffening behavior. The deviations of ${G}_L^{\prime }$ and ${G}_M^{\prime }$ from G′ at small strains were attributed to unsteady and irregular flows due to low applied strain at the beginning of the experiment. Additionally, all yogurt samples showed higher minimum strain viscosities than large strain viscosities in the nonlinear viscoelastic region (${\eta}_M^{\prime }$ > ${\eta}_L^{\prime }$), which was in agreement with the information obtained through the viscous Lissajous curves that indicated intracycle shear thinning for the yogurt samples analyzed.

Fig. 15

${G}_L^{\prime },{G}_M^{\prime }$ and ${\eta}_L^{\prime },{\eta}_M^{\prime }$ values for yogurts with different fat levels at 1 rad/s

All of these outcomes were found to be consistent with the ratios of the third order Chebyshev coefficients to the first order Chebyshev coefficients (e₃/e₁, ν₃/ν₁) extracted from the LAOS data obtained both in the linear and nonlinear viscoelastic regions (Fig. 16). All yogurt samples showed strain-stiffening behavior (e₃/e₁ > 0) in the nonlinear viscoelastic region. Furthermore, all national brand yogurts and the non-fat store brand yogurt showed continuously increasing strain-stiffening behavior up to the highest applied strain (1000%), whereas low-fat and high-fat store brand yogurts showed increasing strain-stiffening followed by a plateau at 1000% strain, indicating a decrease in the intensity of strain stiffening at high strain compared to the other samples. The intensity of strain-stiffening behavior was found to be higher for the national brand yogurts (Fig. 16a) compared to the store brand yogurts (Fig. 16b). For store brand yogurts, intracycle strain stiffening behavior and its intensity were dependent on the fat level, which was consistent with the information obtained through the raw stress responses (Fig. 11).

Fig. 16

e₃/e₁ and ν₃/ν₁ values for yogurts with different fat levels at 1 rad/s

Store brand yogurts all showed shear-thinning behavior (v₃/v₁ < 0) in the nonlinear viscoelastic region (Fig. 16d). The intensity of the intracycle shear-thinning behavior for the low-fat store brand yogurt was found to be the lowest. All national brand yogurts showed slight shear-thickening behavior between 2% and 10% strain followed by shear-thinning behavior in the nonlinear viscoelastic region (Fig. 16c). The shear-thickening behavior observed for the national brand yogurts right after the onset of the nonlinear viscoelastic region was attributed to the formation of aggregate proteins spheres in the microstructures as a result of the disruption of the yogurt gel structure by the increasing strain. As strain increased further, the transition from shear-thickening to shear-thinning behavior may have been due to further breakdown of the aggregate spheres into their constituents, such as caseins, micelles, and bacterial cells. Store brand yogurts showed an onset of intracycle shear-thinning behavior at smaller strains, which concurred with the information obtained through the three-dimensional Lissajous plots (Fig. 12).

The transition from the linear viscoelastic response to the nonlinear viscoelastic response was further analyzed using the dimensionless LAOS parameters S (strain-stiffening ratio) and T (shear-thickening ratio). Positive S values (S > 0) were obtained for both national brand and store brand yogurts at 1 rad/s (Fig. 17a, b). The store brand yogurts showed T values that were slightly below zero (T ≤ 0), whereas the national brand yogurts all showed negative values (T < 0) of a significantly higher magnitude than those of the store brand yogurts, indicating that they had a higher level of shear-thinning behavior (Fig. 17c, d). This information concurred with the information obtained by the viscous Lissajous curves (Figs. 13 and 14). The irregularities observed for the S and T values of the store brand yogurts at initial strains (0.01–0.1%) were attributed to wall slip and the unsteady local velocities occurring within the sample. In general, the information obtained from the S and T values solidified the evaluations of the nonlinear viscoelastic rheological behavior yogurt samples through the analyses of the SAOS and LAOS parameters, along with the elastic and viscous Lissajous curves.

Fig. 17

Strain stiffening ratio (S) and shear thickening ratio (T) values for the yogurt samples with different fat levels at 1 rad/s

3.4 LAOS Behavior of Tomato Paste and Mayonnaise

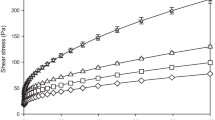
LAOS tests conducted within the strain range of 0.01–200% at 1 rad/s frequency showed that tomato paste and mayonnaise samples displayed nonlinearity at strain values of 1.24% and 4.3%, respectively (Duvarci et al. 2017a). Although a longer viscoelastic region was found for mayonnaise, tomato paste had higher G′ and G″ values. An overshoot was observed for mayonnaise G″ values at the onset of the nonlinear viscoelastic region with the maximum occurring at 12% strain, while both moduli values for tomato paste decreased with increasing strain. The information obtained through the strain sweep data revealed that tomato paste showed Type I nonlinearity and mayonnaise showed Type III nonlinearity based on the classification proposed by Hyun et al. (2002). Both tomato paste and mayonnaise displayed intracycle strain stiffening captured through the upward turn of the elastic stress versus strain curves at large strains. The counterclockwise rotation of the ellipses suggested a gradual softening for both mayonnaise and tomato paste as the strain increased. Secondary loops were observed at the lowest frequency (0.5 rad/s) for tomato paste Lissajous-Bowditch curves, indicating reversible structural deformation and thixotropic behavior (Duvarci et al. 2017b). Both tomato paste and mayonnaise showed slight strain-stiffening (e₃/e₁ > 0, S > 0) and shear-thickening (v₃/v₁ > 0, T > 0) behaviors in the nonlinear viscoelastic region at 1 and 15 rad/s, which decreased at larger strains. At 0.5 rad/s, negative and decreasing v₃/v₁ and T values over strain rate were observed for tomato paste, while these values showed a maximum followed by a decrease for mayonnaise in the nonlinear viscoelastic region, similar to the trend observed for the G″ values (Duvarci et al. 2017a). These findings indicated that large strain rates were the driving force behind the gradual softening observed for tomato paste and mayonnaise, while unraveling the differences in the nonlinearities of these two concentrated dispersions.

3.5 Additional Selected LAOS Studies

LAOS analysis has also been used to evaluate the effects of food formulation changes and chemical composition on their rheological behaviors. For example, the effect of formulating mashed potato with different potato starch preparations (Joyner (Melito) and Meldrum 2016), the impact of particle size and addition of soy lecithin to dark chocolate (van der Vaart et al. 2013), the addition of xanthan gum and pectin to egg white foams (Ptaszek et al. 2016), and the effect of debranching on waxy rice starch gels (Precha-Atsawanan et al. 2018) have been studied. Increased starch damage in mashed potato composition was reported to cause an increase in viscous-dominant rheological behavior and a decrease in nonlinear viscoelastic behavior at large strains, which may have been due to granule shape and size enabling damaged granules to more easily flow past each other. All samples, except for the sample prepared directly from potato starch, displayed shifts from elastic- to viscous-dominated behavior at large strains, which was captured by Lissajous-Bowditch curves and phase angle values (Joyner (Melito) and Meldrum 2016). In dark chocolate, a larger particle size of solids, such as sugar and cocoa, resulted in higher strain-stiffening intensity, while added lecithin did not significantly impact the strain-stiffening behavior. On the other hand, dark chocolate shear-thinning behavior was found to increase as the particle size increased, and the onset of shear thickening occurred at lower strains. Low levels of added lecithin decreased shear-thinning behavior, which could be attributed to its lubricating effect (van der Vaart et al. 2013). The addition of pectin , which is capable of gelling, and xanthan gum, which behaves like a soft gel but does not form a three-dimensional network structure on its own, eliminated the secondary loops associated with thixotropic behavior in egg white foams. Addition of xanthan gum and pectin to egg white foams also caused a shift to strain-hardening behavior in the nonlinear viscoelastic region, compared to the strain-softening behavior observed in egg white foams without these stabilizers (Ptaszek et al. 2016). Debranching increased the strain-stiffening and shear-thinning intensities in waxy rice gels. S values were positive above 1% strain for debranched gels, while positive values did not appear until 100% strain for waxy gels. At high strains, elastic Lissajous curves for debranched gels displayed an almost square shape, indicating abrupt yielding; their viscous curves exhibited an S-shape, showing a high degree of shear-thinning. Elastic and viscous Lissajous-Bowditch curves for waxy starch gels changed from an elliptical to a rhomboidal shape, indicating less pronounced strain-stiffening and lower shear-thinning behavior along with gradual yielding (Precha-Atsawanan et al. 2018).

As discussed in Sect. 1.1.4, e₃/e₁ and v₃/v₁ can be used to determine nonlinear viscoelastic behaviors (Ewoldt et al. 2008). Specifically, the profile of these ratios over the applied strain range can provide an in-depth understanding about how nonlinear viscoelastic material behavior changes with strain. The difference between hard and soft red winter wheat flour doughs in terms of gluten quantity and quality was probed by the decay observed on the intensities of e₃/e₁ within the applied strain range (Yazar et al. 2016a, b). Dough samples from both flours showed intracycle strain stiffening. However, as the strain amplitude increased from 44% to 70%, strain-stiffening behavior decreased for the soft wheat flour dough as observed by the decrease in the intensity of e₃/e₁. Hard wheat flour doughs showed a similar decrease at ~100% strain. These results revealed that the hard wheat flour dough had higher stability against large deformations due to its stronger gluten network.

These Chebyshev coefficients have been used to analyze the nonlinear viscoelastic behavior of other foods. For example, LAOS analysis of brittle and ductile fats showed that fat crystals had increasing v₃/v₁ values as strain increased towards the onset of nonlinearity; after the onset of nonlinear viscoelastic behavior, these values decreased, indicating a shift from intracycle shear-thickening to shear-thinning behavior. Positive e₃/e₁ values (intracycle strain stiffening) were recorded in the nonlinear viscoelastic region, showing that the elastic softening in fat crystals was driven by large strain rates. Additionally, brittle fats were reported to exhibit stronger nonlinearities as evidenced by higher positive elastic Chebyshev coefficients and lower negative viscous Chebyshev coefficients (Macias-Rodriguez et al. 2018).

Chebyshev coefficients have also been used to show that tomato paste and mayonnaise at 1 rad/s (Duvarci et al. 2017a) and agarose gels (Melito et al. 2012) exhibited strain-softening and shear-thinning behavior at the beginning of their nonlinear viscoelastic regions; they displayed strain stiffening and shear-thickening behaviors at higher strains. In contrast to the rheological behavior of these systems, dark chocolate (van der Vaart et al. 2013), egg white protein foams (Ptaszek et al. 2016), and fat crystals (Macias-Rodriguez et al. 2018) showed strain-stiffening and shear-thickening behavior in the linear viscoelastic region and strain-stiffening and shear-thinning behavior in the nonlinear viscoelastic region.

Another example of the complex rheological behavior captured through e₃/e₁ values was observed for buckwheat flour dough (Yazar et al. 2017a). Strain stiffening behavior was observed at the beginning of the nonlinear viscoelastic region (e₃/e₁ > 0). As strain increased gradually at a constant frequency of 10 rad/s, strain softening behavior occurred (e₃/e₁ < 0) due to the lack of a network formation such as that formed by gluten in wheat flour doughs, followed by strain stiffening behavior at >100% strain. At lower frequencies, this strain softening behavior was not observed. Furthermore, shear thinning dominated the rheological behavior in the nonlinear viscoelastic region at all applied frequencies. This shows frequency mainly affected the nonlinearity for the elastic component in the buckwheat flour dough. Evaluation of the stored and dissipated energy mechanisms simultaneously in the nonlinear viscoelastic region is not possible by the application of a rheological test other than LAOS. It is possible in the linear viscoelastic region through SAOS applications. However, linking nonlinear viscoelasticity to macroscopic performance is more relevant, since materials are exposed to large deformations under processing conditions.

The emergence of third order and higher harmonics due to significant nonlinear viscoelastic behaviors during the transition from SAOS to LAOS was also reported to be important to capturing microstructural differences (Ewoldt and Bharadwaj 2013). This transition region, termed the intrinsic regime, comprises relatively low strains covering a range from linear viscoelastic behavior to the onset of nonlinearity. This region is idea for physical interpretation of higher-order harmonics because the experimental errors associated with the magnitude of the third harmonic observed at large strains (e.g. wall slip, secondary flows) are minimized. Ewoldt and Bharadwaj (2013) defined the material functions in the intrinsic region using a single-mode Giesekus model; they obtained a slope of 2 when log(e₃/e₁) and log(v₃/v₁) are plotted against log(γ). Yazar et al. (2017b) evaluated the intrinsic behavior of crude gluten fractions at 0.6–10% strain. They scaled the first harmonic moduli (${G}_1^{\prime }$ and ${G}_1^{\prime \prime }$) using the value of the complex modulus G^* obtained in the intrinsic region. Third-order harmonic Chebyshev coefficients (e₃ and ν₃) were scaled using the corresponding linear viscoelastic material function (G′ = e₁ and G″ = ν₁) at the same frequency within the intrinsic region. Slope values ranging between 0.45 and 2 were obtained for both gluten fractions. Higher slope values were obtained for gliadin, suggesting that the model to characterize intrinsic LAOS function (Ewoldt and Bharadwaj 2013) was a better fit for gliadin than glutenin.

As discussed in Sect. 1.1.1, the first-order viscoelastic moduli , ${G}_1^{\prime }$ and ${G}_1^{\prime \prime }$, can also be used to provide useful material characterization when plotted as a function of stress amplitude (τ₁). For example, ductile fat crystals exhibited a steady decrease in ${G}_1^{\prime }$ and ${G}_1^{\prime \prime }$ at around 1000 Pa, whereas brittle fat crystals showed a gradual decrease at 1500 Pa followed by a sudden drop and a backward bending at 4000 Pa. These significantly different responses were also captured through plotting the stress amplitude (τ₁) versus strain amplitude. Ductile fat showed a maximum stress of 4000 Pa, whereas brittle fat crystals had a maximum stress of 4900 Pa. After reaching the maximum stress, ductile fat crystals displayed a plateau in stress values. However, an instantaneous drop in stress was observed for brittle fats. These data were reported to be consistent with the qualitative behavior provided by third-order harmonic Fourier data (Macias-Rodriguez et al. 2018).

Another LAOS analysis method uses the profile of ${G}_1^{\prime }$ and ${G}_1^{\prime \prime }$ as a function of input strain amplitude to provide information related to the microstructure of complex fluids. Four different types of nonlinear viscoelastic behavior are defined as Type I, or strain thinning; Type II, or strain hardening; Type III, or weak strain overshoot; and Type IV, or strong strain overshoot (Hyun et al. 2002). Studies conducted on food materials showed that fresh gels of gelatin-alginate (1:1 concentration ratio) exhibited Type IV behavior, in which both G′ and G″ increased to a maximum and then decreased in the nonlinear viscoelastic region. Layer gels, however, showed Type III behavior, with steadily decreasing G′ values and increasing and then decreasing (overshoot) G″ values (Goudoulas and Germann 2017). Crosslinked tapioca starch with added guar gum and xanthan gum showed Type III behavior, while gels made with crosslinked tapioca starch and either guar gum or xanthan gum showed Type I behavior, with both G′ and G″ values decreasing continuously in the nonlinear viscoelastic region (Fuongfuchat et al. 2012). Fat crystals have also been shown to exhibit Type III behavior (Macias-Rodriguez et al. 2018).

Several studies on food products have linked LAOS data to applications that impose large deformations on materials. Dough development throughout farinograph mixing was monitored for wheat dough samples through LAOS tests (Yazar et al. 2016a, b). ${G}_L^{\prime }$ and ${G}_{\mathrm{M}}^{\prime }$ values for gluten-free dough samples were correlated to loaf volume of the resulting bread samples (Yazar et al. 2017a). This correlation generated a better understanding of how final product quality was impacted by both the deformations dough samples undergo during fermentation and baking and the capacity of the dough to endure these deformations. LAOS behavior has also been linked to tribological parameters of concentrated emulsions with added fish gelatin–gum Arabic mixture (Anvari and Joyner (Melito) 2018) and Alyssum homolocarpum seed gum (Anvari et al. 2018). The results of both LAOS and tribological tests were attributed to the different molecular structure features of the samples, as well as how those molecular structures were disturbed during testing. Determining relationships between food microstructure and LAOS and other rheological data is important, as it can provide information about food mechanical and friction properties that may contribute to their sensory behaviors.

4 Conclusions

LAOS parameters can be utilized to capture the unique nonlinear behaviors of semisolid foods such as yogurt, wheat flour dough, gluten, mayonnaise, and tomato paste. The emergence of nonlinearities are observed by the change in the shape of the periodic stress response to a sinusoidal strain input, typically displayed as a Lissajous-Bowditch plot. These plots can display the total stress versus strain, the elastic stress versus strain, or the viscous stress versus strain rate. In addition, nonlinear viscoelastic information can be determined from the intracycle strain moduli (${G}_L^{\prime }$, ${G}_M^{\prime }$) and instantaneous viscosities (${\eta}_L^{\prime }$, ${\eta}_M^{\prime }$) (Ewoldt et al. 2008). Moreover, G′ and G″ for the whole strain range help determine the overall type of nonlinear viscoelastic behavior exhibited by a given semisolid food (Hyun et al. 2002), while Chebyshev coefficients (particularly e₃/e₁ and v₃/v₁, since the signs of the third-order harmonics indicate the driving cause of the deviation from linearity) provide insights regarding the dominating intracycle strain-stiffening or -softening and shear-thickening or -thinning behavior (Ewoldt and Bharadwaj 2013). This information can be coupled with the information obtained through the Lissaous-Bowditch curves and S and T parameters. The LAOS technique is therefore a useful tool that can mimic the large deformations these food products are exposed to during manufacturing and oral processing. A wide range of examples for utilizing LAOS parameters on different semisolid foods revealed that the LAOS technique is able to probe the differences occurring in material nonlinearities due to production process parameters, oral processing, and formulation variation that cannot be fully probed by empirical rheological testing methods or fundamental SAOS tests.