Abstract
We provide generic and black box transformations from any chosen plaintext secure Attribute-Based Encryption (ABE) or One-sided Predicate Encryption system into a chosen ciphertext secure system. Our transformation requires only the IND-CPA security of the original ABE scheme coupled with a pseudorandom generator (PRG) with a special security property.
In particular, we consider a PRG with an n bit input \(s \in \{0,1\}^n\) and \(n \cdot \ell \) bit output \(y_1, \ldots , y_n\) where each \(y_i\) is an \(\ell \) bit string. Then for a randomly chosen s the following two distributions should be computationally indistinguishable. In the first distribution \(r_{s_i, i} = y_i\) and \(r_{\bar{s}_i, i}\) is chosen randomly for \(i \in [n]\). In the second distribution all \(r_{b, i}\) are chosen randomly for \(i \in [n], b \in \{0,1\}\).
We show that such PRGs can be built from either the computational Diffie-Hellman assumption (in non-bilinear groups) or the Learning with Errors (LWE) assumption (and potentially other assumptions). Thus, one can transform any IND-CPA secure system into a chosen ciphertext secure one by adding either assumption. (Or by simply assuming an existing PRG is hinting secure.) In addition, our work provides a new approach and perspective for obtaining chosen ciphertext security in the basic case of public key encryption.
B. Waters—Supported by NSF CNS-1908611, CNS-1414082, DARPA SafeWare and Packard Foundation Fellowship.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
1 Introduction
In Attribute-Based Encryption [42] (ABE) every ciphertext \(\mathrm {CT}\) that encrypts a message m is associated with an attribute string x, while each secret, as issued by an authority, will be associated with a predicate function C. A user with a secret key \(\mathsf {sk}\) that is associated with function C will be able to decrypt a ciphertext associated with x and recover the message if and only if \(C(x)=1\). Additionally, security of ABE systems guarantees that an attacker with access to several keys cannot learn the contents of an encrypted message so long as none of them are so authorized.
Since the introduction of Attribute-Based Encryption and early constructions [26] over a decade ago, there have been many advances in the field ranging from supporting expressive functionality [6, 23], to techniques for adaptive security [1, 12, 30, 32, 37, 44, 45], short sized ciphertexts [2], multi-authority [10, 11, 31] and partially hiding attributes [24, 25, 46] to name just a few. In almost all of these cases and in most other papers, the treatment of ABE focused on the chosen plaintext (IND-CPA) definition of ABE. This is despite the fact that chosen ciphertext security [13, 36, 40]—where the attacker can make oracle decryption queries to keys it does not have—is arguably the right definition of security for the same reasons it is the right definition for standard public key cryptography [43]. Likely, most of these works target IND-CPA security since the authors already have their hands full with putting forth new concepts and techniques in manuscripts that often run for many pages. In these circumstances it seems reasonable for such works to initially target chosen plaintext definitions and then for later works to circle back and build toward chosen ciphertext security.
Unfortunately, closing the loop to chosen ciphertext security can be tricky in practice. First, there are a rather large and growing number of ABE constructions. Writing papers to address moving each of these to chosen ciphertext security seems burdensome to authors and program committees alike. One line of work [4, 26, 34, 47] to mediate this problem is to identify features in ABE constructions, which if present mean that CPA security implies chosen ciphertext security. Yamada et al. [47] showed that certain delegability or verifiability properties in ABE systems imply chosen ciphertext security by the Canetti-Halevi-Katz [9] transformation.
Their generality, however, is limited by the need to manually inspect and prove that each construction has such a property. In fact, many schemes might not have these properties. Recent trends for both functionality and proofs techniques might actually work against these properties. For example, an ABE scheme has the verification property roughly if it is possible to inspect a ciphertext and determine if it is well formed and what keys can decrypt it. This property emerged naturally in many of the pairing-based schemes prominent at the time, but is less obvious to prove in LWE-based constructions and actually can run contrary to the predicate encryption goal of hiding an attribute string x from users that cannot decrypt. See for example the one-sided predicate encryption constructions of [24, 25, 46].
If we desire a truly generic transformation to chosen ciphertext security, then there are essentially two pathways available. The first option is to apply some variant of the Fujisaki-Okamoto [20] transformation (first given for transforming from IND-CPA to IND-CCA security in public key encryption). Roughly, the encryption algorithm will encrypt as its message the true message m appended with a random bitstring r using the random coins H(r) where H is a hash function modeled as a random oracle. The CCA-secure decryption algorithm will apply the original decryption algorithm to a ciphertext \(\mathrm {CT}\) and recover \(m'|r'\). Next, it re-encrypts the ciphertext under \(H(r')\) to get a ciphertext \(\mathrm {CT}'\) and outputs the message if \(\mathrm {CT} = \mathrm {CT}'\); otherwise it rejects. The upside of this approach is that the added overhead is fairly low as it just adds one additional call to encryption as part of the decryption routine. On the downside the security analysis of this technique appears intrinsically tied to the random oracle model [3].
The second option is to augment encryption by appending a non-interactive zero knowledge proof [5] that a ciphertext was well formed. This approach has been well studied and explored in the context of standard public key encryption [36] and should translate to the ABE context. Additionally, there are standard model NIZK proof assumptions under factoring and pairing-based and lattice based [38] assumptions.Footnote 1 A drawback of this approach is that applying any generic gate by gate NIZK to an encryption system will be quite expensive in terms of computational overhead—this will be needed for any generic conversion.
1.1 Our Contribution
In this work we provide a black box transformation for chosen ciphertext security of any ABE or one-sided predicate encryption system.Footnote 2
Our transformation requires only the existence of a IND-CPA secure ABE system as well as a pseudorandom generator (PRG) with a special security property which we call the hinting property. This special security property can either be assumed for an “ordinary” (e.g., AES-based) PRG or provably obtained from either the Computational Diffie-Hellman assumption or the Learning with Errors assumption. Our transformation increases ciphertext size by roughly a factor of the security parameter—it requires \(2\,\cdot \,n\) sub-ciphertexts for a parameter n. Additionally, it requires about 2n additional encryptions of the original system for both the new encryption and decryption routines. While this overhead is an increase over the original CPA system and will likely incur more overhead than hand-tailored CCA systems, it is a significant performance improvement over NIZKs that operate gate by gate over the original encryption circuit.
We also wish to emphasize that our transformation applies to ordinary public key encryption as well as ABE. While chosen ciphertext security for PKE has been known for sometime from the CDH and LWE assumptions, we believe that our work provides new insights into the problem and might lead to furthering the understanding of whether IND-CPA security ultimately implies chosen ciphertext security.
Hinting Property for PRGs: Let \(\mathsf {PRG}\) be a function that maps n bits to \((n\,+\,1) \cdot n\) bits (output to be parsed as \(n\,+\,1\) strings, each of length n). Consider the following experiment between a challenger and an adversary. The challenger chooses an n bit string s, computes \(\mathsf {PRG}(s) = z_0 z_1 z_2 \ldots z_n\) (each \(z_i \in \{0,1\}^n\)). Next, it chooses n uniformly random strings \(v_1, v_2, \ldots , v_n\) each from \(\{0,1\}^n\). It then constructs a \(2\times n\) matrix M as follows: if the \(i^{th}\) bit of s is 0, then \(M_{0,i} = z_i, M_{1,i} = v_i\), else \(M_{0,i} = v_i, M_{1,i} = z_i\).Footnote 3 Finally, the challenger either outputs \(z_0\) together with M, or it outputs \(2n+1\) uniformly random strings. A pseudorandom generator is said to satisfy the hinting property if any polynomial time adversary has negligible advantage in this experiment. Note that the seed s is used at two places: first to compute the strings \(z_0, z_1, z_2, \ldots , z_n\), and then to decide where to place each \(z_i\) in the matrix M. Hence, the second piece of information (i.e. the position of \(z_i\) strings serves as an extra hint on the PRG). One could simply assume this property of a particular pseudo random generator. Indeed, this seems rather plausible that ordinary types of PRGs would have it. Alternately, we show how to construct PRGs that provably have this property under either the Computational Diffie-Hellman assumption or the LWE assumption. Our constructions of these PRGs use techniques that closely follow previous works [8, 14,15,16, 22] for a related group of primitives going under a variety of names: Chameleon Encryption, One-Time Signature with Encryption, Batch Encryption, One Way Function with Encryption. We note that while the technical innards for the CDH and LWE realizations of our PRG are similar to the above works, (unlike the above examples) our definition itself does not attach any new functionality requirements to PRG; it simply demands a stronger security property.
Next, we present an overview of our CCA construction. As a warm-up, we will first show how to use any CPA-secure public key encryption (PKE) scheme, together with hinting PRGs to construct a CCA-1 secure PKE scheme. Recall, CCA-1 security is a weaker variant of the CCA security game where the adversary is allowed decryption queries only before sending the challenge messages. After sending the challenge messages, the adversary receives the challenge ciphertext, and must send its guess.
CCA-1 secure PKE from CPA-secure PKE and hinting PRGs. The construction also uses a (standard) pseudorandom generator G with sufficiently long stretch. Let \((\mathsf {Setup}, \mathsf {Enc}, \mathsf {Dec})\) be any CPA secure scheme, and \(H : \{0,1\}^n \rightarrow \{0,1\}^{(n+1)\cdot n}\) a hinting PRG. We require the CPA scheme to have two properties which can be obtained ‘for free’. First, we require that the scheme should have perfect decryption correctness for most public/secret keys. This can be obtained via the transformation of [17]. Next, we require that any ciphertext can be decrypted given the encryption randomness. This is also easily obtained by choosing a random string r during encryption, and appending a one-time pad of the message using r.
The setup of our CCA-1 scheme runs the PKE setup 2n times, obtaining 2n public key/secret key pairs \(\left\{ \mathsf {pk}_{b,i}, \mathsf {sk}_{b,i}\right\} _{i \in [n], b\in \{0,1\}}\). It also chooses a uniformly random tag \(t = t_1 t_2 \ldots t_n\), where each \(t_i\) is a sufficiently long string. The new public key consists of the 2n public keys \(\left\{ \mathsf {pk}_{b,i}\right\} _{i \in [n], b \in \{0,1\}}\) and tag t, while the new secret key includes only of n out of the 2n secret keys, namely \(\left\{ \mathsf {sk}_{0,i}\right\} _{i\in [n]}\) (this secret hiding principle [18] has been used in many CCA constructions, including the initial CCA systems [13, 36]). To encrypt a message m, the encryption algorithm first chooses a seed \(s \leftarrow \{0,1\}^n\) and computes \(H(s) = z_0 z_1 \ldots z_n\). It uses \(z_0\) to mask the message m; that is, it computes \(c= m \oplus z_0\). The remaining ciphertext will contain n ‘signals’ that help the decryption algorithm to recover s bit by bit, which in turn will allow it to compute \(z_0\) and hence unmask \(c\).
The \(i^{th}\) signal (for each \(i\in [n]\)) has three components \(c_{0,i}, c_{1,i}, c_{2,i}\). If the \(i^{th}\) bit of s is 0, then \(c_{0,i}\) is an encryption of a random string \(x_i\) using the public key \(\mathsf {pk}_{0,i}\) and randomness \(z_i\), \(c_{1,i}\) is an encryption of \(0^n\) using \(\mathsf {pk}_{1,i}\) (encrypted using true randomness), and \(c_{2,i}= G(x_i)\). If the \(i^{th}\) bit of s is 1, then \(c_{0,i}\) is an encryption of \(0^n\) using public key \(\mathsf {pk}_{0,i}\) (encrypted using true randomness), \(c_{1,i}\) is an encryption of a random string \(x_i\) using public key \(\mathsf {pk}_{1,i}\) and randomness \(z_i\), and \(c_{2,i}= G(x_i) + t_i\) (recall \(t_i\) is the \(i^{th}\) component in the tag). So half the ciphertexts are encryptions of zero, while the remaining are encryptions of random strings (with blocks of the hinting PRG output being used as randomness), and the positioning of the zero/random encryptions reveals the seed s.
The final ciphertext includes the ‘main’ component \(c\), and n signals \((c_{0,i}, c_{1,i}, c_{2,i})\). A noteworthy point about the ciphertext: first, the components \(\left\{ c_{2,i}\right\} _i\) serve as a perfectly-binding commitment to the seed s.
To decrypt, the decryption algorithm first decrypts each \(c_{0,i}\) (recall the secret key is \(\left\{ \mathsf {sk}_{0,i}\right\} _{i \in [n]}\)) to obtain \(y_1 y_2 \ldots y_n\). It then checks if \(G(y_i) = c_{2,i}\). If so, it guesses that \(s_i = 0\), else it guesses that \(s_i = 1\). With this estimate for s, the decryption algorithm can compute \(H(s) = z_0 z_1 \ldots z_n\) and then compute \(c\oplus z_0\) to learn the message m. While this decryption procedure works correctly, we would like to prevent malicious decryption queries (made during the CCA/CCA-1 experiment), and hence the decryption algorithm needs to enforce additional checks. In particular, the decryption algorithm therefore needs to check that the guess for s is indeed correct. If the \(i^{th}\) bit of s is guessed to be 0, then the decryption algorithm checks that \(c_{0,i}\) is a valid ciphertext - it simply re-encrypts \(y_i\) and checks if this equals \(c_{0,i}\). If the \(i^{th}\) bit of s is guessed to be 1, then the decryption algorithm first recovers the message underlying ciphertext \(c_{1,i}\). Note that \(c_{1,i}\) should be encrypted using randomness \(z_i\), hence using \(z_i\), one can recover message \(\tilde{y}_i\) from \(c_{1,i}\) (using the randomness recovery property of the PKE scheme). It then re-encrypts \(\tilde{y}_i\) and checks if it is equal to \(c_{1,i}\), and also checks that \(c_{2,i}= G(\tilde{y}_i) + t_i\). Finally, if all these checks pass, the decryption algorithm outputs \(z_0 \oplus c\).
To summarize, at a very high level, we build a partial trapdoor where the decryption algorithm will recover some of the coins used for encryption. These are then used to partially re-encrypt the ciphertext and test for validity. Influenced by Garg and Hajiabadi [22], we will prove security not by removing the signals for each bit position, but by adding misinformation that drowns out the original signal. Note that to prove security, we need to remove the information of \(z_0\) (and hence information of s) from two places - first, from the commitment \(\left\{ c_{2,i}\right\} _i\); second, from the positions where the \(z_i\) values are used for encrypting. For the first one, in the proof, we set the challenge tag \(t^*\) such that the signal is ambiguous at each index. More formally, in the challenge ciphertext \(c_{0,i}^*\) is an encryption of \(y_i\), \(c_{1,i}^*\) is encryption of \(\tilde{y}_i\), and \(G(y_i) = G(\tilde{y}_i) + t^*_i\). Replacing the encryptions of zeroes with encryptions of these carefully chosen strings involves a delicate argument, which crucially relies on the perfect correctness of our scheme (see discussion in Sect. 4 for more details).
When this is done for all indices, all information about s will be lost from the message space and we are almost done; however, one loose end remains. Each ciphertext at position \((s_i, i)\) will be encrypted under randomness \(r_i\) which came from running the pseudorandom generator on s; whereas each ciphertext at position \((\bar{s}_i, i)\) will be encrypted under fresh random coins. To complete the proof we need a computational assumption that will allow us to change all the encryption coins to being chosen freshly at random. Here, we use the security of hinting PRGs, and that completes our proof.
CCA Security. To achieve CCA security, we need to make a few tweaks to the above scheme. The setup algorithm also chooses n pairwise independent hash functions \(h_1, h_2, \ldots , h_n\). The encryption algorithm chooses a signing/verification key for a (one-time) signature scheme. Next, instead of using the tag t from the public key, it sets \(t_i = h_i(\mathsf {vk})\) (where \(\mathsf {vk}\) is the verification key). Finally, the encryption algorithm computes a signature on all the ciphertext components, and the final ciphertext consists of all these components together with the signature and the verification key. This idea of using signatures to go from ‘tag-based’ security to CCA security has been used in several previous CCA constructions, starting with the work of [28]. To prove security, we first ensure that none of the decryption queries correspond to the challenge ciphertext’s verification key (this follows from the security of the signature scheme). After this point, the proof follows along the lines of the CCA-1 scheme.
Moving to Attribute Based Encryption/Predicate Encryption - For ABE/PE, the scheme is altered as follows. First, the public key consists of n ABE/PE public keys and n PKE public keys. Let \(\mathsf {pk}_{0,i}\) denote the \(i^{th}\) ABE/PE public key, and \(\mathsf {pk}_{1,i}\) the \(i^{th}\) PKE public key. The master secret key only consists of the n ABE/PE master secret keys. The main difference in the encryption algorithm is that the ciphertexts \(c_{0,i}\) are now ABE/PE ciphertexts. Suppose we want to encrypt message m for attribute x. Then m is masked using \(z_0\) as before, and the \(c_{0,i}\) component is an encryption of zero/random message for attribute x using public key \(\mathsf {pk}_{0,i}\) and randomness being truly random/\(z_i\), depending on the \(i^{th}\) bit of seed s.
We conclude by remarking that while this work focuses on Attribute-Based Encryption and One-sided Predicate Encryption, we believe our transformation could apply to other specialized forms of encryption. For example, we believe it should immediately translate to any secure broadcast encryption [19] system. As another example, we believe our technique should also apply to ABE systems that are IND-CPA secure under a bounded number of key generation queries. Our technique, however, does not appear to apply to standard predicate encryption as defined in [7, 27] (notions very similar to full blown functional encryption). The core issue is that to test the validity of a ciphertext our decryption algorithm needs to obtain the attribute string x to perform re-encryption. In one-sided predicate encryption, if a user has a secret key for C and \(C(x)=1\) we essentially give up on hiding x and allow this to be recovered; whereas for full hiding we might want to still hide information about x even if \(C(x)=1\).
Finally, we note that even if we cast the notions of ABE aside our work might provide another path to exploring the longstanding open problem of achieving chosen ciphertext security from chosen plaintext security. The primary barrier is in how to achieve a PRG with this hinting security.
1.2 Constructions of Hinting PRGs
Our realizations of hinting PRG largely follow in line with recent works [8, 14,15,16, 22]. In particular, our CDH realization follows closely to [15] and our LWE realization to [8, 16]. It may have been possible to build our hinting PRG from one of the previous abstractions, but we chose to provide direct number theoretic realizations. We believe that one important distinction is that our hinting PRG is simply a PRG with stronger security properties; unlike the above abstractions our definition in of itself does not ask for expanded functionality. An intriguing open question is if this can be leveraged to obtain further instances with provable security. Below, we provide a high level description of our hinting PRG construction based on the DDH assumption.
In this work, we construct hinting PRG with setup. The setup algorithm outputs public parameters, which are then used for evaluating the PRG. For simplicity, here we assume the PRG maps n bits to \(n^2\) bits. Let p be an n bit prime, and \(\mathcal {G}\) a group of order p. The setup algorithm first chooses 2n random group elements \(\left\{ g_{i,b}\right\} \) and 2n random integers \(\left\{ \rho _{i,b}\right\} \) from \(\mathbb {Z}_p\). Next, it uses these group elements and integers to publish 2n tables, and each table has 2n entries. Let us consider the \((i,b)-th\) table. In this table, the \((i, \overline{b})-th\) entry is \(\perp \); and for all \((k,\beta ) \ne (i,\overline{b})\), the (k, b)th entry is \(g_{k,\beta }^{\rho _{i,b}}\).
Let us now consider the evaluation procedure. The PRG evaluation on input \(x = x_1 x_2 \ldots x_n\) wil output n group elements, where the \(i^{th}\) one is derived from the \((i, x_i)th\) table as follows - compute product of elements (in table \((i, x_i)\)) at position \((k, x_k)\). More formally, the \(i^{th}\) group element in the output is \(\left( \prod g_{k, x_k} \right) ^{\rho _{i,b}}\).
To prove security, we use the DDH assumption to argue that given all the 2n tables in the public parameters, it will still be hard to learn \(g_{i,b}^{\rho _{i,\overline{b}}}\), for all (i, b). There are a few subtleties though; in particular, we also need a ‘lossiness’ argument for the proof to work. We refer the reader to the full version of our paper.
1.3 Additional Comparisons
It is instructive to take a closer look at how our work relates to and builds upon the trapdoor function construction of Garg and Hajiabadi [22]. Briefly and in our terminology, Garg and Hajiabadi gave a framework where the evaluation algorithm chooses an input \(s \in \{0,1\}^n\) and use this to first produces a value y that produces part of the output. Next, for each position \((s_i, i)\) the evaluation algorithm produces a signal using s and the public parameters of the TDF using a primitive called “one way function with encryption”. At the opposite position \((\bar{s}_i, i)\) the evaluation algorithm outputs a random string \(r_i\) of sufficient length. With very high probability the random string \(z_i\) will not correspond to the valid signal for y at position \((\bar{s}_i, i)\). The inversion algorithm will use knowledge of the TDF secret key plus y to go recover the input s bit by bit. At each position i if a signal is present at (0, i) it records \(s_i=0\) and sets \(s_i=1\) if the signal is at (1, i). If the signal is at both 0 and 1, then recovery fails. One can observe that for almost all choices of public parameters there exist some valid inputs that will cause failure on inversion. To prove security the reduction algorithm at each position change the string \(z_i\) from random to a signal under y. The security properties of the one way function with encryption make this undetectable. Once, this is done the only information about s will be contained in y. Since many choices of s will map to y, inverting to the chosen s at this point will be statistically infeasible.
Our work as described above follows a similar approach in that a seed s is signaled bit by bit. And that a step of proving security is to add misinformation in by adding a counter signal in at positions \((\bar{s}_i, i)\). An important distinction is that in the work of Garg and Hajiabadi the signaling and inversion process is very tightly coupled in the one way function with encryption primitive. One could imagine trying to build an Attribute-Based version of one way function with encryption and then try to yield a CCA encryption from the resulting trapdoor. This runs into two problems. First, it would require a tailored construction for each type of ABE scheme that we want and then we are back to hacking CCA into each type of ABE variant. Second, since the GH scheme allows for ambiguous inputs, it can be difficult for mapping into chosen ciphertext secure schemes. In particular, this issue caused GH to need an adaptive version of one way function with encryption to bridge from TDFs to CCA security and this adaptive version was not realizable from the CDH assumption.
In our work the signaling strategy is decoupled from the recovery of the signals. In particular, the form of the signals comes from our computation of the (non-hinting) PRG, while recovery is realized from simply invoking the ABE decryption algorithm. We also get perfect correctness since a non-signal will be an encryption of the all 0’s string. Also, with high probability our setup algorithm will choose parameters for which it is (information theoretically) impossible to create ambiguous signals. So once the ABE parameters are setup by an honest party (and with overwhelming probability, land in a good spot), there will be no further opportunity to take advantage of conflicting signals by an attacker via a decryption query.
We also believe that it might be interesting to swing some of our techniques back to the trapdoor function regime. For example, consider the GH TDF, but where we added values \(a_1, \ldots , a_n\) to the public parameters. We could modify the evaluation algorithm such that at position i, the algorithm gives the one-way function with encryption output \(e_i\) if \(s_i =0\) and gives \(e_i \oplus a_i\) if \(s_i=1\). This modification would allow us to drop the additional \(z_i\) values from the GH construction and make the output of the TDF shorter. In addition, while there would still be a negligible correctness error, it could be possible to rest this error solely in the choice of public parameters and for a “good” choice of parameters there would be no further error from evaluation. This last claim would require making sure that the \(a_i\) values were sufficiently long relative to y. We believe the techniques from [41] can be used here to achieve CCA security.
Independent Work. Independently, Garg, Gay and Hajiabadi [21] recently built upon the work of [22] to build trapdoors from one way function with encryption that has improved correctness properties. In particular, the base construction of [21] generates parameters that with high probability will allow inversion on all inputs, whereas any parameters generated from the [22] construction will always have inversion failure on some small fraction of inputs. They then build upon using erasure codes and a “smoothness” property to get CCA secure determinstic encryption with shorter ciphertexts. In addition, they show a modification to the Peikert-Waters [39] DDH-based Lossy TDF that gets a better ciphertext rate. The initial direction of getting better correctness in TDFs is similar to our “swinging techniques back” comment above, but otherwise the works pursue separate goals and techniques.
Subsequent Work. Subsequent to our work Kitagawa, Matsuda and Tanaka [29] proposed a variant of our CCA transformation for public key encryption. Their transformation had two significant differences (along with some minor ones) from ours. The first is that they showed how to execute the transformation with using just two public/private key pairs as opposed to the 2n public/private key pairs in our transformation. In our construction setup we generate \((\mathsf {cpa}{.}\mathsf {sk}_{b,i}, \mathsf {cpa}{.}\mathsf {pk}_{b,i}) \leftarrow \mathsf {CPA}{.}\mathsf {Setup}(1^\lambda )\) for each \(b\in \{0,1\}\), \(i \in [n]\). They essentially show that one can replace this with a pair of calls to generate \((\mathsf {cpa}{.}\mathsf {sk}_{b}, \mathsf {cpa}{.}\mathsf {pk}_{b}) \leftarrow \mathsf {CPA}{.}\mathsf {Setup}(1^\lambda )\) for each \(b\in \{0,1\}\) where the ‘i’ subscript can be dropped in the construction and the keys essentially reused. Doing this requires a modified analysis where the hybrids are reordered. One will first change about half of the ciphertext components using IND-CPA security of the PKE scheme. Next, the decryption algorithm will be (undetectably) modified. Finally, IND-CPA security will be invoked a second time to change the other half of the ciphertexts.
The second major difference is that for the final “tie-off” step in the proof they will use a symmetric key encryption scheme with key-dependent message security as opposed to a hinting PRG. Like hinting PRGs these encryption schemes are also realizable from DDH, CDH and LWE, but also contain realizations from the Learning Parity with Noise (LPN) assumption for certain parameters. We remark that these two modifications (shorter keys and using key-dependent message security) appear to be orthogonal and one could choose adopt one without the other.
In other work Lombardi, Quach, Rothblum, Wichs and Wu [33] showed how to adapt our transformation to achieve a single key secure Attribute-Based Encryption scheme with a function hiding property. Suppose that a user has a secret key for a function f in an ABE system. The function hiding property roughly states that an attacker with access to decryption oracle cannot learn any more about what that user’s function f is beyond what must be inherently learnable. The authors show that this property is sufficient for achieving designated verifier non-interactive zero knowledge proofs.
1.4 Toward Bridging Chosen Ciphertext Security in PKE
One classical open problem in cryptography is whether chosen plaintext security implies chosen ciphertext security in standard public key encryption. From a cursory glance one can see that it is easy to swap out the ABE system from our construction for a plain old public key encryption system and the same proof will go through—this time for obtaining chosen ciphertext secure public key encryption. Thus the “only” barrier for moving from IND-CPA to IND-CCA security is in the hinting PRG.
An interesting open question is just how strong this barrier is. From our viewpoint, the hinting security is something that most natural PRGs would likely have. In trying to understand whether it or something similar could be built from general assumptions (e.g. PKE or one way functions) it could be useful to first try to build a separation from our hinting PRG and a standard one. Do there exist PRGs that do not meet the security definition of hinting PRG?
As a first stab at the problem, one might consider PRGs where there is an initial trusted setup algorithm that produces a set of public parameters, which are then used for every subsequent evaluation. In this setting one could imagine a counterexample where the public parameters produced by the setup algorithm include an obfuscated program which will assist in breaking the hinting security, but not be helpful enough to break standard security. Using obfuscation in a similar manner has been useful for achieving other separation results. If we consider PRGs that do not allow for such setup, the task appears to be more challenging. One could try to embed such an obfuscated program in the first block of the PRG output, but this block would need to still look random for standard PRG security.
However, as it turns out there is a much simpler way to achieve a separation. Consider the case where \(\ell =1\) then the identity function on the seed will be a pseudorandom function for the trivial reason that it does not expand. However, this function will not be hinting secure. To get a separation with expansion one can consider a PRG G that takes as input an n bit seed s and outputs \(z_0 z_1 \ldots z_n \ldots z_{2n}\). Now, let \(G'\) be a function that takes 2n bits as input, and maps \((s', s)\) to \((z_0, s'_1 z_1, \ldots , s'_n z_n, z_{n+1}, \ldots , z_{2n}\). One can check that \(G'\) is a secure PRG, but is not a hinting PRG.
Altogether we believe that our work opens up a new avenue for exploring the connection of chosen plaintext and ciphertext security.
2 One-Sided Predicate Encryption
A predicate encryption (PE) scheme \(\mathcal {PE}\), for set of attribute spaces \(\mathcal {X}= \left\{ {\mathcal {X}}_\lambda \right\} _{\lambda \in \mathbb {N}}\), predicate classes \(\mathcal {C}= \left\{ {\mathcal {C}}_\lambda \right\} _{\lambda \in \mathbb {N}}\) and message spaces \(\mathcal {M}= \left\{ {\mathcal {M}}_\lambda \right\} _{\lambda \in \mathbb {N}}\), consists of four polytime algorithms \((\mathsf {Setup}, \mathsf {Enc}, \mathsf {KeyGen}, \mathsf {Dec})\) with the following syntax.
-
\(\mathsf {Setup}(1^{\lambda }) \rightarrow (\mathsf {pp}, \mathsf {msk})\). The setup algorithm takes as input the security parameter \(\lambda \) and a description of attribute space \(\mathcal {X}_\lambda \), predicate class \(\mathcal {C}_\lambda \) and message space \(\mathcal {M}_\lambda \), and outputs the public parameters \(\mathsf {pp}\) and the master secret key \(\mathsf {msk}\).
-
\(\mathsf {Enc}(\mathsf {pp}, m, x) \rightarrow \mathsf {ct}\). The encryption algorithm takes as input public parameters \(\mathsf {pp}\), a message \(m \in \mathcal {M}_{\lambda }\) and an attribute \(x \in \mathcal {X}_\lambda \). It outputs a ciphertext \(\mathsf {ct}\).
-
\(\mathsf {KeyGen}(\mathsf {msk}, C) \rightarrow \mathsf {sk}_C\). The key generation algorithm takes as input master secret key \(\mathsf {msk}\) and a predicate \(C \in \mathcal {C}_\lambda \). It outputs a secret key \(\mathsf {sk}_C\).
-
\(\mathsf {Dec}(\mathsf {sk}_C, \mathsf {ct}) \rightarrow m \text { or} \perp \). The decryption algorithm takes as input a secret key \(\mathsf {sk}_C\) and a ciphertext \(\mathsf {ct}\). It outputs either a message \(m \in \mathcal {M}_\lambda \) or a special symbol \(\perp \).
Correctness. A key-policy predicate encryption scheme is said to be correct if for all \(\lambda \in \mathbb {N}\), \((\mathsf {pp}, \mathsf {msk}) \leftarrow \mathsf {Setup}(1^{\lambda })\), for all \(x \in \mathcal {X}_\lambda \), \(C \in \mathcal {C}_\lambda \), \(m \in \mathcal {M}_\lambda \), \(\mathsf {sk}_C \leftarrow \mathsf {KeyGen}(\mathsf {msk}, C)\), \(\mathsf {ct}\leftarrow \mathsf {Enc}(\mathsf {pp}, m, x)\), the following holds
where \(\mathsf {negl}(\cdot )\) are negligible functions, and the probabilities are taken over the random coins used during key generation and encryption procedures.
Recovery from Randomness Property. A key-policy predicate encryption scheme is said to have recovery from randomness property if there is an additional algorithm \(\mathsf {Recover}\) that takes as input public parameters \(\mathsf {pp}\), ciphertext \(\mathsf {ct}\), string r and outputs \(y \in \left( \mathcal {M}_\lambda \times \mathcal {X}_\lambda \right) \cup \{\perp \}\) and satisfies the following condition: for all \(\lambda \in \mathbb {N}\), \((\mathsf {pp}, \mathsf {msk}) \leftarrow \mathsf {Setup}(1^{\lambda })\), for all \(x \in \mathcal {X}_\lambda \), \(m \in \mathcal {M}_\lambda \), \(\mathsf {ct}= \mathsf {Enc}(\mathsf {pp}, m, x; r)\), \(\mathsf {Recover}(\mathsf {pp}, \mathsf {ct}, r) = (m, x)\). If there is no (m, x, r) tuple such that \(\mathsf {ct}= \mathsf {Enc}(\mathsf {pp}, m, x; r)\), then \(\mathsf {Recover}(\mathsf {pp}, \mathsf {ct}, r)\,=\,\perp \).
Security. In this work, we will be considering predicate encryption systems with one-sided security. One can consider both security against chosen plaintext attacks and chosen ciphertext attacks. First, we will present one-sided security against chosen plaintext attacks.
Definition 1
(One-Sided Security against Chosen Plaintext Attacks). A predicate encryption scheme \(\mathcal {PE}= (\mathsf {Setup}, \mathsf {Enc}, \mathsf {KeyGen}, \mathsf {Dec})\) is said to be one-sided secure against chosen plaintext attacks if for every stateful PPT adversary \(\mathcal {A}\), there exists a negligible function \(\mathsf {negl}(\cdot )\), such that the following holds:
where every predicate query C, made by adversary \(\mathcal {A}\) to the \(\mathsf {KeyGen}(\mathsf {msk}, \cdot )\) oracle, must satisfy the condition that \(C(x_0) = C(x_1) = 0\).
The notion of one-sided security against chosen plaintext attacks could alternatively be captured by a simulation based definition [24]. Goyal et al. [25] showed that if a PE scheme satisfies Definition 1, then it also satisfies the simulation based definition of [24].
Next, we present the definition for capturing chosen ciphertext attacks on predicate encryption schemes. Here, we will assume that the key generation algorithm is deterministic.
Definition 2
(One-Sided Security against Chosen Ciphertext Attacks). A predicate encryption scheme \(\mathcal {PE}= (\mathsf {Setup}, \mathsf {Enc}, \mathsf {KeyGen}, \mathsf {Dec})\) with deterministic key generation is said to be one-sided secure against chosen ciphertext attacks if for every stateful PPT adversary \(\mathcal {A}\), there exists a negligible function \(\mathsf {negl}(\cdot )\), such that the following event’s probability is at most \(1/2 + \mathsf {negl}(\lambda )\):
-
the oracle \(\mathcal {O}_{\mathrm {Dec}}(\mathsf {msk}, \cdot , \cdot )\) takes as input a ciphertext \(\mathsf {ct}\) and a circuit C. It computes \(\mathsf {sk}_C = \mathsf {KeyGen}(\mathsf {msk}, C)\) and outputs \(\mathsf {Dec}(\mathsf {sk}_C, \mathsf {ct})\).
-
every predicate query C, made by adversary \(\mathcal {A}\) to the \(\mathsf {KeyGen}(\mathsf {msk}, \cdot )\) oracle, must satisfy the condition that \(C(x_0) = C(x_1) = 0\).
-
every post-challenge query \((C, \mathsf {ct})\) made by the adversary \(\mathcal {A}\) to \(\mathcal {O}_{\mathrm {Dec}}\) must satisfy the condition that either \(\mathsf {ct}\ne \mathsf {ct}^*\) or if \(\mathsf {ct}= \mathsf {ct}^*\), then \(C(x_0) = C(x_1) = 0\).
Remark 1
Note that the above definition addresses chosen ciphertext attacks against systems with deterministic key generation. An analogous definition for general schemes (that is, with randomized key generation) would involve maintaining key handles and allowing the adversary to choose the key to be used for the decryption queries. We choose the simpler definition since any scheme’s key generation can be made deterministic by using a pseudorandom function. In particular, the setup algorithm chooses a PRF key K which is included as part of the master secret key. To derive a key for circuit C, the algorithm first computes \(r=\mathrm {PRF}(K, C)\) and then uses r as randomness for the randomized key generation algorithm.
2.1 PE Schemes with ‘Recovery from Randomness’ Property
Any PE scheme satisfying one-sided CPA security can be transformed into another PE scheme that is also one-sided CPA secure, and has the ‘recovery from randomness’ property. The encryption algorithm simply uses part of the randomness to compute a symmetric key encryption of the message and attribute, with part of the randomness as the encryption key.
More formally, let \(E = (\mathsf {Setup}, \mathsf {Enc}, \mathsf {KeyGen}, \mathsf {Dec})\) be a PE scheme that satisfies one-sided CPA security (see Definition 1), and let \((\mathsf {SKE{.}Setup}, \mathsf {SKE{.}Enc}, \mathsf {SKE{.}Dec})\) be a symmetric key CPA secure encryption scheme. consider the following scheme \(E' = (\mathsf {Setup}', \mathsf {Enc}', \mathsf {KeyGen}', \mathsf {Dec}', \mathsf {Recover})\), where \(\mathsf {Setup}' = \mathsf {Setup}\) and \(\mathsf {KeyGen}' = \mathsf {KeyGen}\).
-
\(\mathsf {Enc}'(\mathsf {pk}, m, x)\): The encryption algorithm first samples three random strings \(r_1, r_2, r_3\). It computes \(\mathsf {ct}_1 = \mathsf {Enc}(\mathsf {pk}, m, x; r_1)\). Next, it computes \(\mathsf {ske{.}sk}= \mathsf {SKE{.}Setup}(1^\lambda ; r_2)\). Finally, it computes \(\mathsf {ct}_2 = \mathsf {SKE{.}Enc}(\mathsf {ske{.}sk}\), (m, x); \(r_3)\) and outputs \((\mathsf {ct}_1, \mathsf {ct}_2)\).
-
\(\mathsf {Dec}'(\mathsf {sk}, (\mathsf {ct}_1, \mathsf {ct}_2))\): The decryption algorithm simply decrypts \(\mathsf {ct}_1\) using \(\mathsf {sk}\), and ignores \(\mathsf {ct}_2\). It outputs \(\mathsf {Dec}(\mathsf {sk}, \mathsf {ct}_1)\).
-
\(\mathsf {Recover}((\mathsf {ct}_1, \mathsf {ct}_2), r = (r_1, r_2, r_3))\): The recovery algorithm first computes \(\mathsf {ske{.}sk}= \mathsf {SKE{.}Setup}(1^\lambda ; r_2)\). It outputs \(y \leftarrow \mathsf {SKE{.}Dec}(\mathsf {ske{.}sk}, \mathsf {ct}_2)\).
Assuming the symmetric key encryption scheme satisfies perfect correctness, this PE scheme has perfect recovery from randomness property. To argue CPA security, we can first use the security of the SKE scheme to switch \(\mathsf {ct}_2\) to an encryption of \(0^{|m| + |x|}\). Then, we can use the one-sided CPA security.
3 Hinting PRGs
A hinting PRG scheme is a PRG with a stronger security guarantee than standard PRGs. A hinting PRG takes n bits as input, and outputs \(n\cdot \ell \) output bits. In this security game, the challenger outputs 2n strings, each of \(\ell \) bits. In one scenario, all these 2n strings are uniformly random. In the other case, half the strings are obtained from the PRG evaluation, and the remaining half are uniformly random. Moreover, these 2n strings are output as a \(2\times n\) matrix, where in the \(i^{th}\) column, the top entry is pseudorandom if the \(i^{th}\) bit of the seed is 0, else the bottom entry is pseudorandom. As a result, these 2n strings give a ‘hint’ about the seed, and hence this property is stronger than regular PRGs. Note, if this hint is removed and the top entries in each column were pseudorandom (and the rest uniformly random), then this can be achieved using regular PRGs.
Below, we define this primitive formally. The informal description above had two simplifications. First, the definition below considers PRGs with setup (although one can analogously define such a primitive without setup). Second, we assume the PRG outputs \((n+1)\cdot \ell \) bits, where the first \(\ell \) bits do not contain any extra hint about the seed. Finally, for our CCA application, we introduce some notation in order to represent the \(n+1\) blocks of the PRG output. Instead of describing the PRG as a function that outputs \((n+1)\cdot \ell \) bits, we have an evaluation algorithm that takes as input an index \(i \in \left\{ 0, 1, \ldots , n\right\} \), and outputs the \(i^{th}\) block of the PRG output.
Let \(n(\cdot , \cdot )\) be a polynomial. A n-hinting PRG scheme consists of two PPT algorithms \(\mathsf {Setup}, \mathsf {Eval}\) with the following syntax.
-
\(\mathsf {Setup}(1^\lambda , 1^\ell )\): The setup algorithm takes as input the security parameter \(\lambda \), and length parameter \(\ell \), and outputs public parameters \(\mathsf {pp}\) and input length \(n = n(\lambda , \ell )\).
-
\(\mathsf {Eval}\left( \mathsf {pp}, s \in \{0,1\}^{n}, i \in [n] \cup \{0\} \right) \): The evaluation algorithm takes as input the public parameters \(\mathsf {pp}\), an n bit string s, an index \(i \in [n] \cup \{0\}\) and outputs an \(\ell \) bit string y.
Definition 3
A hinting PRG scheme \((\mathsf {Setup}, \mathsf {Eval})\) is said to be secure if for any PPT adversary \(\mathcal {A}\), polynomial \(\ell (\cdot )\) there exists a negligible function \(\mathsf {negl}(\cdot )\) such that for all \(\lambda \in \mathbb {N}\), the following event’s probability is at most \(1/2 + \mathsf {negl}(\lambda )\):
4 CCA Secure Public Key Encryption Scheme
Let \(\mathsf {PKE}_{\mathsf {CPA}}= (\mathsf {CPA}{.}\mathsf {Setup}\), \(\mathsf {CPA}{.}\mathsf {Enc}\), \(\mathsf {CPA}{.}\mathsf {Dec})\) be a  secure public key encryption scheme with randomness-decryptable ciphertexts and perfect decryption correctness, \(\mathsf {S}= (\mathsf {ss}{.}\mathsf {Setup}, \mathsf {ss}{.}\mathsf {Sign}, \mathsf {ss}{.}\mathsf {Verify})\) a strongly unforgeable one time signature scheme and \(\mathsf {HPRG}= (\mathsf {HPRG}{.}\mathsf {Setup}, \mathsf {HPRG}{.}\mathsf {Eval})\) a hinting PRG scheme. We will assume that our encryption scheme has message space \(\{0,1\}^{\lambda + 1}\). Let \(\ell _{\mathsf {PKE}}(\cdot )\) be a polynomial representing the number of bits of randomness used by \(\mathsf {CPA}{.}\mathsf {Enc}\), and \(\ell _{\mathsf {vk}}(\cdot )\) the size of verification keys output by \(\mathsf {ss}{.}\mathsf {Setup}\). For simplicity of notation, we will assume \(\ell (\cdot ) = \ell _{\mathsf {PKE}}(\cdot )\), \(\ell _{\mathrm {out}}(\lambda ) = \ell _{\mathsf {vk}}(\lambda ) + 3\lambda \) and \(\mathsf {PRG}_\lambda : \{0,1\}^{\lambda } \rightarrow \{0,1\}^{\ell _{\mathrm {out}}(\lambda )}\) a family of secure pseudorandom generators.
secure public key encryption scheme with randomness-decryptable ciphertexts and perfect decryption correctness, \(\mathsf {S}= (\mathsf {ss}{.}\mathsf {Setup}, \mathsf {ss}{.}\mathsf {Sign}, \mathsf {ss}{.}\mathsf {Verify})\) a strongly unforgeable one time signature scheme and \(\mathsf {HPRG}= (\mathsf {HPRG}{.}\mathsf {Setup}, \mathsf {HPRG}{.}\mathsf {Eval})\) a hinting PRG scheme. We will assume that our encryption scheme has message space \(\{0,1\}^{\lambda + 1}\). Let \(\ell _{\mathsf {PKE}}(\cdot )\) be a polynomial representing the number of bits of randomness used by \(\mathsf {CPA}{.}\mathsf {Enc}\), and \(\ell _{\mathsf {vk}}(\cdot )\) the size of verification keys output by \(\mathsf {ss}{.}\mathsf {Setup}\). For simplicity of notation, we will assume \(\ell (\cdot ) = \ell _{\mathsf {PKE}}(\cdot )\), \(\ell _{\mathrm {out}}(\lambda ) = \ell _{\mathsf {vk}}(\lambda ) + 3\lambda \) and \(\mathsf {PRG}_\lambda : \{0,1\}^{\lambda } \rightarrow \{0,1\}^{\ell _{\mathrm {out}}(\lambda )}\) a family of secure pseudorandom generators.
We will now describe our \(\mathsf {CCA}\) secure public key encryption scheme \(\mathsf {PKE}_{\mathsf {CCA}}\) = (\(\mathsf {CCA}{.}\mathsf {Setup}\), \(\mathsf {CCA}{.}\mathsf {Enc}\), \(\mathsf {CCA}{.}\mathsf {Dec}\)) with message space \(\mathcal {M}_\lambda = \{0,1\}^{\ell (\lambda )}\). For simplicity of notation, we will skip the dependence of \(\ell \) and \(\ell _{\mathrm {out}}\) on \(\lambda \).
-
\(\mathsf {CCA}{.}\mathsf {Setup}(1^{\lambda })\): The setup algorithm performs the following steps.
-
1.
It chooses \((\mathsf {HPRG}{.}\mathsf {pp}, 1^{n}) \leftarrow \mathsf {HPRG}{.}\mathsf {Setup}(1^{\lambda }, 1^{\ell })\).
-
2.
It chooses 2\(n\) different \(\mathsf {PKE}_{\mathsf {CPA}}\) keys. Let \((\mathsf {cpa}{.}\mathsf {sk}_{b,i}, \mathsf {cpa}{.}\mathsf {pk}_{b,i}) \leftarrow \mathsf {CPA}{.}\mathsf {Setup}(1^\lambda )\) for each \(b\in \{0,1\}\), \(i \in [n]\).
-
3.
It then chooses \(a_i \leftarrow \{0,1\}^{\ell _{\mathrm {out}}}\) for each \(i \in [n]\) and \(B\leftarrow \{0,1\}^{\ell _{\mathrm {out}}}\).
-
4.
It sets \(\mathsf {cca}{.}\mathsf {pk}\) = \(\left( \mathsf {HPRG}{.}\mathsf {pp}, B, \left( a_i, \mathsf {cpa}{.}\mathsf {pk}_{b,i} \right) _{b \in \{0,1\}, i \in [n]} \right) \) and \(\mathsf {cca}{.}\mathsf {sk}= \left( \mathsf {cpa}{.}\mathsf {sk}_{0,i} \right) _{i\in [n]}\).
-
1.
-
\(\mathsf {CCA}{.}\mathsf {Enc}(\mathsf {cca}{.}\mathsf {pk}, m, x)\): Let \(\mathsf {cca}{.}\mathsf {pk}\) = \(\left( \mathsf {HPRG}{.}\mathsf {pp}, B, \left( a_i, \mathsf {cpa}{.}\mathsf {pk}_{b,i} \right) _{b\in \{0,1\}, i \in [n]} \right) \). The encryption algorithm does the following:
-
1.
It first chooses \(s \leftarrow \{0,1\}^{n}\). It sets \(c= \mathsf {HPRG}{.}\mathsf {Eval}(\mathsf {HPRG}{.}\mathsf {pp}, s, 0) \oplus m\).
-
2.
Next, it chooses signature keys \((\mathsf {ss}{.}\mathsf {sk}, \mathsf {ss}{.}\mathsf {vk}) \leftarrow \mathsf {ss}{.}\mathsf {Setup}(1^\lambda )\).
-
3.
For each \(i \in [n]\), it chooses \(v_i \leftarrow \{0,1\}^{\lambda }\) and \(r_i \leftarrow \{0,1\}^\ell \), sets \(\widetilde{r_i}= \mathsf {HPRG}{.}\mathsf {Eval}(\mathsf {HPRG}{.}\mathsf {pp}, s, i)\).
-
4.
Next, for each \(i \in [n]\), it does the following:
-
If \(s_i = 0\), it sets \(c_{0,i}= \mathsf {CPA}{.}\mathsf {Enc}(\mathsf {cpa}{.}\mathsf {pk}_{0,i}, 1|v_i; \widetilde{r_i})\), \(c_{1,i}= \mathsf {CPA}{.}\mathsf {Enc}(\mathsf {cpa}{.}\mathsf {pk}_{1,i}, 0^{\lambda +1}; r_i)\) and \(c_{2,i}= \mathsf {PRG}(v_i)\).
-
If \(s_i = 1\), it sets \(c_{0,i}= \mathsf {CPA}{.}\mathsf {Enc}(\mathsf {cpa}{.}\mathsf {pk}_{0,i}, 0^{\lambda +1}; r_i)\), \(c_{1,i}= \mathsf {CPA}{.}\mathsf {Enc}(\mathsf {cpa}{.}\mathsf {pk}_{1,i}, 1|v_i; \widetilde{r_i})\) and \(c_{2,i}= \mathsf {PRG}(v_i) + a_i + B\cdot \mathsf {ss}{.}\mathsf {vk}\).Footnote 4
-
-
5.
Finally, it sets \(M = \left( c, \left( c_{0,i}, c_{1,i}, c_{2,i} \right) _{i \in [n]} \right) \), computes \(\sigma \leftarrow \mathsf {ss}{.}\mathsf {Sign}(\mathsf {ss}{.}\mathsf {sk}, M)\) and outputs \(\left( \mathsf {ss}{.}\mathsf {vk}, M, \sigma \right) \) as the ciphertext.
-
1.
-
\(\mathsf {CCA}{.}\mathsf {Dec}(\mathsf {cca}{.}\mathsf {sk}, \mathsf {cca}{.}\mathsf {pk}, \mathsf {cca}{.}\mathsf {ct})\): Let the ciphertext \(\mathsf {cca}{.}\mathsf {ct}\) be parsed as \(\left( \mathsf {ss}{.}\mathsf {vk}, M=\left( c, \left( c_{0,i},c_{1,i},c_{2,i} \right) _{i \in [n]} \right) , \sigma \right) \) and \(\mathsf {cca}{.}\mathsf {sk}\) = \(\left( \left( \mathsf {cpa}{.}\mathsf {sk}_{0,i} \right) _{i \in [n]} \right) \). The decryption algorithm does the following:
-
1.
It first verifies the signature \(\sigma \). It checks if \(\mathsf {ss}{.}\mathsf {Verify}(\mathsf {ss}{.}\mathsf {vk}, M, \sigma ) = 1\), else it outputs \(\perp \).
-
2.
Next, the decryption algorithm computes
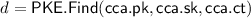 (where
(where  is defined in Fig. 1), and outputs \(\mathsf {PKE}{.}\mathsf {Check}(\mathsf {cca}{.}\mathsf {pk}\), \(\mathsf {cca}{.}\mathsf {ct}\), d) (where \(\mathsf {PKE}{.}\mathsf {Check}\) is defined in Fig. 2).
is defined in Fig. 1), and outputs \(\mathsf {PKE}{.}\mathsf {Check}(\mathsf {cca}{.}\mathsf {pk}\), \(\mathsf {cca}{.}\mathsf {ct}\), d) (where \(\mathsf {PKE}{.}\mathsf {Check}\) is defined in Fig. 2).
-
1.
4.1 Discussion
We will now make a few observations about our construction and then proceed to give a brief overview our proof that appears in the next subsection.
First, for each \(i \in [n]\) if \(s_i=0\) the encryption algorithm will choose a random \(v_i\) and ‘signal’Footnote 5 that this bit is a 0 by encrypting \(1 | v_i\) to the position (0, i) and giving \(c_{2,i}= \mathsf {PRG}(v_i)\) in the clear. In the opposite position of (1, i) it will encrypt the all 0’s string. Likewise, if \(s_i=1\) it will signal a 1 by encrypting \(1 | v_i\) to the position (1, i) and giving \(c_{2,i}= \mathsf {PRG}(v_i) + a_i + B\cdot \mathsf {ss}{.}\mathsf {vk}\) in the clear. With all but negligible probability it is impossible to signal both 0 and 1 simultaneously for an index i. This follows from the fact that \(a_i\) is chosen randomly and that the space of verification keys is much smaller than \(2^{\ell _{\mathrm {out}}(\lambda )}\). We observe that this argument has some flavor of Naor’s bit commitment scheme [35].
Second, we observe that even though one is supposed to encrypt the all 0’s string to position \((\bar{s}_i, i)\) the  routine will not immediately quit if discovers something else. Instead it simply sets \(d_i=0\) if decryption outputs \(1|v_i\) and \(c_{2,i}=\mathsf {PRG}(v_i)\); otherwise it sets \(d_i=1\). Thus, the decryption routine may refrain from immediately aborting even though when it “knows” the ciphertext was not formed entirely correctly. This will be critical to a proof step.
routine will not immediately quit if discovers something else. Instead it simply sets \(d_i=0\) if decryption outputs \(1|v_i\) and \(c_{2,i}=\mathsf {PRG}(v_i)\); otherwise it sets \(d_i=1\). Thus, the decryption routine may refrain from immediately aborting even though when it “knows” the ciphertext was not formed entirely correctly. This will be critical to a proof step.
Our proof of security will be organized as a sequence of security games which we show to be indistinguishable. In the first proof step we apply a standard argument using strongly unforgeable signatures to change the decryption oracle to reject all ciphertexts corresponding to \(\mathsf {ss}{.}\mathsf {vk}^{*}\) where \(\mathsf {ss}{.}\mathsf {vk}^{*}\) is the verification key used by the challenge ciphertext.
Next, for each i we choose the public parameter values \(a_i\) such that it is possible for one to signal both 0 and 1 at index i, but that this ambiguity is only possible for a ciphertext corresponding to \(\mathsf {ss}{.}\mathsf {vk}^{*}\). To do this it chooses uniformly random \(w_i \leftarrow \{0,1\}^{\lambda }\), and sets \(a_i = \mathsf {PRG}(v^{*}_i) -\mathsf {PRG}(w_i) - \mathsf {ss}{.}\mathsf {vk}^{*}\cdot B\) if \(s^{*}_i = 0\), else \(a_i = \mathsf {PRG}(w_i) - \mathsf {PRG}(v^{*}_i) -\mathsf {ss}{.}\mathsf {vk}^{*}\cdot B\). This change can be shown to be undetectable by a standard pseudorandom generator argument. The effect of this change is that it allows the possibility of ambiguous signaling at both 0 and 1 in the challenge ciphertext. However, for all possible decryption queries where \(\mathsf {ss}{.}\mathsf {vk}\ne \mathsf {ss}{.}\mathsf {vk}^{*}\) this remains impossible.
Our next goal will be to use the IND-CPA security of the underlying PKE scheme to introduce signals on the opposite path \(\overline{s^{*}}\). To do this, however, for all i where \(s^{*}_i=1\) we must first change the decryption routine to use \(\mathsf {cpa}{.}\mathsf {sk}_{1,i}\) to decrypt the sub-ciphertext at position (1, i) instead of using \(\mathsf {cpa}{.}\mathsf {sk}_{0,i}\) (at position (0, i)). Consider a particular ciphertext query and let \(d_i\) be the bit reported by the original find algorithm on that ciphertext query and \(d'_i\) be the bit reported by a the new decryption procedure on that same ciphertext. We want to argue that if \(d_i \ne d'_i\) then the \(\mathsf {PKE}{.}\mathsf {Check}\) procedure will abort and output \(\bot \) on both encryptions. The first possibility is that \(d_i =0 \) and \(d'_i=1\); however, that should be information theoretically impossible as it would entail signaling both a 0 and 1 for a query with \(\mathsf {ss}{.}\mathsf {vk}\ne \mathsf {ss}{.}\mathsf {vk}^{*}\). The other possibility is that \(d_i =1 \) and \(d'_i=0\); i.e. that there is not a signal present at either side. In this case the first decryption routine will have \(d_i=1\), but then when running \(\mathsf {PKE}{.}\mathsf {Check}\) it will fail to find a signal at position (1, i) and abort. Likewise, the second decryption routine will have \(d'_i=0\), but then fail to find a signal at position (0, i), so both routines will behave identically in this case as well.
Once the oracle decryption is set to follow the seed \(s^{*}\) we can straightforwardly use CPA security to introduce ambiguous signals in the messages for all positions \((\overline{s^{*}}_i, i)\). Once this change is made we can change the oracle decryption routine again. This time it will only decrypt at positions (1, i) for all \(i \in [n]\) and only use \(\mathsf {cpa}{.}\mathsf {sk}_{1,i}\). A similar argument to before can be applied to make this change.
All information about s is gone except to the lingering amount in the random coins used to encrypt. We can immediately apply the hinting PRG to change to a game where these values can be moved to be uniformly at random. At this point the message will be hidden.
4.2 Security Proof
We will now show that the above construction satisfies the CCA security definition. Our proof proceeds via a sequence of hybrids. First, we will describe all hybrids, and then show that the hybrids are computationally indistinguishable.
Hybrids
Hybrid \(H_0\): This corresponds to the original security game.
-
Setup Phase
-
1.
The challenger first chooses \(\left( \mathsf {HPRG}{.}\mathsf {pp}, 1^{n} \right) \leftarrow \mathsf {HPRG}{.}\mathsf {Setup}(1^\lambda , 1^\ell )\).
-
2.
Next it chooses \(2n\) different \(\mathsf {PKE}_{\mathsf {CPA}}\) keys. Let \((\mathsf {cpa}{.}\mathsf {sk}_{b,i}, \mathsf {cpa}{.}\mathsf {pk}_{b,i}) \leftarrow \mathsf {CPA}{.}\mathsf {Setup}(1^\lambda )\) for each \(i \in [n]\), \(b\in \{0,1\}\).
-
3.
The challenger chooses \(s^{*}\leftarrow \{0,1\}^{n}\), \(v^{*}_i \leftarrow \{0,1\}^{\lambda }\) for each \(i \in [n]\), and \((\mathsf {ss}{.}\mathsf {sk}^{*}, \mathsf {ss}{.}\mathsf {vk}^{*}) \leftarrow \mathsf {ss}{.}\mathsf {Setup}(1^{\lambda })\). It sets \(\widetilde{r_i}^{*}= \mathsf {HPRG}{.}\mathsf {Eval}(\mathsf {HPRG}{.}\mathsf {pp}, s^{*}, i)\). (These components will be used during the challenge phase.)
-
4.
It then chooses \(a_i \leftarrow \{0,1\}^{\ell _{\mathrm {out}}}\) for each \(i \in [n]\) and \(B\leftarrow \{0,1\}^{\ell _{\mathrm {out}}}\).
-
5.
It sends \(\mathsf {cca}{.}\mathsf {pk}\) = \(\left( \mathsf {HPRG}{.}\mathsf {pp}, B, \left( a_i, \mathsf {cpa}{.}\mathsf {pk}_{b,i} \right) _{b\in \{0,1\}, i \in [n]} \right) \) to \(\mathcal {A}\), and sets the secret key \(\mathsf {cca}{.}\mathsf {sk}= \left( \mathsf {cpa}{.}\mathsf {sk}_{0,i} \right) _{i\in [n]}\).
-
1.
-
Pre-challenge Query Phase
-
Decryption Queries
-
1.
For each query \(\left( \mathsf {ct}= \left( \mathsf {ss}{.}\mathsf {vk}, M = \left( c, \left( c_{0,i}, c_{1,i}, c_{2,i} \right) _{i} \right) , \sigma \right) \right) \), the challenger first checks the signature \(\sigma \).
-
2.
Next, the challenger first computes
 .
. -
3.
It outputs \(\mathsf {PKE}{.}\mathsf {Check}\left( \mathsf {cca}{.}\mathsf {pk}, \mathsf {cca}{.}\mathsf {ct}, d \right) \).
-
1.
-
-
Challenge Phase
-
1.
The adversary sends two challenge messages \((m^{*}_0, m^{*}_1)\).
-
2.
The challenger chooses a bit \(\beta \in \{0,1\}\).
-
3.
It sets \(c^{*}= \mathsf {HPRG}{.}\mathsf {Eval}(\mathsf {HPRG}{.}\mathsf {pp}, s, 0) \oplus m^{*}_\beta \).
-
4.
It sets \((c_{0,i}^{*}, c_{1,i}^{*}, c_{2,i}^{*})\) as follows.
-
If \(s^{*}_i = 0\), it sets \(c_{0,i}^{*}= \mathsf {CPA}{.}\mathsf {Enc}(\mathsf {cpa}{.}\mathsf {pk}_{0,i}, 1|v^{*}_i; \widetilde{r_i}^{*})\), \(c_{1,i}^{*}\leftarrow \mathsf {CPA}{.}\mathsf {Enc}(\mathsf {cpa}{.}\mathsf {pk}_{1,i}, 0^{\lambda +1})\) and \(c_{2,i}^{*}= \mathsf {PRG}(v^{*}_i)\).
-
If \(s^{*}_i = 1\), it sets \(c_{0,i}^{*}\leftarrow \mathsf {CPA}{.}\mathsf {Enc}(\mathsf {cpa}{.}\mathsf {pk}_{0,i}, 0^{\lambda + 1})\), \(c_{1,i}^{*}= \mathsf {CPA}{.}\mathsf {Enc}(\mathsf {cpa}{.}\mathsf {pk}_{1,i}, 1|v^{*}_i; \widetilde{r_i}^{*})\) and \(c_{2,i}^{*}= \mathsf {PRG}(v^{*}_i) + a_i + B\cdot \mathsf {ss}{.}\mathsf {vk}^{*}\).
-
-
5.
Finally, it computes a signature \(\sigma ^{*}\) on \(M^{*}= \left( c^{*}, \left( c_{0,i}^{*}, c_{1,i}^{*}, c_{2,i}^{*} \right) \right) \) using \(\mathsf {ss}{.}\mathsf {sk}^{*}\) and sends \(\left( \mathsf {ss}{.}\mathsf {vk}^{*}, M^{*}, \sigma ^{*} \right) \) to \(\mathcal {A}\).
-
1.
-
Post-challenge Query Phase
-
Decryption Queries. These are handled as in the pre-challenge phase, with the restriction that all queries \((\mathsf {ct}, C)\) must satisfy that \(\mathsf {ct}\ne \mathsf {ct}^{*}\).
-
-
Finally, the adversary sends its guess \(b\).
Hybrid \(H_1\): This hybrid is similar to the previous one, except that during the decryption queries, the challenger checks if \(\mathsf {ss}{.}\mathsf {vk}= \mathsf {ss}{.}\mathsf {vk}^{*}\). If so, it rejects. ***
Hybrid \(H_2\): In this hybrid, the challenger changes Step 4 of the setup phase. It chooses uniformly random \(w_i \leftarrow \{0,1\}^{\lambda }\), and sets \(a_i = \mathsf {PRG}(v^{*}_i) -\mathsf {PRG}(w_i) - \mathsf {ss}{.}\mathsf {vk}^{*}\cdot B\) if \(s^{*}_i = 0\), else \(a_i = \mathsf {PRG}(w_i) - \mathsf {PRG}(v^{*}_i) -\mathsf {ss}{.}\mathsf {vk}^{*}\cdot B\).
Hybrid \(H_3\): This hybrid is similar to the previous one, except that the challenger modifies the way decryption queries are handled. Instead of using  , the challenger uses
, the challenger uses  (defined in Fig. 3). The
(defined in Fig. 3). The  routine decrypts only the \(c_{0,i}\) values. If decryption works, it guesses \(d_i = 0\), else it guesses \(d_i = 1\). The
routine decrypts only the \(c_{0,i}\) values. If decryption works, it guesses \(d_i = 0\), else it guesses \(d_i = 1\). The  routine decrypts either \(c_{0,i}\) or \(c_{1,i}\), depending on the \(i^{th}\) bit of \(s^{*}\). Note that the \(\mathsf {PKE}{.}\mathsf {Check}\) routine is identical in both experiments.
routine decrypts either \(c_{0,i}\) or \(c_{1,i}\), depending on the \(i^{th}\) bit of \(s^{*}\). Note that the \(\mathsf {PKE}{.}\mathsf {Check}\) routine is identical in both experiments.
Hybrid \(H_4\): In this step, the challenger modifies the challenge ciphertext. For all \(i \in [n]\) such that \(s^{*}_i = 0\), the challenger sets \(c_{1,i}^{*}\leftarrow \mathsf {CPA}{.}\mathsf {Enc}(\mathsf {cpa}{.}\mathsf {pk}_{1,i}, 1|w_i)\).
Hybrid \(H_5\): In this step, the challenger modifies the challenge ciphertext. For all \(i \in [n]\) such that \(s^{*}_i = 1\), the challenger sets \(c_{0,i}^{*}\leftarrow \mathsf {CPA}{.}\mathsf {Enc}(\mathsf {cpa}{.}\mathsf {pk}_{0,i}, 1|w_i)\).Footnote 6
Hybrid \(H_6\): This step is similar to the previous one, except for the decryption queries in the pre-challenge/post-challenge phase. Instead of using  , the challenger uses
, the challenger uses  (defined in Fig. 4).Footnote 7
(defined in Fig. 4).Footnote 7
Hybrid \(H_7\): This hybrid is identical to the previous one, and the only difference here is change of variable names. In particular, we will swap the variable names \(v^{*}_i\) and \(w_i\) if \(s^{*}_i = 1\). This change affects the setup phase (where the \(a_i\) values are set), and the challenge phase (where we set \(c_{0,i}^{*}\) and \(c_{1,i}^{*}\)). Also, we rename the \(\widetilde{r_i}^{*}\) and \(r^{*}_i\) variables to \(r^{*}_{i,0}\) and \(r^{*}_{i,1}\), depending on \(s^{*}_i\). For clarity, we present the entire setup and challenge phase in the full version of our paper.
Hybrid \(H_8\): In this hybrid, the challenger chooses both \(r^{*}_{i,b}\) uniformly at random from \(\{0,1\}^\ell \). It also chooses \(c^{*}\) uniformly at random.
Analysis. Let \(\mathsf {adv}_{\mathcal {A}}^x\) denote the advantage of an adversary \(\mathcal {A}\) in Hybrid \(H_x\).
Lemma 1
Assuming \(\mathsf {ss}\) is a strongly unforgeable one-time signature scheme, for any PPT adversary \(\mathcal {A}\), there exists a negligible function \(\mathsf {negl}(\cdot )\) such that for all \(\lambda \in \mathbb {N}\), \(|\mathsf {adv}_{\mathcal {A}}^0 - \mathsf {adv}_{\mathcal {A}}^1| \le \mathsf {negl}(\lambda )\).
Proof
This proof follows from the security of \(\mathsf {ss}\). The only difference between these two hybrids is that the challenger, on receiving a decryption query, rejects if it contains \(\mathsf {ss}{.}\mathsf {vk}^{*}.\) Suppose there exists a PPT adversary \(\mathcal {A}\) such that \(|\mathsf {adv}_{\mathcal {A}}^0 - \mathsf {adv}_{\mathcal {A}}^1|\) is non-negligible. We can use \(\mathcal {A}\) to break the security of \(\mathsf {ss}\). The reduction algorithm \(\mathcal {B}\) receives a verification key \(\mathsf {vk}^{*}\) from the signature scheme’s challenger. The reduction algorithm chooses all other components by itself. Next, during the pre-challenge decryption queries, if any decryption query has \(\mathsf {vk}^{*}\) in it and the signature verification passes, then the reduction algorithm outputs this as a forgery.
During the challenge phase, the reduction algorithm receives \((m^{*}_0, m^{*}_1)\). It chooses \(\beta \), and computes \(M^{*}= \left( c^{*}_0, \left( c_{0,i}^{*}, c_{1,i}^{*}, c_{2,i}^{*} \right) \right) \) as in \(H_0\). Finally, it sends \(M^{*}\) to the challenger, and receives signature \(\sigma ^{*}\). It sends \(\left( \mathsf {vk}^{*}, M^{*}, \sigma ^{*} \right) \) to \(\mathcal {A}\).
The adversary then makes polynomially many decryption/key generation queries. If there exists some decryption query with verification key \(\mathsf {vk}^{*}\) that verifies, then the reduction algorithm outputs the corresponding message and signature as a forgery.
Clearly, \(\mathcal {B}'s\) advantage is at least \(\mathsf {adv}_{\mathcal {A}}^1 - \mathsf {adv}_{\mathcal {A}}^2\).
Lemma 2
Assuming \(\mathsf {PRG}\) is a secure pseudorandom generator, for any PPT adversary \(\mathcal {A}\), there exists a negligible function \(\mathsf {negl}(\cdot )\) such that for all \(\lambda \in \mathbb {N}\), \(|\mathsf {adv}_{\mathcal {A}}^1 - \mathsf {adv}_{\mathcal {A}}^2| \le \mathsf {negl}(\lambda )\).
Proof
The proof of this lemma follows from the security of \(\mathsf {PRG}\). The only difference between the two hybrids is the choice of \(a_i\). In \(H_1\), all \(a_i\) are chosen uniformly at random. In \(H_2\), the challenger chooses \(w_i \leftarrow \{0,1\}^\lambda \) for each i, and sets \(a_i\) as either \(\mathsf {PRG}(v^{*}_i) - \mathsf {PRG}(w_i) - \mathsf {ss}{.}\mathsf {vk}^{*}\cdot B\) or \(\mathsf {PRG}(w_i) - \mathsf {PRG}(v^{*}_i) - \mathsf {ss}{.}\mathsf {vk}^{*}\cdot B\), depending on \(s_i\). Since \(w_i\) is not used anywhere else in both these hybrid experiments, we can use PRG security to argue that any PPT adversary has nearly identical advantage in \(H_1\) and \(H_2\).
Lemma 3
Assuming correctness for decryptable ciphertexts for \(\mathsf {PKE}\) scheme, for any adversary \(\mathcal {A}\), there exists a negligible function \(\mathsf {negl}(\cdot )\) such that for all \(\lambda \in \mathbb {N}\), \(|\mathsf {adv}_{\mathcal {A}}^2 - \mathsf {adv}_{\mathcal {A}}^3| \le \mathsf {negl}(\lambda )\).
Proof
This is an information-theoretic step, and holds for all adversaries (not necessarily polynomial time). The only difference between these two hybrids is with respect to the decryption queries. In \(H_2\), the challenger uses the routine  to get a string d, and then checks if d is valid (using \(\mathsf {PKE}{.}\mathsf {Check}\)). In \(H_3\), the challenger uses
to get a string d, and then checks if d is valid (using \(\mathsf {PKE}{.}\mathsf {Check}\)). In \(H_3\), the challenger uses  to compute the string d. In fact, one can prove a more general statement: note that
to compute the string d. In fact, one can prove a more general statement: note that  corresponds to
corresponds to  with last input set to be \(0^n\). We can show that for any two strings \(s^{*}\) and \(s'\), decryption using
with last input set to be \(0^n\). We can show that for any two strings \(s^{*}\) and \(s'\), decryption using  is statistically indistinguishable from decryption using
is statistically indistinguishable from decryption using  . For simplicity, we will present indistinguishability of \(H_2\) and \(H_3\), where in \(H_2\), the challenger uses
. For simplicity, we will present indistinguishability of \(H_2\) and \(H_3\), where in \(H_2\), the challenger uses  for decryption queries.
for decryption queries.
We will argue that with overwhelming probability, for any decryption query \(\mathsf {ct}\), either  and
and  output the same d, or they output d and \(d'\) respectively but \(\mathsf {PKE}{.}\mathsf {Check}\) rejects both. In particular, it suffices to show that there exists a negligible function \(\mathsf {negl}(\cdot )\) such that for all \(\lambda \in \mathbb {N}\), \(s^{*}\in [n]\) and \(\mathsf {ss}{.}\mathsf {vk}^{*}\), the following event’s probability (denoted by p, parameterized by \(s^{*}\) and \(\mathsf {ss}{.}\mathsf {vk}^{*}\)) is at most \(\mathsf {negl}(\lambda )\):
output the same d, or they output d and \(d'\) respectively but \(\mathsf {PKE}{.}\mathsf {Check}\) rejects both. In particular, it suffices to show that there exists a negligible function \(\mathsf {negl}(\cdot )\) such that for all \(\lambda \in \mathbb {N}\), \(s^{*}\in [n]\) and \(\mathsf {ss}{.}\mathsf {vk}^{*}\), the following event’s probability (denoted by p, parameterized by \(s^{*}\) and \(\mathsf {ss}{.}\mathsf {vk}^{*}\)) is at most \(\mathsf {negl}(\lambda )\):

where the probability is over the random coins used in \(\mathsf {CCA}{.}\mathsf {Setup}\). Now, \(p \le p_0 + p_1\), where \(p_b\) is defined as the following event’s probability:

We will show that \(p_b \le \mathsf {negl}(\cdot )\) for both \(b\in \{0,1\}\). To prove this, let us first consider the following event:
where the probability is over the choice of \(B\leftarrow \{0,1\}^{\ell _{\mathrm {out}}}\) and \(v^{*}_i, w_i \leftarrow \{0,1\}^\lambda \). Then \(p_b \le p_{\mathsf {PRG}} + p'_b\), where \(p'_b\) is like \(p'_b\), except for an additional condition that \(\forall \gamma , \delta , \mathsf {PRG}(\gamma ) \ne \mathsf {PRG}(\delta ) + a_i + B\cdot \mathsf {ss}{.}\mathsf {vk}\). It is formally defined as the following event’s probability:

Hence, it suffices to show that \(p_{\mathsf {PRG}}\le \mathsf {negl}(\lambda )\), \(p'_{0} \le \mathsf {negl}(\lambda )\) and \(p'_{1} \le \mathsf {negl}(\lambda )\).
Claim 1
\(p_{\mathsf {PRG}} \le \mathsf {negl}(\lambda )\).
Proof
We will prove a stronger statement: for all \(\mathsf {ss}{.}\mathsf {vk}^{*}\),\( s^{*}\) and \(\left\{ v_i, w_i\right\} _{i\in [n]}\), the following probability is at most \(n\cdot 2^{-\lambda }\):
where the probability is over the choice of \(B\). Fix any integer \(i \in [n]\). Consider the following sets.
The set S has size at most \(2^\lambda \). As a result, the set \(S^-\) has size at most \(2^{2\lambda }\). Finally, the set \(S^-_{\mathsf {vk}}\) has size at most \(2^{2\lambda + \ell _{\mathsf {vk}}}\). If we choose a uniformly random element from \(\{0,1\}^{\ell _{\mathrm {out}}} \equiv \{0,1\}^{3\lambda + \ell _{\mathsf {vk}}}\), then this element falls in \(S^-_{\mathsf {vk}}\) with probability at most \(2^{-\lambda }\). This concludes our proof.
Claim 2
\(p'_0 = 0.\)
Proof
This follows from the definitions of  ,
,  and \(p'_0\). Note that
and \(p'_0\). Note that  sets \(d_i = 0\) only if the decrypted value \(1|v_i\) satisfies \(\mathsf {PRG}(v_i) = c_{2,i}\), and
sets \(d_i = 0\) only if the decrypted value \(1|v_i\) satisfies \(\mathsf {PRG}(v_i) = c_{2,i}\), and  sets \(d_i = 1\) only if the decrypted value \(1|w_i\) satisfies \(\mathsf {PRG}(w_i) + a_i + B\cdot \mathsf {ss}{.}\mathsf {vk}= c_{2,i}\). This, together with the requirement in \(p'_0\) that \(\forall ~\gamma , \delta \), \(\mathsf {PRG}(\gamma ) \ne \mathsf {PRG}(\delta ) + a_i + B\cdot \mathsf {ss}{.}\mathsf {vk}\), implies that \(p'_0 = 0\).
sets \(d_i = 1\) only if the decrypted value \(1|w_i\) satisfies \(\mathsf {PRG}(w_i) + a_i + B\cdot \mathsf {ss}{.}\mathsf {vk}= c_{2,i}\). This, together with the requirement in \(p'_0\) that \(\forall ~\gamma , \delta \), \(\mathsf {PRG}(\gamma ) \ne \mathsf {PRG}(\delta ) + a_i + B\cdot \mathsf {ss}{.}\mathsf {vk}\), implies that \(p'_0 = 0\).
Claim 3
Assuming correctness for decryptable ciphertexts , \(p'_1 = 0\).
Proof Intuition. We will first present an overview of the proof, and discuss a subtle but important point in the construction/proof.
Let \(E'_1\) denote the event corresponding to \(p'_1\). For this event to happen, there exists an index i such that \(s^{*}_i = 1\), and the \(i^{th}\) iteration of both  and
and  fail to find a signal (that is, either the decryption fails, or the PRG check fails). Let d be the string output by
fail to find a signal (that is, either the decryption fails, or the PRG check fails). Let d be the string output by  , and \(d'\) the string output by
, and \(d'\) the string output by  (therefore \(d_i = \overline{d'_i} = 1\)). We need to show that \(\mathsf {PKE}{.}\mathsf {Check}\) outputs \(\perp \) for both d and \(d'\). Suppose \(\mathsf {PKE}{.}\mathsf {Check}\) does not output \(\perp \) for d. Then, this means that there exists a v such that \(c_{1,i}\) is a PKE encryption of 1|v and \(\mathsf {PRG}(v) + a_i + B\cdot \mathsf {ss}{.}\mathsf {vk}= c_{2,i}\). In this case, the \(i^{th}\) iteration of
(therefore \(d_i = \overline{d'_i} = 1\)). We need to show that \(\mathsf {PKE}{.}\mathsf {Check}\) outputs \(\perp \) for both d and \(d'\). Suppose \(\mathsf {PKE}{.}\mathsf {Check}\) does not output \(\perp \) for d. Then, this means that there exists a v such that \(c_{1,i}\) is a PKE encryption of 1|v and \(\mathsf {PRG}(v) + a_i + B\cdot \mathsf {ss}{.}\mathsf {vk}= c_{2,i}\). In this case, the \(i^{th}\) iteration of  should set \(d'_i = 1\), which is a contradiction.
should set \(d'_i = 1\), which is a contradiction.
The other case, where \(\mathsf {PKE}{.}\mathsf {Check}\) does not output \(\perp \) for \(d'\), is similar. This means there exists v, x such that \(c_{0,i}\) is an encryption of 1|v for attribute x, \(C(x) = 1\) and \(\mathsf {PRG}(v) = c_{2,i}\). Using perfect correctness of the PKE scheme, we can argue that  should have set \(d_i = 0\), which is a contradiction.
should have set \(d_i = 0\), which is a contradiction.
Proof
Suppose \(s^{*}_i = 1\), \(d_i = 1\), \(d'_i = 0\), and \(\mathsf {PKE}{.}\mathsf {Check}\) outputs different value for both d and \(d'\). Let \(\widetilde{r_i}= \mathsf {HPRG}{.}\mathsf {Eval}(\mathsf {HPRG}{.}\mathsf {pp}, d, i)\), \(\widetilde{r_i}' = \mathsf {HPRG}{.}\mathsf {Eval}(\mathsf {HPRG}{.}\mathsf {pp}, d', i)\), \(m \leftarrow \mathsf {CPA}{.}\mathsf {Recover}(\mathsf {cpa}{.}\mathsf {pk}_{1,i}, c_{1,i}, \widetilde{r_i})\), \(m' \leftarrow \mathsf {CPA}{.}\mathsf {Recover} (\mathsf {cpa}{.}\mathsf {pk}_{0,i},c_{0,i}, \widetilde{r_i}')\). Since \(\mathsf {PKE}{.}\mathsf {Check}\) outputs different values for d and \(d'\), it does not output \(\perp \) for at least one of them in the \(i^{th}\) iteration. We will consider two cases.
 : As a result, \(m = 1|v\), \(c_{1,i}= \mathsf {CPA}{.}\mathsf {Enc}(\mathsf {cpa}{.}\mathsf {pk}_{1,i}\), m; \(\widetilde{r_i})\) and \(\mathsf {PRG}(v)+a_i + B\cdot \mathsf {ss}{.}\mathsf {vk}= c_{2,i}\). This means that \(\mathsf {CPA}{.}\mathsf {Dec}(\mathsf {sk}_{1,i}, c_{1,i}) = 1|v\) (by perfect correctness of the \(\mathsf {PKE}\) decryption algorithm). However, this means \(d'_i = 1\) (by definition of
: As a result, \(m = 1|v\), \(c_{1,i}= \mathsf {CPA}{.}\mathsf {Enc}(\mathsf {cpa}{.}\mathsf {pk}_{1,i}\), m; \(\widetilde{r_i})\) and \(\mathsf {PRG}(v)+a_i + B\cdot \mathsf {ss}{.}\mathsf {vk}= c_{2,i}\). This means that \(\mathsf {CPA}{.}\mathsf {Dec}(\mathsf {sk}_{1,i}, c_{1,i}) = 1|v\) (by perfect correctness of the \(\mathsf {PKE}\) decryption algorithm). However, this means \(d'_i = 1\) (by definition of  ). Hence Case 1 cannot occur.
). Hence Case 1 cannot occur.
 : As a result, \(m = 1|v\), \(c_{0,i}= \mathsf {CPA}{.}\mathsf {Enc}(\mathsf {cpa}{.}\mathsf {pk}_{0,i}\), m; \(\widetilde{r_i})\), and \(\mathsf {PRG}(v) = c_{2,i}\). This means that \(\mathsf {CPA}{.}\mathsf {Dec}(\mathsf {cpa}{.}\mathsf {sk}_{0,i}, c_{0,i}) = 1|v\) (since we have perfect correctness for \(\mathsf {PKE}\) decryption). However, by definition of
: As a result, \(m = 1|v\), \(c_{0,i}= \mathsf {CPA}{.}\mathsf {Enc}(\mathsf {cpa}{.}\mathsf {pk}_{0,i}\), m; \(\widetilde{r_i})\), and \(\mathsf {PRG}(v) = c_{2,i}\). This means that \(\mathsf {CPA}{.}\mathsf {Dec}(\mathsf {cpa}{.}\mathsf {sk}_{0,i}, c_{0,i}) = 1|v\) (since we have perfect correctness for \(\mathsf {PKE}\) decryption). However, by definition of  , \(d_i = 0\). Hence Case 2 cannot occur.
, \(d_i = 0\). Hence Case 2 cannot occur.
Lemma 4
Assuming \(\mathsf {PKE}\) is  secure, for any PPT adversary \(\mathcal {A}\), there exists a negligible function \(\mathsf {negl}(\cdot )\) such that for all \(\lambda \in \mathbb {N}\), \(|\mathsf {adv}_{\mathcal {A}}^3 - \mathsf {adv}_{\mathcal {A}}^4| \le \mathsf {negl}(\lambda )\).
secure, for any PPT adversary \(\mathcal {A}\), there exists a negligible function \(\mathsf {negl}(\cdot )\) such that for all \(\lambda \in \mathbb {N}\), \(|\mathsf {adv}_{\mathcal {A}}^3 - \mathsf {adv}_{\mathcal {A}}^4| \le \mathsf {negl}(\lambda )\).
Proof
The only difference in the two hybrids is with respect to the challenge ciphertext. In \(H_3\), the challenger sets \(c_{1,i}^{*}\) to be encryption of \(0^{\lambda +1}\) for all \(i \in [n]\) such that \(s^{*}_i = 0\). In \(H_4\), the challenger sets \(c_{1,i}^{*}\) to be encryption of \(1|w_i\). Note that the decryption queries require \(\mathsf {cpa}{.}\mathsf {sk}_{1,i}\) only if \(s^{*}_i = 1\). As a result, using the  security of \(\mathsf {PKE}\), it follows that the two hybrids are computationally indistinguishable.
security of \(\mathsf {PKE}\), it follows that the two hybrids are computationally indistinguishable.
Lemma 5
Assuming \(\mathsf {PKE}\) is  secure, for any PPT adversary \(\mathcal {A}\), there exists a negligible function \(\mathsf {negl}(\cdot )\) such that for all \(\lambda \in \mathbb {N}\), \(|\mathsf {adv}_{\mathcal {A}}^4 - \mathsf {adv}_{\mathcal {A}}^5| \le \mathsf {negl}(\lambda )\).
secure, for any PPT adversary \(\mathcal {A}\), there exists a negligible function \(\mathsf {negl}(\cdot )\) such that for all \(\lambda \in \mathbb {N}\), \(|\mathsf {adv}_{\mathcal {A}}^4 - \mathsf {adv}_{\mathcal {A}}^5| \le \mathsf {negl}(\lambda )\).
Proof
The proof of this lemma is similar to the proof of the previous lemma (Lemma 4). In \(H_4\), the challenger sets \(c_{0,i}^{*}\) to be encryption of \(0^{\lambda +1}\) for all \(i \in [n]\) such that \(s^{*}_i = 1\). In \(H_5\), the challenger sets \(c_{0,i}^{*}\) to be encryption of \(1|w_i\). Note that the decryption queries require \(\mathsf {cpa}{.}\mathsf {sk}_{0,i}\) only if \(s^{*}_i = 0\). As a result, using the  security of \(\mathsf {PKE}\), it follows that the two hybrids are computationally indistinguishable.
security of \(\mathsf {PKE}\), it follows that the two hybrids are computationally indistinguishable.
Lemma 6
Assuming correctness for decryptable ciphertexts for \(\mathsf {PKE}\) scheme, for any adversary \(\mathcal {A}\), there exists a negligible function \(\mathsf {negl}(\cdot )\) such that for all \(\lambda \in \mathbb {N}\), \(|\mathsf {adv}_{\mathcal {A}}^5 - \mathsf {adv}_{\mathcal {A}}^6| \le \mathsf {negl}(\lambda )\).
Proof
This proof is similar to the proof of Lemma 3. In particular, recall that the proof of Lemma 3 works for any \(s^{*}, s'\), and note that  simply corresponds to
simply corresponds to  .
.
Lemma 7
\(\mathsf {adv}_{\mathcal {A}}^6 = \mathsf {adv}_{\mathcal {A}}^7\).
Proof
This follows from the definition of the two hybrids. The only difference between \(H_6\) and \(H_7\) is that the variable names \(v^{*}_i\) and \(w_i\) are swapped if \(s^{*}_i = 1\). As a result, any adversary has identical advantage in both hybrids.
Lemma 8
Assuming \(\mathsf {HPRG}\) satisfies Definition 3, for any PPT adversary \(\mathcal {A}\), there exists a negligible function \(\mathsf {negl}(\cdot )\) such that for all \(\lambda \in \mathbb {N}\), \(|\mathsf {adv}_{\mathcal {A}}^7 - \mathsf {adv}_{\mathcal {A}}^8| \le \mathsf {negl}(\lambda )\).
Proof
Suppose there exists a PPT adversary \(\mathcal {A}\) such that \(|\mathsf {adv}_{\mathcal {A}}^7 - \mathsf {adv}_{\mathcal {A}}^8| = \epsilon \). We will use \(\mathcal {A}\) to build a PPT reduction algorithm \(\mathcal {B}\) that breaks the security of \(\mathsf {HPRG}\).
The reduction algorithm first receives \(\mathsf {HPRG}{.}\mathsf {pp}\) and \(\left( r^{*}_0, \left( r^{*}_{b,i} \right) _{i \in [n], b\in \{0,1\}} \right) \) from the challenger. It chooses \(\left\{ v^{*}_i, w_i\right\} \), \((\mathsf {ss}{.}\mathsf {sk}^{*}, \mathsf {ss}{.}\mathsf {vk}^{*})\), sets \(\left\{ a_i\right\} \), chooses \(B\leftarrow \{0,1\}^{\ell _{\mathrm {out}}}\), \(\left\{ (\mathsf {cpa}{.}\mathsf {pk}_{b,i}, \mathsf {cpa}{.}\mathsf {sk}_{b,i}) \leftarrow \mathsf {CPA}{.}\mathsf {Setup}(1^\lambda )\right\} \) and sends \(\left( \mathsf {HPRG}{.}\mathsf {pp}, B,\right. \left. \left( a_i, \mathsf {cpa}{.}\mathsf {pk}_{b,i} \right) \right) \) to \(\mathcal {A}\). Next, it receives decryption queries, which can be handled using \(\left\{ \mathsf {cpa}{.}\mathsf {sk}_{1,i}\right\} \) (as in \(H_6\)/\(H_7\)). For the challenge ciphertext, it chooses \(\beta \leftarrow \{0,1\}\), sets \(c^{*}_0 = m^{*}_b \oplus r^{*}_0\), computes \(c_{0,i}^{*}= \mathsf {CPA}{.}\mathsf {Enc}(\mathsf {cpa}{.}\mathsf {pk}_{0,i}, 1|v^{*}_i; r^{*}_{0,i})\), \(c_{1,i}^{*}= \mathsf {CPA}{.}\mathsf {Enc}(\mathsf {cpa}{.}\mathsf {pk}_{1,i}, 1|w_i; r^{*}_{1,i})\), \(c_{2,i}^{*}= \mathsf {PRG}(v^{*}_i) = \mathsf {PRG}(w^{*}_i) + a_i + B\cdot \mathsf {ss}{.}\mathsf {vk}^{*}\) and finally computes a signature on \(\left( c^{*}, \left( c_{0,i}^{*}, c_{1,i}^{*}, c_{2,i}^{*} \right) \right) \). It sends the ciphertext to the adversary. The post-challenge queries are handled as the pre-challenge queries. Finally, the adversary sends its guess \(\beta '\). If \(\beta \ne \beta '\), the reduction algorithm guesses that all \(r^{*}_{b,i}\) are uniformly random. This reduction algorithm has advantage \(\epsilon \) in the hinting PRG security game.
Lemma 9
For any adversary \(\mathcal {A}\), \(\mathsf {adv}_{\mathcal {A}}^8 = 0\).
Proof
Note that in hybrid \(H_8\), there is no information about \(m_\beta \) in the challenge ciphertext, since \(c^{*}_0\) is uniformly random.
5 CCA Secure Predicate Encryption Scheme
Let \(\mathsf {PredE}\) = (\(\mathsf {PredE}{.}\mathsf {Setup}\), \(\mathsf {PredE}{.}\mathsf {Enc}\), \(\mathsf {PredE}{.}\mathsf {KeyGen}\), \(\mathsf {PredE}{.}\mathsf {Dec})\) be a predicate encryption scheme with randomness-decryptable ciphertexts and one-sided security against chosen plaintext attacks, \(\mathsf {PKE}\) = (\(\mathsf {CPA}{.}\mathsf {Setup}\), \(\mathsf {CPA}{.}\mathsf {Enc}\), \(\mathsf {CPA}{.}\mathsf {Dec})\) an  secure public key encryption scheme with randomness-decryptable ciphertexts, \(\mathsf {S}= (\mathsf {ss}{.}\mathsf {Setup}, \mathsf {ss}{.}\mathsf {Sign}, \mathsf {ss}{.}\mathsf {Verify})\) a strongly unforgeable one time signature scheme and \(\mathsf {HPRG}= (\mathsf {HPRG}{.}\mathsf {Setup}, \mathsf {HPRG}{.}\mathsf {Eval})\) a hinting PRG scheme. We will assume both our encryption schemes have message space \(\{0,1\}^{\lambda + 1}\). Let \(\ell _{\mathsf {PredE}}(\cdot )\) be a polynomial representing the number of bits of randomness used by \(\mathsf {PredE}{.}\mathsf {Enc}\), \(\ell _{\mathsf {PKE}}(\cdot )\) the number of random bits used by \(\mathsf {CPA}{.}\mathsf {Enc}\), and \(\ell _{\mathsf {vk}}(\cdot )\) the size of verification keys output by \(\mathsf {ss}{.}\mathsf {Setup}\). For simplicity of notation, we will assume \(\ell (\cdot ) = \ell _{\mathsf {PredE}}(\cdot ) = \ell _{\mathsf {PKE}}(\cdot )\),Footnote 8 \(\ell _{\mathrm {out}}(\lambda ) = \ell _{\mathsf {vk}}(\lambda ) + 3\lambda \) and \(\mathsf {PRG}_\lambda : \{0,1\}^{\lambda } \rightarrow \{0,1\}^{\ell _{\mathrm {out}}(\lambda )}\) a family of secure pseudorandom generators.
secure public key encryption scheme with randomness-decryptable ciphertexts, \(\mathsf {S}= (\mathsf {ss}{.}\mathsf {Setup}, \mathsf {ss}{.}\mathsf {Sign}, \mathsf {ss}{.}\mathsf {Verify})\) a strongly unforgeable one time signature scheme and \(\mathsf {HPRG}= (\mathsf {HPRG}{.}\mathsf {Setup}, \mathsf {HPRG}{.}\mathsf {Eval})\) a hinting PRG scheme. We will assume both our encryption schemes have message space \(\{0,1\}^{\lambda + 1}\). Let \(\ell _{\mathsf {PredE}}(\cdot )\) be a polynomial representing the number of bits of randomness used by \(\mathsf {PredE}{.}\mathsf {Enc}\), \(\ell _{\mathsf {PKE}}(\cdot )\) the number of random bits used by \(\mathsf {CPA}{.}\mathsf {Enc}\), and \(\ell _{\mathsf {vk}}(\cdot )\) the size of verification keys output by \(\mathsf {ss}{.}\mathsf {Setup}\). For simplicity of notation, we will assume \(\ell (\cdot ) = \ell _{\mathsf {PredE}}(\cdot ) = \ell _{\mathsf {PKE}}(\cdot )\),Footnote 8 \(\ell _{\mathrm {out}}(\lambda ) = \ell _{\mathsf {vk}}(\lambda ) + 3\lambda \) and \(\mathsf {PRG}_\lambda : \{0,1\}^{\lambda } \rightarrow \{0,1\}^{\ell _{\mathrm {out}}(\lambda )}\) a family of secure pseudorandom generators.
We will now describe our CCA-one-sided secure predicate encryption scheme \(\mathsf {PredE}_{\mathsf {CCA}}\) = (\(\mathsf {PredE}_{\mathsf {CCA}}{.}\mathsf {Setup}\), \(\mathsf {PredE}_{\mathsf {CCA}}{.}\mathsf {Enc}\), \(\mathsf {PredE}_{\mathsf {CCA}}{.}\mathsf {KeyGen}\), \(\mathsf {PredE}_{\mathsf {CCA}}{.}\mathsf {Dec}\)) with message space \(\mathcal {M}_\lambda = \{0,1\}^{\ell (\lambda )}\). For simplicity of notation, we will skip the dependence of \(\ell \) and \(\ell _{\mathrm {out}}\) on \(\lambda \).
-
\(\mathsf {PredE}_{\mathsf {CCA}}{.}\mathsf {Setup}(1^{\lambda })\): The setup algorithm first chooses \((\mathsf {HPRG}{.}\mathsf {pp}, 1^{n}) \leftarrow \mathsf {HPRG}{.}\mathsf {Setup}(1^{\lambda }, 1^{\ell })\). Next it chooses \(n\) different \(\mathsf {PredE}\) keys and \(\mathsf {PKE}\) keys. Let \((\mathsf {pred}{.}\mathsf {msk}_i, \mathsf {pred}{.}\mathsf {pk}_i) \leftarrow \mathsf {PredE}{.}\mathsf {Setup}(1^\lambda )\), \((\mathsf {cpa}{.}\mathsf {sk}_i, \mathsf {cpa}{.}\mathsf {pk}_i) \leftarrow \mathsf {CPA}{.}\mathsf {Setup}(1^{\lambda })\) for each \(i \in [n]\). It then chooses \(a_i \leftarrow \{0,1\}^{\ell _{\mathrm {out}}}\) for each \(i \in [n]\) and \(B\leftarrow \{0,1\}^{\ell _{\mathrm {out}}}\). It sets \(\mathsf {pe{.}cca}{.}\mathsf {pk}= \left( \mathsf {HPRG}{.}\mathsf {pp}, B, \left( a_i, \mathsf {pred}{.}\mathsf {pk}_i, \mathsf {cpa}{.}\mathsf {pk}_i \right) _{i \in [n]} \right) \) and \(\mathsf {pe{.}cca}{.}\mathsf {msk}= \left( \mathsf {pred}{.}\mathsf {msk}_i, \mathsf {cpa}{.}\mathsf {sk}_i \right) _{i\in [n]}\).
-
\(\mathsf {PredE}_{\mathsf {CCA}}{.}\mathsf {Enc}(\mathsf {pe{.}cca}{.}\mathsf {pk}, m, x)\): Let \(\mathsf {pe{.}cca}{.}\mathsf {pk}\) = \(\left( \mathsf {HPRG}{.}\mathsf {pp}, B, \left( a_i, \mathsf {pred}{.}\mathsf {pk}_i,\right. \right. \left. \left. \mathsf {cpa}{.}\mathsf {pk}_i \right) _{i \in [n]} \right) \). The encryption algorithm first chooses \(s \leftarrow \{0,1\}^{n}\). It sets \(c_0 = \mathsf {HPRG}{.}\mathsf {Eval}(\mathsf {HPRG}{.}\mathsf {pp}, s, 0) \oplus m\). Next, it chooses signature keys \((\mathsf {ss}{.}\mathsf {sk}, \mathsf {ss}{.}\mathsf {vk}) \leftarrow \mathsf {ss}{.}\mathsf {Setup}(1^\lambda )\). For each \(i \in [n]\), it chooses \(v_i \leftarrow \{0,1\}^{\lambda }\) and \(r_i \leftarrow \{0,1\}^\ell \), sets \(\widetilde{r_i}= \mathsf {HPRG}{.}\mathsf {Eval}(\mathsf {HPRG}{.}\mathsf {pp}, s, i)\) and does the following:
-
If \(s_i = 0\), it sets \(c_{0,i}= \mathsf {PredE}{.}\mathsf {Enc}(\mathsf {pred}{.}\mathsf {pk}_i, 1|v_i, x; \widetilde{r_i})\), \(c_{1,i}= \mathsf {CPA}{.}\mathsf {Enc}(\mathsf {cpa}{.}\mathsf {pk}_i, 0^{\lambda +1}; r_i)\) and \(c_{2,i}= \mathsf {PRG}(v_i)\).
-
If \(s_i = 1\), it sets \(c_{0,i}= \mathsf {PredE}{.}\mathsf {Enc}(\mathsf {pred}{.}\mathsf {pk}_i, 0^{\lambda +1}, x; r_i)\), \(c_{1,i}= \mathsf {CPA}{.}\mathsf {Enc}(\mathsf {cpa}{.}\mathsf {pk}_i, 1|v_i; \widetilde{r_i})\) and \(c_{2,i}= \mathsf {PRG}(v_i) + a_i + B\cdot \mathsf {ss}{.}\mathsf {vk}\).Footnote 9.
Finally, it sets \(M = \left( c_0, \left( c_{0,i}, c_{1,i}, c_{2,i} \right) _{i \in [n]} \right) \), computes \(\sigma \leftarrow \mathsf {ss}{.}\mathsf {Sign}(\mathsf {ss}{.}\mathsf {sk}, M)\) and outputs \(\left( \mathsf {ss}{.}\mathsf {vk}, M, \sigma \right) \) as the ciphertext.
-
-
\(\mathsf {PredE}_{\mathsf {CCA}}{.}\mathsf {KeyGen}(\mathsf {pe{.}cca}{.}\mathsf {msk}, C)\): Let \(\mathsf {pe{.}cca}{.}\mathsf {msk}\) = \(\left( \mathsf {pred}{.}\mathsf {msk}_i, \mathsf {cpa}{.}\mathsf {sk}_i \right) _{i\in [n]}\). The key generation algorithm computes \(\mathsf {pred}{.}\mathsf {sk}_i \leftarrow \mathsf {PredE}{.}\mathsf {KeyGen}(\mathsf {pred}{.}\mathsf {msk}_i, C)\) and outputs \(\mathsf {pe{.}cca}{.}\mathsf {sk}= \left( C, \left( \mathsf {pred}{.}\mathsf {sk}_i \right) _{i \in [n]} \right) \).
-
\(\mathsf {PredE}_{\mathsf {CCA}}{.}\mathsf {Dec}(\mathsf {pe{.}cca}{.}\mathsf {sk}, \mathsf {pe{.}cca}{.}\mathsf {pk}, \mathsf {pe{.}cca}{.}\mathsf {ct})\): Let the ciphertext \(\mathsf {pe{.}cca}{.}\mathsf {ct}\) be parsed as \(\left( \mathsf {ss}{.}\mathsf {vk}, M=\left( c_0, \left( c_{0,i}, c_{1,i}, c_{2,i} \right) _{i \in [n]} \right) , \sigma \right) \) and \(\mathsf {pe{.}cca}{.}\mathsf {sk}\) = \(\left( C, \left( \mathsf {pred}{.}\mathsf {sk}_i \right) _{i \in [n]} \right) \). The decryption algorithm first verifies the signature \(\sigma \). It checks if \(\mathsf {ss}{.}\mathsf {Verify}(\mathsf {ss}{.}\mathsf {vk}, M, \sigma ) = 1\), else it outputs \(\perp \).
Next, the decryption algorithm computes \(d = \mathsf {Find}(\mathsf {pe{.}cca}{.}\mathsf {pk}\), \(\mathsf {pe{.}cca}{.}\mathsf {sk}\), \(\mathsf {pe{.}cca}{.}\mathsf {ct}\)) (where \(\mathsf {Find}\) is defined in Fig. 5), and outputs \(\mathsf {Check}(\mathsf {pe{.}cca}{.}\mathsf {pk}\), \(\mathsf {pe{.}cca}{.}\mathsf {ct}\), C, d) (where \(\mathsf {Check}\) is defined in Fig. 6).
5.1 Security Proof
The security proof works via a sequence of hybrid experiments, and the hybrid experiments are very similar to the ones used for the PKE construction. Due to space constraints, the proof of security is included in the full version of our paper.
Notes
- 1.
The realization of NIZKs from the Learning with Errors assumption is a very recent and exciting development [38] and occured after the initial posting of this work.
- 2.
The original definition of predicate encryption [7, 27] required hiding whether an attribute string of a challenge ciphertext was \(x_0\) or \(x_1\) from an attacker that had a key C where \(C(x_0)=C(x_1)\). A weaker form of predicate encryption is where this guarantee is given only if \(C(x_0)=C(x_1)=0\), but not when \(C(x_0)=C(x_1)=1\). This weaker form has been called predicate encryption with one-sided security and anonymous Attribute-Based Encryption. For this paper we will use the term one-sided predicate encryption.
- 3.
More compactly, \(M_{s_i, i} = z_i\) and \(M_{\overline{s_i}, i} = v_i\).
- 4.
Here, we assume the verification key is embedded in \(\mathbb {F}_{2^{\ell _{\mathrm {out}}}}\), and the addition and multiplication are performed in \(\mathbb {F}_{2^{\ell _{\mathrm {out}}}}\). Also, the function \(h(x) = a_i + B\cdot x\) serves as a pairwise independent hash function.
- 5.
By signaling, we mean that any party that has the secret key for decryption can learn the bits of s one after another, by using the ciphertext components \(c_{0,i},c_{1,i},c_{2,i}\).
- 6.
Note that hybrids \(H_4\) and \(H_5\) could have been clubbed into a single hybrid. We chose this distinction so that the hybrids for the PKE CCA proof are similar to the hybrids for our Predicate Encryption security proof.
- 7.
We could have simplified this step by using
 instead of using
instead of using  . However, looking ahead, our proof for ABE/PE systems will require an analogous
. However, looking ahead, our proof for ABE/PE systems will require an analogous  routine. Hence, we chose to add this minor additional complication here as well.
routine. Hence, we chose to add this minor additional complication here as well. - 8.
Alternatively, we could set \(\ell \) to be max of these two polynomials.
- 9.
Here, we assume the verification key is embedded in \(\mathbb {F}_{2^{\ell _{\mathrm {out}}}}\), and the addition and multiplication are performed in \(\mathbb {F}_{2^{\ell _{\mathrm {out}}}}\).
References
Attrapadung, N.: Dual system encryption via doubly selective security: framework, fully secure functional encryption for regular languages, and more. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 557–577. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-55220-5_31
Attrapadung, N., Libert, B., de Panafieu, E.: Expressive key-policy attribute-based encryption with constant-size ciphertexts. In: Catalano, D., Fazio, N., Gennaro, R., Nicolosi, A. (eds.) PKC 2011. LNCS, vol. 6571, pp. 90–108. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-19379-8_6
Bellare, M., Rogaway, P.: Random oracles are practical: a paradigm for designing efficient protocols. In: ACM Conference on Computer and Communications Security, pp. 62–73 (1993)
Blömer, J., Liske, G.: Construction of fully CCA-secure predicate encryptions from pair encoding schemes. In: Sako, K. (ed.) CT-RSA 2016. LNCS, vol. 9610, pp. 431–447. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-29485-8_25
Blum, M., Feldman, P., Micali, S.: Non-interactive zero-knowledge and its applications. In: STOC, pp. 103–112 (1988)
Boneh, D., et al.: Fully key-homomorphic encryption, arithmetic circuit ABE and compact garbled circuits. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 533–556. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-55220-5_30
Boneh, D., Waters, B.: Conjunctive, subset, and range queries on encrypted data. In: Vadhan, S.P. (ed.) TCC 2007. LNCS, vol. 4392, pp. 535–554. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-70936-7_29. http://dl.acm.org/citation.cfm?id=1760749.1760788
Brakerski, Z., Lombardi, A., Segev, G., Vaikuntanathan, V.: Anonymous IBE, leakage resilience and circular security from new assumptions. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018, Part I. LNCS, vol. 10820, pp. 535–564. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78381-9_20
Canetti, R., Halevi, S., Katz, J.: Chosen-ciphertext security from identity-based encryption. In: Cachin, C., Camenisch, J.L. (eds.) EUROCRYPT 2004. LNCS, vol. 3027, pp. 207–222. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24676-3_13
Chase, M.: Multi-authority attribute based encryption. In: Vadhan, S.P. (ed.) TCC 2007. LNCS, vol. 4392, pp. 515–534. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-70936-7_28
Chase, M., Chow, S.S.M.: Improving privacy and security in multi-authority attribute-based encryption. In: ACM Conference on Computer and Communications Security, pp. 121–130 (2009)
Chen, J., Gay, R., Wee, H.: Improved dual system ABE in prime-order groups via predicate encodings. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015, Part II. LNCS, vol. 9057, pp. 595–624. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46803-6_20
Dolev, D., Dwork, C., Naor, M.: Non-malleable cryptography (extended abstract). In: Proceedings of the 23rd Annual ACM Symposium on Theory of Computing, New Orleans, Louisiana, USA, 5–8 May 1991, pp. 542–552 (1991)
Döttling, N., Garg, S.: From selective IBE to full IBE and selective HIBE. In: Kalai, Y., Reyzin, L. (eds.) TCC 2017, Part I. LNCS, vol. 10677, pp. 372–408. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70500-2_13
Döttling, N., Garg, S.: Identity-based encryption from the Diffie-Hellman assumption. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017, Part I. LNCS, vol. 10401, pp. 537–569. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63688-7_18
Döttling, N., Garg, S., Hajiabadi, M., Masny, D.: New constructions of identity-based and key-dependent message secure encryption schemes. In: Abdalla, M., Dahab, R. (eds.) PKC 2018, Part I. LNCS, vol. 10769, pp. 3–31. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-76578-5_1
Dwork, C., Naor, M., Reingold, O.: Immunizing encryption schemes from decryption errors. In: Cachin, C., Camenisch, J.L. (eds.) EUROCRYPT 2004. LNCS, vol. 3027, pp. 342–360. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24676-3_21
Feige, U., Shamir, A.: Witness indistinguishable and witness hiding protocols. In: Proceedings of the 22nd Annual ACM Symposium on Theory of Computing, Baltimore, Maryland, USA, 13–17 May 1990, pp. 416–426 (1990)
Fiat, A., Naor, M.: Broadcast encryption. In: Stinson, D.R. (ed.) CRYPTO 1993. LNCS, vol. 773, pp. 480–491. Springer, Heidelberg (1994). https://doi.org/10.1007/3-540-48329-2_40
Fujisaki, E., Okamoto, T.: Secure integration of asymmetric and symmetric encryption schemes. In: Wiener, M. (ed.) CRYPTO 1999. LNCS, vol. 1666, pp. 537–554. Springer, Heidelberg (1999). https://doi.org/10.1007/3-540-48405-1_34
Garg, S., Gay, R., Hajiabadi, M.: New techniques for efficient trapdoor functions and applications. Cryptology ePrint Archive, Report 2018/872 (2018). https://eprint.iacr.org/2018/872
Garg, S., Hajiabadi, M.: Trapdoor functions from the computational Diffie-Hellman assumption. In: Shacham, H., Boldyreva, A. (eds.) CRYPTO 2018, Part II. LNCS, vol. 10992, pp. 362–391. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96881-0_13
Gorbunov, S., Vaikuntanathan, V., Wee, H.: Attribute-based encryption for circuits. In: STOC (2013)
Gorbunov, S., Vaikuntanathan, V., Wee, H.: Predicate encryption for circuits from LWE. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015, Part II. LNCS, vol. 9216, pp. 503–523. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48000-7_25
Goyal, R., Koppula, V., Waters, B.: Lockable obfuscation. In: 58th IEEE Annual Symposium on Foundations of Computer Science, FOCS 2017, pp. 612–621 (2017)
Goyal, V., Pandey, O., Sahai, A., Waters, B.: Attribute-based encryption for fine-grained access control of encrypted data. In: Proceedings of the 13th ACM Conference on Computer and Communications Security, CCS 2006 (2006)
Katz, J., Sahai, A., Waters, B.: Predicate encryption supporting disjunctions, polynomial equations, and inner products. In: Smart, N. (ed.) EUROCRYPT 2008. LNCS, vol. 4965, pp. 146–162. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78967-3_9
Kiltz, E.: Chosen-ciphertext security from tag-based encryption. In: Halevi, S., Rabin, T. (eds.) TCC 2006. LNCS, vol. 3876, pp. 581–600. Springer, Heidelberg (2006). https://doi.org/10.1007/11681878_30
Kitagawa, F., Matsuda, T., Tanaka, K.: CCA security and trapdoor functions via key-dependent-message security. Cryptology ePrint Archive, Report 2019/291 (2019). https://eprint.iacr.org/2019/291
Lewko, A.B., Okamoto, T., Sahai, A., Takashima, K., Waters, B.: Fully secure functional encryption: attribute-based encryption and (hierarchical) inner product encryption. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 62–91. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13190-5_4
Lewko, A.B., Waters, B.: Decentralizing attribute-based encryption. In: Paterson, K.G. (ed.) EUROCRYPT 2011. LNCS, vol. 6632, pp. 568–588. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-20465-4_31
Lewko, A.B., Waters, B.: New proof methods for attribute-based encryption: achieving full security through selective techniques. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 180–198. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32009-5_12
Lombardi, A., Quach, W., Rothblum, R.D., Wichs, D., Wu, D.J.: New constructions of reusable designated-verifier NIZKs. In: Boldyreva, A., Micciancia, D. (eds.) CRYPTO 2019. LNCS, vol. 11694, pp. 670–700. Springer, Heidelberg (2019). https://eprint.iacr.org/2019/242
Nandi, M., Pandit, T.: Generic conversions from CPA to CCA secure functional encryption. Cryptology ePrint Archive, Report 2015/457 (2015). https://eprint.iacr.org/2015/457
Naor, M.: Bit commitment using pseudo-randomness. In: Brassard, G. (ed.) CRYPTO 1989. LNCS, vol. 435, pp. 128–136. Springer, New York (1990). https://doi.org/10.1007/0-387-34805-0_13
Naor, M., Yung, M.: Public-key cryptosystems provably secure against chosen ciphertext attacks. In: Proceedings of the 22nd Annual ACM Symposium on Theory of Computing, Baltimore, Maryland, USA, 13–17 May 1990, pp. 427–437 (1990)
Okamoto, T., Takashima, K.: Fully secure functional encryption with general relations from the decisional linear assumption. In: Rabin, T. (ed.) CRYPTO 2010. LNCS, vol. 6223, pp. 191–208. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-14623-7_11
Peikert, C., Shiehian, S.: Noninteractive zero knowledge for NP from (plain) learning with errors. Cryptology ePrint Archive, Report 2019/158 (2019). https://eprint.iacr.org/2019/158
Peikert, C., Waters, B.: Lossy trapdoor functions and their applications. In: Proceedings of the 40th Annual ACM Symposium on Theory of Computing, Victoria, British Columbia, Canada, 17–20 May 2008, pp. 187–196 (2008)
Rackoff, C., Simon, D.R.: Non-interactive zero-knowledge proof of knowledge and chosen ciphertext attack. In: Feigenbaum, J. (ed.) CRYPTO 1991. LNCS, vol. 576, pp. 433–444. Springer, Heidelberg (1992). https://doi.org/10.1007/3-540-46766-1_35
Rosen, A., Segev, G.: Chosen-ciphertext security via correlated products. SIAM J. Comput. 39(7), 3058–3088 (2010)
Sahai, A., Waters, B.: Fuzzy identity-based encryption. In: Cramer, R. (ed.) EUROCRYPT 2005. LNCS, vol. 3494, pp. 457–473. Springer, Heidelberg (2005). https://doi.org/10.1007/11426639_27
Shoup, V.: Why chosen ciphertext security matters (1998)
Waters, B.: Dual system encryption: realizing fully secure IBE and HIBE under simple assumptions. In: Halevi, S. (ed.) CRYPTO 2009. LNCS, vol. 5677, pp. 619–636. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-03356-8_36
Wee, H.: Dual system encryption via predicate encodings. In: Lindell, Y. (ed.) TCC 2014. LNCS, vol. 8349, pp. 616–637. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54242-8_26
Wichs, D., Zirdelis, G.: Obfuscating compute-and-compare programs under LWE. In: 58th IEEE Annual Symposium on Foundations of Computer Science, FOCS 2017, pp. 600–611 (2017)
Yamada, S., Attrapadung, N., Hanaoka, G., Kunihiro, N.: Generic constructions for chosen-ciphertext secure attribute based encryption. In: Catalano, D., Fazio, N., Gennaro, R., Nicolosi, A. (eds.) PKC 2011. LNCS, vol. 6571, pp. 71–89. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-19379-8_5
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 International Association for Cryptologic Research
About this paper
Cite this paper
Koppula, V., Waters, B. (2019). Realizing Chosen Ciphertext Security Generically in Attribute-Based Encryption and Predicate Encryption. In: Boldyreva, A., Micciancio, D. (eds) Advances in Cryptology – CRYPTO 2019. CRYPTO 2019. Lecture Notes in Computer Science(), vol 11693. Springer, Cham. https://doi.org/10.1007/978-3-030-26951-7_23
Download citation
DOI: https://doi.org/10.1007/978-3-030-26951-7_23
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-26950-0
Online ISBN: 978-3-030-26951-7
eBook Packages: Computer ScienceComputer Science (R0)







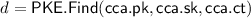 (where
(where  is defined in Fig.
is defined in Fig. 
 .
.





 instead of using
instead of using  . However, looking ahead, our proof for ABE/PE systems will require an analogous
. However, looking ahead, our proof for ABE/PE systems will require an analogous  routine. Hence, we chose to add this minor additional complication here as well.
routine. Hence, we chose to add this minor additional complication here as well.