Abstract
In this survey paper we present the existing generalizations of the proximal point method from scalar to vector optimization problems, discussing some of their advantages and drawbacks, respectively, presenting some open challenges and sketching some possible directions for future research.
Dedicated to the memory of J.M. Borwein
Access provided by Autonomous University of Puebla. Download chapter PDF
Similar content being viewed by others
Keywords
- Vector optimization problem
- Proximal point algorithm
- Weakly efficient solution
- Efficient solution
- Splitting method
- Multiobjective optimization problem
- Vector function
- Scalarization function
AMS 2010 Subject Classification
11.1 Introduction
The usual way to solve a vector optimization problem is by scalarizing it, i.e. by attaching to it a scalar optimization problem whose optimal solutions are also optimal in some sense to the original problem. However, this approach can often lead to unbounded scalar optimization problems, hence the necessity to address the vector optimization problems directly, especially when it comes to numerically solving them. One can find some results on the choice of scalarizing parameters in order to guarantee the existence of optimal solutions of the scalarized problems in the literature, but the imposed conditions are quite restrictive (see [47, 62]) and their verification, when possible, may prove to be too expensive from a computational point of view. There are some scalarization methods (for instance the one with the scalarization function introduced by Tammer (Gerstewitz) in [43] or by means of a (semi-)norm, see also [49, Chapter 4]) that lead to scalar optimization problems that are bounded from below, however the objective functions of the latter consist of compositions of functions that are often unsuitable for the existing algorithms. This situation has motivated research on iterative methods for directly solving multiobjective or vector optimization problems consisting in vector-minimizing a vector function, sometimes subject to (geometric) constraints, that are more or less immediate extensions of scalar algorithms. Some of the first contributions to this direction can be found in [54,55,56, 64] and the interest towards such algorithms remained active during the next decades (see, for instance, [11, 60, 61]), several other methods being adapted or developed. More recently, one can find generalizations from the scalar case to the vector one of several classical methods for solving both smooth optimization problems, such as the Newton’s method (cf. [42]), the projected gradient method (cf. [46]) or the steepest descent method (cf. [48]), and nonsmooth ones, for instance the proximal point method (cf. [24, 75]), the proximal bundle one (cf. [58]) or the subgradient method (cf. [40]). Moreover, one can find even methods for solving vector optimization problems that rely on dynamical systems, such as the ones proposed in [5,6,7].
In this survey we focus on the existing generalizations of the proximal point method from scalar to vector optimization problems, briefly presenting them and discussing about their advantages and drawbacks, respectively, mentioning some open problems and sketching some possible directions for future research. The (already classical) proximal point algorithm was first proposed by Martinet in [59] and shortly afterwards developed and extended by Rockafellar for solving monotone inclusions, in particular convex (scalar) optimization problems. Since then there were many contributions to this area of research, proximal point type algorithms being now available for various complexly structured convex optimization problems as well as for some classes of nonconvex optimization problems. We refer the reader to [9] for more on the state of the art on this topic.
The first major contribution to extending the proximal point method from scalar to vector optimization problems is the paper [24] due to Bonnel, Iusem and Svaiter. One could argue that the earlier contributions [61] and [45, Section 4.2] contain some proximal point type algorithms for solving vector optimization problems, too, however, in the introduction of [24] the authors explicitly address this issue, stressing that in these works the proximal point steps are actually applied on scalar optimization problems. The mentioned work, written roughly fifteen years ago and cited over one hundred times (according to google scholar) is still the (gold) standard in the field and basically every further paper containing a proximal point type method for solving vector optimization problems builds on it. In the following we discuss around thirty such subsequent contributions (see [4, 12,13,14,15,16,17, 19, 27,28,29,30,31,32,33,34,35,36,37,38,39, 41, 51,52,53, 67,68,69,70,71,72,73,74,75]) where one finds algorithms for solving vector optimization problems of various types, where the objective functions are cone-convex, cone-quasiconvex, differences of cone-convex functions or sums of such, have a special structure or are arbitrary and map from Euclidean, Hilbert, Banach or even Hadamard spaces to Euclidean or Banach ones, being minimized over the whole space or only over some sets or even subject to some other explicitly formulated constraints. In some of these papers the proximality paradigm is present in a classical manner, in some the proximal terms contain Bregman distances, quasi-distances, or are formulated via viscosity functions. There are also two papers where inertial/memory effects or hybrid constructions are added to the algorithm, and we mention, too, some contributions where the regularization is performed by means of a Tikhonov type function instead of the Moreau-Yosida one from the proximal point algorithms.
The method proposed in [24] and extended and refined in subsequent contributions does not directly scalarize the original vector optimization problem. The proximal step of the algorithm consists in choosing as the next iterate a weakly efficient solution of the intermediate vector optimization problem corresponding to the current iteration. The intermediate vector optimization problems are constructed by means of a Moreau-Yosida type regularization and, consequently, they always have weakly efficient solutions. Moreover, the scalarized optimization problems attached to them by any nonzero linear continuous functional from the dual cone of the ordering cone have optimal solutions and, thus, deliver weakly efficient solutions to the intermediate vector optimization problems. This observation is used in the convergence proof, however it does not mean that the original vector optimization problem or the intermediate ones have to be actually scalarized when the algorithm is running. Note also that most of the proximal point type algorithms for vector optimization problems deliver weakly efficient solutions or even, in the nonconvex case, critically efficient solutions to them. The convergence to efficient solutions can be then guaranteed under additional hypotheses.
Note that we have used in this survey the vector optimization problems as they were considered in the original works, i.e. in Euclidean, Hilbert or Banach spaces and with or without constraints, respectively. In order to maintain a reasonable length of the work, we gave for each algorithm only a convergence statement, not other related results such as well definiteness of the iterations.
Most of the proximal point type algorithms for solving vector optimization problems are formulated as theoretical schemes and some of them are accompanied by inexact versions that should be more suitable for implementation. While the papers presenting algorithms for solving scalar optimization problems usually contain applications and computational results, this is rarely the case for the ones dealing with methods for solving vector optimization problems. The algorithm introduced in [24] is explicitly presented as a theoretical scheme meant to be implemented someday and many of its followers are introduced in a similar manner. We discuss later the difficulties encountered while trying to actually numerically test such algorithms. However, making use of additional methods in order to solve the intermediate problems, various authors managed to provide viable implementations of the proximal point type algorithms they introduced for solving vector optimization problems and hence to deliver concrete computational results. We mention in the following, where applicable, on which classes of problems were the considered algorithms tested.
11.2 Preliminaries
In the following we present the general framework we consider within this study, following [24]. Where necessary we mention the changes to this setting. Note, however, that this work is not completely self-contained and the reader is referred to the original sources for some definitions and more properties of notions that are only briefly employed or mentioned within this study.
Let X be a Hilbert space and (Y, ∥⋅∥) a separable Banach space that is partially ordered by a pointed closed convex cone C ⊆ Y . Recall that C ⊆ Y is said to be a cone when tC ⊆ C for all t ≥ 0, that is called pointed when − C ∩ C = {0}. The partial ordering induced by C on Y is denoted by “\(\leqq _C\)” (i.e. it holds x ≦C
y when y − x ∈ C, where x, y ∈ Y ) and we write x ≤C
y if x ≦C
y and x ≠ y. A greatest element with respect to “\(\leqq _C\)” denoted by ∞
C which does not belong to Y is attached to this space, and let Y
• = Y ∪{∞
C}. Then for any y ∈ Y one has y ≤C
∞
C and we consider on Y
• the operations y + ∞
C = ∞
C + y = ∞
C for all y ∈ Y
• and t ⋅∞
C = ∞
C for all t ≥ 0. By 〈y
∗, y〉 we denote the value at y ∈ Y of the linear continuous functional y
∗∈ Y
∗, where (Y
∗, ∥⋅∥∗) is the dual space of Y , and by convention we take 〈y
∗, ∞
C〉 = +∞ for all y
∗∈ C
∗, where C
∗ = {y
∗∈ Y
∗ : 〈y
∗, y〉≥ 0 ∀y ∈ C} is the dual cone to C. The restricted polar to the cone C is K
δ = {z
∗∈ Y
∗ : 〈z
∗, y〉≥ δ∥y∥∥z
∗∥ for all y ∈ C} for some δ > 0. Given a subset U of X, by \( \operatorname *{\mathrm {cl}} U\), \( \operatorname *{\mathrm {cone}} U\), \( \operatorname *{\mathrm {int}} U\) and δ
U we denote its closure, conical hull, interior and indicator function, respectively. As \( \operatorname *{\mathrm {int}} C \cup \{0\}\) is a convex cone, too, we also write x <C
y when \(y-x\in \operatorname *{\mathrm {int}} C\). A set W ⊆ Y is said to have the domination property with respect to C, if there exists w ∈ Y such that W ⊆ w + C. The closed unit ball of Y is denoted by \(\mathcal {B}_Y\) and its unit sphere by \(\mathcal {S}_Y\). The convergence in the (corresponding) weak topology is denoted by “\(\rightharpoonup \)”, \( \operatorname *{\mathrm {id}}_X:X\to X\) is the identity operator on X and by \( \operatorname *{\mathrm {Pr}}_U\) we denote the projection onto the (closed convex) set U ⊆ X. When Y is finitely dimensional we consider it endowed with the Euclidean norm, unless otherwise specified. Denote also  .
.
A Banach space (Z, ∥⋅) is said to be strictly convex if ∥(1∕2)(x + y)∥ < 1 for all x, y ∈ Z with ∥x∥ = ∥y∥ = 1 and x ≠ y, and uniformly convex if limn→+∞∥x n − y n∥ = 0 for any two sequences \((x_n)_n, (y_n)_n \subseteq \mathcal {S}_Z\) such that limn→+∞(∥x n + y n∥)∕2 = 1. One says that Z is (uniformly) smooth if the limit limt→0(∥x + ty∥x∥)∕t exists (and is attained uniformly) for all \(x, y \in \mathcal {S}_Z\). The normalized duality mapping of Z is \(J_Z : Z \to 2^{Z^*}\) defined by \(J_Z(x) = \{x^* \in Z^* : \langle x^*, x\rangle = \|x\|{ }^2 = \|x^*\|{ }_*^2\}\).
When \(f:X\rightarrow \overline {\mathbb {R}}=\mathbb {R}\cup \{\pm \infty \}\) is proper (i.e. is nowhere equal to −∞ and has at least a real value) and ε ≥ 0, if \(f(x)\in \mathbb {R}\) the (convex) ε-subdifferential of f at x is ∂ ε f(x) = {x ∗∈ X ∗ : f(y) − f(x) ≥〈x ∗, y − x〉− ε ∀y ∈ X}, while if f(x) = +∞ we take by convention ∂ ε f(x) = ∅. The ε-subdifferential of f becomes in case ε = 0 its classical (convex) subdifferential denoted by ∂f. Then \(\bar x\in X\) is a minimum of f if and only if \(0\in \partial f(\bar x)\). Denote also by \([t]_+ = \max \{t, 0\}\) for any \(t\in \mathbb {R}\).
A vector function F : X → Y • = Y ∪{∞ C} is said to be proper if its domain \( \operatorname {{\mathrm {dom}}} F = \{x\in X: F(x)\in Y\}\) is nonempty, (strictly) C-convex if F(tx + (1 − t)y) ≦C(<C)tF(x) + (1 − t)F(y) for all x, y ∈ X and all t ∈ (0, 1) and positively C-lower semicontinuous (in the literature also star C-lower semicontinuous) when the function x↦〈z ∗, F(x)〉, further denoted by \((z^*F):X\rightarrow \overline {\mathbb {R}}\), is lower semicontinuous for all z ∗∈ C ∗∖{0}. A slightly stronger generalization of the classical lower semicontinuity to vector functions is the one due to Penot and Théra (cf. [66]) who called F to be C-lower semicontinuous x ∈ X if for any neighborhood V of 0 and for any b ∈ Y satisfying \(b\leqq _C F(x)\), there exists a neighborhood U of x in X such that F(U) ⊆ b + V + C ∪{∞ C}. Last but not least, F is called (cf. [36, 37, 39]) positively partially continuous if (z ∗ F) is continuous on every closed convex subset of \( \operatorname {{\mathrm {dom}}} F\) for every z ∗∈ C ∗, and C ∗-asymptotically uniformly continuous when for every bounded sequences (x n)n, (y n)n ⊆ X such that limn→+∞∥x n − y n∥ = 0 and each sequence \((z_n^*)_n \subseteq C^*\) weakly∗-converging to some z ∗∈ C ∗ there holds \(\lim _{n\to +\infty }\langle F(x_n)-F(y_n), z_n^*-z^*\rangle =0\). Related to this one can also define F to be C ∗-uniformly semicontinuous (on some closed convex set S ⊆ X) when for every weakly convergent sequence (x n)n ⊆ S to some x ∈ S and each sequence \((z_n^*)_n \subseteq C^*\) weakly∗-converging to some z ∗∈ C ∗, one has \(\lim _{n\to +\infty }|\langle z^*_n, F(x_n)-F(y_n)\rangle - \langle z^*, F(x)-F(y_n)\rangle |=0\) for any sequence (y n)n ⊆ S for which limn→+∞∥x n − y n∥ = 0. A generalization of the (convex) ε-subdifferential for vector functions is necessary for our presentation, too. When \(F:\mathbb {R}^n\rightarrow \mathbb {R}^m\), \(K\subseteq \mathbb {R}^m\) is a convex cone and ε ≥ 0, the (vector) ε-subdifferential of F at \(x\in \mathbb {R}^n\) is \(\partial _{\varepsilon } F (x)=\{V\in \mathbb {R}^{m\times n}: F(x)+ V^T(y-x)\leqq _K F(y)+\varepsilon e\) ∀y ∈ X} and it becomes the (vector) subdifferential of F denoted by ∂F when ε = 0.
Some notions of nonconvex nonsmooth analysis are necessary as well. Let \(f :\mathbb {R}^n \to \mathbb {R}\) be locally Lipschitz at \(x \in \mathbb {R}^n\) and \(d \in \mathbb {R}^n\). The Clarke directional derivative of f at x in the direction d is defined as f C(x;d) =limt↓0supy→x(f(y + td) − f(y))∕t, while the Clarke subdifferential of f at x is \(\partial ^C f (x) = \{w\in \mathbb {R}^n: w^\top d \leq f^C (x; d)\) \(\forall d \in \mathbb {R}^ n\}\).
In order to introduce some generalized distances, the following notions are necessary. A function \(d : \mathbb {R}^n \times \mathbb {R}^ n \to R_+ \cup \{+\infty \}\) is said to be a proximal distance with respect to a nonempty open convex set \(S \subseteq \mathbb {R}^n\) (cf. [8]) if for each y ∈ S it satisfies the following properties
-
(P1)
d(⋅, y) is proper, convex and continuously differentiable on S;
-
(P2)
\( \operatorname {{\mathrm {dom}}} d(\cdot , y) \subseteq \operatorname *{\mathrm {cl}} S\) and \( \operatorname {{\mathrm {dom}}} \nabla _1 d(\cdot ,y) = S\), where ∇1 denotes the gradient map with respect to the first variable;
-
(P3)
d(⋅, y) is level bounded on \(\mathbb {R}^n\), i.e., lim∥x∥→+∞ d(x, y) = +∞;
-
(P4)
d(y, y) = 0.
Moreover, a function \(H : \mathbb {R}^n \times \mathbb {R}^n \to \mathbb {R}_+\cup \{+\infty \}\) is called the induced proximal distance to a given proximal distance d if H is finitely valued on \( \operatorname *{\mathrm {cl}} S \times S\) and for each y, z ∈ S it satisfies H(y, y) = 0, ∇1 d(z, y)⊤(x − z) ≤ H(x, y) − H(x, z) for all \(x\in \operatorname *{\mathrm {cl}} S\) and H(x, ⋅) is level bounded on S, for all \(x \in \operatorname *{\mathrm {cl}} S\). One denotes by \(\mathcal {F}^*( \operatorname *{\mathrm {cl}} S)\) the set of pairs (d, H) as introduced above that satisfy the following two additional properties
-
(P5)
if (y n)n ⊆ S is a bounded sequence in S and \(\bar y \in \operatorname *{\mathrm {cl}} S\) such that \(\lim _{n\to +\infty } H(\bar y, y_n)=0\), then \(\lim _{n\to +\infty } y_n=\bar y\);
-
(P6)
if (y n)n ⊆ S converges to y, then at least one of the relations limn→+∞ H(y, y n) = 0 and \(\lim _{n\to +\infty } H(\bar y, y_n)=+\infty \) for all \(\bar y\in S\) such that \(\bar y\neq y\) holds true.
On the other hand, one says that \(q:\mathbb {R}^n\times \mathbb {R}^n\to \mathbb {R}_+\) is a quasi-distance (cf. [72]) when for any \(x, y, z\in \mathbb {R}^n\) it holds
-
(Q1)
q(x, y) = q(y, x) = 0 ⇔ x = y;
-
(Q2)
q(x, z) ≤ q(x, y) + q(y, z).
In [33] a vector-valued Bregman distance function was introduced. Let the proper, strictly C-convex and C-lower semicontinuous vector function \(G:\mathbb {R}^n\to (\mathbb {R}^m)^{\bullet }\) whose domain is closed, convex and has a nonempty interior, on which it is Gâteaux differentiable with the Gâteaux derivative DG(⋅). The vector-valued Bregman distance with respect to G is the map \(B_G : \operatorname {{\mathrm {dom}}} G \times \operatorname *{\mathrm {int}}( \operatorname {{\mathrm {dom}}} G)\to \mathbb {R}^m\), defined by B G(z, x) = G(z) − G(x) − DG(x)(z − x). Moreover, G is said to be a vector-valued Bregman distance function if it satisfies the following hypotheses
-
(A1)
for any \(x, y, z\in \operatorname *{\mathrm {int}} ( \operatorname {{\mathrm {dom}}} G)\), if \((DG(x)-DG(y))^\top (z-x)\notin - \operatorname *{\mathrm {int}} C\), then (DG(x) − DG(y))⊤(z − x) ∈ C;
-
(A2)
for any \(x \in \operatorname {{\mathrm {dom}}} G\), \(\lambda \in \{a\in \mathbb {R}^m_+: \|a\|=1\}\), bounded sequences \((x_n)_n, (y_n)_n\subseteq \operatorname *{\mathrm {int}} ( \operatorname {{\mathrm {dom}}} G)\) such that limn→+∞∥x n − y n∥ = 0, it holds limn→+∞(B G(x, x n) − B G(x, y n))⊤ λ = 0;
-
(A3)
for any bounded sequences \((x_n)_n, (y_n)_n\subseteq \operatorname *{\mathrm {int}} ( \operatorname {{\mathrm {dom}}} G)\) such that limn→+∞ y n = y and, for any \(\lambda \in \{a\in \mathbb {R}^m_+: \|a\|=1\}\), limn→+∞ B G(x n, y n)⊤ λ = 0, one has limn→+∞ x n = y.
A vector-valued Bregman distance function \(G:\mathbb {R}^n\to (\mathbb {R}^m)^{\bullet }\) that satisfies also the condition
-
(A4)
for every \(y\in \mathbb {R}^n\) and \(\lambda \in \mathbb {R}^m_+\cap \mathcal {S}_{\mathbb {R}^m}\), there exists \(x\in \operatorname *{\mathrm {int}} ( \operatorname {{\mathrm {dom}}} G)\) such that DG(x)⊤ λ = y;
is said to be a strengthened vector-valued Bregman distance function.
On the other hand, a vector-valued coercive viscosity function \(G : \mathbb {R}^n \to (\mathbb {R}^m)^{\bullet }\) is a proper, strictly C-convex and C-lower semicontinuous vector function with a closed convex domain with a nonempty interior, that is Gâteaux differentiable on the interior of its domain and whose Gâteaux derivative DG(⋅) is nonexpansive on \( \operatorname {{\mathrm {dom}}} G\) such that there exists an \(x \in \operatorname {{\mathrm {dom}}} G\) with ∥x∥ < +∞ such that DG(x) = 0.
When Z is a smooth Banach space, one defines the Lyapunov functional as \(L : Z \times Z \to \mathbb {R}_+\), defined by L(x, y) = ∥x∥2 − 2〈J Z(y), x〉 + ∥y∥2, x, y ∈ Z. For further properties of this function that are relevant for the algorithms discussed in this paper the reader is referred to [35, Section 2].
Let S ⊆ X. A mapping A : S → X is said to be monotone when 〈Ax − Ay, x − y〉≥ 0 for all x, y ∈ S. Using it, one can define a monotone variational inequality problem that consists of determining an x ∈ S such that 〈Ax, y − x〉≥ 0 for all y ∈ S and whose set of solutions is denoted by V I(A, S).
Assume further, unless explicitly stated otherwise, that \( \operatorname *{\mathrm {int}} C \neq \emptyset \). Consider the vector optimization problem
(V P) \( \operatorname *{\mathrm {Min}} \limits _{x \in X} F(x)\),
where F : X → Y
• is a proper vector function. When \(Y=\mathbb {R}^m\) we usually write  .
.
In case the vector minimization of F is considered subject to some nonempty subset S of X such that \( \operatorname {{\mathrm {dom}}} F\cap S\neq \emptyset \), we consider the vector optimization problem
(V PG) \( \operatorname *{\mathrm {Min}} \limits _{x \in S} F(x)\).
Later in Remark 11.33 a vector optimization problem with both geometric and equality constraints is briefly discussed, while in Section 11.5 we consider other vector optimization problems whose objective functions consist of sums or differences of (C-convex) vector functions.
In the literature one can find different solution notions for vector optimization problems. We present here the ones needed for our presentation. An element \(\bar x\in \operatorname {{\mathrm {dom}}} F\) is said to be an efficient solution to (V P) if there is no x ∈ X such that \(F(x)\leq _C F(\bar x)\) and a weakly efficient solution to (V P) if \((F(\bar x) - \operatorname *{\mathrm {int}} C)\cap F( \operatorname {{\mathrm {dom}}} F)=\emptyset \), respectively. We denote by \(\mathcal {E}(VP)\) the efficiency set to (V P), i.e. set of all efficient solutions to (V P), and by \(\mathcal {W}\mathcal {E} (VP)\) the one of all weakly efficient ones, i.e. the weak efficiency set. Moreover, \(\bar x\in \operatorname {{\mathrm {dom}}} F\) is a properly efficient solution (in the sense of Henig and Lampe) to (V P) if there is a pointed closed convex cone K ⊆ Y such that \(C\setminus \{0\} \subseteq \operatorname *{\mathrm {int}} K\) and \((F( \operatorname {{\mathrm {dom}}} F)-F(\bar x)) \cap (-K) =\{0\}\), and we denote this by \(\bar x\in \mathcal {P}\mathcal {E} (VP)\). Another proper efficiency notion considered in this presentation is the following (for other types of properly efficient solutions to (V P), such as the ones due to Borwein from [25, 26], we refer to [21, Section 2.4]). We say, for δ ∈ (0, 1], that \(\bar x\in \operatorname {{\mathrm {dom}}} F\) is a properly efficient solution (with respect to K
δ
) to (V P) when there exists some z
∗∈ K
δ ∖{0} such that \(\langle z^*, F(\bar x)\rangle \leq \langle z^*, F(x)\rangle \) for all x ∈ X and we write this \(\bar x\in \mathcal {P}\mathcal {E}_{\delta } (VP)\). The corresponding efficiency notions for (V PG) are defined analogously, by replacing X by S and \( \operatorname {{\mathrm {dom}}} F\) by \( \operatorname {{\mathrm {dom}}} F\cap S\) in the definitions. Further, when \(X=\mathbb {R}^n\), \(Y=\mathbb {R}^m\) and \(F:\mathbb {R}^n\to \mathbb {R}^m\) is locally Lipschitz, an element \(\bar x\in \mathbb {R}^n\) is said to be a (Pareto-Clarke) critically efficient solution to (V P) if, for any direction \(d \in \mathbb {R}^n\), there exists a  , such that \(F_j^C (\bar x; d) \geq 0\). When F can be written as the difference of two C-convex functions \(F_1,F_2:\mathbb {R}^n\to \mathbb {R}^m\) the last definition collapses to the existence of a \(u\in C^*\cap \mathcal {S}_{\mathbb {R}^m}\) such that 0 ∈ (∂F
1(x) − ∂F
2(x))⊤
u. Theoretically nice, but without much practical relevance are the so-called ideally efficient solutions to (V P) in case \(Y=\mathbb {R}^m\), defined as those \(\bar x\in \operatorname {{\mathrm {dom}}} F\) for which \(F_j(\bar x)\leq F_j(x)\) for all x ∈ X, where
, such that \(F_j^C (\bar x; d) \geq 0\). When F can be written as the difference of two C-convex functions \(F_1,F_2:\mathbb {R}^n\to \mathbb {R}^m\) the last definition collapses to the existence of a \(u\in C^*\cap \mathcal {S}_{\mathbb {R}^m}\) such that 0 ∈ (∂F
1(x) − ∂F
2(x))⊤
u. Theoretically nice, but without much practical relevance are the so-called ideally efficient solutions to (V P) in case \(Y=\mathbb {R}^m\), defined as those \(\bar x\in \operatorname {{\mathrm {dom}}} F\) for which \(F_j(\bar x)\leq F_j(x)\) for all x ∈ X, where  .
.
From [21, Corollary 2.4.26] one has the following characterization of the weakly efficient solutions to (V P) in the convex setting.
Lemma 11.1
If F is also C-convex, then \(\bar x\in \mathcal {W}\mathcal {E} (VP)\) if and only if
Remark 11.1
As noted above, there are quite simple vector optimization problems where an unfortunate choice of the scalarizing function can often lead to unbounded scalar optimization problems. Take, for instance, the example presented in [24, Remark 1], where \(X=Y=\mathbb {R}^2\), \(C=\mathbb {R}_+^2\) and \(F(x_1, x_2)=(x_1^2-x_2, x_2)^\top \). For every \(z^* = (z^*_1, z^*_2)^\top \in C^*=\mathbb {R}_+^2\) with \(z^*_1 \neq z^*_2\) the scalarized optimization problem infx ∈ X(z ∗ F)(x) is unbounded from below, hence it has no optimal solutions and is of little use in identifying the weakly efficient solutions to the original vector optimization problem. Only the scalarization functionals based on \(z^* = (z^*_1, z^*_2)^\top \in \mathbb {R}_+^2\setminus \{0\}\) with \(z^*_1=z^*_2\) generate scalarized optimization problems that have optimal solutions, delivering hence weakly efficient solutions to the original vector optimization problem.
For guaranteeing the convergence of many of the algorithms that are presented in this work the following notion is necessary. Note that it is defined in a more general framework in [57, Definition 3.2]. It is followed by a weaker version needed only for the convergence of the method from [28, 38] (see Theorem 11.15 and Theorem 11.16).
Definition 11.1 (cf. [24])
Given x ∈ X, the set F(X) ∩ (F(x) − C) is said to be C-complete when for all sequences (a n)n ⊆ X with a 0 = x such that F(a n+1) ≦C F(a n) for all n ≥ 1 there exists an a ∈ X such that F(a) ≦C F(a n) for all n ≥ 1.
Definition 11.2 (cf. [28])
Given x ∈ S, where S ⊆ X is a closed convex set, the set F(S) ∩ (F(x) − C) is said to be C-quasicomplete for S when for all sequences (a n)n ⊆ X with a 0 = x such that F(a n+1) ≦C F(a n) for all n ≥ 1 one has F(a) ≦C F(a n) for all n ≥ 1 and all \(a\in \mathcal {W}\mathcal {E} (VP) \cap VI(S, A)\), where A : S → X is a monotone mapping.
11.3 The Original Proximal Point Type Method for Vector Optimization Problems
As mentioned above, the first work where the classical proximal point method was actually extended from scalar optimization to vector optimization problems is [24]. The algorithm introduced there, on which basically all the future contributions to this field rely on, is the following one.
Algorithm 1
Choose the starting point \(x_1\in \operatorname {{\mathrm {dom}}} F\) and the exogenous sequences (α n)n ⊆ (0, α], with α > 0, and \((e_n)_n\subseteq \operatorname *{\mathrm {int}} C\) such that ∥e n∥ = 1 for all n ≥ 1. Consider the following iterative steps
-
1
let n = 1;
-
2
if \(x_n\in \mathcal {W}\mathcal {E}(VP)\) , then x n+p = x n for all p ≥ 1;
-
3
otherwise find \(x_{n+1}\in \mathcal {W}\mathcal {E} \Big \{F(x) + \frac {\alpha _n}{2}\|x-x_n\|{ }^2 e_n: x\in \varOmega _n\Big \}\) , where Ω n = {x ∈ X : F(x) ≦C F(x n)};
-
4
take n := n + 1 and go to Step 2.
Under usual convexity and topological hypotheses applied on F one can prove the following weak convergence result.
Proposition 11.1 (cf. [24, Proposition 3.3])
Let F be C-convex and positively C-lower semicontinuous. If the sequence (x n)n generated by Algorithm 1 has a weak cluster point, then it is weakly convergent towards a weakly efficient solution to (V P).
However, in order to prove the weak convergence of this algorithm towards a weakly efficient solution to (V P) regardless of the knowledge available only after running it, an additional hypothesis is necessary.
Theorem 11.1 (cf. [24, Theorem 3.1])
Let F be C-convex and positively C-lower semicontinuous and assume that F(X) ∩ (F(x 1) − C) is C-complete. Then any sequence (x n)n generated by Algorithm 1 converges weakly towards a weakly efficient solution to (V P).
Some comments are in order.
Remark 11.2
When \(Y=\mathbb {R}\) and \(C=\mathbb {R}_+\) (i.e. in the scalar case), Algorithm 1 collapses to the classical proximal point method for scalar optimization problems, supporting thus the fact that it is a direct extension of the latter.
Remark 11.3
In every iteration of Algorithm 1 a different intermediate vector optimization problem is addressed, each of them having a smaller feasible set than its predecessor.
Remark 11.4
The operation that takes place in Step 3 of Algorithm 1 can be considered as a vector counterpart of determining the proximal point of a scalar function at a given point, i.e. one could call the set-valued mapping
where Ω v = {x ∈ X : F(x) ≦C F(v)}, vector proximal point operator. Of course the analogy is not perfect, since the scalar (Moreau) proximal point operator is single-valued if the involved scalar function is proper, convex and lower-semicontinuous. Note also that the \( \operatorname *{\mbox{arg min}}\) operation within is unconstrained. However, (11.1) is at the moment the closest construction to the scalar (Moreau) proximal point operator one has in the vector case and when particularized to the scalar framework it coincides with the latter.
Remark 11.5
The construction of x n+1 in Algorithm 1 guarantees the decreasing monotonicity of the sequence (F(x n))n with respect to the cone C. However, this is not enough to guarantee its convergence.
Remark 11.6
Alternate stopping rules to the one used in the formulation of Algorithm 1 can be found in [24, Remark 2 and Proposition 3.2]. Since it is usually not an easy task to verify whether \(x_n\in \mathcal {W}\mathcal {E}(VP)\), one can instead check if x n+1 = x n.
Remark 11.7
At a first look the construction of the new iterate in Algorithm 1 contradicts the basic fact that the subproblems that are employed in an iterative process have to be simpler and more easily solvable than the original optimization problem one aims to solve with the method in discussion, as the intermediate problems have more complicated objective functions than (V P) and, on the top of it, they are constrained (in a world where the proximal point methods still lack the ability to solve general constrained optimization problems even in the scalar setting). However, any z ∗∈ C ∗∖{0} provides a suitable scalarization functional (whose existence is guaranteed by Lemma 11.1 under the hypotheses of Theorem 11.1) for the vector optimization problems in Step 3 of Algorithm 1. This endows the method with additional flexibility properties that may prove to be useful when implementing it. Moreover, even if the function
has, because it is lower semicontinuous and strongly convex, exactly one minimum that is x n+1, the sequence (x n)n is not uniquely determined because for each choice of z ∗∈ C ∗∖{0} one deals with a different such function. This does not mean that the vector optimization problem (V P) is a priori scalarized by means of a linear continuous functional, because this scalarization is applied to the intermediate vector optimization problems not to (V P).
Remark 11.8
Different to the classical proximal point method, in the convergence statement Theorem 11.1 it is not necessary to assume the existence of a solution of the considered optimization problem, i.e. a weakly efficient solution to (V P), in order to prove the convergence of Algorithm 1. The role of such a hypothesis in showing the convergence of the method has been fully covered in the proof of Theorem 11.1 (see [24, Theorem 3.1]) by the assumed C-completeness hypothesis. Considering the former instead of the latter, the role of ∩n≥1 Ω n would be taken by \(\mathcal {W}\mathcal {E}(VP)\) in the proof of Theorem 11.1 (i.e. [24, Theorem 3.1]). However, then is the inclusion \(\mathcal {W}\mathcal {E}(VP)\subseteq \varOmega _n\) for all n ≥ 1 not obviously guaranteed by construction and should be separately investigated (or imposed). Note moreover that assuming the existence of some \(\bar x \in \mathcal {W}\mathcal {E}(VP)\) does not automatically deliver the corresponding scalarizing parameter \(\bar z^*\) that exists according to Lemma 11.1, which would probably be needed in formulating the algorithm under the mentioned hypothesis.
Remark 11.9
In the scalar setting (i.e. when \(Y = \mathbb {R}\) and \(C=\mathbb {R}_+\)), when the set of minimizers of a function \(f:X\to \overline {\mathbb {R}}\) is nonempty, for every \(x_1\in \operatorname {{\mathrm {dom}}} F\) the intersection \((f(x_1)-\mathbb {R}_+) \cap f(X)\) is \(\mathbb {R}_+\)-complete, i.e. the C-completeness hypothesis of Theorem 11.1 is always satisfied. However, in even slightly more complex frameworks this hypothesis is no longer automatically valid and its eventual fulfillment is not always easy to verify. Sufficient conditions for guaranteeing that F(X) ∩ (F(x 1) − C) is C-complete were proposed in [57, Lemma 3.5], namely
-
the set (F(x 1) − C) ∩ F(X) is compact;
-
the set (F(x 1) − C) ∩ F(X) is weakly compact;
-
the set (F(x 1) − C) ∩ F(X) is closed and has a lower bound and the cone C has the Daniell property (i.e., any decreasing net having a lower bound converges to its infimum).
On the other hand, it could be interesting to investigate whether the weaker hypothesis of C-quasicompleteness imposed on F(X) ∩ (F(x 1) − C) in Theorem 11.15 and Theorem 11.16 could prove to be sufficient for convergence for other algorithms as well.
Remark 11.10
For determining the optimal solutions of the scalarized optimization problems attached to the vector optimization problems in Step 3 of Algorithm 1 one can try to employ a splitting type algorithm designed for finding the optimal solutions of optimization problems consisting in minimizing sums of convex functions, like the ones proposed in [9, 18, 20, 22]. However, the processing of the functions \(\delta _{\varOmega _n}\), n ≥ 1, may prove to be quite difficult, due to the special structure of the sets Ω n, n ≥ 1. A way to go round this nuisance is, as seen in [4, 19, 52, 53, 67,68,69], by employing some other algorithms for solving the intermediate scalar optimization problems, for instance one based on interior point methods.
In [24, Section 4] it is discussed about the additional hypotheses needed by Algorithm 1 in order to deliver efficient solutions to (V P) instead of weakly efficient ones. In this case it is not necessary to have \( \operatorname *{\mathrm {int}} C\neq \emptyset \).
Theorem 11.2 (cf. [24, Theorem 4.1])
Let F be C-convex and positively C-lower semicontinuous and assume that F(X) ∩ (F(x 1) − C) is C-complete and that there exists some δ > 0 such that the set K δ is nonempty. Then any sequence (x n)n generated by Algorithm 1 with the selection
where \((z^*_n)_n\subseteq K_\delta \) , converges weakly towards an efficient solution to (V P).
Last but not least, an inexact version of Algorithm 1 is proposed in [24, Section 5] for the purpose of providing an implementable iterative scheme, that, however, was not concretely tested on an example or an application. As the authors put it, the Step 3 in Algorithm 2 is formulated in a scalar manner in order to avoid unnecessary complications, but x n+1 could be as well taken as some approximate weakly efficient solution to the corresponding intermediate vector optimization problem in Algorithm 1.
Algorithm 2
Choose the starting point \(x_1\in \operatorname {{\mathrm {dom}}} F\) , the relative error tolerance σ ∈ [0, 1) and the exogenous sequences (α n)n ⊆ (0, α], with α > 0, \((e_n)_n\subseteq \operatorname *{\mathrm {int}} C\) such that ∥e n∥ = 1 for all n ≥ 1 and \((z^*_n)_n\in C^*\) such that \(\|z^*_n\|=1\) for all n ≥ 1. Consider the following iterative steps
-
1
let n = 1;
-
2
if \(x_n\in \mathcal {E}(VP)\) , then x n+p = x n for all p ≥ 1;
-
3
otherwise find x n+1 ∈ X as a solution of the inclusion \(0\in \partial _{\varepsilon _n} \langle z^*_n, F(x) + \delta _{\varOmega _n}\rangle + {\alpha _n}\langle z^*_n, e_n\rangle (x-x_n)\) , where \(\varepsilon _n\leq \sigma \frac {\alpha _n}{2}\langle z^*_n, e_n\rangle \|x-x_n\|{ }^2\) ;
-
4
take n := n + 1 and go to Step 2.
The convergence of Algorithm 2 is obtained in a similar manner to the one of Algorithm 1 and in [24, Remark 6] it is stated that one can also obtain efficient solutions to (V P) under the additional hypotheses from Theorem 11.2.
Theorem 11.3 (cf. [24, Theorem 5.1])
Let F be C-convex and positively C-lower semicontinuous and assume that F(X) ∩ (F(x 1) − C) is C-complete. Then any sequence (x n)n generated by Algorithm 2 converges weakly towards a weakly efficient solution to (V P).
Remark 11.11
As noted in [19, Remark 11], vector optimization problems with the ordering cones of the image spaces having empty interiors, but nonempty generalized interiors can be found in finance mathematics (see, for instance, [1, 44]) and other research fields. This has motivated the weakening of the definition of the weakly efficient solutions to (V P) (cf. [44, 49, 50]) for the case when \( \operatorname *{\mathrm {int}} C=\emptyset \) by replacing this hypothesis with the nonemptiness of the quasi interior of C (i.e. the set of all y ∈ Y such that \( \operatorname *{\mathrm {cl}}( \operatorname *{\mathrm {cone}}(V-y))=Y\)). In order to characterize these more general weakly efficient solutions to (V P) one can use [50, Corollary 9] instead of Lemma 11.1. However, since the key result [23, Lemma 2.2] does not hold in case \( \operatorname *{\mathrm {int}} C=\emptyset \), the proof of the algorithm convergence statement Theorem 11.1 has to be modified, for instance, by scalarizing all the subproblems with the same \(\bar z^*\in C^*\setminus \{0\}\). On the other hand, in finitely dimensional spaces so-called relatively weakly efficient solutions to (V P) can be defined when C has an empty interior but a nonempty relative interior and they can be characterized by means of linear scalarization (cf. [49]) while the impediment mentioned above does not occur due to the equivalence of the corresponding weak and strong topologies.
Remark 11.12
Algorithm 1 is applied in [31] for vector-minimizing in the finitely dimensional setting where \(X=\mathbb {R}^n\) and \(Y=\mathbb {R}^m\) the composition of a vector function with a linear continuous mapping subject to a geometric constraint. We have not included this method in Section 11.5 because the author merely replaced in Algorithm 1 the vector function \(F:\mathbb {R}^p\to (\mathbb {R}^m)^\bullet \) with its composition with the considered linear continuous mapping \(A:\mathbb {R}^n\to \mathbb {R}^p\) and did not apply some splitting method in order to process F and A separately during the iterative process. In order to guarantee the convergence of the method towards a weakly efficient solution to the considered vector optimization problem no C-completeness hypothesis is employed, however the domination property of the image of the objective vector function is imposed and the weak efficiency set is taken to be compact.
Remark 11.13
In the literature one can find contributions where the convergence of Algorithm 1 (or of its inexact version) is proven under different hypotheses than the ones of Theorem 11.1, in the sense that the objective function F of the considered vector optimization problem needs not be C-convex in order to achieve the desired result. In the following we discuss briefly the results of [4, 12, 14, 15, 69]. Consider the finitely dimensional setting with \(X=\mathbb {R}^n\), \(Y=\mathbb {R}^m\) and, moreover, \(C=\mathbb {R}^m_+\). In [12] Algorithm 1 (with the difference that the elements of the sequence (x n)n are additionally asked to lie in S) is employed for solving (V PG) (the geometrically constrained counterpart of (V P)). The components of the vector function F are asked to be locally Lipschitz and, under some additional hypotheses imposed on the involved sequences it is shown in [12, Theorem 3] that every cluster point of (x n)n is a critically efficient solution to (V PG). Taking the components of F to be quasiconvex and imposing the \(\mathbb {R}^m_+\)-completeness hypothesis, the convergence of the generated sequence (x n)n towards a critically efficient solution to (V PG) is achieved. An application to the compromise solution problem is discussed, however no numerical results are provided. The same algorithm is employed in [15] for vector minimizing a vector function \(F:\mathbb {R}^n\to \mathbb {R}^m\) whose components are maxima of continuously differentiable functions over some given subset of \(\mathbb {R}^n\). In [15, Theorem 1] the convergence of the iterative method is investigated and it is shown that each cluster point of the generated sequence is a critically efficient solution to (V PG). Under additional hypotheses the convergence of the generated sequence towards a weakly efficient solution to (V PG) is achieved. Further, in [14] a proximal point type algorithm that solves at each step a scalarized version (by means of a special case of the Tammer scalarization function - the so-called maximum scalarization, see also Remark 11.31 and Remark 11.32) of the corresponding intermediate vector optimization problem from Algorithm 1 is proposed, with the convergence of the generated sequence towards a critically efficient solution to (V P) shown under quasiconvexity hypotheses imposed on the components of F in [14, Theorem 4.1]. It is also shown that under stronger assumptions the sequence can converge towards a weakly efficient solution to (V P) and even an efficient one in [14, Theorem 4.3], while an application to behavioural science is also discussed. Last but not least in [4, 69] one finds proximal point type algorithms for solving (V P) with the components of F taken quasiconvex, where the iterations are defined as zeros of subdifferential inclusions, in the vein of Algorithm 2 but without the error sequence (ε n)n and with the Clarke and Fréchet subdifferential, respectively, instead of the convex one. The convergence of the generated sequence is guaranteed towards critically efficient solutions (and, under additional convexity hypotheses imposed on the components of F, also towards weakly efficient solutions) to (V P) in [4] and towards a minimizing set (and, under additional continuity hypotheses imposed on the components of F, also towards weakly efficient, and, if these are taken also convex, even efficient solutions) to (V P). Worth noticing, however, is that in both these papers computational results obtained in matlab are presented, too. Note also that in [4] one can find an application to location theory, while in [69] an inexact version of the considered algorithm and an application to consumer demand theory are given as well.
11.4 Modifications and Extensions of the Original Method
Several authors have proposed various modifications and extensions of the proximal point type method introduced in [24]. Besides the extensions towards nonconvex vector optimization problems mentioned in Remark 11.13, there are algorithms where the norm distance from the classical proximal point iteration is replaced by a quasi-distance, a Bregman distance, a Lyapunov distance or is formulated by means of a viscosity function and proximal point type algorithms with inertial/memory effects or hybrid constructions. Generalizations of the algorithm from [24] towards Hadamard and Banach spaces were proposed, too. We also briefly mention some contributions where the regularization is performed by means of a Tikhonov type function instead of the Moreau-Yosida type one from the proximal point algorithms.
We begin with algorithms where the classical distance expressed via a norm is replaced by a generalization of it.
11.4.1 Algorithms with Bregman-Type Distances
In [75], a so-called interior proximal method is proposed for solving a geometrically constrained version of (V P) in finitely-dimensional spaces, i.e. (V PG), where \(F:\mathbb {R}^n\rightarrow (\mathbb {R}^m)^{\bullet }\) is a proper vector function and \(S\subseteq \mathbb {R}^n\) is a closed convex set with nonempty interior. The algorithm employs a proximal distance d with respect to \( \operatorname *{\mathrm {int}} S\) and before formulating it one assumes that \(S\subseteq \operatorname {{\mathrm {dom}}} F\).
Algorithm 3
Choose the starting point \(x_1\in \operatorname *{\mathrm {int}} S\) and the exogenous sequences (α n)n ⊆ (0, α], with α > 0, and \((e_n)_n\subseteq \operatorname *{\mathrm {int}} C\) such that ∥e n∥ = 1 for all n ≥ 1. Consider the following iterative steps
-
1
let n = 1;
-
2
if \(x_n\in \mathcal {W}\mathcal {E}(VPG)\) , then x n+p = x n for all p ≥ 1;
-
3
otherwise find \(x_{n+1}\in \mathcal {W}\mathcal {E} \Big \{F(x) + \alpha _n d(x,x_n) e_n: x\in \varOmega _n\Big \}\) ;
-
4
take n := n + 1 and go to Step 2.
For the statement on convergence towards a weakly efficient solution to (V PG), the following additional hypotheses are required
-
(B1)
\(\exists \tilde z\in C^*\setminus \{0\}\) such that \(\tilde z^\top F(x)>-\infty \) for all x ∈ S;
-
(B2)
d(⋅, u) is coercive for any u ∈ S in \(\mathbb {R}^n\).
Theorem 11.4 (cf. [75, Theorem 4.1])
Let F be C-convex and positively C-lower semicontinuous and assume that F(S) ∩ (F(x 1) − C) is C-complete, the conditions (B1) − (B2) hold and \((d, H)\in \mathcal {F}^*( \operatorname *{\mathrm {cl}} S)\) . Then any sequence (x n)n generated by Algorithm 3 converges towards a weakly efficient solution to (V PG).
Remark 11.14
In [75, Section 5] an inexact version of Algorithm 3 was proposed, too, with the corresponding convergence towards a weakly efficient solution to (V PG) obtained in [75, Theorem 5.1] under some additional hypotheses.
Remark 11.15
Another inexact algorithm based on a proximal distance was proposed in [17] for vector minimizing a vector function \(F:\mathbb {R}^n\to \mathbb {R}^m\) whose components are maxima of continuously differentiable functions over some given subset of \(\mathbb {R}^n\), like the one treated in [15]. In [17, Theorem 4.1] the convergence of the iterative method is investigated and it is shown that each cluster point of the generated sequence is a critically efficient solution to (V PG). An application to a problem of distributive justice is also presented together with some ideas for future research.
A somehow similar algorithm was proposed in [33] for solving (V PG), with the difference that the authors take \(F:S\rightarrow (\mathbb {R}^m)^{\bullet }\) and assume that \( \operatorname *{\mathrm {int}} S\cap \operatorname {{\mathrm {dom}}} F \neq \emptyset \). In order to introduce it, one needs to consider a strengthened vector-valued Bregman distance function \(G:\mathbb {R}^n\to (\mathbb {R}^m)^{\bullet }\).
Algorithm 4
Assume that a starting point \(x_1\in \operatorname *{\mathrm {int}} S\cap \operatorname {{\mathrm {dom}}} F\) such that \(\{x\in \mathbb {R}^n: F(x)\leqq _C F(x_1)\}\subseteq \operatorname {{\mathrm {dom}}} F \cap \operatorname *{\mathrm {int}} ( \operatorname {{\mathrm {dom}}} G)\) exists and choose the exogenous sequence (α n)n ⊆ (0, α], with α > 0. Consider the following iterative steps
-
1
let n = 1;
-
2
if \(x_n\in \mathcal {W}\mathcal {E}(VPG)\) , then x n+p = x n for all p ≥ 1;
-
3
otherwise find \(x_{n+1}\in \mathcal {W}\mathcal {E} \Big \{F(x) + \frac {\alpha _n}{2} B_G(x,x_n): x\in \varOmega _n\Big \}\) ;
-
4
take n := n + 1 and go to Step 2.
The statement on convergence of the sequence generated via Algorithm 4 towards a weakly efficient solution to (V PG) follows. Note that, unlike its counterparts presented above, it requires no C-completeness in order to achieve the convergence, however the domination property of the image of the objective vector function is imposed.
Theorem 11.5 (cf. [33, Theorem 3.3])
Let F be C-convex and C-lower semicontinuous such that \(F(\mathbb {R}^n)\) has the domination property, \(\mathcal {W}\mathcal {E}(VPG)\) is nonempty and compact and DG is norm-to-norm continuous. Then any sequence (x n)n generated by Algorithm 4 converges towards a weakly efficient solution to (V PG).
Further generalizations of the classical distance function can be found in the class of the so-called quasi-distances. Successfully employed in proximal point type algorithms, they ended up being used in iterative methods for determining weakly efficient solutions to vector optimization problems, too, for instance in [72], as follows, where  , \(C=\mathbb {R}^m_+\) and \(q:\mathbb {R}^n\times \mathbb {R}^n\to \mathbb {R}_+\) is a quasi-distance.
, \(C=\mathbb {R}^m_+\) and \(q:\mathbb {R}^n\times \mathbb {R}^n\to \mathbb {R}_+\) is a quasi-distance.
Algorithm 5
Choose the starting point \(x_1\in \mathbb {R}^n\) and the exogenous sequence (α n)n ⊆ (η, α], with 0 < η < α. Consider the following iterative steps
-
1
let n = 1;
-
2
if \(x_n\in \mathcal {W}\mathcal {E}(VP)\) , then x n+p = x n for all p ≥ 1;
-
3
otherwise find \(x_{n+1}\in \mathcal {W}\mathcal {E} \Big \{F(x) + \frac {\alpha _n}{2} q^2(x,x_n): x\in \varOmega _n\Big \}\) ;
-
4
take n := n + 1 and go to Step 2.
The convergence statement of Algorithm 5 follows, noting that the uniqueness of the cluster point of the sequence generated by the method is not guaranteed. Worth noticing is also that the considered hypotheses imply the usual C-completeness assumption needed in the rest of the paper for guaranteeing the convergence of the considered algorithms.
Theorem 11.6 (cf. [72, Theorem 3.1])
Let F
i be convex,  , and assume that there is some
, and assume that there is some  such that lim∥x∥→+∞
F
j(x) = +∞. Suppose there are positive constants a and b such that a∥x − y∥≤ q(x, y) ≤ b∥x − y∥ for any \(x, y \in \mathbb {R}^n\)
. Then any cluster point of any sequence (x
n)n generated by Algorithm 5 is a weakly efficient solution to (V P).
such that lim∥x∥→+∞
F
j(x) = +∞. Suppose there are positive constants a and b such that a∥x − y∥≤ q(x, y) ≤ b∥x − y∥ for any \(x, y \in \mathbb {R}^n\)
. Then any cluster point of any sequence (x
n)n generated by Algorithm 5 is a weakly efficient solution to (V P).
Remark 11.16
Computational results obtained by implementing Algorithm 5 in matlab are presented in [72, Section 4].
Remark 11.17
An inexact version of Algorithm 5 was proposed in [70] by means of the limiting subdifferential. The usage of this nonsmooth subdifferential instead of the classical convex one is justified by the fact that even if F is taken \(\mathbb {R}^m_+\)-convex, the quasi-distance needs not be convex.
11.4.2 Algorithms with Viscosity Functions and Tikhonov Type Regularizations
In order to present the proximal point type algorithms for solving vector optimization problems where the regularization is done by means of viscosity functions that were introduced in [30, 39] one needs to take \(X=\mathbb {R}^n\) and \(Y=\mathbb {R}^m\) within this subsection. Moreover, let \(G:\mathbb {R}^n\to \mathbb {R}^m\) be a vector-valued coercive viscosity function such that \( \operatorname {{\mathrm {dom}}} F\cap \operatorname *{\mathrm {int}} ( \operatorname {{\mathrm {dom}}} G)\neq \emptyset \).
We begin with the method proposed in [30] for determining weakly efficient solutions to (V P).
Algorithm 6
Choose the starting point \(x_1\in \operatorname {{\mathrm {dom}}} F\cap \operatorname *{\mathrm {int}} ( \operatorname {{\mathrm {dom}}} G)\) and the exogenous sequences (α n)n ⊆ (0, +∞), with limn→+∞ α n = +0, and (β n)n ⊆ [0, 1] with limn→+∞ β n = 0. Consider the following iterative steps
-
1
let n = 1;
-
2
if \(x_n\in \mathcal {W}\mathcal {E}(VP)\) , then x n+p = x n for all p ≥ 1;
-
3
otherwise find \(y_{n+1}\in \mathcal {W}\mathcal {E} \Big \{F(x) + \alpha _n G(x): x\in \varOmega _n\Big \}\) ;
-
4
take x n+1 = (1 − β n)y n + β n x n ;
-
5
take n := n + 1 and go to Step 2.
The convergence statement of Algorithm 6 follows. Note that the constructions considered in this subsection do not require the usual C-completeness hypothesis needed in the rest of the paper for guaranteeing the convergence of the considered algorithms, its role being covered by asking \(\mathcal {W}\mathcal {E}(VP)\) to be nonempty and compact. Connected to this issue see also the discussion in Remark 11.8.
Theorem 11.7 (cf. [30, Theorem 3.3])
Let F be C-convex, C-lower semicontinuous and C ∗ -asymptotically uniformly continuous such that \(\mathcal {W}\mathcal {E}(VP)\) is nonempty and compact. Further suppose that there exist a sequence \((\eta _n)_n \in \mathbb {R}\) such that ∥y n − x n∥≤ η n for all n ≥ 1 and ∑n≥1 η n < +∞, where (x n)n and (y n)n are sequences generated by Algorithm 6 . Then (x n)n converges towards a weakly efficient solution to (V P).
Remark 11.18
An legitimate question regarding Theorem 11.7 concerns the necessity of both topological assumptions imposed on F, the C-lower semicontinuity and the C ∗-asymptotically uniform continuity in order to achieve the statement. However, at the moment we are unaware of any result connecting or comparing these two notions in some way.
A modification of Algorithm 6 proposed in [39] guarantees the convergence of the generated sequence towards an efficient solution to (V P). More precisely, instead of determining weakly efficient solutions of the intermediate problems, one looks in Step 3 for properly efficient ones with respect to K δ. In this case it is not necessary to have \( \operatorname *{\mathrm {int}} C\neq \emptyset \).
Algorithm 7
Choose the starting point \(x_1\in \operatorname {{\mathrm {dom}}} F\cap \operatorname *{\mathrm {int}} ( \operatorname {{\mathrm {dom}}} G)\) and the exogenous sequences (α n)n ⊆ (0, +∞), with limn→+∞ α n = +0, and (β n)n ⊆ [0, 1] with limn→+∞ β n = 0. Assume moreover that there exists some δ ∈ (0, 1] such that the set K δ is nonempty. Consider the following iterative steps
-
1
let n = 1;
-
2
if \(x_n\in \mathcal {E}(VP)\) , then x n+p = x n for all p ≥ 1;
-
3
otherwise find \(y_{n+1}\in \mathcal {P}\mathcal {E}_{\delta } \Big \{F(x) + \alpha _n G(x): x\in \varOmega _n\Big \}\) ;
-
4
take x n+1 = (1 − β n)y n + β n x n ;
-
5
take n := n + 1 and go to Step 2.
The convergence statement [39, Theorem 3.4] is different to the others presented so far since it does not guarantee the convergence of the sequence generated by Algorithm 7 (towards an efficient solution to (V P)). Adding to it an additional hypothesis from Theorem 11.7 guarantees the unicity of the cluster point of this sequence.
Theorem 11.8 (cf. [39, Theorem 3.4])
Let F be C-convex, C-lower semicontinuous, positively partially continuous and C ∗ -asymptotically uniformly continuous such that \(\mathcal {W}\mathcal {E}(VP)\) is nonempty and compact. Further suppose that there exist a sequence \((\alpha _n)_n \in \mathbb {R}\) such that ∥y n − x n∥≤ α n for all n ≥ 1 and ∑n≥1 α n < +∞, where (x n)n and (y n)n are sequences generated by Algorithm 7 . Then (x n)n converges towards an efficient solution to (V P).
Remark 11.19
Examining the proof of [39, Theorem 3.4] (and that of [37, Theorem 3.2], cited below as Theorem 11.13), one can note that the usage of the property of positive C-lower semicontinuity of F can be covered by its positive partial continuity, so the firstly mentioned hypothesis seems to be redundant. On the other hand, at least at a first look, the role of the second hypothesis in the proof is not crucial and it can be replaced by the first one as well. Connected to this issue, a discussion on whether a positively partially continuous vector function is in general also positively C-lower semicontinuous could prove to be interesting as well, taking also in consideration that positively partially continuous vector functions (at least under this name) can be found only in [36, 37, 39].
Related to Algorithm 6 and Algorithm 7 from which special cases can be derived when β n = 0 for all n ≥ 1 and \(G=\|\cdot \| \tilde e\), for some suitable \(\tilde e\in \mathbb {R}^m_+\) (respectively \(\tilde e\in C\)) are the methods proposed in [34, 36] where the regularization in the iterative steps is performed by means of a Tikhonov type function instead of the Moreau-Yosida type one from the proximal point algorithms.
The algorithm proposed in [34] for determining weakly efficient solutions to (V PG) is the following, where \( \operatorname {{\mathrm {dom}}} F\cap \operatorname *{\mathrm {int}} S \neq \emptyset \).
Algorithm 8
Choose the starting point \(x_1\in \operatorname {{\mathrm {dom}}} F\cap \operatorname *{\mathrm {int}} S\) and the exogenous sequences (α n)n ⊆ (0, +∞), with limn→+∞ α n = +0, and \((e_n)_n\subseteq \mathbb {R}^m_+\) with ∥e n∥ = 1 for all n ≥ 1. Consider the following iterative steps
-
1
let n = 1;
-
2
if \(x_n\in \mathcal {W}\mathcal {E}(VGP)\) , then x n+p = x n for all p ≥ 1;
-
3
otherwise find \(x_{n+1}\in \mathcal {W}\mathcal {E} \Big \{F(x) + \alpha _n \|x\|{ }^2 e_n: x\in \varOmega _n\Big \}\) ;
-
4
take n := n + 1 and go to Step 2.
Theorem 11.9 (cf. [34, Theorem 3.2])
Let F be C-convex and C-lower semicontinuous, S be closed and convex, and \(\mathcal {W}\mathcal {E}(VPG)\) nonempty and compact. Then any sequence (x n)n generated by Algorithm 8 converges towards a weakly efficient solution to (V PG).
Finally, we also present the algorithm proposed in [36] for determining efficient solutions to (V P). In this case it is not necessary to have \( \operatorname *{\mathrm {int}} C\neq \emptyset \).
Algorithm 9
Choose the starting point \(x_1\in \operatorname {{\mathrm {dom}}} F\) and the exogenous sequences (α n)n ⊆ (0, +∞), with limn→+∞ α n = 0, and (e n)n ⊆ C with ∥e n∥ = 1 for all n ≥ 1. Assume moreover that there exists some δ ∈ (0, 1] such that the set K δ is nonempty. Consider the following iterative steps
-
1
let n = 1;
-
2
if \(x_n\in \mathcal {E}(VP)\) , then x n+p = x n for all p ≥ 1;
-
3
otherwise find \(x_{n+1}\in \mathcal {P}\mathcal {E}_\delta \Big \{F(x) + \alpha _n \|x\|{ }^2 e_n: x\in \varOmega _n\Big \}\) ;
-
4
take n := n + 1 and go to Step 2.
The corresponding convergence statement follows, although in a different manner than many of the other ones presented in this survey, as the unicity of the cluster point of the sequence generated by Algorithm 9 is not guaranteed. The idea presented in Remark 11.19 is valid for this result as well.
Theorem 11.10 (cf. [36, Theorem 3.1])
Let F be C-convex, C-lower semicontinuous and positively partially continuous, and \(\mathcal {E}(VP)\) is nonempty and compact. Then any sequence (x n)n generated by Algorithm 9 converges towards an efficient solution to (V P).
11.4.3 Algorithms with Lyapunov-Type Distances
A more general framework, even than the one in [24], is considered in the papers [32, 35, 37], where algorithms of proximal point type for solving (V P) are formulated by means of the Lyapunov functional. In this subsection let (X, ∥⋅∥) be a uniformly convex and uniformly smooth Banach space. We begin with the algorithm proposed in [35].
Algorithm 10
Choose the starting point \(x_1\in \operatorname {{\mathrm {dom}}} F\) and the exogenous sequences (α n)n ⊆ (0, α], with α > 0, and \((e_n)_n\subseteq \operatorname *{\mathrm {int}} C\) such that ∥e n∥ = 1 for all n ≥ 1. Consider the following iterative steps
-
1
let n = 1;
-
2
if \(x_n\in \mathcal {W}\mathcal {E}(VP)\) , then x n+p = x n for all p ≥ 1;
-
3
otherwise find \(x_{n+1}\in \mathcal {W}\mathcal {E} \Big \{F(x) + \frac {\alpha _n}{2} L(x,x_n) e_n: x\in \varOmega _n\Big \}\) ;
-
4
take n := n + 1 and go to Step 2.
Because of the more general framework, the convergence of the method towards a weakly efficient solution to (V P) can be guaranteed under some additional hypotheses to the ones in Theorem 11.1.
Theorem 11.11 (cf. [35, Theorem 3.5])
Let F be C-convex and positively C-lower semicontinuous and assume that F(S) ∩ (F(x 1) − C) is C-complete, \(\mathcal {W}\mathcal {E}(VP)\) is nonempty and J X is weak-to-weak continuous. Then any sequence (x n)n generated by Algorithm 10 converges weakly towards a weakly efficient solution to (V P).
Remark 11.20
In the proof of [35, Theorem 3.5] it is claimed that the weak limit of the sequence generated by Algorithm 10 under the hypotheses of Theorem 11.11 was the only weakly efficient solution to (V P). However, nothing supports this fact, as there it is shown only that any such sequence has a unique weak cluster point. Moreover, the hypothesis of nonemptiness of \(\mathcal {W}\mathcal {E}(VP)\) in Theorem 11.11 seems, in the light of Remark 11.8, superfluous.
Closely related to this method is the approximate one proposed in [32].
Algorithm 11
Choose the starting point \(x_1\in \operatorname {{\mathrm {dom}}} F\) and the exogenous sequences (α n)n ⊆ (0, α], with α > 0, and \((e_n)_n\subseteq \operatorname *{\mathrm {int}} C\) such that ∥e n∥ = 1 for all n ≥ 1, as well as the error sequence (𝜖 n)n ⊆ X ∗ satisfying ∑n≥1∥𝜖 n∥∗ < +∞. Consider the following iterative steps
-
1
let n = 1;
-
2
if \(x_n\in \mathcal {W}\mathcal {E}(VP)\) , then x n+p = x n for all p ≥ 1;
-
3
otherwise find \(x_{n+1}\in \mathcal {W}\mathcal {E} \Big \{F(x) + \frac {\alpha _n}{2} (L(x,x_n)-\langle \epsilon _{n+1}, x\rangle ) e_n: x\in \varOmega _n\Big \}\) ;
-
4
take n := n + 1 and go to Step 2.
The corresponding convergence statement is similar to Theorem 11.11 to which a hypothesis regarding the error sequence and involving the generated sequence is added. Note that Remark 11.20 applies for the following statement, too.
Theorem 11.12 (cf. [32, Theorem 3.5])
Let F be C-convex and positively C-lower semicontinuous and assume that F(S) ∩ (F(x 1) − C) is C-complete, \(\mathcal {W}\mathcal {E}(VPG)\) is nonempty and J X is weak-to-weak continuous. Then any sequence (x n)n generated by Algorithm 11 converges weakly towards a weakly efficient solution to (V P) when ∑n≥1〈𝜖 n, x n〉 exists and is finite.
A modification of Algorithm 11 proposed in [37] delivers efficient solutions to (V P). In this case it is not necessary to have \( \operatorname *{\mathrm {int}} C\neq \emptyset \).
Algorithm 12
Choose the starting point \(x_1\in \operatorname {{\mathrm {dom}}} F\) and the exogenous sequences (α n)n ⊆ (0, α], with α > 0, and \((e_n)_n\subseteq \operatorname *{\mathrm {int}} C\) such that ∥e n∥ = 1 for all n ≥ 1, as well as the error sequence (𝜖 n)n ⊆ X ∗ satisfying ∑n≥1∥𝜖 n∥∗ < +∞. Assume moreover that there exists some δ > 0 such that the set K δ is nonempty. Consider the following iterative steps
-
1
let n = 1;
-
2
if \(x_n\in \mathcal {E}(VP)\) , then x n+p = x n for all p ≥ 1;
-
3
otherwise find \(x_{n+1}\in \mathcal {P}\mathcal {E}_{\delta } \Big \{F(x) + \frac {\alpha _n}{2} (L(x,x_n)-\langle \epsilon _{n+1}, x\rangle ) e_n: x\in \varOmega _n\Big \}\) ;
-
4
take n := n + 1 and go to Step 2.
The convergence statement contains both the hypotheses of Theorem 11.12 and the additional requirement imposed on F to be positively partially continuous.
Theorem 11.13 (cf. [37, Theorem 3.2])
Let F be C-convex, positively C-lower semicontinuous and positively partially continuous, and assume that F(S) ∩ (F(x 1) − C) is C-complete, and J X is weak-to-weak continuous. Then any sequence (x n)n generated by Algorithm 12 converges weakly towards an efficient solution to (V P) when ∑n≥1〈𝜖 n, x n〉 exists and is finite.
11.4.4 Algorithms with Hybrid and Inertial Steps
In this subsection we have gathered some algorithms for solving vector optimization problems where the proximal point steps are combined with other ideas, leading to so-called hybrid methods and inertial type algorithms.
In [29] one can find the following method for determining weakly efficient solutions to vector optimization problems.
Algorithm 13
Choose the starting point \(x_1\in \operatorname {{\mathrm {dom}}} F\) and the sequences (α n)n ⊆ (0, α), where α > 0, (β n)n ⊆ [0, 1], (θ n)n ⊆ X and \((e_n)_n\subseteq \operatorname *{\mathrm {int}} C\) such that ∥e n∥ = 1 for all n ≥ 1. Consider the following iterative steps
-
1
let n = 1;
-
2
if \(x_n\in \mathcal {W}\mathcal {E}(VP)\) , then x n+p = x n for all p ≥ 1;
-
3
find \(y_n\in \mathcal {W}\mathcal {E} \Big \{F(x) + \frac {\alpha _n}{2}\|x-x_n-\theta _n\|{ }^2 e_n: x\in \varOmega _n\Big \}\) ;
-
4
take x n+1 = β n x n + (1 − β n)y n ;
-
5
take n := n + 1 and go to Step 2.
Different to Algorithm 1 is not only the fact that an additional iterative sequence (y n)n was employed in order to define the one that will converge towards a weakly efficient solution to (V P) (as seen below), but also the usage of another sequence (θ n)n in the proximal step. The corresponding convergence statement follows, with a dynamic condition that cannot be verified before running the algorithm. Note also that the comment from Remark 11.18 applicable here, too.
Theorem 11.14 (cf. [29, Theorem 3.1])
Let F be C-convex, positively C-lower semicontinuous and C ∗ -asymptotically uniformly continuous and assume that F(S) ∩ (F(x 1) − C) is C-complete. Let the sequences (x n)n and (y n)n be generated by Algorithm 13 . If there is a bounded sequence (η n)n ⊆ (0, +∞) such that \(\sum _{n\geq 1} \eta _n^2<+\infty \) and ∥θ n∥≤ η n∥x n − y n∥ and a constant δ ∈ (0, 1) such that 0 ≤ β n ≤ 1 − δ for all n ≥ 1, and it holds limn→+∞ β n = 0, then (x n)n converges weakly towards a weakly efficient solution to (V P).
In [29] one can find also a modification of Algorithm 13 where the usual distance is replaced by a Bregman type one as follows, where \(h:X\to \mathbb {R}\) is a strictly convex function that is Gâteaux differentiable with the Gâteaux derivative Dh(⋅) and \(B_h:X\times X\to \mathbb {R}\) is the corresponding Bregman distance with respect to h, namely B h(x, y) = h(x) − h(y) − Dh(y)(x − y).
Algorithm 14
Choose the starting point \(x_1\in \operatorname {{\mathrm {dom}}} F\) and the sequences (α n)n ⊆ (0, α), where α > 0, (β n)n ⊆ [0, 1], (θ n)n ⊆ X and \((e_n)_n\subseteq \operatorname *{\mathrm {int}} C\) such that ∥e n∥ = 1 for all n ≥ 1. Consider the following iterative steps
-
1
let n = 1;
-
2
if \(x_n\in \mathcal {W}\mathcal {E}(VP)\) , then x n+p = x n for all p ≥ 1;
-
3
find \(x_n\in \mathcal {W}\mathcal {E} \Big \{F(x) + \frac {\alpha _n}{2}(2h(x) + \|x-Dh(x_n)-\theta _n\|{ }^2) e_n: x\in \varOmega _n\Big \}\) ;
-
4
take n := n + 1 and go to Step 2.
Remark 11.21
The weak convergence of Algorithm 14 towards a weakly efficient solution to (V P) is achieved in [29, Theorem 4.1]. Different to Theorem 11.14, the hypothesis of C ∗-asymptotically uniform continuity of F seems no longer necessary, however Dh is required to be weak-to-weak sequentially continuous and the boundedness condition imposed on the sequence (θ n)n is replaced with \(\|\theta _n\| \leq \eta _n D_h^{1/2}(x_{n+1}, x_n)\).
Remark 11.22
In [29] one can also find an inexact version of Algorithm 13 called relative approximate proximal algorithm, whose weak convergence towards a weakly efficient solution to (V P) is obtained in [29, Theorem 5.1]. Interestingly, the hypothesis of C ∗-asymptotically uniform continuity of F seems no longer necessary for this statement either.
A further development of Algorithm 13 can be found in [28] in the form of a hybrid proximal point type algorithm for finding weakly efficient solutions to (V PG), where the iterative steps contain projections and involve monotone mappings, while a variational inequality is involved in the convergence statement. Note that in this case actually four sequences are generated during the iterative process in order to construct the one that actually converges towards a weakly efficient solutions to (V PG). Let S be closed and convex and A : S → X be monotone.
Algorithm 15
Choose the starting point \(x_1\in \operatorname {{\mathrm {dom}}} F\cap S\) and the sequences (α n)n ⊆ (0, α), where α > 0, (λ n)n ⊆ (0, 1), (β n)n ⊆ [0, 1], (η n)n ⊆ [0, 1], (θ n)n ⊆ X and \((e_n)_n\subseteq \operatorname *{\mathrm {int}} C\) such that ∥e n∥ = 1 for all n ≥ 1. Consider the following iterative steps
-
1
let n = 1;
-
2
if \(x_n\in \mathcal {W}\mathcal {E}(VPG)\) , then x n+p = x n for all p ≥ 1;
-
3
take \(y_n= \operatorname *{\mathrm {Pr}}_S(x_n-\lambda _nAx_n)\) ;
-
4
take \(z_n=\eta _nx_n + (1-\eta _n) \operatorname *{\mathrm {Pr}}_S (x_n - \lambda _n Ay_n)\) ;
-
5
find \(w_n\in \mathcal {W}\mathcal {E} \Big \{F(x) + \frac {\alpha _n}{2}\|x-z_n-\theta _n\|{ }^2 e_n: x\in \varOmega _n\Big \}\) ;
-
6
take x n+1 = β n x n + (1 − β n)w n ;
-
7
take n := n + 1 and go to Step 2.
The convergence statement is apparently more complicated than the others, as it solves not only the considered vector optimization problem but also an attached variational inequality.
Theorem 11.15 (cf. [28, Theorem 3.1])
Let F be C-convex, positively C-lower semicontinuous and C ∗ -uniformly semicontinuous and assume that F(S) ∩ (F(x 1) − C) is C-quasicomplete. Assume that A is Lipschitz continuous with the Lipschitz constant κ > 0, such that \(\mathcal {W}\mathcal {E}(VPG)\cap VI (S, A)\neq \emptyset \) and that there is a bounded sequence (η n)n ⊆ (0, +∞) such that \(\sum _{n\geq 1} \eta _n^2<+\infty \) and ∥θ n∥≤ η n∥x n − y n∥, where the sequences (x n)n and (y n)n are generated by Algorithm 15 . When there are some 𝜖, δ ∈ (0, 1) such that (β n)n ⊆ (𝜖, δ), c ∈ [0, 1) such that (η n)n ⊆ [0, c) and a, b ∈ (0, 1∕κ) such that (λ n)n ⊆ [a, b], then (x n)n converges weakly towards a weakly efficient solution to (V PG) that also lies in V I(S, A).
Remark 11.23
In [28] one can also find a modification of Algorithm 15 where the usual distance is replaced by a Bregman type one in the spirit of Algorithm 14 as well as an inexact version of Algorithm 15 called relative hybrid approximate proximal algorithm, whose weak convergences towards weakly efficient solutions to (V PG) (that also lie in V I(S, A)) are obtained in [28, Theorem 4.3 & Theorem 5.1], respectively, under some additional hypotheses to the ones from Theorem 11.15. Like above (see Remark 11.22), the hypothesis of C ∗-asymptotically uniform semicontinuity of F seems no longer necessary for these statements.
Another modification of Algorithm 15 is available in [38], where it is shown to deliver efficient solutions to (V PG). In this case it is not necessary to have \( \operatorname *{\mathrm {int}} C\neq \emptyset \).
Algorithm 16
Choose the starting point \(x_1\in \operatorname {{\mathrm {dom}}} F\cap S\) and the sequences (α n)n ⊆ (0, α), where α > 0, (λ n)n ⊆ (0, 1), (β n)n ⊆ [0, 1], (η n)n ⊆ [0, 1], (θ n)n ⊆ X and \((e_n)_n\subseteq \operatorname *{\mathrm {int}} C\) such that ∥e n∥ = 1 for all n ≥ 1. Assume moreover that there exists some δ ∈ (0, 1] such that the set K δ is nonempty. Consider the following iterative steps
-
1
let n = 1;
-
2
if \(x_n\in \mathcal {E}(VPG)\) , then x n+p = x n for all p ≥ 1;
-
3
take \(y_n= \operatorname *{\mathrm {Pr}}_S(x_n-\lambda _nAx_n)\) ;
-
4
take \(z_n=\eta _nx_n + (1-\eta _n) \operatorname *{\mathrm {Pr}}_S (x_n - \lambda _n Ay_n)\) ;
-
5
find \(w_n\in \mathcal {P}\mathcal {E}_\delta \Big \{F(x) + \frac {\alpha _n}{2}\|x-z_n-\theta _n\|{ }^2 e_n: x\in \varOmega _n\Big \}\) ;
-
6
take x n+1 = β n x n + (1 − β n)w n ;
-
7
take n := n + 1 and go to Step 2.
For the convergence one basically needs the hypotheses of Theorem 11.15.
Theorem 11.16 (cf. [38, Theorem 3.1])
Let F be C-convex, positively C-lower semicontinuous and C ∗ -uniformly semicontinuous and assume that F(S) ∩ (F(x 1) − C) is C-quasicomplete. Assume that A is Lipschitz continuous with the Lipschitz constant κ > 0 and that there is a bounded sequence (η n)n ⊆ (0, +∞) such that \(\sum _{n\geq 1} \eta _n^2<+\infty \) and ∥θ n∥≤ η n∥x n − y n∥, where the sequences (x n)n and (y n)n are generated by Algorithm 15 . When there are some 𝜖, δ ∈ (0, 1) such that (β n)n ⊆ (𝜖, δ), c ∈ [0, 1) such that (η n)n ⊆ [0, c) and a, b ∈ (0, 1∕κ) such that (λ n)n ⊆ [a, b], then (x n)n converges weakly towards a weakly efficient solution to (V PG) that, when \(x_n\notin \mathcal {E}(VPG)\) for all n ≥ 1, also lies in V I(S, A).
Remark 11.24
In [38] one can also find a modification of Algorithm 16 where the usual distance is replaced by a Bregman type one in the spirit of Algorithm 14 as well as an inexact version of Algorithm 16 called relative hybrid approximate proximal algorithm, whose weak convergences towards efficient solutions to (V PG) (that also lie in V I(S, A) provided that \(x_n\notin \mathcal {E}(VPG)\) for all n ≥ 1) are obtained in [38, Theorem 4.1 & Theorem 5.1], respectively, under some additional hypotheses to the ones from Theorem 11.16. Like above (see Remark 11.22), the hypothesis of C ∗-asymptotically uniform semicontinuity of F seems no longer necessary for these statements.
Further we also present an inertial proximal point algorithms with memory effects for solving vector optimization problems. The inertial proximal point methods with memory effects, first proposed by Alvarez and Attouch (cf. [2, 3]), were inspired from heavy ball with friction dynamical systems and have as a characteristic feature the fact that an iteration variable depends on the previous two elements of the same sequence, not only on its predecessor as it is usually the case for many algorithmic approaches. This modification accelerates the original proximal point method and makes it more robust. We propose an inertial version of Algorithm 1 that is slightly more general than the special case of Algorithm 19 (introduced later in Section 11.5) that can be employed for solving (V P). For completeness sake, since it cannot be found in the published literature, the proof of the convergence of this algorithm towards a weakly efficient solution to (V P) is provided in an Appendix at the end of the paper.
Algorithm 17
Choose the starting points \(x_0, x_1\in \operatorname {{\mathrm {dom}}} F\) and the sequences (λ n)n ⊆ (0, +∞), (α n)n ⊆ [α, +∞), where α > 0, (β n)n ⊆ [0, β), where 0 < β < 1∕3, and \((e_n)_n\subseteq \operatorname *{\mathrm {int}} C\) such that (α n)n is bounded, (β n)n is nondecreasing and ∥e n∥ = 1 for all n ≥ 1. Consider the following iterative steps
-
1
let n = 1;
-
2
if \(x_n\in \mathcal {W}\mathcal {E}(VP)\) , then x n+p = x n for all p ≥ 1;
-
3
find \(x_{n+1}\in \mathcal {W}\mathcal {E} \Big \{\lambda _n F(x) + \frac {\alpha _n}{2}\|x-x_n-\beta _n(x_n-x_{n-1})\|{ }^2 e_n: x\in \varOmega _n\Big \}\) ;
-
4
take n := n + 1 and go to Step 2.
Remark 11.25
When β n = 0 and λ n = 1 for all n ≥ 1, Algorithm 17 collapses to Algorithm 1. On the other hand, when \(Y=\mathbb {R}\) and \(C=\mathbb {R}_+\), Algorithm 17 becomes the inertial proximal point method for scalar optimization problems that can be derived from the algorithm for finding zeros of maximally monotone operators proposed in [3].
Theorem 11.17
Let F be C-convex and positively C-lower semicontinuous and F(X) ∩ (F(x 1) − C) be C-complete. Then any sequence (x n)n generated by Algorithm 17 converges weakly towards a weakly efficient solution to (V P).
Remark 11.26
The conclusion of Theorem 11.17 remains valid when the sequence (x n)n generated by Algorithm 17 fulfills the condition \(\sum _{n=1}^{+\infty } \beta _n\|x_n-x_{n-1}\|{ }^2 < +\infty \), in which case (β n)n needs not necessarily be nondecreasing and one can take β ∈ [0, 1). However, this dynamic condition might be more difficult to verify since it involves the generated sequence (x n)n, while the static hypotheses considered above can simply be imposed while defining the parameters β and (β n)n, respectively. Different to the inertial proximal methods proposed in the literature for solving scalar optimization problems or monotone inclusions (see, for instance, [3]), in Theorem 11.17 it is not necessary to assume the existence of a weakly efficient solution to (V P) in order to prove the convergence of Algorithm 17. Analogous to Remark 11.8, in this case the role of such a hypothesis in showing the convergence of the method has been fully covered by the assumed C-completeness hypothesis.
Remark 11.27
Motivated by Remark 11.6, one can consider also in Algorithm 17 a stopping rule that is easier to check than the original one. It can be shown in a similar manner to [24, Proposition 3.2] that if three consecutive iterations of the sequence (x n)n generated by Algorithm 17 coincide, they represent a weakly efficient solution to (V P).
One can provide an inexact version of Algorithm 17 inspired by Algorithm 2 as follows.
Algorithm 18
Choose the starting points \(x_0, x_1\in \operatorname {{\mathrm {dom}}} F\) , the sequences (λ n)n ⊆ (0, +∞), (α n)n ⊆ [α, +∞), where α > 0, (β n)n ⊆ [0, β), where 0 < β < 1∕4, \((z_n^*)_n \subseteq C^*\setminus \{0\}\) , and \((e_n)_n\subseteq \operatorname *{\mathrm {int}} C\) such that (α n)n is bounded, (β n)n is nondecreasing, \(\|z_n^*\|=1\) and ∥e n∥ = 1 for all n ≥ 1, as well as the constant σ ∈ [0, 1 − 4β). Consider the following iterative steps
-
1
let n = 1;
-
2
if \(x_n\in \mathcal {W}\mathcal {E}(VP)\) , then x n+p = x n for all p ≥ 1;
-
3
find \(x_{n+1}\in \operatorname {{\mathrm {dom}}} F\) such that
$$\displaystyle \begin{aligned}0\in \partial _{\varepsilon_n} (\langle z^*_n, F(\cdot)\rangle + \delta_{\varOmega_n}) (x_{n+1}) + \alpha_n\langle z^*_n, e_n\rangle (x_{n+1}-x_n -\beta_n(x_n-x_{n-1}))\end{aligned}$$for some \(0\leq \varepsilon _n \leq \sigma \frac {\alpha _n}{2}\langle z^*_n, e_n\rangle \|x_{n+1}-x_n -\beta _n(x_n-x_{n-1})\|{ }^2\) ;
-
4
take n := n + 1 and go to Step 2.
Remark 11.28
When β n = 0 and λ n = 1 for all n ≥ 1 and β ↓ 0, Algorithm 18 collapses to Algorithm 2.
The convergence of Algorithm 18 towards a weakly efficient solution to (V P) can be guaranteed under the same hypotheses as the one of its exact version Algorithm 17, the proof relying on the ones of Theorem 11.17 and [24, Theorem 5.1].
Theorem 11.18
Let F be C-convex and positively C-lower semicontinuous and F(X) ∩ (F(x 1) − C) be C-complete. Then any sequence (x n)n generated by Algorithm 17 converges weakly towards a weakly efficient solution to (V P).
Remark 11.29
Another possible way to provide an inexact version of Algorithm 17 may be investigated by making use of the approximative inertial type proximal scheme proposed in [2, Section 3.2].
Remark 11.30
Another inertial type proximal point method was proposed in [27] for determining ideally efficient solutions to (V P) in case \(Y=\mathbb {R}^m\). We opted not to present it here because of the limited significance of the ideally efficient solutions to (V P) and also due to the way it is constructed that required introducing maximally monotone operators. Note however that this algorithm is accompanied by applications to convex feasibility problems and to the problem of common fixed points for nonexpansive potential mappings and also that some convergence rates are derived for the method.
Remark 11.31
In the literature there are also some proximal point type algorithms for solving vector optimization problems whose objective functions map from Hadamard manifolds to Euclidean spaces. The algorithmic schemes are not much different from the ones presented above, however one needs to define the whole Hadamard manifolds setting in order to give the corresponding convergence statements. In [13] a proximal point type scheme is proposed for determining weakly efficient solutions to the Hadamard version of (V PG), where F is taken as mentioned above. Weakly efficient elements to the Hadamard version of (V P) are obtained in [16] by means of a proximal point type algorithm where the intermediate optimization problems are scalarized versions of the ones in [13] by means of a special case of the scalarization function introduced by Tammer (then Gerstewitz) in [43]. An inexact version of the method that converges towards weakly efficient elements to the considered vector optimization problem is proposed as well. Another special case of Tammer’s scalarization function, the so-called maximum scalarization, is employed in [74] for proposing an inexact proximal point method for determining efficient solutions to the Hadamard version of (V P). Because of the special structure of its objective function, the scalarized optimization problem should apparently be not so difficult to solve and a rate of convergence of the proposed method is provided, too.
Remark 11.32
One could include in this section also the algorithms in [41, 51, 71, 73], as they are proximal point type methods for solving vector optimization problems as well. However, in all of them the new iteration x n+1 is calculated as an optimal solution to a scalar optimization problem that is a scalarization of a vector one, not as some sort of an efficient solution to some vector optimization problem, failing thus to satisfy the criteria stated in [24]. The algorithm proposed in [41] employs the Tammer scalarization function (see also Remark 11.31). This function leads to scalar optimization problems that are bounded from below by 0, excluding thus the possibility to have to deal with unbounded scalar optimization problems that may occur when working with the linear scalarization. However, the objective functions of the scalar optimization problems derived by means of this scalarization contain compositions of functions that are unfortunately still unsuitable for the existing proximal point type algorithms and, moreover, this scalarization does not guarantee a descent property for the values of the objective function either. On the other hand, worth noticing is that the intermediate optimization problems in the algorithm designed in [41] for delivering weakly efficient solutions to (V P) are unconstrained, i.e. they do not require defining the sets Ω n, n ≥ 1. An inexact method that converges towards weakly efficient elements to the considered vector optimization problem is proposed in the Hadamard manifolds framework discussed in Remark 11.31 in [73] by means of a generalized proximal distance, where the original problem is scalarized by a special case of the Tammer scalarization function. In [51, 71] there are proposed some logarithmic proximal point type algorithms for solving (V P) in Euclidean spaces. However, these are essentially methods for minimizing some scalar functions called strict scalar representations of the objective function of the original vector optimization problem. Note that the method proposed in [51] can be modelled, to some extent, to deal also with vector optimization problems with convex inequality constraints. On the other hand, the one from [71] employs a quasi-distance instead of the classical distance induced by a norm in the proximal step and is employed for numerically solving some test problems.
Remark 11.33
There are some papers where proximal point type algorithms for solving vector optimization problems consisting in vector-minimizing a vector function subject to both geometric and linear equality constraints are proposed, in the finitely dimensional framework where \(X=\mathbb {R}^n\), S ⊆ X is convex and compact, \(Y=\mathbb {R}^m\), \(C\subseteq \mathbb {R}^m\) is a convex cone, \(A\in \mathbb {R}^{p\times n}\), \(b\in \mathbb {R}^p\) and \(F:\mathbb {R}^n\to \mathbb {R}^m\). The constrained vector optimization problem considered in [67, 68] is
(V PC) \( \operatorname *{\mathrm {WMin}} \limits _{\substack {Ax=b,\\ x \in S}} F(x)\).
However, the methods proposed in the mentioned papers for determining weakly efficient and efficient solutions to (V PC) fail to satisfy the criteria stated in [24] (see also Remark 11.32), as they consist of solving some minmax scalar optimization problems that contain scalarizations of the objective function of (V PC) and some other terms based on the equality constraint. The algorithms are shown to converge towards weakly efficient solutions to (V PC) and, under additional assumptions, towards efficient ones (called strongly efficient in [68]) to it. Applications to supply chain network risk management and computational results obtained in matlab are provided, too in both these works, despite the fact that usually minmax optimization problems are not easy to solve numerically. Note also that in [72, Remark 3.3] a vector optimization problem with a linear objective function and both geometric and linear inequality constraints is mentioned and a numerical scheme for solving it is sketched, however without actually exploiting the structure of the constraint set.
11.5 Proximal Point Type Algorithms for Other Vector Optimization Problems
In this section we present proximal point type algorithms for solving vector optimization problems with more complicated structure than (V P) (or its constrained counterparts (V PG) and (V PC)), namely ones with a sum or difference of vector functions as an objective function. Many of the remarks we gave in Section 11.3 remain valid for some of these classes of vector optimization problems as well and we will not mention them again here.
11.5.1 Vector-Minimization of Sums of Vector Functions
Consider next the so-called composite vector optimization problem consisting in vector-minimizing the sum of two vector functions, whose weakly efficient solutions were obtained in [19] by means of a forward-backward proximal point method with inertial/memory effects
(V PS) \( \operatorname *{\mathrm {WMin}} \limits _{x \in X} \big [F(x)+G(x)\big ]\),
where F : X → Y • is a proper vector function and G : X → Y is a Fréchet differentiable vector function with an L-Lipschitz continuous gradient ∇G.
The exact proximal inertial forward-backward iterative method proposed in [19] for determining the weakly efficient solutions to (V PS) is the following.
Algorithm 19
Choose the starting points x 0, x 1 ∈ X and the sequences (β n)n ⊆ [0, β), \((z^*_n)_n\subseteq C^*\setminus \{0\}\) and \((e_n)_n\subseteq \operatorname *{\mathrm {int}} C\) such that (β n)n is nondecreasing, β < 1∕9, \(\|z^*_n\|=1\) and \(\langle z^*_n, e_n\rangle =1\) for all n ≥ 1. Consider the following iterative steps
-
1
let n = 1;
-
2
if \(x_n\in \mathcal {W}\mathcal {E}(VPS)\) , then x n+p = x n for all p ≥ 1;
-
3
find \(x_{n+1}\in \mathcal {W}\mathcal {E} \Big \{F(x) + \frac {L}{2}\big \|x-\big (x_n+\beta _n(x_n-x_{n-1}) - \frac 1L \nabla (z_n^*G)(x_n)\big )\big \|{ }^2 e_n: x\in \varOmega _n^S\Big \}\) , where \(\varOmega _n^S = \{x\in X: (F+G)(x)\leqq _C (F+G)(x_n)\}\) ;
-
4
take n := n + 1 and go to Step 2.
Remark 11.34
When G ≡ 0, Algorithm 19 becomes an inertial proximal point method for solving vector optimization problems that is a special case of Algorithm 17, and by additionally taking β n = 0 for all n ≥ 1 it collapses into the proximal point method for vector-minimizing a nonsmooth vector function introduced in [24] and presented above as Algorithm 1. On the other hand, when \(Y=\mathbb {R}\) and \(C=\mathbb {R}_+\) (i.e. in the scalar case), Algorithm 19 becomes the inertial proximal-gradient method for scalar optimization problems, that can be derived from the algorithm for finding zeros of maximally monotone operators proposed in [63]. When, furthermore, G ≡ 0, it collapses into the one from [3], while when β n = 0 for all n ≥ 1 it becomes the celebrated ISTA method, however in a more general framework.
The convergence of Algorithm 19 is achieved in a similar setting to the one of Algorithm 1.
Theorem 11.19 (cf. [19, Theorem 2.1])
Let F be C-convex and positively C-lower semicontinuous, G be C-convex and assume that (F + G)(X) ∩ (F(x 1) + G(x 1) − C) is C-complete. Then any sequence (x n)n generated by Algorithm 19 converges weakly towards a weakly efficient solution to (V PS).
Remark 11.35
The conclusion of Theorem 11.19 remains valid when one takes only F + G to be C-convex instead of both F and G and Remark 11.26 applies here as well. The additional hypotheses of Theorem 11.2 guarantee the weak convergence of any sequence (x n)n generated by Algorithm 19 towards an efficient solution to (V PS), too. Note also that the intermediate vector optimization problems can be solved as such or can be scalarized for this, in which case an obvious choice for the scalarizing functional are the corresponding \(z^*_n\)’s. Of course, the sequence \((z_n^*)_n\) can be taken constant, situation in which the intermediate vector optimization problems differ despite having the same objective vector function because their feasible sets become smaller at each iteration. This does not mean that the vector optimization problem (V PS) is a priori scalarized by means of a linear continuous functional, because this scalarization is applied to the intermediate vector optimization problems not to (V PS).
Remark 11.36
For implementation purposes one can provide an inexact version of Algorithm 19 as well, where Step 3 is replaced by
-
3’
find x n+1 ∈ X such that
$$\displaystyle \begin{aligned}0\in \partial_{\varepsilon_n} (\langle z^*_n, F(\cdot) &+ \frac{L}{2}\|\cdot-x_n-\beta_n(x_n-x_{n-1}) + \frac 1L \nabla (z_n^*G)(x_n)\|{}^2 e_n \rangle\\ &+ \delta_{\varOmega_n^S} (\cdot)) (x_{n+1}),\end{aligned} $$
where the additional sequence of tolerable nonnegative errors (ε n)n fulfills some hypotheses, such as the ones considered in [24] or those from [2, 63]. Employing the later, i.e. ∑n≥1 ε n < +∞, the convergence statement obtained by correspondingly modifying Theorem 11.19 remains valid. Moreover, as an alternative stopping rule that is easier to check than Step 2 of Algorithm 19 one can verify whether three consecutive iterations of the sequence (x n)n generated by the method coincide, in which case they represent a weakly efficient solution to (V PS). Note also that x n−1 = x n does not necessarily imply that x n+1 coincides with them, too. This can prove to be useful when starting the algorithm because one can begin with x 0 = x 1 without affecting the convergence of the method.
In [19] also the following (Nesterov type) modification of Algorithm 19 was proposed, the difference between them residing in the point where the value of \(\nabla (z_n^*G)\) is calculated. The above remarks remain basically valid for it as well.
Algorithm 20
Choose the starting points x 0, x 1 ∈ X and the sequences (β n)n ⊆ [0, β), \((z^*_n)_n\subseteq C^*\setminus \{0\}\) and \((e_n)_n\subseteq \operatorname *{\mathrm {int}} C\) such that (β n)n is nondecreasing, β < 1∕9, \(\|z^*_n\|=1\) and \(\langle z^*_n, e_n\rangle =1\) for all n ≥ 1. Consider the following iterative steps
-
1
let n = 1;
-
2
if \(x_n\in \mathcal {W}\mathcal {E}(VPS)\) , then x n+p = x n for all p ≥ 1;
-
3
find \(x_{n+1}\in \mathcal {W}\mathcal {E} \Big \{F(x) + \frac {L}{2}\big \|x-\big (x_n+\beta _n(x_n-x_{n-1}) - \frac 1L \nabla (z_n^*G)(x_n+\beta _n(x_n-x_{n-1}))\big )\big \|{ }^2 e_n: x\in \varOmega _n^S\Big \}\) ;
-
4
take n := n + 1 and go to Step 2.
Remark 11.37
In the scalar case, when \(Y=\mathbb {R}\) and \(C=\mathbb {R}_+\), Algorithm 20 becomes a more general version of the celebrated FISTA method from [10], that can be recovered by taking β n = (t n − 1)∕t n+1, where \(t_{n+1}=(1+\sqrt {1+4t_n^2})/2\), n ≥ 1, with t 1 = 1, and restricting the framework to finitely dimensional spaces.
The convergence statement concerning Algorithm 20 is similar to Theorem 11.19.
Theorem 11.20 (cf. [19, Theorem 3.1])
Let F be C-convex and positively C-lower semicontinuous, G be C-convex and assume that (F + G)(X) ∩ (F(x 1) + G(x 1) − C) is C-complete. Then any sequence (x n)n generated by Algorithm 20 converges weakly towards a weakly efficient solution to (V PS).
Remark 11.38
One can additionally provide, following [10, Theorem 4.4], when the sequence \((z_n^*)_n\) is constant and for the choice of the parameters β n, n ≥ 1, mentioned in Remark 11.37, a convergence rate statement for the values of the objective functions of the scalarized intermediate problems in Algorithm 20. Moreover, when taking the sequence \((z_n^*)_n\) constant it is no longer necessary to take \(\|z^*_n\|=1\) for all n ≥ 1.
Stripping any of Algorithm 19 or Algorithm 20 of its inertial terms, it collapses into a forward-backward method, whose convergence is derivable from Theorem 11.19 or Theorem 11.20, as follows.
Algorithm 21
Choose the starting point x 1 ∈ X and the sequences \((z^*_n)_n\subseteq C^*\setminus \{0\}\) and \((e_n)_n\subseteq \operatorname *{\mathrm {int}} C\) such that \(\|z^*_n\|=1\) and \(\langle z^*_n, e_n\rangle =1\) for all n ≥ 1. Consider the following iterative steps
-
1
let n = 1;
-
2
if \(x_n\in \mathcal {W}\mathcal {E}(VPS)\) , then x n+p = x n for all p ≥ 1;
-
3
find \(x_{n+1}\in \mathcal {W}\mathcal {E} \Big \{F(x) + \frac {L}{2}\big \|x-\big (x_n - \frac 1L \nabla (z_n^*G)(x_n)\big )\big \|{ }^2 e_n: x\in \varOmega _n^S\Big \}\) ;
-
4
take n := n + 1 and go to Step 2.
A convergence rate statement for the values of the objective functions of the scalarized intermediate problems in Algorithm 21 can be deduced analogously to [10, Theorem 3.1].
Theorem 11.21 (cf. [19, Theorem 2.2])
Let F be C-convex and positively C-lower semicontinuous, G be C-convex and assume that (F + G)(X) ∩ (F(x 1) + G(x 1) − C) is C-complete. Consider the sequence (x n)n generated by Algorithm 21 , where one takes \(z_n^*=z^*\in C^*\setminus \{0\}\) , n ≥ 1. Then for any n ≥ 1 and \(\tilde x\in \cap _{n\geq 1} \varOmega _n^S\) one has
Remark 11.39
Unlike most of the mentioned papers where iterative methods for solving vector optimization problems were proposed, but their implementation was left for later due to the difficulty of solving the employed subproblems, in [19, Section 4] a concrete application in finance mathematics was solved in matlab via the inexact versions of both Algorithm 19 and Algorithm 21, whose performances are then compared, showing that a good choice of the inertial parameters can considerably reduce the resources needed for identifying a weakly efficient solution to (V PS).
11.5.2 Vector-Minimization of Differences of Cone-Convex Vector Functions
The last class of vector optimization problems considered in this survey consists in vector-minimizing the difference of two cone-convex (DC) vector functions subject to a geometric constraint in finitely dimensional spaces. One can find in [52, 53] proximal point type algorithms for solving such problems, however, due to their structure, only critically efficient solutions are determined. In the convex case the critically efficient solutions turn out to be weakly efficient, however this cannot happen in this setting. Consider the DC vector optimization problem
(V PD) \( \operatorname *{\mathrm {WMin}} \limits _{x \in S} \big [F(x)-G(x)\big ]\),
where \(F, G:\mathbb {R}^n\rightarrow \mathbb {R}^m\) are proper C-convex vector functions, \(C\subseteq \mathbb {R}^m\) being a convex cone, and \(S\subseteq \mathbb {R}^n\) is a closed convex set.
The proximal point type algorithm for solving (V PD) proposed in [53] is the following.
Algorithm 22
Choose the starting point \(x_1\in \mathbb {R}^n\) , the exogenous sequence (α n)n ⊆ (0, +∞) and ε > 0. Consider the following iterative steps
-
1
let n = 1;
-
2
find V n ∈ ∂G(x n);
-
3
find
 ;
;
-
4
if ∥x n+1 − x n∥≤ ε: STOP;
-
5
take n := n + 1 and go to Step 2.
The convergence statement regarding Algorithm 22 follows. Note however that only the fact that every cluster point of (x n)n is a critically efficient solution to (V PD) is guaranteed and that even for this a condition involving the structure of the sequence (x n)n is imposed.
Theorem 11.22 (cf. [53, Theorem 7])
Let S be bounded and assume that for n ≥ 1 large enough there is some \(u\in C^*\cap \mathcal {S}_{\mathbb {R}^m}\) such that \(x_{n+1}\in S\cap \big (\partial G^\top u + \alpha _n \operatorname *{\mathrm {id}}_{\mathbb {R}^n}\big )^{-1} \big (V_n^\top u+ \alpha _nx_n\big )\) , where the sequence (x n)n is generated by Algorithm 22 and it has infinitely many iterations. Then any cluster point of (x n)n is a critically efficient solution to (V PD).
Remark 11.40
In [53] one can find also a second proximal point type algorithm for solving (V PD) where the role of α n is taken by \(r_n^\top u\), where \((r_n)_n\subseteq \mathbb {R}^m\) is some iterative sequence that satisfies \(r_n^\top u >0\). Moreover, an inexact version of Algorithm 22 called ε-proximal algorithm is proposed, where the vector subdifferential of G is replaced (also in the hypotheses of the convergence statement) by its vector ε-subdifferential.
Remark 11.41
A special case of Algorithm 22 obtained when \(C=\mathbb {R}^m_+\) can be found in the earlier paper [52] together with an inexact version and an application to portfolio optimization that is also numerically solved in matlab, some computational results being provided.
Remark 11.42
Note that in Algorithm 22 the sets Ω n play no role and the intermediate problems are only geometrically constrained. On the other hand, at the first look they do not satisfy the criterion mentioned in [24] (see Remark 11.32), as they are scalar minmax optimization problems. However we opted to include Algorithm 22 here and not only to mention it in a remark because it employs the vector subdifferential of G and not one of some scalarization of it and, on the other hand, since the method can be seen as a splitting type one where the involved functions are processed separately, as one determines an element of the vector subdifferential of G and then uses it in a sort of a backward step. Another argument for the inclusion of this algorithm in this work is the fact that in [53] it is applied for numerically solving in matlab a problem of probabilistic lot sizing with service levels and computational results are provided, too. Note also that the hypotheses of the convergence statement do not include the usual C-completeness assumption considered in most of its counterparts gathered in this survey.
11.6 Conclusions and Further Research Directions
At the moment one can find more than thirty papers whose authors claim to introduce new proximal point type algorithms for solving vector optimization problems or to refine some existing ones. In most of these the method proposed in the seminal contribution due to Bonel, Iusem and Svaiter is extended in some way, usually by replacing the norm distance in the iterative step by some other (quasi-)distance function or by relaxing the hypotheses that are necessary for ensuring the convergence of the algorithm. Moreover, there are some contributions where one also has constraints or the objective function has a more complicated structure, being a sum or difference of vector functions or a composition of such a function with a linear operator.
The first conclusion one can draw is that in the decade and a half since the mentioned paper was published the interest around iteratively solving vector (and multiobjective) optimization problems by means of proximal point methods has steadily increased. Various techniques were extended from scalar to vector optimization and it seems that others would follow soon. There are proximal point type algorithms for approaching nonconvex vector optimization problems and some that deliver efficient (and not only weakly efficient) solutions to the considered vector optimization problem. The authors of the original paper have actually admitted that their algorithm was merely a theoretical scheme and many of the ones who followed it contain no numerical results either, however in some recent contributions one can find concrete applications with computational results.
On the other hand, one can notice that the algorithmic scheme of Bonel, Iusem and Svaiter is still the standard in this research area, as many of the subsequent contributions are mostly theoretical variations or improvements. Despite the progress in relaxing the hypotheses of the convergence statement, there are still no real alternatives to the cone-completeness hypothesis, as the compactness of the (weak) efficiency set cannot usually be a priori verified. However, the most important issue relies in the construction of the intermediate vector optimization problems that have to be solved in the iterative steps. The fact that these are constrained makes the existing splitting proximal point methods not really useful in approaching them and they have to be solved via other algorithms or solvers. The role of these constraints is to ensure that the values of the objective function decrease with respect to the ordering cone, thus a possible idea could be here to find another way to guarantee this descending property of the generated sequence without making the intermediate problems constrained. Moreover, there are almost no results on convergence rates for such algorithms and the existing ones require quite restrictive hypotheses. On the other hand, with or without constraints, there is still room for improvements with respect to the implementations of this class of algorithms, as only a few contributions contain actual computational results.
Of course, the difficulties encountered while trying to adapt techniques from scalar optimization into the vector optimization framework are far from being trivial. For instance, at each iteration one has to deal with a different intermediate vector optimization problem, while in the scalar case the objective function of the considered problem is usually not modified as the algorithm advances. Moreover, at the moment there is still no characterization via a monotone inclusion of the efficient solutions of a vector optimization problem, so directly adapting a method from that area without going through the scalar case is still out of the question. And, as mentioned above, the constraints of the intermediate vector optimization problems are not making the life easier.
Besides these, there are many other challenges regarding proximal point methods for solving vector optimization problems that are more or less solvable. We list in the following some of them. A first one would be to identify weaker hypotheses or the necessary modifications of the existing algorithms in order to guarantee the identification of (properly) efficient solutions to the considered vector optimization problems instead of weakly efficient or even critically efficient ones. Some the methods known at the moment to function only in Euclidean spaces are expected to work, under additional assumptions, in infinitely dimensional settings such as Hilbert spaces, too. As suggested in a paper by Bento, da Cruz Neto and Soubeyran, and, on the other hand, in one due to Rocha, Oliveira, Gregório and Souza, in the nonconvex case one can try to employ functions having the Kurdyka-Łojasiewicz property, too. Things are at the moment only at the beginning with respect to vector optimization problems with objective functions consisting of sums or differences of vector functions and/or compositions with linear continuous mappings. Other splitting schemes besides the forward-backward one could be applied. Speaking of the later, as mentioned in the cited paper of Boţ and the author, it would be interesting to identify a way to modify the proposed forward-backward algorithms in order to encompass as a special case also the projected gradient method proposed by Graña Drummond and Iusem for vector-minimizing a smooth cone-convex vector function. Adding constraints to the considered vector optimization problems obviously complicates things, however since the intermediate problems are already constrained it would be interesting to find some ways to approach these both, too, maybe by means of duality. Last but not least, as the ordering cones that occur in vector optimization often have empty interiors, modifications of the existing algorithms in order to maintain their convergence towards weakly efficient solutions defined by means of generalized interiors should be taken into consideration as well.
References
Aliprantis, C., Florenzano, M., da Rocha, V.M., Tourky, R.: Equilibrium analysis in financial markets with countably many securities. Journal of Mathematical Economics 40, 683–699 (2004)
Alvarez, F.: On the minimizing property of a second order dissipative system in Hilbert spaces. SIAM Journal on Control and Optimization 38, 1102–1119 (2000)
Alvarez, F., Attouch, H.: An inertial proximal method for maximal monotone operators via discretization of a nonlinear oscillator with damping. Set-Valued Analysis 9, 3–11 (2001)
Apolinário, H., Quiroz, E.P., Oliveira, P.: A scalarization proximal point method for quasiconvex multiobjective minimization. Journal of Global Optimization 64, 79–96 (2016)
Attouch, H., Garrigos, G.: Multiobjective optimization - an inertial dynamical approach to Pareto optima. arXiv 1506.02823 (2015)
Attouch, H., Garrigos, G., Goudou, X.: A dynamic gradient approach to Pareto optimization with nonsmooth convex objective functions. Journal of Mathematical Analysis and Applications 422, 741–771 (2015)
Attouch, H., Goudou, X.: A continuous gradient-like dynamical approach to Pareto-optimization in Hilbert spaces. Set-Valued and Variational Analysis 22, 189–219 (2014)
Auslender, A., Teboulle, M.: Interior gradient and proximal methods for convex and conic optimization. SIAM Journal on Optimization 16, 697–725 (2006)
Bauschke, H., Combettes, P.: Convex Analysis and Monotone Operator Theory in Hilbert Spaces. CMS Books in Mathematics / Ouvrages de mathématiques de la SMC. Springer-Verlag, New York (2011)
Beck, A., Teboulle, M.: A fast iterative shrinkage-tresholding algorithm for linear inverse problems. SIAM Journal on Imaging Sciences 2, 183–202 (2009)
Benker, H., Hamel, A.H., Tammer, C.: An algorithm for vectorial control approximation problems. In: Multiple Criteria Decision Making (Hagen, 1995), Lecture Notes in Economics and Mathematical Systems, vol. 448, pp. 3–12. Springer-Verlag, Berlin (1997)
Bento, G.C., da Cruz Neto, J.X., López, G., Soubeyran, A., Souza, J.C.O.: The proximal point method for locally Lipschitz functions in multiobjective optimization with application to the compromise problem. SIAM Journal on Optimization 28, 1104–1120 (2018)
Bento, G.C., da Cruz Neto, J.X., de Meireles, L.V.: Proximal point method for locally Lipschitz functions in multiobjective optimization of Hadamard manifolds. Journal of Optimization Theory and Applications 179, 37–52 (2018)
Bento, G.C., da Cruz Neto, J.X., Soubeyran, A.: A proximal point-type method for multicriteria optimization. Set-Valued and Variational Analysis 22, 557–573 (2014)
Bento, G.C., Ferreira, O.P., Junior, V.L.S.: Proximal point method for a special class of nonconvex multiobjective optimization functions. Optimization Letters 12, 311–320 (2018)
Bento, G.C., Ferreira, O.P., Pereira, Y.R.L.: Proximal point method for vector optimization on Hadamard manifolds. Operations Research Letters 46, 13–18 (2018)
Bento, G.C., Ferreira, O.P., Soubeyran, A., de Sousa Júnior, V.L., Valdinês, L.: Inexact multi-objective local search proximal algorithms: application to group dynamic and distributive justice problems. Journal of Optimization Theory and Applications 177, 181–200 (2018)
Boţ, R.I., Csetnek, E.R., Heinrich, A.: A primal-dual splitting algorithm for finding zeros of sums of maximal monotone operators. SIAM Journal on Optimization 23, 2011–2036 (2013)
Boţ, R.I., Grad, S.M.: Inertial forward-backward methods for solving vector optimization problems. Optimization 67, 959–974 (2018)
Boţ, R.I., Hendrich, C.: A variable smoothing algorithm for solving convex optimization problems. TOP 23(1), 124–150 (2015)
Boţ, R.I., Grad, S.M., Wanka, G.: Duality in Vector Optimization. Vector Optimization. Springer-Verlag, Berlin (2009)
Boţ, R.I., Hendrich, C.: A Douglas-Rachford type primal-dual method for solving inclusions with mixtures of composite and parallel-sum type monotone operators. SIAM Journal on Optimization 23, 2541–2565 (2013)
Bolintineanu, Ş.: Approximate efficiency and scalar stationarity in unbounded nonsmooth convex vector optimization problems. Journal of Optimization Theory and Applications 106, 265–296 (2000)
Bonnel, H., Iusem, A.N., Svaiter, B.F.: Proximal methods in vector optimization. SIAM Journal on Optimization 15, 953–970 (2005)
Borwein, J.M.: Proper efficient points for maximizations with respect to cones. SIAM Journal on Control and Optimization 15, 57–63 (1977)
Borwein, J.M.: The geometry of Pareto efficiency over cones. Mathematische Operationsforschung und Statistik Series Optimization 11, 235–248 (1980)
Buong, N.: Inertial proximal point regularization algorithm for unconstrained vector convex optimization problems. Ukrainian Mathematical Journal 60, 1483–1491 (2008)
Ceng, L.C., Mordukhovich, B.S., Yao, J.C.: Hybrid approximate proximal method with auxiliary variational inequality for vector optimization. Journal of Optimization Theory and Applications 146, 267–303 (2010)
Ceng, L.C., Yao, J.C.: Approximate proximal methods in vector optimization. European Journal of Operational Research 183, 1–19 (2007)
Chen, Z.: Generalized viscosity approximation methods in multiobjective optimization problems. Computational Optimization and Applications 49, 179–192 (2011)
Chen, Z.: Asymptotic analysis in convex composite multiobjective optimization problems. Journal of Global Optimization 55, 507–520 (2013)
Chen, Z., Huang, H., Zhao, K.: Approximate generalized proximal-type method for convex vector optimization problem in Banach spaces. Computers & Mathematics with Applications 57, 1196–1203 (2009)
Chen, Z., Huang, X.X., Yang, X.Q.: Generalized proximal point algorithms for multiobjective optimization problems. Applicable Analysis 90, 935–949 (2011)
Chen, Z., Xiang, C., Zhao, K., Liu, X.: Convergence analysis of Tikhonov-type regularization algorithms for multiobjective optimization problems. Applied Mathematics and Computation 211, 167–172 (2009)
Chen, Z., Zhao, K.: A proximal-type method for convex vector optimization problem in Banach spaces. Numerical Functional Analysis and Optimization 30, 70–81 (2009)
Chuong, T.D.: Tikhonov-type regularization method for efficient solutions in vector optimization. Journal of Computational and Applied Mathematics 234, 761–766 (2010)
Chuong, T.D.: Generalized proximal method for efficient solutions in vector optimization. Numerical Functional Analysis and Optimization 32, 843–857 (2011)
Chuong, T.D., Mordukhovich, B.S., Yao, J.C.: Hybrid approximate proximal algorithms for efficient solutions in vector optimization. Journal of Nonlinear and Convex Analysis 12, 257–286 (2011)
Chuong, T.D., Yao, J.C.: Viscosity-type approximation method for efficient solutions in vector optimization. Taiwanese Journal of Mathematics 14, 2329–2342 (2010)
Cruz, J.Y.B.: A subgradient method for vector optimization problems. SIAM Journal on Optimization 23, 2169–2182 (2013)
Durea, M., Strugariu, R.: Some remarks on proximal point algorithm in scalar and vectorial cases. Nonlinear Functional Analysis and Applications 15, 307–319 (2010)
Fliege, J., Graña Drummond, L.M., Svaiter, B.F.: Newton’s method for multiobjective optimization. SIAM Journal on Optimization 20, 602–626 (2009)
Gerstewitz, C.: Nichtkonvexe Dualität in der Vektoroptimierung. Wissenschaftliche Zeitschrift der Technischen Hochschule Carl Schorlemmer Leuna-Merseburg 25, 357–364 (1983)
Gong, X.H.: Optimality conditions for Henig and globally proper efficient solutions with ordering cone has empty interior. Journal of Mathematical Analysis and Applications 307, 12–31 (2005)
Göpfert, A., Riahi, H., Tammer, C., Zălinescu, C.: Variational Methods in Partially Ordered Spaces. CMS Books in Mathematics / Ouvrages de mathématiques de la SMC. Springer-Verlag, New York, New York (2003)
Graña Drummond, L.M., Iusem, A.N.: A projected gradient method for vector optimization problems. Computational Optimization and Applications 28, 5–29 (2004)
Graña Drummond, L.M., Maculan, N., Svaiter, B.F.: On the choice of parameters for the weighting method in vector optimization. Mathematical Programming 111, 201–216 (2008)
Graña Drummond, L.M., Svaiter, B.F.: A steepest descent method for vector optimization. Journal of Computational and Applied Mathematics 175, 395–414 (2005)
Grad, S.M.: Vector Optimization and Monotone Operators via Convex Duality. Vector Optimization. Springer-Verlag, Cham (2015)
Grad, S.M., Pop, E.L.: Vector duality for convex vector optimization problems by means of the quasi interior of the ordering cone. Optimization 63, 21–37 (2014)
Gregório, R.M., Oliveira, P.R.: A logarithmic-quadratic proximal point scalarization method for multiobjective programming. Journal of Global Optimization 49, 281–291 (2011)
Ji, Y., Goh, M., de Souza, R.: Proximal point algorithms for multi-criteria optimization with the difference of convex objective functions. Journal of Optimization Theory and Applications 169, 280–289 (2016)
Ji, Y., Qu, S.: Proximal point algorithms for vector DC programming with applications to probabilistic lot sizing with service levels. Discrete Dynamics in Nature and Society - Article ID 5675183 (2017)
Kiwiel, K.C.: An aggregate subgradient descent method for solving large convex nonsmooth multiobjective minimization problems. In: A. Straszak (ed.) Large Scale Systems: Theory and Applications 1983, International Federation of Automatic Control Proceedings Series, vol. 10, pp. 283–288. Pergamon Press, Oxford (1984)
Kiwiel, K.C.: An algorithm for linearly constrained nonsmooth convex multiobjective minimization. In: A. Sydow, S.M. Thoma, R. Vichnevetsky (eds.) Systems Analysis and Simulation 1985 Part I: Theory and Foundations, pp. 236–238. Akademie-Verlag, Berlin (1985)
Kiwiel, K.C.: A descent method for nonsmooth convex multiobjective minimization. Large Scale Systems 8, 119–129 (1985)
Luc, D.T.: Theory of Vector Optimization, Lecture Notes in Economics and Mathematical Systems, vol. 319. Springer-Verlag, Berlin (1989)
Mäkelä, M.M., Karmitsa, N., Wilppu, O.: Proximal bundle method for nonsmooth and nonconvex multiobjective optimization. In: Mathematical Modeling and Optimization of Complex Structures, Computational Methods in Applied Sciences, vol. 40, pp. 191–204. Springer-Verlag, Cham (2016)
Martinet, B.: Régularisation d’inéquations variationelles par approximations succesives. Revue Française de d’Informatique et de Recherche Opérationnelle 4, 154–159 (1970)
Miettinen, K., Mäkelä, M.M.: An interactive method for nonsmooth multiobjective optimization with an application to optimal control. Optimization Methods and Software 2, 31–44 (1993)
Miettinen, K., Mäkelä, M.M.: Interactive bundle-based method for nondifferentiable multiobjective optimization: nimbus. Optimization 34, 231–246 (1995)
Miglierina, E., Molho, E., Recchioni, M.C.: Box-constrained multi-objective optimization: a gradient-like method without “a priori” scalarization. European Journal of Operational Research 188, 662–682 (2008)
Moudafi, A., Oliny, M.: Convergence of a splitting inertial proximal method for monotone operators. Journal of Computational and Applied Mathematics 155, 447–454 (2003)
Mukai, H.: Algorithms for multicriterion optimization. IEEE Transactions on Automatic Control 25, 177–186 (1980)
Opial, Z.: Weak convergence of the sequence of successive approximations for nonexpansive mappings. Bulletin of the American Mathematical Society 73, 591–597 (1967)
Penot, J.P., Théra, M.: Semi-continuous mappings in general topology. Archiv der Mathematik (Basel) 38, 158–166 (1982)
Qu, S., Goh, M., Ji, Y., de Souza, R.: A new algorithm for linearly constrained c-convex vector optimization with a supply chain network risk application. European Journal of Operational Research 247, 359–365 (2015)
Qu, S.J., Goh, M., de Souza, R., Wang, T.N.: Proximal point algorithms for convex multi-criteria optimization with applications to supply chain risk management. Journal of Optimization Theory and Applications 163, 949–956 (2014)
Quiroz, E.A.P., Apolinário, H.C.F., Villacorta, K.D.V., Oliveira, P.R.: A linear scalarization proximal point method for quasiconvex multiobjective minimization. arXiv 1510.00461 (2015)
Rocha, R.A., Gregório, R.M.: Um algoritmo de ponto proximal inexato para programaçao multiobjetivo. In: Proceeding Series of the Brazilian Society of Applied and Computational Mathematics, vol. 6 (2018)
Rocha, R.A., Oliveira, P.R., Gregório, R.M., Souza, M.: Logarithmic quasi-distance proximal point scalarization method for multi-objective programming. Applied Mathematics and Computation 273, 856–867 (2016)
Rocha, R.A., Oliveira, P.R., Gregório, R.M., Souza, M.: A proximal point algorithm with quasi-distance in multi-objective optimization. Journal of Optimization Theory and Applications 171, 964–979 (2016)
Souza, J.C.O.: Proximal point methods for Lipschitz functions on Hadamard manifolds: scalar and vectorial cases. Journal of Optimization Theory and Applications 179, 745–760 (2018)
Tang, F.M., Huang, P.L.: On the convergence rate of a proximal point algorithm for vector function on Hadamard manifolds. Journal of the Operations Research Society of China 5, 405–417 (2017)
Villacorta, K.D.V., Oliveira, P.R.: An interior proximal method in vector optimization. European Journal of Operational Research 214, 485–492 (2011)
Acknowledgements
This work was partially supported by FWF (Austrian Science Fund), project M-2045 and DFG (German Research Foundation), project GR3367∕4 − 1 The author is grateful to an anonymous reviewer for making him aware of the paper [73] and for carefully reading this survey, and to the editors of this volume for the invitation to the CMO-BIRS Workshop on Splitting Algorithms, Modern Operator Theory, and Applications (17w5030) in Oaxaca.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendix: Proof of Theorem 11.17
Appendix: Proof of Theorem 11.17
In the following we provide an example of a convergence proof for a proximal point algorithm for determininig weakly efficient solutions to a vector optimization problem. It originates from an earlier version of [19] and incorporates some ideas from the proofs of [24, Theorem 3.1] and [3, Theorem 2.1 and Proposition 2.1]. Before formulating it, we recall the celebrated Opial’s Lemma (cf. [65]).
Lemma 11.2
Let (x n)n ⊆ X a sequence such that there exists a nonempty set S ⊆ X such that
-
(a)
limn→+∞∥x n − x∥ exists for every x ∈ S;
-
(b)
if \(x_{n_j} \rightharpoonup \hat x\) for a subsequence n j → +∞, then \(\hat x\in S\).
Then, there exists an \(\bar x \in S\) such that \(x_k \rightharpoonup \bar x\) when k → +∞.
Theorem 11.17
Let F be C-convex and positively C-lower semicontinuous and F(X) ∩ (F(x 1) − C) be C-complete. Then any sequence (x n)n generated by Algorithm 17 converges weakly towards a weakly efficient solution to (V P).
Proof
We show first that the algorithm is well-defined. Assuming that we have obtained an x n, where n ≥ 1, we have to secure the existence of x n+1. Take a \(z^*_n\in C^*\setminus \{0\}\) and without loss of generality assume that \(\|z^*_n\|=1\) for all n ≥ 1. Then \(\langle z^*_n, e_n\rangle > 0\) and the function
is lower semicontinuous, being a sum of continuous and lower semicontinuous functions, respectively, and strongly convex, as the sum of some convex functions and a squared norm, having thus exactly one minimum. By Lemma 11.1 this minimum is a weakly efficient solution to the vector optimization problem in Step 3 of Algorithm 17 and we denote it by x n+1.
The next step is to show the Fejér monotonicity of the sequence (x n)n with respect to the set Ω = {x ∈ X : F(x) ≦C F(x k) ∀k ≥ 0}, that is nonempty because of the C-completeness hypothesis. Let n ≥ 1. The function \(x\mapsto \langle z^*_n, \lambda _n F(x) + ({\alpha _n}/{2})\|x-x_n-\beta _n(x_n-x_{n-1})\|{ }^2 e_n \rangle + \delta _{\varOmega _n} (x)\) attains its only minimum at x n+1, and this fact can be equivalently written as
Using the continuity of the norm, this yields (e.g. via [21, Theorem 3.5.6]) \(0\in \partial \big (\langle z^*_n, \lambda _n F(\cdot ) \rangle + \delta _{\varOmega _n} (\cdot )\big ) (x_{n+1}) + \partial \big (({\alpha _n}/{2})\langle z^*_n, e_n\rangle \|\cdot -x_n-\beta _n (x_n-x_{n-1})\|{ }^2 \big )(x_{n+1}) = \partial \big (\langle z^*_n, \lambda _n F(\cdot ) \rangle + \delta _{\varOmega _n} (\cdot )\big ) (x_{n+1})\) \(+ \alpha _n \langle z^*_n, e_n\rangle (x_{n+1}-x_n-\beta _n (x_n-x_{n-1}))\). Then, since x n+1 ∈ Ω n, for any x ∈ Ω n it holds
Let us take an element \(\tilde x\in \varOmega \). By construction \(\tilde x\in \varOmega _n\), thus (11.2) yields, after taking into consideration that \(F(\tilde x)\leqq _C F(x_{n+1})\), λ n > 0 and \(z^*_n\in C^*\setminus \{0\}\), that \( \alpha _n \langle z^*_n, e_n\rangle \langle x_{n+1}-x_n-\beta _n (x_n-x_{n-1}), \tilde x-x_{n+1}\rangle \geq 0\).
For each k ≥ 0 denote \(\varphi _k=(1/2)\|x_k-\tilde x\|{ }^2\). The previous inequality, after dividing with the positive number \(\alpha _n \langle z^*_n, e_n\rangle \), can be rewritten as
and, since \(\langle x_n-x_{n-1}, x_{n+1}-\tilde x\rangle = \varphi _n-\varphi _{n-1} + (1/2)\|x_n-x_{n-1}\|{ }^2+ \langle x_n-x_{n-1}, x_{n+1}-x_n\rangle \), it turns into
Since the right-hand side of (11.3) is less than or equal to ((β n − 1)∕2)∥x n+1 − x n∥2 + β n∥x n − x n−1∥2, denoting μ k = φ k − β k φ k−1 + β k∥x k − x k−1∥2, k ≥ 1, it follows that
thus the sequence (μ k)k is nonincreasing, as n ≥ 1 was arbitrarily chosen. Then φ n ≤ β n φ 0 + μ 1∕(1 − β) and one also gets ∥x n+1 − x n∥2 ≤ (2∕(1 − 3β))(μ n − μ n+1). Employing (11.4), one obtains then
in particular
The right-hand side of (11.3) can be rewritten as (1∕2)(β n(β n + 1)∥x n − x n−1∥2 −∥x n+1 − x n − β n(x n − x n−1)∥2). Denoting τ k+1 = x k+1 − x k − β k(x k − x k−1), θ k = φ k − φ k−1 and δ k = β k∥x k − x k−1∥2 for k ≥ 0 and taking into consideration that β n ∈ [0, 1∕3), (11.3) yields
Then [θ n+1]+ ≤ (1∕3)[θ n]+ + δ n, followed by \([\theta _{n+1}]_+ \leq (1/3^n) [\theta _1]_+ + \sum _{k=0}^{n-1}\delta _{n-k}/3^k\). Hence \(\sum _{k=0}^{+\infty }[\theta _{k+1}]_+ \leq 3/2 ( [\theta _1]_+ + \sum _{k=0}^{+\infty }\delta _k)\) and, as the right-hand side of this inequality is finite due to (11.5), so is \(\sum _{k=1}^{+\infty }[\theta _k]_+\), too. This yields that the sequence (w k)k defined as \(w_k=\varphi _k - \sum _{j=1}^k [\theta _j]_+\), k ≥ 0, is bounded. Moreover, \(w_{k+1}-w_k = \varphi _{k+1}-\varphi _k - [\varphi _{k+1}-\varphi _k]_+ = \varphi _{k+1}-\varphi _k + \min \{0, \varphi _k - \varphi _{k+1}\} \leq 0\) for all k ≥ 1, thus (w k)k is convergent. Consequently, \(\lim _{k \rightarrow +\infty } \varphi _k = \lim _{k \rightarrow +\infty } w_k + \sum _{j=1}^{+\infty }[\theta _{j+1}]_+\), therefore (φ k)k is convergent. Finally, \((\|x_k-\tilde x\|{ }^2)_k\) is convergent, too, i.e. (a) in Lemma 11.2 with S = Ω is fulfilled.
We show now that (x k)k is weakly convergent. The convergence of (φ k)k implies that (x k)k is bounded, so it has weak cluster points. Let \(\hat x\in X\) be one of them and \((x_{k_j})_j\) the subsequence that converges towards it. Then, as F is positively C-lower semicontinuous and C-convex, it follows that for any z ∗∈ C ∗ the function 〈z ∗, F(⋅)〉 is lower semicontinuous and convex, thus
with the last equality following from the fact that the sequence (F(x k))k is by construction nonincreasing. Assuming that there exists a k ≥ 0 such that \(F(\hat x)\nleqq _C F(x_k)\), there exists a \(\tilde z\in C^*\setminus \{0\}\) such that \(\langle \tilde z, F(\hat x) - F(x_k)\rangle > 0\), which contradicts (11.7), consequently \(F(\hat x)\leqq _C F(x_k)\) for all k ≥ 0, i.e. \(\hat x\in \varOmega \), therefore one can employ Lemma 11.2 with S = Ω since its hypothesis (b) is fulfilled as well. This guarantees then the weak convergence of (x k)k to a point \(\bar x\in \varOmega \).
The last step is to show that \(\bar x \in \mathcal {W}\mathcal {E}(VP)\). Assuming that \(\bar x\notin \mathcal {W}\mathcal {E} (VP)\), there exists an x′∈ X such that \(F(x')< _C F(\bar x)\). This yields x′∈ Ω. As \(\|z^*_k\|=1\) for all k ≥ 0, the sequence \((z_k^*)_k\) has a weak∗ cluster point, say \(\bar z^*\), that is the limit of a subsequence \((z^*_{k_j})_j\). Because \(z^*_k\in C^*\) for all k ≥ 0 and C ∗ is weakly∗ closed, it follows that \(\bar z^*\in C^*\). Moreover, \(\bar z^*\neq 0\), since it can be shown via [23, Lemma 2.2] that \(\langle \bar z^*, c\rangle > 0\) for any \(c\in \operatorname *{\mathrm {int}} C\). Consequently, \(\langle \bar z^*, F(x') - F(\bar x)\rangle < 0\). For any j ≥ 0 it holds by (11.2)
Because of (11.5), (∥x k − x k−1∥)k converges towards 0 for k → +∞, therefore so does the last expression in the inequality chain (11.8) when j → +∞ as well. Letting j converge towards + ∞, (11.8) yields \(\langle \bar z^*, F(x') - F(\bar x)\rangle \geq 0\), contradicting the inequality obtained above. Consequently, \(\bar x \in \mathcal {W}\mathcal {E}(VP)\). □
Remark 11.43
In order to guarantee the lower semicontinuity of the functions \(\delta _{\varOmega _n}\), n ≥ 1, it is enough to have the vector function F only C-level closed (i.e. the set {x ∈ X : F(x) ≦C y} is closed for any y ∈ Y ), a hypotheses weaker than the positive C-lower semicontinuity imposed on F in Theorem 11.17 and Theorem 11.18. However, the latter is also necessary in the proofs of these statements in order to guarantee the lower semicontinuity of the functions \((z^*_nF)\), n ≥ 1.
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Grad, SM. (2019). A Survey on Proximal Point Type Algorithms for Solving Vector Optimization Problems. In: Bauschke, H., Burachik, R., Luke, D. (eds) Splitting Algorithms, Modern Operator Theory, and Applications. Springer, Cham. https://doi.org/10.1007/978-3-030-25939-6_11
Download citation
DOI: https://doi.org/10.1007/978-3-030-25939-6_11
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-25938-9
Online ISBN: 978-3-030-25939-6
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)



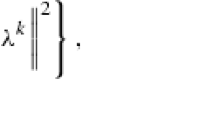
 ;
;