Abstract
This paper studies indistinguishability against quantum chosen-ciphertext attacks (IND-qCCA security) of key-encapsulation mechanisms (KEMs) in quantum random oracle model (QROM). We show that the SXY conversion proposed by Saito, Yamakawa, and Xagawa (EUROCRYPT 2018) and the HU conversion proposed by Jiang, Zhang, and Ma (PKC 2019) turn a weakly-secure deterministic public-key encryption scheme into an IND-qCCA-secure KEM scheme in the QROM. The proofs are very similar to that for the IND-CCA security in the QROM, easy to understand, and as tight as the original proofs.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Quantum Superposition Attacks: Scalable quantum computers will threaten classical cryptography because of efficient quantum algorithms, e.g., Grover’s algorithm for DB search [Gro96] and Shor’s algorithms for factorization and discrete logarithms [Sho97]. Hence, we study classical cryptography secure against quantum adversaries (see e.g., the technical report from NIST [CJL+16]). Moreover, several researchers studied stronger quantum adversaries that can mount quantum superposition attacks, that is, quantum adversaries that can obtain the result of quantum computations with secret. For example, the adversary can obtain  by querying
by querying  , where D is a decryption circuit of a symmetric-key encryption scheme and k is a secret key. There are several quantum superposition attacks that break classically-secure cryptographic primitives: Kuwakado and Morii [KM12] presented a quantum chosen-plaintext attack against the Even-Mansour construction of a block cipher if the inner permutation is publicly available as quantum oracle, which employed Simon’s algorithm [Sim97] neatly. Kaplan, Leurent, Leverrier, and Naya-Plasencia [KLLN16] also studied quantum superposition attacks against several block ciphers and modes.Footnote 1 Boneh and Zhandry [BZ13b] also gave a block cipher that is secure against chosen-plaintext-and-ciphertext attacks but vulnerable against quantum chosen-ciphertext attacks.
, where D is a decryption circuit of a symmetric-key encryption scheme and k is a secret key. There are several quantum superposition attacks that break classically-secure cryptographic primitives: Kuwakado and Morii [KM12] presented a quantum chosen-plaintext attack against the Even-Mansour construction of a block cipher if the inner permutation is publicly available as quantum oracle, which employed Simon’s algorithm [Sim97] neatly. Kaplan, Leurent, Leverrier, and Naya-Plasencia [KLLN16] also studied quantum superposition attacks against several block ciphers and modes.Footnote 1 Boneh and Zhandry [BZ13b] also gave a block cipher that is secure against chosen-plaintext-and-ciphertext attacks but vulnerable against quantum chosen-ciphertext attacks.
The stronger attack model in which adversaries can issue quantum queries is worth investigating. We motivate to investigate this model from following arguments:
-
If a source code containing secret information is available, then a quantum adversary can implement a quantum machine containing secret information by itself and mount quantum superposition attacks. For example, a reverse engineering of a physical machine containing secret information allows an adversary to obtain an obfuscated code containing secret information. Moreover, white-box cryptography and obfuscation allows us to publish an obfuscated code containing secret information [GHS16].Footnote 2
-
In the future, quantum machines and quantum channels will be ubiquitous. Protocols and primitives will handle quantum data as discussed in Damgård, Funder, Nielsen, and Salvail [DFNS14].
-
Even if they handle classical data, we can consider the quantum-ubiquitous world as Boneh and Zhandry discussed [BZ13a, BZ13b]. In this world, the end-user device is quantum and, thus, the device should measure the final quantum state and output a classical information, which prevents the quantum superposition attacks. This last step would be eventually avoided by an implementation bug or be circumvented by a neat hack of a quantum adversary in the future.
-
Moreover, if they handle classical data and are implemented in classical machines, one can consider special techniques that force the classical machines behave quantumly. For example, Damgård, Funder, Nielsen, and Salvail [DFNS14] and Gagliardoni, Hülsing, and Schaffner [GHS16] discussed the ‘frozen smart-card’ scenario.
Security of PKE and KEM against Quantum Chosen-Ciphertext Attacks: Boneh and Zhandry [BZ13b] introduced the security against quantum chosen-ciphertext attacks (\({ \textsc {qCCA}}\) security in short) for public-key encryption (PKE), which is the security against quantum adversaries that make quantum decryption queries. Boneh and Zhandry [BZ13b] showed that a PKE scheme obtained by applying the Canetti-Halevi-Katz conversion [BCHK07] to an identity-based encryption (IBE) scheme and one-time signature is  -secure if the underlying IBE scheme is selectively-secure against quantum chosen-identity queries and the underlying one-time signature scheme is (classically) strongly, existentially unforgeable against chosen-message attacks. They also showed that if there exists an IND-CCA-secure PKE, then there exists an ill-formed PKE that is IND-CCA-secure but not
-secure if the underlying IBE scheme is selectively-secure against quantum chosen-identity queries and the underlying one-time signature scheme is (classically) strongly, existentially unforgeable against chosen-message attacks. They also showed that if there exists an IND-CCA-secure PKE, then there exists an ill-formed PKE that is IND-CCA-secure but not  -secure [BZ13b].
-secure [BZ13b].
As far as we know, this is the only known PKE scheme that is proven to be  secure (excluding the concurrent work by Zhandry [Zha18, 2018-08-14 ver.]).
secure (excluding the concurrent work by Zhandry [Zha18, 2018-08-14 ver.]).
1.1 Our Contribution
We show that the SXY conversion in Saito, Yamakawa, and Xagawa [SXY18] and the HU conversion proposed by Jiang, Zhang, and Ma [JZM19] turn a PKE scheme into an  -secure KEM scheme in the QROM, if the underlying PKE scheme is perfectly-correct and disjoint-simulatable. We also observed that the perfect correctness can be relaxed as \(\delta \)-correctness with negligible \(\delta \) [HHK17].
-secure KEM scheme in the QROM, if the underlying PKE scheme is perfectly-correct and disjoint-simulatable. We also observed that the perfect correctness can be relaxed as \(\delta \)-correctness with negligible \(\delta \) [HHK17].
Our idea is summarized as follows: In the last step of the IND-CCA security proofs of the above conversions, the challenger should simulate the decapsulation oracle on a query of any ciphertext c except the challenge ciphertext \(c^*\). Roughly speaking, we observe that, if this simulation is “history-free,” i.e., if the simulation does not depend on previously made queries at all, this procedure can be quantumly simulated by implementing this procedure in the quantum way.Footnote 3 For example, in the last step of the IND-CCA security proof in [SXY18], the decapsulation oracle on input c returns \(K = \mathsf {H}_q(c)\) if \(c \ne c^*\), where \(\mathsf {H}_q\) is a random function chosen by the reduction algorithm. Therefore, intuitively speaking, this simulation is “history-free” and can be implemented quantumly.
1.2 Concurrent Works
Zhandry [Zha18, 2018-08-14 ver.] showed that the PKE scheme obtained by applying the Fujisaki-Okamoto conversion [FO13] to a PKE scheme \(\mathsf {PKE}\) and a DEM scheme \(\mathsf {DEM}\) is  -secure in the QROM, if \(\mathsf {PKE}\) is
-secure in the QROM, if \(\mathsf {PKE}\) is  -secure and well-spread, \(\mathsf {DEM}\) is OT-secureFootnote 4. Zhandry proposed recording and testing techniques to simulate the decryption oracles. We note that his security proof is non-tight unlike ours.
-secure and well-spread, \(\mathsf {DEM}\) is OT-secureFootnote 4. Zhandry proposed recording and testing techniques to simulate the decryption oracles. We note that his security proof is non-tight unlike ours.
1.3 Organizations
Section 2 reviews basic notations and definitions. Section 3 reviews security notions of PKE and KEM. Section 4 gives our new qCCA-security proof for the KEM in [SXY18] as known as the SXY conversion. Section 5 gives our new qCCA-security proof for the KEM in [JZM19] as known as the HU conversion.
2 Preliminaries
2.1 Notation
A security parameter is denoted by \(\kappa \). We use the standard O-notations: O, \({\mathrm \Theta }\), \({\mathrm \Omega }\), and \(\omega \). DPT and PPT stand for deterministic polynomial time and probabilistic polynomial time. A function \(f(\kappa )\) is said to be negligible if \(f(\kappa ) = \kappa ^{-\omega (1)}\). We denote a set of negligible functions by  . For two finite sets
. For two finite sets
 and
and
 denote a set of all functions whose domain is
denote a set of all functions whose domain is
 and codomain is
and codomain is
 .
.
For a distribution \(\chi \), we often write “\(x \leftarrow \chi \),” which indicates that we take a sample x from \(\chi \). For a finite set S, U(S) denotes the uniform distribution over S. We often write “\(x \leftarrow S\)” instead of “\(x \leftarrow U(S)\).” For a set S and a deterministic algorithm \(\mathsf {A}\), \(\mathsf {A}(S)\) denotes the set \(\{\mathsf {A}(x) \mid x \in S\}\).
If \(\mathsf {inp}\) is a string, then “\(\mathsf {out} \leftarrow \mathsf {A}(\mathsf {inp})\)” denotes the output of algorithm \(\mathsf {A}\) when run on input \(\mathsf {inp}\). If \(\mathsf {A}\) is deterministic, then \(\mathsf {out}\) is a fixed value and we write “\(\mathsf {out} := \mathsf {A}(\mathsf {inp})\).” We also use the notation “\(\mathsf {out} := \mathsf {A}(\mathsf {inp};r)\)” to make the randomness r explicit.
For the Boolean statement P, \(\mathsf {boole}(P)\) denotes the bit that is 1 if P is true, and 0 otherwise. For example, \(\mathsf {boole}(b' \mathbin {{\mathop {=}\limits ^{?}}}b)\) is 1 if and only if \(b' = b\).
2.2 Quantum Computation
We refer to [NC00] for basic of quantum computation.
Quantum Random Oracle Model. Roughly speaking, the quantum random oracle model (QROM) is an idealized model where a hash function is modeled as a publicly and quantumly accessible random oracle. See [BDF+11] for a more detailed description of the model.
Lemma. We review useful lemmas regarding the quantum oracles.
Lemma 2.1
Let \(\ell \) be an integer. Let
 and
and
 be two independent random oracles. If an unbounded time quantum adversary
be two independent random oracles. If an unbounded time quantum adversary
 makes a query to \(\mathsf {H}\) at most \(q_{\mathsf {H}}\) times, then we have
makes a query to \(\mathsf {H}\) at most \(q_{\mathsf {H}}\) times, then we have

where all oracle accesses of
 can be quantum.
can be quantum.
Though this seems to be a folklore, Saito et al. [SXY18] and Jiang et al. [JZC+18] gave the proof.
The second one is the hardness of generic search problem. If the oracle F rarely returns 1, then it is hard to distinguish F from the zero oracle N.
Lemma 2.2
(Generic Search Problem ([ARU14, Lemma 37], [HRS16, Thm.1], [JZC+18])). Let \(\gamma \in {[0,1]}\). Let
 be a finite set. Let
be a finite set. Let
 be the following function: For each z, \(F(z) = 1\) with probability \(p_z\) at most \(\gamma \) and \(F(z) = 0\) else. Let N be the zero function, that is, \(N(z) = 0\) for any
be the following function: For each z, \(F(z) = 1\) with probability \(p_z\) at most \(\gamma \) and \(F(z) = 0\) else. Let N be the zero function, that is, \(N(z) = 0\) for any
 . If an oracle algorithm
. If an oracle algorithm
 makes at most Q quantum queries to F (or N), then
makes at most Q quantum queries to F (or N), then

Particularly, the probability that
 finds a z satisfying \(F(z) = 1\) is at most \(2q \sqrt{\gamma }\).
finds a z satisfying \(F(z) = 1\) is at most \(2q \sqrt{\gamma }\).
Simulation of Random Oracle. In the original quantum random oracle model introduced by Boneh et al. [BDF+11], they do not allow a reduction algorithm to access a random oracle, so it has to simulate a random oracle by itself. In contrast, in this paper, we give a random oracle access to a reduction algorithm. We remark that this is just a convention and not a modification of the model since we can simulate a random oracle against quantum adversaries in several ways; (1) 2q-wise independent hash function [Zha12], where q is the maximum number of queries to the random oracle, (2) quantumly-secure PRF [BDF+11], and (3) hash function modeled as quantum random oracle [KLS18]. In addition, Zhandry proposed a new technique to simulate the quantum random oracle, the compressed oracle technique [Zha18]. His new simulation of the quantum random oracle is perfect even for unbounded number of queries. In what follows, we use \(t_{\mathsf {RO}}\) to denote a time needed to simulate a quantum random oracle.
3 Definitions
3.1 Public-Key Encryption (PKE)
The model for PKE schemes is summarized as follows:
Definition 3.1
A PKE scheme \(\mathsf {PKE}\) consists of the following triple of polynomial-time algorithms \((\mathsf {Gen}, \mathsf {Enc}, \mathsf {Dec})\).
-
\(\mathsf {Gen}(1^{\kappa };r_g) \rightarrow ( ek , dk )\): a key-generation algorithm that on input \(1^\kappa \), where \(\kappa \) is the security parameter, outputs a pair of keys \(( ek , dk )\). \( ek \) and \( dk \) are called the encryption key and decryption key, respectively.
-
\(\mathsf {Enc}( ek ,m;r_e) \rightarrow c\): an encryption algorithm that takes as input encryption key \( ek \) and message
 and outputs ciphertext
and outputs ciphertext
 .
. -
\(\mathsf {Dec}( dk ,c) \rightarrow m/\bot \): a decryption algorithm that takes as input decryption key \( dk \) and ciphertext c and outputs message
 or a rejection symbol
or a rejection symbol
 .
.
Definition 3.2
We say a PKE scheme \(\mathsf {PKE}\) is deterministic if \(\mathsf {Enc}\) is deterministic. DPKE stands for deterministic public key encryption.
We review \(\delta \)-correctness in Hofheinz, Hövelmanns, and Kiltz [HHK17].
Definition 3.3
(\(\delta \)-Correctness [HHK17]). Let \(\delta = \delta (\kappa )\). We say that \(\mathsf {PKE}= (\mathsf {Gen},\mathsf {Enc},\mathsf {Dec})\) is \(\delta \)-correct if

In particular, we say that \(\mathsf {PKE}\) is perfeclty correct if \(\delta = 0\).
We also define key’s accuracy.
Definition 3.4
(Accuracy). We say that a key pair \(( ek , dk )\) is accurate if for any \(m \in \mathcal {M}\),
Remark 3.1
We observe that if \(\mathsf {PKE}\) is deterministic, then \(\delta \)-correctness implies that
In other words, if \(\mathsf {PKE}\) is deterministic and \(\delta \)-correct, then a key pair is accurate with probability \(\ge 1-\delta \). We finally stress that, if \(\mathsf {PKE}\) is deterministic but derandomized by the random oracle, then we cannot apply the above argument.
Disjoint Simulatability. Saito et al. defined disjoint simulatability of DPKE [SXY18]. Intuitively speaking, a DPKE scheme is disjoint-simulatable if there exists a simulator that is only given an encryption key and generates a “fake ciphertext” that is computationally indistinguishable from a real ciphertext of a random message. Moreover, we require that a fake ciphertext falls in a valid ciphertext space with negligible probability. The formal definition is as follows.
Definition 3.5
(Disjoint simulatability [SXY18]). Let  denote an efficiently sampleable distribution on a set
denote an efficiently sampleable distribution on a set  . A deterministic PKE scheme \(\mathsf {PKE}= (\mathsf {Gen},\mathsf {Enc},\mathsf {Dec})\) with plaintext and ciphertext spaces
. A deterministic PKE scheme \(\mathsf {PKE}= (\mathsf {Gen},\mathsf {Enc},\mathsf {Dec})\) with plaintext and ciphertext spaces  and
and
 is
is  -disjoint-simulatable if there exists a PPT algorithm
-disjoint-simulatable if there exists a PPT algorithm
 that satisfies the followings.
that satisfies the followings.
-
(Statistical disjointness:)

is negligible, where
 denotes a randomness space for \(\mathsf {Gen}\).
denotes a randomness space for \(\mathsf {Gen}\). -
(Ciphertext-indistinguishability:) For any PPT adversary
 ,
, 
is negligible.
IND-QCCA. Boneh and Zhandry showed that if we consider a quantum challenge oracle, then there exists a quantum adversary that can distinguish the superposition of plaintexts [BZ13b]. They showed that indistinguishability against fully-quantum chosen-plaintext attack (IND-fqCPA) and indistinguishability against fully-quantum chosen-left-right-plaintext attack ( ) is impossible. (For the details, see their paper [BZ13b].) Thus, we only consider a classical challenge oracle.
) is impossible. (For the details, see their paper [BZ13b].) Thus, we only consider a classical challenge oracle.
We need to define the result of \(m \oplus \bot \), where  . In order to do so, we encode \(\bot \) as a bit string outside of the message space. The security definition follows:
. In order to do so, we encode \(\bot \) as a bit string outside of the message space. The security definition follows:
Definition 3.6
( for PKE [BZ13b]). For any adversary \(\mathcal {A}\), we define its
for PKE [BZ13b]). For any adversary \(\mathcal {A}\), we define its  advantages against a PKE scheme \(\mathsf {PKE}= (\mathsf {Gen},\mathsf {Enc},\mathsf {Dec})\) as follows:
advantages against a PKE scheme \(\mathsf {PKE}= (\mathsf {Gen},\mathsf {Enc},\mathsf {Dec})\) as follows:

where
 is an experiment described in Fig. 1. We say that \(\mathsf {PKE}\) is
is an experiment described in Fig. 1. We say that \(\mathsf {PKE}\) is  -secure if
-secure if
 is negligible for any PPT adversary
is negligible for any PPT adversary
 .
.
3.2 Key Encapsulation Mechanism (KEM)
The model for KEM schemes is summarized as follows:
Definition 3.7
A KEM scheme \(\mathsf {KEM}\) consists of the following triple of polynomial-time algorithms \((\mathsf {Gen}, \mathsf {Encaps}, \mathsf {Decaps})\):
-
\(\mathsf {Gen}(1^{\kappa };r_g) \rightarrow ( ek , dk )\): a key-generation algorithm that on input \(1^\kappa \), where \(\kappa \) is the security parameter, outputs a pair of keys \(( ek , dk )\). \( ek \) and \( dk \) are called the encapsulation key and decapsulation key, respectively.
-
\(\mathsf {Encaps}( ek ;r_e) \rightarrow (c,K)\): an encapsulation algorithm that takes as input encapsulation key \( ek \) and outputs ciphertext
 and key
and key
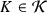 .
. -
\(\mathsf {Decaps}( dk ,c) \rightarrow K/\bot \): a decapsulation algorithm that takes as input decapsulation key \( dk \) and ciphertext c and outputs key K or a rejection symbol
 .
.
Definition 3.8
(\(\delta \)-Correctness). Let \(\delta = \delta (\kappa )\). We say that \(\mathsf {KEM}= (\mathsf {Gen},\mathsf {Encaps},\mathsf {Decaps})\) is \(\delta \)-correct if
In particular, we say that \(\mathsf {KEM}\) is perfeclty correct if \(\delta = 0\).
IND-qCCA. We also define indistinguishability under quantum chosen-ciphertext attacks (denoted by  ) for KEM by following [BZ13b].
) for KEM by following [BZ13b].
Definition 3.9
( for KEM). For any adversary \(\mathcal {A}\), we define its
for KEM). For any adversary \(\mathcal {A}\), we define its  advantage against a KEM scheme \(\mathsf {KEM}= (\mathsf {Gen}, \mathsf {Encaps}, \mathsf {Decaps})\) as follows:
advantage against a KEM scheme \(\mathsf {KEM}= (\mathsf {Gen}, \mathsf {Encaps}, \mathsf {Decaps})\) as follows:

where  is an experiment described in Fig. 2.
is an experiment described in Fig. 2.
We say that \(\mathsf {KEM}\) is  -secure if
-secure if
 is negligible for any PPT adversary
is negligible for any PPT adversary
 .
.
4 IND-qCCA Security of \(\mathsf {SXY}\)
Let \(\mathsf {PKE}_1 = (\mathsf {Gen}_1,\mathsf {Enc}_1,\mathsf {Dec}_1)\) be a deterministic PKE scheme and let
 and
and
 be random oracles. We review the conversion \(\mathsf {SXY}\) in Fig. 3. We show that \(\mathsf {KEM}:= \mathsf {SXY}[\mathsf {PKE}_1,\mathsf {H},\mathsf {H}']\) is
be random oracles. We review the conversion \(\mathsf {SXY}\) in Fig. 3. We show that \(\mathsf {KEM}:= \mathsf {SXY}[\mathsf {PKE}_1,\mathsf {H},\mathsf {H}']\) is  -secure if the underlying \(\mathsf {PKE}_1\) is a disjoint-simulatable DPKE.
-secure if the underlying \(\mathsf {PKE}_1\) is a disjoint-simulatable DPKE.
Theorem 4.1
( security of \(\mathsf {SXY}\) in the QROM). Let \(\mathsf {PKE}_1\) be a \(\delta \)-correct DPKE scheme. Suppose that \(\mathsf {PKE}_1\) is
security of \(\mathsf {SXY}\) in the QROM). Let \(\mathsf {PKE}_1\) be a \(\delta \)-correct DPKE scheme. Suppose that \(\mathsf {PKE}_1\) is  -disjoint-simulatable with a simulator
-disjoint-simulatable with a simulator
 . For any
. For any  quantum adversary
quantum adversary
 against \(\mathsf {KEM}\) issuing \(q_{\mathsf {H}}\) and \(q_{\mathsf {H}'}\) quantum random oracle queries to \(\mathsf {H}\) and \(\mathsf {H}'\) and \(q_{\overline{\mathsf {Dec}}}\) decapsulation queries, there exists an adversary
against \(\mathsf {KEM}\) issuing \(q_{\mathsf {H}}\) and \(q_{\mathsf {H}'}\) quantum random oracle queries to \(\mathsf {H}\) and \(\mathsf {H}'\) and \(q_{\overline{\mathsf {Dec}}}\) decapsulation queries, there exists an adversary
 against the disjoint simulatability of \(\mathsf {PKE}_1\) such that
against the disjoint simulatability of \(\mathsf {PKE}_1\) such that

and
 .
.
We note that the proof of Theorem 4.1 is essentially equivalent to that of the CCA security in the QROM in [SXY18] except that at the final game we require quantum simulation of decapsulation oracle.
Security Proof. We use a game-hopping proof. The overview of all games is given in Table 1.
\(\mathsf {Game}_0\): This is the original game,
 .
.
\(\mathsf {Game}_{1}\): This game is the same as \(\mathsf {Game}_0\) except that \(\mathsf {H}'(s,c)\) in the decapsulation oracle is replaced with \(\mathsf {H}_q(c)\) where
 is another random oracle. We remark that
is another random oracle. We remark that
 is not given direct access to \(\mathsf {H}_q\).
is not given direct access to \(\mathsf {H}_q\).
\(\mathsf {Game}_{1.5}\): This game is the same as \(\mathsf {Game}_1\) except that the random oracle \(\mathsf {H}(\cdot )\) is simulated by \(\mathsf {H}'_q(\mathsf {Enc}_1( ek ,\cdot ))\) where \(\mathsf {H}'_q\) is yet another random oracle. We remark that a decapsulation oracle and generation of \(K_0^*\) also use \(\mathsf {H}'_q(\mathsf {Enc}_1( ek ,\cdot ))\) as \(\mathsf {H}(\cdot )\) and that
 is not given direct access to \(\mathsf {H}'_q\).
is not given direct access to \(\mathsf {H}'_q\).
\(\mathsf {Game}_{2}\): This game is the same as \(\mathsf {Game}_{1.5}\) except that the random oracle \(\mathsf {H}(\cdot )\) is simulated by \(\mathsf {H}_q(\mathsf {Enc}_1( ek ,\cdot ))\) instead of \(\mathsf {H}'_q(\mathsf {Enc}_1( ek ,\cdot ))\). We remark that the decapsulation oracle and generation of \(K_0^*\) also use \(\mathsf {H}_q(\mathsf {Enc}_1( ek ,\cdot ))\) as \(\mathsf {H}(\cdot )\).
\(\mathsf {Game}_{3}\): This game is the same as \(\mathsf {Game}_2\) except that \(K_0^*\) is set as \(\mathsf {H}_q(c^*)\) and the decapsulation oracle always returns \(\mathsf {H}_q(c)\) as long as \(c \ne c^*\). We denote the modified decapsulation oracle by \(\textsc {qDec'}\).
\(\mathsf {Game}_{4}\): This game is the same as \(\mathsf {Game}_3\) except that \(c^*\) is set as
 .
.
The above completes the descriptions of games. We clearly have

by the definition. We upperbound this by the following lemmas.
Lemma 4.1
We have

Proof
This is obvious from Lemma 2.1. \(\square \)
Lemma 4.2
Let  and
and  denote the event that the key pair \(( ek , dk )\) is accurate and inaccurate, respectively. We have
denote the event that the key pair \(( ek , dk )\) is accurate and inaccurate, respectively. We have

Proof
By the definition, we have

We have

as we wanted. \(\square \)
Lemma 4.3
We have

Proof
Since we assume that the key pair \(( ek , dk )\) of \(\mathsf {PKE}_1\) is accurate, \(\mathsf {Enc}_1( ek ,\cdot )\) is injective. Therefore, if \(\mathsf {H}'_q(\cdot )\) is a random function, then \(\mathsf {H}'_q(\mathsf {Enc}_1( ek ,\cdot ))\) is also a random function. Remarking that access to \(\mathsf {H}'_q\) is not given to
 , it causes no difference from the view of
, it causes no difference from the view of
 if we replace \(\mathsf {H}(\cdot )\) with \(\mathsf {H}'_q(\mathsf {Enc}_1( ek ,\cdot ))\). \(\square \)
if we replace \(\mathsf {H}(\cdot )\) with \(\mathsf {H}'_q(\mathsf {Enc}_1( ek ,\cdot ))\). \(\square \)
Lemma 4.4
We have

Proof
We say that a ciphertext c is valid if we have \(\mathsf {Enc}_1( ek ,\mathsf {Dec}_1( dk ,c))=c\) and invalid otherwise. We remark that \(\mathsf {H}_q\) is used only for decrypting an invalid ciphertext c as \(\mathsf {H}_q(c)\) in \(\mathsf {Game}_{1.5}\). This means that a value of \(\mathsf {H}_q(c)\) for a valid c is not used at all in \(\mathsf {Game}_{1.5}\).
On the other hand, any output of \(\mathsf {Enc}_1( ek ,\cdot )\) is valid due to the accuracy of \(( ek , dk )\). Since \(\mathsf {H}'_q\) is only used for evaluating an output of \(\mathsf {Enc}_1( ek ,\cdot )\), a value of \(\mathsf {H}_q'(c)\) for an invalid c is not used at all in \(\mathsf {Game}_{1.5}\).
Hence, it causes no difference from the view of
 if we use the same random oracle \(\mathsf {H}_q\) instead of two independent random oracles \(\mathsf {H}_q\) and \(\mathsf {H}'_q\). \(\square \)
if we use the same random oracle \(\mathsf {H}_q\) instead of two independent random oracles \(\mathsf {H}_q\) and \(\mathsf {H}'_q\). \(\square \)
Lemma 4.5
We have

Proof
Since we set \(\mathsf {H}(\cdot ):=\mathsf {H}_q(\mathsf {Enc}_1( ek ,\cdot ))\), for any valid c and \(m:=\mathsf {Dec}_1( dk ,c)\), we have \(\mathsf {H}(m)=\mathsf {H}_q(\mathsf {Enc}_1( ek ,m))=\mathsf {H}_q(c)\). Therefore, responses of the decapsulation oracle are unchanged. We also have \(\mathsf {H}(m^*)=\mathsf {H}_q(c^*)\). \(\square \)
Lemma 4.6
We have

Proof
We have

In the third inequality, we use the fact that for any reals a, b, and c with \(c \ge 0\), we have  . (See Lemma A.1 for the proof.) We use this inequality by setting
. (See Lemma A.1 for the proof.) We use this inequality by setting  , \(b = 1/2\) and
, \(b = 1/2\) and  . \(\square \)
. \(\square \)
Lemma 4.7
There exists a quantum adversary
 such that
such that

and
 .
.
Proof
We construct an adversary
 , which is allowed to access two random oracles \(\mathsf {H}_q\) and \(\mathsf {H}'\), against the disjoint simulatability as followsFootnote 5.
, which is allowed to access two random oracles \(\mathsf {H}_q\) and \(\mathsf {H}'\), against the disjoint simulatability as followsFootnote 5.
-
 It picks \(b\leftarrow \{0,1\}\), sets
It picks \(b\leftarrow \{0,1\}\), sets
 , and invokes
, and invokes
 where
where
 oracles are simulated as follows.
oracles are simulated as follows.-
\(\mathsf {H}(\cdot )\) is simulated by \(\mathsf {H}_q(\mathsf {Enc}_1( ek ,\cdot ))\).
-
\(\mathsf {H}'\) can be simulated because
 has access to an oracle \(\mathsf {H}'\).
has access to an oracle \(\mathsf {H}'\). -
\(\textsc {qDec'}(\cdot )\) is simulated by filtering \(c^*\) and using \(\mathsf {H}_q(\cdot )\); that is, on input
 ,
,
 returns
returns  .
.
Finally,
 returns \(\mathsf {boole}(b\mathbin {{\mathop {=}\limits ^{?}}}b')\).
returns \(\mathsf {boole}(b\mathbin {{\mathop {=}\limits ^{?}}}b')\). -
This completes the description of
 . It is easy to see that
. It is easy to see that
 perfectly simulates \(\mathsf {Game}_3\) if \(c^*=\mathsf {Enc}_1( ek ,m^*)\) and \(\mathsf {Game}_4\) if
perfectly simulates \(\mathsf {Game}_3\) if \(c^*=\mathsf {Enc}_1( ek ,m^*)\) and \(\mathsf {Game}_4\) if
 . Therefore, we have
. Therefore, we have

as wanted. Since \(\mathsf {H}\) is simulated by one evaluation of \(\mathsf {Enc}_1\) plus one evaluation of a random oracle \(\mathsf {H}_q\), and \(\mathsf {H}'\) and \(\textsc {qDec'}\) are simulated by one evaluation of random oracles, we have
 . \(\square \)
. \(\square \)
Lemma 4.8
We have

Proof
Let \(\mathsf {Bad}\) denote the event that \(c^*\) is in  in \(\mathsf {Game}_4\). It is easy to see that we have
in \(\mathsf {Game}_4\). It is easy to see that we have

When \(\mathsf {Bad}\) does not occur, i.e.,
 obtains no information about \(K_0^*=\mathsf {H}_q(c^*)\). This is because queries to \(\mathsf {H}\) only reveal \(\mathsf {H}_q(c)\) for
obtains no information about \(K_0^*=\mathsf {H}_q(c^*)\). This is because queries to \(\mathsf {H}\) only reveal \(\mathsf {H}_q(c)\) for  , and \(\textsc {qDec'}(c)\) returns \(\bot \) if \(c=c^*\). Therefore, we have
, and \(\textsc {qDec'}(c)\) returns \(\bot \) if \(c=c^*\). Therefore, we have
Combining the above, we have

as we wanted. \(\square \)
Proof
(Proof of Theorem 4.1). Combining all lemmas in this section, we obtain the following inequality:

\(\square \)
5 IND-qCCA Security of \(\mathsf {HU}\)
Very recently, Jiang, Zhang, and Ma [JZM19] proposed a conversion \(\mathsf {HU}\), which allows an explicit rejection but requires additional hash value \(c_2\) of m. Let \(\mathsf {PKE}_1 = (\mathsf {Gen}_1,\mathsf {Enc}_1,\mathsf {Dec}_1)\) be a deterministic PKE scheme and let
 and
and
 be random oracles. We review the conversion \(\mathsf {HU}\) in Fig. 4. We show that \(\mathsf {KEM}:= \mathsf {HU}[\mathsf {PKE}_1,\mathsf {H},\mathsf {H}']\) is
be random oracles. We review the conversion \(\mathsf {HU}\) in Fig. 4. We show that \(\mathsf {KEM}:= \mathsf {HU}[\mathsf {PKE}_1,\mathsf {H},\mathsf {H}']\) is  -secure if the underlying \(\mathsf {PKE}_1\) is a disjoint-simulatable DPKE.
-secure if the underlying \(\mathsf {PKE}_1\) is a disjoint-simulatable DPKE.
Theorem 5.1
( security of \(\mathsf {HU}\) in the QROM). Let \(\mathsf {PKE}_1\) be a \(\delta \)-correct DPKE scheme. Suppose that \(\mathsf {PKE}_1\) is
security of \(\mathsf {HU}\) in the QROM). Let \(\mathsf {PKE}_1\) be a \(\delta \)-correct DPKE scheme. Suppose that \(\mathsf {PKE}_1\) is  -disjoint-simulatable with a simulator
-disjoint-simulatable with a simulator  . For any
. For any  quantum adversary
quantum adversary
 against \(\mathsf {KEM}\) issuing \(q_{\mathsf {H}}\) and \(q_{\mathsf {H}'}\) quantum random oracle queries to \(\mathsf {H}\) and \(\mathsf {H}'\) and \(q_{\overline{\mathsf {Dec}}}\) decapsulation queries, there exists an adversary
against \(\mathsf {KEM}\) issuing \(q_{\mathsf {H}}\) and \(q_{\mathsf {H}'}\) quantum random oracle queries to \(\mathsf {H}\) and \(\mathsf {H}'\) and \(q_{\overline{\mathsf {Dec}}}\) decapsulation queries, there exists an adversary
 against the disjoint simulatability of \(\mathsf {PKE}_1\) such that
against the disjoint simulatability of \(\mathsf {PKE}_1\) such that

and
 .
.
The proof of Theorem 5.1 follows.
Security Proof. We use a game-hopping proof. The overview of all games is given in Table 2.
\(\mathsf {Game}_{0}\): This is the original game,  .
.
\(\mathsf {Game}_{1}\): This game is the same as \(\mathsf {Game}_{0}\) except that the random oracle \(\mathsf {H}(\cdot )\) and \(\mathsf {H}'(\cdot )\) are simulated by \(\mathsf {H}_q(\mathsf {Enc}_1( ek ,\cdot ))\) and \(\mathsf {H}'_q(\mathsf {Enc}_1( ek ,\cdot ))\), respectively, where
 and
and
 are random oracles. We remark that a decapsulation oracle and generation of \(K_0^*\) also use \(\mathsf {H}_q(\mathsf {Enc}_1( ek ,\cdot ))\) as \(\mathsf {H}(\cdot )\), and generation of \(c_2^*\) uses \(\mathsf {H}_q'(\mathsf {Enc}_1( ek ,\cdot ))\) as \(\mathsf {H}'(\cdot )\). We also remark that
are random oracles. We remark that a decapsulation oracle and generation of \(K_0^*\) also use \(\mathsf {H}_q(\mathsf {Enc}_1( ek ,\cdot ))\) as \(\mathsf {H}(\cdot )\), and generation of \(c_2^*\) uses \(\mathsf {H}_q'(\mathsf {Enc}_1( ek ,\cdot ))\) as \(\mathsf {H}'(\cdot )\). We also remark that
 is not given direct access to \(\mathsf {H}_q\) and \(\mathsf {H}_q'\).
is not given direct access to \(\mathsf {H}_q\) and \(\mathsf {H}_q'\).
\(\mathsf {Game}_{2}\): This game is the same as \(\mathsf {Game}_{1}\) except that the decapsulation oracle returns \(K := \mathsf {H}_q(c_1)\) if \(c_1 = \mathsf {Enc}_1( ek ,m)\) and \(\mathsf {H}_q'(c_1) = c_2\), instead returns \(K := \mathsf {H}(m)\) if \(c_1 = \mathsf {Enc}_1( ek ,m)\) and \(\mathsf {H}'(m) = c_2\).
\(\mathsf {Game}_{3}\): This game is the same as \(\mathsf {Game}_{2}\) except that the decapsulation oracle returns \(K := \mathsf {H}_q(c_1)\) if \(\mathsf {H}_q'(c_1) = c_2\). That is, the decapsulation oracle never use the re-encryption check.
\(\mathsf {Game}_{4}\): This game is the same as \(\mathsf {Game}_3\) except that \(c_1^*\) is set as
 .
.
The above completes the descriptions of games. We clearly have

by the definition. We upperbound this by the following lemmas.
Lemma 5.1
Let  denote the event that the key pair \(( ek , dk )\) is accurate. We have
denote the event that the key pair \(( ek , dk )\) is accurate. We have

We omit the proof, since the proof is the same as that of Lemma 4.2.
Lemma 5.2
We have

Proof
Since we assume that the key pair is accurate, \(\mathsf {Enc}_1( ek ,\cdot )\) is injective. Therefore, if \(\mathsf {H}_q(\cdot )\) (and \(\mathsf {H}_q'(\cdot )\), resp.) is a random function, then \(\mathsf {H}_q(\mathsf {Enc}_1( ek ,\cdot ))\) (and \(\mathsf {H}'_q(\mathsf {Enc}_1( ek ,\cdot ))\), resp.) is also a random function. Remarking that access to \(\mathsf {H}_q\) and \(\mathsf {H}'_q\) is not given to
 , it causes no difference from the view of
, it causes no difference from the view of
 if we replace \(\mathsf {H}(\cdot )\) (and \(\mathsf {H}'(\cdot )\), resp.) with \(\mathsf {H}_q(\mathsf {Enc}_1( ek ,\cdot ))\) (and \(\mathsf {H}'_q(\mathsf {Enc}_1( ek ,\cdot ))\), resp.). \(\square \)
if we replace \(\mathsf {H}(\cdot )\) (and \(\mathsf {H}'(\cdot )\), resp.) with \(\mathsf {H}_q(\mathsf {Enc}_1( ek ,\cdot ))\) (and \(\mathsf {H}'_q(\mathsf {Enc}_1( ek ,\cdot ))\), resp.). \(\square \)
Lemma 5.3
We have

Proof
This change is just conceptual. Suppose that \(c_1 = \mathsf {Enc}_1( ek ,m)\). We have that \(c_2 = \mathsf {H}'(m)\) holds if and only if \(c_2 = \mathsf {H}_q'(c_1)\) and \(K = \mathsf {H}(m) = \mathsf {H}_q(c_1)\). \(\square \)
Lemma 5.4
We have

Proof
Recall that we have \(\mathsf {H}'(m) = \mathsf {H}_q'(\mathsf {Enc}( ek ,m))\) and \(\mathsf {H}_q'(c_1) = c_2\).
Let us see the details how the decapsulation oracle treats the query  . Let \(m = \mathsf {Dec}_1( dk ,c_1)\).
. Let \(m = \mathsf {Dec}_1( dk ,c_1)\).
-
Case 1 that \(c_1 = \mathsf {Enc}_1( ek ,m)\): in this case, the decapsulation oracles in both games return
 , where \(K := \mathsf {H}_q(c_1)\) or \(\bot \) depending on that \(c_2 = \mathsf {H}_q'(c_1)\).
, where \(K := \mathsf {H}_q(c_1)\) or \(\bot \) depending on that \(c_2 = \mathsf {H}_q'(c_1)\). -
Case 2 that \(c_1 \ne \mathsf {Enc}_1( ek ,m)\) and \(c_2 \ne \mathsf {H}_q'(c_2)\): In this case, the decapsulation oracles in both games return
 .
. -
Case 3 that \(c_1 \ne \mathsf {Enc}_1( ek ,m)\) and \(c_2 = \mathsf {H}_q'(c_1)\): In this case, the decapsulation oracle in \(\mathsf {Game}_2\) returns
 , but the decapsulation oracle in \(\mathsf {Game}_3\) returns
, but the decapsulation oracle in \(\mathsf {Game}_3\) returns  .
.
If the query is classical, we can argue the difference as in [JZM19]: Since the adversary cannot access to \(\mathsf {H}_q'\) directly, it cannot know the value of \(\mathsf {H}_q'(c_1)\) if \(c_1\) lies outside of \(\mathsf {Enc}( ek ,\cdot )\). Therefore, any \(c_2\) hits the value \(\mathsf {H}_q'(c_1)\) with probability at most
 .
.
Even if the query is quantum, the problem is distinguishing problem and we invoke Lemma 2.2. We now reduce from generic search problem to distinguishing \(\mathsf {Game}_2\) with \(\mathsf {Game}_3\). We define the distribution
 over
over
 as follows: for each
as follows: for each
 , choose
, choose
 uniformly at random and set
uniformly at random and set
For each \((c_1,h)\), we have
 .
.
The reduction algorithm is defined as follows: Suppose that we are given
 , which is chosen according to
, which is chosen according to
 or set as the zero function N. We construct \(\mathsf {H}\), \(\mathsf {H}'\), and the decapsulation oracle as follows:
or set as the zero function N. We construct \(\mathsf {H}\), \(\mathsf {H}'\), and the decapsulation oracle as follows:
-
\(\mathsf {H}_q\) and \(\mathsf {H}_q'\): we choose
 and
and  uniformly at random.
uniformly at random. -
\(\mathsf {H}\): on input
 , it returns
, it returns  .
. -
\(\mathsf {H}'\): on input
 , it returns
, it returns  .
. -
\({ \textsc {qDec}}_{c^*}\): On input
 , it computes \(m = \mathsf {Dec}_1( dk ,c_1)\) and computes K as follows:
, it computes \(m = \mathsf {Dec}_1( dk ,c_1)\) and computes K as follows:-
if \(c_1 = c_1^*\) and \(c_2 = c_2^*\), then let \(K = \bot \).
-
if \(c_1 = \mathsf {Enc}_1( ek ,m)\) and \(c_2 = \mathsf {H}_q'(c_1)\), then let \(K = \mathsf {H}_q(c_1)\).
-
if \(c_1 = \mathsf {Enc}_1( ek ,m)\) and \(c_2 \ne \mathsf {H}_q'(c_1)\), then let \(K = \bot \).
-
if \(c_1 \ne \mathsf {Enc}_1( ek ,m)\) and \(f(c_1,c_2) = 1\), then let \(K = \mathsf {H}_q(c_1)\).
-
if \(c_1 \ne \mathsf {Enc}_1( ek ,m)\) and \(f(c_1,c_2) = 0\), then let \(K = \bot \).
it returns
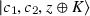 .
. -
If \(f = N\), then this algorithm perfectly simulates \(\mathsf {Game}_2\). On the other hand, if  , then this algorithm perfectly simulates \(\mathsf {Game}_3\), since any adversary cannot access \(\mathsf {H}_q'\) on
, then this algorithm perfectly simulates \(\mathsf {Game}_3\), since any adversary cannot access \(\mathsf {H}_q'\) on
 . Thus, according to Lemma 2.2, we have upperbound
. Thus, according to Lemma 2.2, we have upperbound
 as we wanted. \(\square \)
as we wanted. \(\square \)
Lemma 5.5
We have

We omit the proof, since the proof is the same as that of Lemma 4.6.
Lemma 5.6
There exists an adversary
 such that
such that

and
 .
.
Proof
Let \(g(\cdot ) := \mathsf {Enc}_1( ek ,\cdot )\). For ease of notation, we define a new function
 as follows:
as follows:
We construct an adversary
 , which is allowed to access two random oracles \(\mathsf {H}_q\) and \(\mathsf {H}_q'\), against the disjoint simulatability as follows (See footnote 5).
, which is allowed to access two random oracles \(\mathsf {H}_q\) and \(\mathsf {H}_q'\), against the disjoint simulatability as follows (See footnote 5).
-
 It picks \(b\leftarrow \{0,1\}\), sets \(K_0^*:=\mathsf {H}_q(c_1^*)\) and
It picks \(b\leftarrow \{0,1\}\), sets \(K_0^*:=\mathsf {H}_q(c_1^*)\) and
 , and invokes
, and invokes
 where
where
 oracles are simulated as follows.
oracles are simulated as follows.-
\(\mathsf {H}(\cdot )\) is simulated by \(\mathsf {H}_q(\mathsf {Enc}_1( ek ,\cdot ))\).
-
\(\mathsf {H}'(\cdot )\) is simulated by \(\mathsf {H}_q'(\mathsf {Enc}_1( ek ,\cdot ))\).
-
\(\overline{\mathsf {Dec}}'(\cdot )\) is simulated by filtering \(c_1^*\); on input
 ,
,
 returns
returns 
Finally,
 returns \(\mathsf {boole}(b\mathbin {{\mathop {=}\limits ^{?}}}b')\).
returns \(\mathsf {boole}(b\mathbin {{\mathop {=}\limits ^{?}}}b')\). -
This completes the description of
 .
.
Since \(c_2^* := \mathsf {H}_q(c_1^*)\), if \(c_2 \ne c_2^*\), then the decapsulation oracle in both games and \(f_{\mathsf {H}_q,\mathsf {H}_q'}\) return \(\bot \) on input \((c_1^*,c_2)\). Thus, we have

and
 perfectly simulate the decapsulation oracle.
perfectly simulate the decapsulation oracle.
It is easy to see that
 perfectly simulates \(\mathsf {Game}_3\) if \(c_1^*=\mathsf {Enc}_1( ek ,m^*)\) and \(\mathsf {Game}_4\) if
perfectly simulates \(\mathsf {Game}_3\) if \(c_1^*=\mathsf {Enc}_1( ek ,m^*)\) and \(\mathsf {Game}_4\) if
 . Therefore, we have
. Therefore, we have

as wanted. We have
 , since
, since
 invokes
invokes
 once, \(\mathsf {H}\) is simulated by one evaluation of \(\mathsf {Enc}_1\) plus one evaluation of a random oracle, and \(\mathsf {H}'\) and \(\overline{\mathsf {Dec}}'\) are simulated by two evaluations of random oracles. \(\square \)
once, \(\mathsf {H}\) is simulated by one evaluation of \(\mathsf {Enc}_1\) plus one evaluation of a random oracle, and \(\mathsf {H}'\) and \(\overline{\mathsf {Dec}}'\) are simulated by two evaluations of random oracles. \(\square \)
Lemma 5.7
We have

Proof
Let \(\mathsf {Bad}\) denote the event that  happens in \(\mathsf {Game}_4\). It is easy to see that we have
happens in \(\mathsf {Game}_4\). It is easy to see that we have

When \(\mathsf {Bad}\) does not occur, i.e.,
 obtains no information about \(K_0^*=\mathsf {H}_q(c_1^*)\). This is because queries to \(\mathsf {H}\) only reveal \(\mathsf {H}_q(c)\) for
obtains no information about \(K_0^*=\mathsf {H}_q(c_1^*)\). This is because queries to \(\mathsf {H}\) only reveal \(\mathsf {H}_q(c)\) for
 , and \(\overline{\mathsf {Dec}}'(c)\) returns \(\bot \) if \(c=c_1^*\). Therefore, we have
, and \(\overline{\mathsf {Dec}}'(c)\) returns \(\bot \) if \(c=c_1^*\). Therefore, we have
Combining the above, we have

as we wanted. \(\square \)
Proof
(Proof of Theorem 5.1). Combining all lemmas in this section, we obtain the following inequality:

\(\square \)
Notes
- 1.
We also note that Anand, Targhi, Tabia, and Unruh [ATTU16] showed several modes are secure against quantum superposition attacks if the underlying block cipher is quantumly-secure PRF.
- 2.
This means that if there is quantum chosen-plaintext or quantum chosen-ciphertext attack that breaks a cryptographic scheme easily, we should not publish an obfuscated code by the white-box cryptography or obfuscation.
- 3.
Boneh et al. [BDF+11] defined history-free reductions for signature schemes. They also discussed the difficulties to model history-free reductions in the case of (public-key) encryption schemes. We also do not define history-free property of reductions for KEMs.
- 4.
Any efficient adversary cannot distinguish \(E(k,m_0)\) from \(E(k,m_1)\) even if it chooses \(m_0\) and \(m_1\) with
 .
. - 5.
We allow a reduction algorithm to access the random oracles. See Subsect. 2.2 for details.
References
Ambainis, A., Rosmanis, A., Unruh, D.: Quantum attacks on classical proof systems: the hardness of quantum rewinding. In: 55th FOCS, pp. 474–483. IEEE Computer Society Press, October 2014
Anand, M.V., Targhi, E.E., Tabia, G.N., Unruh, D.: Post-quantum security of the CBC, CFB, OFB, CTR, and XTS modes of operation. In: Takagi, T. (ed.) PQCrypto 2016. LNCS, vol. 9606, pp. 44–63. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-29360-8_4
Boneh, D., Canetti, R., Halevi, S., Katz, J.: Chosen-ciphertext security from identity-based encryption. SIAM J. Comput. 36(5), 1301–1328 (2007)
Boneh, D., Dagdelen, Ö., Fischlin, M., Lehmann, A., Schaffner, C., Zhandry, M.: Random oracles in a quantum world. In: Lee, D.H., Wang, X. (eds.) ASIACRYPT 2011. LNCS, vol. 7073, pp. 41–69. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-25385-0_3
Boneh, D., Zhandry, M.: Quantum-secure message authentication codes. In: Johansson, T., Nguyen, P.Q. (eds.) EUROCRYPT 2013. LNCS, vol. 7881, pp. 592–608. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-38348-9_35
Boneh, D., Zhandry, M.: Secure signatures and chosen ciphertext security in a quantum computing world. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8043, pp. 361–379. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40084-1_21
Chen, L., et al.: Report on post-quantum cryptography. Technical report, National Institute of Standards and Technology (NIST) (2016)
Damgård, I., Funder, J., Nielsen, J.B., Salvail, L.: Superposition attacks on cryptographic protocols. In: Padró, C. (ed.) ICITS 2013. LNCS, vol. 8317, pp. 142–161. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-04268-8_9
Fujisaki, E., Okamoto, T.: Secure integration of asymmetric and symmetric encryption schemes. J. Cryptol. 26(1), 80–101 (2013)
Gagliardoni, T., Hülsing, A., Schaffner, C.: Semantic security and indistinguishability in the quantum world. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9816, pp. 60–89. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53015-3_3
Grover, L.K.: A fast quantum mechanical algorithm for database search. In: 28th ACM STOC, pp. 212–219. ACM Press, May 1996
Hofheinz, D., Hövelmanns, K., Kiltz, E.: A modular analysis of the Fujisaki-Okamoto transformation. In: Kalai, Y., Reyzin, L. (eds.) TCC 2017. LNCS, vol. 10677, pp. 341–371. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70500-2_12
Hülsing, A., Rijneveld, J., Song, F.: Mitigating multi-target attacks in hash-based signatures. In: Cheng, C.-M., Chung, K.-M., Persiano, G., Yang, B.-Y. (eds.) PKC 2016. LNCS, vol. 9614, pp. 387–416. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49384-7_15
Jiang, H., Zhang, Z., Chen, L., Wang, H., Ma, Z.: IND-CCA-secure key encapsulation mechanism in the quantum random oracle model, revisited. In: Shacham, H., Boldyreva, A. (eds.) CRYPTO 2018. LNCS, vol. 10993, pp. 96–125. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96878-0_4
Jiang, H., Zhang, Z., Ma, Z.: Key encapsulation mechanism with explicit rejection in the quantum random oracle model. In: Lin, D., Sako, K. (eds.) PKC 2019. LNCS, vol. 11443, pp. 618–645. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17259-6_21
Kaplan, M., Leurent, G., Leverrier, A., Naya-Plasencia, M.: Breaking symmetric cryptosystems using quantum period finding. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9815, pp. 207–237. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53008-5_8
Kiltz, E., Lyubashevsky, V., Schaffner, C.: A concrete treatment of fiat-shamir signatures in the quantum random-oracle model. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018. LNCS, vol. 10822, pp. 552–586. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78372-7_18
Kuwakado, H., Morii, M.: Security on the quantum-type even-mansour cipher. In: Proceedings of the International Symposium on Information Theory and its Applications, ISITA 2012, Honolulu, HI, USA, 28–31 October 2012, pp. 312–316. IEEE (2012)
Nielsen, M.A., Chuang, I.L.: Quantum Computation and Quantum Information. Cambridge University Press, Cambridge (2000)
Shor, P.W.: Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM J. Comput. 26(5), 1484–1509 (1997)
Simon, D.R.: On the power of quantum computation. SIAM J. Comput. 26(5), 1474–1483 (1997)
Saito, T., Xagawa, K., Yamakawa, T.: Tightly-secure key-encapsulation mechanism in the quantum random oracle model. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018. LNCS, vol. 10822, pp. 520–551. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78372-7_17
Zhandry, M.: Secure identity-based encryption in the quantum random oracle model. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 758–775. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32009-5_44
Zhandry, M.: How to record quantum queries, and applications to quantum indifferentiability. Cryptology ePrint Archive, Report 2018/276 (2018). https://eprint.iacr.org/2018/276
Acknowledgments
We would like to thank Haodong Jiang and anonymous reviewers of PQCrypto 2019 for insightful comments.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
A Simple Lemma
A Simple Lemma
Lemma A.1
For any reals a, b, and c with \(c \ge 0\), we have

Proof
We consider the three cases below:
-
Case \(a-b \ge c \ge 0\): In this case, we have \(a-b-c \ge 0\). Thus, we have
 .
. -
Case \(a-b \le 0 \le c\): In this case, we have \(a-b-c \le 0\). We have
 .
. -
Case \(0 \le a-b \le c\): Again, we have \(a-b-c \le 0\). We have
 .
.
In all three cases, we have  as we wanted. \(\square \)
as we wanted. \(\square \)
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Xagawa, K., Yamakawa, T. (2019). (Tightly) QCCA-Secure Key-Encapsulation Mechanism in the Quantum Random Oracle Model. In: Ding, J., Steinwandt, R. (eds) Post-Quantum Cryptography. PQCrypto 2019. Lecture Notes in Computer Science(), vol 11505. Springer, Cham. https://doi.org/10.1007/978-3-030-25510-7_14
Download citation
DOI: https://doi.org/10.1007/978-3-030-25510-7_14
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-25509-1
Online ISBN: 978-3-030-25510-7
eBook Packages: Computer ScienceComputer Science (R0)





 and outputs ciphertext
and outputs ciphertext
 .
. or a rejection symbol
or a rejection symbol
 .
.
 denotes a randomness space for
denotes a randomness space for  ,
, 

 and key
and key
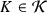 .
. .
.

 It picks
It picks  , and invokes
, and invokes
 where
where
 oracles are simulated as follows.
oracles are simulated as follows. has access to an oracle
has access to an oracle  ,
,
 returns
returns  .
. returns
returns 
 , where
, where  .
. , but the decapsulation oracle in
, but the decapsulation oracle in  .
. and
and  uniformly at random.
uniformly at random. , it returns
, it returns  .
. , it returns
, it returns  .
. , it computes
, it computes 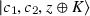 .
. It picks
It picks  , and invokes
, and invokes
 where
where
 oracles are simulated as follows.
oracles are simulated as follows. ,
,
 returns
returns 
 returns
returns  .
. .
. .
. .
.