Abstract
Limited automata are single-tape Turing machines with severe rewriting restrictions. They have been introduced in 1967 by Thomas Hibbard, who proved that they have the same computational power as pushdown automata. Hence, they provide an alternative characterization of the class of context-free languages in terms of recognizing devices. After that paper, these models have been almost forgotten for many years. Only recently limited automata were reconsidered in a series of papers, where several properties of them and of their variants have been investigated. In this work we present an overview of the most important results obtained in these researches. We also discuss some related models and possible lines for future investigations.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
1 A Short Introduction with a Classical Example
This paper is devoted to limited automata. These devices have been introduced, with the aim of generalizing the notion of determinism in context-free languages, by Thomas N. Hibbard in 1967, who originally called them scan limited automata. We present an overview of the most important results on limited automata: we discuss their computational power, their descriptional complexity, the relationships between deterministic and nondeterministic versions. Finally, we shortly discuss some variants of these devices and some related models. In the paper we will also address some problems related to these devices which, in our opinion, deserve investigation.
In order illustrate the model, we start by presenting a classical example which will turn out to be useful in the paper.
Suppose we need to verify that a sequence of brackets is correctly balanced. A quite natural way to proceed is to start from the first opening bracket and search for the corresponding closing bracket. To locate it, a counter which is incremented for each opening bracket and decremented for each closing bracket can be helpful. When during this process the counter reaches the initial value, the closing bracket is reached. These operations can be iterated for each opening bracket in order to verify the matching of all the pairs of brackets and the correct nesting in the sequence.
We could use a different and perhaps more simple strategy. Instead of locating the first opening bracket, we start by locating the first closing one: the corresponding opening bracket is necessarily the last bracket before it, that must be of the same type. If these two brackets are removed or rewritten by a different symbol, the same procedure can be repeated on the sequence so modified: locate the first closing bracket, check if the last bracket before it is of the same type, and overwrite these two brackets. When no more closing brackets are left in the sequence, even none opening bracket can be left. In this case the original sequence was balanced. Otherwise, in the following cases the sequence is not balanced:
-
At the end, the sequence left on the tape contains some opening bracket.
-
After locating a closing bracket, no opening bracket before it is found.
-
After locating a closing bracket, the last opening bracket found before it is of a different type.
Suppose now that the sequence of brackets is written on a Turing machine tape, one bracket per cell, and suppose that the computation of the machine starts, as usual, with the head scanning the cell containing the first input symbol. In this way, each input cell is reached for the first time while moving the head from left to right. We can observe that, applying the above described strategy, the following facts hold:
-
A cell containing a closing bracket is overwritten only when the head visits it for the first time. After that operation the head is moved back to the left to search an opening bracket.
-
A cell containing an opening bracket is overwritten only when the head visits it for the second time. In this case the cell is entered by the head from the right.
-
After one of these two active visits, a cell can be visited further many times, but it cannot be overwritten, so it is “frozen”.
As we will discuss in the paper, each context-free language can be recognized by a strategy similar to the one we just described. In particular, each context-free language can be recognized by a single-tape machine which is able to overwrite the contents of each tape cell only in the first two visits. This is the basic idea under the computational model of limited automata that we discuss in this work. The device we have outlined for this specific case is called 2-limited automaton, since each cell can be overwritten only in the first two visits and, after that, it is never modified.
2 Limited Automata
Given an integer \(d\ge 0\), a d-limited automaton is a Turing machine with a single tape, which initially contains the input, one symbol for each tape cell. At the left and at the right of the input there are cells containing the two special symbols \({\mathord {\vartriangleright }}\) and \({\mathord {\vartriangleleft }}\) called, respectively, the left and the right end-markers. The machine head cannot leave the tape segment delimited by the two end-markers, i.e., it cannot move to the left of the cell containing \({\mathord {\vartriangleright }}\) and to the right of cell containing \({\mathord {\vartriangleleft }}\).
In d-limited automata, each tape cell can be overwritten only in the first d visits. After that the cell is “frozen”, so it cannot be further modified. The cells containing the two end-markers cannot be never overwritten.
Acceptance is defined in a standard way, as for Turing machines. More technical details can be found in [28, 29].Footnote 1
We will now discuss the computational power of these models, in the nondeterministic and deterministic cases. Then, we will present descriptional complexity aspects and several open problems. We will conclude the section by shortly discussing time complexity.
2.1 Computational Power, Determinism and Nondeterminism
In Sect. 1 we described how a 2-limited automaton can accept the language of balanced sequences of brackets. We remind the reader that such a language is called Dyck language. More precisely, given an alphabet \(\varOmega _k\) containing k types of brackets (hence 2k symbols) we denote by \(D_k\) the Dyck language over it.
Dyck languages are important in the investigation of context-free languages, because they capture the recursive structure of any context-free language. This fact is formalized in the following famous result:
Theorem 1
(Chomsky-Schützenberger Theorem [2]). Each context-free language L over an alphabet \(\varSigma \) can be represented as a homomorphic image \(L=h(D_k\cap R)\), for some integer \(k>0\), where \(R\subseteq \varOmega _k^*\) is a regular language and \(h:\varOmega _k\rightarrow \varSigma ^*\) is a homomorphism.
Theorem 1 suggests a way to build, for any context-free language L, a recognizer which is the combination of the following devices, as depicted in Fig. 1:
-
A one-way nondeterministic machine T that on each input \(w\in \varSigma ^*\) produces a string \(z\in h^{-1}(w)\).
-
A machine \(A_D\) recognizing the Dyck language \(D_k\).
-
A one-way finite automaton \(A_R\) accepting the regular language R.
As machine \(A_D\) we can use the 2-limited automaton for the recognition of \(D_k\) outlined in Sect. 1. Using the fact that the homomorphism h can be supposed to be non-erasing [20], it is possible to combine these machines in such a way that also the resulting machine accepting the given context-free language L is a 2-limited automaton. (Details can be found in [26, 28]). This allows to conclude that each context-free language is accepted by a 2-limited automaton.
The converse also holds. Furthermore, by allowing a larger, but still constant number of initial visits in which rewritings are possibles, the computational power does not increase. By summarizing:
Theorem 2
([9]). For each \(d\ge 2\), the class of languages accepted by d-limited automata coincides with the class of context-free languages.
The just outlined conversion from context-free languages to 2-limited automata is intrinsically nondeterministic. Actually, the conversion presented by Hibbard is different and preserves the determinism. Hence, each deterministic context-free language is accepted by a deterministic 2-limited automaton. However, determinism is not preserved by the converse transformation in the form presented in [9]. Indeed, the problem of the equivalence between the class of deterministic context-free language and the class of languages accepted by deterministic 2-limited automata was left open in that paper. This problem was recently solved in [29], by giving a transformation from 2-limited automata to pushdown automata which preserves the determinism. The transformation is based on an extension of transition tables, originally introduced by Shepherdson [32] to obtain a simulation of two-way finite automata by equivalent one-way ones.
Theorem 3
([29]). The class of languages accepted by deterministic 2-limited automata coincides with the class of deterministic context-free languages.
It is an easy observation that Theorem 3 cannot be extended to \(d>2\). For instance, the following language, which is not deterministic, can be accepted by a deterministic 3-limited automaton A:
To recognize L, A can scan the tape from left to right, to locate the right end-marker and, moving back, it can read the last input symbol. If the symbol is a c, then A has to verify whether or not the number of the a’s in the input coincides with the number of the b’s. To this aim, A continues to move to the left, to find a cell containing an a, which is rewritten by the symbol  . Then it moves to the right to search a cell containing a b, which is also rewritten by the symbol
. Then it moves to the right to search a cell containing a b, which is also rewritten by the symbol  . This process is repeated up to reach the left end-marker while searching an a. When the last symbol of the input is a d, the only difference in the procedure is that for each a the automaton A has to overwrite two occurrences of the letter b.
. This process is repeated up to reach the left end-marker while searching an a. When the last symbol of the input is a d, the only difference in the procedure is that for each a the automaton A has to overwrite two occurrences of the letter b.
We point out that the main motivation of the original work of Hibbard was to extend the notion of determinism for context-free languages (indeed, the title of [9] is “A Generalization of Context-Free Determinism”). With respect to the number d of initial visits in which rewriting are allowed, by extending the last example he proved the existence of an infinite hierarchy of deterministic languages:
Theorem 4
([9]). For each \(d>2\) there exists a language which is recognized by a deterministic d-limited automaton, but which cannot be accepted by any deterministic \((d-1)\)-limited automaton.
In [9] it is claimed (without proof) that the set of palindromes cannot be accepted by deterministic d-limited automata, for any integer d. As a consequence, the above hierarchy of deterministic languages does not cover all the class of context-free languages. It would be interesting to have a formal proof of this fact.
Results comparing the degrees of nondeterminism that can be defined according to the above hierarchy and measures of nondeterminism for pushdown automata are presented in [18].
By allowing to overwrite tape cells only in the first visit, the computational power of limited automata reduces to the class of regular languages.
Theorem 5
([34, Thm. 12.1]). The class of languages accepted by 1-limited automata coincides with the class of regular languages.
Concerning the computational power of limited automata, we finally mention the case where the number of initial visits to each cell in which rewritings are possible is not constant, but it is bounded by a function f(n) of the input length n. This case was studied by Wechsung and Brandstädt which gave a characterization in terms of languages accepted by space bounded one-way auxiliary pushdown automata, namely pushdown automata with a one-way input tape, extended with a two-way work tape. The space is measured by taking into account only the work tape.
Theorem 6
([36]). For any recursive function f(n), the class of languages accepted by f(n)-limited automata coincides with the class of languages accepted by auxiliary pushdown automata in space O(f(n)).
2.2 Descriptional Complexity
To study the descriptional complexity of a formal system, we have to consider the size of its description, namely the number of symbols which are used to write down its description. In the case of limited automata over a given input alphabet \(\varSigma \), the size is a polynomial in the cardinalities of the state set and of the working alphabet. For pushdown automata we also have to take into account how many symbols can be written on the pushdown store in one single move. However, if each move is allowed to increase the height of the pushdown by adding at most one symbol, then the size is polynomial in the number of states and in the cardinality of the pushdown alphabet. In a similar way, to define the size of context-free grammars, we have to take into account the maximal length of the right-hand sides of productions. For grammars in Chomsky normal form or, more in general, grammars in which the production right-hand sides have length at most 2, the size is polynomial in the number of variables. Finally, for finite automata, the size is polynomial with respect to the number of states.
We introduce a family of languages which will be useful to discuss descriptional complexity results.
For each integer \(n>0\), let \(K_n\) be the set of all strings over the alphabet \(\{a,b\}\) consisting of the concatenation of blocks of length n, where the last block is equal to one of the previous blocks. Formally:
A deterministic 2-limited automaton for \(K_n\)
To accept \(K_n\), a deterministic 2-limited automaton \(M_n\) can first make a scan from left to right of the input to locate the right end-marker (this “consumes” the first visit to each tape cell). Then \(M_n\) inspects each block \(x_j\) of length n starting from \(j=k\) up to \(j=1\), and compares it, symbol by symbol, with the last block x. This can be done by moving the head back and forth between the block under consideration and the last block, using a counter modulo n to identify the corresponding positions that need to be compared in the two blocks, while marking the symbols of \(x_j\). In this phase or in the first scan, \(M_n\) also checks if the length of the input is a multiple of n. The implementation of \(M_n\) can be done by using O(n) states and a working alphabet of O(1) symbols.
A nondeterministic 1-limited automaton for \(K_n\)
In a first complete scan of the tape, the automaton nondeterministically marks two cells. No more rewriting operations are possible after this phase. The first marked cell is guessed to be the leftmost position of the required block \(x_j\), while the other one is guessed to be the leftmost position of the last block x. In a second phase, using a counter modulo n, the machine can verify that the input length is a multiple of n, the last marked position corresponds to the leftmost symbol of the last block of length n, and the other marked position is the leftmost symbol of another block of length n. Finally, the automaton makes n scans of the part of the tape which contains the two selected blocks: in the ith scan it checks if the ith symbols in the marked blocks are equal. The implementation produces a nondeterministic 1-limited automaton with O(n) states.
Lower bounds for \(K_n\)
The following lower bounds for the recognition of \(K_n\) by pushdown and finite automata can be proved:
-
To accept and to generate \(K_n\), pushdown automata and context-free grammars require exponential size in n.
The proof can be done by using the interchange lemma for context-free languages [19]. The argument is similar to that used in [29] for a slightly different language.
-
Any one-way deterministic automaton accepting \(K_n\) requires a number of states double exponential in n.
The proof uses distinguishability arguments. Let \(x_1,x_2,\ldots ,x_{2^n}\) be a list of all strings in \(\{a,b\}^n\), in some fixed order, and F be the set of all functions from \(\{1,2,\ldots ,2^n\}\) to \(\{0,1\}\). For each \(f\in F\), consider the string \(w_f=x_1^{f(1)}x_2^{f(2)}\cdots x_{2^n}^{f(2^n)}\). Given \(f,g\in F\), with \(f\ne g\), it can be verified that any string \(x_i\) with \(f(i)\ne g(i)\) distinguishes \(w_f\) and \(w_g\). Since \(\#F=2^{2^n}\), the lower bound follows.
The size cost of the simulation of 2-limited automata by pushdown automata has been investigated in [29] by proving an exponential upper bound. The result has been recently improved, by showing that the upper bound remains exponential if we simulate a d-limited automaton, with \(d>2\), by a pushdown automaton [14]. Considering the lower bound given for the size of pushdown automata accepting \(K_n\), we obtain:
Theorem 7
([14, 29]). For each \(d>1\), the size cost of the transformation of d-limited automata into equivalent pushdown automata is exponential.
Concerning the transformation of deterministic 2-limited automata into equivalent deterministic pushdown automata, it has been proved a double exponential upper bound, which reduces to a simple exponential if the input is given to the pushdown automaton with an extra special symbol marking the right end. The optimality of the exponential bounds can be proved using \(K_n\). We conjecture that the double exponential upper bound cannot be reduced.
For the converse transformations, we have the following result:
Theorem 8
([29]). The size cost of the transformation of pushdown automata into 2-limited automata is polynomial. Furthermore, the polynomial transformation preserves determinism.
By Theorem 5, 1-limited automata have the same power of finite state automata. The proof of this result was obtained by Wagner and Wechung by adapting the Shepherdson’s technique for the transformation of two-way finite automata into equivalent one-way ones [32]: given a 1-limited automaton, a nondeterministic one-way automaton is created which keeps in its state a transition table corresponding to the portion of the tape at the left of the head. The table is used to replace parts of computations that from the current head position finally reach for the first time the position to the right of it, by making a sequence of moves which visit some of the already scanned tape cells.
By analyzing the cost of such a simulation and by considering the family of languages \(K_n\), the following costs can be obtained:
Theorem 9
([28]). The size costs of the transformation of 1-limited automata into equivalent one-way nondeterministic and deterministic finite automata are exponential and double exponential, respectively.
We point out that the double exponential cost in Theorem 9 is related to a double role of the nondeterminism in 1-limited automata. When the head of a 1-limited automaton reaches for the first time a tape cell, it overwrites the contents according to a nondeterministic choice.Footnote 2 Furthermore, the set of nondeterministic choices that are allowed during the next visits to the same cell depends on the symbol that has been chosen to rewrite it in the first visit and that cannot be further changed, namely it depends on the nondeterministic choice which was made during the first visit.
When the given 1-limited automaton is deterministic, the same simulation produces a one-way deterministic finite automaton of exponential size. The optimality can be easily proved by considering the reversal of the language \(K_n\).
We briefly discuss the unary case, namely, the case of languages defined over a one-letter alphabet. It is well known that, under this restriction, the classes of context-free and of regular languages coincide [4]. Hence, for each \(d\ge 0\), unary d-limited automata recognize only regular languages. Since the family \(K_n\) of witness languages used in Theorem 9 is defined over a binary alphabet, it is quite natural to ask if there is any difference in the unary case.
A first result comparing the sizes of unary 1-limited automata and those of equivalent two-way nondeterministic finite automata was presented in [28]. Kutrib and Wendlandt proved state lower bounds for the simulation of unary d-limited automata by different variants of finite automata [14, 15]. More recently, the following result has been proved:
Theorem 10
([30]). For each integer \(n>0\), the singleton language \(\{a^{2^n}\}\) is accepted by a deterministic 1-limited automaton of size O(n), while each one-way nondeterministic finite automaton accepting it needs \(2^n+1\) states.
The upper bound in Theorem 10 was obtained by making use of the construction and of the properties of the binary carry sequence, an infinite sequence of integers related base 2 representation [33].
With a small modification, it can be shown that for each \(n>0\) even the language \(\{a^{2^n}\}^*\) can be accepted by a deterministic 1-limited automaton of size O(n), while each two-way nondeterministic finite automaton accepting it requires \(2^n\) states [30].
The results comparing the sizes of finite automata and 1-limited automata are summarized in Fig. 2. The upper bounds in the diagram follow from the simulations of 1-limited automata by finite automata (see Theorem 9 and the discussion after it). All the lower bounds, with the exception of those from 1-limited automata to one-way deterministic finite automata (arrow (a) in Fig. 2) and to deterministic 1-limited automata (b), are witnessed by the unary language \(\{a^{2^n}\}^*\). For the double exponential lower bound from 1-limited automata to one-way deterministic automata (a), the binary witness \(K_n\) can be used. It is an open problem if the same gap can be achieved in the unary case. From our experience on unary languages we conjecture a negative answer. The exponential lower bound from 1-limited automata to deterministic 1-limited automata (b) is a consequence of the double exponential lower bound to one-way deterministic automata (a) and of the cost of the simulation of deterministic 1-limited automata by one-way deterministic automata (d).
At the moment we do not know direct simulations of 1-limited automata by deterministic 1-limited automata (b) and by two-way deterministic automata (c). For instance, it should be interesting to know if simulating 1-limited automata by two-way (instead of one-way) deterministic automata the cost reduces from a double exponential to a simple exponential.
By summarizing, we can propose the following problems:
Problem 1
Study the size cost of the simulation of unary 1-limited automata by one-way deterministic finite automata (unary version of (a)).
Problem 2
Study the size cost of the simulation of 1-limited automata by deterministic 1-limited automata, in the general and in the unary case (b).
Problem 3
Study the size cost of the simulation of 1-limited automata by two-way deterministic finite automata, in the general and in the unary case (c).
We point out that the last two problems are variants of the question of the cost of the elimination of nondeterminism from two-way automata, proposed by Sakoda and Sipser in 1978 [31], which is still open (for a recent survey, see [25]). In particular, concerning Problem 2, we observe that for the elimination of the nondeterminism from 1-limited automata an exponential lower bound is known, while for the corresponding problem in two-way finite automata the best known lower bound is polynomial [3].
It could be also interesting to study a “relaxed” version of the problem of Sakoda and Sipser, in which the simulating machine could overwrite the contents of tape cells during the first visit:
Problem 4
Study the size costs of the simulations of one-way and two-way nondeterministic finite automata by deterministic 1-limited automata.
A relaxed version of the Sakoda and Sipser problem has been recently considered in [5], by proving a polynomial blowup from two-way nondeterministic automata to single-tape deterministic machines working in linear time. Since each 1-limited automaton can be converted into an equivalent one working in linear time also preserving determinism (see Theorem 11 below), proving that the simulation proposed in Problem 4 costs polynomial would improve that result.
Problem 4 can be further relaxed by considering simulations by deterministic d-limited automata, for \(d>1\).
2.3 Time Complexity
While one-way and two-way finite automata can always accept in linear time, with respect to the input length, there are 1-limited automata that use quadratic time [6].
The Shepherdson’s technique, used by Wagner and Wechsung to prove Theorem 5, has been recently refined to prove that, with only a polynomial increase in the size, 1-limited automata can be forced to work in linear time. Roughly, the main idea is that the running time of 1-limited automata can be reduced by avoiding computation paths which move back to the left and visit too many tape cells before reaching again the current position. This is done with a tricky simulation which stores transition tables on a tape track.
Theorem 11
([6]). With a polynomial size increase, each 1-limited automaton can be transformed into an equivalent 1-limited automaton which works in linear time. Furthermore, determinism can be preserved in such a conversion.
We point out that the machine obtained in Theorem 11 is also a Hennie machines, namely, a single-tape Turing machine working in linear time. It is known that these devices can recognize only regular languages.Footnote 3
In our knowledge, at the moment there are no other results concerning the time complexity of limited automata.
3 Strongly Limited Automata
In Sect. 2, using the Chomsky-Schützenberger representation theorem (Theorem 1), we discussed how to construct for any context-free language a 2-limited automaton accepting it. We remind the reader that such a 2-limited automaton is obtained by combining three machines T, \(A_R\) and \(A_D\), as summarized in Fig. 1. While T and \(A_R\) are finite state machines, \(A_D\) is the only “context-free component” in the construction. In fact, its purpose is that of recognizing a Dyck language \(D_k\). \(A_D\) can be implemented as the 2-limited automaton described in Sect. 1. However, we can notice that in order to recognize \(D_k\), \(A_D\) does not use all the capabilities of 2-limited automata. For instance, it moves from left to right only to search closing brackets: in this phase, \(A_D\) does not need neither to change the state nor to make any rewriting, except when it finally reaches the cell containing a closing bracket, where it starts to move to the left to search a symbol not yet overwritten, which is expected to be the corresponding opening bracket. While moving to the left, \(A_D\) ignores the contents of cells that have been already overwritten.
Since, as we wrote, \(A_D\) is the only “context-free component” in the construction and it can be implemented without using all the capabilities of 2-limited automata, we can ask if it is possible to restrict the moves of 2-limited automata, without reducing the computational power.
In [27] we gave a positive answer to this question, by introducing strongly limited automata, a restriction of 2-limited automata which closely imitates the moves that are used by limited automata to accept Dyck languages. In particular, strongly limited automata satisfy the following restrictions:
-
While moving to the right, a strongly limited automaton always uses the initial state \(q_0\) until a cell (which has not been yet overwritten) is modified. Then, it enters a different state and starts to move to the left.
-
While moving to the left, the automaton ignores the cells that have been already overwritten and, without changing its internal state, overwrites the other ones it meets, up to some position where it enters \(q_0\) and starts again to move to the right.
-
In the final phase of the computation, which starts when the right end-marker is reached, the automaton inspects all tape cells, to check whether or not the string which is finally on the tape belongs to a given 2-strictly locally testable language. Roughly, this means that all the factors of two letters of this string (including the end-markers) belong to a given set.
We shortly discuss some examples (for more examples see [26, 27]).
Example 1
The language \(L=\{a^nb^n\mid n\ge 0\}\) can be accepted by a strongly limited automaton which in the initial state \(q_0\) moves the head to the right to search the first cell containing a b. When it finds such a cell, it rewrites the contents by the symbol  and moves the head to the left, until it finds the first not overwritten symbol, which is expected to be an a. If so, the symbol is overwritten, the automaton re-enters the state \(q_0\) to search another b. When no more b’s are left on the tape, the head reaches the right end-marker. At this point the automaton verifies if the string on the tape is of the form
and moves the head to the left, until it finds the first not overwritten symbol, which is expected to be an a. If so, the symbol is overwritten, the automaton re-enters the state \(q_0\) to search another b. When no more b’s are left on the tape, the head reaches the right end-marker. At this point the automaton verifies if the string on the tape is of the form  .
.
Example 2
A more interesting example is the recognition of the deterministic context-free language \(\{a^nb^{2n}\mid n\ge 0\}\), which can be done by a strongly limited automaton that guesses the position of each second b, using the following strategy:
-
Moving the head from left to right, when the automaton reads an a it continues to move to the right, while when it reads a b it makes a nondeterministic choice between further moving to the right (so leaving the b in the cell) or rewriting the cell by
 and turning the head to the left.
and turning the head to the left. -
Moving the head from right to left, when the automaton reads a b it rewrites it by
 and continues to move to the left (notice that such a b was left unchanged in the previous visit, when moving from left to right), while when it reads an a, it replaces the contents by
and continues to move to the left (notice that such a b was left unchanged in the previous visit, when moving from left to right), while when it reads an a, it replaces the contents by 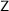 , turning the head to the right.
, turning the head to the right. -
In the final scan, which starts when the right end-marker is reached, the machine accepts if and only if the string on the tape belongs to
 .
.
We can modify the above algorithm in order to recognize the language \(\{a^nb^n\mid n\ge 0\}\cup \{a^nb^{2n}\mid n\ge 0\}\). While moving from left to right, when the head reaches a cell containing b three actions are possible: either the automaton continues to move to the right, without any rewriting, or it rewrites the cell by  , turning to the left, or it rewrites the cell by
, turning to the left, or it rewrites the cell by  , also turning the head to the left. While moving from right to left, the automaton behaves as the one above described for \(\{a^nb^{2n}\mid n\ge 0\}\). The input is accepted if and only if the string which is finally on the tape belongs to
, also turning the head to the left. While moving from right to left, the automaton behaves as the one above described for \(\{a^nb^{2n}\mid n\ge 0\}\). The input is accepted if and only if the string which is finally on the tape belongs to  . \(\square \)
. \(\square \)
In spite of the restrictions on moves, strongly limited automata have the same computational power as limited automata, namely they characterize context-free languages. Furthermore they are polynomially related in size to pushdown automata:
Theorem 12
([27]).
-
(i)
Each context-free language L is accepted by a strongly limited automaton whose description has a size which is polynomial with respect to the size of a given context-free grammar generating L or of a given pushdown automaton accepting L.
-
(ii)
Each strongly limited automaton \(\mathcal M\) can be simulated by a pushdown automaton of size polynomial with respect the size of \(\mathcal M\).
The proof of (i) was obtained using a variant of the representation theorem of Chomsky-Schützenberger, proved by Okhotin [20], where Dyck languages extended with neutral symbols and letter-to-letter homomorphisms are used. (ii) was proven by providing a direct simulation.
In Example 2 we described a strongly limited automaton accepting the deterministic context-free language \(\{a^nb^{2n}\mid n\ge 0\}\). The automaton makes use of nondeterministic choices. It is not difficult to prove that this cannot be avoided (see [27]). Hence:
Theorem 13
([27]). The class of languages accepted by deterministic strongly limited automata is properly included in the class of deterministic context-free languages.
Strongly limited automata are allowed to change state only when they reverse the head direction. If we remove this restriction, the language \(\{a^nb^{2n}\mid n\ge 0\}\) (and other deterministic context-free languages which are not accepted by deterministic strongly limited automata) can be easily recognized in a deterministic way. In order to have a model polynomially related in size to pushdown automata and whose deterministic version is equivalent to deterministic pushdown automata, in [27] almost strongly limited automata have been proposed. They are obtained from strongly limited automata by relaxing some of the restrictions on state changes. In almost strongly limited automata there is a set of states \(Q_R\), including the initial state \(q_0\), which can be used while moving to the right, and a set of states \(Q_L\) which can be used while moving to the left. State changes are possible while moving to the left or to the right (which is not possible in strongly limited automata), except on the cells that have been already overwritten. Furthermore, almost strongly limited automata have to satisfy all the other restrictions given for strongly limited automata.
By adapting the arguments used to prove Theorem 12, it can be shown that almost strongly limited automata characterize context-free languages and are polynomially related in size to pushdown automata. Since almost strongly limited automata are restrictions of 2-limited automata, from Theorem 3 it follows that each deterministic almost strongly limited automaton recognizes a deterministic context-free language. At the moment, we do not know if the converse holds.
Problem 5
Does the class of languages accepted by deterministic almost strongly limited automata coincide with the class of deterministic context-free languages?
4 Some Related Models
In this section we shortly discuss some restricted variants of Turing machines, presented in the literature, which recognize context-free languages.
4.1 Wechsung’s Model
We have seen that limited automata are single-tape Turing machines defined by limiting the active visits to each tape cell from the beginning of the computation: in a d-limited automaton only the first d visits to each cell can modify the contents.
We can consider a similar restriction, where for a fixed integer d, only the last d visits to each cell can be active.
Such a model was implicitly introduced by Wechsung, by considering a complexity measure for one-tape Turing machines called return complexity [35, 36]. Indeed, this measure counts the maximum number of visits to a tape cell, starting from the first visit which modifies the cell contents. Machines with return complexity 1 characterize regular languages (each cell, after the first rewriting, will be never visited again, hence rewritings are useless). Furthermore, it has been shown that for each \(d\ge 2\), return complexity d characterizes context-free languages.Footnote 4 Even with respect to return complexity, there exists a hierarchy of deterministic languages (cf. Theorem 4 in the case of limited automata). However, this hierarchy is not comparable with the class of deterministic context-free languages. For instance, it can be easily seen that the set of palindromes, which is not a deterministic context-free language, can be recognized by a deterministic machine with return complexity 2. However, there are deterministic context-free languages that cannot be recognized by any deterministic machine with return complexity d, for any integer d [22, 23].
It seems interesting to investigate the possibility of finding a class of machines containing both limited automata and Wechsung’s machines and still characterizing context-free languages. One natural attempt can be that of considering machines such that for each tape cell the number of visits counted starting from the first active visit up to the last one is bounded by a given constant.
4.2 Forgetting, Deleting and Restarting Automata
With motivations deriving mainly from linguistics, in a series of papers Jancar, Mráz, and Plátek introduced and studied forgetting automata [10,11,12]. These devices are single-tape machines that can erase tape cells by rewriting their contents with a unique special symbol, that cannot be further overwritten. However, overwritten cells are kept on the tape and are still considered during the computation. For instance, the state can be changed while visiting an erased cell. Different variants, depending on the allowed operations, have been investigated.
In a variant of forgetting automata that characterizes context-free languages, when a cell which contains an input symbol is visited while moving to the left, it is rewritten by the unique special symbol, while it can remain unchanged while moving to the right. This way of operating has some similarities with that of strongly limited automata, which, however, can use nonunary rewriting alphabets.Footnote 5 Furthermore, in strongly limited automata overwritten cells are completely ignored (namely, the head direction and the state cannot be changed while visiting them) except in the final scan of the tape from the right to the left end-marker.
If erased cells are completely ignored in forgetting automata, the resulting computational model, called deleting automata, is less powerful. In fact it is not able to recognize all context-free languages [12].
A modification of forgetting automata, called restarting automata, was introduced in [13] and widely considered in the literature. Variants of restarting automata characterizing context-free languages have been obtained. For more details see [21].
4.3 No Space Overhead Machines
With the aim of investigating computations with very restricted resources, Hemaspaandra, Mukherji, and Tantau studied single-tape Turing machine with absolutely no space overhead [7]. The model is very close to “realistic computations”, where the space is measured without any hidden constants. To this aim, these machines use the binary alphabet \(\varSigma =\{0,1\}\) (plus two end-marker symbols) and only the portion of the tape which at the beginning of the computation contains the input. Furthermore, no other symbols are available, namely only symbols from \(\varSigma \) can be used to rewrite the tape. Despite these strong restrictions, these machines are able to recognize in polynomial time all context-free languages over \(\varSigma \).
5 Further Remarks
In this work we presented limited automata, discussed some of their main properties, in particular concerning computational power, descriptional complexity, determinism versus nondeterminism. We shortly discussed some related models.
This overview is only partial. Much more space would be necessary to make an exhaustive and more detailed work.
We conclude by adding a couple of further remarks.
First we point out that reversibility in limited automata has been investigated in [16]. Probabilistic extensions of limited automata have been recently introduced and studied in [37].
We do not know any result relating limited automata, or their variants, with input-driven pushdown automata, also known as nested word automata [1, 17]. It is known that these devices recognize a proper subclass of deterministic context-free languages, which properly contains the class of regular languages. It should be interesting to know if this class can be characterized by some restricted versions of limited automata.
Notes
- 1.
Actually, the original definition of d-limited automata was given by Hibbard by considering some kinds of rewriting systems [9]. It is not difficult to reformulate it, as we did, in terms of Turing machines.
- 2.
We could have moves that do not change the contents of a cell even in the first visit, as we seen in the above example of 1-limited automaton accepting \(K_n\). For a such a move, we can imagine that the cell is rewritten by the same symbol which is already in it.
- 3.
- 4.
The maximum number of visits to a cell up to the last rewriting, namely the measure corresponding to limited automata, is sometimes called dual return complexity [34].
- 5.
A nonunary rewriting alphabet is necessary for strongly limited automata to recognize all context-free languages. For instance, to recognize the set of palindromes, a working alphabet of at least 3 symbols is required [27].
References
Alur, R., Madhusudan, P.: Adding nesting structure to words. J. ACM 56(3), 16:1–16:43 (2009). https://doi.org/10.1145/1516512.1516518
Chomsky, N., Schützenberger, M.: The algebraic theory of context-free languages. In: Braffort, P., Hirschberg, D. (eds.) Computer Programming and Formal Systems, Studies in Logic and the Foundations of Mathematics, vol. 35, pp. 118–161. Elsevier (1963). https://doi.org/10.1016/S0049-237X(08)72023-8
Chrobak, M.: Finite automata and unary languages. Theoret. Comput. Sci. 47(3), 149–158 (1986). https://doi.org/10.1016/0304-3975(86)90142-8. Errata: 302(1–3), 497–498 (2003)
Ginsburg, S., Rice, H.G.: Two families of languages related to ALGOL. J. ACM 9(3), 350–371 (1962). https://doi.org/10.1145/321127.321132
Guillon, B., Pighizzini, G., Prigioniero, L., Průša, D.: Two-way automata and one-tape machines. In: Hoshi, M., Seki, S. (eds.) DLT 2018. LNCS, vol. 11088, pp. 366–378. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-98654-8_30
Guillon, B., Prigioniero, L.: Linear-time limited automata. Theoret. Comput. Sci. (2019, in press). https://doi.org/10.1016/j.tcs.2019.03.037
Hemaspaandra, L.A., Mukherji, P., Tantau, T.: Context-free languages can be accepted with absolutely no space overhead. Inform. Comput. 203(2), 163–180 (2005). https://doi.org/10.1016/j.ic.2005.05.005
Hennie, F.C.: One-tape, off-line Turing machine computations. Inf. Control 8(6), 553–578 (1965)
Hibbard, T.N.: A generalization of context-free determinism. Inf. Control 11(1/2), 196–238 (1967)
Jančar, P., Mráz, F., Plátek, M.: Characterization of context-free languages by erasing automata. In: Havel, I.M., Koubek, V. (eds.) MFCS 1992. LNCS, vol. 629, pp. 307–314. Springer, Heidelberg (1992). https://doi.org/10.1007/3-540-55808-X_29
Jancar, P., Mráz, F., Plátek, M.: A taxonomy of forgetting automata. In: Borzyszkowski, A.M., Sokołowski, S. (eds.) MFCS 1993. LNCS, vol. 711, pp. 527–536. Springer, Heidelberg (1993). https://doi.org/10.1007/3-540-57182-5_44
Jančar, P., Mráz, F., Plátek, M.: Forgetting automata and context-free languages. Acta Inform. 33(5), 409–420 (1996). https://doi.org/10.1007/s002360050050
Jančar, P., Mráz, F., Plátek, M., Vogel, J.: Restarting automata. In: Reichel, H. (ed.) FCT 1995. LNCS, vol. 965, pp. 283–292. Springer, Heidelberg (1995). https://doi.org/10.1007/3-540-60249-6_60
Kutrib, M., Pighizzini, G., Wendlandt, M.: Descriptional complexity of limited automata. Inform. Comput. 259(2), 259–276 (2018). https://doi.org/10.1016/j.ic.2017.09.005
Kutrib, M., Wendlandt, M.: On simulation cost of unary limited automata. In: Shallit, J., Okhotin, A. (eds.) DCFS 2015. LNCS, vol. 9118, pp. 153–164. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-19225-3_13
Kutrib, M., Wendlandt, M.: Reversible limited automata. Fund. Inform. 155(1–2), 31–58 (2017). https://doi.org/10.3233/FI-2017-1575
Mehlhorn, K.: Pebbling mountain ranges and its application to DCFL-recognition. In: de Bakker, J., van Leeuwen, J. (eds.) ICALP 1980. LNCS, vol. 85, pp. 422–435. Springer, Heidelberg (1980). https://doi.org/10.1007/3-540-10003-2_89
Nasyrov, I.R.: Deterministic realization of nondeterministic computations with a low measure of nondeterminism. Cybernetics 27(2), 170–179 (1991). https://doi.org/10.1007/BF01068368
Ogden, W.F., Ross, R.J., Winklmann, K.: An “interchange lemma” for context-free languages. SIAM J. Comput. 14(2), 410–415 (1985). https://doi.org/10.1137/0214031
Okhotin, A.: Non-erasing variants of the Chomsky–Schützenberger theorem. In: Yen, H.-C., Ibarra, O.H. (eds.) DLT 2012. LNCS, vol. 7410, pp. 121–129. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-31653-1_12
Otto, F.: Restarting automata and their relations to the Chomsky hierarchy. In: Ésik, Z., Fülöp, Z. (eds.) DLT 2003. LNCS, vol. 2710, pp. 55–74. Springer, Heidelberg (2003). https://doi.org/10.1007/3-540-45007-6_5
Peckel, J.: On a deterministic subclass of context-free languages. In: Gruska, J. (ed.) MFCS 1977. LNCS, vol. 53, pp. 430–434. Springer, Heidelberg (1977). https://doi.org/10.1007/3-540-08353-7_164
Peckel, J.: A deterministic subclass of context-free languages. Časopis pro pěstování matematiky 103(1), 43–52 (1978). http://eudml.org/doc/21335
Pighizzini, G.: Nondeterministic one-tape off-line Turing machines. J. Autom. Lang. Comb. 14(1), 107–124 (2009). https://doi.org/10.25596/jalc-2009-107. http://arXiv.org/abs/0905.1271
Pighizzini, G.: Two-way finite automata: old and recent results. Fund. Inform. 126(2–3), 225–246 (2013). https://doi.org/10.3233/FI-2013-879
Pighizzini, G.: Guest column: one-tape Turing machine variants and language recognition. SIGACT News 46(3), 37–55 (2015). https://doi.org/10.1145/2818936.2818947
Pighizzini, G.: Strongly limited automata. Fund. Inform. 148(3–4), 369–392 (2016). https://doi.org/10.3233/FI-2016-1439
Pighizzini, G., Pisoni, A.: Limited automata and regular languages. Internat. J. Found. Comput. Sci. 25(7), 897–916 (2014). https://doi.org/10.1142/S0129054114400140
Pighizzini, G., Pisoni, A.: Limited automata and context-free languages. Fund. Inform. 136(1–2), 157–176 (2015). https://doi.org/10.3233/FI-2015-1148
Pighizzini, G., Prigioniero, L.: Limited automata and unary languages. Inform. Comput. 266, 60–74 (2019). https://doi.org/10.1016/j.ic.2019.01.002
Sakoda, W.J., Sipser, M.: Nondeterminism and the size of two way finite automata. In: Lipton, R.J., Burkhard, W.A., Savitch, W.J., Friedman, E.P., Aho, A.V. (eds.) Proceedings 10th Annual ACM Symposium on Theory of Computing (STOC 1978), pp. 275–286. ACM (1978). https://doi.org/10.1145/800133.804357
Shepherdson, J.C.: The reduction of two-way automata to one-way automata. IBM J. Res. Dev. 3(2), 198–200 (1959). https://doi.org/10.1147/rd.32.0198
Sloane, N.J.A.: The on-line encyclopedia of integer sequences. http://oeis.org/A007814
Wagner, K.W., Wechsung, G.: Computational Complexity. D. Reidel Publishing Company, Dordrecht (1986)
Wechsung, G.: Characterization of some classes of context-free languages in terms of complexity classes. In: Bečvář, J. (ed.) MFCS 1975. LNCS, vol. 32, pp. 457–461. Springer, Heidelberg (1975). https://doi.org/10.1007/3-540-07389-2_233
Wechsung, G., Brandstädt, A.: A relation between space, return and dual return complexities. Theoret. Comput. Sci. 9, 127–140 (1979). https://doi.org/10.1016/0304-3975(79)90010-0
Yamakami, T.: Behavioral strengths and weaknesses of various models of limited automata. In: Catania, B., Královič, R., Nawrocki, J., Pighizzini, G. (eds.) SOFSEM 2019. LNCS, vol. 11376, pp. 519–530. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-10801-4_40
Acknowledgment
I am very grateful to Luca Prigioniero for his valuable and helpful comments.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 IFIP International Federation for Information Processing
About this paper
Cite this paper
Pighizzini, G. (2019). Limited Automata: Properties, Complexity and Variants. In: Hospodár, M., Jirásková, G., Konstantinidis, S. (eds) Descriptional Complexity of Formal Systems. DCFS 2019. Lecture Notes in Computer Science(), vol 11612. Springer, Cham. https://doi.org/10.1007/978-3-030-23247-4_4
Download citation
DOI: https://doi.org/10.1007/978-3-030-23247-4_4
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-23246-7
Online ISBN: 978-3-030-23247-4
eBook Packages: Computer ScienceComputer Science (R0)







 and turning the head to the left.
and turning the head to the left. and continues to move to the left (notice that such a b was left unchanged in the previous visit, when moving from left to right), while when it reads an a, it replaces the contents by
and continues to move to the left (notice that such a b was left unchanged in the previous visit, when moving from left to right), while when it reads an a, it replaces the contents by 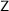 , turning the head to the right.
, turning the head to the right. .
.