Supersingular Isogeny Diffie–Hellman Authenticated Key Exchange

Abstract

We propose two authenticated key exchange protocols from supersingular isogenies. Our protocols are the first post-quantum one-round Diffie–Hellman type authenticated key exchange ones in the following points: one is secure under the quantum random oracle model and the other resists against maximum exposure where a non-trivial combination of secret keys is revealed. The security of the former and the latter is proven under isogeny versions of the decisional and gap Diffie–Hellman assumptions, respectively. We also propose a new approach for invalidating the Galbraith–Vercauteren-type attack for the gap problem.

1 Introduction

All conventional cryptosystems from discrete logarithm and/or factorization intractability assumptions would be totally broken by the emergence of quantum computers, i.e., by Shor’s algorithm [27]. In the post-quantum era, it is important to confirm whether classical cryptographic techniques are still secure against quantum adversaries. Recently, strong security notions and constructions against quantum computers have been intensively studied (e.g., [1, 3, 10, 32, 33]). Moreover, National Institute of Standards and Technology has initiated a process to standardize quantum-resistant public-key cryptographic algorithms [24], so, to study quantum-resistant cryptosystems is a hot research area.

Key establishing over insecure channels is one of important cryptographic techniques. In a key establishing protocol, two parties exchange some messages, and then, they can share a key. Recent researches on this have lead to authenticated key exchange (AKE). In the post-quantum era, it is preferable to have an AKE protocol secure based on a problem which resists against quantum adversaries. We then propose two quantum-resistant AKE schemes from a (relatively) new mathematical foundation, i.e., supersingular isogenies.

Supersingular Isogeny Diffie–Hellman (SIDH). Computing a sequence of isogenies of elliptic curves is a new cryptographic basic operation in some applications. For example, a cryptographic hash function from expander graphs, proposed in [6], consists of computing an isogeny sequence, which is based on the hardness of constructing an isogeny between two (randomly chosen) isogenous curves. Diffie–Hellman (DH) type key exchange protocols based on isogenies are given by Rostovtsev and Stolbunov [26] and De Feo et al. [11], which were considered as candidates for post-quantum public-key primitives.

Childs et al. [7] considered the isogeny computation problem for ordinary elliptic curves, and obtained a subexponential-time quantum algorithm. In contrast, the algorithm cannot be applied to the supersingular case (because of non-commutativity of endomorphism rings). Therefore, both applications above, i.e., hash function and key exchange, need to employ supersingular elliptic curves (and the graph consisting of them). In particular, supersingular isogeny Diffie–Hellman (SIDH) protocol proposed by De Feo et al. [11] has short public keys compared to other post-quantum candidates, and has been intensively studied for serving as a drop-in replacement to existing Internet protocols [2, 8, 9].

Very recently, Petit [25] proposed a mathematical attack for the security of SIDH, but also showed that the security is not affected by the attack if we use appropriate public parameters as is given in Sect. 3.

Authenticated Key Exchange. In an AKE protocol, two parties have own static public keys, exchange ephemeral public keys, and compute a session key based on the public keys and the related secret keys. AKE protocols achieve that honest parties can establish a session key, and any malicious party cannot guess the session key. The latter condition is formulated in an indistinguishability game.

Regarding to this security game, several models have been invented, and the Canetti–Krawczyk (CK) model was proposed to capture leakage of the session state [5]. After the proposal, several security requirements have been indicated such as key compromise impersonation (KCI), weak perfect forward secrecy (wPFS), and maximal exposure attacks (MEX) (refer to [21] for KCI, wPFS, and MEX). The CK model has been integrated with KCI, wPFS, and MEX to the CK$^{+}$ model [13].

Recently, several SIDH AKE protocols have been proposed [14, 22, 23, 31].

Galbraith proposed a one-round¹ protocol (SIDH TS2) in [14] based on the Unified Model DH protocol by Jeong, Katz, and Lee [18]. The protocol is CK-secure under a decisional problem in classical random oracle model (ROM).

Longa shows a two-round SIDH AKE protocol (AKE-SIDH-SIKE) which is CK$^{+}$-secure from a KEM scheme [23]. However, it is based on a generic construction known already.

LeGrow, Jao, and Azarderakhsh defined a security model in which the adversary is allowed to make quantum queries, and proposed a quantum CK secure (qCK secure) protocol [22]. The protocol, we call it LJA, is secure in the quantum random oracle model (QROM) however it is two-round.

Xu et al. proposed a two-round protocol (AKE$_{\mathrm {SIDH}\text {-}2}$) in [31], and the protocol is CK$^{+}$-secure under a decisional problem in classical random oracle model (ROM).

It is worth to note here that all the existing SIDH AKE protocols shown above only achieve two-pass protocols except the SIDH TS2 protocol. In a one-round protocol, two parties can simultaneously exchange their ephemeral keys, while in a two-pass one, a party has to wait for the ephemeral key from the other party. Moreover, a one-round AKE protocol has several advantages of efficiency, e.g., each party can pre-compute ephemeral keys in advance.

Supersingular Isogeny Gap DH Problem. Traditional DH AKE protocols have been constructed from several forms of DH assumptions, i.e., computational, decisional and gap DH assumptions, for attaining various trade-offs between security and efficiency. Recently, Galbraith and Vercauteren [16] and Thormarker [29] independently proposed attacks, called GV-type attack in this paper, on the supersingular isogeny computational DH (SI-CDH) problem with access to decision degree oracle, which determines whether two supersingular curves are isogenous of some specific degree or not. While the attack can be extended to some form of SI version of gap DH (SI-GDH) problem, still, there exist possible approaches to formulate a secure form of SI-GDH problem (and assumption) for which the above attack is ineffective. Therefore, it is important to find and establish such secure SI-GDH assumptions to rescue (a wide range of) SIDH-based AKE schemes on the gap assumptions. (For surveys on SIDH-related computational problems, refer to [16, 30].)

Contributions. We propose two one-round authenticated key exchange protocols from supersingular isogenies: one is a protocol secure in the CK model with a quantum adversary under a supersingular isogeny version of the DDH assumption, and the other is a protocol secure in the CK$^{+}$ model with a classical adversary under a supersingular isogeny version of the gap DH assumption.

We call the latter assumption degree-insensitive (di-)SI-GDH assumption in which an adversary has access to a degree-insensitive SI-DDH oracle, and then cannot employ the GV-type attack for which degree distinction is crucial. We expect that the new assumption is of independent interest. Then, both protocols have several advantages of efficiency and wide applicability in practical situations as they retain a simple one-round Diffie–Hellman structure, and are realized in exchanging a single elliptic curve with an auxiliary smooth-order torsion basis, which can be efficiently compressed [2, 8]. We give a comparison table of the existing SIDH AKE protocols and our proposals in Table 1.

Table 1. Comparison of SIDH AKE protocols.

Notations. When A is a set, $y \in _{R}A$ denotes that y is uniformly selected from A. When A is a random variable, $y \leftarrow _{R}A$ denotes that y is randomly selected from A according to its distribution. We denote the finite field of order q by $\mathbb {F}_q$.

2 Security Models: CK-Security and CK$^{+}$-Security

This section outlines the CK and CK$^{+}$ security definitions for two-pass PKI-based authenticated key exchange protocols. Note that, in our post-quantum CK and CK$^{+}$ models, all parties are modeled by probabilistic polynomial-time (ppt) Turing machines while the adversary is modeled by a polynomial time quantum machine. For further CK and CK$^{+}$ details and explanations, see [12, 21]. It is worth to note here that the proposed protocols are one-round and thus, it is enough to describe the security model as for two-pass AKE because a two-pass model includes a one-round one.

We denote a party’s identity $\hat{A}$, $\hat{B}$, $\hat{C}$, $\dots$, where the ID space is $\mathbf {IDS}$. A party honestly generates its own keys, static public and static secret ones, and the static public key is linked with the party’s identity in some systems like PKI.² The maximum numbers of parties and sessions are polynomially bound in the security parameter.

We outline our models for a two-pass AKE protocol where parties, $\hat{A}$ and $\hat{B}$, exchange ephemeral public keys, X and Y, i.e., $\hat{A}$ sends X to $\hat{B}$ and $\hat{B}$ sends Y to $\hat{A}$, and thereafter derive a session key. The session key depends on the exchanged ephemeral keys, identifiers of the parties, the static keys, and the protocol instance that is used.

Keys. The public key owned by each party and its secret key are called static public key and static secret key, respectively. The one-time use session information exchanged in the protocol is called ephemeral public key as the information is generated from a temporary secret called ephemeral secret key.

Session. An invocation of a protocol is called a session. A session is activated via an incoming message of the forms $(\varPi$, $\mathcal {I}$, $\hat{A}$, $\hat{B})$ or $(\varPi$, $\mathcal {R}$, $\hat{A}$, $\hat{B}$, Y), where $\varPi \in \mathbf {PRS}$ is a protocol identifier in the protocol ID space, $\mathbf {PRS}$. If $\hat{A}$ is activated with $(\varPi$, $\mathcal {I}$, $\hat{A}$, $\hat{B})$, then $\hat{A}$ is the session initiator, otherwise it is the session responder. We say that $\hat{A}$ is the owner (resp. peer) of session $\mathtt {sid}$ if the third (resp. fourth) coordinate of $\mathtt {sid}$ is $\hat{A}$. After activation, session initiator $\hat{A}$ creates ephemeral public key X and a new session identified with $(\varPi$, $\mathcal {I}$, $\hat{A}$, $\hat{B}$, X, $\perp )$, and sends $(\varPi$, $\mathcal {R}$, $\hat{B}$, $\hat{A}$, X) to the session responder $\hat{B}$, who then prepares ephemeral public key Y and a new session identified with $(\varPi$, $\mathcal {R}$, $\hat{B}$, $\hat{A}$, X, Y), computes the session key and sends $(\varPi$, $\mathcal {I}$, $\hat{A}$, $\hat{B}$, X, Y) to $\hat{A}$. Upon receiving $(\varPi$, $\mathcal {I}$, $\hat{A}$, $\hat{B}$, X, Y), $\hat{A}$ updates the session identifier $(\varPi$, $\mathcal {I}$, $\hat{A}$, $\hat{B}$, X, $\perp )$ with $(\varPi$, $\mathcal {I}$, $\hat{A}$, $\hat{B}$, X, Y) and computes a session key for that session. We say that a session is completed if its owner computes a session key.

If $\hat{A}$ is the initiator of a session, the session is identified via $\mathtt {sid}=(\varPi$, $\mathcal {I}$, $\hat{A}$, $\hat{B}$, X, $\perp )$ or $\mathtt {sid}=(\varPi$, $\mathcal {I}$, $\hat{A}$, $\hat{B}$, X, Y). If $\hat{B}$ is the responder of a session, the session is identified via $\mathtt {sid}=(\varPi$, $\mathcal {R}$, $\hat{B}$, $\hat{A}$, X, Y). The matching session of the session identified via $(\varPi$, $\mathcal {I}$, $\hat{A}$, $\hat{B}$, X, Y) is a session with identifier $(\varPi$, $\mathcal {R}$, $\hat{B}$, $\hat{A}$, X, Y) and vice versa.

Adversary. Adversary $\mathcal {M}$ is modeled as a probabilistic Turing machine that controls all communications including session activation. Activation is performed via a $\mathsf {Send}(\textsc {message})$ query. The $\textsc {message}$ has one of the following forms: $(\varPi$, $\mathcal {I}$, $\hat{A}$, $\hat{B})$, $(\varPi$, $\mathcal {R}$, $\hat{A}$, $\hat{B}$, X), or $(\varPi$, $\mathcal {I}$, $\hat{A}$, $\hat{B}$, X, Y). Each party submits its responses to adversary $\mathcal {M}$, who decides the global delivery order.

The secret information of a party is not accessible to adversary $\mathcal {M}$; however, leakage of secret information is obtained via the following adversary queries.

• $\mathsf {SessionKeyReveal}(\mathtt {sid})$: $\mathcal {M}$ obtains the session key for the session with session identifier $\mathtt {sid}$, provided that the session is completed.

• $\mathsf {SessionStateReveal}(\mathtt {sid})$: $\mathcal {M}$ obtains the session state of the owner of session $\mathtt {sid}$ if the session is not completed (the session key is not established yet). The session state includes all ephemeral secret keys and intermediate computation results except for immediately erased information but does not include the static secret key.

• $\mathsf {Corrupt}(\hat{A})$: The query allows $\mathcal {M}$ to obtain all information of party $\hat{A}$. If a party, $\hat{A}$, is corrupted by a $\mathsf {Corrupt}(\hat{A})$ query issued by $\mathcal {M}$, then we call the party, $\hat{A}$, dishonest. If not, we call the party honest.

Definition 1

(Freshness). Let $\mathtt {sid}^{*}$ be the session identifier of a completed session, owned by an honest party $\hat{A}$ with an honest peer $\hat{B}$. If the matching session exists, then let $\overline{\mathtt {sid}^{*}}$ be the session identifier of the matching session of $\mathtt {sid}^{*}$. Define $\mathtt {sid}^{*}$ to be fresh if none of the following conditions hold:

• $\mathcal {M}$ issues $\mathsf {SessionKeyReveal}(\mathtt {sid}^{*})$, or $\mathsf {SessionKeyReveal}(\overline{\mathtt {sid}^{*}})$ if $\overline{\mathtt {sid}^{*}}$ exists.

• $\overline{\mathtt {sid}^{*}}$ exists and $\mathcal {M}$ makes either of the following queries

  • $\mathsf {SessionStateReveal}(\mathtt {sid}^{*})$ or $\mathsf {SessionStateReveal}(\overline{\mathtt {sid}^{*}})$,

• $\overline{\mathtt {sid}^{*}}$ does not exist and $\mathcal {M}$ makes the following query

  • $\mathsf {SessionStateReveal}(\mathtt {sid}^{*})$.

Security Experiment. Initially, adversary $\mathcal {M}$ is given a set of honest parties, for whom $\mathcal {M}$ selects identifiers. Then the adversary makes any sequence of the queries described above. During the experiment, $\mathcal {M}$ makes a special query $\mathsf {Test}(\mathtt {sid}^{*})$, where $\mathtt {sid}^{*}$ is the session identifier of a fresh session, and is given with equal probability either the session key held by $\mathtt {sid}^{*}$ or a random key; the query does not terminate the experiment. The experiment continues until $\mathcal {M}$ makes a guess whether the key is random or not. The adversary wins the game if the test session $\mathtt {sid}^{*}$ is still fresh and if the guess by $\mathcal {M}$ was correct. The advantage of quantum adversary $\mathcal {M}$ in the AKE experiment with AKE protocol $\varPi$ is defined as

$$ \mathbf {Adv}_{\varPi }^{AKE }(\mathcal {M}) = \Pr [\mathcal {M}\text { wins}] - \frac{1}{2}. $$

Definition 2

(Post-quantum CK security). We say that an AKE protocol $\varPi$ is post-quantum secure in the CK model if the following conditions hold:

• 1. If two honest parties complete matching sessions, then, except with negligible probability, they both compute the same session key.

• 2. For any polynomial-time quantum adversary $\mathcal {M}$, $\mathbf {Adv}_{\varPi }^{AKE }(\mathcal {M})$ is negligible in security parameter $\lambda$ for the test session $\mathtt {sid}^{*}$,

  • (a) if $\overline{\mathtt {sid}^{*}}$ does not exist, or

  • (b) if $\overline{\mathtt {sid}^{*}}$ exists, and the static secret key of the owner of $\mathtt {sid}^{*}$ and the static secret key of the owner of $\overline{\mathtt {sid}^{*}}$ are given to $\mathcal {M}$.

Definition 3

(Post-quantum CK$^{+}$ security). We say that an AKE protocol $\varPi$ is post-quantum secure in the CK$^{+}$ model if the following conditions hold:

• 1. If two honest parties complete matching sessions, then, except with negligible probability, they both compute the same session key.

• 2. For any polynomial-time quantum adversary $\mathcal {M}$, $\mathbf {Adv}_{\varPi }^{AKE }(\mathcal {M})$ is negligible in security parameter $\lambda$ for the test session $\mathtt {sid}^{*}$,

  • (a) if $\overline{\mathtt {sid}^{*}}$ does not exist, and the static secret key of the owner of $\mathtt {sid}^{*}$ is given to $\mathcal {M}$,

  • (b) if $\overline{\mathtt {sid}^{*}}$ does not exist, and the ephemeral secret key of the owner of $\mathtt {sid}^{*}$ is given to $\mathcal {M}$,

  • (c) if $\overline{\mathtt {sid}^{*}}$ exists, and the static secret key of the owner of $\mathtt {sid}^{*}$ and the static secret key of the owner of $\overline{\mathtt {sid}^{*}}$ are given to $\mathcal {M}$,

  • (d) if $\overline{\mathtt {sid}^{*}}$ exists, and the ephemeral secret key of the owner of $\mathtt {sid}^{*}$ and the ephemeral secret key of the owner of $\overline{\mathtt {sid}^{*}}$ are given to $\mathcal {M}$,

  • (e) if $\overline{\mathtt {sid}^{*}}$ exists, and the static secret key of the owner of $\mathtt {sid}^{*}$ and the ephemeral secret key of the owner of $\overline{\mathtt {sid}^{*}}$ are given to $\mathcal {M}$, or

  • (f) if $\overline{\mathtt {sid}^{*}}$ exists, and the ephemeral secret key of the owner of $\mathtt {sid}^{*}$ and the static secret key of the owner of $\overline{\mathtt {sid}^{*}}$ are given to $\mathcal {M}$.

The static and ephemeral public keys of our schemes include supersingular curves and points on them. We can test supersingularity of curves in polynomial time, e.g., [28]. We make an important remark: While Krawczyk mentions a strong adversary model where a corrupted party can choose to register any public key of its choice at any point during the protocol as a variant of the CK($^{+}$) model in [21], we do not allow the re-registration of static public key (similar to the CK($^{+}$) model), and the initial public key is honestly generated and has been used until the end of the protocol. It is because that an active attack which Galbraith et al. [15] proposed for revealing static keys might be considered as an effective attack when we adopt the above flexible key re-registration.

3 Supersingular Isogeny Diffie–Hellman (SIDH)

We describe the SIDH protocol, whose implementation is investigated in detail in [9] and subsequently in [2, 4, 8, 19, 20]. The security is studied in [15, 25]. For making user secret keys short, we follow the description in the SIKE document [17], that is, the user key is given as just one scalar, e.g., $k_{\mathtt {A}} \in \mathbb {Z}/\ell _{\mathtt {A}}^{e_{\mathtt {A}}}\mathbb {Z}$.

3.1 Original (Concrete) Description of SIDH

For two small primes $\ell _{\mathtt {A}}, \ell _{\mathtt {B}}$ (e.g., $\ell _{\mathtt {A}}=2, \ell _{\mathtt {B}}=3$), we choose a large prime p such that $p\pm 1 = f \cdot \ell _{\mathtt {A}}^{e_{\mathtt {A}}} \ell _{\mathtt {B}}^{e_{\mathtt {B}}}$ for a small f and $\ell _{\mathtt {A}}^{e_{\mathtt {A}}} \approx \ell _{\mathtt {B}}^{e_{\mathtt {B}}} = 2^{\varTheta (\lambda )}$, where $\lambda$ is a security parameter. Then, we also choose a random supersingular elliptic curve E over $\mathbb {F}_{p^2}$ with $E(\mathbb {F}_{p^2}) \simeq ({\mathbb Z}/(p\pm 1) {\mathbb Z})^2 \supseteq ({\mathbb Z}/\ell _{\mathtt {A}}^{e_{\mathtt {A}}} {\mathbb Z})^2 \oplus ({\mathbb Z}/\ell _{\mathtt {B}}^{e_{\mathtt {B}}} {\mathbb Z})^2$. We use isogenies, $\phi _{\mathtt {A}}$ and $\phi _{\mathtt {B}}$, with kernels of orders, $\ell _{\mathtt {A}}^{e_{\mathtt {A}}}$ and $\ell _{\mathtt {B}}^{e_{\mathtt {B}}}$, respectively, and the following commutative diagram for the SIDH key exchange between Alice and Bob.

Below we first choose generators $P_{\mathtt {A}}, Q_{\mathtt {A}}, P_{\mathtt {B}}, Q_{\mathtt {B}}$ such that $E[\ell _{\texttt {A}}^{e_{\mathtt {A}}}] = \langle P_{\mathtt {A}}, Q_{\mathtt {A}} \rangle ,$ $E[\ell _{\mathtt {B}}^{e_{\mathtt {B}}}] = \langle P_{\texttt {B}}, Q_{\mathtt {B}} \rangle$ and then set the random curve $E/\mathbb {F}_{p^2}$ and the above generators as public parameters, i.e., we define the generator as $\mathsf {pk}^{\mathsf {sidh}}=(\mathfrak {g}=(E; \ P_{\mathtt {A}}, \ Q_{\mathtt {A}}, \ P_{\mathtt {B}}, \ Q_{\mathtt {B}}), \ \mathfrak {e}=(\ell _{\mathtt {A}}, \ell _{\mathtt {B}}, e_{\mathtt {A}}, e_{\mathtt {B}})) \leftarrow _{R}\mathsf {Gen}^\mathsf {sidh}(1^\lambda )$. Secret-key spaces for Alice and Bob are given as $SK _{\mathtt {A}} =\mathbb {Z}/\ell _{\mathtt {A}}^{e_{\mathtt {A}}}\mathbb {Z}$ and $SK _{\mathtt {B}} =\mathbb {Z}/\ell _{\mathtt {B}}^{e_{\mathtt {B}}}\mathbb {Z}$, respectively. DH-type key exchange is given as below (Fig. 1). Here, since $\langle \phi _{\mathtt {B}}(P_{\mathtt {A}}) + k_{\mathtt {A}} \, \phi _{\mathtt {B}}(Q_{\mathtt {A}}) \rangle = \langle \phi _{\mathtt {B}}(R_{\mathtt {A}}) \rangle = \ker \phi _{\mathtt {B}\mathtt {A}}$ and $\langle \phi _{\mathtt {A}}(P_{\mathtt {B}}) + k_{\mathtt {B}} \, \phi _{\mathtt {A}}(Q_{\mathtt {B}}) \rangle = \langle \phi _{\mathtt {A}}(R_{\mathtt {B}}) \rangle = \ker \phi _{\mathtt {A}\mathtt {B}}$ hold, we have the equality of the j-invariants $K_{\texttt {Alice}} = j(E_{\mathtt {B}}/\ker \phi _{\mathtt {B}\mathtt {A}}) = j(E/\langle R_{\mathtt {A}},R_{\mathtt {B}} \rangle ) = j(E_{\texttt {A}}/\ker \phi _{\mathtt {A}\mathtt {B}}) = K_{\texttt {Bob}}$, and $K=K_{\texttt {Alice}} = K_{\texttt {Bob}}$ is a shared key. Alice’s output includes $\phi _{\mathtt {A}}(P_{\mathtt {B}})$ and $\phi _{\mathtt {A}}(Q_{\mathtt {B}})$ as well as $E_{\mathtt {A}}$, and the security is based on the hardness of isogeny problem with the auxiliary inputs.

Fig. 1.

Outline of SIDH protocol (original description).

3.2 Crypto-Friendly Description of SIDH

We prepare an alternative crypto-friendly description of SIDH for a simple presentation of our proposed AKE.

We set

$$\begin{aligned}&\mathfrak {g}=(E; \ P_{\mathtt {A}}, \ Q_{\mathtt {A}}, \ P_{\mathtt {B}}, \ Q_{\mathtt {B}}), \ \mathfrak {a}=k_{\mathtt {A}}, \ \mathrm {and} \ \mathfrak {b}=k_{\mathtt {B}}. \end{aligned}$$

Let the sets of supersingular curves and those with an auxiliary torsion basis be

$$\begin{aligned}&SSEC _p =\{\text {supersingular elliptic curve} \ E \ \text {over} \ \mathbb {F}_{p^2} \\&\ \ \ \ \ \ \ \ \ \ \ \ \ \text {with} \, E(\mathbb {F}_{p^2}) \simeq ({\mathbb Z}/(p\pm 1) {\mathbb Z})^2 \supseteq ({\mathbb Z}/\ell _{\mathtt {A}}^{e_{\mathtt {A}}} {\mathbb Z})^2 \oplus ({\mathbb Z}/\ell _{\mathtt {B}}^{e_{\mathtt {B}}} {\mathbb Z})^2 \}, \\&SSEC _{p,\mathtt {A}} =\{(E; \, P'_\mathtt {B}, \, Q'_\mathtt {B}) \,|\, E \in SSEC _p, \, (P'_\mathtt {B}, \, Q'_\mathtt {B}) : \text {basis of} \ E[\ell _{\mathtt {B}}^{e_{\mathtt {B}}}] \}, \\&SSEC _{p,\mathtt {B}} =\{(E; \, P'_\mathtt {A}, \, Q'_\mathtt {A}) \,|\, E \in SSEC _p, \, (P'_\mathtt {A}, \, Q'_\mathtt {A}) : \text {basis of} \ E[\ell _{\mathtt {A}}^{e_{\mathtt {A}}}] \}. \end{aligned}$$

Thus, SIDH public keys of ${\mathtt {A}}$ and ${\mathtt {B}}$ are given elements of $SSEC _{p,\mathtt {A}}$ and $SSEC _{p,\mathtt {B}}$, respectively. Then, we define

$$\begin{aligned}&\mathfrak {g}^{\mathfrak {a}} =(E_{\mathtt {A}}; \ \phi _{\mathtt {A}}(P_{\mathtt {B}}), \ \phi _{\mathtt {A}}(Q_{\mathtt {B}})) \in SSEC _{p,\mathtt {A}}, \ \\&\ \ \ \ \ \text {where} \ R_{\mathtt {A}} =P_{\mathtt {A}} + k_{\mathtt {A}} Q_{\mathtt {A}}, \ \phi _{\mathtt {A}}: E \rightarrow E_{\mathtt {A}} =E/\langle R_{\mathtt {A}} \rangle , \\&\mathfrak {g}^{\mathfrak {b}} =(E_{\mathtt {B}}; \ \phi _{\mathtt {B}}(P_{\mathtt {A}}), \ \phi _{\mathtt {B}}(Q_{\mathtt {A}})) \in SSEC _{p,\mathtt {B}}, \ \\&\ \ \ \ \ \text {where} \ R_{\mathtt {B}} =P_{\mathtt {B}} + k_{\mathtt {B}} Q_{\mathtt {B}}, \ \phi _{\mathtt {B}}: E \rightarrow E_{\mathtt {B}} =E/\langle R_{\mathtt {B}} \rangle , \\&\left( \mathfrak {g}^{\mathfrak {b}} \right) ^{\mathfrak {a}} =j(E_{\texttt {BA}}), \\&\ \ \ \ \ \text {where} \ R_{\texttt {BA}} =\phi _{\mathtt {B}}(P_{\mathtt {A}}) + k_{\mathtt {A}} \phi _{\mathtt {B}}(Q_{\mathtt {A}}), \ \phi _{\texttt {BA}}: E_{\mathtt {B}} \rightarrow E_{\texttt {BA}} =E_{\mathtt {B}}/\langle R_{\texttt {BA}} \rangle , \\&\left( \mathfrak {g}^{\mathfrak {a}} \right) ^{\mathfrak {b}} =j(E_{\texttt {AB}}), \\&\ \ \ \ \ \text {where} \ R_{\texttt {AB}} =\phi _{\mathtt {A}}(P_{\mathtt {B}}) + k_{\mathtt {B}} \phi _{\mathtt {A}}(Q_{\mathtt {B}}), \ \phi _{\texttt {AB}}: E_{\mathtt {A}} \rightarrow E_{\texttt {AB}} =E_{\mathtt {A}}/\langle R_{\texttt {AB}} \rangle . \end{aligned}$$

We describe SIDH using this notation below (Fig. 2). Public parameters are $\mathfrak {g}=(E; \ P_{\mathtt {A}}, \ Q_{\texttt {A}}, \ P_{\mathtt {B}}, \ Q_{\mathtt {B}})$ and $\mathfrak {e}=(\ell _{\mathtt {A}}, \ell _{\mathtt {B}}, e_{\mathtt {A}}, e_{\mathtt {B}})$. Here, shared secret is given as $K_{\texttt {Alice}} = \left( {\mathfrak {g}}^\mathfrak {b}\right) ^\mathfrak {a}= \left( \mathfrak {g}^{\mathfrak {a}} \right) ^{\mathfrak {b}} = K_{\texttt {Bob}}$, which shows correctness of the SIDH protocol.

4 Post-quantum Assumptions from SIDH

We define SI-CDH, SI-DDH, ds- and di-SI-GDH assumptions against quantum adversaries based on the notation in Sect. 3.2. The SI-DDH assumption is needed for indistinguishability security of SIDH shared keys. Moreover, all of the following assumptions excluding ds-SI-GDH (see Proposition 1) are considered reasonable at present.

Fig. 2.

Outline of SIDH protocol (crypto-friendly description).

Definition 4

(SI-CDH Assumption). Let $\mathcal {S}$ be a quantum machine adversary. For $\mathsf {pk}^{\mathsf {sidh}}=(\mathfrak {g}=(E; \ P_{\mathtt {A}}, \ Q_{\mathtt {A}}, \ P_{\mathtt {B}}, \ Q_{\mathtt {B}}), \ \mathfrak {e}=(\ell _{\mathtt {A}}, \ell _{\mathtt {B}}, e_{\mathtt {A}}, e_{\mathtt {B}})) \leftarrow _{R}\mathsf {Gen}^\mathsf {sidh}(1^\lambda )$ and $\mathfrak {a}\in _{R} SK _{\mathtt {A}}, \ \mathfrak {b}\in _{R} SK _{\mathtt {B}}$, $\mathcal {S}$ receives $(\ \mathsf {pk}^{\mathsf {sidh}}, \ \mathfrak {g}^\mathfrak {a}, \ \mathfrak {g}^\mathfrak {b})$, and $\mathcal {S}$ outputs ${\mathfrak {h}} \in \mathbb {F}_{p^2}$. If $\mathfrak {h}= \left( \mathfrak {g}^\mathfrak {a}\right) ^\mathfrak {b}(= \left( \mathfrak {g}^\mathfrak {b}\right) ^\mathfrak {a})$, $\mathcal {S}$ wins. We define the advantage of $\mathcal {S}$ for the SI-CDH problem as $\mathbf {Adv}_{{\mathfrak {g},\mathfrak {e}}}^{\mathrm {SI}\text {-}\mathrm {CDH}}(\mathcal {S})=\Pr [\mathcal {S}\text { wins} ]$. The SI-CDH assumption is: For any polynomial-time quantum machine adversary $\mathcal {S}$, the advantage of $\mathcal {S}$ for the SI-CDH problem is negligible in security parameter $\lambda$.

Definition 5

(SI-DDH Assumption). Let $\mathcal {S}$ be a quantum machine adversary. For $\mathsf {pk}^{\mathsf {sidh}}=(\mathfrak {g}=(E; \ P_{\mathtt {A}}, \ Q_{\mathtt {A}}, \ P_{\mathtt {B}}, \ Q_{\mathtt {B}}), \ \mathfrak {e}=(\ell _{\mathtt {A}}, \ell _{\mathtt {B}}, e_{\mathtt {A}}, e_{\mathtt {B}})) \leftarrow _{R}\mathsf {Gen}^\mathsf {sidh}(1^\lambda )$ and $\mathfrak {a}, \mathfrak {r}\in _{R} SK _{\mathtt {A}}, \ \mathfrak {b}, \mathfrak {s}\in _{R} SK _{\mathtt {B}}$, $\mathcal {S}$ receives $\mathcal {X}_b$ for $b \in _{R}\{ 0,1 \}$, that is defined by

$$\begin{aligned} \mathcal {X}_0 =(\ \mathsf {pk}^{\mathsf {sidh}}, \ \mathfrak {g}^\mathfrak {a}, \ \mathfrak {g}^\mathfrak {b}, \ \left( \mathfrak {g}^\mathfrak {a}\right) ^\mathfrak {b}\ ) \ \ \mathrm {and} \ \ \mathcal {X}_1 =(\ \mathsf {pk}^{\mathsf {sidh}}, \ \mathfrak {g}^\mathfrak {a}, \ \mathfrak {g}^\mathfrak {b}, \ \left( \mathfrak {g}^{\mathfrak {r}} \right) ^{\mathfrak {s}} \ ), \end{aligned}$$

$\mathcal {S}$ outputs a guess bit $b'$. If $b = b'$, $\mathcal {S}$ wins. We define the advantage of $\mathcal {S}$ for the SI-DDH problem as $\mathbf {Adv}_{{\mathfrak {g},\mathfrak {e}}}^{\mathrm {SI}\text {-}\mathrm {DDH}}(\mathcal {S})=\Pr [ \mathcal {S}\text { wins} ]-1/2$. The SI-DDH assumption is: For any polynomial-time quantum machine adversary $\mathcal {S}$, the advantage of $\mathcal {S}$ for the SI-DDH problem is negligible in security parameter $\lambda$.

Definition 6

(ds- and di-SI-GDH Assumption). Let $\mathcal {S}$ be a quantum machine adversary. For $\mathsf {pk}^{\mathsf {sidh}}=(\mathfrak {g}=(E; \ P_{\mathtt {A}}, \ Q_{\mathtt {A}}, \ P_{\mathtt {B}}, \ Q_{\mathtt {B}}), \ \mathfrak {e}=(\ell _{\mathtt {A}}, \ell _{\mathtt {B}}, e_{\mathtt {A}}, e_{\mathtt {B}})) \leftarrow _{R}\mathsf {Gen}^\mathsf {sidh}(1^\lambda )$ and $\mathfrak {a}\in _{R} SK _{\mathtt {A}}, \ \mathfrak {b}\in _{R} SK _{\mathtt {B}}$, $\mathcal {S}$ receives $(\mathsf {pk}^{\mathsf {sidh}}, \ \mathfrak {g}, \ \mathfrak {g}^\mathfrak {a}, \ \mathfrak {g}^\mathfrak {b})$, and $\mathcal {S}$ access SI-DDH oracle for any input $\mathcal {X}=( \mathsf {pk}^{\mathsf {sidh}}, (E'_{\mathtt {A}}; P'_{\mathtt {A}\mathtt {B}}, Q'_{\mathtt {A}\mathtt {B}}), \ (E'_{\mathtt {B}}; P'_{\mathtt {B}\mathtt {A}},$ $Q'_{\mathtt {B}\mathtt {A}}), \ \mathfrak {h}' )$ where $P'_{\mathtt {A}\mathtt {B}}, Q'_{\mathtt {A}\mathtt {B}}$ (resp. $P'_{\mathtt {B}\mathtt {A}}, Q'_{\mathtt {B}\mathtt {A}}$) are points in $E'_{\mathtt {A}}(\mathbb {F}_{p^2})$ (resp. $E'_{\mathtt {B}}(\mathbb {F}_{p^2})$) and ${\mathfrak {h}}' \in \mathbb {F}_{p^2}$, and then outputs ${\mathfrak {h}} \in \mathbb {F}_{p^2}$. If $\mathfrak {h}= \left( \mathfrak {g}^\mathfrak {a}\right) ^\mathfrak {b}(= \left( \mathfrak {g}^\mathfrak {b}\right) ^\mathfrak {a})$, $\mathcal {S}$ wins. According to the behavior of SI-DDH oracle, we have two types of SI-GDH problem, i.e.,

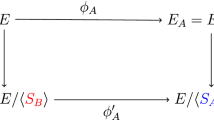
• degree-sensitive SI-GDH (ds-SI-GDH) problem. The ds-SI-DDH oracle answers true if there exist a supersingular elliptic curve $E'_{\mathtt {A}\mathtt {B}}$ and isogenies $(\phi '_{\mathtt {A}},$ $\phi '_{\mathtt {B}},$ $\phi '_{\mathtt {A}\mathtt {B}},$ $\phi '_{\mathtt {B}\mathtt {A}})$ among $E, E'_{\mathtt {A}}, E'_{\mathtt {B}}, E'_{\mathtt {A}\mathtt {B}}$ which form a commutative diagram as in Fig. 3 such that

  • 

    and

  • $P'_{\mathtt {A}\mathtt {B}} = \phi '_{\mathtt {A}}(P_{\mathtt {B}}), \ Q'_{\mathtt {A}\mathtt {B}} = \phi '_{\mathtt {A}}(Q_{\mathtt {B}})$ and $P'_{\mathtt {B}\mathtt {A}} = \phi '_{\mathtt {B}}(P_{\mathtt {A}}),\ Q'_{\mathtt {B}\mathtt {A}} = \phi '_{\mathtt {B}}(Q_{\mathtt {A}})$ where points $(P_{\mathtt {A}}, Q_{\mathtt {A}}, P_{\mathtt {B}}, Q_{\mathtt {B}})$ are given in public key $\mathsf {pk}^{\mathsf {sidh}}$, and ${\mathfrak {h}}' = j(E'_{\mathtt {A}\mathtt {B}})$,

  and false otherwise. We call this case degree-sensitive SI-GDH (ds-SI-GDH) problem.

• degree-insensitive SI-GDH (di-SI-GDH) problem. The di-SI-DDH oracle answers true if there exist a supersingular elliptic curve $E'_{\mathtt {A}\mathtt {B}}$ and isogenies $(\phi '_{\mathtt {A}},$ $\phi '_{\mathtt {B}},$ $\phi '_{\mathtt {A}\mathtt {B}},$ $\phi '_{\mathtt {B}\mathtt {A}})$ among $E, E'_{\mathtt {A}}, E'_{\mathtt {B}}, E'_{\mathtt {A}\mathtt {B}}$ which form a commutative diagram as in Fig. 3 such that

  • and

  • $P'_{\mathtt {A}\mathtt {B}} = \phi '_{\mathtt {A}}(P_{\mathtt {B}}), \ Q'_{\mathtt {A}\mathtt {B}} = \phi '_{\mathtt {A}}(Q_{\mathtt {B}})$ and $P'_{\mathtt {B}\mathtt {A}} = \phi '_{\mathtt {B}}(P_{\mathtt {A}}),\ Q'_{\mathtt {B}\mathtt {A}} = \phi '_{\mathtt {B}}(Q_{\mathtt {A}})$ where points $(P_{\mathtt {A}}, Q_{\mathtt {A}}, P_{\mathtt {B}}, Q_{\mathtt {B}})$ are given in public key $\mathsf {pk}^{\mathsf {sidh}}$, and ${\mathfrak {h}}' = j(E'_{\mathtt {A}\mathtt {B}})$,

  and false otherwise. We call this case degree-insensitive SI-GDH (di-SI-GDH) problem.

We define the advantage of adversary $\mathcal {S}$ for the ds–SI-GDH and di-SI-GDH problems as $\mathbf {Adv}_{{\mathfrak {g},\mathfrak {e}}}^{\mathrm {ds}\text {-}\mathrm {SI}\text {-}\mathrm {GDH}}(\mathcal {S})=\Pr [\mathcal {S}\text { wins} ]$ and $\mathbf {Adv}_{{\mathfrak {g},\mathfrak {e}}}^{\mathrm {di}\text {-}\mathrm {SI}\text {-}\mathrm {GDH}}(\mathcal {S})=\Pr [\mathcal {S}\text { wins}]$, respectively. The ds-SI-GDH (resp. di-SI-GDH) assumption is: For any polynomial-time quantum machine adversary $\mathcal {S}$, the advantage of $\mathcal {S}$ for the ds-SI-GDH (resp. di-SI-GDH) problem is negligible in security parameter $\lambda$.

Fig. 3.

Commutative diagram for true instances of SI-DDH oracles, in which it holds that $\ker (\phi '_{\mathtt {B}\mathtt {A}}) = \phi '_{\mathtt {B}}(\ker (\phi '_{\mathtt {A}}))$ and $\ker (\phi '_{\mathtt {A}\mathtt {B}}) = \phi '_{\mathtt {A}}(\ker (\phi '_{\mathtt {B}}))$.

Proposition 1

(adapted from [16]). The ds-SI-GDH assumption does not hold, i.e., there exists a ppt adversary against the ds-SI-GDH problem.

Proof Sketch

Very recently, Galbraith and Vercauteren proposed an attack on the SI-CDH problem with access to the decision degree (DD) oracle [16], which determines whether two supersingular curves are isogenous of some specific degree or not. As a basic building block, first, we describe an attack on the SI-CDH problem using the DD oracle. The input of the problem is $(\mathsf {pk}^{\mathsf {sidh}}=(\mathfrak {g}=(E; \ P_{\mathtt {A}}, \ Q_{\mathtt {A}}, \ P_{\mathtt {B}}, \ Q_{\mathtt {B}}), \ \mathfrak {e}=(\ell _{\mathtt {A}}, \ell _{\mathtt {B}}, e_{\mathtt {A}}, e_{\mathtt {B}})), E_{\mathtt {A}}, P_{\mathtt {A}\mathtt {B}}, Q_{\mathtt {A}\mathtt {B}})$, where $\phi _{\mathtt {A}}: E \rightarrow E_{\mathtt {A}}$ is an $\ell _{\mathtt {A}}^{e_{\mathtt {A}}}$-isogeny, $P_{\mathtt {A}\mathtt {B}} =\phi _{\mathtt {A}}(P_{\mathtt {B}})$, and $Q_{\mathtt {A}\mathtt {B}} =\phi _{\mathtt {A}}(Q_{\mathtt {B}})$. The goal of the adversary $\mathcal S$ is to reveal $\phi _{\mathtt {A}}$. For that, $\mathcal S$ calculates integer u such that $u \cdot \ell _{\mathtt {A}} \equiv 1$ (mod $\ell _{\mathtt {B}}$), and then one $\ell _{\mathtt {A}}$-isogeny $\psi : E_{\mathtt {A}} \rightarrow E'$. $\mathcal S$ send

$$ (\tilde{\mathsf {pk}}^{\mathsf {sidh}}=(\mathfrak {g}, \ \tilde{\mathfrak {e}} =(\ell _{\mathtt {A}}, \ell _{\mathtt {B}}, e_{\mathtt {A}}-1, e_{\mathtt {B}}), E', u \cdot \psi (P_{\mathtt {A}\mathtt {B}}), u \cdot \psi (Q_{\mathtt {A}\mathtt {B}})) $$

to the DD oracle. Here, we note that the exponent $e_{\mathtt {A}}-1$ is used instead of $e_{\mathtt {A}}$ for the implicitly defined $\ell _{\mathtt {A}}$-power isogeny. That is, the oracle distinguishes the degree (or length) of the isogeny, in other words, whether $E'$ is $\ell _{\mathtt {A}}^{e_{\mathtt {A}}-1}$-isogenous to E or $\ell _{\mathtt {A}}^{e_{\mathtt {A}}+1}$-isogenous to E. See the left hand side of Fig. 4. Then, the adversary reveals all the isogeny by repeating this $\ell _{\mathtt {A}}$-backtracking decision.

Next, we extend the above strategy to solve the ds-SI-GDH problem. Namely, an ds-SI-GDH adversary obtains an input $(\mathsf {pk}^{\mathsf {sidh}}=(\mathfrak {g}=(E; \ P_{\mathtt {A}}, \ Q_{\mathtt {A}}, \ P_{\mathtt {B}}, \ Q_{\mathtt {B}}), \ \mathfrak {e}=(\ell _{\mathtt {A}}, \ell _{\mathtt {B}}, e_{\mathtt {A}}, e_{\mathtt {B}})), E_{\mathtt {A}}, P_{\mathtt {A}\mathtt {B}}, Q_{\mathtt {A}\mathtt {B}}, \ldots )$, where $\phi _{\mathtt {A}}: E \rightarrow E_{\mathtt {A}}$ is an $\ell _{\mathtt {A}}^{e_{\mathtt {A}}}$-isogeny, $P_{\mathtt {A}\mathtt {B}} =\phi _{\mathtt {A}}(P_{\mathtt {B}})$, and $Q_{\mathtt {A}\mathtt {B}} =\phi _{\mathtt {A}}(Q_{\mathtt {B}})$. The goal of the adversary $\mathcal S$ is to reveal $\phi _{\mathtt {A}}$. For that, $\mathcal S$ calculates one $\ell _{\mathtt {A}}$-isogeny $\psi : E_{\mathtt {A}} \rightarrow E'$ as before. Moreover, $\mathcal S$ calculates degree $\ell _{\mathtt {B}}^{e_{\mathtt {B}}}$-isogenies $E \rightarrow E'_{\mathtt {B}}$ and $E' \rightarrow E'_{\mathtt {A}\mathtt {B}}$ that makes commutative SIDH diagram $(E,E',E'_{\mathtt {B}},E'_{\mathtt {A}\mathtt {B}})$. Then, $\mathcal S$ send

$$ (\tilde{\mathsf {pk}}^{\mathsf {sidh}}=(\mathfrak {g}, \ \tilde{\mathfrak {e}} =(\ell _{\mathtt {A}}, \ell _{\mathtt {B}}, e_{\mathtt {A}}-1, e_{\mathtt {B}}), E', E'_{\mathtt {B}}, \ldots , j(E'_{\mathtt {A}\mathtt {B}})) $$

to the ds-SI-DDH oracle and determine whether $\psi$ is a backtracking step in $\phi _{\mathtt {A}}$ or not. See the right hand side of Fig. 4. From here on, repeating this procedure, $\mathcal S$ can reveal $\phi _{\mathtt {A}}$. Also, $\mathcal S$ can compute $E_{\mathtt {A}\mathtt {B}}$ by using $E_{\mathtt {B}}$ and $\phi _{\mathtt {A}}$, which solves the ds-SI-GDH problem.    $\square$

Fig. 4.

Diagrams for the GV-type attack. The right (resp. left) hand side shows the strategy for the ds-SI-GDH problem (resp. the SI-CDH problem with access to the DD oracle). The attacker distinguishes which one of the $e_{\mathtt {A}}+1$ left arrows of $\ell _{\mathtt {A}}$-isogenies from $E_{\mathtt {A}}$ is backtracking by using the ds-SI-DDH (resp. the DD) oracle.

As described in the above proof, to distinguish the degree of isogeny (or distance between two elliptic curves in the $\ell _{\mathtt {A}}$-isogeny graph) is crucial for the GV-type attack. Since the ability for the distinction is given by the ds-SI-DDH oracle, the GV-type attack adversaries have no advantages in the di-SI-GDH problem. Therefore, in contrast to the ds-SI-GDH problem, we may assume that the di-SI-GDH problem cannot be solved by any efficient adversaries, and can be used for the basis of the security of our biclique scheme.

Note that auxiliary points $\phi '_{\mathtt {A}}(P_{\mathtt {B}}), \phi '_{\mathtt {A}}(Q_{\mathtt {B}}), \phi '_{\mathtt {B}}(P_{\mathtt {A}}), \phi '_{\mathtt {B}}(Q_{\mathtt {A}})$ in true instance $\mathcal {X}$ for di-SI-DDH oracle impose some restrictions on implicitly defined isogenies $\phi '_{\mathtt {A}}, \phi '_{\mathtt {B}}$ (and $\phi '_{\mathtt {A}\mathtt {B}}, \phi '_{\mathtt {B}\mathtt {A}}$) used in Fig. 3. However, since degrees $d'_{\mathtt {A}}$ and $d'_{\mathtt {B}}$ of $\phi '_{\mathtt {A}}$ and $\phi '_{\mathtt {B}}$ can be chosen as any powers of $\ell _{\mathtt {A}}$ and $\ell _{\mathtt {B}}$ respectively, a wide range of tuples $(E'_{\mathtt {A}}, E'_{\mathtt {B}}, E'_{\mathtt {A}\mathtt {B}})$ can be accepted for forming the commutative diagram in Fig. 3. Therefore, as an extreme possible case, any tuple of supersingular elliptic curves $(E'_{\mathtt {A}}, E'_{\mathtt {B}}, E'_{\mathtt {A}\mathtt {B}})$ might form the commutative diagram in Fig. 3, that is, any tuple of such curves would be true instances in the hypothetical case. We cannot exclude such possibility from our present knowledge of the di-SI-GDH problem. A satisfiable analysis of the di-SI-GDH problem seems to need more understanding of the Ramanujan graph of $\ell$-isogenies of supersingular curves.

Lemma 3.2 and Theorem 3.3 in [30] also show some interesting connection between computational and decisional SIDH problems. However, we notice that answers of all the oracles $(O_{E,1})_{\ell ^e}, (O_{E,2})_{\ell ^e}$ and $(O_{E,3})_{\ell ^e}$ (for $\ell ^e=\ell _1^{e_1}$ or $\ell _2^{e_2}$) are related to isogenies of degrees dividing $\ell ^e$, which is defined by public parameters. In particular, all the isogeny degrees have smaller or equal than $\ell ^e$. Our di-SI-GDH problem is related to unbounded degrees which are just a power of $\ell$. Thus, Lemma 3.2 and Theorem 3.3 in [30] are now unrelated with our situation, but, we think seeking relationships between the di-SI-GDH problem and the results in [30] is an interesting research direction.

5 Proposed SIDH UM Protocol

In this section, we propose the SIDH UM protocol, where it can be proved in the quantum random oracle model under the SI-DDH assumption.

Before describing the protocol, we explain that each party needs to have two static public keys. The public parameter, $\mathfrak {g}$, contains two parameters, $(P_{1}, \ Q_{1})$ and $(P_{2}, Q_{2})$. A party has a key on $(P_{1}, \ Q_{1})$ and the other key on $(P_{2}, Q_{2})$. Then, $(P_{1}, \ Q_{1})$ is used to generate the ephemeral public key of the initiator and $(P_{2}, \ Q_{2})$ is used to generate the ephemeral public key of the responder. When the role is exchanged, each party uses the other static key which is not used before.

This double construction in public parameter and static public keys gives resistance to reflection attacks. To the best of our knowledge, the previous researches of key exchange on supersingular isogenies have lacked this consideration.

5.1 Useful Techniques for Quantum Random Oracle Model

A problem on security proofs in the quantum random oracle model is how to generate random values for exponentially many positions in order to simulate outputs of the hash function. For a hash function $H : Dom \rightarrow Rng$, in the quantum random oracle model, the adversary poses a superposition $|\phi \rangle = \varSigma \alpha _x | x \rangle$ and the oracle returns $\varSigma \alpha _x | H(x) \rangle$. If $Rng$ is large for a quantum polynomial-time simulator, it is difficult to generate all random output values of H to compute $\varSigma \alpha _x | H(x) \rangle$. Zhandry [33] showed a solution with the notion of k-wise independent function.

A weight assignment on a set $\mathcal {X}$ is a function $D : \mathcal {X} \rightarrow \mathbb {R}$ such that $\varSigma _{x \in \mathcal {X}} D(x) = 1$. A distribution on $\mathcal {X}$ is a weight-assignment D such that $D(x) \ge 0$ for all $x \in \mathcal {X}$. Consider the set of functions $H : \mathcal {X} \rightarrow \mathcal {Y}$ for sets $\mathcal {X}$ and $\mathcal {Y}$, denoted by $H_{\mathcal {X},\mathcal {Y}}$. We define the marginal weight assignment $D_\mathcal {W}$ of D on $H_{\mathcal {X},\mathcal {Y}}$ where the weight of a function $H_\mathcal {W} : \mathcal {W} \rightarrow \mathcal {Y}$ is equal to the sum of the weights of all $H \in H_{\mathcal {X},\mathcal {Y}}$ that agree with $H_\mathcal {W}$ on $\mathcal {W}$.

Definition 7

(k-wise equivalence). We call two weight assignments $D_1$ and $D_2$ on $H_{\mathcal {X},\mathcal {Y}}$ k-wise equivalent if for all $\mathcal {W} \subseteq \mathcal {X}$ of size k, the marginal weight assignments $D_{1,\mathcal {W}}$ and $D_{2,\mathcal {W}}$ (of $D_1$ and $D_2$) over $H_{\mathcal {X},\mathcal {Y}}$ are identical.

Definition 8

(k-wise independent function). We call a function f k-wise independent function if f is k-wise equivalent to a random function.

Lemma 1

(Theorem 3.1 in [33]). Let A be a quantum algorithm making q quantum queries to an oracle $H : \mathcal {X} \rightarrow \mathcal {Y}$. If we draw H from some weight assignment D, then for every z, the quantity $\Pr _{H \leftarrow D}[A^H()=z]$ is a linear combination of the quantities $\Pr _{H \leftarrow D}[H(x_i) = r_i \forall i \in {1,\dots ,2q}]$ for all possible settings of the $x_i$ and $r_i$.

Lemma 2

(Theorem 6.1 in [33]). If there exists $2q_i$-wise independent function, then any quantum algorithm A making $q_i$ quantum queries to random oracles $O_i$ can be efficiently simulated by a quantum algorithm B, which has the same output distribution, but makes no queries.

Hence, a quantum algorithm B can simulate quantum random oracles in a polynomial-time. We use this simulation technique to simulate outputs of the hash function in the security proof of the SIDH UM protocol.

On the other hand, the other problem on security proofs in the quantum random oracle model is how to insert intended random values as the outputs of corresponding oracle inputs. Zhandry [33] showed a solution with the notion of semi-constant distributions $\mathbf {SC}_{\omega }$.

Definition 9

(Semi-constant distribution). Define $\mathbf {SC}_{\omega }$, the semi-constant distribution, as the distribution over $H_{\mathcal {X},\mathcal {Y}}$ resulting from the following process:

• First, pick a random element y from $\mathcal {Y}$.

• For each $x \in \mathcal {X}$, do one of the following:

  • With probability $\omega$, set $H(x) = y$. We call x a distinguished input to H.

  • Otherwise, set H(x) to be a random element in $\mathcal {Y}$.

Lemma 3

(Corollary 4.3 in [33]). The distribution of outputs of a quantum algorithm making $h$ queries to an oracle drawn from $\mathbf {SC}_{\omega }$ is at most a distance $\frac{3}{8}h^4\omega ^2$ away from the case when the oracle is drawn from the uniform distribution.

We suppose that the simulation succeeds with probability $\epsilon$ if the adversary uses an inserted random value as the outputs of corresponding oracle inputs. If the probability that the adversary uses one of the points is $\omega$, then the simulation succeeds with probability $\epsilon \omega - \frac{3}{8}h^4\omega ^2$. By choosing $\omega$ to maximize the success probability, the simulation succeeds with probability $O(\epsilon ^2/h^4)$. We use this simulation technique to insert a SI-DDH instance into the hash function in the security proof of the SIDH UM protocol.

5.2 Description of SIDH UM Protocol

We give our SIDH UM protocol using the notation in Sect. 3.2. Public parameters are $\mathfrak {g}=(E; \ P_{1}, \ Q_{1}, \ P_{2}, \$ $Q_{2})$ and $\mathfrak {e}=(\ell _{1}, \ell _{2}, e_{1}, e_{2})$. We set $\varPi = \mathrm {SIDHUM}$, that is, the protocol ID is “SIDHUM.” Static and ephemeral keys are the same as our biclique SIDH protocol. Let two secret-key spaces for initiators and responders be given as $SK _1 =\mathbb {Z}/\ell _1^{e_1}\mathbb {Z}$ and $SK _2 =\mathbb {Z}/\ell _2^{e_2}\mathbb {Z}$, respectively.

User $\hat{A}$ has two static public keys, $A_{1}=\mathfrak {g}^{\mathfrak {a}_{1}}$ and $A_{2}=\mathfrak {g}^{\mathfrak {a}_{2}}$, where $\mathfrak {a}_{1} =k_{\mathtt {A}, 1} \in _{R} SK _1$, $\mathfrak {a}_{2} =k_{\mathtt {A}, 2} \in _{R} SK _2$, and $\mathfrak {a}_{1}$ and $\mathfrak {a}_{2}$ are $\hat{A}$’s static secret keys. User $\hat{B}$, also, has two static public keys, $B_{1}=\mathfrak {g}^{\mathfrak {b}_{1}}$ and $B_{2}=\mathfrak {g}^{\mathfrak {b}_{2}}$, where $\mathfrak {b}_{1} =k_{\mathtt {B}, 1} \in _{R} SK _1$, $\mathfrak {b}_{2} =k_{\mathtt {B}, 2} \in _{R} SK _2$, and $\mathfrak {b}_{1}$ and $\mathfrak {b}_{2}$ are $\hat{B}$’s static secret keys. Here, ephemeral secret keys for $\hat{A}$ and $\hat{B}$ are given as

$$ \mathfrak {x}=k_{\mathtt {X}} \in _{R} SK _1, \ \text {and} \ \ \mathfrak {y}=k_{\mathtt {Y}} \in _{R} SK _2, $$

respectively. $\hat{A}$ sends a ephemeral public key X as $X=g^{\mathfrak {x}}$ to $\hat{B}$, $\hat{B}$ sends back a ephemeral public key Y as $Y=g^{\mathfrak {y}}$ to $\hat{A}$.

$\hat{A}$ computes $Z_{1}=B_{2}^{\mathfrak {a}_1}$, and $Z_{2}=Y^{\mathfrak {x}}$, and then, obtains the session key K as $K=H(\varPi , Z_{1}, Z_{2}, \hat{A}, \hat{B},$ X, Y), where H is a hash function.

$\hat{B}$ can computes the session key K as $K=H(\varPi , Z_{1}, Z_{2}, \hat{A}, \hat{B}, X, Y)$ from $Z_{1}=A_{1}^{\mathfrak {b}_{2}}$, and $Z_{2}=X^{\mathfrak {y}}$.

It is clear that the session keys of both parties are equal (Fig. 5).

Fig. 5.

Outline of SIDH UM protocol.

Fig. 6.

Outline of Biclique SIDH protocol.

5.3 Security

Theorem 1

Suppose that $H$ is modeled as a quantum random oracle and that the SI-DDH assumption hold for $(\mathfrak {g}, \mathfrak {e})$. Then the SIDH UM protocol is a post-quantum CK-secure authenticated key exchange protocol in the quantum random oracle model.

In particular, for any AKE quantum adversary $\mathcal {M}$ against the SIDH UM protocol that runs in time at most t, involves at most $n$ honest parties and activates at most $s$ sessions, and makes at most $h$ queries to the quantum random oracle and $q$ $\mathsf {SessionKeyReveal}$ queries, there exists an SI-DDH quantum adversary $\mathcal {S}$ such that

$$ \mathbf {Adv}_{{\mathfrak {g},\mathfrak {e}}}^{\mathrm {SI}\text {-}\mathrm {DDH}}(\mathcal {S})\ge \frac{2\mathbf {Adv}_{{\mathrm {SIDHUM}}}^{\mathrm {AKE}}(\mathcal {M})^2}{n^2 s^2 (8hq+ 3(h+q+1)^4)}, $$

where $\mathcal {S}$ runs in time t plus time to perform $\mathcal {O}\big ((n+ s) \lambda \big )$ low-degree isogeny operations.

An intuition of the security proof is given in Sect. 5.1. The SI-DDH assumption used in Theorem 1 can be degree-sensitive. Hence, it implies security under the SI-CDH assumption by using the reduction in Proposition 1. However, an additional reduction cost is necessary. It is not trivial to directly prove security under the SI-CDH assumption because of the no-cloning theorem. Specifically, in the reduction to the CK security, the SI-CDH solver wants to extract the answer of the SI-CDH problem from a random oracle query by the AKE adversary. However, the query is a quantum state, and the solver cannot record a copy of the input. Thus, this proof strategy does not work. Recently, Zhandry [34] introduced a technique to record quantum queries. How to apply this technique to the proof is an open problem.

6 Proposed Biclique SIDH Protocol

In this section, we propose the biclique SIDH protocol, where it can be proved in the random oracle model under the di-SI-GDH assumption.

It is worth to note here that the SIDH UM protocol is secure in the quantum random oracle model under the SI-DDH assumption, and therefore, the SIDH UM protocol is superior than the biclique SIDH protocol in the following points: the computational model of adversaries and the assumption relaying to the security. However, the biclique SIDH protocol can be shown to be secure in the CK$^{+}$ model, that is, the protocol resists against maximum exposure where a non-trivial combination of secret keys is revealed. This shows that the biclique SIDH protocol is superior than the SIDH UM protocol in this sense.

As our SIDH UM protocol in Sect. 5, the public parameter, $\mathfrak {g}$, contains two parameters, $(P_{1}, \ Q_{1})$ and $(P_{2}, Q_{2})$ in our biclique SIDH protocol. A party has a key on $(P_{1}, \ Q_{1})$ and the other key on $(P_{2}, Q_{2})$.

6.1 Description of Biclique SIDH Protocol

We give our biclique SIDH protocol using the notation in Sect. 3.2. Public parameters are $\mathfrak {g}=(E; \ P_{1}, \ Q_{1}, \$ $P_{2}, \ Q_{2})$ and $\mathfrak {e}=(\ell _{1}, \ell _{2}, e_{1}, e_{2})$. We set $\varPi = \mathrm {BCSIDH}$, that is, the protocol ID is “BCSIDH.” Let two secret-key spaces for initiators and responders be given as $SK _1 =\mathbb {Z}/\ell _1^{e_1}\mathbb {Z}$ and $SK _2 =\mathbb {Z}/\ell _2^{e_2}\mathbb {Z}$, respectively.

User $\hat{A}$ has two static public keys, $A_{1}=\mathfrak {g}^{\mathfrak {a}_{1}}$ and $A_{2}=\mathfrak {g}^{\mathfrak {a}_{2}}$, where $\mathfrak {a}_{1} =k_{\mathtt {A}, 1} \in _{R} SK _1$, $\mathfrak {a}_{2} =k_{\mathtt {A}, 2} \in _{R} SK _2$, and $\mathfrak {a}_{1}$ and $\mathfrak {a}_{2}$ are $\hat{A}$’s static secret keys. User $\hat{B}$, also, has two static public keys, $B_{1}=\mathfrak {g}^{\mathfrak {b}_{1}}$ and $B_{2}=\mathfrak {g}^{\mathfrak {b}_{2}}$, where $\mathfrak {b}_{1} =k_{\mathtt {B}, 1} \in _{R}SK_1$, $\mathfrak {b}_{2} =k_{\mathtt {B}, 2} \in _{R}SK_2$, and $\mathfrak {b}_{1}$ and $\mathfrak {b}_{2}$ are $\hat{B}$’s static secret keys. Here, ephemeral secret keys for $\hat{A}$ and $\hat{B}$ are given as

$$ \mathfrak {x}=k_{\mathtt {X}} \in _{R} SK _1, \ \text {and} \ \ \mathfrak {y}=k_{\mathtt {Y}} \in _{R} SK _2, $$

respectively. $\hat{A}$ sends an ephemeral public key X as $X=g^{\mathfrak {x}}$ to $\hat{B}$, $\hat{B}$ sends back an ephemeral public key Y as $Y=g^{\mathfrak {y}}$ to $\hat{A}$.

$\hat{A}$ computes the non-trivial combinations of the ephemeral and static public keys as $Z_{1}=Y^{\mathfrak {a}_{1}}$, $Z_{2}=B_{2}^{\mathfrak {x}}$, $Z_{3}=B_{2}^{\mathfrak {a}_1}$, and $Z_{4}=Y^{\mathfrak {x}}$, and then, obtains the session key K as $K=H(\varPi , Z_{1}, Z_{2}, Z_{3}, Z_{4}, \hat{A}, \hat{B}, X, Y)$, where H is a hash function.

$\hat{B}$ can computes the session key K as $K=H(\varPi , Z_{1}, Z_{2}, Z_{3}, Z_{4}, \hat{A}, \hat{B}, X, Y)$ from $Z_{1}=A_{1}^{\mathfrak {y}}$, $Z_{2}=X^{\mathfrak {b}_{2}}$, $Z_{3}=A_{1}^{\mathfrak {b}_{2}}$, and $Z_{4}=X^{\mathfrak {y}}$.

It is clear that the session keys of both parties are equal (Fig. 6).

Charles et al. [6] proposed a hash function secure against quantum adversaries from the isogeny computation intractability. Hence, we can use the isogeny-based hash function in the real implementation for H, however, H is modeled as a random oracle in the security proof below.

6.2 Security

Theorem 2

Suppose that $H$ is modeled as a random oracle and that the di-SI-GDH assumption hold for $(\mathfrak {g}, \mathfrak {e})$. Then the biclique SIDH protocol is a post-quantum CK$^{+}$-secure authenticated key exchange protocol in the random oracle model.

In particular, for any AKE quantum adversary $\mathcal {M}$ against the biclique SIDH protocol that runs in time at most t, involves at most $n$ honest parties and activate at most $s$ sessions, and makes at most $h$ queries to the random oracle, there exists a di-SI-GDH quantum adversary $\mathcal {S}$ such that

$$ \mathbf {Adv}_{{\mathfrak {g},\mathfrak {e}}}^{\mathrm {di}\text {-}\mathrm {SI}\text {-}\mathrm {GDH}}(\mathcal {S})\ge \min \Big \{\frac{1}{sn},\frac{1}{n^2},\frac{1}{s^2}\Big \} \cdot \mathbf {Adv}_{{\mathrm {BCSIDH}}}^{\mathrm {AKE}}(\mathcal {M}), $$

where $\mathcal {S}$ runs in time t plus time to perform $\mathcal {O}\big ((n+ s) \lambda \big )$ low-degree isogeny operations and make $\mathcal {O}(h+ s)$ queries to di-SI-DDH oracle.

As we consider a case where the security model is CK$^{+}$, an adversary may access to a non-trivial combination of secret keys. However, it means that the adversary cannot access to the other combination of the secret key. Thus, the di-SI-GDH solver can embedded an instance to the public keys where secret key are not revealed. As we assume the random oracle model, the adversary has to make a query which contains the di-SI-GDH answer, and then, the theorem can be proved. Note here that the di-SI-DDH oracle is necessary to keep consistency between the answers by the di-SI-GDH solver on adversary’s questions.

We consider how to extend our security proof in the random oracle model to that in the quantum random oracle model as in the SIDH UM protocol. For completing the simulation, we need to extend the di-SI-GDH assumption (Definition 6). Namely, in random oracle simulation, $\mathcal {S}$ first checks compatibility of input elements using di-SI-DDH oracle. Hence, in the quantum ROM situation, since inputs are given in quantum superposition form, we should extend the di-SI-DDH oracle to take as input the superpositions. If the di-SI-GDH quantum adversary allows the extended di-SI-DDH oracle access, then our security proof can be converted to quantum ROM secure one.

7 Conclusion

We proposed two authenticated key exchange protocols from supersingular isogenies: SIDH UM and biclique SIDH. We also discussed a new approach for invalidating the Galbraith–Vercauteren attack for the gap problem on the supersingular isogeny Diffie–Hellman, and defined the di-SI-GDH assumption.

The SIDH UM protocol is secure in the CK and quantum random oracle models under the SI-DDH assumption. The biclique SIDH protocol is secure in the CK$^{+}$ and random oracle models under the di-SI-GDH assumption.

Our protocols are the first post-quantum one-round Diffie–Hellman type authenticated key exchange ones in the following points: one is secure under the quantum random oracle model and the other resists against maximum exposure where a non-trivial combination of secret keys is revealed.