Group Search and Evacuation

Abstract

Group search and evacuation are fundamental tasks performed by a set of co-operating, autonomous mobile agents. The two tasks are similar in that they both aim to search a given domain so as to locate a target which has been placed at an unknown location in the domain. However they also differ in that the former terminates when the first searcher in the group reaches the target while the latter when the last searcher in the group reaches the target. Variations where termination is determined by some designated agent have also been considered. Depending on the domain being explored we distinguish linear search when the target is placed on the infinite line and circular search when the target is placed on the perimeter of a disk. The agents move with their own maximum speed, and the goal is to design algorithms that minimize the worst case termination time. Two communication models between the robots are being considered: in the non-wireless (or face-to-face) communication model, robots exchange information only when simultaneously located at the same point, and wireless communication in which robots can communicate with one another anywhere at any time. In this paper we survey some of the most interesting recent algorithmic results on search and evacuation concerning mobile agents with and without faults.

Research supported in part by NSERC Discovery grants.

1 Introduction

Search in theoretical computer science is primarily concerned with the algorithmic probing of a well-defined (data-) domain in order to find a stored target object. The main focus of this survey, is on presenting recent algorithmic developments on search performed by a group of collaborating autonomous agents. During the search, the mobile agents are pursuing their own trajectories and are required to locate a target and conclude the task in the minimum amount of time. To begin we introduce some basic concepts and ideas that will be used in later sections.

Searchers

Throughout this paper the terms mobile agent, searcher and robot will be identical. We assume that n robots are initially placed at a start position on a geometric domain. The robots can move on a continuous trajectory with a predefined maximum speed (usually one) along a geometric domain (which is either an infinite line or a cycle in the plane).

Search and Evacuation

We distinguish between search and evacuation. The former succeeds when the first searcher in the group reaches the target and the latter when the last searcher in the group reaches the target. Variations where only distinguished searchers need to reach the target are also considered. In all cases, the target can be identified only by robots that reach its location.

Linear and Circular Search

The search domain may be either on an infinite line or on a closed curve, like disk. In the first case it is called linear search and was first proposed by Bellman [9] and independently by Beck [8] in a stochastic setting and by [6, 7]) in a deterministic setting. In the linear search model the environment is an infinite line and the robots start at a given point, called the origin, on this line. An hidden object/target (exit) is placed on the line at a location which is unknown to the robots. In the second case it is sometimes called circular search and the model was first studied in [17]. In the unit disk search model the environment is a disk, usually of unit radius; the robots start their movement either at the center of the disk (and they can move anywhere on the plance) or on the disk (and they can move only on the perimeter). The only information robots have is that the target has been placed at an unknown location on the perimeter.

Communication

Two models of communication between the robots are being considered: in the non-wireless (or face-to-face) communication model, robots exchange information only when they are simultaneously located at the same point, and wireless communication in which robots can communicate with one another anywhere at any time.

Performance Metrics

When operating in geometric environments, performance is measured by the geometric distance traveled, while in discrete settings the number of hops in a trajectory. By default, algorithmic performance is measured with respect to worst case analysis. The competitive ratio of an algorithm is the worst case ratio between the performance of the algorithm and the performance of the best offline algorithm, i.e., an algorithm that knows in advance the location of the “hidden” object. In traditional search the task ends when the first agent finds the object. This is different for evacuation since we are interested in the search makespan which refers to the max (or even, total) length of the search strategy when all the agents (or sometimes a specific number of the agents) have finished processing their respective tasks.

Some Related Literature

There is a vast literature investigating all aspects of search. Several papers are cited throughout the survey but here we mention only a few books. It is worth cittng the classical book on optimal search [36], the compendium of search problems in [1] and the game theoretic approach in the treatise [5]. Applications of search to foraging and evolution can be found in [30, 35]. Further, [33] provides an introduction to the analysis and design of dynamic multiagent networks, and [14] an introduction to the distributed control of robotic networks with a blend of computer science and control theory. Additional specialized monographs are [10, 11] as well as the pleasant monograph [34] which provides a different perspective with chases and escapes.

2 Linear Search

In this section we focus on linear search on an infinite line and discuss search for robots which may suffer from crash and/or byzantine faults. In the last part of the section we also explore search on linear terrains (a generalization of the infinite line).

2.1 Crash Faults

In this section we present the linear search by a collection of robots, some of which may turn out to be faulty [24].

Model Specifics and Problem Definition

By A(n, f) we denote a linear search problem using n mobile robots where at most f robots may turn out to be faulty. The robots are placed at the origin of an infinite line. Robots may walk along the line with the same unit speed. At some point on the line, at distance d from the origin, is placed a stationary target that needs to be found by the collection of robots. A robot finds the target when it visits the position of the line where the target is located. A sub-collection of up to f robots may experience crash faults. A faulty robot cannot identify the target despite visiting its location. The search is completed when at least one non-faulty robot finds the target.

The bound f on the number of faulty robots is known to the search algorithm. However, the identities of the faulty robots are unknown to the algorithm. Consequently, the set of the faulty robots is controlled by the adversary, which knows the search algorithm in advance. The distance d to the target position is also unknown to the algorithm, but the performance of the algorithm is measured as a function of d. More exactly, the algorithm efficiency is defined by a competitive ratio, which is the worst case ratio of the arrival of the first reliable robot to the target, and the distance d from the source to the target.

For any potential target position, the best adversarial strategy is to choose the first f robots incoming to such position to be faulty. It is clear that, when $n \ge 2f+2$, there exists a simple algorithm with competitive ratio 1 that sends two groups of $f+1$ robots in each direction of the line. Below we focus on efficient search strategies when $f< n < 2f+2$.

Zig-Zag Strategies

For $n < 2f+2$, the trajectories of all robots considered are using zig-zag strategies, i.e. solutions in which each robot walks alternately in both directions, where its turning points for each direction are more and more distant from the origin. It is useful to illustrate the zig-zag movements using the Cartesian plane in which x-axis corresponds to the line of robots’ movement and t-axis represent time. The trajectory of a robot is represented by a function of time t whose absolute slope is bounded by 1 (as robots move using maximal unit speed). By a turning point $(x_i, t_i)$ we mean that at time $t_i$ the robot is at point $x_i$ of the line and it changes the direction of its movement.

The strategies used are such that the turning points $(x_i, t_i)$ belong to some geometric cone of the Cartesian plane. Let $C_{\beta }$ denote the cone starting at the origin and extending in the positive direction of t-axis such that it is bounded by two semi-lines, each having angle ${\beta }$ with the t-axis. We have

Definition 1

Suppose that at time $a \beta$ a robot visits point a of the line. We say that the robot follows a zig-zag movement defined by cone $C_{\beta }$ and point $(a, a \beta )$ if the robot walks with unit speed inside the cone $C_{\beta }$ starting at point $(a, a \beta )$ and that it reverses its direction whenever it arrives at the boundary of $C_{\beta }$.

Figure 1 illustrates movements of robots defined by the cone $C_{\beta }$.

It is possible to prove the following lemma.

Lemma 1

([24]). Let $x_0$ be the initial position of a robot on the line at time $t_0$. Consider the zig-zag movement of this robot defined by point $(x_0, t_0)$ and the cone $C_{\beta }$, where $\beta >1$. The turning points of the robot are given by the formula

$$\begin{aligned} x_i&= x_0 \left( \frac{\beta +1}{\beta -1} \right) ^i (-1)^i \end{aligned}$$

(1)

Proportional Schedules

When several robots participate in the search, they all move according to zig-zag strategies using the same cone $C_{\beta }$, but the choice of the parameter ${\beta }$ depends on the ratio of assumed bound of the faulty robots. Moreover, the most efficient search is achieved when the robots’ trajectories are forming so-called proportional schedules (see Fig. 1). Roughly speaking, for a proportional schedule, the infinite sequence of the consecutive positive x-coordinates of the turning points of all robots form a geometric progression. The same is true for the consecutive negative x-coordinates of all turning points. More precisely, we give the following definition.

Definition 2

Suppose that a collection of robots performs zig-zag movements defined by the same cone $C_{\beta }$. Consider the infinite sequence of the consecutive positive turning points $0< \tau _0< \tau _1 < \cdots$ obtained from the zig-zag movements of all the robots of the collection. We say that the schedule is proportional if for some real value r, the ratio $\frac{\tau _{i+1} - \tau _i}{\tau _i - \tau _{i-1}} = r$, for $i=1,2,\ldots$. We call r the proportionality ratio of the schedule.

Fig. 1.

Proportional schedule for n robots $a_0, a_1, \ldots , a_{n-1}$, in the cone $C_{\beta }$.

We have the following lemma.

Lemma 2

([24]). Consider any constant $\beta > 1$ and n robots performing zig-zag movements defined by the cone $C_{\beta }$. Suppose that the movements of the robots constitute the proportional schedule $S_{\beta } (n)$. The proportionality ratio of schedule $S_{\beta } (n)$ equals

$$\begin{aligned} r&= \left( \frac{\beta +1}{\beta -1} \right) ^{2/n}. \end{aligned}$$

(2)

Moreover, suppose that $\tau _i, \tau _{i+1}$ are two consecutive, positive turning points of some two robots a, b, such that robot a visited $\tau _i$ at time $t_i$ and robot b visited $\tau _{i+1}$ at time $t_{i+1}$. Then we have $t_{i+1} = t_i + \tau _i \beta (r-1)$ and $\tau _{i+1} = r \tau _i$. Note that by symmetry a similar result applies to negative turning points.

Suppose that n robots, which may include at most f faulty ones execute a proportional schedule $S_\beta (n)$ using cone $C_{\beta }$. Let $CR_{\beta }^{n,f}$ denote the competitive ratio of schedule $S_\beta (n)$. The following lemma proves the upper bound on the competitive ratio of the proportional schedule $S_\beta (n)$.

Lemma 3

([24]). Let $S_{\beta } (n)$ be a proportional schedule executed by n robots, which may include at most f faulty ones, where $f<n< 2f+2$. Then we have the following bound on the competitive ratio of this proportional schedule:

$$\begin{aligned} CR_{\beta }^{n,f}&= \left( \beta +1 \right) ^{\frac{2f+2}{n}} \left( \beta -1 \right) ^{1-\frac{2f+2}{n}} + 1 . \end{aligned}$$

(3)

For any configuration of parameters n, f it is possible to find the value of $\beta$ which minimizes the function $F(\beta ) := (\beta +1)^{\frac{2f+2}{n}} (\beta -1)^{1-\frac{2f+2}{n} } + 1$, where $\beta > 1$. This can be done by taking the derivative of F with respect to $\beta$ and setting it equal to 0. Such optimal vale of $\beta$ turns out to be $\beta = \frac{4f+4}{n} - 1$.

Consequently, we conclude with the following theorem.

Theorem 1

([24]). Consider a collection of n robots up to f of which are faulty. Then there exists an algorithm A(n, f) performing search on infinite line, whose competitive ratio is at most equal to

$$\begin{aligned} \left( \frac{4f+4}{n} \right) ^{\frac{2f+2}{n}} \left( \frac{4f+4}{n} -2\right) ^{1-\frac{2f+2}{n} } + 1 \end{aligned}$$

(4)

Figure 2 illustrates the search algorithm for three robots containing one that may turn out to be faulty. Inside the cone $C_\beta$ may be identified the region R bound by bold polygonal lines (that reminds the Sacrada Familia Barcelonian church). Each point (x, t) inside region R has the property that before time t point x of the line has been visited by at least two robots, hence it is considered successfully searched. If point (x, t) is outside region R, that means that only one robot visited x before time t (as that robot may be faulty, x cannot be declared as successfully searched). The competitive ratio of the algorithm is determined by the two lines that pass through the origin, belong to R and have maximal and minimal slopes (thin grey lines OA and OB on Fig. 2). Indeed, the competitive ratio equals the smaller of the absolute values of both slopes. An interested reader may verify that if we perturb slightly the movement of any robot by changing slightly the positions where its trajectory touches the cone $C_\beta$ (i.e. the zig-zag strategy becomes not proportional) the competitive ratio becomes larger. This suggest that the proportional strategies are optimal. Indeed, the optimality of the proportional strategies has been formally proven in the recent work of Kupavskii and Welzl [31].

Fig. 2.

Searching by three robots one of which is faulty.

2.2 Byzantine Faults

The section presents linear search when a collection of searchers contains Byzantine robots (cf. [23]). A Byzantine robot may fail to see the target or it may communicate to other robots a position of the target that is not the real one.

Model Specifics and Problem Definition

A collection of n robots is initially placed at the origin of an infinite line. Each robot can move left or right along the line with a speed that does not exceed its maximum speed (which is the same for all robots). Robots have a distinct identity and they may communicate wirelessly, so a message sent by any robot is instantaneously heard by all other robots. As the trajectories of all robots are determined in advance, the only possible message that a robot may communicate is that it found the target. Some robots may turn out to experience Byzantine faults and they may fail to communicate a position of the target they find or they may communicate a position of the target which is wrong. Each communicated message is associated with the identity of the robot sending it and it is assumed that a Byzantine robot cannot lie on its identity. There are at most f robots which may behave in Byzantine way.

The search algorithm is designed by a central authority, which knows the bound f on the number of faulty robots, but is unaware which subset of robots is faulty, neither is their behavior predictable (i.e. faulty robots may misreport their findings). The search algorithm does not have a knowledge of the distance d to the target from the origin. The trajectory of each robot is designed so it may be possibly altered when robot hears about a potential position of the target announced by some other, clearly identified robot.

We suppose that the adversary knows our algorithm and may choose the subset of (at most) f Byzantine robots and their malicious actions in order to delay the moment when the target position is known. By $S_d(n,f)$ we denote the search time, i.e. the time it takes for a search algorithm using a collection of n robots at most f of which are faulty, to find the location of a target placed at an a priori unknown distance d from the origin of the line. The corresponding competitive ratio is defined as $S(n,f)=\sup _d S_d(n,f)/d$, which is the worst case ratio of the algorithm’s search time and the lower bound d on the time taken by any algorithm for the problem.

Observe that if $n \ge 4f+2$ it is possible to obtain an optimal algorithm (with competitive ratio 1). Indeed, we can partition the set into two groups of $2f+1$ robots and make one group to walk together in the left direction and the other group in the right direction. When the target is found, it is announced by all non-faulty robots arriving at its location at time d. As that group contains at least $f+1$ non-faulty robots, by the majority vote the target position is clearly identified. On the other hand, if $n \le 2f$, there does not exist any algorithm that may decide the position of the target, as no majority voting is possible. Consequently, the non-trivial solutions are interesting only when $2f< n < 4f+2$.

Algorithms for Single Byzantine Robot

Following the last observation, and when $f=1$, it is interesting to consider only the cases of $n=3,4$ or 5. The simplest case concerns the collection of $n=4$ robots.

Case 1: $n=4$. The algorithm instructs two groups of 2 robots to walk together in opposite directions. As each group contains at least one reliable robot, at some point a target position is announced, say at some position at distance x from the origin. If two robots announce (i.e. report that the target is found), then the algorithm finishes in time $d=x$. Otherwise, i.e. when only one robot announces, the groups are instructed to swap their positions and then continue in the opposite directions. If the target is confirmed by the robots arriving at the position being announced, the algorithm finishes in time 3d. Otherwise, a Byzantine robot is identified and the remaining robots continue, not reacting on any further announcements of the identified Byzantine robot. An announcement by any other robot (at time $2x+d$) finishes the algorithm. As $x < d$, we conclude that

$$ S(4,1) \le 3. $$

Case 2: $n=5$. Two groups of 2 robots continue in opposite directions as in Case 1, and the fifth robot waits, stationary at the origin. Again an announcement must be made at some time x and in case when two robots make the announcement the algorithm finishes at time $d=x$. Suppose then that a single robot makes that announcement. Then the robot which was stationary walks to the announcement point (for simplicity suppose that all other robots wait motionless for time x, until the fifth robot reaches the announced position). If this robot may confirm the announcement, then in time $2x=2d$ the target is found. Otherwise the Byzantine robot is identified, the robots restart walking in the same direction and a further announcement by any other robot concludes the algorithm. The search time equals $x+d$, and as $x < d$ we have

$$ S(5,1) \le 2. $$

Case 3: $n=3$. In this case, [23] conjectured that the best search algorithm was for all three robots to walk together performing a standard cow-path trajectory, that finishes in time $S_d (5,1) < 9d$. However only a lower bound $S (5,1) > 3.93$ was proven in [23]. This lower bound was later improved in [31] to

$$ S(3,1) > \frac{8}{3} \root 3 \of {4} \approx 5.23. $$

Algorithms for Large Collections of Robots

The proposed upper bounds of the algorithms for large number of robots are usually a function of ratio $r=f/n$. As previously observed, we are interested in the interval $2f+1 \le n < 4f+2$, so we are interested in the case when $1/2 \ge r \ge 1/4$. Observe first, that already for $n=2f+1$, the problem is feasible, i.e. there exists an algorithm, which finds the target in finite time. More exactly, for any $f \ge 0$ we have

$$ S(2f+1,f) \le 9. $$

Indeed, we can instruct the robots to walk together along the path and the majority vote before time 9d concludes the algorithm.

Asymptotically, for $1/2< r < 1/4$ we have the competitive ratio

$$ 1 \le S(f/r+c,f) \le 9, $$

where c denotes some constant value. More formally, we can define

$$\begin{aligned} \hat{S}(r) = \min ~\left\{ q ~|~ \exists \text { constant } c_{r} \text { such that } \forall f > 0, ~S\left( f/r + c_{r}, f \right) \le q \right\} \end{aligned}$$

(5)

Clearly, the larger is the proportion $1-r$ of the non-faulty robots, the better is the competitive ratio that may be expected from an efficient search. Below is the example of an upper bound for some particular density of Byzantine robots.

Proposition 1

([23]). $S\left( \frac{14f +4}{5}, f \right) \le 3$ provided $f \equiv 4 \mod 5$.

The idea of the algorithm providing the bound claimed in Proposition 1 is the following. Two groups of robots, L and R, each containing $\frac{7f +2}{5}$ participants, walk in left and right directions, respectively. Suppose that an announcement is made at time x. If less than $\frac{2f+2}{5}$ robots vote that target is at x or they vote that the target is not at x, then this subgroup is eliminated from consideration (as identified Byzantine robots) and both groups continue walking in their respective directions. So we can assume that the vote is such that each group voting on point x contains at least $\frac{2f+2}{5}$ robots. By symmetry, suppose that the announcement has been made by a sub-collection of group R (i.e. when visiting point $x >0$). At this point, we send $\frac{3f+3}{5}$ robots belonging to group L to move from their current position at $-x$ to point x. At the same time the sub-collections of $\frac{2f+2}{5}$ robots that voted YES and $\frac{2f+2}{5}$ that voted NO are sent from x to $-x$. Once the groups sent swap their positions from $-x$ to x and from x to $-x$, two cases are possible. If the exit is confirmed at x (note that altogether $\frac{7f +2}{5}+\frac{3f+3}{5}=2f+1$ robots visited x so the state of point x is decided), then the algorithm terminates in time $3x=3d$. Otherwise we can eliminate from the consideration a set of at least $\frac{2f+2}{5}$ Byzantine robots (present now at point $-x$), so there exist still at most $f'=f-\frac{2f+2}{5}= \frac{3f-2}{5}$ undisclosed Byzantine robots. At that point the number of robots $l'$ present at $-x$ whose state is unknown equals at least

$$ l' \ge \frac{7f +2}{5} - \frac{3f+3}{5} + \frac{2f+2}{5} = \frac{6f+1}{5}. $$

At point x we have then $r'$ robots and

$$ r' \ge \frac{7f +2}{5} - 2\left( \frac{2f+2}{5}\right) + \frac{3f+3}{5} = \frac{6f+1}{5}. $$

As $l'=r' \ge 2f'+1$ we have at both points $-x$ and x the sub-collections of robots, each containing more reliable than Byzantine robots. Both groups continue searching away from the origin until a majority vote is present, which concludes the search. The cost of the algorithm is the sum of the search time d and the swap time 2x. As $x \le d$ the claim of Proposition 1 is true.

The algorithms for larger values of the ratio r of Byzantine robots may include more than one swap between the groups L and R during the search. The results for these cases are summarized in Table 1.

Table 1. Upper bounds on the asymptotic competitive search ratio $\hat{S}(r)$ for various ranges of r. Recall that for $r > \frac{1}{2}$ the search problem is infeasible.

2.3 Linear Terrains

We now explore a setting (first considered in [26]) which generalizes the infinite straight line setting first considered in [6, 7] and [8, 9], in which the search domain is no longer a straight line but rather a linear terrain with “hills” and valleys. By this we mean that the search is along a curve which is formed by a continuous function (depicted in Fig. 3 whose representation $y=f(x)$ may be known to the robot. As an example, f(x) may be a monotone polygon consisting of n straight-line segments, for some integer $n \ge 1$.

Fig. 3.

Search in an infinite one-dimensional terrain $y=f(x)$. The robot may move in either direction along the terrain, the point O is the origin (considered as the starting position of the robot) and the exit is located on the terrain at a position unknown to the robot.

Model Specifics and Problem Definition

The objective is to design search algorithms that achieve good competitive ratios for the time spent by the robot to complete its search divided by the time spent by an omniscient robot that knows the location of the target. Searching for the exit, could involve variants of the well-known zig-zag, doubling search strategies along the linear terrain. However, the traditional doubling strategy leading to an optimal competitive ratio of 9 for linear search may no longer be adequate and one is required to investigate different approaches and more elaborate strategies for searching that take the shape of the linear terrain $y=f(x)$ into account.

The canonical zig-zag search algorithm (or strategy) is parametrized by an infinite sequence of positive distances $X=\{x_k\}_{k\ge 1}$ from the origin O that specifies the turning points of the robot. Obviously, to ensure progress in searching, each trip of the robot away from the origin must cover more distance than the previous trip in the same direction. A natural measure of the efficacy of the zig-zag search strategy X, is how well it performs in competition with an omniscient adversary that knows the exact location of the target. If d is the unknown distance of the target from the origin, let $\sigma _X(d)$ be the ratio between the time taken by the robot using the zig-zag strategy X to reach an unknown target divided by the time taken by the adversary to proceed directly to the target (placed at distance d from the origin). In addition, $\sigma _X \triangleq \sup _{d>1} ~\sigma _X(d)$ denotes the competitive ratio of the strategy X. We denote the optimal competitive ratio by $\sigma ^*$.

In general, and unlike traditional linear search, the speed of the robot may depend on the physical properties of the terrain. Further, the robot’s speed may depend on the direction of travel along the terrain, or on the profile of the terrain, e.g. when the line is inclined the robot may accelerate or decelerate depending on whether it is moving uphill or downhill, respectively. For example, on uphill segments the robot moves with speed 1 while on the i-th downhill segment it moves with speed $s_i$, where $s_i = 1 + g \sin \alpha _i\ge 1$, g is the well-known gravitation constant (which is approximately equal to $9.8~m/s^2$), and $\alpha _i$ is the angle of inclination of the i-th (downhill) segment, for $i=1,2,\ldots ,n$.

Search Strategies

The first class of models considered is depicted in Fig. 4 and concerns two-speed models of linear search: tailwind (unit speed going left and tailwind speed $s>1$ going right), beacon (unit speed moving away from the origin and speed s moving towards it), and exploration history (the robot explores unknown regions slowly and deliberately with unit speed, but is able to search faster–with speed s–when it encounters a region already seen earlier in its search). Here are some of the results obtained in [26] (Note that Theorem 3 was independently proved also by [12]).

Fig. 4.

Two-speed models based on (a) absolute direction and (b) direction relative to origin

Theorem 2

(Tailwind Model, [26]). Assume the robot has speed $s \ge 1$ when moving left to right and speed 1 otherwise. For $\alpha , r$ such that $\alpha = (1-s + \sqrt{(s-1)^2 + 4r^2 s})/(2r)$, $r = \sqrt{ 2 + ({s+1})/{\sqrt{s}} }$, and $X=\{s, \alpha r, r^2s, \alpha r^3, \ldots \}$ we have that

$$\begin{aligned}&2 + 1/s \le \sigma ^* \le \sigma _X,\nonumber \\&\sigma _X \le 1+ \frac{s+2\sqrt{s}+1}{s+\sqrt{s}+1} \cdot \frac{s+1}{2s} \cdot \left( s+1 + \sqrt{(s-1)^2 + 8s + 4 \sqrt{s} (s+1)} \right) \end{aligned}$$

(6)

Theorem 3

(Beacon Model, [26]). The doubling strategy D is optimal for the beacon model, i.e.

$$\begin{aligned} \sigma ^* = \sigma _D = 5+\frac{4}{s}. \end{aligned}$$

(7)

Theorem 4

(Exploration History Model, [26]). Let $r= 1+\sqrt{2/(s+1)}$, and $X=(r^0,r^1,r^2,\ldots )$ be an expansion strategy. Then, with this strategy, the zig-zag algorithm’s competitive ratio satisfies

$$\begin{aligned} 2 + 1/s \le \sigma ^* \le \sigma _X=2+\frac{1}{s} \left( 3+2\sqrt{2s+2} \right) . \end{aligned}$$

(8)

Fig. 5.

Constant acceleration models: (a) Line (b) Inclined line (c) Hill (d) Valley

The second class of models is depicted in Fig. 5 and concerns constant acceleration models of linear terrain search. In inclined linear terrains (the robot can operate in two modes where it is moving with unit speed when moving uphill and with constant acceleration when moving downhill. The different terrains include an inclined line, a symmetric hill with the hill-top at the origin, or a symmetric valley with the valley-bottom at the origin). Here are some of the results obtained in [26].

Theorem 5

(Constant acceleration in both directions, [26]). Assume the robot is searching with constant acceleration c in either direction, starting from rest initially, as well as at turning points. Then:

$$\begin{aligned} 3 (\sqrt{2} + 1 / \sqrt{2}) \le \sigma ^* \le \sigma _D \le \frac{2\sqrt{3} }{\sqrt{2}-1} + \sqrt{3} + 1 \end{aligned}$$

(9)

Theorem 6

(Moving on an inclined line, [26]). Assume the robot moves with acceleration c in the positive direction, and constant speed 1 in the negative direction using the doubling strategy D. Then for any $d \ge 1$,

$$\begin{aligned} \sqrt{2c}\sqrt{d}<\sigma _D(d) \le \sqrt{8 c} \cdot \sqrt{d} + O(1). \end{aligned}$$

(10)

Furthermore, $\sigma ^* \ge \sup _{d>1} \min \{ 2 + \sqrt{2/(cd)}, \sqrt{2} + \sqrt{cd/2} \}$.

Theorem 7

(Starting at the top of a hill, [26]). Assume that the robot travels with constant acceleration c away from the origin, and with unit speed towards the origin. Then $\sigma _D(d) = \varTheta (\sqrt{d})$ and this is optimal.

Theorem 8

(Starting at the bottom of a valley, [26]). Assume that the robot travels with constant acceleration c towards the origin, and with unit speed away from the origin. Then for any $d \ge 1$:

$$\sigma _D(d) \le 5+ O(d^{-1/2})$$

Furthermore, $\sigma ^* \ge 5$.

3 Evacuation

In this section we discuss search and evacuation which takes place on the perimeter of a closed domain, like circle, triangle or square. We also consider the case of faulty robots.

3.1 Evacuating from a Disk

Consider k mobile robots inside a circular disk of unit radius. The robots are required to evacuate the disk through an unknown exit point situated on its perimeter. We assume all robots have the same (unit) maximal speed and start at the centre of the disk. The robots may communicate in order to inform themselves about the presence (and its position) or the absence of an exit. The goal is for all the robots to evacuate through the exit in minimum time.

A single ($k=1$) robot can find the exit by going to the perimeter and traversing in the clockwise, say, direction. This takes time $1+2\pi$ to reach the exit, in the worst case. It is clear that for any $\epsilon >0$ the robot can cover at most a length $2\pi -\epsilon$ of the perimeter (because its maximum speed is one and the adversary can place the exit in the unvisited portion of the perimeter). Therefore $1+2\pi -\epsilon$ is a lower bound for evacuation, for any $\epsilon >0$. Hence, $1+2\pi$ is also a tight bound for evacuation of one robot.

Model Specifics and Problem Definition

In general, if the k robots are placed in arbitrary initial positions in the interior of the disk then the resulting optimization problem is very difficult and very few (if any) non-trivial evacuation algorithms are known. For this reason in the sequel, the robots are placed at the start at the center of the disk.

An exit is represented as a point on the perimeter of the disk and the robot may locate the exit only if it is colocated with it. Further, two communication models are being considered. F2F (Face-to-Face) which requires that the two robots may communicate only if they are colocated at the same time, and Wireless in which the robots can communicate regardless of their distance. The more general case where the robots have limited communication range $r>0$ has never been discussed in the scientific literature.

Fig. 6.

Evacuating two robots from a disk. The robots start at the center K of the disk and the (unknown) exit is located at B. Left picture depicts the algorithm in the F2F, while the right picture in the wireless communication model.

Evacuation for Two Robots

In the sequel we analyze in somewhat detail the evacuation problem for two robots.

Figure 6 depicts two evacuation algorithms which were originally published in [17]: Left-hand-side figure depicts the F2F model and the right-hand-side figure depicts the wireless communication model. There are two robots that need to evacuate from an unknown exit. One robot is represented by the bold arrow and the other by the blank arrow. In both communication models the robots start at the same time at the center K of the disk. In the first part, the two algorithms are identical. The robots move together to the perimeter, say to point A, and from there they move in opposite direction along the perimeter. This is where the similarities end.

• 1. In the F2F model (see left picture of Fig. 6) when the robot represented by the bold arrow, say, finds the exit at B it makes a cross-cut along the interior of the disk and travels to meet the robot represented by the bold arrow at D. From this point on the two robots move together along the interior of the disk to the exit B.

• 2. In the Wireless model (see right picture of Fig. 6) when the robot represented by the blank arrow, say, finds the exit at B it communicates to the robot represented by the bold arrow that it has found the exit and the latter robot moves to the exit B along the interior of the disk.

We can summarize the performance of the two algorithms in the following theorem.

Theorem 9

(Upper Bounds for 2 Robots, [17]). Consider two robots starting at the same time from the center of a unit disk.

• 1. (Wireless Model) There is an algorithm for evacuating two robots from an unknown exit located on the perimeter of the disk which takes time at most $1 + \frac{2\pi }{3}+ \sqrt{3} \approx 4.826$.

• 2. (F2F Model) There is an algorithm for evacuating the robots from an unknown exit located on the perimeter of the disk which takes time $1 + \alpha / 2+ 3 \sin (\alpha /2)$ where the angle $\alpha$ satisfies the equation $\cos (\alpha /2) = - 1/3$. It follows that the evacuation algorithm takes time ${\sim }5.74$.

Proof

For the proof below, we refer to the two pictures in Fig. 6 (left for the F2F and right for wireless model).

First we consider the F2F model. We calculate the time required until both robots reach the exit. Denote . The total time required is $g (\alpha ) = 1 + x + 2y$. Observe that $\alpha = 2x +y, \text { and } y = 2 \sin (\alpha /2)$, because y is a chord of the angle $\alpha$. Substituting x and y in the function f we can express the evacuation time as a function of the angle $\alpha$ as follows

$$\begin{aligned} g (\alpha )= & {} 1 + \frac{\alpha - y}{2} + 2y = 1 + \frac{\alpha }{2} + \frac{3y}{2} = 1 + \frac{\alpha }{2} + 3 \sin (\alpha /2) . \end{aligned}$$

Now we differentiate with respect to $\alpha$ and we obtain: $\frac{dg (\alpha )}{d \alpha } = \frac{1}{2} + \frac{3}{2} \cos (\alpha / 2).$ Set the derivative equal to 0 to find the maximum of the function $g (\alpha )$, which yields as value for $\alpha$ the solution of $\cos (\alpha /2) = -1 /3$. This completes the analysis for the F2F communication model.

Second we consider the Wireless model. We refer to Fig. 6. If the angular distance between A and B equals x, then the length of the chord taken by the robot $r_2$ equals to $c(x) = 2\sin (\pi - x)$. Thus the evacuation time T satisfies

$$ T \le \max _{0\le x \le \pi }\{1 + x + 2 \sin (\pi - x)\} = \max _{0\le x \le \pi }\{1 + x + 2 \sin x\} . $$

The function $h(x) = 1+x + 2 \sin x$ in the interval $[0,\pi ]$ is maximized at the point $x^* = 2\pi / 3$ and $h(x^*) = 1+ 2\pi /3 + \sqrt{3}$. This completes the analysis for the Wireless communication model.    $\square$

We also mention the lower bounds for two robots, but the proof is more technical and we refer the reader to [17] for additional details.

Theorem 10

(Lower Bounds for 2 Robots, [17]). Consider two robots starting at the same time from the center of a unit disk.

• 1. (Wireless Model) For any algorithm it takes at least $1 + \frac{2\pi }{3}+ \sqrt{3}$ ($\approx 4.826$) time in the worst case for two robots to evacuate from an unknown exit located in the perimeter of the disk.

• 2. (F2F Model) It takes at least $3 + \frac{\pi }{4} + \sqrt{2}$ ($\approx 5.199$) time units for two robots to evacuate from an unknown exit located in the perimeter of the disk.

Note that the bounds for the F2F communication model are not tight. Table 2 summarizes what is known and indicates the existing gap.

Table 2. Upper and lower bounds for the evacuation of 2 robots in the F2F communication model.

Evacuation for $\varvec{k \ge 3}$ Robots

It is apparent that the evacuation time improves by the collaboration of the robots. This is because a robot can share the search results of its exploration with the other robots in the group (using either F2F or Wireless communication). Therefore it is not surprising that the evacuation time should improve as the number of robots increases. This is in fact confirmed by the results as listed in Table 3.

Table 3. Upper and Lower bounds for $k\ge 3$ robots as proved in [17].

Nevertheless, it is much harder to obtain good bounds for the evacuation of any small number of robots, say three. For example, for three robots [17] gives upper and lower bounds for both the F2F and the wireless communication models, but they are not tight (see Table 3). The interested reader can find additional details for the case of $k=3$ robots in [17].

Fortunately, it is possible to obtain asymptotically tight bounds for evacuation as the number k of robots tends to infinity. The basic idea is for the robots to explore different parts of the perimeter and share with each other their search results. However the main difficulty is to ensure that when a robot finds (respectively, announces) the exit the rest of the robots are as close to it as possible. An outline of the algorithms are given below.

• 1. (F2F Model) The k robots “spread” at equal angles $2\pi /k$ and upon reaching the perimeter, they all move clockwise (along the perimeter) for $2 \pi /k$ time units. In one additional time unit, all robots move to the center of the disk. Since at least one robot has found the exit it can inform the remaining robots and in one additional time unit all robots move to the exit.

• 2. (Wireless Model) The k robots are divided into two groups: Group $G_{\alpha }$ of size $k_{\alpha }= \lceil k^{2/3} \rceil$, and Group $G_{\beta }$ of size $k_{\beta } = k-k_{\alpha }$. The robots in group $G_{\alpha }$ are assigned to “spread” and search a continuos arc 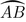of length of length $\pi - 2\sqrt{\pi } k^{-1/3}$, while the robots in group $G_{\beta }$ are assigned to “spread” and search the complement of arc . The robots explore specifically assigned subarcs of the arcs of length , respectively, and upon receiving a notification about the position of the discovered exit they all cut across a chord to the exit.

We can prove that the two algorithms above are asymptotically optimal in their respective communication model (see [17] for additional details).

Theorem 11

(F2F Model, [17]). It is possible to evacuate k robots from an unknown exit located on the perimeter of the disk in time $3 + \frac{2\pi }{k}$. It takes time at least $3 + \frac{2 \pi }{k} - O(k^{-2})$ in the worst case to evacuate k robots from an unknown exit located on the perimeter of the disk.

Theorem 12

(Wireless Model, [17]). If $k\ge 100$ then it is possible to evacuate k robots from an unknown exit located in the perimeter of the disk in time $3 + \frac{\pi }{k} + O(k^{-4/3})$. Moreover, it takes at least $3 + \frac{\pi }{k}$ time in the worst case to evacuate $k \ge 2$ robots from an unknown exit located on the perimeter of the disk.

3.2 Evacuating from Triangles and Squares

Two of the main requirements of the algorithms designed for evacuating robots from a disk were that the robots agree in advance on the search strategy they will follow and also have knowledge of the “shape” of the perimeter on which they need to search for the exit. The former was important so that robots can estimate each other’s position at any given time and the latter for traversing the perimeter. Further, any robot that finds the exit can take a “straight-line” short-cut through the interior of the disk so as to either meet another robots or go to the exit. These assumptions can be easily satisfied by any “convex” closed curve (e.g., triangles and squares as depicted in Fig. 7) though this will not necessarily make the optimization problem any simpler regardless of the communication model.

Fig. 7.

General setting of robot evacuation from equilateral triangles and squares. Robots start in general positions at the interior (or perimeter) and the exit is located on the perimeter of the triangle or square.

Model Specifics and Problem Definition

Throughout this section we assume the wireless communication model. Consider an equilateral triangle or square with sides of length 1. A number of robots starting at the same location on the perimeter or in the interior of the triangle or square are required to evacuate from an exit which is located at an unknown location on its perimeter. At any time the robots can move at identical speed equal to 1, and they can cooperate by communicating with each other wirelessly. Thus, if a robot finds the exit it can broadcast “exit found” to the remaining robots which then move in a straight line segment towards the exit to evacuate. Our task is to design robot trajectories that minimize the evacuation time of the robots, i.e., the time the last robot evacuates from the exit. Designing such optimal algorithms turns out to be a very intricate problem and even the case of equilateral triangles turns out to be challenging.

Evacuation Algorithm

Consider the case where the robots start at a point P on the perimeter of triangle ABC and at distance x from the midpoint of edge BC (see Fig. 8). Now consider the following algorithm. From the midpoint the robots move in opposite directions along the perimeter, i.e. Robot 1 towards vertex A via vertex B, and the other Robot 2 towards vertex A via vertex C. When a robot finds the exit it broadcasts “Exit found” to the other robot which immediately goes in a straight line segment to the exit. A similar approach is required when the two robots start together at an interior point of the triangle.

These algorithms are not difficult to analyze and we can prove the following theorems (details can be found in [25]).

Fig. 8.

Evacuating from an equilateral triangle. Left: the two robots start at a point P at distance x from the midpoint of edge BC. Right: the starting position of the two robots is in $\triangle AFD$. N, M, D are the midpoints of the corresponding sides.

Theorem 13

(Robots starting on the perimeter, [25]). Assume that two robots are initially located on the perimeter of an equilateral triangle at distance x from the closest midpoint of an edge of the triangle. Then $x + \frac{3}{2}$ is a tight bound for evacuating these two robots.

Theorem 14

(Robots start in the interior, [25]). Assume that two robots are initially located at point s inside the equilateral triangle, and let $x = \min \{d(s, m) \mid m \text { is a mid point of an edge} \}.$ Then $x + \frac{3}{2}$ is a tight bound for evacuating these two robots.

Similar techniques can be used to analyze evacuation in unit squares. To sum up the results obtained in [25] include the following.

• 1. Equilateral Triangle. Optimal evacuation trajectories (algorithms) for 2 robots and for any (same) starting position. 3 or more robots starting on the perimeter cannot achieve better evacuation time than two robots.

• 2. Square. Optimal evacuation trajectories (algorithms) for 2 robots for starting positions on the perimeter. 3 or more robots starting at one of the corners cannot achieve better evacuation time than 2 robots.

Additional results for more robots and more generally for regular polygons can be found in [25]. For evacuation from an equilaterla triangle in the F2F model see [16]. An interesting problem concerns evacuation on an ellipse or an arbitrary convex polygon.

3.3 Evacuation with Faulty Agents

Evacuating robots from the disk is a well studied problem, first introduced and studied in [17]. In particular when the communication model between robots is wireless, i.e. information can be shared between them instantaneously, nearly tight upper and lower bounds are known. Of course, in such a model what becomes particularly relevant is that information shared among agents is reliable. In contrast, operational algorithmic solutions need to be, in practice, robust against malfunctions. This translates to robots that either fail to report their findings, or even to misreports. The fundamental question that arises then is how is evacuation time affected in the presence of faulty robots. Note that the minimum number n of robots for which the problem is non degenerate is $n=3$, out of which 1 robot is faulty. This is the subject of study in [22].

Model Specifics and Problem Definition

$\textsc {FE}_{}$ is an evacuation problem whose search domain is the disk of radius 1. In this problem, 3 non-distinguishable robots (searchers) of maximum speed 1 start from the center of the disk, and they can communicate with each other their findings instantaneously, i.e. they operate under the wireless model. Somewhere on the perimeter of the disk lies a hidden object (exit) that can be identified only if a robot goes over it. Among the searchers there is distinct robot, thereafter referred as faulty. An evacuation algorithm is a search trajectory for all three robots, in which eventually all robots reach the hidden object. Given a placement of the hidden object, the cost of the search algorithm is the time till the last non-faulty robot reaches the hidden item. The evacuation time of the algorithm is defined as the worst case cost of the algorithm.

Clearly, given a search algorithm, and in the spirit of worst case analysis, the adversary controls not only where the hidden object is placed, but also which of the searchers is faulty. In the same direction, the adversary also controls the actions of the faulty robot, and therefore one needs to determine the limitations of such adversarial choices. In the crash-faulty model, the faulty robot may only fail to report that the hidden object is found, whereas in the byzantine-faulty model, the faulty robot may misreport at any moment its findings. We denote the two evacuation problems in the corresponding faulty models as $\textsc {FE}_{c}$ and $\textsc {FE}_{b}$, respectively.

Disk Evacuation Against Crash Faults

The advantage of trying to evacuate 3 robots in the crash-fault model is that once the location of the hidden object is reported, the remaining non-faulty robot may abandon searching and move toward the exit along a shortest (line segment) path. Maybe the simplest family of algorithms one may consider first is a symmetric-type, in which robots partition the circle in three contiguous arcs. The robots deploy to the endpoints of these arcs, and start searching in the same direction, each of them its own contiguous arc till the exit is found (reported). It is not hard to prove that the best algorithm of this family deploys the searchers in equidistant points, i.e. the three arcs are of length $2\pi /3$ each, and the induced evacuation time is $1+4\pi /3+\sqrt{3}$.

One of the main contributions of [22] is to show how a non-symmetric algorithm can evacuate the two non-faulty robots efficiently. Practically, one may again define a family of, non-symmetric evacuation trajectories this time, as follows. Fix parameter $\beta$. Two robots deploy to an arbitrary point of the disk, with the intension to explore in opposite directions. The third robot is deployed to a point of the disk at arc distance $\beta$ from the deployment point of the other robots, with the intention to explore toward the closest robot (and hence in opposite direction than that robot), see Fig. 9.

Fig. 9.

The deployment of the three robots, and their initial direction of movements for the algorithm the shows the upper bound of Theorem 15

Consider now the following two adversarial choices. First, the two non-fault robots are those at arc distance $\beta$ moving toward each other. Assuming that $\beta \le 4\pi /3$ one can show that the worst placement of the exit is at time $2\pi /3$, after they search their in-between arc segment (this is because the maximizer of function $x+2\sin \left( {x/2}\right)$ is attained at $x=2\pi /3$) inducing cost $1+\beta /2+2\pi /3+\sqrt{3}$. Second, assume that the non-faulty robots are those moving in the same direction. It is easy to see that the worst placement of the exit makes the non-faulty robots search the perimeter for $2\pi -\beta$, which maintain throughout the exploration arc distance $\beta$ (hence the last robot needs additional time $2\sin \left( {\beta /2}\right)$ to reach the exit). Overall, this second case induces worst evacuation time $1+2\pi -\beta + 2\sin \left( {\beta }\right)$. The best algorithm known for $\textsc {FE}_{c}$ is exactly the one above that uses as $\beta$ the value that equates the evacuation costs in the aforementioned adversarial inputs.

Theorem 15

([17]). Let $\beta _0$ be the solution to equation $3\beta _0/2-2\sin \left( {\beta _0/2}\right) =4\pi /3-\sqrt{3}$, where $\beta _0 \approx 2.966$. Then $\textsc {FE}_{c}$ admits solution with evacuation time at most $1+\beta _0/2+2\pi /3+\sqrt{3}\approx 6.309$.

Disk Evacuation Against Byzantine Faults

The best performance achieved for $\textsc {FE}_{c}$ with symmetric algorithms turns out to be the best performance known for $\textsc {FE}_{b}$, but remarkably with a different type of algorithm. The inherent difference in the byzantine-fault model is that once the exit is reported, it firsts needs to be confirmed as a reliable message before the non faulty robot attempts to reach it, as otherwise performance would be suboptimal. Indeed, evacuating in the presence of a byzantine faulty robot who may misreport her findings, all robots are asked to first explore, in the same direction, a contiguous arc segment of length $2\pi /3$. Depending on the report(s) that have been circulated, robots have information to either go to the exit or continue searching the circle for additional time $\frac{2\pi }{3}$. The fact that each point is searched twice, allows them to resolve any conflicts and deduce the real location of the exit. This idea gives rise to the following upper bound.

Theorem 16

([17]). $\textsc {FE}_{b}$ admits solution with evacuation time at most $1+4\pi /3+\sqrt{3}\approx 6.92$.

A Unified Lower Bound Argument

As it is common in lower bounds arguments, in order to show negative results for $\textsc {FE}_{}$, one has to identify special time moments in which, independently of the algorithm considered, certain points in the search domain have not all been explored by non-faulty robots. Specifically for $\textsc {FE}_{}$, the following predicate $P(\cdot )$, given any evacuation algorithm, plays a crucial role in the lower bound argument.

P(T): At time T, there are two critical points on the circle at arc distance $2\pi /3$, and none of them is visited more than once by any of the three searchers.

One of the main technical contributions in [22] was to prove that $P\left( 1+ \frac{13}{7}\sqrt{3}\right)$ is true. Now in $\textsc {FE}_{b}$, there must be a robot that has visited none of the two critical points. The adversary can chose that robot to be non-faulty, and clearly that robot requires extra at least $\sqrt{3}/2$ to reach any of them. For $\textsc {FE}_{b}$, the adversary has more power to mislead non-faulty robots, and in fact can call a potentially misreport of the exit. Independently of the performance of the evacuation algorithm, it is shown that the non-faulty robot must be at least $2\pi /3$ away from the true location of the exit, inducing extra cost $2\sin \left( {2\pi /3}\right) =\sqrt{3}$. Overall, the results of the lower bound arguments are summarized below.

Theorem 17

([17]). Let $T_0 = 1+ \frac{13}{7}\sqrt{3}$. Then no algorithm can solve $\textsc {FE}_{c}$ with evacuation time less than $T_0 + \sqrt{3}/2 \approx 5.082$. Also, no algorithm can solve $\textsc {FE}_{b}$ with evacuation time less than $T_0 + \sqrt{3}\approx 5.948$.

4 Multiple Targets on a Circle

Evacuation type problems emerged by requiring collections of robots to identify the location of a hidden item, and to reach it as fast as possible. It is natural to also assume variations in which there may be more than one objects hidden in the domain, and search termination to be defined as the latest time in which the last robot reaches any of the hidden objects. From a practical perspective, the hidden objects can be thought as available exits that are placed in the underlying domain in which searchers collectively try to reach any of them (and evacuate) efficiently, possibly using as partial information the relative distance of the exits, but not their locations. The main reference work for this model with multiple exits described above is [21].

Model Specifics and Problem Definition

$\textsc {FE}_{k}$ is an evacuation problem whose search domain is the circle of perimeter 1 (i.e. of radius $1/2\pi$). In this problem, k hidden and identical (non distinuishable) objects (exits) are located on the circle. The relative distance between the hidden items is known, thereafter referred as the map, but not their locations. Two identical robots are placed at arc distance L on the circle, they can move at speed 1, and they can see each other. They can see any of the hidden object only if they are collocated with the object, and they can communicate wirelessly and instantaneously their findings. Their goal is that each of them reaches any of the hidden objects (exits). The evacuation time is defined as the worst case time of the last robot to reach an(y) exit.

There are two variations of the problem, where the initial placement (relative distance) L of the robots is either part of the input, or is the subject of an algorithmic choice based on the provided map. In both variations, the goal is to design trajectories for the two searchers on the circle so as to minimize their evacuation time.

Multiple Exit Evacuation with Given Robot Placement

Maybe the simplest case of all is the one when the map contains only one exit. The two robots start at known arc distance L, and they try to minimize the time that the last robot reaches the exit. It is convenient for the moment to think that the two robots are co-located. Very naturally the robots should start exploring in opposite directions till the exits is found, say at time $x\le \frac{1}{2}$. Then, the other robot is notified, and can evacuate choosing the shortest route (along the circle) of length $\min \{2x,1-2x\}$. Given that the adversary controls the location of the exit, that would induce worst case performance

$$ \max _{x\in [0,1/2]}\left\{ x+\min \{2x,1-2x\} \right\} = 3/4. $$

If on the other hand the robots are at distance L, then it is natural to first have them explore the arc between them, taking time L / 2, and then running the previous algorithm of extra cost 3 / 4. It turns out that this simple idea is also optimal.

Theorem 18

([21]). When the initial arc distance $L\in [0,1/2]$ of the two robots is part of the input, $\textsc {EME}_{1}$ can be solved with evacuation time $\frac{3}{4} + \frac{1}{2}L$. Moreover this is optimal.

$\textsc {EME}_{k}$ becomes more interesting for $k\ge 2$. Since exits are not distinguishable, one needs to identify the critical information that can be deduced from every map. Given an instance of $\textsc {EME}_{k}$, e.g. a map for the placement of k exits, the critical parameter that can be utilized algorithmically turns out to be longest arc length of the circle that does not strictly contain any exit. This can be also thought as a pessimistic estimation for the distance of a hidden item from the location of an exit currently found (and reported). A map in which the longest arc not strictly containing an exit has length D will be called a map with critical value D, see also Fig. 10 for an example of an $\textsc {EME}_{k}$ instance. Note that by definition, any map of $\textsc {EME}_{k}$ has critical value $D\in [1/k,1]$.

Fig. 10.

An instance of $\textsc {EME}_{3}$. Robots placements are depicted with circles R, and exit placements are depicted by squares E.

Theorem 19

([21]). When the initial arc distance $L\in [0,1/2]$ of the two robots is part of the input, a map of $\textsc {EME}_{k}$ with critical distance D can be evacuated in time

$$ \frac{3}{4}D+\frac{1}{2}L. $$

Moreover no algorithm can have evacuation time better than $\frac{3}{4}D-\frac{1}{2}L$.

The upper bound for Theorem 19 is due to an algorithm similar to the optimal algorithm for $\textsc {EME}_{1}$. Indeed, when there is only 1 exit, the critical value of the map is $D=1$, whereas for general critical value $D\in [1/k,1]$, each of the two robots performs, in the worst case, within an arc of length D, which is similar to performing on a circle of perimeter D. Nevertheless this argument is not strong enough to derive a matching upper and lower bound. In contrast, when all consecutive exits are equidistant, we do know the best possible evacuation time.

Theorem 20

([21]). When the initial arc distance $L\in [0,1/2]$ of the two robots is part of the input, a map of $\textsc {EME}_{k}$ with critical distance $D=1/k$ can be evacuated it time $\frac{3}{4}D+\frac{1}{2}\lambda ,$ where

$$ \lambda = \left\{ \begin{array}{lr} L \bmod \frac{1}{k}, &{} \text {if } L \bmod \frac{1}{k} \le \frac{1}{2k}\\ \frac{1}{k} - L \bmod \frac{1}{k}, &{} \text {if } L \bmod \frac{1}{k} > \frac{1}{2k} \end{array} \right. $$

Moreover this performance is optimal.

The heart of the argument for proving Theorem 20 relies on the idea of reducing $\textsc {EME}_{k}$ on the circle of perimeter 1 to $\textsc {EME}_{1}$ on a circle of perimeter 1 / k (which is possible due to that all consecutive exits are equispaced). The fact that evacuation performance is non-monotonic has to do with the initial distance of the robots. When the circle is partitioned in arcs of length 1 / k, their original distance L evaluated $\bmod 1/k$ can be either larger or smaller than 1 / 2k. If $\lambda _0=L\bmod 1/k \le 1/2k$, then the problem is equivalent to $\textsc {EME}_{1}$ on the circle of perimeter 1 / k, with initial robots distance $\lambda _0$. Otherwise, the distance of the two robots in the new instance is $1/k-\lambda _0$.

Multiple Exit Evacuation with Chosen Robot Placement

Evacuation problem $\textsc {EME}_{k}$, when the initial relative distance L of the robots can be chosen as a function of the given map of critical value D, i.e. when we allow $L=L(D)$, requires a more elaborate analysis. At a high level, given initial distance L of the robots, optimal, or near-optimal evacuation trajectories are known. For these trajectories, an adversary can choose when the first exit is found, say at time $x \le \frac{1}{2} - \frac{1}{2}L$. If the induced evacuation cost is denoted by g(D, L, x), then the evacuation cost of the algorithm is given by $\max _{x\in [0,\frac{1}{2} - \frac{1}{2}L]}\left\{ g(D,L,x) \right\}$. If in addition we allow the algorithm to pick $L=L(D)$, then one has to solve optimization problem

$$\min _{L\in [0,1/2]}\max _{x\in [0,\frac{1}{2} - \frac{1}{2}L]}\left\{ g(D,L,x) \right\} $$

in order to determine the best possible evacuation algorithm. This is exactly what the next theorem describes.

Theorem 21

([21]). When the initial arc distance $L\in [0,1/2]$ of the two robots can be chosen algorithmically based on a map of $\textsc {EME}_{k}$ with critical distance $D\in [1/k,1]$, there is an evacuation algorithm with cost at most

$$ \left\{ \begin{array}{lll} \frac{3}{4}D, &{} \text {if } D\in [1/k,4/5), &{} \text {achieved for } L=0\\ 1-\frac{1}{2}D, &{} \text {if } D\in [4/5,6/7) &{}\text {achieved for } L=\frac{5}{2}D-2\\ \frac{5}{4}D-\frac{1}{2}, &{} \text {if } D\in [6/7,1], &{}\text {achieved for } L=1-D . \end{array} \right. $$

5 Search and Fetch

Search and Fetch type problems are common in search-and-rescue operations where a hidden object (a victim) not only has to be located, but also has to be carried (fetched) to a designated spot. From a theoretical perspective, which is the focus of the current work, such problems fall under the generic evacuation type problems, where evacuation has to be accomplished only by a subset of the involved objects/mobile agents, hence delivering a combinatorial flavor to the problem. An attempt to model and study such search and fetch problems on the plane with 1 and 2 mobile agents appeared first in [28] and [27], respectively.

Model Specifics and Problem Definition

$\textsc {TE}_{\alpha }^{n}$ is an evacuation-type problem whose domain is the unit disk. In this problem, $n\in \{1,2\}$ mobile agents start from the center of the disk and can move at maximum speed 1 anywhere on the plane. Two hidden objects, a treasure T and an exit E, reside on the perimeter of the disk at known arc distance $\alpha$. E is immobile, while T can be moved by any mobile agent. Any of the hidden objects can be located only by a robot that walks over it.

An evacuation algorithm for $\textsc {TE}_{\alpha }^{n}$ is composed by the trajectory for each of the n robots which guarantees that T reaches E in a finite amount of time. For any placement of the objects (at known arc distance $\alpha$), the completion time is defined as the time it takes T to reach E, i.e. the time to evacuate T. The completion (evacuation) time for an evacuation algorithm for $\textsc {TE}_{\alpha }^{n}$ is the worst case evacuation time over all placements of hidden objects T, E. Finally, the evacuation time of $\textsc {TE}_{\alpha }^{n}$ is the minimum completion time over all evacuation algorithms.

Relevant Literature

$\textsc {TE}_{\alpha }^{1}$ is closely related to search-type problems that involve a searcher and a hider in numerous variants for which the literature is vast [3, 4]. Evacuation-type problems similar to $\textsc {TE}_{\alpha }^{2}$ in which the model of computation between the robots becomes relevant but without the fetching/combinatorial component, have been studied is a series of papers [13, 17, 20, 21, 25, 32]. From a practical perspective, search-and-rescue problems have been studied since the late 90’s by the robotics community, e.g. see [29], and extensively by the operations research community, e.g., see [15]. Maybe the most similar problem to $\textsc {TE}_{\alpha }^{n}$ studied before is the one introduced by Alpern in [2], where the domain was discrete (a tree), and the goal of the rescuer was to fetch a treasure hidden in a leaf back to the root of the tree.

Model Motivation

The underlying model of $\textsc {TE}_{\alpha }^{n}$ is admittedly simplistic, yet its’ importance is fivefold.

First, as it will be clear in the remaining of the section, solving optimally either $\textsc {TE}_{\alpha }^{1}$, $\textsc {TE}_{\alpha }^{2}$ seems a particularly challenging task. Moreover any upper or lower bounds for $\textsc {TE}_{\alpha }^{1}$, $\textsc {TE}_{\alpha }^{2}$ require non-trivial and sometimes technical arguments. Together with the fact the known upper and lower bounds are far from being matched, solving $\textsc {TE}_{\alpha }^{n}$ qualifies as a challenging mathematical puzzle.

Second, $\textsc {TE}_{\alpha }^{n}$ is by definition an online problem where an algorithm is asked to perform well against an unknown input (here the position of the hidden objects). A fundamental subject of theoretical computer science is exactly to study the boundaries of computational capabilities given limited resources, and for $\textsc {TE}_{\alpha }^{n}$ that would be the knowledge of the input. In that direction, $\textsc {TE}_{\alpha }^{n}$ proposes a compromise between no information and full information about the input. From an algorithmic perspective, $\textsc {TE}_{\alpha }^{n}$ asks the fascinating question of utilizing the partial information available about the input (the distance between the two hidden objects) in order to improve upon an algorithm with no information about the input.

Third, $\textsc {TE}_{\alpha }^{n}$ is maybe the first attempt to inject a combinatorial flavour to evacuation type problems. This far, evacuation problems treated robots equivalently, meaning that completion time was oblivious to robot’s identities. In contrast, $\textsc {TE}_{\alpha }^{n}$ requires a specific immobile robot, the treasure, to be fetched to a hidden exit, and specifically it poses no constraints to the facilitators (other robots) which try to expedite the evacuation of the treasure. Only very recently, two more papers studied evacuation problems with similar combinatorial-type requirements [18, 19].

Fourth, and when $n\ge 2$, $\textsc {TE}_{\alpha }^{n}$ emphasizes the relevance of the communication protocol between robots in search-and-rescue operations. Indeed, when access to information is overall restricted in online problems, i.e. no information about hidden objects is available, search protocols where robots are allowed to communicate wirelessly are expected to outperform search protocols where robots can exchange information only by meeting (face-to-face model). In contrast, when partial information becomes available, in our case the distance between the hidden objects, a face-to-face algorithm is better equipped against the uncertainty that even wireless algorithms face, allowing possibly for solutions whose costs do not differ by much in the two communication models.

Fifth, the domain of $\textsc {TE}_{\alpha }^{n}$ as well as robots specifications follow closely model specifications of fundamental problems in search theory and rendezvous, and as such $\textsc {TE}_{\alpha }^{n}$ proposes a natural extension of them. Since all of these problems intend to introduce fundamental search/algorithmic techniques with applicability to real life search-and-rescue operations, $\textsc {TE}_{\alpha }^{n}$ in particular becomes relevant when rescuers performance is quantified not by their evacuation time, rather by the evacuation time of the victim they are trying to save.

5.1 Searching with One Robot

Search and fetch with one robot, i.e. $\textsc {TE}_{\alpha }^{1}$, has been studied in two variations depending on the precise knowledge regarding the location of the two hidden objects. In one of them, a bound $\alpha$ is known for the exact distance of the objects, while in the other, $\alpha$ is guaranteed to be the distance of the objects. Clearly, the first variation gives rise to an optimal completion time which at least as costly than the one of the second variation. However, somehow surprisingly, providing an optimal algorithm for the first variation is a relatively easy task, compared to the other variation where a similar result is still eluding.

Knowledge of a Bound of the Critical Distance

Consider the variation of $\textsc {TE}_{\alpha }^{1}$ where the online algorithm has access to a lower bound $\alpha$ of the actual distance $\ell$ of the two hidden objects, i.e. $\ell \ge \alpha$. In other words, one tries to minimize the worst case completion time of fetching the treasure T to the exit E, assuming that the arc-distance between T, E is at least $\alpha$. We denote this variant as $\textsc {TE}_{\ge \alpha }^{1}$.

Theorem 22

([28]). An instance of $\textsc {TE}_{\ge \alpha }^{1}$ where T, E are at arc distance $\ell \ge \alpha$ can be solved with worst case completion time $1+2\pi -\alpha +2\sin \left( {\alpha /2}\right) +2\sin \left( {\ell /2}\right)$, and this is optimal.

Notice that the description of a treasure evacuation algorithm concerns only the part of the execution till the locations of both objects are identified. Then, robot(s) may fetch the treasure to the exit in an optimal way, given objects’ and robot’s locations. The algorithm that proves the upper bound of Theorem 22 utilizes nicely the key component to all evacuation protocols for all $\textsc {TE}_{\alpha }^{n}$, and concerns an “arc-avoidance” step during the exploration phase of the algorithm. Indeed, assume that a robot explores the perimeter of the disk, searching still for the first hidden object, and assume that already an arc of length at least $\alpha$ has been explored. Once the first hidden item is located, the other has to be arc-distance at least $\alpha$ away. Therefore cross-cutting along the corresponding chord of length $2\sin \left( {\alpha /2}\right)$ induces total savings of $\alpha -2\sin \left( {\alpha /2}\right)$. Note that such a move is beneficial independently of whether the first item found is the treasure or the exit. From an adversarial perspective, the first item to be found has to be the exit, so that an extra $2\sin \left( {\ell /2}\right)$ is required for the fetching phase, as well as the two hidden items are to be located (in the worst case) as late in the time horizon as possible. Overall, this explains why the worst case evacuation time of the following algorithm is indeed $1+2\pi -\alpha +2\sin \left( {\alpha /2}\right) +2\sin \left( {\ell /2}\right)$.

The lower bound of Theorem 22 is based on a simple observation regarding any evacuation algorithm. If a robot has explored less than $2 \pi - \alpha$ of the perimeter of the disk, then there is a chord of length at least $2 \sin (\alpha /2)$ (say of corresponding arc length $\ell$) neither of whose endpoints has been visited by the robot. Therefore, any adversary could let any algorithm run for $1+2\pi -\alpha -\epsilon$, before she fixes the locations of the two hidden points, and she can do that by making the first explored point to be the exit.

Knowledge of the Exact Critical Distance

Now we turn our attention to the variant of $\textsc {TE}_{\alpha }^{1}$, denoted as $\textsc {TE}_{=\alpha }^{1}$, in which the two hidden items are exactly at arc distance $\alpha$, and $\alpha$ is known. Notably, Algorithm 1 is still applicable, and it is no surprise that Theorem 22 predicts its worst case performance to be equal to $1+2\pi -\alpha +4\sin \left( {\alpha /2}\right)$. With some technical work, one can improve upon the previous upper bound.

The main idea behind the best algorithm known for $\textsc {TE}_{=\alpha }^{1}$ relies on the partition of the search space, i.e. the perimeter of the disk, into contiguous segments that will be searched, and others that can be “skipped”. Indeed, fix some $\alpha$, and consider a robot having searched an arc of length $a_1\ge \alpha$. If any of the hidden items lies within $b_1\le \alpha$ arc distance from the robot, then the location of the other hidden item can be deduced. Hence, the robot has an incentive to move along the chord of length $2\sin \left( {b_1}\right)$ (without ever missing both hidden items), and continue searching a new arc. If the latter has length $b_2\ge \alpha$, then the previous argument applies again.

Consider now a partition of the disk into arc of length $a_1, b_1, \ldots , a_n, b_n,a_{n+1}$, such that $b_i \le \alpha \le a_i$. A robot can search each of the arcs of length $a_i$, following a “jump” along the chords of length $2\sin \left( {b_i}\right)$, till one of the hidden items is found. Call the search strategy associated with such a partition greedy. If the first hidden item is found by the greedy algorithm while searching arc $a_i, i\le n$, then the robot may have to check two locations for the second hidden object. However, any jump saves locally time $b_i - 2\sin \left( {b_i/2}\right) >0$, as long as $b_i>0$. Moreover, $b_i - 2\sin \left( {b_i/2}\right)$ is monotone in $b_i$, hence it is intuitive that one should choose a partition of the disk that induces as much savings as possible. In that direction, it is natural to pack as many maximal jumps as possible of length $b_i=\alpha$, making sure that if a hidden object is found in the last arc to be searched, then the other object location is deduced from the searched space. Omitting several technicalities, one can show that the number $n_\alpha$ of such jumps must be equal to

$$ n_\alpha :=\left\lfloor \frac{2\pi -3\alpha -2\sin \left( {\alpha }\right) }{2\alpha } \right\rfloor $$

giving rise to the following positive result.

Theorem 23

([28]). For an instance of $\textsc {TE}_{=\alpha }^{1}$, consider a greedy search algorithm using disk partition $a_1, b_1, a_2, b_2, \ldots , a_{n_\alpha }, b_{n_\alpha },a_{n_{\alpha }+1}$. If $n_\alpha < \frac{\pi -\sin \left( {\alpha }\right) }{\alpha }-2$, then the worst evacuation time of the algorithm is

$$ 2\pi -(n_\alpha +2)\alpha +2(n_\alpha +3)\sin \left( {\alpha /2}\right) $$

and otherwise, the worst evacuation time is

$$ (n_{\alpha }+2)\alpha +2(n_{\alpha }+2) \sin \left( {\alpha /2}\right) + 2\sin \left( {\frac{2n_{\alpha }+3}{2}\alpha +\sin \alpha }\right) +2\sin \alpha $$

Moreover the analysis it tight.

Although it is conjectured that the above upper bound is the best possible, a tight lower bound is still eluding. At the same time, a non trivial lower bound can be obtained by consider a “weaker” adversary that is restricted to choose the locations of the two hidden items after a search algorithm has left only one contiguous unexplored arc of length $\alpha$. Given such a restricted adversary, it is not difficult to show that the most efficient algorithms must be greedy, hence, their trajectories must be determined by a sequence of non-negative reals $a_1, b_1, a_2, b_2, \ldots , a_{l-1}, b_{l-1},a_{l}$ for some integer $l\ge 1$, with $b_i \le \alpha$. Placing the two hidden objects at the very end of the search (where the first item found is the exit) induces cost $1+\sum _{i=1}^l a_i + \sum _{i=1}^{l-1} 2 \sin (b_i/2)+4\sin (\alpha /2)$. Hence, the values of the following family of Non-Linear Programs gives a lower bound for the best evacuation time for $\textsc {TE}_{=\alpha }^{1}$

$$\begin{aligned} \mathbf{minimize}&\quad 1+\sum _{i=1}^l a_i + \sum _{i=1}^{l-1} 2 \sin (b_i/2)+4\sin (\alpha /2) \\ \mathbf{subject \ to }&\quad \sum _{i=1}^l a_i + \sum _{i=1}^l b_i = 2 \pi \\&\quad b_i \le \alpha \text { for } i=1,2,\ldots , l \\&\quad a_i, b_i \ge 0 \text { for } i=1,2,\ldots , l \end{aligned}$$

Some technical work is required to obtain the maximum value of the optimization problems above (over all intefers $l\ge 1$), resulting in the following theorem.

Theorem 24

([28]). No algorithm for $\textsc {TE}_{=\alpha }^{1}$ has evacuation time better than

$$ 1+ \pi + \min \left\{ \begin{array}{l} 4\sin \frac{\alpha }{2}+2\left( \left\lceil \frac{\pi }{\alpha }\right\rceil -1\right) \sin \frac{\pi -\alpha }{2\left( \left\lceil \frac{\pi }{\alpha }\right\rceil -1\right) }, \\ \pi -\alpha \left\lfloor \frac{\pi }{\alpha }\right\rfloor +2\left( \left\lfloor \frac{\pi }{\alpha }\right\rfloor +1\right) \sin \frac{\alpha }{2} \end{array} \right\} $$

5.2 Searching with Two Robots

Known results for $\textsc {TE}_{\alpha }^{1}$ indicate that optimal trajectories for $\textsc {TE}_{\alpha }^{2}$ must employ complicated trajectories for the two robots using alternating arcs of the disk that are to be searched and skipped. Such complications seem unnecessary, given that efficient algorithms for $\textsc {TE}_{\alpha }^{2}$ are far from being plain-vanilla type, especially in the face-to-face model. Indeed, the work in [27] indicates that even if one considers a special family of search algorithms in which robots do not abandon searching before at least one hidden item is found, efficient search trajectories do require ingenuity.

Upper Bound in the Wireless Model

It is worthwhile investigating a simple-minded algorithm for $\textsc {TE}_{\alpha }^{2}$, demonstrating the need for algorithms that are adaptive in $\alpha$, especially given that in the wireless model, robots share information instantaneously.

Indeed, consider an algorithm, thereafter referred as $\mathcal {A}_1^w$, that deploys two robots in an arbitrary point on the disk, and robots start searching in opposite directions till the first hidden object is found, after time, say, x. Due to the communication model, robots can coordinate in order to explore all possible locations of the second hidden object, fetching the treasure to the exit in an optimal way (from the time that both objects have been found).

It turns out that $\mathcal {A}_1^w$ performs well when $\alpha$ is not too big, and indeed, one can show that the worst case evacuation time is at most $1+\pi -\alpha +4\sin \left( {\alpha /2}\right)$, as long as $\alpha \le 2\pi /3$. Performance analysis is based on case analysis as to where the hidden objects are placed. It is not difficult to see that one of the worst input configurations occur when the first object found is the exit, say after time x, see Fig. 11. If $2x\le \alpha$, there is still uncertainty as to where the treasure is, even though it must be at distance $2\sin \left( {\alpha /2}\right)$ from the found object. The two robots can search independently the two candidate locations, and as long as x is not too big, the exit founder reaches the actual location of the treasure after the other robot, overall inducing cost at least

$$1+\alpha /2-\arcsin \left( \sin \left( {\alpha /2}\right) -\sin \left( {\alpha }\right) \right) +4\sin \left( {\alpha /2}\right) ,$$

which provably exceeds the bound of $1+\pi -\alpha +4\sin \left( {\alpha /2}\right)$ for large enough $\alpha$.

Fig. 11.

An example of robots’ trajectories in which the first interesting point found is the exit, depicted with the square E. At distance $\delta =2\sin \left( {\alpha /2}\right)$ is the other interesting point. The actual location of the treasure is depicted with the square T and it’s other possible location by the square?

To circumvent the poor behavior of $\mathcal {A}_1^w$, we employ another search strategy, that we call $\mathcal {A}_2^w$. In this algorithm, robots deploy in two antipodal points of the disk, and search the perimeter in the same direction till the first hidden item is found, say at time x. In this case, uncertainty about the location of the second item occurs when $x\le \alpha$ and when $\pi -x \le \alpha$, and hence the algorithm can deduce the location of both items in more cases, when $\alpha$ is large enough. In fact, one can show that if $\alpha \ge 2\pi /3$, then the worst evacuation time of $\mathcal {A}_2^w$ is at most $1+\pi -\alpha +4\sin \left( {\alpha /2}\right)$. Overall, we have algorithms $\mathcal {A}_1^w, \mathcal {A}_2^w$, each achieving the same upper bound (as a function of $\alpha$) for complementary values of $\alpha$ concluding the following theorem.

Theorem 25

([27]). $\textsc {TE}_{\alpha }^{2}$ admits a solution in the wireless model with evacuation time $1+\pi -\alpha +4\sin \left( {\alpha /2}\right)$.

Upper Bound in the Face-to-Face Model

The optimal strategy known in the wireless model for $\textsc {TE}_{\alpha }^{2}$ indicates that strategies adaptive to the value of $\alpha$ are necessary in order to achieve efficient evacuation times. Such strategies become more relevant in the face-to-face model where information cannot be shared by the searchers from distance.

In order to circumvent the lack of communication, it is no surprise that efficient algorithms for $\textsc {TE}_{\alpha }^{2}$ in the face-to-face model need to adapt not only with $\alpha$, but as well as with the timing of certain findings. For example, it is natural to aim for search strategies that change behavior as a function of when the first hidden object is found, and of the type of the hidden object. Especially challenging seems that task of having the robots coordinate their trajectories from distance, given that any findings cannot be shared unless the searchers meet. Nevertheless, robots may be able to indirectly exchange information from distance given that they have agreed in advance to meet in predetermined locations assuming certain configurations have been encountered by the robots. If the meeting is realized, then clearly robots exchange information regarding their findings. Similarly, if the meeting is not realized, robots may preclude certain configurations, hence deducing information about the topology of hidden objects indirectly. Of course the challenge with such an approach is (a) to coordinate the robots properly and independently of the encountered configurations, and (b) to achieve the same upper bound for all possible placements of the hidden objects.

In this direction, [27] invented various search strategies in the face-to-face model, each of them performing well for different values of $\alpha$, achieving the following result.

Theorem 26

([27]). $\textsc {TE}_{\alpha }^{2}$ admits a solution in the face-to-face model with evacuation time $1+\pi -\alpha /2+3\sin \left( {\alpha /2}\right)$.

There are three different search algorithms $\mathcal {A}_1^f, \mathcal {A}_2^f, \mathcal {A}_3^f$, that need to be employed in order to achieve the bound of Theorem 26, which we briefly outline next. All of them, deploy both robots to an arbitrary point of the disk, and have them start exploring in opposite directions till the first hidden object is found, and the algorithms are distinguished with respect to what happens next. Figure 12 depicts possible executions of the three algorithms.

Fig. 12.

Possible executions of algorithms $\mathcal {A}_1^f, \mathcal {A}_2^f, \mathcal {A}_3^f$. On the left, the first robot that finds an interesting point, depicted with square I, tries one of the possible locations of the other interesting point. In the middle, the founder of the first interesting point which is the treasure, goes to the center of the circle, and waits till it collects enough information as to where the exit is (possible trajectories depicted with dotted arrows). On the right, the founder of the treasure follows a special chord specified by points A, B, C, D (described in the definition of $\mathcal {A}_3^f$ below) only up to a total length y. Thereafter, there are two possibilities of movements depicted with the dotted arrows, and that depend on the information the robot will have collected about the location of the exit.

In $\mathcal {A}_1^f$, each robot greedily tries to find locations of the hidden items, and the treasure founder fetches the treasure to the exit without attempting coordination (or any exchange of information via a coordinated meeting) as if there was only one searcher. Some technical analysis shows that this algorithm works well (see Theorem 26) as long as $\alpha$ is not large enough.

$\mathcal {A}_2^f$ is employed either when $\alpha$ is between two critical values, and the treasure is found within a carefully predetermined time window. In this case, the treasure founder goes to the center of the disk, and waits for as long as it would take the other robot to find the exit in a candidate location and come to notify the treasure holder. No matter whether the meeting is realized or not, the treasure holder deduces the location of the exit, and fetches it inducing worst case evacuation time equal to the one promised by Theorem 26.

Finally, $\mathcal {A}_3^f$ is employed in all other cases and utilizes the most involved trajectories and is based, at a high level, on the following idea. Suppose a hidden object is located at point A, and that object is the treasure. If there is uncertainty about the location of the exit, then this must be at arc distance $\alpha$ either cw or ccw, forming an imaginary triangle ABC. What would induce a bad performance is the treasure holder to check points B, C alone. Instead, the treasure founder can utilize her knowledge that her peer robot is searching one of the arcs AB or AC, and the length of these arcs is known since robots started exploring the disk from the same point. So say that arc is AB. Had the other robot found the exit at point B, that would induce for her another triangle ABD with the possible locations of the second hidden object. In fact, $\mathcal {A}_3^f$ instructs such a robot to check point D for the object, and if failed to start moving toward point A to notify the treasure founder. Hence, the treasure founder has an incentive, instead of checking her candidate points B, C to first start moving toward point D, just in case the other robot has already encountered the other hidden object. No matter whether the meeting is realized, the treasure holder would be able to deduce the location of the exit, fetching to it the treasure efficiently.

Lower Bounds for

The only lower bound known for $\textsc {TE}_{\alpha }^{2}$ is for the face-to-face model and relies on an adversary that waits for the two robots to explore the disk until there are three points A, B, C on the disk, where arcs AB, BC are both of length $\alpha$ and at most one of the points A, B, C has been visited. One can argue that this has to take every algorithm time at least $1+\pi /3$. Now depending on the value of $\alpha$, an adversary can fix the locations of the two hidden items in the other two locations, inducing different worst case evacuation times that are summarized in the next theorem.

Theorem 27

([27]). No face-to-face search algorithm can solve $\textsc {TE}_{\alpha }^{2}$ with evacuation time less than

$$ 1+\pi /3+2\sin \left( {\alpha /2}\right) + \left\{ \begin{array}{ll} 2\sin \left( {\alpha /2}\right) , &{} if \ 0\le \alpha \le 2\pi /3\\ 2\sin \left( {\alpha }\right) , &{} o.w. \end{array} \right. $$

6 Conclusion

Search has always been an inexhaustible source of challenging mathematical optimization problems. In this paper a brief survey has been provided of recent developments in group search and evacuation in linear and circular search domains. The paper is no doubt biased in favor of recent work by the authors and their collaborators. Also note that the survey is not meant to be exhaustive but rather provide the reader with the flavor of some of the recent, challenging and exciting questions on this topic.