Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

Introduction

This chapter addresses the use of technology in the assessment of mathematics. Using technology calls for new emphases in the learning of mathematics and the goals of the curriculum which, in turn, require different kinds of assessment to probe students’ anticipated new skills and capabilities. New technology can also provide new assistance for the work of assessment both for the teacher within the classroom and for monitoring standards at the system level. This chapter reviews the challenges and opportunities for mathematics assessment posed by the use of technology. It examines issues concerning what should be assessed under these new modes of learning; the potential for deeper, more informative assessment; and how assessment might be conducted. Throughout this chapter, the term mathematics is used to refer to all of the mathematical sciences, including statistics.

There is a large literature on research and development in computer-based testing, which identifies many different approaches to all components of testing. In this literature, distinctions are sometimes made between testing for summative and formative purposes, between fixed and adaptive item presentation (where the items presented to students depends on their success on previous items), between Web-based and other delivery systems which differ in the nature and timing of feedback to the student (if any), according to the measurement theory employed (if any), and on many other features. In this broad literature, mathematics is often selected as the content domain for research. In the present article, all forms of testing using electronic technology are included (and referred to) as “computer-based” and issues are chosen for discussion because of their relevance to mathematics teaching, learning and assessment rather than to general issues of assessment practices or measurement theory. Computer-based testing is also at the heart of intelligent tutoring, since it links the “student model” and the “tutor model,” but again this is not considered beyond the issues that arise specifically in mathematics.

The Potential of Technology

Technology has potential to alter all of the aspects of the assessment process. There are new possibilities for the ways in which tasks are selected for use in assessments, in the way they are presented to students, in the ways that students operate while responding to the task, in the ways in which evidence generated by students is identified, and how evidence is accumulated across tasks (Almond, Steinberg, & Mislevy, 2003). Technology can improve the ways we assess the traditional mathematics curriculum, but it can also support the assessment of a wider “bandwidth” of mathematical proficiency to meet the changes in emphases of learning for the future.

Computer-based testing allows the automated generation of different items with similar psychometric properties. This allows different students to take different items or students to take the same test at different times without giving them access to items before taking the test (Irvine, 2002).

Acting as a communications infrastructure, computer-based platforms enhance item presentation, as will be demonstrated below. For the student, there may be a dynamic stimulus, three-dimensional objects may be rotated, and flexible access to complex information from multiple sources can be provided. A particularly important feature of computer-based testing is that it can ensure students comply with constraints in a problem to ensure engagement with the desired mathematics. A wider range of response types is now possible. For example, “drag-and-drop” items or the use of “hotspots” on an image may allow students to respond to more items non-­verbally, giving a more rounded picture of mathematical literacy. In paper-based assessment, the validity of assessment in mathematics for some individuals has been limited by the necessity to decode written instructions for mathematical items and to express mathematical answers and ideas clearly. The software may also take into account the steps taken by a student in reaching a solution, as well as the solution itself. Computer-based platforms also support the presentation of problems with large amounts of (possibly redundant) information, mimicking the real-world scheduling and purchasing problems that are common in everyday life in the Internet age.

Automated scoring of responses has been possible for multiple-choice items for 80 years (Wiliam, 2005), but in recent years there have been significant advances in the automated scoring of items where students have to construct an answer, rather than just choose among given alternatives (see, e.g., Williamson, Mislevy, & Bejar, 2006). Computer-based assessment offers possibilities for providing more detailed information to students and teachers at lower cost, including profile scoring and other forms of diagnostic feedback that can be used to improve instruction. Automated scoring is also increasingly used in online learning systems, both “stand-alone” instructional packages and supplements to classroom instruction with integrated assessments. Such systems can give diagnostic feedback to the student during the instructional activity, as well as providing information about the final outcomes, as a single final score, or a detailed breakdown. Some interactivity may also be possible. Automated scoring also makes it easier to supply reports showing trends in performance over time. For the assessor and teacher, sophisticated reports on the assessment enable ready tracking of progress of individuals, classes and systems. Unobtrusive measurement of new aspects of student–task interaction may also be reported. Features of student-constructed drawings, displays and procedures that are impractical to code manually, can be efficiently assessed, and strong database facilities are available for statistical analysis.

Acting as a computational and representational infrastructure, the computer-based platform can enable students to demonstrate aspects of mathematical literacy that benefit from the use of the mathematics analysis tools embedded in computer and calculator technology. Without the “burden of computation,” student attention can be focused on problem-solving strategies, concepts, and structures, rather than mechanical processes. They can work with multiple representations that are “hot-linked” so that a change in one representation automatically produces a change in another (e.g., a change in a data table produces a change in a chart).

Chapter Outline

The first major section of this chapter examines assessment in situations where the technology is principally used for the purpose of assessment, rather than by students in an open way for solving the mathematics items. There are subsections on items and item types, increasing the bandwidth of assessment, scoring, feedback to students, and reporting to teachers, and the comparison of computer-based and paper-based assessment. As Threlfall, Pool, Homer, and Swinnerton (2007) note, “the medium of pen-and-paper has been an inseparable part of assessment, and a change to the medium of presentation threatens that highly invested arrangement, and seems to risk losing some of what is valued” (p. 335). Most of the studies reviewed in this section assume that the mathematics curriculum and approved mathematical practices are unchanged, and what changes are the opportunities to assess these.

The second major section of this chapter considers assessment when students can use the mathematical capabilities of technology in the mathematical performance that is being assessed. This section responds particularly to the advent of mathematically-able calculators and computer software and the need to accommodate them in learning, teaching and assessment. From such a perspective, it is generally accepted that both curriculum goals and accepted mathematical practices will change.

The themes of both the major sections (the ability to use new tools for mathematics, and the changing nature of mathematical tasks) are being reflected in mathematics assessment at all levels. For example, the OECD’s 2012 international PISA survey of mathematics will include an optional computer-based assessment of mathematics (Programme for International Student Assessment Governing Board, 2010). Some of the computer-based items would be suitable for paper-based delivery but the presentation will be enhanced by computer delivery. Most of the items in the computer-based assessment, however, will test aspects of mathematical literacy that depend on the additional mathematical tools that are provided by information technology, and the whole PISA assessment is now on a trajectory towards computer delivery. The intention is to move “from a paper-based assessment towards a technology-rich assessment in 2015 as well as from the traditional items to the innovative assessment formats which computer-delivery would enable” (p. 6).

The chapter concludes with reflections on the state of the art and presents some principles that can be used to guide future work in this field.

Using Technology to Assess Mathematics

This major section examines changes technology is making to assessment, organized under the various components of assessment. The first subsection examines the new possibilities for items. The following section looks at developments in automated scoring of responses. The third subsection examines progress in providing feedback to students, especially in the context of formative assessment, which has been shown to be a major strategy for improving learning (Black & Wiliam, 1998). In this first main section, technology is principally being used for enhanced item presentation, more convenient and reliable scoring, and for immediate and personalized feedback to students. In the subsequent section, attention is focused on assessments where the technology is being used by the student as a mathematical assistant, with the associated issues of changed goals for the curriculum in addition to changed procedures. As will be seen in both main sections, computer-based assessment can serve traditional goals as well as providing new opportunities to assess aspects of mathematical proficiency that relate to higher-order thinking and greater real-world relevance.

Before beginning the section proper, we note that computer-based assessment is often adopted because such test administration provides multiple points of convenience for students, teachers and educational systems. Students can often take tests at a time and place to suit themselves, and may receive immediate feedback. Teachers (and even school systems) may be freed from the burden of grading, and can receive well-designed reports by class, student or item. The expansion of online learning systems has also encouraged the use of computer-based assessment and the major commercial products have teacher-friendly tools for constructing straightforward computer-based assessment within them. Many reports in the literature discuss these features. For example, Pollock (2002) reported on a change of the teaching and assessment of “basic mathematics skills” in a course for prospective teachers. The course already used a computer-aided learning system and so adopted an associated computer-based assessment system to enable a switch from assessing with examinations to continuous assessment. Previously, such a system had been regarded as too demanding of staff time. Since the aspects of computer-based assessment related to test administration are for the most part not specifically related to mathematics, they are not discussed further.

Similarly, although access to the substantial infrastructure required for computer-based assessment is certainly a barrier to its use (by individual students, classes within schools, schools as a whole, and systems) because this does not specifically relate to mathematics, the difficulties of access are recognized but not further discussed here.

Expanding Assessment: Items and Solutions

New possibilities for computer-based items.

Consider Figure 23.1 below, which shows part of two versions of an item on estimating with percentages, taken from the developmental work on “smart-tests” (see Stacey, Price, Steinle, Chick, & Gvozdenko, 2009).

Figure 23.1.
figure 1

Computer-based assessment allows a wider range of item types.

Full size image

The paper-based item is multiple choice. The pom-pom tree in year 1 is shown and students have to select A, B, C D, or E to indicate the height of the pom-pom tree in year 2, when its top has blown off and it is 35% shorter. This item is easily scored by hand or by computer. On the right hand side, a new version only feasible in computer-based assessment is shown. Students indicate their estimate of the height by pulling up a slider. In the figure, a student has pulled up the slider for the fir tree, but has not yet started on the pom-pom tree. The handle of its slider is visible near ground level. There are at least three advantages to the computer-based item. First, estimation is tested in a direct and active way, without guessing from alternatives (and, possibly, with less ­cognitive load because the choices do not need to be processed). Second, whereas such an item would be very tedious to mark by hand, it is easily marked by computer, and partial credit based on the accuracy of the estimate can easily be allocated. Third, the image can be in colour, so the presentation is more attractive to students, without the substantial cost of colour printing.

Figure 23.2 shows an online mathematics question for 12–14 year olds from the example items for the “World Class Tests” (World Class Arena, 2010).

Figure 23.2.
figure 2

Computer screen for “Rotato,” an example item from the World Class Arena.

Full size image

These tests are designed to challenge able students, requiring creative thinking, logic and clear communication of thought processes. Solving the item in Figure 23.2 requires using the interface first in an exploratory way, gradually coming to understand the effect of certain moves (e.g., rotating twice around one point) and finally assembling a strategy to make the required shift in less than 12 moves. The computer provides the dynamic image, and itself counts the number of moves (other features of the solution could also be tracked). The item stem requires many fewer words than would be required in a paper-based version, and the item response is entirely non-verbal, which means that the mathematical proficiency of students with less developed verbal skills can be better assessed. It is hard to imagine a feasible paper-based version of this item, although it could be the basis for a mathematical investigation producing a report for teacher assessment.

As noted above, a computer-based assessment platform offers an infrastructure for communication that can enhance item presentation, the range of mathematics assessed, interaction between the student and the item, the way in which the response is provided by the student and the information that is extracted from the response. There is great potential for creatively expanding the nature of assessment items and students’ experience of engaging with assessment.

Authentic Assessment

We live in a society “awash in numbers” and “drenched with data” (Steen, 2001), where “computers meticulously and relentlessly note details about the world around them and carefully record these details. As a result, they create data in increasing amounts every time a purchase is made, a poll is taken, a disease is diagnosed, or a satellite passes over a section of terrain” (Steen, 2001). Knowledge workers need to make sense of these data and citizens need to be able to respond intelligently to reports from such data. This requires a change in the mathematics being learned. Full participation in society and in the workplace in this information-rich world, therefore requires an extended type of mathematical competence. For this reason, there has been increased interest in recent years in the development of “authentic” assessment in mathematics—assessment that directly assesses the competence of students in performing valued mathematics rather than relying on proxies such as multiple-choice tests that may correlate well with the desired outcomes, but may create incentives for classroom practice to focus on the proxy measures, rather than the valued mathematics.

Medication calculation is an important part of the numeracy required for nurses, since patients’ lives can depend on this. NHS Education for Scotland funded the development by Coben et al. (2010) of a computerized assessment of medication calculations related to tablets, liquids, injections and intravenous infusions, using high-fidelity images of hospital equipment. In this “authentic assessment,” the task for the student replicated the workplace task as faithfully as possible. As well as facilitating item presentation, computer-based administration of the test included automatic marking, rapid collation of group and individual results, error determination and feedback. A concurrent validity study compared the computer-based test with a “gold-standard” practical simulation test, where the students also prepared the actual dose for delivery (for example in a syringe). The two methods of assessment were essentially equivalent for determining calculation competence and ability to select an appropriate measurement vehicle (e.g., syringe, medicine pot). However, the computer assessment did not assess practical measurement errors, such as failing to displace air bubbles from a syringe. Coben et al. concluded that medication calculation assessment can be thought of in two parts: computational competence (which is best assessed by computer, especially since the whole range of calculation types can be included) and competence in practical measurement. Performance assessment, being very labour-intensive, should be restricted to assessing practical measurement.

In many cases, authentic assessment is undertaken through setting investigative projects. This is a longstanding practice, for example, in statistics education and in mathematical modelling. Since these assessments usually involve the use of mathematically-able software, they are discussed in the second main section of this paper.

Assessment with Support

A standard paper-based assessment generally aims to measure what a student can do alone and with a very limited range of tools. In the second main section, we discuss the changes when students have access to mathematically-able software when they are undertaking assessment. However, there are many other possibilities for including tools in computer-based assessments. Two educational concepts are particularly relevant here. The first is the idea of distributed cognition. Pea (1987) and others have pointed out that much cognitive activity is not carried out “in the head” but is distributed between the individual and the tools that are available for the task. The obvious consequence is that assessment of what a person can do should acknowledge tool use. The second important idea is Vygotsky’s distinction between the psychological processes an individual can deploy on his or her own, and those that can be deployed when working with a teacher or a more advanced peer (see, e.g., Allal & Pelgrims Ducrey, 2000). These two ideas raise the possibility of using technology to create very different kinds of educational assessments—those that are focussed on the supports that are needed for successful performance rather than the degree of success when unsupported (Ahmed & Pollitt, 2004).

For example, Peltenburg, van den Heuvel-Panhuizen, and Robitzsch (2010) were concerned to improve the assessment of students with special education needs. Traditional assessments of these students indicated that they were operating several years below grade level, but the researchers were keen to investigate what the students might do with support. The study compared a standardized assessment with a computer-based “dynamic assessment” (Lidz & Elliott, 2001), which provided digital manipulatives that students could use to assist with subtraction questions. Students’ results were better when the manipulatives were available, because the assessment showed more of what the students knew than could be inferred simply from an incorrect answer. Software running in the background also captured data on how the students used the manipulatives. Interestingly, in several instances these were not the methods that had been predicted when designing the tools.

Scoring and Gathering Other Data on Performance

In this subsection, we first examine progress in automating the work that a teacher does in evaluating the work of a student. Then, we look at non-traditional measures of the interaction between students and items that may contribute to a fuller assessment of student performance and learning.

Scoring constructed response mathematics items.

Computer-based assessment, since its inception in the 1970s, has been limited by the nature of responses that can be scored reliably. The dominance of the multiple-choice format and single entry number answers, which still persists today, highlights the problem. Yet there is much more to mathematics than producing such simple responses: ideally, assessment across the full bandwidth of mathematics should deal with multiple-step calculations, checking each step as a teacher might, analyzing arguments and explanations, and certainly, as will be illustrated below, providing full credit for all solutions that are mathematically correct but differ in mathematical form. Although automated scoring that is as good as the best human scorers, if it can ever be achieved, is many years away, considerable progress has been made in recent years on assessing certain kinds of constructed-response mathematics items.

An advertisement for the commercial product WebAssign in the March 2011 edition of the Notices of the American Mathematical Society showed grading by two automated assessment systems of a student’s response to a constructed response item. The item was “Find the derivative of y  =  2sin(3x  –  π),” and the response given was \( \frac{\text{d}y}{\text{d}x}=-6 \mathrm{cos} 3x\). The expected pen-and-paper response (by applying the chain rule) to this item would be \( 6 \mathrm{cos} \left(3x-\pi \right)\), which is of course equivalent to the given response of \( -6 \mathrm{cos} 3x\). The advertisement made the point that the online assessment system WebAssign correctly graded this “unexpected” simplified response, whereas many other online grading systems would have graded it as incorrect (see WebAssign, n.d.). The difference lies in the computational engine (if any) being used for scoring complex constructed response mathematical answers. A powerful computer algebra system (CAS) can create items fitting specified criteria, compute the correct answer, and check students’ responses.

Within the limited realm of school mathematics, less powerful mathematical software is effective. The equivalence of different algebraic expressions can be established by numerically evaluating the correct response (supplied by the item setter) and the student response at a number of points. The “m-rater” scoring engine developed by the Educational Testing Service does just this, by choosing the points to be evaluated at random, but also allows item creators to specify additional points to be evaluated. This approach has roughly the same level of accuracy as symbolic manipulation (Educational Testing Service, 2010).

In the report of the 17th ICMI Study on technology in mathematics education, only one paper specifically focussed on assessment. Sangwin, Cazes, Lee, and Wong (2010) considered the use of technologies such as CAS and dynamic geometry to generate an outcome from a student response that is a mathematical object (e.g., an algebraic expression, a graph, or a dynamic geometry object). The outcome may be right/wrong feedback to the student, a numerical mark along with automated written feedback to the student, or statistics for the teacher about the cohort of students.

Sangwin et al. first made the point that a CAS needs a range of additional capabilities to support good computer-aided assessment (CAA). As a simple example, they noted that a mainstream CAS recognizes x 2  +  2x  +  1 and x  +  1  +  x  +  x 2 as algebraically equivalent (and hence can mark either as correct), but for useful feedback to a student, a CAA system should be able to recognize the incomplete simplification and provide appropriate feedback to the student. Another simple example was an item where students needed to rotate one point about a central point. The resulting dynamic geometry diagram could be analyzed to see if the student has the correct distance and the correct angular position, opening possibilities for both partial credit and informative feedback. Drawing on examples of classroom observations the article described the development of quality feedback, useful cohort data for teachers, and new styles of mathematical tasks for which informative feedback can be given. It also described the pitfalls when a system can only examine the end product instead of examining the strategies that students use. Technology in this area is developing rapidly, and product development cycles often overtake educational research. Sangwin et al. concluded that new CAA tools require new modes of thought and action on the part of institutions, teachers and students alike.

Interest in assessment of constructed responses has been given further impetus by the shift towards integrated online learning and assessment systems, especially in tertiary education. For example, the WebAssign system mentioned earlier identifies its strongest features as convenience, reliability and security, compatibility with popular learning management systems, automated and customizable reporting to teachers by student or item, and easy creation or selection of assessment items. Partnerships with major textbook companies provide prepared databases of practice and assessment items and tutorial materials linked to popular textbooks, and questions can also be selected from open resources or those created by the teacher.

Another example is Maple T.A. (Maplesoft, 2011), which, being powered by the long-standing computer algebra system Maple, is specifically designed for technical courses that involve mathematics. Advertised strengths include the capacity to use conventional mathematical notation in both questions and student responses, the comprehensive coverage of mathematics and its capacity to support complex, free-form entry of mathematical equations and intelligent, automated evaluation of student responses graded for true mathematical equivalence with feedback available for the student. Maple T.A. can support open-ended questions with infinitely many answers, flexible partial credit scoring, and offers the assessment designer a high degree of mathematical control over randomly generated items, so that different students see different items testing the same content or to provide virtually unlimited on-demand practice. Maple visualization tools such as 2D and 3D plots are available to test creators and test takers.

Reports on the use of Maple T.A. and other systems are now appearing. For example, Jones (2008) reported on its ability to provide regular feedback and practice questions to engineering students. The article discussed how partial credit may be awarded, how account had been taken of techniques for designing good questions that incorporate randomly generated parameters, the coding required by the instructor, and strategies for reducing cheating in the on-line environment. Students’ difficulties with the syntax for entering mathematics into the computer are commonly reported across much of the computer-based mathematics literature. Jones (2008) recommended the use of practice questions at the beginning of the course to reduce this. In this way, some of the barriers to a more expert computer-based scoring of constructed mathematical responses are now being overcome.

Awarding of partial credit is an important feature of human scoring in mathematics, but this presents significant challenges for automated scoring (Beevers, Youngson, McGuire, Wild, & Fiddes, 1999). In view of the difficulty of replicating the judgments made by humans in awarding partial credit, designers of computer-based assessments have explored a range of ways of approximating partial-credit scoring with simple dichotomous scoring.

Ashton, Beevers, Korabinski, and Youngson (2006) trialled two methods of awarding partial credit in automatically-scored high-stakes pass/fail examinations. In the “steps method,” some questions required the student to choose whether to enter a single response, which would be scored as correct or incorrect, or to opt to answer a series of sub-questions that led to the full answer, each of which would be assessed individually. For example, students asked to find the equation of a tangent to a curve could either choose to input the equation (for which they would either get full credit or no marks), or they could answer a series of sub-questions, requiring the coordinates of the point of tangency, the general form of the derivative, the slope of the tangent at the point and then its equation. Fewer marks were awarded for the structured approach because students did not demonstrate the ability to plan a solution strategy for themselves. The second method of approximating human-scored partial credit assessment explored by Ashton et al. simply informed students whether their submitted answer was correct or incorrect and gave them the opportunity to resubmit. The logic here is that partial credit is commonly awarded when students make small slips and so feedback would enable students to correct these small slips, bringing their score up closer to a human-assessed score. Although the total marks awarded in both methods were statistically indistinguishable from standard partial credit marking, Ashton et al. recommended adoption of the “steps” method because the correct/incorrect feedback method appeared to promote guessing rather than careful review.

The choice of a digital tool as a mathematical assistant depends on many aspects of the teaching context. For example, the Digital Math Environment (http://www.fi.uu.nl/wisweb/en/) has been designed to help secondary school students as they learn pen-and-paper algebra. It provides students with a facility to solve problems (e.g., to solve a quadratic equation) step by step, with the program providing feedback on accuracy at each step. In this way, it is primarily a learning tool, providing immediate formative assessment as the student works through problems, but summative assessment is also available.

Unobtrusive Measurement of Student–Task Interaction

Computer-based testing allows the collection and analysis of a range of data beyond a student’s response, including response time and number of attempts. In cognitive psychology, response time has for many years been regarded as an important measure in the investigation of mental processing (Eysenck & Keane, 2005), and computer-based testing allows data on response times on a larger scale, and in naturalistic settings. Response time has been used for many purposes, including to inform item selection by complementing accuracy data, to identify cheating, to monitor test takers’ motivation (for example, by flagging rapid guessing), and to track the development of automaticity, which is especially relevant to consolidating mathematical skills.

Gvozdenko (2010) studied the uses that teachers and test designers can make of information about student response times, using data from preservice primary teacher education mathematics courses. He found that response–time measurements provide a valuable supplement to performance data for: (a) evaluating difference in cognitive load of items; (b) identifying the presence of multiple solution strategies; and (c) monitoring the impact of teaching on specific cohort sub-groups across a teaching period.

Figure 23.3 gives an example from Gvozdenko (2010) of three versions of a test item that were intended to be classically parallel (i.e., the items should be interchangeable). The facility (percentages of students correct) and mean ­question response times (MQRT) of versions 1 and 3 were both similar. Version 2 looks similar from the facility data (only 6% lower) but it has a substantially greater MQRT. The 50% greater MQRT draws attention to the greater cognitive load in version 2, probably due to having two different rotated elements and a higher order of rotational symmetry.

Figure 23.3.
figure 3

Three versions of a task, and associated mean question response times (MQRT) and facility (Adapted with permission from Gvozdenko, 2010).

Full size image

Gvozdenko’s (2010) study of preservice primary teacher education students also showed how response time can provide a supplementary measure of learning. Many students in such a course are able to solve primary-school level problems on entry, but their knowledge is not sufficiently automatic, robust, and strongly founded for flexible use in the immediacy of teaching a class. Measuring response time can give an additional indicator of developing competence for teaching. Another item from Gvozdenko (2010) involved the conversion of square metres to hectares. Conversion of 12,560 m2 to hectares (answer 1.256) had a facility of 77%, but conversion of 690 m2 to hectares (answer 0.069) had a facility of 72%. This group of students seems equally competent at these items. However, the MQRT of the first was 44 s, and for the second 62 s. This reveals a difference in the robustness of the knowledge that may show up in the pressured environment of the classroom.

Providing Feedback

The provision of feedback that is focussed on what a learner needs to do to improve, rather than on how well the individual compared with others, has been shown to impact significantly on learning (Wiliam, 2011). Indeed, over the last quarter century, a number of reviews of research have demonstrated that there are few interventions that have such a great impact on student achievement (Hattie, 2008). It is not surprising, therefore, that a major priority in the development of computer-based assessment software has been providing detailed feedback to test takers. Traditionally, assessment has been concerned with placing a student at a particular point on a scale. Although this may be adequate for many of the functions that assessments serve, it does not give feedback to students about what to do next. Rather, a feedback system needs to focus less on measurement, and more on classification—the assessment should indicate that the student has a particular state of knowledge that is likely to benefit from a specific intervention.

Livne, Livne, and Wight (2007) developed an online parsing system for students preparing to take college-level courses in mathematics designed to classify errors in student numerical answers, mathematical expressions, and equations as either structural (indicating the possibility of a conceptual difficulty) or computational (for example, the kinds of errors that would result from transcription errors). In terms of overall scoring, correlation between the automated scoring system and human scoring was very high (0.91). However, the automated scoring system appeared to be considerably better than human scorers at identifying patterns of errors in students’ responses.

Shute, Hansen, and Almond (2008) investigated how summative and formative assessment could be linked by examining how an assessment system might be modified to include some elements of instruction for 15-year-old students learning algebra. They investigated the impact on student learning when feedback was added to an assessment system and when the presentation of items in the assessment was adaptive (responding to student answers) rather than in a fixed sequence. They found that the validity, reliability and efficiency of the summative assessment was unaffected by the provision of feedback, even when the feedback was elaborated (i.e., showing detailed solutions immediately after the item was completed). Students who received adaptive items learned as much as students who received items in the fixed sequence and students who received the elaborated feedback learned more than those who received no feedback or received feedback only on the correctness of their answers. The results suggest that it may be possible, in the near future, to derive data for summative purposes (e.g., for accountability) from experiences primarily designed to promote learning. In the authors’ phrase, it may be possible to fatten the hog with the same instrument used to weigh it.

A particularly fruitful area for such research in recent years has been the development of Bayesian inference networks, or Bayesian nets for short. The basic idea is that for a particular domain, a proficiency model is specified that details the elements needed for successful performance in that domain. For each individual, a student model is constructed by observing the student’s performance on a number of tasks, and using Bayes’ theorem to update the likelihood that the student does indeed possess particular knowledge given the performance evidence. Such models are widely used in intelligent tutors, both to track student competence (the assessment task) and also to make decisions on what tasks a student should tackle next (Korb & Nicholson, 2011; Stacey, Sonenberg, Nicholson, Boneh, & Steinle, 2003; VanLehn, 2006).

Diagnostic Feedback for Teachers

Although diagnostic feedback direct to students has proven educational benefits, there is also a case for providing detailed diagnostic feedback to teachers, especially when it is able to enhance their pedagogical content knowledge. Stacey et al. (2009) described a system, now in use in schools, of “Specific Mathematics Assessments that Reveal Thinking” (SMART, 2008). These “smart-tests” are designed to provide teachers with a simple way to conduct assessment to support learning. Using the Internet, students undertake a short test that is focussed narrowly on a topic selected by their teacher. Students’ stages of development are diagnosed, and are immediately available to the teacher.

The programming behind the diagnosis links individual student’s answers across questions to pool the evidence for particular misconceptions or missing conceptions in a way that would be impractical for teachers to do manually. Where possible, items have been derived from international research and then adapted for computer-based delivery. Online teaching resources (when available) are linked to each diagnosis, to guide teachers in moving students to the next stage. Many smart-tests are now being trialled in schools and their impact on students’ and teachers’ learning is being evaluated.

Comparing Computer-Based and Paper-Based Assessment

When an important goal of an assessment is to compare results over time with an unchanged content expectation, the question of how a computer-based assessment compares with a paper-based assessment for mathematics is important. One common example of such a context is when governments monitor achievement standards in schools from year to year. In response to such concerns, the European Commission Joint Research Centre commissioned a report (Scheuermann & Björnssen, 2009) on the transition to computer-based assessment for a wide range of purposes.

Research studies comparing effects of modes of assessment have shown mixed results (Hargreaves, Shorrocks-Taylor, Swinnerton, Tait, & Threlfall, 2004; Threlfall et al., 2007). There were differences in student performance in both directions and also no differences. Kingston (2009) conducted a meta-analysis of studies for 10 years up to 2007 and found that the comparability between traditional mathematics tested with computer-based and paper-based formats is slightly less than the comparability between tests of reading and science in these two formats. This difference was attributed to the need, in many items in the mathematics test, for students to shift their focus between the computer screen and writing paper. The difficulty of typing mathematics into a computer means that students undertaking computer-based mathematics assessment still usually need to do a lot of the work on paper, and transfer this to the computer when it is complete.

Hargreaves et al. (2004) found no significant difference between computer-based and paper-based testing for 10-year-old children and no advantage for students with greater familiarity with computers. In a study of complex problem solving involving fractions content, Bottge, Rueda, Kwon, Grant, and LaRoque (2009) found no difference by mode of presentation in the results of the assessment for any ability group. In general, computer-based testing creates both constraints and affordances for students; computer-based presentation can limit the strategies that students can use for solving problems, but can also afford more interesting and dynamic approaches to assessment. Items often change when converted from paper-based to computer-based assessment, but it does not seem possible to predict, in general, whether such conversion is likely to make items easier or more difficult.

Threlfall et al. (2007) explored how changing items designed originally for paper-based tests into a computer-based form altered what students do, and therefore what the items assess. The study examined only a narrow range of computer-based items, created by transferring paper-based items to the screen as closely as possible and marking as similarly as possible. Overall results were similar but some items showed large differences in facility. Computer-based items that supported exploratory solutions, and which enabled a solution to be adjusted, generally had higher facilities than the paper-based equivalent. For example, students ordering 4 lengths by size could drag the symbols into position and then check all of the pair-wise comparisons, rearranging if necessary. Students placing circles to make a figure symmetric could drag them into position, and then check if the result looked symmetric, whereas on the paper-based item this approach was not possible. The computer-based presentation for such items enabled more sequential processing and hence effectively reduced cognitive load. However, some items where the computer allowed exploratory activity were less well done than in the paper-based version; an example was given of how the computer program did not provide exploration that was well controlled. Items where performance was better in the paper-based mode included those in which students did written calculation on scrap paper but where students tried to work mentally in the computer-based assessment. Students often do not use paper in a computer-based assessment even if it is available. Threlfall et al. concluded that each item needs to be examined to see which of the solution methods afforded by the media most closely correspond to the behaviours that the item is designed to assess. Using different item presentation media can affect performance, but the relationship with validity is complex—higher scores do not necessarily indicate greater validity.

The awkwardness of using the computer palette or other input device to construct mathematical expressions remains a potential source of construct-irrelevant variance for assessing mathematics by computer. A study of beginning tertiary quantitatively-able students by Gallagher, Bennett, Cahalan, and Rock (2002) found that ability to use the entry interface did not affect performance on a test where all answers were symbolic mathematical expressions. However, examinees overwhelmingly expressed a preference for taking a paper-based rather than computer-based test, because inputting mathematical objects was so cumbersome. The difficulties arising from the sharp contrast between hand written mathematics and keyboard-entered mathematics is a recurring theme in reports of computer-based assessment of all types and at all levels of education. Written mathematics is two-dimensional rather than strictly linear, there are symbols that are not standard on a keyboard, and different representations such as equations, graphs, diagrams, text, and symbols are used together in presenting a solution. All of these features mean that even the best of the current systems is far from ideal. Keyboard input remains a major barrier to computer-based assessment of mathematics.

In addition to whether the mode of presentation affects performance overall, it is also important to examine whether certain kinds of student are disadvantaged, or advantaged, by particular modes of presentation. Martin and Binkley (2009) suggested, for example, that the presentation of dynamic stimuli will advantage boys. Other groups of concern (see, for example, Scheuermann & Björnssen, 2009) include students with disabilities, members of different ethnic groups and students with certain cognitive characteristics. It is likely that there is too much variation in styles of computer-based assessment to obtain simple answers to such questions.

Assessing Mathematics Changed by Technology

The advertisement for WebAssign mentioned above appears to assume that the student differentiates the given expression using pen and paper, then enters the answer into a computer system. However the computer into which the student enters the response has the capacity to carry out the differentiation itself. If the online assessment system has access to a CAS for grading the work, it seems odd that access to this system should be denied to the student. Indeed, the widespread availability of powerful software for doing mathematics, rather than just checking the correctness of mathematics done on paper, raises fundamental issues about what mathematics is valued, how it should be taught and how it should be assessed. This has been a major preoccupation in many countries in recent years, and is the theme of this second major section of the chapter.

There are several reasons why assessment should take into consideration the tools that are used for mathematics outside school. As noted earlier, Pea (1987) has pointed out that tools that assist students in undertaking cognitive tasks have knowledge embedded within them, so the most meaningful unit for assessing competence is the user with the tool, rather than the user artificially working alone for the purpose of assessment. Another argument for the use of technology in formal assessment arises from the principle of validity—the context of the assessment should not differ significantly from the context of instruction. Indeed, where the context of assessment differs greatly from the context of instruction, assessment results are uninterpretable.

The College Board (2010), in the USA, explicitly made the point that the limitations of the use of technology in examination-based assessment should not limit the use of technology in classrooms, but the examination remains a powerful driver of what happens in schools. As will be demonstrated below, assessing mathematics when students are allowed to use technology has been shown to require substantial experimentation, research and a critical examination of values. Specifically, it requires clarity about the constructs to be assessed (Wiliam, 2011). Among other reasons, this is because research has led to a growing realization that mathematical thinking is almost impossible to separate from the tools with which it is learned and practised (Trouche & Drijvers, 2009). Doing mathematics with new tools leads to different ways of thinking about mathematical problems, and, indeed, to somewhat different mathematics.

Mathematical Competence and Computer Technology

Mathematics has a special relationship with computer technology, as its origins lay in the need to deal with extensive computation. An important part of mathematics has always been to develop algorithms for solving problems, and the design of effective algorithms has always had a two-way relationship with the technology of the day, from the abacus, to Napier’s “bones,” to ready reckoners, logarithm tables and slide rules to today’s calculators and computers. Working with electronic technology, whether packaged as calculators, computers or special purpose machines, is now an essential component of doing and using mathematics in everyday life and in the workplace.

The impact of electronic technology on the ways in which individuals use mathematics, and consequently should learn it, has long been discussed, and continues to change rapidly. Thirty years ago, the Cockcroft enquiry into mathematics in UK schools (Committee of Inquiry into the Teaching of Mathematics in Schools, 1982) pointed to a change in the relative importance of methods of arithmetic calculation for personal and occupational use. Pen-and-paper algorithms had diminished in importance, being replaced by mental computation and estimation wherever appropriate and backed up by computer/calculator use when an exact answer to a difficult computation was required. This was an early indication of the need for mathematical competence to be redefined, in relation to electronic technology, with consequent impact on assessment. As Trouche and Drijvers (2009) pointed out, whereas the introduction of computers into mathematics education appears to have had limited impact on classroom practice, the use of handheld technology rapidly overcame the infrastructure limitations in schools and has made a greater difference to practice in mathematics classrooms. In the hands of students, for use at home and school when required rather than housed in a distant computer laboratory, handheld calculators (now with considerable mathematical and statistical power) are now used routinely in assessment in many countries. Much of the research reviewed in this section is therefore centred on the role of handheld technology for senior school mathematics.

The mathematical functionality of mathematically-able software such as graphics calculators, CAS, and statistics programs (especially those focussed on exploratory, rather than confirmatory data analysis) render many of the questions asked in the pen-and-paper era obsolete when looked at from a purely functional point of view. The availability of mathematically-able software shifts significant parts of the work from the student to a machine. For example, a student may decide a problem can be answered by solving two simultaneous equations and so inputs the equations to a graphics calculator using appropriate syntax, requests the graph with a suitable range and domain, examines the output and interprets the coordinates of intersection in terms of the original question. The machine does the graphing and zooming as requested, supported by a myriad of hidden numerical calculations. The student selects the method, establishes the equations, and interprets the output. This example demonstrates that assessment with technology tests very different skills from assessment without technology. Routine calculations and routine graphing can be by-passed by the student, who is left in charge of the strategic plan of solution. Hopefully, with the burden of calculation removed, emphasis can then shift to assessing more than routine skills to encompass a much broader bandwidth of mathematical proficiency, including reasoning, problem solving, modelling and argumentation. Some expansion of the range of assessable mathematical content might also be predicted. For example, non-linear equations can be treated similarly to linear models when graphical, rather than algebraic, methods are used.

Applying Three Principles for Assessment

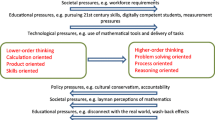
In the USA, the National Research Council Mathematical Sciences Education Board (1993) published a conceptual guide for assessment which emphasized that assessment should make the important measurable rather than making the measurable important. To this end, they proposed the following three principles for the assessment of mathematics that are relevant at the personal, class and system level.

  • The mathematics principle: Assessment should reflect the mathematics that is most important for students to learn. (This was called the “content principle” by MSEB)

  • The learning principle: Assessment should enhance mathematics learning and support good instructional practice.

  • The equity principle: Assessment should support every student’s opportunity to learn important mathematics. (p. 1)

While these three principles are statements of values, rather than the more familiar principles of educational measurement, they do, in effect, subsume traditional concerns such as validity. The main value in the three principles presented above is that the focus was shifted from measurement to education (Carver, 1974).

These three principles do, of course, have implications for assessing traditional mathematics with technology, discussed in the first major section of this chapter. However, the major implications of the three principles, and the interactions between them, are more significant for the kinds of mathematics that can be assessed.

The Mathematics and Learning Principles

The issues at the heart of the mathematics principle and the learning principle are evident when school systems grapple with how to introduce technology into examinations. What mathematics is valued and how can good learning of mathematics be promoted? Drijvers (2009), for example, reported on the use of mathematically-able software (principally graphics calculators and CAS calculators) in 10 European countries. Consistent with earlier studies, he found four policies: technology not allowed; technology allowed but with examination questions designed so that it is of minimal use; technology allowed and useful in solving questions but without any reward for such work; and technology use allowed and rewarded in at least some components of the assessment. Drijvers concluded that the 10 countries he studied were probably moving towards consensus on the policies allowing the use of technology: (a) including some questions where it is definitely useful, and (b) ensuring pen-and-paper algebra/calculus skills are tested in some way, either by not rewarding certain technology-assisted work, or by including a special component of assessment without technology. This is consistent with the policy of several university-entrance examinations, including AP Calculus (College Board, 2010) and some Australian examinations (Victorian Curriculum and Assessment Authority, 2010).

The mathematics principle states that assessment should focus on the mathematics that is most important for students to learn, but of course exactly what this is may be strongly contested. A review of the policies above confirms that there are divided opinions on the use of technology to “do mathematics,” so that compromises (e.g., to have separate components some of which allow and some of which disallow technology) are common. The learning principle is also significant here. The need for students to have basic pen-and-paper competence is widely recognized, even among strong advocates for the use of technology. It is essential, for example, to recognize equivalent algebraic forms when the technology generates an unexpected result. Having a separate component of an examination that does not allow technology is defended by some to ensure that these basic skills are not overlooked in schools. Exactly what skills should be tested and whether such a component is necessary, however, is also a contested matter. It is an interesting contrast that in the statistics education literature, the question whether students should use statistics software is rarely debated (see for example Garfield et al., 2011).

Given the enhanced computational power in the hands of students, one might hypothesize that end-of-school and university-entrance examinations allowing mathematically-able software would show a shift from mechanical questions (requiring students to perform some standard procedure that is cued in the wording of the question) towards questions requiring application in new situations and more complex construction of solutions. This might be seen as a natural outcome of the mathematics principle. However, Brown (2010) observed that the introduction of mathematically-able tools does not necessarily change the character of mathematics being assessed (and hence taught). Brown compared six end-of-school examinations in three jurisdictions, first at a point in time when students could use only a standard scientific calculator and later when students were permitted to use graphics calculators. He found that there was less emphasis on mechanical questions in two of the later examinations, but not in the other four.

Mechanical questions dominated all of the examinations before and after, even in examinations that were supplemented by an additional component where graphics calculator use was not permitted. Brown attributed the general lack of change to the unchanging mathematical values of the question writers, many of whom continue to place a high value on the accurate performance of pen-and-paper procedures. This may not however be the whole reason. For example, Flynn (2003) demonstrated that designing new questions that take advantage of technology requires creativity and experimentation, and it takes time for teachers and assessors to develop the necessary expertise. In a case study of “problems to prove,” Flynn analyzed many sample examination questions, and identified difficulties that arose when the solution tools changed. With symbolic manipulation software (CAS), the key issue is what Flynn called “gobbling up” steps. For example, a student without CAS who shows that (sin x  +  cos x)2  =  1  +  sin 2x demonstrates knowledge of the identities sin2 x  +  cos2 x  =  1 and 2sin x·cos x  =  sin 2x. For the student with CAS, these steps are “gobbled up” by the CAS, and the result is given immediately. Flynn’s paper provided some ways forward for assessing complex reasoning. However, there is much to be done to improve all assessment of the full bandwidth of mathematical proficiency. Having new technologies provides an extra dimension to this challenge as well as new but still embryonic opportunities.

Flynn (2003) also provided a case study of the way in which the symbolic manipulation facility of CAS calculators can actually be used in examinations that permit their use. He analyzed the two first such examinations in Victoria, Australia. Flynn found that questions yielding 12% of the total marks could not be answered with CAS features. These questions typically tested knowledge of features and properties of unspecified mathematical functions such as identifying the graph of f(−x) from multiple-choice options, given the graph of a function with an unspecified rule for f(x). This style of question came to prominence when graphics calculators were first permitted, to test understanding of the fundamental relationship between the graphs of f(x) and f(−x). Previously, this understanding may have been assessed by asking students to sketch the graph for a specified f(x), but graphics calculators changed the cognitive demand of this task from mainly mathematical knowledge to mainly syntax and button pushing because they can automatically graph f(−x) where f(x) is given.

Flynn found that symbolic manipulation would have advantaged students in questions worth 31% of the total marks. Most of these questions were similar to those that Brown (2010) termed mechanical questions, requiring rehearsed procedures such as factoring or differentiation—with CAS they require little more than button pushing. Perhaps surprisingly, these questions were generally well within the pen-and-paper algebraic skills of most students and hence many students would have completed them most efficiently without CAS. In fact, since examiners had probably derived the answers by hand, it was sometimes the case that multiple-choice questions presented answers in algebraic forms that favour pen-and-paper methods. There were no clear examples of questions that required algebra skills beyond expected pen-and-paper competence and in this sense took full advantage of the CAS, although subsequently this has occasionally occurred.

In questions leading to 56% of the marks, Flynn judged that a CAS calculator would give no advantage to a good student, although for a large proportion of such questions, the symbolic capability offered an additional solution or checking method, a phenomenon known as “explosion of methods.” Figure 23.4 illustrates an examination question of this type.

Figure 23.4.
figure 4

VCAA 2002 Mathematical Methods (CAS) Examination 1, Part I, Question 3.

Full size image

For the question in Figure 23.4, the following methods are available:

  1. 1.

    Locating when the maximum temperature occurs from the graph of the function;

  2. 2.

    Solving sin(πt/12)  =  −1 (the known minimum value of sine) using either the symbolic capabilities of CAS, with pen-and-paper, or directly from knowledge that the sine function has a minimum value at 3π/2;

  3. 3.

    Solving dy/dt  =  0 for t either with pen-and-paper or by using the symbolic capabilities for differentiation and/or solving;

  4. 4.

    Using a built-in facility on some calculators to find the maximum of a function;

For a student without technology, only the pen-and-paper versions of methods 2 and 3 are feasible; having a graphing facility adds methods (1) and (4), whereas with symbolic manipulation as well, all of the algebraic work is supported, as it would be in a question with parameters instead of specific values, when algebra would be the only viable solution method.

The large proportion of marks for questions where the newly permitted CAS facility had little or no impact demonstrate a continuity in examination practice, a continuity in what mathematics is valued, and the need for time and experience to develop a range of new question types. A broadening of the range of available solution methods is a main effect of the introduction of CAS into this examination system. Other effects of having CAS available are that it can compensate for some students’ algebraic weakness, or enable them to check their own work, or simply be a strategic decision to save time.

Equity Principle

The purpose of assessment is to allow valid and reliable inferences about student learning to be made. For this reason, it is imperative that all students be given a fair chance to show what they have learned. In assessment with technology, there are many dimensions where the equity principle is relevant, including socio-economic circumstances, and certain physical disabilities. The College Board (2010) makes the point that teacher professional development is an important equity issue, as is convenient access to calculators or computers and the ancillary equipment (e.g., data projectors, calculator view screens, networks, etc.) to make the most of the technology in class. Education systems have tended to manage the latter issues by slowing the pace of change that might otherwise be desirable.

Gender is a potential equity issue, since boys are often said to be more “technically minded” than girls, and there are numerous research studies which confirm this “digital divide.” Pierce, Stacey, and Barkatsas (2007) showed that although secondary school boys and girls (on average) approach learning mathematics with technology differently, this does not seem to affect their school use of technology for learning. Others, however, proposed that examinations with advanced technology disadvantage girls. Forgasz and Tan (2010), for example, proposed, on the basis of results from a special sample, that girls are disadvantaged when the more advanced CAS calculators are used instead of graphics calculators: this proposal awaits confirmation with a well-constructed sample, and a theoretical explanation of why the addition of symbolic manipulation to an already powerful technology might have such an effect.

One of the most important questions facing assessment with technology is how it can be conducted fairly if students use equipment of different quality or different brands or models with different capabilities. Of course, this is hardly a new issue. When fountain pens were first available, some worried that students rich enough to afford one would be at an advantage compared to those who had to dip the pen repeatedly in the ink-well. The examinations in Australia discussed above require students to have a calculator from a list of approved models (Victorian Curriculum and Assessment Authority, 2010), and the list is created with students’ economic circumstances in mind. Any capability of the calculator can be used. Because modern calculators have the ability to store text (some more than others, and with different ease of access), students are permitted to bring notes into examinations. In other settings such as AP Calculus (College Board, 2010), any calculator can be used but only a restricted range of their capabilities can be used, with pen-and-paper working required for other processes.

As with the mathematics principle and the learning principle, the equity principle requires that assessors have a strong knowledge of the capabilities of the permitted technologies. Even when there is a list of approved calculators which have the same broad capabilities, assessors need to be certain that students are not advantaged by using one calculator over another, certainly over the whole examination and preferably in individual questions. Differences between brands and models can occur in architecture (e.g., ease of linking of representations or accessing commands, menus and keys), user-friendliness of syntax, capabilities (e.g., operations and transformations) and outputs (e.g., privileged forms and possible inconsistencies). The study of Victorian Certificate of Education questions by Flynn (2003) cited above found that 20% of available marks were affected by differences between the three permitted calculators, although when the examination was considered as a whole, these differences cancelled out. A major source of differences is that a symbolic manipulation package auto-simplifies mathematical expressions. A good example from Flynn and Asp (2002) is provided in Figure 23.5. To solve part (c) (ii), a  =  tan−1(3/4) can be substituted into the expression for the derivative. One CAS calculator produces the answer nearly as required, but another gives an answer that is disconcerting to both students and teachers (see Figure 23.6).

Figure 23.5.
figure 5

International Baccalaureate Mathematical Methods Standard Level 2000 Paper 2, Question 7.

Full size image
Figure 23.6.
figure 6

Different answers from different CAS calculators.

Full size image

In fact, the CAS2 solution can be simplified to give the same answer, but few students (or for that matter, teachers) are likely to be confident that the initial answer is on the correct path. This interesting example raises another issue related to the Mathematics Principle: does this technology-assisted solution constitute the proof required for this question?

After noting that users of different brands and models of technology may have “unfair” advantages on some questions, Flynn (2003) concluded that the most important goal is a fair examination, where small advantages to some on some questions balance out, thereby providing a fair overall result. This requires examinations to be rigorously scrutinized by assessors knowledgeable about all the technologies in use and about how students are likely to use them.

Assessing Project Work that Is Supported by Technology

In classroom projects and investigations, students can use technology to explore mathematical ideas for themselves, undertake more substantial work than is possible in a timed examination and deal with complex data sets, including real data, or undertake mathematical modelling of real problems, formulating relationships and interpreting results. For example, dynamic geometry programs provide excellent assistance for students to experiment, make hypotheses and test them, before creating formal proofs. In this way, students can demonstrate a wide range of abilities. Spreadsheets and statistics programs similarly enable students to search for relationships in authentic data and provide excellent graphical representations of datasets, and are ideal tools to use in project work. These are important aspects of mathematics and statistics that are difficult, if not impossible, to assess validly in traditional examinations. Since both the mathematics principle and the learning principle invite us to ensure that these “higher-order” skills do indeed feature in assessments, assessment of students using technology in investigations is important.

Rijpkema, Boon, van Berkum, and Di Bucchianico (2010) described how the program StatLab can be used to teach and assess engineers about the design of experiments. The StatLab program assists in assessing application of theoretical knowledge to practical situations by providing part of the grading and feedback to students. Bulmer (2010) described a course based around a virtual island with many inhabitants who were used by his students as subjects in virtual experiments. He described how this provided support for rich tasks that engaged students in realistic scientific practice where they confronted statistical issues, and he also described how Internet technology facilitated the assessment of project work for a large number of students by providing ready access to peer and tutor feedback. Bulmer commented that students could carry out the virtual experiments without access to statistical software, although the realism and modelling of good statistical practice would suffer from the necessarily limited samples. Callingham (2010) surveyed assessment of statistics using technology, giving examples of technology used in various phases of the assessment process, including an instance where Grade 9 students used technology to create graphs of data. Callingham concluded that more research is needed, especially on the assessment of statistical concepts.

The lack of research is surprising, given that for several decades many practitioners have expected students to use technology in statistics assignments, as a tool for calculation and for handling data. For example, the Victorian Certificate of Education, which combines both timed written examinations and school-based assessments, requires students to use statistical analysis systems in relevant topics and has done so for over 20 years (Victorian Curriculum and Assessment Authority, 2010).

Assessment from Classroom Connectivity

The vision of a connected classroom where teachers and students can exchange electronic information instantaneously and in a usefully collated form has been around for many years. In 1990, a software package called Discourse enabled teachers to set tasks for students, for students to respond, for teachers to monitor students’ responses as they were generated, and, in later versions, to select an individual student’s work and display it for the whole class, either with or without attribution (Heller Reports, 2002). This provides substantial opportunities for immediate formative assessment. However, the promise of such “classroom aggregation technologies” (Roschelle, Abrahamson, & Penuel, 2004) is still to be fully realized.

There have been several studies of the use of classroom aggregation technology for mathematics, such as the wireless-based Texas Instruments Navigator system, which has features like Discourse along with CAS and graphics calculator capabilities. Clark-Wilson (2010) reported on her own and other studies which found more opportunities for students to peer-assess other work and self-assess their own. They found that teachers used student responses to make decisions about the direction of subsequent work. In her study of seven teachers, Clark-Wilson found that all teachers reported new opportunities for formative assessment. By providing better opportunities to monitor students’ work as entered into calculators, teachers gained additional insights, which enabled them to provide thoughtful interventions. They reported various mechanisms by which the discourse in the classroom was enhanced (e.g., discussing an interesting approach by a student to a problem), and in turn this enriched the teacher’s awareness of student thinking. Additionally teachers reported many instances where students changed their opinions and moderated their responses when they saw other students’ work: this provided additional opportunities for peer-assessment and self-assessment. However, learning to teach well with data arriving throughout the lesson appeared to challenge some teachers.

King and Robinson (2009) found that the use of electronic voting systems (which can also be used for immediate formative assessment providing information to teachers and students) in undergraduate mathematics classrooms was viewed positively by most students, and did increase student engagement—even for those students who did not view the electronic voting systems as positive. However, they found no relationship between increased use of electronic voting systems and student achievement.

Reflections

This review of the ways in which technology is changing assessment in mathematics was organized around two broad themes. First, the increasing sophistication and power of technology has supported five main categories of changes in the ways that assessment is conducted:

  1. 1.

    Item preparation and selection: better understanding of what makes items difficult has enabled the automated generation of items with predictable psychometric properties that reduce the cost of assessments, and make it easier to produce practice tests for students to prepare for high-stakes assessments. Technology also permits adaptive testing where the items are selected according to student responses to earlier items, thus increasing test reliability (or, equivalently, reducing test length).

  2. 2.

    Item presentation: technology allows items to be presented to students in ways that would not be possible with paper alone—for example, through the use of assessment models that focus not on how far through an item a student progresses, but the amount of support needed for successful completion of the task, thus improving the assessment experience for the student.

  3. 3.

    Operation: technology allows students to engage in tasks in different ways, and can also ensure that students adhere to constraints imposed on solutions, thus improving the validity of the assessment and expanding characteristics that are assessed, especially by reducing the reliance on verbal communication. Possibilities for authentic assessment are expanded.

  4. 4.

    Evidence identification: technology allows automatic scoring of some responses constructed by students, thus reducing the cost of scoring and supporting automated diagnostic analysis of response patterns. It allows different types of evidence (e.g., response time) to be collected unobtrusively, analyzed and reported.

  5. 5.

    Evidence accumulation: technology supports the development of models of student proficiency that go beyond simple unidimensional scales measuring competence to multidimensional models that allow the provision of detailed feedback to students and teachers.

These changes are blurring the boundaries between teaching and assessment, allowing assessment to become better integrated with instruction, and ultimately offer the prospect of integrated systems of assessment that can serve both formative and summative functions. However, several major obstacles still exist. What is possible now is a promise rather than a reality even in rich countries, not least because existing assessment systems tend to be well accepted in the contexts in which they operate, so change tends to be slow (Black & Wiliam, 2005). Furthermore, moving from pen-and-paper, human-scored systems to technology-based systems involves substantial initial investment costs. Perhaps most significantly, most current human–computer interfaces for mathematics require non-intuitive keyboard-based inputs, and students’ solution processes need to combine paper-based work with computer input.

The second major theme of this chapter has been that technology prompts significant changes in the nature of mathematics that is assessed, and this creates new challenges for teachers and examiners. Creativity is needed to design assessment items which show what mathematical values are held important, and to design systems that are equitable, encourage good learning and focus the attention of teachers and students on mathematical knowledge that is important for the future.

Assessment should focus on the mathematical knowledge and skills that are most valuable. Technology, including dynamic geometry, spreadsheets, and calculators, enables students to explore mathematical ideas for themselves, formulating and testing and resolving hypotheses, so some assessment with technology needs to be without time pressure so that students can show these abilities. Similarly, some extended assessment can look at the whole modelling cycle, from formulating a problem mathematically, to solving it and interpreting the results; a process which technology assists at a number of points. Since technology takes over much of the routine work of solving, even examinations now need to look beyond assessing a narrow bandwidth of mathematical activity. Good assessment practices which permit technology use will be powerful in ensuring that systems achieve the higher-order thinking benefits that educators seek from technology in schools. Designing good assessments with technology also needs to pay attention to equity. High performance in school mathematics is often associated with social advantage, so it is important that use of technology in class or in assessment does not operate to limit further the achievement of socially and economically disadvantaged students. To accomplish all of these goals, assessors need to be very familiar with the capabilities of the technologies permitted and the sometimes unexpected ways in which students might use them.

In summary, new technologies offer considerable potential to provide the capability to support authentic assessments of complex mathematical activity, and to monitor unobtrusively how students interact with the tasks, thus supporting the development of sophisticated models of student proficiency that support the provision of high-quality feedback. Although recent developments in assessment with technology seems to have focussed primarily on the delivery of rich audio–visual content, the real power of computerized assessment is likely, in the future, to be in the creation of learning environments in which students use a range of information resources, engage with powerful software for problem solving, and collaborate with other students.