Keywords

Introduction

The work presented in this chapter is located in the overlapping area of four research and development domains of education which have recently received growing attention. (1) Information communication technologies (ICT) have proliferated in all areas of life, including school learning. The ubiquitous ICT has made it more realistic to transfer all assessment to computerised platforms; therefore, technology-based assessment can be widely utilised to support everyday educational processes (Csapó, Ainley, Bennett, Latour, & Law, 2012). (2) Adapting education to the individual needs of students, and thus giving special support to those who really need it, has always been an intention of educators, but such a goal required assessment instruments that could diagnose students’ difficulties early enough and monitor their progress. Therefore, assessment for learning, i.e. formative and diagnostic assessment, has recently become a dominant field within the research on educational assessment (Black & Wiliam, 1998), especially technology-based assessment. (3) Research has shown that preschool development and the first school years determine later success (Aunola, Leskinen, Lerkkanen, & Nurmi, 2004; Watts, Duncan, Siegler, & Davis-Kean, 2014); therefore early childhood education is one of the most rapidly growing areas in educational research, which development is strongly supported by the means of technology-based formative and diagnostic assessment. (4) Finally, mathematics is one of the most important school subjects; success in learning it has a strong impact on a number of other areas of education, including science. Due to its importance in modern societies in everyday life as well as in science and technology-related professions, mathematics education has become one of the focal areas in improving educational systems. Besides reading and science, it is one of the three most frequently tested domains, both in international and national assessment programmes, thus attracting broad public attention.

There are many initiatives in progress, and a number of computer-based tests are available in the field of mathematics, but they are mainly developed for summative assessment, as well as the large-scale international (OECD PISA, IEA TIMSS) and national assessment programmes (e.g. MAP, Missouri Assessment Program, Missouri; SOL, Standards of Learning, Virginia; OAKS, Oregon Assessment of Knowledge and Skills, Oregon; SBAC, Smarter Balanced Assessment Consortium; PARCC, The Partnership for Assessment of Readiness for College and Careers). There are much fewer formative or diagnostic tests available, especially for measuring younger students’ mathematics knowledge and skills. In general, there is a lack of research-based online diagnostic mathematics tests available for everyday classroom applications. Although there are several initiatives for online assessments (see, e.g. Pearson’s MyMathLab (n.d.); Let’s Go Learn (n.d.); The Diagnostic assessment part of PARCC (n.d.); Math Garden from the University of Amsterdam (n.d.); PAT: Mathematics in New Zealand (n.d.)), but these are all commercial products not completely and freely available for students and teachers.

As an exception, Panamath is available for free, but it is measuring only one part of mathematics’ knowledge, students’ approximate number system (ANS) aptitude. In the Panamath tasks, students are presented two sets of dots (blue and yellow), and they have to decide in a brief flash whether the number of blue or yellow dots is greater. The result tells about the accuracy of the test takers’ basic sense for numbers. It can be used across the entire lifespan from 2-year-olds to old adults (DeWind & Brannon, 2016).

As there are large differences between students in a number of dimensions, successful mathematics education, especially in the first school years, requires differentiated and personalised teaching. This includes early identification of learning difficulties, frequent feedback, individualised well-targeted interventions, and continuous monitoring of development. An assessment system which can diagnose learning difficulties and can be used frequently enough must be built on a deeper understanding of students’ developmental processes, the impacts of mathematics education on it, and the organisation of students’ knowledge in general.

The first part of this chapter presents the advantages and possibilities of technology-based assessment. It describes how technology and its advantages initiated to rethink the purpose of assessment focusing more on diagnostic instead of summative assessment and realising efficient testing for personalised learning. The second part of the chapter summarises the scientific foundations for the diagnostic assessments. The theoretical foundations of framework development have resulted in a three-dimensional framework that outlines mathematics learning and the development of mathematical abilities and skills in three dimensions. These dimensions cover students’ psychological development, the applicability of their knowledge, and the curricular content of teaching. To implement the diagnostic assessment, a complex online platform called eDia has been constructed to support the entire assessment process from item writing through item banking, test delivery, and storing and analysing the data to providing feedback to students and their teachers. The third part of the chapter shows how the mathematics framework has been mapped into an item bank containing over a thousand items by dimension for the first six grades of primary school. The diagnostic assessment system has been offered to schools for application in everyday practice. The fourth part shows the implementation process, some early results from field testing, scaling issues, and framework validation. Finally, the last part discusses how the system can be further developed and how it can be integrated into everyday educational processes to support personalised education and provide customised support for atypical learners of mathematics.

Advantages and Possibilities of Technology-Based Assessment: The Move from Summative to Diagnostic Assessment to Realise Efficient Testing for Personalised Learning

The most prominent educational developments of the past few decades have been aimed at establishing the feedback mechanisms of different levels of educational systems. Therefore, both the theory and the practice of educational assessment have seen considerable advances. Large-scale international assessments have become regularly administered by collaborative teams of experts of the leading test centres of the world. As a result, a huge improvement of data transfer technology and data analysis methods could be witnessed. Systems of assessment and evaluation in national contexts taking into account both the international trends and the local characteristics have been gradually set up. Due to the rapid development, the means of paper-based assessments most widespread and accepted at the millennium imposed serious constraints on their usability. To facilitate potential improvement and meet the twenty-first century needs of the new kinds of assessment and evaluation, an essential qualitative change had to be made (Scheuermann & Pereira, 2008). The direction of the change was mainly determined by technology. The fact that technology has developed, spread, and become accessible offers extraordinary opportunities for the improvement of the practice of educational assessment. Applying technology allows more exact and more varied testing procedures of significantly more complex skills and abilities by devising tasks in more realistic, application-oriented, and authentic testing environments than those of the earlier, paper-based assessments (Beller, 2013; Bennett, 2002; Breiter, Groß, & Stauke, 2013; Bridgeman, 2010; Christakoudis, Androulakis, & Zagouras, 2011; Csapó, Ainley, et al., 2012; Farcot & Latour, 2009; Kikis, 2010; Martin, 2010; Martin & Binkley, 2009; Moe, 2010; Ripley, 2010; van Lent, 2010). Its effectiveness and the increase of effectiveness under certain conditions could be detected on every level of assessment and evaluation.

  • The economy of testing (Bennett, 2003; Choi & Tinkler, 2002; Farcot & Latour, 2008; Peak, 2005).

  • The diversity of test editing and development (Csapó, Ainley, et al., 2012) and the speed of test administration and data flow (Csapó, Lőrincz, & Molnár, 2012).

  • The opportunity to provide instant, objective, and standardised feedback (Becker, 2004; Dikli, 2006; Mitchell, Russel, Broomhead, & Aldridge, 2002; Valenti, Neri, & Cucchiarelli, 2003).

  • The motivation of the students for testing changes (Meijer, 2010; Sim & Horton, 2005).

  • Innovative item development opportunities, multimedia, dynamic, and interactive items, applying second- and third-generation tests (Pachler, Daly, Mor, & Mellar, 2010; Strain-Seymour, Way, & Dolan, 2009), which were impracticable in a paper-based form (Molnár, Greiff, Wüstenberg, & Fischer, 2017).

  • An adaptive test algorithm has become available, which allows a more exact assessment of levels of knowledge and skills and abilities (Frey, 2007; Jodoin, Zenisky, & Hambleton, 2006).

  • The circle of test takers could be extended (e.g. audio version of tasks and instructions could be played, which makes testing of children who cannot read possible) (Csapó, Molnár, & Nagy, 2014).

  • Technology serves as an effective means of logging and analysing contextual data (e.g. the time needed for the execution of a task could be measured; besides the number of attempts made by the student to modify their solutions, the number and location of a student’s clicks during a test could also be mapped) (Csapó et al., 2014). Consequently, instead of the only indicator used in paper-based testing, which is the test result, a rich and well-structured database is available, which makes a more thorough following and analysis of the student’s movements and behaviour possible during the test (Molnár & Lőrincz, 2012).

  • Indicators of test goodness criteria could increase (Csapó et al., 2014; Jurecka & Hartig, 2007; Ridgway & McCusker, 2003).

Although approaching the problem from different perspectives, major relevant research and development projects in an international context (e.g. Assessment and Teaching of 21st Century Skills – ATC21S, Class of 2020 Action Plan; Griffin, McGaw, & Care, 2012; SETDA, 2008) have all agreed that the direction for improvement could be computer-based testing exclusively (Csapó, Ainley, et al., 2012; Pearson, 2012; Scheuermann & Björnsson, 2009). Today computer-based assessment permits more effective assessments than traditional face-to-face or paper-based testing. Therefore, within a reasonably foreseeable time, all important assessment will probably be put on a technological basis. International summative tests have already shown such a tendency. Furthermore, given the opportunity to provide instant feedback on assessments, besides the predominantly summative approach, recently, there has been an emphasis on individualised diagnostic testing in order to enhance fast and effective learning by means of exploiting the learning supporting function of diagnostic testing (Kettler, 2011; Redecker & Johannessen, 2013; Van der Kleij, Eggen, Timmers, & Veldkamp, 2012). Traditional paper-based tests are not suitable for diagnostic assessment, which bottom line is sufficiently frequent student assessment. The development of technology together with that of assessment and evaluation in the past 15 years has created numerous new opportunities in early childhood assessment, which so far have mainly been based on individual data collection (Csapó et al., 2014).

Theoretical Foundations of Framework Development: A Three-Dimensional Model of Mathematical Knowledge

In the history of mathematics education, three perennial goals have remained clear from the very beginning of the history of schooling up to present-day approaches. To create a diagnostic assessment system which can precisely identify students’ weaknesses and strengths, a framework must be created which clearly distinguishes these three directions, three types of goals.

Cultivating general cognitive abilities has always been one of the main declared goals of learning mathematics. Adjusting learning to students’ mental development is a precondition of successful teaching, while obtaining feedback on how maths teaching stimulates the developing mind requires regular testing. To create assessment instruments to meet this goal, psychological processes must be studied.

Another obvious goal is that mathematics education should provide learners with practical skills applicable outside the school context. Seneca’s often cited aphorism, “Non scholae sed vitae discimus”, expresses the expectations of modern societies as well, and this aim, making mathematics education more relevant for the average learner, is embodied in national and international assessment projects.

Finally, mathematics is one of the oldest and best organised bodies of human knowledge. As Banach has formulated his admiration, “Mathematics is the most beautiful and most powerful creation of the human spirit”. To comprehend the organisation of this branch of knowledge, students must study mathematics as a discipline, including its specific terminology, its axioms, theorems, definitions, proofs, etc. Another set of goals can be deduced from this need which can be further shaped taking into account the educational requirements of those students who prepare to be professional users of mathematics, becoming research mathematicians or dealing with high-level applications in a number of other areas of research and development.

A Three-Dimensional Model of Students’ Knowledge for Diagnostic Assessment in Early Education

The arguments for assessing students’ progress in three dimensions may be further elaborated by analysing some national and international assessment frameworks. Large-scale international assessment programmes publish their frameworks well before the actual assessment. The first international assessment programmes in mathematics were conducted by the IEA (International Association for the Assessment of Educational Progress) in the early 1970s and 1980s, and the assessments became regular since 1995 under the acronym TIMSS (Trends in International Mathematics and Science Studies). The early IEA assessments focused on the curricular content of mathematics teaching and were closer to the disciplinary view of mathematics. Although the curricula in the participating countries remained the primary source of content for recent TIMSS assessments, they distinguish the content domains (covering the main domains of mathematics as a discipline) and the cognitive domains which are knowing, applying, and reasoning (Mullis & Martin, 2013).

The other large-scale international programme launched in 2000 under the aegis of the OECD, PISA (Programme for International Student Assessment), aims to assess the knowledge and skills that students are expected to possess at the age of 15 to be prepared for the challenges they will face in modern societies. To characterise the type of broadly applicable knowledge, PISA extended the conception of literacy and termed the assessment domains reading literacy, mathematical literacy, and scientific literacy. For mathematical literacy, a novel definition was developed:

Mathematical literacy is defined in PISA as: the capacity to identify, to understand, and to engage in mathematics and make well-founded judgments about the role that mathematics plays, as needed for an individual’s current and future private life, occupational life, social life with peers and relatives, and life as a constructive, concerned, and reflective citizen. (OECD, 2000, p. 50)

Based on this definition, the framework was elaborated in three dimensions, dealing with mathematical processes, mathematical content, and situations and contexts of applying mathematical knowledge. Both the definition of mathematical literacy and the detailed framework proceeding from it as well as item development placed much stronger emphasis on the application of knowledge as the disciplinary content and the mathematical processes were embedded in contexts and situations relevant for young students living in developed societies. Over the assessment cycles, the conception of mathematical literacy further evolved, and its core idea remained very similar to the original:

Mathematical literacy is an individual’s capacity to formulate, employ and interpret mathematics in a variety of contexts. It includes reasoning mathematically and using mathematical concepts, procedures, facts and tools to describe, explain and predict phenomena. It assists individuals to recognize the role that mathematics plays in the world and to make the well-founded judgments and decisions needed by constructive, engaged and reflective citizens. (OECD, 2016, p. 65)

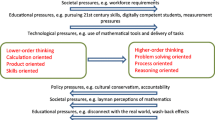
Following the traditions of framework development in international assessment projects and taking into account several further theoretical considerations (see Csapó, 2004, 2010) and empirical results (Csapó, 2007), a three-dimensional model of teaching and learning goals was proposed. This approach (outlined in Fig. 40.1) assumes that these three aspects of teaching should be present at the same time in school education, to develop the intellect and to cultivate thinking and general cognitive abilities. These goals must not exclude each other, and they should not compete for teaching time. Focusing on one of these goals, e.g. teaching the disciplinary content (which traditionally happens in many education systems), is not satisfying in modern societies; students are expected to apply their mathematical knowledge in a broad variety of contexts (as PISA assesses it), and they should be able to solve problems in unknown, novel situations (as was assessed, e.g. in PISA 2012 in the domain of problem-solving, see OECD, 2014). These goals (teaching disciplinary content knowledge in mathematics, preparing students to apply it in a broad range of contexts, and developing thinking skills; see Csapó & Szendrei, 2011) have been competing with each other for teaching time over the past few decades. One or another became from time to time dominant in the curricula; however, they should receive equal attention for interacting and reinforcing each other.

Fig. 40.1
An illustration with three boxes is labeled as follows. 1. Internal or psychological. 2. Social and cultural. 3. Disciplinary or content dimensions linked.

A three-dimensional model for developing a framework of diagnostic assessments. (Csapó, 2007)

Full size image

The model in Fig. 40.1 has been elaborated for each assessment domain taking into account the specific characteristics of the particular domain and has been published in three parallel volumes (see Csapó & Csépe, 2012 for reading; Csapó & Szendrei, 2011 for mathematics; and Csapó & Szabó, 2012 for science). The similarities and differences of these frameworks highlighted the specific roles each domain plays in education. Reading is the basis for all further learning, including mathematics, while mathematics provides foundations for learning certain sciences. Further developmental work (creating items and carrying out assessments with them) based on this three-dimensional framework indicates the validity of the approach in educational practice.

As for mathematics, each dimension has been separately considered and elaborated in detail in the light of literature from the particular field of research. It is of great use to separate these different dimensions in diagnostic assessments because a precise identification of areas of delayed differences is a precondition of personalised interventions. The scope of studying these dimensions is also different. The roots of the psychological development of mathematical reasoning may be universal as far as early neurocognitive development in children is alike across cultures and societies. Studies related to the application dimension can mostly be shared with researchers dealing with the contexts and expectations of developed countries, while the curricular content is related to the national educational system.

The psychological dimension has been conceptualised as the interaction between students’ cognitive development and learning mathematics at school (Nunes & Csapó, 2011). The questions in this dimension are how well mathematics education is adjusted to students’ psychological development, on the one hand, and how learning mathematics can contribute to the development of specific reasoning skills and how effectively it stimulates students’ general cognitive development, on the other. Research in this field provides rich resources ranging from the classical works of Piaget (see, e.g. Inhelder & Piaget, 1958) to the most recent neurocognitive studies. A long list of skills can be taken into account in this field that are strongly embedded in psychological development, such as counting skills, additive and multiplicative reasoning as well as spatial, probabilistic, combinatorial, and proportional reasoning, and so on. Assessments of a number of such skills are especially crucial at the beginning of schooling and in the first school years, as their developmental level determines later success (see Nguyen et al., 2016).

The application dimension of the goals of learning mathematics is interpreted as mastering mathematical literacy, the type of skills that make mathematics useful in areas other than the immediate school context. Mathematics is applied in a number of areas, ranging from other school subjects to a broad cross section of everyday life (Csíkos & Verschaffel, 2011). The key questions in this field are how students can construct mathematical models of problems they face and how well they can mobilise mathematical knowledge to solve those problems. Transfer of knowledge to new contexts is not automatic, and children must learn and practise applying their knowledge. Research on realistic mathematical modelling is the most useful source for elaborating the assessment framework of this dimension (see, e.g. Verschaffel, De Corte, & Lasure, 1994). The tasks that can be taken into account for the measurement of this dimension range from pseudo-real-world to real-world problems which embed mathematical knowledge in a number of relevant contexts and real-life situations.

The disciplinary dimension can be defined as the mathematics content knowledge described in the national core curriculum. This is the prescribed content on which textbooks, local curricula, and teachers’ actual work are based (Szendrei & Szendrei, 2011). A precise translation of the core curriculum into an assessment framework and later on into test tasks makes it possible to monitor how students progress with their daily mathematics studies. Previous research has indicated that mastering and reproducing the immediate teaching material does not necessarily have a long-term impact on students’ cognitive development (see, e.g. Csapó, 2007), but for a precise diagnosis, it is necessary to know if students actually learn what they are expected to in mathematics lessons.

Teaching students disciplinary content knowledge in mathematics, preparing them to apply it, and developing their thinking skills are not considered as exclusive alternatives but processes that reinforce and interact with each other. That is, education must achieve these objectives in an integrated way, but for diagnostic purposes the tests must be able to show if there is insufficient progress in one or another of these dimensions, thus they should be treated as distinct dimensions in diagnostic assessments.

Taking this principle into account and considering the specific aspects of early education and the diagnostic orientation of the assessment, the former tridimensional model was further developed and used as a foundation for item development. The continuum of the first six grades has been divided into 2-year sections, and the test items have been prepared to cover these periods (Csíkos & Csapó, 2011, see Fig. 40.2).

Fig. 40.2
An image illustrating the multidimensional organization of the content of assessments in grades 1 to 6. The dimensions are dimensions of learning, content, and grade.

The model of mathematical knowledge to develop the framework for diagnostic assessment in Grades 1–6. (Csíkos & Csapó, 2011)

Full size image

The three-dimensional approach indicates that these aspects of learning are not independent of each other. Disciplinary content is the means of developing students’ reasoning skills, and this is what students are then expected to apply in other contexts. The following sections show how items were developed for these dimensions, how students’ knowledge is measured in these dimensions, and how their disciplinary knowledge, reasoning skills, and applicable knowledge are related.

Creating an Assessment System: Online Platform Building and Innovative Item Writing

Based on the model of mathematical knowledge described in the previous section, an item bank was constructed for diagnostic assessments. This item bank contains 6182 tasks (each task consists of several items) to measure disciplinary content knowledge in mathematics (MD; n = 2119), mathematical reasoning (MR; n = 1965), and mathematical literacy (MA; n = 2098) in first to sixth grades (age 6–12). The content of the assessment as a function of the three dimensions of learning and target population is shown in Fig. 40.2.

The tasks were grouped into clusters (4–5 tasks per cluster), meaning 15–20 items per cluster for the lower grades and 20–25 items for the higher grades. One 45-min test contains at least three clusters (at least 45–50 items).

In the first to third grades, instructions are provided both in written form and online by a prerecorded voice to prevent reading difficulties and ensure the validity of the results. Thus, students must use headphones during the administration of the tests. After listening to the instructions, they must indicate their answer using the mouse or keyboard (in the case of desktop computers, which is the most common infrastructure in the Hungarian educational system) or directly tapping, typing, or dragging the elements of the tasks with their fingers on tablets. It takes no more than 45 min (one school lesson) to complete the test.

At the beginning of the tests, participants are provided with instructions, including a trial (warm-up) task with immediate feedback, in which they can learn how to use the programme: (1) at the top of the screen, a yellow bar indicates how far the have advanced in the test; (2) they must click on the speaker to be able to listen to the task instruction; (3) to move on to the next task, they must click on the “next” button; and, finally, (4) after completing the last task, they receive game-based immediate feedback with one to ten balloons depending on their achievement. The better their results are, the more balloons they will see over Piglet’s head. The immediate feedback also contains their achievement in each dimension of knowledge.

The feedback system, which is available for the teacher, is more elaborated. As the tasks in the item bank have been scaled by means of IRT, students’ achievement can be objectively compared. Teachers receive feedback on students’ achievements both in percentage and in ability scores, which are comparable to each other and also contain a point of reference to the national standards. In each of the grades and fields, the national-level average achievement was transferred to 500 points with a 100-point standard deviation, which constructs the point of reference to the students’ achievement.

Mathematical Reasoning Items

Based on the framework for the diagnostic assessment of mathematics (Csapó & Szendrei, 2011), reasoning items encompass the measurement of inductive reasoning, deductive reasoning, combinative reasoning, systematisation skills, and proportional reasoning. The task presented in Fig. 40.3 combines the mathematical concept of whole numbers with the assessment of students’ inductive reasoning skills within the context of a famous Hungarian cartoon. In the task, students must discover regularities by detecting dissimilarities with respect to attributes of different objects. In this operation, they must use their knowledge of quantities and their understanding of the relations of greater than, less than and the same. According to Klauer’s definition (1993) of inductive reasoning, students must use the operation of discrimination in this item. In the present case, students can provide their answers by clicking on the “odd-one-out” element, scoring a maximum of 4 points, one in each group of chocolate bars. As demonstrated, inductive reasoning tasks are often connected to other areas of mathematics, in this case to whole numbers and computation.

Fig. 40.3
An illustration of 20 chocolates arranged in four rows and five columns. Each chocolate bar has three columns and four rows. Each chocolate bar represents each group of remaining chocolate.

Mathematical reasoning task: combining the mathematical concept of whole numbers with the assessment of students’ inductive reasoning skills in a familiar Hungarian cartoon

Full size image

In the task presented in Fig. 40.4, students’ systematisation skills and their level of understanding of the number concept are assessed. The formulation and development of the number concept must be supported from three directions: number symbols, the name of the numbers, and the quantities indicated by the numbers.

Fig. 40.4
An illustration of 16 lily pads with numbers on them. The numbers are 4, 7, 13, 10, 7, 12, 5, 16, 9, 18, 8, 19, 10, 20, 4, and 14. Frogs are sitting on lily pads 4, 7, 9, and 10.

Mathematical reasoning task: recognising and combining number symbols and quantities

Full size image

The tasks, which support the connections between these representations, are suitable for diagnostic purposes for the reasoning dimension of counting. The present task provides an example of the combination of number symbols and quantities in a reasoning context. Students need to recognise number symbols and then connect them to quantities and place them in increasing order by clicking on the numbers. In short, the order of the clicking was evaluated.

Mathematical Literacy Items

In the lower grades, mathematical problems become realistic when everyday experiences and observations come to play an active role in the problem-solving process. It is easier to interpret the problem if it is supported by a relevant picture or situation. The word problems can be made realistic if they can be solved with the accompanying picture or by manipulating the pictures given. The task presented in Fig. 40.5 using online technology encompasses an important feature of an authentic problem beyond the real-life-like context; namely, several solutions are possible, and the students can interact with the problem environment. With the scoring procedure, it is all the same which of the teddy bears are placed – dragged and dropped – on the bed; only the number of teddy bears counts. All of the combinations are accepted. The task measures skill level addition up to 10 in a realistic application context.

Fig. 40.5
A cartoon illustration of two teddy bears placed on a bed. Eight bears are placed on the floor.

Mathematical literacy task: adding up to ten in a realistic application context

Full size image

The task presented in Fig. 40.6 illustrates that it is impossible to split the tasks of the three dimensions from each other. It is a mathematical literacy type task, which measures number concept and relations and functions in a realistic application context. The aim is to measure students’ ability to follow, recognise, and continue periodically repeating rhythms and movements by detecting similarities in relations among objects in an application context. Task scoring is automatised for all of the tasks in the item bank, even those with several correct answers. In the present case (Fig. 40.6), students had the option of typing their answer for the number of beads used in the bracelet in several ways, e.g. using number symbols or letters, using small letters or capitals or a mixture of them, or using spaces. All of these possibilities were accepted by the scoring system.

Fig. 40.6
An illustration of the four steps of making a bracelet. The steps include adding beads in a pattern. The beads are red and green.

Mathematical literacy task: following, recognising, and continuing periodically repeating rhythms and movements in a realistic application context

Full size image

Items that Assess Disciplinary Mathematics Knowledge

In early mathematics education, among the most effective teaching methods are learning-by-doing activities. This is also the case for geometry, where students need to discover three-dimensional forms through different activities. The experience gained during these activities provides the foundations and in many cases determines the conceptual building work in lower and higher grades. In an online environment, the possibilities of manipulation play an important role. The task presented in Fig. 40.7 illustrates this. Students need to connect three-dimensional forms built out of cubes with other three-dimensional forms consisting of the same number of cubes by clicking on them to draw the connections. As GeoGebra elements and tasks uploaded from GeoGebraTube can be used in the eDia system, students can even rotate and engage in a manipulative interaction with these three-dimensional geometric forms.

Fig. 40.7
An illustration of eight structures formed with 7 cubes. A structure formed with nine cubes.

Mathematical disciplinary task from geometry involving learning-by-doing with the possibility of manipulative interaction

Full size image

In the first few years of schooling, operations with whole numbers, which build the foundations for additive reasoning, form an essential part of mathematics education. They include not only the operation of addition but all the knowledge elements for comparing quantities and numerosities. By reading the different numbers, sums, and differences, students are prepared for the mathematical concepts of addition and subtraction. In the process of understanding and interpreting addition and subtraction, the number line plays an important role. The task presented in Fig. 40.8 integrates the understanding of number symbols, the operation of addition, the comparison of quantities and numerosities, and the knowledge of relation symbols. During the solution process, students had to click on the name of the child who scored the least points and then choose the right relation symbol from the drop-down menus.

Fig. 40.8
An illustration of a dart board with the markings of John, Mark, Lisa, Mary, and Paul. Their markings are differentiated with various colors. Buttons labeled, click here, are present near the color representation.

Mathematical disciplinary task: integrating the understanding of number symbols, the operation of addition, the comparison of quantities and numerosities, and the knowledge of relation symbols

Full size image

Field Trial and Empirical Validation of the Theoretical Model

We launched a field trial study to ascertain the applicability of computer-based tests in regular educational practice for assessing students at the beginning of schooling and for the empirical validation of the theoretical model of mathematical knowledge introduced above. The objectives of the study were threefold. First, we examined the applicability of an online diagnostic assessment system in the field of mathematics for students at the beginning of schooling. We then empirically validated the three-dimensional model of mathematical knowledge based on research results collected with first graders using eDia, the Hungarian online diagnostic assessment system. Finally, we examined the relationship between disciplinary content knowledge (MD), mathematical reasoning (MR), and mathematical literacy (ML) and answered the research question: how are the three different dimensions of mathematical knowledge related?

The sample was drawn from first-grade students in Hungarian primary schools. School classes formed the sampling units. 5115 first graders were involved in the study. The proportion of girls and boys was about the same.

The instrument was only a part of the whole test battery; it consisted of 48 items, which measured MD, ML, and MR in that order. To prevent reading difficulties, instructions were provided online using a prerecorded voice. Children had to indicate their answer by using the mouse or keyboard. Testing took place in the computer labs at the participating schools. Test completion lasted no more than 45 min (one school lesson). The tests were automatically scored, and students received immediate feedback at the end of the testing.

Reliability, time-on-task, and missing and achievement data were analysed to test the applicability of the online assessment system by first graders. The Rasch model was used to scale the data and draw the three-dimensional item-person map of mathematics. We conducted confirmatory factor analyses (CFA) within structural equation modelling (SEM; Bollen, 1989) to test the underlying measurement model of mathematical knowledge with the three different dimensions: disciplinary knowledge, literacy, and reasoning. Bivariate correlations, partial correlations, and SEM analyses were employed to test construct validity, that is, the relations between the three dimensions of mathematical knowledge.

Why have we conducted confirmatory factor analyses and what is it good for? Confirmatory factor analysis is a special form of factor analyses. In the present case, it is used to test whether the model based on the empirical data is consistent with our understanding of the nature and of the three-dimensional model of mathematical knowledge. That is, the objective of confirmatory factor analysis is to test whether the data fit a hypothesised measurement model, which is based on the three-dimensional theory of knowledge.

Bivariate correlation indicates the numerical relationship, the strength of the association between two measured variables, while partial correlation measures the degree of this association with the effect of controlling variables removed. Bivariate correlations can give misleading results if there is another variable that is related to both of the examined variables. This misleading information can be avoided by computing the partial correlation coefficient. Both of the coefficients take on a value in the range from −1 to 1. The value 0 conveys that there is no relationship, the value −1 means a perfect negative correlation, and the value 1 conveys a perfect positive association.

Construct validity describes the degree to which a test measures what it claims, indicating how well it really covers the targeted content; whether the scale behaves like the theory predicts a measure of that construct should behave. It describes the degree to which empirical evidence and theoretical rationales support the adequacy and appropriateness of inferences and actions based on test scores (Messick, 1995).

Applicability of the Diagnostic System in Everyday School Practice

The results confirmed our hypotheses. The internal consistency of the mathematics test proved to be high both on the test (α = 0.942) and subtest levels (α_MD = 0.89; α_MR = 0.83; α_ML = 0.89), so the results are reliable and generalisable. Less than 0.4%, that is, 18 students out of 5115, were not able to finish the test on time (within 45 min). As none of them completed more than 70% of the test and reached the third subtest, all of their data were deleted from the databases that form the data for the 5097 students involved in the analyses. Generally, the students managed to finish the test within the given timeframe, 1690 seconds on average (sd = 673).

Scaling and Item Difficulty

Participants’ score distribution on the mathematics test also confirmed the applicability of the online assessment system. The mean achievement was about 50% (49.39%, sd = 23.87). The subtest level achievement distribution changed (M_md = 42.29, s = 26.66; M_ml = 53.96, s = 26.67; M_mr = 53.18, s = 28.14) and was significantly different (t_md_ml = −40.96, p < 0.01; M_md_mr = −33.45, p < 0.01; M_ml_mr = 2.35, p < 0.05). The level of standard deviations indicated that the test could be used to test the variability of the sample even on a subtest level.

The three-dimensional item-person map (Fig. 40.9) shows the match between the item difficulty distribution and the distribution of students’ Rasch-scaled achievement estimates for MD, MA, and MR. For any person engaged with an item located at that person’s level, the Rasch model routinely sets the probability of success on the item at 50% on an item-person logit scale.

Fig. 40.9
An illustration of an item-person map of first graders' mathematical knowledge.

The three-dimensional item-person map of first graders’ mathematical knowledge

Full size image

The probability of success increases to 75% for an item that is 1 logit easier or decreases to 25% for an item that is 1 logit more difficult. The MD (green signs) and MA (blue signs) items were well matched to the sample (“x” and number are parallel), and with MR some hard and easy items were missing from the test. The achievement distribution in MD was the highest; there were more low-developed students than in the two other dimensions. Generally, the test was suitable for measuring and discriminating student achievement based on the three-dimensional model of mathematical knowledge in first grade in an online environment.

Gender-level achievement differences changed between the different dimensions. Girls’ achievement proved to be significantly higher on the test level (M_girl = 50.36, s_girl = 23.46, M_boy = 49.01, s_boy = 23.92, t = −2.011, p = 0.044); however, the level of significance might only have been caused by the large sample size. On the subtest level, there were no gender-level achievement differences on the MD and MA subtests, while significant differences could be detected on the reasoning part of the test (t = −2.923, p < 0.01), thus causing the gender-level differences on the test level.

Based on this result, we can conclude that, first, computer-based assessment can be carried out even at the very beginning of schooling without any modern touch screen technology on normal desktop computers using a general browser and the school infrastructure, and, second, the online diagnostic system can be used to test students’ mathematics knowledge at the beginning of schooling in a school context.

Dimensionality and Structural Validity

In validating the three-dimensional model of mathematical knowledge, SEM analyses were outperformed. The three-dimensional measurement model for mathematics showed a good model fit (Table 40.1), based on Hu and Bentler’s (1999) recommended cut-off values. The comparative fit index (CFI) and the Tucker-Lewis index (TLI) value above 0.95 and the root mean square error of approximation (RMSEA) below 0.06 indicate a good global model fit. As significant and high correlations were found between the pairs of dimensions (rMD_MR = 0.685, rMD_ML = 0.749, rML_MR = 0.634, p < 0.001) on a latent level – latent variables are not directly observed but are inferred from other variables that are observed (directly measured) – within the three-dimensional model, we also tested the one-dimensional model with the three dimensions combined under one general factor. With the one-dimensional model, the fit indices decreased considerably.

Table 40.1 Goodness of fit indices for testing dimensionality of mathematics
Full size table

In order to test which model fitted the data better, a special χ2-difference test was carried out in Mplus, which showed that the three-dimensional model fitted significantly better than the one-dimensional model (χ2 = 3389.111; df = 6; p < 0.001). In summary, the three-dimensional model fitted well and better than the one-dimensional model. Thus, the disciplinary, literacy, and reasoning dimensions of mathematical knowledge were empirically distinguished, supporting our hypothesis.

The bivariate correlations between MD, ML, and MR were high, ranging from 0.63 to 0.71 (Fig. 40.10). The relationships proved to be similar between MR and either ML or MD (r = 0.63 and 0.64, p < 0.001, respectively), and they were significantly weaker than the correlation between ML and MD (r = 0.71, p < 0.001).

Fig. 40.10
An illustration between M R, M L, and M D. They are connected with lines and curves. M R is linked to M D with a line labeled, .64 and with a curve labeled, .35. M D is linked to M L with a line labeled, .71 and with a curve labeled, .51. M L is linked to M R with a line labeled, .63 and with a curve labeled, .32.

Relations between MR, ML, and MD (Solid lines depict bivariate correlations; dotted lines represent partial correlations. All coefficients are significant at the p < 0.001 level)

Full size image

Partial correlations were significantly lower as all bivariate relationships were influenced by the third construct (rMR_ML = 0.32; rMR_MD = 0.35; rML_MD = 0.51, p < 0.001). Like the bivariate correlations, the partial correlation coefficients between MR and either ML or MD were of the same strength (p < 0.001), while the partial correlation between ML and MD proved to be the highest. This is supported and was indicated by the correlation coefficients on a latent level as well (see above).

We assumed that disciplinary knowledge and mathematical reasoning predict performance in literacy, the application dimension of mathematics, since we need that dimension of mathematics most in everyday life. Thus, we regressed MD and MR on ML and estimated the proportion of variance explained. The results showed that MD and MR explained performance in ML on a high level (90%) but with a different effect (see Fig. 40.11). The residuals of measures of MD and MR were still correlated on a moderate level (r = 0.35), indicating common aspects of MD and MR that are separable from ML. The model fit well (CFI = 1.000, TLI = 1.000, RMSEA = 0.000).

Fig. 40.11
An illustration of a structural model with M D, M R, and M L. M D and M R are linked with a two-way arrow.

A structural model of mathematical knowledge: disciplinary knowledge and mathematical reasoning as predictors of mathematical literacy (*p < 0.01)

Full size image

To sum up, our results showed that MD, MR, and ML are highly correlated constructs, though not identical. Students’ levels of disciplinary knowledge and mathematical reasoning strongly influence and predict achievement in the context of mathematical application. That is, if we enhance disciplinary knowledge in mathematics and students’ thinking skills, we can expect a stronger transfer from the disciplinary to the application contexts. This suggests that beyond factual knowledge, thinking skills should become an integral part of school agendas (de Koning, 2000) and should be incorporated into a broad range of school-related mathematical learning activities.

Conclusions and Further Research and Development

In this chapter, we have presented the theoretical foundations and technological realisation of an online diagnostic assessment system in the domain of mathematics. The applicability of this system in educational practice was demonstrated in an ecologically valid context, when the online tests were administered to a large sample in real school settings. The assumption that computer-based assessment is applicable even in the early school grades was confirmed. We validated the three-dimensional model of mathematical knowledge empirically, having addressed the psychological, application, and disciplinary dimensions of knowledge. These results strengthen the foundations for a complex online diagnostic assessment platform called eDia, which contains about 2000 tasks (8000 items) per dimension for the first six grades of primary school.

According to the empirical results, the three-dimensional approach is valid; the disciplinary, application, and reasoning aspects of learning are neither independent of nor identical to each other. Consequently, each of these three aspects of knowledge must be enhanced at the same level and at the same time at school, and all of them must be incorporated into a broad range of mathematical learning activities and must not be mutually exclusive. In modern societies, it is neither sufficient nor satisfying to focus on only one of these goals, a common tendency in many education systems in which the teaching of disciplinary content is favoured.

The system can be used to identify students with atypical development, that is, children whose achievement is significantly lower in one of the three dimensions. Teachers receive prompt feedback about their students’ development in each of the dimensions separately in a comparable way. At this moment, in the phase of system development, the system administers the tests having different difficulty levels to the students in a random way; it is not enough to provide only percentage-based feedback to the teachers, as they are strictly taken not objectively comparable to each other. The feedback is based on students IRT-based ability levels in ability points, which can be referred to the national mean ability values that is transferred to 500 (with 100-point standard deviation) in each grade, which constructs the point of reference to the students’ achievement. Beyond the student-level results and national standards, teachers receive feedback about their class-level and school-level achievement with comparison to the other class-level, school-level, regional-level, and strata-level achievements. Our future plan is to put the test administration on an adaptive level.

Training programmes adjusted to their specific deficiencies can then be implemented to help them catch up. The efficacy of such a training can also be monitored with the assessment system. Further research can be carried out with the diagnostic assessment system to explore the reason for an atypical mathematical development and the ways in which the different dimensions of mathematical knowledge can be effectively enhanced.