Analysis of the Single-Period Problem under Carbon Emissions Policies

Abstract

We investigate the classical single-period (newsvendor) problem under carbon emissions policies including the mandatory carbon emissions capacity, the carbon emissions tax, and the cap-and-trade system. Specifically, under each policy, we find a firm’s optimal production quantity and corresponding expected profit, and draw analytic managerial insights. We show that, in order to reduce carbon emissions by a certain percentage, the tax rate imposed on the high-margin firm should be less than that on the low-margin firm for the high-profit perishable products, whereas the high-margin firm should absorb a high tax than the low-margin firm for the low-profit products. Under the cap-and-trade policy, the emissions capacity should be set to a level such that the marginal profit of the firm is less than the carbon credit purchasing price. We also derive the specific (closed-form) conditions under which, as a result of implementing the cap-and-trade policy, the firm’s expected profit is increased and carbon emissions are reduced.

1 Introduction

The past three decades have clearly witnessed an increasingly serious impact of carbon dioxide on the environment. Carbon dioxide has been regarded as the main pollutant that is warming the Earth. It is a greenhouse gas that is emitted through transport, land clearance, and the production and consumption of food, fuels, manufactured goods, materials, wood, roads, buildings, and services CO2List.org (2006). For the purpose of environmental protection, many governments and organizations have been contributing to carbon emissions reduction with a common goal that carbon emissions should be reduced by at least half by 2050, as reported by, e.g., the International Energy Agency (2008).

In practice, a great number of governments have implemented some policies to control carbon emissions. In Congress of the United States (2008), the Congressional Budget Office (CBO) of the Congress of the United States provided a comprehensive study on the policy options for reducing CO₂emissions. We find from the CBO’s study that there are four majorcarbon emissions policies as follows: (i) a mandatory capacity on the amount of carbon emitted by each firm; (ii) a tax imposed to each firm on the amount of carbon emissions; (iii) a cap-and-trade system implemented to allow the emission trading; and (iv) an investment made by each firm in the carbon offsets to meet its carbon capacity requirement. In Sect. 13.2.2, we shall specify these four major policies, and show that the fourth policy can be per se regarded as a special case of the third Policy and it should be thus necessary, and interesting, to investigate the first, the second, and the third policies.

In this paper, we analyze the impact of the three policies on a profit-oriented firm’s production quantity decision. We note that many profit-oriented firms have also observed the importance of the carbon emissions reduction, and responded by developing low-carbon technologies and adopting new and renewable energy resources. Furthermore, the Barloworld Optimus—the logistics arm of the multinational corporation “Barloworld”—reported that, even though over 80% of carbon savings are usually achieved at the product design stage, each firm can reduce carbon emissions by optimizing its operations in production, inventory, and transportation; see, for example, Benjaafar et al. (2010) and BuySmart network (2008). A survey by Accenture.com (2009) indicated that more than 86% supply chain executives have undertaken at least one green initiative in the areas such as recycling, lighting management, and energy-efficient systems. We also learn from Accenture.com (2009) that 10% of companies have actively modeled their supply chain carbon footprints and implemented successful sustainability initiatives.

For our analysis of carbon emissions policies, we focus on the optimal quantity decision of a firm making a perishable item with a short lifespan. The production of the item results in carbon emissions. It is realistic to consider the perishable item for the firm. For example, in the Huber Group (2003), the Huber Group—which provides facility services to commercial, industrial, educational, medical, retail, government, and institutional customers—released a technical information regarding the impact of newspaper printing with the carbon-based ink on the environment. In addition, as reported in Environmental News Energies Correspondent (2009), Carbon Trust, a British governmental organization, suggests that consumers should use real Christmas trees instead of artificial equivalents, because the carbon footprint left by artificial trees is at least ten times greater than real Christmas trees. However, in today’s market, the demand for artificial Christmas trees is still very high; for example, Tesco—the largest British supermarket chain—sold 300,000 artificial Christmas trees in December 2009.

To examine how each carbon emissions policy affects the firm’s production quantity decision, we shall involve a corresponding parameter into the classical single-period model, and address the following questions:

• 1. What are the firm’s optimal production quantity decision and corresponding maximum expected profit under each carbon emissions policy?

• 2. How does the implementation of a policy influence the carbon emissions reduction and the expected profits of the low-margin, the moderate-margin, and the high-margin firms?

• 3. Does there exist a “win–win” scenario in which the carbon emissions are decreased while the firm’s expected profit is not reduced?

Our paper contributes to the literature by analyzing the single-period problem under carbon emissions policies and presenting managerial discussion on the incentive of the firm on the carbon emissions reduction. Even though our discussions on the policies are motivated by the practice of the U.S., our analytic approach and results should be useful to any government who intends to choose a proper policy to reduce carbon emissions. The remainder of this paper is organized as follows: In Sect. 13.2, we briefly review the relevant literature in Sect. 13.2.1, which shows the originality of this paper; and we present our discussion on existing carbon emissions policies in Sect. 13.2.2. In Sect. 13.3, we consider three policies, and for each policy analyze the single-period model to find the corresponding optimal quantity decision. Numerical study with sensitivity analysis are provided in Sect. 13.4. This paper ends with a summary of our results in Sect. 13.5. In addition, a list of major notations used in this paper is given in Table 13.1.

Table 13.1 A list of major notations that are used in this paper

2 Preliminaries: Literature Review and Carbon Emissions Policies

In this section, we briefly review major relevant publications and discuss four carbon emissions policies, which are preliminaries to our analysis of the single-period problem under carbon emissions policies.

2.1 Brief Literature Review

We now review major publications that are closely related to this paper where we analyze the classical single-period model in the presence of carbon emissions policies. For a detailed description of the classical model, see, e.g., Hadley and Whitin (1963). The single-period model has been widely used to investigate a variety of problems in the operations management (OM) area. Khouja (1999) proposed a literature review of various single-period problems. In today’s OM area, many scholars still extend the classical model to incorporate different objectives and utility functions, address different pricing policies, analyze the value of the demand information, etc.

Starting from the middle of 1990s, the carbon emissions-related issues have been attracting the OM scholars’ attention. As a seminal publication, Penkuhn et al. (1997) considered the emission taxes and developed a nonlinear programming model for a production planning problem. Letmathe and Balakrishnan (2005) constructed two analytic models to determine a firm’s production quantities under different environmental constraints. Kim et al. (2009) investigated the relationship between transportation costs and CO₂emissions using the multi-objective optimization method. Cachon (2009) discussed how a reduction in carbon footprints affects supply chain operations and structures.

In recent two years, an increasing number of OM scholars examine some carbon emissions-related issues. For example, Hoen et al. (2010) investigated the effects of two regulation mechanisms on the decision on the transportation mode selection. Benjaafar et al. (2010) discussed how the carbon emissions concerns could be involved into the operational decision-making models with regard to procurement, production, and inventory management. They also provided insights that highlight the impact of operational decisions on the carbon emissions and the importance of the operational models in assessing the benefits of investments in more carbon-efficient technologies. Hua et al. (2010) investigated how firms manage the carbon emissions in their inventory control under the carbon emissions- trading mechanism. They derived the EOQ model, and analytically examined the impact of carbon trade, carbon price, and carbon capacity on order decisions, carbon emissions, and total cost.

In this paper, we consider the classical single-period problem under three carbon emissions policies, which significantly distinguishes our analysis and those by, e.g., Benjaafar et al. (2010) and Hua et al. (2010). Moreover, we quantify the impact of different policies on the emissions reduction and the expected profit of the firm. This further shows the originality of our paper.

2.2 Description of Carbon Emissions Policies

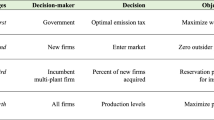
We now describe four major carbon emissions policies that are discussed by the Congressional Budget Office of the Congress of the United States (2008). We begin by presenting a summary of these four policies as given in Table 13.2, where Qdenotes a firm’s production quantity of the items that emit the carbon, and Q _cmeans the mandatory capacity of the production that results in carbon emissions. Moreover, in Table 13.2, τ represents the tax amount paid by the firm for each unit of the item that emits the carbon; and, β and α denote the firm’s unit sale price and unit purchasing price of the carbon credits in the cap-and-trade system, respectively.

Table 13.2 Four major carbon emission policies discussed by the Congressional Budget Office of the Congress of the United States

Next, we discuss the four policies listed in Table 13.2to determine which policies shall be later used to analyze the single-period problem. For our single-period problem under Policy 1 (“mandatory carbon emissions capacity”), the firm’s optimal decision is subject to the mandatory capacity. That is, the firm needs to determine an optimal production quantity that maximizes its profit under the constraint that the firm’s production quantity Qis smaller than or equal to the mandatory capacity Q _c, i.e., Q ≤ Q _c. Note that, to simplify our analysis and facilitate our managerial discussion, we measure the carbon emissions-related parameters and constraints on the product-unit basis throughout the paper. This is justified as follows: In reality, carbon emissions can be generated from production, transportation, inventory, etc. Letting edenote the average carbon emissions generated by making one unit of product over the single period, we find that, when the firm has to adhere to a fixed carbon capacity C, he cannot produce more than ${Q}_{\mathrm{c}} = C/e$products (that is, Q ≤ Q _c). This implies that it is reasonable to use Q _cinstead of Cfor our analysis of the single-period problem.

For our problem under Policy 2 (“carbon emissions tax”), there is no carbon emissions constraint; but, the firm absorbs the tax on the amount of carbon emissions. Specifically, denoting by τ the carbon tax charged for one unit of product, we can calculate the firm’s total tax payment as τQ. Under Policy 3 (“cap-and-trade”), the firm has prescribed carbon credits from the policy-maker, which allow the firm to produce at most Q _c units of products. However, the firm can trade extra (unused) carbon credits through a cap-and-trade system to vary its carbon capacity. This means that, in the cap-and-trade system, the firm can buy and sell the “right to emit.”

Under Policy 4 (“investment in the carbon offsets”), the firm can invest in the carbon emissions-reduction projects to offset emissions in excess of the capacity Q _c. We note that the investment under Policy 4 is per sethe same as the credit purchase in a cap-and-trade system under Policy 3 with β = 0. That is, if the firm’s unused carbon credits cannot be sold, i.e., β = 0, then Policy 3 is equivalent to Policy 4 because α can be assumed to be the unit investment cost. Hence, Policy 4 can be regarded as a special case of Policy 3. For generality, we do not analyze our single-period problem under Policy 4 in this paper.

According to the above, we subsequently investigate the impact of Policies 1, 2, and 3 on the optimal decision in the single-period problem.

3 Analysis of the Single-Period Problem Under Carbon Emissions Policies

In this section, we analyze the classical single-period inventory model under three carbon emissions policies—i.e., Policies 1, 2, and 3 in Table 13.2. Our analytic results are also compared to investigate the impact of the three policies on the reduction in carbon emissions and the firm’s expected profit. Next, we start with the firm’s single-period inventory problem under Policy 1.

3.1 The Single-Period Problem Under Policy 1 (Mandatory Carbon Emissions Capacity)

For our analysis of the classical single-period problem, we let Xdenote the aggregate demand, which is assumed to be a random variable with the probability density function (p.d.f.) f(x) and the cumulative distribution function (c.d.f.) F(x). In addition, pis the selling price per unit of the perishable product; cis the firm’s unit acquisition cost; sis the shortage (stockout) cost for each unsatisfied demand; and vis the salvage value per unit of the unsold product. Then, c _o ≡ c − vis the unit overage cost, and ${c}_{\mathrm{u}} \equiv p + s - c$represents the unit underage cost. Note that Qdenotes the firm’s order quantity, as defined in Table 13.1.

Using the above, we write the firm’s expected profit function as,

$$\begin{array}{rlrlrl} J\left (Q\right ) & = \left (p - v\right )\int \limits _{0}^{Q}xf\left (x\right )\mathrm{d}x + \left (p + s - c\right ){\int \nolimits \nolimits }_{Q}^{\infty }Qf\left (x\right )\mathrm{d}x & & \\ &\quad \,\, - s \int \nolimits _{Q}^{\infty }xf\left (x\right )\mathrm{d}x -\left (c - v\right )\int \limits _{0}^{Q}Qf\left (x\right )\mathrm{d}x. &\end{array}$$

(13.1)

We learn from our discussion in Sect. 13.2.2that, in order to find optimal quantity Q ^∗under Policy 1 (“mandatory carbon emissions capacity”), the firm should maximize its expected profit $J\left (Q\right )$in (13.1) under the constraint that Q ≤ Q _c, where Q _cis the mandatory capacity. That is, the firm’s maximization problem under Policy 1 is written as follows: ${\max }_{\mathrm{Q\leq {Q}_{\mathrm{c}}}}J(Q)$.

Theorem 1.

For the single-period problem under Policy 1 (mandatory carbon emissions capacity), the optimal quantity decision is found as ${Q}_{1}^{{_\ast}} =\min \left ({Q}^{{_\ast}},{Q}_{\mathrm{c}}\right )$ , where Q ^∗ is optimal solution of the classical single-period problem, i.e.,

$${Q}^{{_\ast}} = {F}^{-1}\left (w\right ),\quad \mathrm{where}\ w \equiv \frac{{c}_{\mathrm{u}}} {{c}_{\mathrm{u}} + {c}_{\mathrm{o}}} = \frac{p + s - c} {p + s - v}\mathrm{.}$$

(13.2)

Proof.

For a proof of this theorem and the proofs of all subsequent theorems, see 13.5​.

From the above theorem, we note that Policy 1 is effective only when the mandatory capacity Q _cdoes not exceed the Q ^∗, i.e., Q _c ≤ Q ^∗. Otherwise, if Q _c > Q ^∗, then the firm always determines its optimal solution as Q ^∗for any value of Q _c, which means that the firm’s optimal solution under Policy 1 is the same as that with not any policy. It thus follows that, in order to effectivelyreduce carbon emissions generated by the firm, the policy-maker needs to set the mandatory capacity as a value lower than the firm’s optimal decision under no policy constraint.

Theorem 1also indicates that we can compute Q ₁ ^∗when the c.d.f. F(x) is explicitly given. For simplicity, we hereafter assume that the aggregate demand Xfor the perishable product is normally distributed with mean μ and standard deviation σ, i.e., X ∼ N(μ, σ). We thus have,

$$J\left ({Q}^{{_\ast}}\right ) = \mu \left (p - c\right ) - \sigma \left ({c}_{\mathrm{ u}} + {c}_{\mathrm{o}}\right )\phi \left ({z}^{{_\ast}}\right )\text{,}$$

(13.3)

where ${z}^{{_\ast}}\equiv ({Q}^{{_\ast}}- \mu )/\sigma$, and ϕ is the p.d.f. of the standard normal distribution.

3.2 The Single-Period Problem Under Policy 2 (Carbon Emissions Tax)

Under the policy, the firm needs to pay the tax $τ for each unit of product, as discussed in Sect. 13.2.2. This means that the firm incurs the per unit cost $τ in addition to its acquisition cost c. Thus, we can easily write the firm’s corresponding profit function, by replacing cin $J\left (Q\right )$given in (13.1) with c + τ. As a result, the optimal production quantity under Policy 2 is given as,

$${Q}_{2}^{{_\ast}} = {F}^{-1}\left (\frac{p + s - c - \tau } {p + s - v} \right ) = {F}^{-1}\left ({w}_{ 2}\right ).$$

(13.4)

Next, we discuss the effect of the carbon tax τ on the reduction in carbon emissions. More specifically, we need to consider the following question: what should be the value of τ if we desire to reduce the firm’s carbon emissions by a certain percentage. Note that, if Policy 2 does not apply, then the firm’s optimal quantity decision is Q ^∗, as given in (13.2); and, if this policy applies, then the optimal decision is Q ₂ ^∗as in (13.4). Therefore, the reduction in carbon emissions can be calculated as $\kappa \equiv ({Q}^{{_\ast}}- {Q}_{2}^{{_\ast}})/{Q}^{{_\ast}}$.

In addition, we should also consider the impact of the profitability-related attributes of the perishable product on the policy-maker’s tax decision. As discussed by Schweitzer and Cachon (2000), in the single-period problem, the perishable product with w ₂ ≥ 0. 5 and that with w ₂ < 0. 5—where wis defined as in Theorem 1—are called a high-profit product and a low-profit product, respectively. Noting that the aggregate demand Xfollows a normal distribution, we find from (13.2) that Q ^∗ ≥ μ for the high-profit products with w ₂ ≥ 0. 5, and Q ^∗ < μ for the low-profit products with w ₂ < 0. 5. Furthermore, it should be interesting to investigate whether or not the firm selling a high-profit product and the firm selling a low-profit product should have the same tax payment if they desire to achieve a same emission-reduction percentage κ.

Theorem 2.

If the firm makes a high-profit perishable product (i.e., w ₂ ≥ 0.5), then the carbon emissions-reduction percentage κ isdecreasing in c, i.e., ∂κ∕∂c < 0. But, if the firm makes a low-profit perishable product (i.e., w ₂ < 0.5), then the carbon emissions-reduction percentage κ isincreasing in c, i.e., ∂κ∕∂c > 0.

As the above theorem indicates, for a high-profit and a low-profit products under Policy 2 with a fixed value of the carbon tax τ, we find that, ceteris paribus, the carbon emissions-reduction percentage κ varies in differentmanners as the unit cost is changed. For a high-profit product, the reduction decreases as cincreases, whereas, for a low-profit product, the reduction increases as cincreases. The result implies an important insight from the perspective of the policy-maker, as given in the following remark.

Remark 1.

The policy-maker should consider the attributes of the perishable product and the unit acquisition cost of the firm, in order to achieve the emissions reduction at a certain desired level. Specifically, for a given value of κ, if the perishable product belongs to the high-profit category, then the tax rate τ imposed on the high-margin firm (i.e., its unit acquisition cost cis small) should be less than that on the low-margin firm (i.e., cis high). On the other hand, for the low-profit product, the high-margin firm should absorb a high tax than the low-margin firm.

3.3 The Single-Period Problem Under Policy 3 (Cap-and-Trade)

Under the policy, the firm has to buy the carbon credits at the per unit price α if it produces more than the prescribed capacity Q _c. We thus calculate the purchasing cost of carbon credits as $\alpha {\left (Q - {Q}_{\mathrm{c}}\right )}^{+}$, where,

$${ \left (Q - {Q}_{\mathrm{c}}\right )}^{+} =\max (Q-{Q}_{\mathrm{ c}},0) = \left \{\begin{array}{ll} Q - {Q}_{\mathrm{c}}\text{,}&\text{ if }Q \geq {Q}_{\mathrm{c}}\text{,} \\ 0\text{,} &\text{ otherwise.} \end{array} \right.$$

(13.5)

Note that, if Q _c ≤ Q, then $\alpha {\left (Q - {Q}_{\mathrm{c}}\right )}^{+} = 0$, which implies that the firm makes no payment if it does not need any extra carbon credits. However, the firm may benefit from emitting less than the capacity Q _cby selling its unused carbon credits in the trading market. In fact, for the single-period problem where the unused credits should be salvaged, the firm has to sell unused credits and thus obtain the revenue as $\beta {\left ({Q}_{\mathrm{c}} - Q\right )}^{+}$.

Therefore, the firm’s expected profit under the cap-and-trade policy can be written as,

$${J}_{3}\left (Q\right ) = J\left (Q\right ) + \alpha {(Q - {Q}_{\mathrm{c}})}^{+} + \beta {({Q}_{\mathrm{ c}} - Q)}^{+}\text{,}$$

(13.6)

where $J\left (Q\right )$is given as in (13.1); and as discussed above, the second and third terms can be regarded as the firm’s “penalties” and “rewards” generated by transferring carbon credits under the cap-and-trade policy, respectively. The firm should maximize ${J}_{3}\left (Q\right )$in (13.6) to find the optimal quantity Q ₃ ^∗under Policy 3.

Theorem 3.

When Policy 3 (“cap-and-trade”) is implemented, we find the firm’s optimal quantity decision Q ₃ ^∗ as given in Table  13.3, where Q ^∗ is the optimal solution for the classical single-period problem, as given in(13.2); and,

$${w}_{\alpha } \equiv \frac{{c}_{\mathrm{u}} - \alpha } {{c}_{\mathrm{u}} + {c}_{\mathrm{o}}}\text{, }{w}_{\beta } \equiv \frac{{c}_{\mathrm{u}} - \beta } {{c}_{\mathrm{u}} + {c}_{\mathrm{o}}}\text{, }\gamma \equiv {\left.\frac{\mathrm{d}J(Q)} {\mathrm{d}Q} \right \vert }_{Q={Q}_{\mathrm{c}}}.$$

(13.7)

Note that γ in(13.7) means the firm’smarginal profit at the point that Q = Q _c . Moreover, the firm’s corresponding expected profit is also calculated as in Table  13.3. ■

We learn from Theorem 3that, if Q _cis sufficiently high such that Q _c ≥ Q ^∗, then the firm’s optimal production quantity should be smaller than the capacity Q _cand the firm should sell its unused carbon credits under the cap-and-trade policy. For this case, the trade-off between reducing the production quantity and selling unused carbon credits is that the revenue reduction generated by decreasing Qfrom Q ^∗to Q ₃ ^∗should be compensated by selling the increments in the unused carbon credits (i.e., Q ^∗ − Q ₃ ^∗).

Remark 2.

Theorem 3indicates that the firm’s carbon emissions could be reduced when a propercap-and-trade policy is implemented. Specifically, the amount of the carbon-emissions reduction depends on the values of α, β, c _u, and γ. In order to assure that the firm’s carbon emissions are reduced to Q _cor less, the policy-maker should set the unit carbon-credit purchasing cost α no less than γ, i.e., α ≥  γ; otherwise, Policy 3 may not be effective in reducing carbon emissions that are generated by the firm.

We find from Theorem 3that Q ₃ ^∗ = 0 when β ≥ c _u. This implies that the firm can profit more from selling carbon credits than from selling perishable products, when the price for carbon credits is extremelyhigh. In practice, the policy-maker should effectively “manage” the cap-and-trade market to prevent the firm from acting as a carbon credit “dealer” instead of as a product “manufacturer.”

Corollary 1.

When Q ^∗ > Q _c and c _u > β > γ, we find that

$$\left \{\begin{array}{cl} {J}_{3}\left ({Q}_{3}^{{_\ast}}\right ) \geq J\left ({Q}^{{_\ast}}\right )\text{,}&\text{ if }\beta \geq {\beta }_{0} \equiv {c}_{\mathrm{u}} -\left ({c}_{\mathrm{u}} + {c}_{\mathrm{o}}\right )F\left (2{Q}_{\mathrm{c}} - {Q}^{{_\ast}}\right )\text{ ;} \\ {J}_{3}\left ({Q}_{3}^{{_\ast}}\right ) < J\left ({Q}^{{_\ast}}\right )\text{,}&\text{ if }\beta < {\beta }_{0}. \end{array} \right.$$

Proof.

For a proof of this corollary, see 13.5​.

From the above corollary, we note that, if Q ^∗ > Q _c, c _u > β > γ, and β ≥ β₀, then, as a result of implementing Policy 3, the firm’s profit is increased (i.e., ${J}_{3}\left ({Q}_{3}^{{_\ast}}\right ) \geq J\left ({Q}^{{_\ast}}\right )$) and its carbon emissions are decreased (i.e., Q ₃ ^∗ < Q _c). That is, under the conditions that Q ^∗ > Q _c, c _u > β > γ, and β ≥ β₀, the firm should be willing to reduce its production quantity under Policy 3 and the policy is thus effective.

Table 13.3 The firm’s optimal quantity decision Q ₃ ^∗under Policy 3 (“cap-and-trade”). Note that w _α, w _β, and γ are defined as in (13.7)

4 Numerical Study

In this section, we provide numerical examples to illustrate our analysis in Sect. 13.3. Since the analysis under Policy 1—which is provided in Sect. 13.3.1—is simple, we next compute the firm’s optimal production quantities and expected profits under Policy 2 (carbon emissions tax) and Policy 3 (cap-and-trade). For simplicity, we assume that the firm does not incur a shortage cost (i.e., s = 0) and does not have a salvage value (i.e., v = 0). In addition, X ∼ N(500, 150), and p = 100. We consider several scenarios that differ in the values of other parameters including the unit acquisition cost c, the carbon tax τ, the unit carbon-credit purchasing cost α, the unit carbon-credit selling price β, and the prescribed emissions capacity Q _c.

4.1 Numerical Example for Policy 2

We now provide an example to illustrate our analysis for Policy 2 in Sect. 13.3.2. In this example, we use four different values of the unit cost cto represent four types of products, which include two high-profit products (c = 15 and c = 35) and two low-profit products (c = 65 and c = 85). For each product, we consider three scenarios, and for each scenario, we compute the corresponding optimal quantity for the firm.

In the first scenario, we assume that there is no capacity constraint. Accordingly, we calculate Q ^∗and $J\left ({Q}^{{_\ast}}\right )$. In the second scenario, we assume that the carbon tax τ is equal to 10, and we calculate Q ₂ ^∗and ${J}_{2}\left ({Q}_{2}^{{_\ast}}\right )$, which are then compared with Q ^∗and $J\left ({Q}^{{_\ast}}\right )$in the first scenario, respectively. We also compute the emissions reduction percentage $\kappa = ({Q}^{{_\ast}}- {Q}_{2}^{{_\ast}})/{Q}^{{_\ast}}$and find the profit decrease percentage $\omega \equiv [J({Q}^{{_\ast}}) - {J}_{2}({Q}_{2}^{{_\ast}})]/J({Q}^{{_\ast}})$. In the third scenario, assuming that the firm desires to reduce carbon emissions by a specific percentage κ (e.g., κ = 10%), we calculate Q ₂ ^∗, ${J}_{2}\left ({Q}_{2}^{{_\ast}}\right )$, and ω; and also compute the corresponding tax rate τ in order to achieve the emissions reduction percentage κ. Our numerical results are presented in Table 13.4.

Table 13.4 The firm’s optimal quantities and corresponding expected profits in three scenarios

As Table 13.4indicates, the firm’s optimal production quantity is reduced as a result of implementing the carbon tax policy. From Scenario 2, we find that, if the per unit tax rate is 10, then the carbon emissions reduction for the high-profit products decreases as the profit margin (p − c) decreases, whereas the reduction for the low-profit products significantly increases (from 9.73% to 26.38%) as the profit margin declines. We also note that the profit reduction percentage ω is strictly increasing in c; that is, if the profit margin is reduced, then the profit reduction percentage is increased.

In Scenario 3, when the carbon-emissions reduction percentage κ is equal to 10% for all products, the tax rate τ imposed on the high-profit product with c = 35 should be higher than that imposed on the high-profit product with c = 15. On the other hand, for the two low-profit products, the tax rate τ should be higher for the product with a smaller value of c. We also find that, even though the profit reduction percentage ω increases as the profit margin decreases, the increases for the four products are not as significant as those in Scenario 2.

4.2 Numerical Example for Policy 3

We now consider two examples to illustrate our analysis for Policy 3 in Sect. 13.3.3. From Theorem 3, we find that the firm’s optimal quantity decision depends on the comparison between Q ^∗and Q _c. Next, we first present an example for the case that Q _c ≥ Q ^∗, using the values of the unit acquisition cost cfor four products as in Sect. 13.4.1. Setting the specific values of Q _cand β for each product, we present our calculation results in Table 13.5, where we find that, for each product, carbon emissions are decreased but the firm’s expected profit is increased.

Table 13.5 The numerical results when Q ^∗ ≤ Q _c

Next, we present another example to illustrate our analysis for the case that Q _c < Q ^∗. We set α = 12. 5 and β = 10, and we select three different values of Q _cfor each product, as given in Table 13.6, where we find the following results. For each product, Q ₃ ^∗is reduced as Q _cis smaller; and, ${J}_{3}\left ({Q}_{3}^{{_\ast}}\right )$is greater than $J\left ({Q}^{{_\ast}}\right )$as long as β > β₀. We also find that Q _cmore significantly impacts Q ₃ ^∗and ${J}_{3}\left ({Q}_{3}^{{_\ast}}\right )$for the low-profit products than for the high-profit products. In addition, if the profit margin is lower, then the impact of the carbon capacity on carbon emissions and the firm’s expected profit are more significant.

Table 13.6 The numerical results when Q ^∗ > Q _c

5 Summary and Concluding Remarks

In this paper, we investigated the single-period problem under three carbon emissions policies including the mandatory carbon emissions capacity, the carbon emissions tax, and the cap-and-trade system. Under each policy, we obtained the optimal production quantity and calculated the corresponding expected profits for the firm. From our analysis, we draw some important analyticmanagerial insights. For example, we showed that, in order to reduce carbon emissions by a certain percentage, the tax rate τ imposed on the high-margin firm should be less than that on the low-margin firm for the high-profit perishable products, whereas the high-margin firm should absorb a higher tax than the low-margin firm for the low-profit products.

We also found that, from the perspective of the policy-maker, the emissions capacity should be set to a level such that the marginal profit of the firm is less than the carbon credit purchasing price, because, otherwise, the firm would produce more than the emissions capacity. We also derived the specific conditions under which, as a result of implementing the cap-and-trade policy, the firm’s expected profit is increased and carbon emissions are reduced. The conditions assure the firm’s and the policy-maker’s incentives on the cap-and-trade policy.

The research problem discussed in this paper could be extended in several directions. In future, we may relax the single-period assumption and consider the quantity decisions of nonperishable products in multiple periods. In another possible research direction, we may also consider pricing decision for the firm, assuming the price-dependent aggregate demand in an additive and a multiplicative function form. In addition, from the policy-maker prospective, it would be nice if one could propose a way for a firm to select the best policy. The method of choosing the best carbon emission reduction policy for a given managerial situation likely has critical business implications for manufacturers.

6 Appendix Appendix A: Proofs of Theorems

Proof of Theorem 1.

Temporarily ignoring the constraint that Q ≤ Q _c, we can solve the classical single-period problem to find that

$$F\left ({Q}^{{_\ast}}\right ) = w \equiv \frac{p + s - c} {p + s - v}.$$

(13.8)

Taking the constraint into consideration, we can easily obtain the result in this theorem.

Proof of Theorem 2.

To discuss the impact of won the effectiveness of the carbon tax policy, we assume that the unit cost cin (13.4) takes two different values, e.g., c ₁and c ₂(w.l.o.g., c ₁ < c ₂); and then, ceteris paribus, the corresponding optimal quantities given by (13.2) are $\hat{{Q}}_{2}^{{_\ast}}$and $\tilde{{Q}}_{2}^{{_\ast}}$, respectively.

Using (13.2) and (13.4), we find that, replacing cwith c + τ, the optimal production quantity is changed from Q ^∗to Q ₂ ^∗. If τ → 0⁺, then ${Q}^{{_\ast}}- {Q}_{2}^{{_\ast}} = -\mathrm{d}{Q}^{{_\ast}}/\mathrm{d}c$. Differentiating both sides of (13.8) once w.r.t. c, we have, $\mathrm{d}{Q}^{{_\ast}}/\mathrm{d}c = -1/[\left (p + s - v\right )f\left ({Q}^{{_\ast}}\right )]$. It thus follows that, as τ → 0⁺, $\kappa = ({Q}^{{_\ast}}- {Q}_{2}^{{_\ast}})/{Q}^{{_\ast}} = 1/[\left (p + s - v\right )f\left ({Q}^{{_\ast}}\right )]$, which is easily shown to be strictly increasing in Q ^∗when Q ^∗ ≥ μ but strictly decreasing in Q ^∗when Q ^∗ < μ. Therefore, for a high-profit product, $\hat{{Q}}_{2}^{{_\ast}} >\tilde{ {Q}}_{2}^{{_\ast}}$, and $\hat{\kappa } \equiv (\hat{{Q}}^{{_\ast}}-\hat{ {Q}}_{2}^{{_\ast}})/\hat{{Q}}^{{_\ast}} >\tilde{ \kappa } \equiv (\tilde{{Q}}^{{_\ast}}-\tilde{ {Q}}_{2}^{{_\ast}})/\tilde{{Q}}^{{_\ast}}$, whereas, for a low-profit product, $\hat{\kappa } <\tilde{ \kappa }$. This theorem is thus proved.

Proof of Theorem 3.

We find from (13.6) that J ₃(Q) is a continuous, piecewise function in Q. We next consider two cases: Q _c < Q ^∗and Q _c ≥ Q ^∗; and for each case, we compute the corresponding optimal decision Q ₃ ^∗.

When Q _c < Q ^∗, we depict four scenarios as shown in Fig. 13.1; and, for each scenario, we compute the optimal solution Q ₃ ^∗as follows: If β ≥ c _u, then we find from Fig. 13.1(1) that J ₃(Q) is strictly decreasing in Qover $\left [0,+\infty \right )$; and thus, the optimal quantity maximizing J ₃is Q ₃ ^∗ = 0, and ${J}_{3}\left ({Q}_{3}^{{_\ast}}\right ) = \beta {Q}_{\mathrm{c}} - s\mu$. If c _u > β > γ, then as Fig. 13.1(2) indicates, Q ₃ ^∗can be obtained as ${Q}_{3}^{{_\ast}} = {F}^{-1}\left ({w}_{\beta }\right )$, which is in the range $\left (0,{Q}_{\mathrm{c}}\right )$. If β ≤ γ ≤ α, then, as Fig. 13.1(3) indicates, J ₃(Q) is increasing in $Q \in \left [0,{Q}_{\mathrm{c}}\right ]$but decreasing in $Q \in \left ({Q}_{\mathrm{c}},+\infty \right )$. The optimal solution Q ₃ ^∗is thus determined as Q ₃ ^∗ = Q _c. If α < γ, then ${Q}_{3}^{{_\ast}} = {F}^{-1}\left ({w}_{\alpha }\right ) \in \left ({Q}_{\mathrm{c}},+\infty \right )$, as shown in Fig. 13.1(4).

Fig. 13.1

The analysis of J ₃(Q) in four scenarios: (1) β > c _u , (2) c _u  > β > γ, (3) β < γ < α, and (4) α < γ

When Q _c ≥ Q, we find from (13.6) that ${J}_{3}(Q) = J\left (Q\right ) + \beta \left ({Q}_{\mathrm{c}} - Q\right )$, which is a concave function of Q. Similarly, we can show that J ₃(Q) is a decreasing, concave function of Qin the range $\left ({Q}_{\mathrm{c}},+\infty \right )$. Thus, the optimal solution Q ₃ ^∗must exist in the range $\left [0,{Q}_{\mathrm{c}}\right ]$. If J ₃(Q) is also strictly decreasing in Q ∈ 0, Q _c, then Q ₃ ^∗ = 0. Otherwise, Q ₃ ^∗should be obtained by solving $\mathrm{d}{J}_{3}(Q)/\mathrm{d}Q = 0$; that is, ${Q}_{3}^{{_\ast}} = {F}^{-1}\left ({w}_{\beta }\right )$. Noting that $\mathrm{d}{J}_{3}(Q)/\mathrm{d}Q{\vert }_{Q=0} < 0$ onlyif β > c _u, we find that Q ₃ ^∗ = 0 if β > c _u; ${Q}_{3}^{{_\ast}} = {F}^{-1}\left ({w}_{\beta }\right )$otherwise. In addition, Q ₃ ^∗ ≤ Q _cbecause w _β ≤ w; and, ${J}_{3}\left ({Q}_{3}^{{_\ast}}\right ) \geq J\left ({Q}^{{_\ast}}\right ) + \beta \left ({Q}_{\mathrm{c}} - {Q}^{{_\ast}}\right ) \geq J\left ({Q}^{{_\ast}}\right )$.

7 Appendix Appendix B: Proof of Corollary 1

We learn from Theorem 3that, if c _u > β > γ, then ${Q}_{3}^{{_\ast}} = {F}^{-1}\left ({w}_{\beta }\right )$and $\Phi \left ({z}_{3}^{{_\ast}}\right ) = {w}_{\beta }$. Hence, z ₃ ^∗is dependent on β, and $\phi \left ({z}_{3}^{{_\ast}}\right )$can be written as $\phi \left ({z}_{3}^{{_\ast}}\right ) = -[1/(p + s - v)] \times (\mathrm{d}\beta /\mathrm{d}{z}_{3}^{{_\ast}})$. Using (13.3), we have,

$$\begin{array}{rlrlrl} {J}_{3}\left ({Q}_{3}^{{_\ast}}\right ) - J\left ({Q}^{{_\ast}}\right ) & = \beta \left ({Q}_{\mathrm{ c}} - \mu \right ) + \sigma \left ({c}_{\mathrm{u}} + {c}_{\mathrm{o}}\right )\left [\phi \left ({z}^{{_\ast}}\right ) - \phi \left ({z}_{ 3}^{{_\ast}}\right )\right ] & & \\ & = \beta \left ({Q}_{\mathrm{c}} - \mu \right ) + \sigma {\beta }^{{\prime}} + \sigma \left ({c}_{\mathrm{ u}} + {c}_{\mathrm{o}}\right )\phi \left ({z}^{{_\ast}}\right ). &\end{array}$$

(13.9)

Equating ${J}_{3}\left ({Q}_{3}^{{_\ast}}\right )$to $J\left ({Q}^{{_\ast}}\right )$and solving the resulting equation for β, we find that

$$\beta = \frac{\sigma \left ({c}_{\mathrm{u}} + {c}_{\mathrm{o}}\right )\phi \left ({z}^{{_\ast}}\right )} {{Q}_{\mathrm{c}} - \mu } [{e}^{({Q}_{\mathrm{c}}-\mu )\left ({z}^{{_\ast}}-{z}_{ 3}^{{_\ast}}\right )/\sigma } - 1].$$

(13.10)

Substituting β in (13.9) into (13.10), we obtain z ₃ ^∗as ${z}_{3}^{{_\ast}} = {z}^{{_\ast}} = 2\left ({Q}_{\mathrm{c}} - \mu \right )/\sigma - {z}^{{_\ast}}$. It is easy to show that the corresponding value of β for z ₃ ^∗is ${\beta }_{0} = {c}_{\mathrm{u}} -\left ({c}_{\mathrm{u}} + {c}_{\mathrm{o}}\right )F\left (2{Q}_{\mathrm{c}} - {Q}^{{_\ast}}\right )$. We also find that ${J}_{3}\left ({Q}_{3}^{{_\ast}}\right ) - J\left ({Q}^{{_\ast}}\right ) >0$for β > β₀, but ${J}_{3}\left ({Q}_{3}^{{_\ast}}\right ) - J\left ({Q}^{{_\ast}}\right ) < 0$for β < β₀.