Topological Hypergraphs

Abstract

Let P be a set of n points in the plane. A topological hypergraphG, on the set of points of P, is a collection of simple closed curves in the plane that avoid the points of P. Each of these curves is called an edge of G, and the points of P are called the vertices of G. We provide bounds on the number of edges of topological hypergraphs in terms of the number of their vertices under various restrictions assuming the set of edges is a family of pseudo-circles.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

A topological graph is a graph drawn in the plane with its vertices drawn as points and its edges drawn as Jordan arcs connecting corresponding points. In this chapter we make an attempt to generalize the notion of a topological graph and consider topological hypergraphs.

Definition 1.1.

Let C be a simple closed Jordan curve in the plane. By Jordan’s theorem, C divides the plane into two regions, only one of which is bounded. We call the bounded region the disc bounded by C and we denote this region by disc(C). Any point x inside disc(C) is said to be surrounded by C, and C is said to be surrounding x.

We are now ready to define a topological hypergraph. A topological hypergraphG is a pair $(P,\mathcal{C})$, where P is a finite set of points in the plane, and $\mathcal{C}$ is a family of simple closed curves in the plane that avoid the points of P. For each curve $C \in \mathcal{C}$, we denote by P _C the set of all points of P surrounded by C. C is called an edge of G and the set P _C is the set of vertices of the edge C. Two edges of G, C ₁ and C ₂, are called parallel if ${P}_{{C}_{1}} = {P}_{{C}_{2}}$. We usually assume that any two curves from $\mathcal{C}$ intersect in a finite number of points and that in each such intersection point the two curves properly cross. G is called k-uniform if, for every $C \in \mathcal{C}$, | P _C  |  = k.

In what follows and throughout the rest of the chapter, we will always assume that the topological hypergraph in question does not contain parallel edges.

A family of simple closed curves in the plane is a family of pseudo-circles if every two curves in the family are either disjoint or properly cross at precisely two points. Any collection of circles in the plane is an example of such a family.

The following simple lemma is a crucial observation.

Lemma 1.

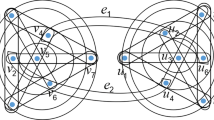
Suppose C ₁ and C ₂ are two pseudo-circles in the plane and ${x}_{1},{y}_{1},{x}_{2},{y}_{2}$ are four distinct points satisfying the following condition: x ₁ and y ₁ are surrounded by C ₁ but not by C ₂ , and x ₂ and y ₂ are surrounded by C ₂ but not by C ₁ . Let e ₁ be a Jordan arc, entirely contained in disc(C ₁ ), connecting x ₁ and y ₁ , and let e ₂ be a Jordan arc, entirely contained in disc(C ₂ ), connecting x ₂ and y ₂ . Then e ₁ and e ₂ cross an even number of times.

Proof.

If C ₁ and C ₂ do not intersect, then disc(C ₁) and disc(C ₂) must be disjoint. Indeed, otherwise one must contain the other; say disc(C ₁) contains disc(C ₂). This is a contradiction to the assumption that x ₂ and y ₂ are two points surrounded by C ₂ but not by C ₁. However, if disc(C ₁) is disjoint from disc(C ₂), then clearly e ₁ and e ₂ cannot intersect.

Therefore, assume that C ₁ and C ₂ intersect in two points u and v. Let S ₁ be the subarc of C ₁ delimited by u and v and contained in disc(C ₂). Denote by S ₂ the subarc of C ₂ delimited by u and v and contained in disc(C ₁). Observe that S ₁ together with S ₂ form a simple closed curve that surrounds exactly the points in $Z = \mbox{ disc}({C}_{1}) \cap \mbox{ disc}({C}_{2})$. Clearly, e ₁ and e ₂ may intersect only at points of Z (see Fig. 1). Since both x ₁ and y ₁ do not belong to Z, as they are not surrounded by C ₂, the intersection of e ₁ with Z consists of a finite number of arcs each of which has both endpoints lying on S ₂. It is enough to show that each of these arcs crosses e ₂ an even number of times. Let g be such an arc whose endpoints on S ₂ are k and ℓ. Let S′ ₂ be the subarc of S ₂ delimited by k and $\mathcal{l}$. g and S′ ₂ form a simple closed curve contained in Z. Consequently, both x ₂ and y ₂ are not surrounded by this closed curve. It follows that e ₂, the Jordan arc connecting x ₂ and y ₂, intersects $g \cup {S^\prime}_{2}$ an even number of times. However, e ₂ does not intersect S′ ₂, as it is a subarc of C ₂. Therefore, e ₂ crosses g an even number of times.

The next theorem is a simple consequence of Lemma 1.

Theorem 2.

Let $G = (P,\mathcal{C})$ be a topological 2-uniform hypergraph on n vertices. If $\mathcal{C}$ is a family of pseudo-circles, then G, viewed as an abstract 2-graph, is a planar graph. In particular, there are at most 3n − 6 curves in $\mathcal{C}$.

Proof.

We draw the graph G as a topological graph in such a way that every pair of edges that are not incident to the same vertex cross an even number of times. Then it is a consequence of Hanani and Tutte’s theorem [2, 9] that G is planar. The drawing rule for G is as follows: For any curve $C \in \mathcal{C}$, let x and y be the two points of P surrounded by C. We draw a Jordan arc connecting x to y so that the arc is contained in disc(C).

Fig. 1

Lemma 1

It remains to show that the above drawing rule provides the desired topological graph. Let e and f be two edges in our drawing that do not share a common vertex. Let x and y be the vertices of e, and let ${C}_{e} \in \mathcal{C}$ be the curve in $\mathcal{C}$ that surrounds both x and y. Let a and b be the vertices of f, and let ${C}_{f} \in \mathcal{C}$ be the curve in $\mathcal{C}$ that surrounds both a and b. Since C _e surrounds x and y and no other vertex, then in particular it does not surround a or b. Similarly, C _f surrounds a and b but none of x and y. Therefore, by Lemma 1, e and f cross an even number of times.

We will now bound the number of edges in a topological hypergraph with more general settings. We use the following lemma [1] (see also [5]).

Lemma 3.

Let ${A}_{1},\ldots,{A}_{n}$ be connected sets in the plane, each of which is also simply connected with boundaries that cross each other a finite number of times. If, for every 1 ≤ i < j ≤ n, ${A}_{i} \cap {A}_{j}$ is connected, then ${A}_{1} \cap \ldots \cap {A}_{n}$ is either connected or empty.

As a consequence of Lemma 3, we obtain the following corollary:

Corollary 4.

If ${C}_{1},\ldots,{C}_{t}$ is any collection of pseudo-circles, then $\mbox{ disc}({C}_{1}) \cap \ldots \cap \mbox{ disc}({C}_{t})$ is either a connected set or the empty set.

Indeed, this is because disc(C _i ) is a simply connected set for every C _i , and $\mbox{ disc}({C}_{i}) \cap \mbox{ disc}({C}_{j})$ is either empty or connected for every C _i and C _j .

The next theorem provides a linear bound in terms of | P | on the number of edges of a 3-uniform topological hypergraph $G = (P,\mathcal{C})$, in the case where $\mathcal{C}$ is a family of pseudo-circles.

Theorem 5.

Let $G = (P,\mathcal{C})$ be a 3-uniform topological graph on n vertices such that $\mathcal{C}$ is a family of pseudo-circles. Then $\vert \mathcal{C}\vert = O(n)$.

Proof.

We draw a topological graph H whose vertices are the points of P and whose edges are all pairs of points that are surrounded by some curve in $\mathcal{C}$. Let x and y be two points of P surrounded by a curve in $\mathcal{C}$, and let ${C}_{1},\ldots,{C}_{l}$ be all the curves in $\mathcal{C}$ that surround both x and y. By Corollary 4, $Z = \mbox{ disc}({C}_{1}) \cap \ldots \cap \mbox{ disc}({C}_{l})$ is a connected set. We draw the edge in H between x and y as a Jordan curve inside the connected region Z.

For every edge e in H, let d(e) denote the number of curves in $\mathcal{C}$ that surround both endpoints of e (and therefore also the entire edge e).

Claim 1.

Let e and f be two edges of H with no common vertex. If e and f cross an odd number of times, then either d(e) ≤ 2, or d(f) ≤ 2, or both.

Proof.

Assume to the contrary that both d(e) and d(f) are greater than or equal to 3. Since d(e) ≥ 3, there are at least three different curves from $\mathcal{C}$ that surround both endpoints of e. Therefore, there is a curve ${C}_{e} \in \mathcal{C}$ that surrounds both endpoints of e but no endpoint of f. Similarly, there is a curve ${C}_{f} \in \mathcal{C}$ that surrounds both endpoints of f but no endpoint of e. By Lemma 1, e and f cross an even number of times, a contradiction.

Let E′ be the set of all edges e of H such that d(e) ≤ 2. By Claim 1, the set of edges in $E \setminus E^\prime$ forms a planar graph, as every two edges in $E \setminus E^\prime$ that do not share a common vertex cross an even number of times. In particular, the cardinality of $E \setminus E^\prime$ is linear in n. We will now show that the cardinality of E′ is also linear in n.

In fact, we will prove even a slightly stronger statement that will be helpful for the proof of Theorem 5.

Claim 7.

Let V be any subset of the vertices of H and let E′(V ) be those edges in E′ both of whose vertices are in V. Then | E′(V ) | ≤ c | V | , where c > 0 is some absolute constant.

Proof.

Let 0 < q < 1 be a positive number to be determined later. Pick every vertex of V with probability q and consider only those edges of E′(V ) both of whose vertices are picked. We thus obtain a random subgraph of H, which we denote by $\tilde{H}$, on a set of vertices $\tilde{V }$. Let e be an edge in $\tilde{H}$, and let x and y be its two vertices. We know that d(e) ≤ 2. Therefore, there exist at most two vertices z ∈ V such that x, y, and z are surrounded by some curve $C \in \mathcal{C}$. We say that e is good if there is no such vertex z in $\tilde{V }$.

Observe that every two good edges with no common vertex cross an even number of times. Indeed, if e and f are two good edges with no common vertex, then there is a curve ${C}_{e} \in \mathcal{C}$ that surrounds both vertices of e but no vertex of f (or else e would not be good). And similarly, there is a curve ${C}_{f} \in \mathcal{C}$ that surrounds both vertices of f but no vertex of e. Hence, by Lemma 1, e and f cross an even number of times. It follows now from the theorem of Hanani and Tutte [2, 9] that the good edges in $\tilde{H}$ constitute a planar graph. Therefore, the number of good edges in $\tilde{G}$ is at most $3\vert \tilde{V }\vert$. This inequality is true also for the expected values of the number of good edges and $\vert \tilde{V }\vert$. Clearly, $Ex(\vert \tilde{V }\vert ) = q\vert V \vert$. As for the expected number of good edges, observe that any edge e ∈ E(V ) is a good edge in $\tilde{H}$ with probability of at least ${q}^{2}{(1 - q)}^{2}$. Indeed, this is the probability in case there are precisely two edges in G that include the vertices of e. If there is only one such edge in G, this probability is be higher, namely, q ²(1 − q).

It follows now that ${q}^{2}{(1 - q)}^{2}\vert E(V )\vert \leq 3q\vert V \vert$. Taking $q = \frac{1} {3}$, we obtain | E(V ) | ≤ 21 | V | .

Considering the graph H again, we deduce that there is an absolute constant c′ such that the number of edges of H induced by any subset V of vertices of H is at most c′ | V | . Indeed, this is true for the subset E′ of edges of H, by Claim 7, and also to the subset of edges $E \setminus E^\prime$, as they constitute a planar graph.

We now show that the number of triangles (that is, cycles of length 3) in the graph H is at most linear in the number of vertices of H. This will be enough to prove Theorem 5 because every pseudo-circle $C \in \mathcal{C}$ corresponds to precisely one triangle in the graph G (the triangle whose vertices are surrounded by C). We prove a more general lemma on abstract graphs:

Lemma 8.

Let H be a graph on m vertices. Assume that there is an absolute constant c′ such that the number of edges of H induced by any subset V of the vertices of H is at most c′|V |. Then for every $\mathcal{l} \geq 2$ , the number of copies of ${K}_{\mathcal{l}}$ (the complete graph on $\mathcal{l}$ vertices) in H is at most ${c}_{\mathcal{l}}m$ , where ${c}_{\mathcal{l}} = \frac{{(2c^\prime)}^{\mathcal{l}-1}} {\mathcal{l}!}$.

Proof.

We prove the lemma by induction on $\mathcal{l}$. For $\mathcal{l} = 2$, there is nothing to prove, as this is the assumption in the lemma. Assume the lemma is true for $\mathcal{l}$. Let ${v}_{1},\ldots,{v}_{m}$ denote the vertices of H and let E denote the set of edges of H. We know that | E | ≤ c′m. For every 1 ≤ i ≤ m, let d _i denote the degree of v _i in H. Fix i and consider the number of copies of ${K}_{\mathcal{l}+1}$ in H that include the vertex v _i . Each such copy of ${K}_{\mathcal{l}+1}$ corresponds to a unique copy of ${K}_{\mathcal{l}}$ among the neighbors of v _i . Therefore, it follows from the induction hypothesis, applied to the subgraph ${H}_{{v}_{i}}$ of H induced by the neighbors of v _i , that the number of copies of ${K}_{\mathcal{l}}$ in ${H}_{{v}_{i}}$ is at most ${c}_{\mathcal{l}}{d}_{i}$. It follows now that that v _i is incident to at most ${c}_{\mathcal{l}}{d}_{i}$ copies of K _{ℓ + 1} in H. Summing over all i between 1 and m, every copy of ${K}_{\mathcal{l}+1}$ is counted exactly $\mathcal{l} + 1$ times. Therefore, the number of copies of ${K}_{\mathcal{l}+1}$ in H is at most $\frac{1} {\mathcal{l}+1}{\sum\nolimits}_{i=1}^{m}{c}_{\mathcal{l}}{d}_{i} = \frac{1} {\mathcal{l}+1}2{c}_{\mathcal{l}}\vert E\vert \leq \frac{1} {\mathcal{l}+1}2{c}_{\mathcal{l}}c^\prime m = {c}_{\mathcal{l}+1}m$.

In particular, the number of triangles in our topological graph H is at most cn, where c is some absolute constant independent of n. This concludes the proof of Theorem 5.

If $G = (P,\mathcal{C})$ is a topological hypergraph and $\mathcal{C}$ is a family of pseudo-circles, but we do not assume that G is uniform, then a linear bound on the number of edges of G is no longer valid. Nevertheless, it is possible to obtain a cubic (that is also tight) bound on the number of edges in G in this case, as we shall now see.

Recall that for a family $\mathcal{F}$ of sets, the VC-dimension [10] of $\mathcal{F}$ is the largest cardinality of a set S that is shattered by $\mathcal{F}$, that is, the largest cardinality of a set S such that for any subset B of S there exists $F \in \mathcal{F}$ with $B = F \cap S$.

Perhaps one of the most fundamental results on VC-dimension is the Perles–Sauer–Shelah theorem [7, 8], which says that a family $\mathcal{F}$ of subsets of {1, …, n} that has VC-dimension d consists of at most $\left({ n \atop 0} \right) + \cdots + \left({ n \atop d} \right) = O({n}^{d})$ members.

Theorem 9.

Let $G = (P,\mathcal{C})$ be a topological hypergraph on n vertices such that $\mathcal{C}$ is a family of pseudo-circles. Then the family $\mathcal{F} =\{ {P}_{C}\mid C \in \mathcal{C}\}$ has VC-dimension at most 3. In particular, by the Perles–Sauer–Shelah theorem, $\vert \mathcal{C}\vert = O({n}^{3})$.

Proof.

We show that $\mathcal{F}$ cannot shatter any set of 4 points. Assume to the contrary that it does, and let $\{{p}_{1},{p}_{2},{p}_{3},{p}_{4}\} \subset P$ be a set of four points shattered by $\mathcal{F}$. For every 1 ≤ i < j ≤ 4, consider the family ${\mathcal{C}}_{ij}$ of all the curves in $\mathcal{C}$ that surround both p _i and p _j . By Corollary 4, the set ${R}_{ij} = {\cap }_{C\in {\mathcal{C}}_{ij}}\mbox{ disc}(C)$ is a connected set. We draw an edge (Jordan arc) e _ij between p _i and p _j inside the region R _ij . We thus get a drawing of K ₄ in the plane. We claim that in this drawing every two edges that do not share a common vertex cross an even number of times. Indeed, consider the edge e _ij between p _i and p _j and the edge e _kl between p _k and p _l (we assume that {i, j, k, l} = { 1, 2, 3, 4}). As $\{{p}_{1},{p}_{2},{p}_{3},{p}_{4}\}$ is shattered by $\mathcal{F}$, there is a curve ${C}_{ij} \in {\mathcal{C}}_{ij}$ that surrounds both p _i and p _j but neither p _k nor p _l . Similarly, there is a curve ${C}_{kl} \in {\mathcal{C}}_{kl}$ that surrounds both p _k and p _l but neither p _i nor p _j . By our construction, ${e}_{ij} \subset \mbox{ disc}({C}_{ij})$ and ${e}_{kl} \subset \mbox{ disc}({C}_{kl})$. It follows now from Lemma 1 that e _ij and e _kl cross an even number of times.

It is easy to observe that by small modifications of the drawing of the edges in a small neighborhood around each point p _i , we may obtain a new drawing in which also every two edges that share a common vertex cross an even number of times (apart from meeting at the same vertex).

For a closed curve S in the plane, not necessarily simple, and a point x not on S, we say that x is surrounded by S if the index of the curve S with respect to the point x is odd. This is equivalent to that any ray (or just a Jordan curve that goes to infinity) emanating from x meets S (as a curve, not as a set) an odd number of times. Observe that this definition generalizes the notion of a point surrounded by a simple closed curve.

Lemma 10.

In any drawing of K ₄ in the plane in which every two edges cross an even number of times, there is a vertex v of K ₄ that is surrounded by the closed curve composed from the three edges of K ₄ not incident to v.

Proof.

Assume not and once again let ${p}_{1},{p}_{2},{p}_{3}$, and p ₄ denote the vertices of K ₄ drawn in the plane. For any three vertices ${p}_{i},{p}_{j}$, and p _k , denote by S _ijk the closed curve composed from the edges ${p}_{i}{p}_{j}$, ${p}_{j}{p}_{k}$, and ${p}_{k}{p}_{i}$. Consider a fixed vertex p _i . Any small enough circular disc D, centered at p _i , is trisected by the edges going from p _i to the three other vertices. Fix such a disc D. We claim the section of D bounded by the edges ${p}_{i}{p}_{j}$ and ${p}_{i}{p}_{k}$ consists of points that are all surrounded by S _ijk . Indeed, otherwise the portion of the edge ${p}_{i}{p}_{l}$ inside D is surrounded by S _ijk . As the edge ${p}_{i}{p}_{l}$ crosses each of the edges ${p}_{i}{p}_{j}$, ${p}_{i}{p}_{k}$, and ${p}_{j}{p}_{k}$ an even number of times, it follows that p _l is also surrounded by S _ijk , a contradiction.

Consider now a point x far away, not surrounded by any of the curves S _ijk . Draw an arc g connecting x to p ₁. Once again let D be a small circular disc centered at p ₁. D is trisected by the edges ${p}_{1}{p}_{i}$ for i = 2, 3, 4. Without loss of generality, assume that $g \cap D$ lies in the portion of D delimited by ${p}_{1}{p}_{2}$ and ${p}_{1}{p}_{3}$. Hence, as x is not surrounded by S ₁₂₃, it follows that g crosses S ₁₂₃ an odd number of times. For the same reasons, it follows that g crosses both S ₁₂₄ and S ₁₃₄ an even number of times because $g \cap D$ is not surrounded by S ₁₂₄ nor by S ₁₃₄.

Denote by t _ij the number of crossings between g and the edge ${p}_{i}{p}_{j}$. Therefore, ${t}_{12} + {t}_{13} + {t}_{23}$ is odd and both ${t}_{12} + {t}_{14} + {t}_{24}$ and ${t}_{13} + {t}_{14} + {t}_{34}$ are even. Summing them all up, we conclude that ${t}_{23} + {t}_{34} + {t}_{24}$ is odd. Therefore, g crosses S ₂₃₄ an odd number of times. Now since x is not surrounded by S ₂₃₄ and g connects x to p ₁, it follows that p ₁ is surrounded by S ₂₃₄, a contradiction.

In view of Lemma 10, assume without loss of generality that p ₄ is surrounded by the closed curve composed from the edges ${p}_{1}{p}_{2}$, ${p}_{2}{p}_{3}$, and ${p}_{3}{p}_{1}$. As $\mathcal{F}$ shatters $\{{p}_{1},{p}_{2},{p}_{3},{p}_{4}\}$, let $C \in \mathcal{C}$ be a curve surrounding ${p}_{1},{p}_{2},$ and p ₃ but not p ₄. Therefore, each of the edges ${p}_{1}{p}_{2}$, ${p}_{2}{p}_{3}$, and ${p}_{3}{p}_{1}$ is contained in disc(C). This is a contradiction because now it is not possible that p ₄ is surrounded by the closed curve composed from the edges ${p}_{1}{p}_{2}$, ${p}_{2}{p}_{3}$, and ${p}_{3}{p}_{1}$, as it is not surrounded by C. This completes the proof of Theorem 9.

For a set A and an integer r ≥ 0, we denote by $\left({ [A] \atop \leq r} \right)$ the family of all subsets of A of cardinality at most r. We will need the following small variant of the original Perles–Sauer–Shelah theorem [7].

Theorem 11.

Let $\mathcal{F} =\{ {A}_{1},\ldots,{A}_{m}\}$ be a family of distinct subsets of {1,2,…,n} and assume that $\mathcal{F}$ has VC-dimension less than or equal to d. Then

$$m \leq \vert {\bigcup \limits_{i=1}^{m}}\left({ [{A}_{i}] \atop \leq d} \right)\vert.$$

Proof.

We prove the theorem by induction on d and n. The theorem is clearly true for d = 0 and any n. For d > 0, assume that $\mathcal{F}$ has VC-dimension at most d and define ${\mathcal{F}}_{1} =\{ A \setminus \{ 1\}\mid A \in \mathcal{F}\}$ and $\mathcal{T} =\{ A \setminus \{ 1\}\mid 1 \in A\mbox{ and }A \setminus \{ 1\} \in \mathcal{F}\}$. It is easy to see that $\vert \mathcal{F}\vert = \vert {\mathcal{F}}_{1}\vert + \vert \mathcal{T}\vert$. Let s denote the number of sets in ${\mathcal{F}}_{1}$ and let t denote the number of sets in $\mathcal{T}$. We rewrite ${\mathcal{F}}_{1} =\{ {F}_{1},\ldots,{F}_{s}\}$ and $\mathcal{T} =\{ {T}_{1},\ldots,{T}_{t}\}$. As the VC-dimension of ${\mathcal{F}}_{1}$ is at most d, we use the induction hypothesis on n to deduce that the family ${\bigcup\nolimits}_{i=1}^{s}\left({ [{F}_{i}] \atop \leq d} \right)$ contains at least s sets.

Observe that the VC-dimension of $\mathcal{T}$ is at most d − 1, for otherwise $\mathcal{F}$ has VC-dimension at least d + 1. Therefore, by the induction hypothesis, there are at least t sets in ${\bigcup\nolimits}_{i=1}^{t}\left({ [{T}_{i}] \atop \leq d-1} \right)$. To each of these sets add the element 1 to obtain t sets in ${\bigcup\nolimits}_{i=1}^{m}\left({ [{A}_{i}] \atop \leq d} \right)$ each containing the element 1 and thus each is different than any set in ${\bigcup\nolimits}_{i=1}^{s}\left({ [{F}_{i}] \atop \leq d} \right)$. The result follows from the fact that $m = s + t$.

Corollary 12.

Let $\mathcal{F} =\{ {A}_{1},\ldots,{A}_{m}\}$ be a family of distinct subsets of {1,2,…,n} with VC-dimension less than or equal to d. Then it is possible to assign to each set A _i a subset of it of size at most d such that no two sets A _i and A _j are assigned to the same set.

Proof.

Consider the bipartite graph in which one set of vertices corresponds to the sets ${A}_{1},\ldots,{A}_{m}$ and the other set of vertices corresponds to the elements in ${\bigcup\nolimits}_{i=1}^{m}\left({ [{A}_{i}] \atop \leq d} \right)$. In this bipartite graph connect each set A _i to all its subsets of size at most d. By Hall’s theorem [3, 4] and by Theorem 11, the desired matching exists.

Theorems 2 and 5 give a linear bound to the number of edges of a 2-uniform and 3-uniform, respectively, topological hypergraphs where the set of edges is a family of pseudo-circles. The next theorem provides a bound to the number of edges in a topological hypergraph $G = (P,\mathcal{C})$ on n vertices, where $\mathcal{C}$ is a family of pseudo-circles and that | P _C  | ≤ k for every $C \in \mathcal{C}$ and a fixed k > 3.

Theorem 13.

Let $G = (P,\mathcal{C})$ be a topological hypergraph on n vertices. Assume that $\mathcal{C}$ is a family of pseudo-circles and that |P _C |≤ k for every $C \in \mathcal{C}$ and a fixed integer k. Then $\vert \mathcal{C}\vert = O({k}^{2}n)$.

Proof.

Consider the family $\mathcal{F} =\{ {P}_{C}\mid C \in \mathcal{C}\}$. By Theorem 9, $\mathcal{F}$ has VC-dimension less than or equal to 3. We use Corollary 12 and assign to each member P _C of $\mathcal{F}$ a subset of it of size at most 3 that we denote by B _C .

We fix a small number 0 < q < 1 ∕ 2 to be determined later and pick every point of P independently with probability q. We call a curve $C \in \mathcal{C}$ good if every point in B _C was picked and no point in ${P}_{C} \setminus {B}_{C}$ was picked. Observe that a curve C in $\mathcal{C}$ is good with probability ${q}^{\vert {B}_{C}\vert }{(1 - q)}^{\vert {P}_{C}\vert -\vert {B}_{C}\vert }\geq {q}^{\vert {B}_{C}\vert }{(1 - q)}^{k-\vert {B}_{C}\vert }\geq {q}^{3}{(1 - q)}^{k-3}$, where the last inequality is because q < 1 ∕ 2 and | B _C  | ≤ 3.

By Theorems 2 and 5, the number of edges in a 2-uniform, or a 3-uniform topological hypergraph on n vertices whose set of edges is a family of pseudo-circles is O(n). Therefore, the number of good curves in $\mathcal{C}$ is at most some absolute constant c times the number of points of P that were picked. Taking the expectation, we see that $\vert \mathcal{C}\vert {q}^{3}{(1 - q)}^{k-3} \leq cqn$. Taking $q = 1/k$, we get the desired result, namely, $\vert \mathcal{C}\vert \leq c^\prime{k}^{2}n$ for some absolute constant c′ > 0.

Remark 1.

It is not hard to show that the bound in Theorem 13 can indeed be attained even by a family $\mathcal{C}$ of circles in the plane.

Definition 1.2.

We denote by f _t (n) the maximum number of edges in a topological graph on n vertices with no t vertex-disjoint edges every two of which cross an odd number of times.

We will need the following estimate on f _t (n) from [6] (see Theorem 3 in [6]):

Theorem 14 ([6]). 

${f}_{t}(n) = O({n\log }^{4t-8}n)$.

In fact, in the sequel, we will only use the fact that ${f}_{t}(n) = o({n}^{2})$.

The next theorem provides even better bounds on the size of $\{{P}_{C}\mid C \in \mathcal{C}\}$, assuming that the intersections of the sets P _C with each other are ”small.”

Theorem 15.

Let $r,{k}_{1},{k}_{2} > 0$ be fixed integers. Let $G = (P,\mathcal{C})$ be a topological hypergraph on n vertices and assume that $\mathcal{C}$ is a family of pseudo-circles. Assume further that ${k}_{1} \leq \vert {P}_{C}\vert \leq {k}_{2}$ for every $C \in \mathcal{C}$ . If, for every r curves ${C}_{1},\ldots,{C}_{r} \in \mathcal{C}$ , we have $\vert {P}_{{C}_{1}} \cap \ldots \cap {P}_{{C}_{r}}\vert < r$ , then ${\sum\nolimits}_{C\in \mathcal{C}}\vert {P}_{C}\vert = O(\frac{{k}_{2}^{2}} {{k}_{1}^{2}} n)$ , where the constant of proportionality depends only on r.

Proof.

We define a topological graph H in the following way: The vertices of H are the points of P. For any pair of vertices x and y that are surrounded by some curve $C \in \mathcal{C}$, consider all curves in $\mathcal{C}$ that surround x and y. Let those curves be ${C}_{1},\ldots,{C}_{l}$ and define $Z = \mbox{ disc}({C}_{1}) \cap \ldots \cap \mbox{ disc}({C}_{l})$. By Corollary 4, Z is a connected set. We draw the edge in H between x and y as a Jordan curve entirely included in Z.

We call an edge of Hbad if its endpoints, and hence the edge as well, are surrounded by at least $(r - 1){2}^{r-2} + 1$ different curves in $\mathcal{C}$; otherwise, it is called good.

Claim 6.

There are no r ² bad edges in H every two of which cross an odd number of times and no two of which share a common vertex.

Proof.

Assume to the contrary that E is a collection of r ² bad edges every two of which cross an odd number of times and no two of which share a common vertex.

Let $e,{e}_{1},\ldots,{e}_{r-2}$ be any r − 1 different edges in E. We claim that among all curves in $\mathcal{C}$ surrounding e, there is at least one curve that does not surround any of the two vertices of some edge among ${e}_{1},\ldots,{e}_{r-2}$. Indeed, otherwise any curve in $\mathcal{C}$ that surrounds e must surround at least one vertex of each of ${e}_{1},\ldots,{e}_{r-2}$. Since e is a bad edge, there are at least $(r - 1){2}^{r-2} + 1$ curves in $\mathcal{C}$ that surround e. Therefore, by the pigeon-hole principle, there must be at least r curves surrounding e as well as the same set of r − 2 vertices (each of which is the endpoint of some edge among ${e}_{1},\ldots,{e}_{r-2}$). This is a contradiction to the assumption that no r curves in $\mathcal{C}$ surround the same set of r vertices.

It follows that apart from at most r − 3 edges in E, for every edge f in E, different from e, there is a curve $C \in \mathcal{C}$ that surrounds e but not any of the two vertices of f. This way, because $E > (r - 1)(r - 2)$, we can find r − 1 edges ${e}_{1},\ldots,{e}_{r-1}$ with the property that for every 1 ≤ i < j ≤ r − 1 there is a curve in $\mathcal{C}$ that surrounds e _i but not any of the two vertices of e _j .

Using once again the argument above, there is a curve C ∈ C and there is an index j between 1 and r − 2 such that C surrounds e _{r − 1}, but C does not surround any of the vertices of e _j . Since j < r − 1, there is a curve $C^\prime \in \mathcal{C}$ that surrounds e _j but that does not surround any of the vertices of e _{r − 1}. By Lemma 1, this implies that e _j and e _{r − 1} cross an even number of times, contradicting our assumption.

It follows from Claim 6 and Theorem 14 that there exists k ₀ that depends only on r such that if ${k}_{1} > {k}_{0}$, then for every $C \in \mathcal{C}$, C surrounds at least k ₁ ² ∕ 4 good edges.

Clearly, we may assume that ${k}_{1} > {k}_{0}$ as by Theorem 13, the collection $\mathcal{C}^\prime$ of all curves $C \in \mathcal{C}$ with $\vert {P}_{C}\vert \leq {k}_{0}$ consists of O(k ₀ ² n) curves and therefore, $\sum\limits_{C\in \mathcal{C}^\prime}\vert C\vert = O(n)$.

Fix a probability 0 < q < 1, to be determined later, and pick every point in P with probability q. Let H ^∗ be the random topological graph whose vertices are those points that were picked and whose edges are those good edges of H both of whose vertices were picked. Call an edge e of H ^∗ nice if there is a curve $C \in \mathcal{C}$ that surrounds no other vertex of H ^∗ but the endpoints of e.

We claim that the subgraph of H ^∗, which consists only of the nice edges, is planar. Indeed, let e and f be two nice edges that do not share a common vertex. Because e is nice, there is a curve ${C}_{e} \in \mathcal{C}$ that surrounds e but does not surround any of the vertices of f. Similarly, there is a curve ${C}_{f} \in \mathcal{C}$ that surrounds f but does not surround any of the vertices of e. By Lemma 1, e and f cross an even number of times. Therefore, by the Hanani–Tutte theorem, H ^∗ is planar. It follows that | E ^∗ | is less than or equal to 3 | V ^∗ | − 6, where E ^∗ is the set of all nice edges and V ^∗ is the set of vertices in H ^∗. This is true also when considering the expected values of | E ^∗ | and | V ^∗ | .

We have Ex( | V ^∗ | ) = qn. We claim that $Ex(\vert {E}^{{_\ast}}\vert ) \geq \vert W\vert {q}^{2}{(1 - q)}^{{k}_{2}-2}$, where W is the set of all good edges. This is because each edge in W is nice with probability of at least ${q}^{2}{(1 - q)}^{{k}_{2}-2}$. Indeed, suppose e ∈ W, and let C _e be any curve in $\mathcal{C}$ that surrounds e. e becomes nice if its two vertices are picked to V ^∗ (which happens with probability q ²) and the other points surrounded by C _e are not picked. The latter happens with probability of at least ${(1 - q)}^{{k}_{2}-2}$ and independently of the event in which the two vertices of e are picked.

Therefore, $\vert W\vert {q}^{2}{(1 - q)}^{{k}_{2}-2} < 3qn$. Taking $q = \frac{1} {{k}_{2}-1}$, we obtain | W |  < 9(k ₂ − 1)n. On the other hand, each good edge is surrounded by at most $(r - 1){2}^{r-1}$ curves in $\mathcal{C}$, and each curve in $\mathcal{C}$ surrounds at least k ₁ ² ∕ 4 good edges. Therefore, $\vert W\vert \geq \frac{{k}_{1}^{2}} {4(r-1){2}^{r-1}} \vert \mathcal{C}\vert$. Hence, $\vert \mathcal{C}\vert < \frac{36(r-1){2}^{r-1}{k}_{ 2}} {{k}_{1}^{2}} n$. The theorem now follows as $\sum\limits_{C\in \mathcal{C}}\vert {P}_{C}\vert \leq \sum\limits_{C\in \mathcal{C}}{k}_{2} \leq 36(r - 1){2}^{r-1}\frac{{k}_{2}^{2}} {{k}_{1}^{2}} n$.

Corollary 17.

Let r > 0 be a fixed integer. Let $G = (P,\mathcal{C})$ be a topological hypergraph on n vertices, and assume that $\mathcal{C}$ is a family of pseudo-circles. If, for every r curves ${C}_{1},\ldots,{C}_{r} \in \mathcal{C}$ , we have $\vert {P}_{{C}_{1}} \cap \ldots \cap {P}_{{C}_{r}}\vert < r$ , then ${\sum\nolimits}_{C\in \mathcal{C}}\vert {P}_{C}\vert = O(n\log n)$.

Proof.

For every 0 ≤ i ≤ log₂ n, let ${\mathcal{C}}_{i}$ denote those curves $C \in \mathcal{C}$ for which ${2}^{i} \leq \vert {P}_{C}\vert \leq {2}^{i+1}$. By Theorem 15, for every 0 ≤ i ≤ log₂ n, we have $\sum\limits_{C\in {\mathcal{C}}_{i}}\vert {P}_{C}\vert = O({(\frac{{2}^{i+1}} {{2}^{i}} )}^{2}n) = O(n)$. Therefore, ${\sum\nolimits}_{C\in \mathcal{C}}\vert {P}_{C}\vert = {\sum\nolimits}_{i=0}^{{\lfloor \log }_{2}n\rfloor }O(n) = O(n\log n)$.

As an example, fix an integer r ≥ 2. Let $G = (P,\mathcal{C})$ be a k-uniform topological hypergraph on n vertices. Assume that for any two curves ${C}_{1},{C}_{2} \in \mathcal{C}$, we have $\vert {P}_{{C}_{1}} \cap {P}_{{C}_{2}}\vert < r$. Then, clearly, for every r curves ${C}_{1},\ldots,{C}_{r} \in \mathcal{C}$, we have $\vert {P}_{{C}_{1}} \cap \ldots \cap {P}_{{C}_{r}}\vert < r$. It follows now from Theorem 15 that

$$k\vert \mathcal{C}\vert ={\sum \limits_{C\in \mathcal{C}}}\vert {P}_{C}\vert = O(\frac{{k}^{2}} {{k}^{2}}n) = O(n).$$

Hence, $\vert \mathcal{C}\vert = O(n/k)$. This roughly says that the sets in the family $\{{P}_{C}\mid C \in \mathcal{C}\}$, each having cardinality k, behave almost as if they were disjoint.