Optimal Multi-Microphone Speech Enhancement in Cars

Abstract

Hands-free speech telephony and speech recognition in cars suffer from additive noise and reverberation. We propose an iterative blind room impulse response (RIR) estimation algorithm based on an analysis-by-synthesis loop closed around a multi-path generalized sidelobe canceller (GSC). By combining a post-filter with the proposed scheme, optimal speech enhancement in practical situations can be achieved. The algorithm is tested using simulated data and real speech recordings from the AVICAR database.

This work was done when Lae-Hoon Kim was with University of Illinois at Urbana-Champaign. He has since joined Qualcomm Inc.

1 Introduction

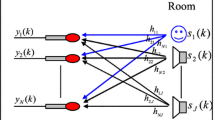
In recent years, although many systems have used multi-microphone arrays for speech enhancement [1, 2] and robust speech recognition [3], few approaches have presented a theoretical basis for multi-microphone speech signal processing under the assumed statistical model of source speech signal, room impulse response (RIR), and noise. One of the few published systems considering a theoretical basis for speech enhancement is that of Balan and Rosca [1], which showed that multi-microphone MMSE spectral amplitude estimation can be factored into a sufficient statistics followed by a single-microphone post-filter. As a straightforward extension of [1], if we know the RIRs, optimal estimation of the speech signal can be achieved using the simple two-step method. However, it is actually not easy to satisfy the assumption of the known RIRs. In this chapter, we address a realistic implementation of the sufficient statistics with unknown RIRs.

If we know the source signal, we can adaptively estimate the RIRs based on an acoustic echo cancelation scheme [4]. Because more correctly beamformed output is nearer to the original source signal, we might be able to use the beamformed output as a reference signal to estimate the RIRs [5]. In this chapter we propose using a delay-and-sum beamformer (DSB) to provide the information necessary for an initial constrained estimate of the RIR, which is then updated iteratively using a multi-path generalized sidelobe canceller (GSC) based on the evolving RIR estimate. Good RIR estimation makes the multi-path GSC more accurate, and this again guarantees better RIR estimation. We demonstrate that, with a reasonable constraint on the sparsity of the room impulse response, the algorithm converges to a useful approximate RIR. Even though we may not get perfect RIR identification, the converged RIR is nevertheless sufficient to compute coefficient vectors for a multi-path fixed beamformer (FBF) which outperforms the naive DSB. By leveraging the converged RIR, we are able to mitigate the common practical problem of multi-path GSC, namely, its tendency to cancel the target signal due the indistinguishability of signal from reverberation at the beamformer.

To visualize the situation in a tractable way, we first show the convergence of a simplified version of the proposed scheme. A simple simulation test shows that this method achieves sufficient blind deconvolution at the output of FBF. We then evaluate the proposed algorithm using real-world moving-car recordings [6].

2 Proposed Method

2.1 Multi-path GSC

Multi-path GSC can be formulated as an optimization problem as shown in (13.1), which is a generalized version of GSC [7] under a known multi-path environment, represented by the RIR as coded into a constraint matrix C:

$$ \mathop{\hbox{argmin}}\limits_{{\vec{w}}} E\left\{ {{{\vec{w}}^T}\vec{y}(n)\vec{y}{{(n)}^T}\vec{w}} \right\}{\hbox{ subject to }}{C^T}\vec{w} = \vec{f}, $$

(13.1)

where ${\hat{s}(n) = {{\vec{w}}^T}\vec{y}(n)}$ is an estimated source signal at the current time $n$, ${{\vec{f} = \left[ {\begin{array}{cccc} 1\ \ 0 \ \ \cdots\ \ 0 \\\end{array} } \right]}^T}$. ${\vec{y}(n)}$ is a noisy signal vector measured by the microphone array, the array of filter coefficients is ${{\vec{w} = \left[ {\begin{array}{cccc} {{w_1}}\ \ {{w_2}}\ \ \cdots\ \ {{w_{{NL}}}} \\\end{array} } \right]}^T}$ encoding the estimated L-tap inverse RIR filters for all of the N recorded signals, and

$$\begin{array}{cccc} {\vec{y}(n) = \left[ {\begin{array}{cccc} {y_{{1}}^{{\left[ {{1:}L} \right]}}(n)} \hfill & {y_{{2}}^{{\left[ {{1:}L} \right]}}(n)} \hfill & \cdots \hfill & {y_N^{{\left[ {{1:}L} \right]}}(n)} \hfill \\\end{array} } \right]}, \end{array}$$

(13.2)

$$ {y_i^{{\left[ {{1:}L} \right]}}(n) = \left[ {\begin{array}{cccc} {{y_i}\left( {n - \left( {i - {1}} \right){n_{{0}}}} \right)} \hfill & {{y_i}\left( {n - \left( {i - {1}} \right){n_{{0}}} - {1}} \right)} \hfill & \cdots \hfill & {{y_i}\left( {n - \left( {i - {1}} \right){n_{{0}}}} \right) - L + {1}} \hfill \\\end{array} } \right]}, $$

(13.3)

where i = 1, 2, … N, steered to a look direction of ${\theta = { \arcsin }\left( { - {n_{{0}}}\frac{c}{{{F_s}d}}} \right)}$ for uniform microphone spacing d, sampling rate Fs, and speed of sound c. Note that n ₀ is introduced in (5) to compensate the inter-microphone channel delay so that the signal from all microphone channels can be aligned. However, n0 may not be an integer number; therefore we may need to deal with non-integer delay compensation [3].

To derive multi-path GSC, we need to manipulate the constraint part in (1). The constraint part has the following convolution form:

$$ {{C^T}\vec{w} = \left[ {\begin{array}{cccc} {{C_{{{h_{{1}}}}}}} \hfill & {{C_{{{h_{{2}}}}}}} \hfill & \cdots \hfill & {{C_{{{h_N}}}}} \hfill \\\end{array} } \right] \cdot \left[ {\begin{array}{cccc} {{w_{{1}}}} \hfill \\{{w_{{2}}}} \hfill \\\vdots \hfill \\{{w_{{NL}}}} \hfill \\\end{array} } \right] = \left[ {\begin{array}{cccc} {1} \hfill \\{0} \hfill \\\vdots \hfill \\{0} \hfill \\\end{array} } \right]}, $$

(13.4)

where ${l_h}$ (length of the RIR) + L-1 by L matrix ${{C_{{{h_i}}}}}$ is constructed from the response ${{{\vec{h}}_i} = \left[ {\begin{array}{cccc} {{h_i}\left( {0} \right)} \hfill \ \ {{h_i}\left( {1} \right)} \hfill \ \ \cdots \hfill & {{h_i}\left( {{l_h} - {1}} \right)} \hfill \\\end{array} } \right]}$,

$$ {{C_{{{h_i}}}} = \left[ {\begin{array}{cccc} {{h_i}\left( {0} \right)} \hfill & {0} \hfill & \cdots \hfill & {0} \hfill \\{{h_i}\left( {1} \right)} \hfill & {{h_i}\left( {0} \right)} \hfill & \ddots \hfill & \vdots \hfill \\\vdots \hfill & {{h_i}\left( {1} \right)} \hfill & \ddots \hfill & {0} \hfill \\{{h_i}\left( {{l_h} - {1}} \right)} \hfill & \vdots \hfill & \ddots \hfill & {{h_i}\left( {0} \right)} \hfill \\{0} \hfill & {{h_i}\left( {{l_h} - {1}} \right)} \hfill & \vdots \hfill & {{h_i}\left( {1} \right)} \hfill \\\vdots \hfill & \ddots \hfill & \ddots \hfill & \vdots \hfill \\{0} \hfill & \cdots \hfill & \cdots \hfill & {{h_i}\left( {{l_h} - {1}} \right)} \hfill \\\end{array} } \right]}, $$

(13.5)

i = 1, 2, …, N. ${{C_{{{h_i}}}}}$ is a typical linear convolution matrix, which has Toeplitz structure. The solution to Eq.13.5 is a channel deconvolution filter, $\vec{w}$ [8]. In standard multi-path GSC, the solution to (1) is computed by projection of $\vec{w}$ onto a blocking matrix, which can be constructed as the null space of the multichannel convolution matrix, C. Now, the problem of identifying the FBF coefficient vector $\vec{w}$ can be regarded as a general multichannel deconvolution problem; therefore it need not be computed directly as the least-squares solution of Eq.13.1; instead, if desired, we can apply any kind of multichannel deconvolution scheme [8–10]. The blocking matrix can also be constructed by using an echo cancelation scheme as in [5], because ideally the output of the fixed beamformer is the deconvolved and beamformed source signal. Although we might be able to apply any kind of multichannel deconvolution scheme for FBF, in the subsequent sections we propose a blind multichannel RIR identification algorithm, which is in fact based on the unique structure of the multi-path GSC.

2.2 Iterative Blind Estimation of RIR Based on Multi-path GSC

2.2.1 Problem Formulation

The channel response estimation follows the optimization process below:

$$\hat h_i(n) = \mathop{{\arg \min }}\limits_{{{{{\hat h}}}_i}(n)} {\left\| {s(n) * \left( {{h_{{1}}}(n) * {w_{{1}}}(n) +\cdots + {h_N}(n) * {w_N}(n)} \right) * {{\hat{h}}_i}(n) - s(n) *{h_i}(n)} \right\|^{{2}}}, $$

(13.6)

where * stands for a convolution, and (7) can be represented in the following with vector notation ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}} {\vec{h}}}_i}$:

$$ {\hat{\vec{h}}_i} = \mathop{{\arg \min }}\limits_{{{{\hat{\vec{h}}}_i}}} {\left\| {\hat{C}{{\hat{\vec{h}}}_i} - {{\vec{h}}_i}} \right\|^2} = {\left( {{{\hat{C}}^T}\hat{C}} \right)^{{ - 1}}}{\hat{C}^T}{\vec{h}_i}, $$

(13.7)

where ${\hat{C} = {C^T}\vec{w}}$ is the convolution matrix obtained with the beamformed outputs of RIRs. Ideally, if ${\hat{C} = I}$, in other words, if the FBF of RIRs produces perfectly deconvolved output, then we can obtain the real RIRs. In addition to (13.7), the estimated RIRs are obtained with the constraint of forcing the magnitude to be zero values except at the estimated time stamps of each dominant reflection in RIRs. This constraint can be interpreted as a sparseness constraint of RIRs.

2.2.2 Algorithm

The proposed algorithm is introduced below step by step based on the assumption that we know the time stamps ${{r_{{i,d}}}}$ of the dominant echo paths occurring in impulse response ${{{\vec{h}}_i}}$, where i = 1, …, N and the number of dominant echo paths d = 1, 2, …, D. Here, we focus on the RIR estimation and deconvolution, because the noise suppression after the deconvolution is straightforward. Estimation of the time stamps for the dominant echo paths will be discussed in Sect.13.2.2.3:

• 1. Initialize estimated impulse response.

• 2. ${h_i}(n) = {1} + \varepsilon \delta \left( {n - {r_{{i,{1}}}}} \right) + \cdots + \varepsilon \delta \left( {n - {r_{{i,D}}}} \right) .$

• 3. Perform multi-path GSC using (13.6) and update ${{h_i}\left( {{r_{{i,d}}}} \right)}$ with the solution of (13.7). Enforce ${{h_i}(n) = {0}}$ for other n.

• 4. Iterate 2 until there is no more significant change in the magnitude of the reflection.

If you follow the first iteration, you will get the first update at the time stamp for the dominant echo paths,

$$ {{{\hat{h}}_i}\left( {{r_{{i,d}}}} \right) \approx {h_i}\left( {{r_{{i,d}}}} \right) - \frac{{1}}{N}\left( {{h_{{1}}}\left( {{r_{{i,d}}}} \right) + \cdots + {h_i}\left( {{r_{{i,d}}}} \right) - \varepsilon + \cdots + {h_N}\left( {{r_{{i,d}}}} \right)} \right)} $$

(13.8)

(13.8) can be illustrated by the situation in which there is only one dominant reflection, with magnitude $\varepsilon$. Then, the deconvolution filter coefficient for the channel at time ${{r_{{i,{1}}}}}$ becomes near to ${ - \varepsilon }$, if the deconvolution filter is long enough, to meet the following condition:

$$ {\left( {\left( {{1} + \varepsilon \delta \left( {t - {r_{{i,{1}}}}} \right)} \right) * \left( {{1} - \varepsilon \delta \left( {t - {r_{{i,{1}}}}} \right)} \right)} \right)(r) = {0}}. $$

(13.9)

Under this circumstance the deconvolution output at ${{r_{{i,{1}}}}}$ with RIR as input becomes ${{h_i}\left( {{r_{{i,{1}}}}} \right) - \varepsilon }$, and the beamformed output with this deconvolution output becomes ${\frac{{1}}{N}\left( {{h_{{1}}}\left( {{r_{{i,{1}}}}} \right) + \cdots + {h_i}\left( {{r_{{i,{1}}}}} \right) - \varepsilon + \cdots + {h_N}\left( {{r_{{i,{1}}}}} \right)} \right)}$. Note that ${{h_i}(n) = 0}$ for every n except n = 0 and n=${{r_{{i,{1}}}}}$. Now, by applying (13.7) for the channel estimation at channel i, (13.8) is obtained and ${{{\hat{h}}_i}\left( {{r_{{i,{1}}}}} \right)}$ can be considered as an updated $\varepsilon$; therefore

$$ {{\varepsilon_{{k + {1}}}} = {h_i}\left( {{r_{{i,{1}}}}} \right) - \frac{{1}}{N}\left( {{h_{{1}}}\left( {{r_{{i,{1}}}}} \right) + \cdots + {h_i}\left( {{r_{{i,{1}}}}} \right) - {\varepsilon_k} + \cdots + {h_N}\left( {{r_{{i,{1}}}}} \right)} \right)} $$

(13.10)

at the kth iteration, which can be expressed as follows:

$$\begin{array}{cccccc} {\varepsilon_{{k + {1}}}} - {h_i}\left( {{r_{{i,{1}}}}} \right) + \frac{{1}}{{N - {1}}}\left( {{h_{{1}}}\left( {{r_{{i,{1}}}}} \right) + \cdots + {h_{{i - {1}}}}\left( {{r_{{i,{1}}}}} \right) + {h_{{i + {1}}}}\left( {{r_{{i,{1}}}}} \right) \cdots + {h_N}\left( {{r_{{i,{1}}}}} \right)} \right) \hfill \cr {\left( {\frac{{1}}{N}} \right)^n}\left( {{\varepsilon_k} - {h_i}\left( {{r_{{i,{1}}}}} \right) + \frac{{1}}{{N - {1}}}\left( {{h_{{1}}}\left( {{r_{{i,{1}}}}} \right) + \cdots + {h_{{i - {1}}}}\left( {{r_{{i,{1}}}}} \right) + {h_{{i + {1}}}}\left( {{r_{{i,{1}}}}} \right) \cdots + {h_N}\left( {{r_{{i,{1}}}}} \right)} \right)} \right) \end{array} $$

(13.11)

By induction,

$$ {{\varepsilon_{\infty }} = {{\hat{h}}_i}\left( {{r_{{i,{1}}}}} \right) = {h_i}\left( {{r_{{i,{1}}}}} \right) - \frac{{1}}{{N - {1}}}\left( {{h_{{1}}}\left( {{r_{{i,{1}}}}} \right) + \cdots + {h_{{i - {1}}}}\left( {{r_{{i,{1}}}}} \right) + {h_{{i + {1}}}}\left( {{r_{{i,{1}}}}} \right) \cdots {h_N}\left( {{r_{{i,{1}}}}} \right)} \right)} $$

(13.12)

which can be interpreted as follows: If ${{{\hat{h}}_i}\left( {{r_{{i,{1}}}}} \right)}$ is bigger than ε, it will be updated until there is no change of ${{{\hat{h}}_i}\left( {{r_{{i,{1}}}}} \right)}$. In the early part of the RIR, echo paths are infrequent, typically ${{h_{{1}}}\left( {{r_{{i,{1}}}}} \right), \cdots, {h_{{i - {1}}}}\left( {{r_{{i,{1}}}}} \right),{h_{{i + {1}}}}\left( {{r_{{i,{1}}}}} \right), \cdots, {h_N}\left( {{r_{{i,{1}}}}} \right){ \ll }{h_i}\left( {{r_{{i,{1}}}}} \right)}$; therefore ${{{\hat{h}}_i}\left( {{r_{{i,{1}}}}} \right) \approx {h_i}\left( {{r_{{i,{1}}}}} \right)}$ in (13.12). Even with background noise in a real situation, ${{{\hat{h}}_i}\left( {{r_{{i,{1}}}}} \right) \approx {h_i}\left( {{r_{{i,{1}}}}} \right)}$ still holds, since we can easily assume that the noise process is zero mean and we take a mean of iteration measurements in (13.12). This one dominant reflection scenario can be extended to the case of multiple reflections, because after deconvolving the most dominant reflection path, the next dominant path can be deconvolved. Note that by specifying all the time stamps for the dominant echo paths, this sequential deconvolution can be performed implicitly. However, also note that due to practical issues such as low-pass filtering (due to sampling of the signal, and/or frequency-dependent reflection coefficients at the walls of the room), the response may not contain perfect impulses.

Such imperfection may produce some errors in estimation of the channel, since the assumption of sparse RIRs will no longer hold with precision. In particular, echo paths with similar direction of arrival (DOA) may not be estimated exactly using this scheme. In most cases, the restriction of channel estimation to sources with DOA different from those of the dominant echoes is not as difficult to meet as the restrictions imposed by other channel estimation algorithms, and in practice, even the imperfections of overlapping and negative-valued echoes seem not to harm channel estimation results using the proposed algorithm.

Figure 13.1 shows the converged result of a two-channel measurement with a seven dominant reflection paths in RIRs, including one negative component and one overlapped component as follows:

Fig. 13.1

(a) FBF output: Blue dotted line is DSB output, black dotted lines are updated FBF output: Red line is the final FBF output after 20 iteration. Updated FBF output produces more impulse-like output by eliminating the effect of the designated echo paths, in other words, more deconvolved output. (b) Estimated channel h1. (c) Estimated channel h2: Red dots show the converged channel response after 20 iteration, and the blue dotted lines are updated responses. The black line is for original RIR. The designated channel responses are almost perfectly identified

$$ {{h_{{1}}}( {{r_{{i,{1}}}}} , \cdots, {h_{{i - {1}}}}({{r_{{i,{1}}}}} ,{h_{{i + {1}}}}( {{r_{{i,{1}}}}} , \cdots, {h_N}( {{r_{{i,{1}}}}} { \ll }{h_i}( {{r_{{i,{1}}}}}}$$

(13.13)

The first three reflection time stamps are assumed to be known and the others are set as zero. We can confirm that with the correct time stamps for a few of the dominant early echo paths (not all), we can estimate the channel responses and perform deconvolution.

2.2.3 Algorithm with Reflection Time Stamp Estimation

In this section, we propose a heuristic method for estimating dominant reflection time stamps. The algorithm is as follows:

• 1. Initially we choose DSB as a first FBF and perform normalized least mean square algorithm to estimate the RIR FIR coefficients using the output of DSB.

• 2. Select the time stamps, in which the estimated RIR magnitudes are above a predefined threshold, which determines the significance level of the reflection.

• 3. Perform the proposed algorithm presented in Sect. 13.2.2.2.

• 4. Iterate 2 and 3 until there is no significant increase on the selected time stamps.

Figure 13.2 shows the converged result, where the simulated output of two channels has been obtained by convolving the channel response with a white Gaussian-noise source and the threshold has been set to 0.08. Note that most of the significant reflection points above the threshold can be estimated almost correctly.

Fig. 13.2

(a) Estimated channel h1. (b) Estimated channel h2: Red dots show the converged channel response after 20 iteration, and the black line is for the original RIR. The designated channel responses above the predefined threshold are almost correctly identified

3 Experiment with Real Car Data

In this section, we test the proposed algorithm using real multichannel sources measured in cars. Before running the algorithm, inter-channel delays are estimated using GCC-PHAT [11] to formulate the DSB. Figure 13.3 shows the two-channel identification results using one of the single-digit utterances from the AVICAR database [6], and no distinctive reflection other than direct path has been estimated. Possible explanation about the result is that the space inside of a car is too small to have sparsely separable, distinctive echo paths. However, because this result also means that there is no significantly correlated reflection in the original signals with the beamformed output using the direct path information as in DSB, we can avoid the signal canceling problem when we use conventional GSC structure only with DSB as FBF. Optimal signal enhancement and isolated digit recognition results with conventional GSC followed by MMSE spectral amplitude estimation have been already reported in [12].

Fig. 13.3

(a) Estimated channel hl. (b) Estimated channel h2

4 Conclusion

In this chapter, we propose a multi-path GSC–based blind channel identification method, which can be plugged in as a realistic replacement of the sufficient statistic for optimal speech enhancement. The simulation with artificially generated sparse channels demonstrates that the proposed algorithm can converge to good estimates of all components in the original channel responses that are above a predefined threshold. Channel estimation experiments with real data measured in a car show that there exists no distinctive significant reflection and support that a conventional GSC followed by a post-filter can produce optimal speech estimation.