Approximations for Probability Distributions and Stochastic Optimization Problems

Abstract

In this chapter, an overview of the scenario generation problem is given. After an introduction, the basic problem of measuring the distance between two single-period probability models is described in Section 15.2. Section 15.3 deals with finding good single-period scenarios based on the results of the first section. The distance concepts are extended to the multi-period situation in Section 15.4. Finally, Section 15.5 deals with the construction and reduction of scenario trees.

1 Introduction

Decision making under uncertainty is based upon

• (i) a probability model for the uncertain values,

• (ii) a cost or profit function depending on the decision variables and the uncertainties, and

• (iii) a probability functional, like expectation, median, etc., to summarize the random costs or profits in a real-valued objective.

We describe the decision model under uncertainty by

$$(Opt) \qquad \max \{ F(x) = {\mathcal A}_{P}[H(x,\xi)] : x \in {\mathbb X} \},$$

((15.1))

where $H(\cdot, \cdot)$ denotes the profit function, with x the decision and ξ the random variable or random vector modeling uncertainty. Both – the uncertain data ξ and the decision x – may be stochastic processes adapted to some filtration ${\mathcal F}$. ${\mathcal A}$ is the probability functional and ${\mathbb X}$ is the set of constraints. P denotes the underlying probability measure.

The most difficult part in establishing a formalized decision model of type (15.1) for a real decision situation is to find the probability model P. Typically, there is a sample of past data available, but not more. It needs two steps to come from the sample of observations to the scenario model:

• (1) In the first step a probability model is identified, i.e., the description of the uncertainties as random variables or random processes by identifying the probability distribution. This step is based on statistical methods of model selection and parameter estimation. If several probability measures represent the data equally well, one speaks of ambiguity. In the non-ambiguous situation, one and only one probability model is selected and this model is the basis for the next step.

• (2) In the following scenario generation step, a scenario model is found, which is an approximation of (15.1) by a finite model of lower complexity than the probability model.

The scenario model differs from the original model (15.1) insofar as P is replaced by $\tilde {P}$, but – especially in multi-period problems – also the feasible set ${\mathbb X}$ is replaced by a smaller, feasible set $\tilde{{\mathbb X}}$:

$$\widetilde{(Opt)} \qquad \max \{ \tilde{F}(\tilde{x}) = {\mathcal A}_{\tilde{P}}[H(\tilde{x},\xi)] : \tilde{x} \in \tilde{{\mathbb X}}\}.$$

((15.2))

It is essential that the scenario model is finite (i.e., only finitely many values of the uncertainties are possible), but a good approximation to the original model as well. The finiteness is essential to keep the computational complexity low, and the approximative character is needed to allow the results to be carried over to the original model. In some cases, which do not need to be treated further here, finitely many scenarios are given right from the beginning (e.g., Switzerland will join the EU in 2015 – yes or no, or UK will adopt the EURO in 2020 and so on). The same is true, if the scenarios are just taken as the historic data without further transformation or information reduction. However, the justification of using just the empirical sample as the scenario model lies in the fact that these samples converge to the true underlying distribution if the sample size increases. For a quantification of this statement see Section 15.3.3 on Monte Carlo approximation below.

When stressing the approximative character of a scenario model we have to think about the consequences of this approximation and to estimate the error committed by replacing the probability model by the scenario model. Consider the diagram below: It is typically impossible to solve problem (15.1) directly due to its complexity. Therefore, one has to go around this problem and solve the simplified problem (15.2). Especially for multi-period problems, the solution of the approximate problem is not directly applicable to the original problem, but an extension function is needed, which extends the solution of the approximate problem to a solution of the original problem. Of course, the extended solution of the approximate problem is typically suboptimal for the original problem. The respective gap is called the approximation error. It is the important goal of scenario generation to make this gap acceptably small.

The quality of a scenario approximation depends on the distance between the original probability P and the scenario probability $\tilde {P}$. Well-known quantitative stability theorems (see, e.g., Dupacova (1990), Heitsch et al. (2006), and Rachev and Roemisch (2002)) establish the relation between distances of probability models on one side and distances between optimal values or solutions on the other side (see, e.g., cite stability). For this reason, distance concepts for probability distributions on ${\mathbb R}^M$ are crucial.

2 Distances Between Probability Distributions

Let ${\mathcal P}$ be a set of probability measures on ${\mathbb R}^M$.

Definition 1.1

A semi-distance on ${\mathcal P}$ is a function ${\mathsf d}(\cdot , \cdot )$ on ${\mathcal P} \times {\mathcal P}$, which satisfies (i) and (ii) as follows:

• (i) Nonnegativity: For all $P_{1}, P_{2} \in {\mathcal P}$

  $${\mathsf d}(P_{1},P_{2}) \ge 0.$$

• (ii) Triangle inequality: For all $P_{1}, P_{2}, P_{3} \in {\mathcal P}$

  $${\mathsf d}(P_{1},P_{2}) \le {\mathsf d}(P_{1},P_{3}) + {\mathsf d}(P_{3},P_{2}).$$

  If a semi-distance satisfies the strictness property

• (iii) Strictness: If ${\mathsf d}(P_{1}, P_{2}) = 0$, then $P_{1} = P_{2}$,

  it is called a distance.

A general principle for defining semi-distances and distances consists in choosing a family of integrable functions ${\mathcal H}$ (i.e., a family of functions such that the integral $\int h(w) \, dP(w)$ exists for all $P \in {\mathcal P}$) and defining

$${\mathsf d}_{{\mathcal H}} (P_{1},P_{2}) = \sup \left\{ | \int h(w) \; {\mathit d} P_{1}(w) - \int h(w) \; {\mathit d} P_{2}(w) | : h \in {\mathcal H}\right\}.$$

We call ${\mathsf d}_{{\mathcal H}}$ the (semi-)distance generated by ${\mathcal H}$.

In general, ${\mathsf d}_{{\mathcal H}}$ is only a semi-distance. If ${\mathcal H}$ is separating, i.e., if for every pair $P_{1}, P_{2} \in {\mathcal P}$ there is a function $h \in {\mathcal H}$ such that $\int h \, {\mathit d} P_{1} \neq \int h \, {\mathit d} P_{2}$, then ${\mathsf d}_{{\mathcal H}}$ is a distance.

2.1 The Moment-Matching Semi-Distance

Let ${\mathcal P}_{q}$ be the set of all probability measures on ${\mathbb R}^1$ which possess the qth moment, i.e., for which $\int \max(1, | w |^q) \, d P(w) < \infty$. The moment-matching semi-distance on ${\mathcal P}_{q}$ is

$${\mathsf d}_{M_{q}}(P_{1}, P_{2}) = \sup \left\{ | \int w^s \; {\mathit d} P_{1}(w) - \int w^s \; {\mathit d} P_{2}(w) | : s \in \{1,2, \dots, q\} \right\}.$$

((15.3))

The moment-matching semi-distance is not a distance, even if q is chosen to be large or even infinity. In fact, there are examples of two different probability measures on ${\mathbb R}^1$, which have the same moments of all orders. For instance, there are probability measures, which have all moments equal to those of the lognormal distribution, but are not lognormal (see, e.g., Heyde (1963)).

A widespread method is to match the first four moments (Hoyland and Wallace 2001), i.e., to work with ${\mathsf d}_{M_{4}}$. The following example shows that two densities coinciding in their first four moments may exhibit very different properties.

Example

Let P ₁ and P ₂ be the two probability measures with densities g ₁ and g ₂ where

$$\begin{array}{rcl}g_{1}(x) &=& 0.39876 \, [ \, \exp(-|x+0.2297|^3) {\mathchoice {\hbox{1\kern -0.27em l}}{\hbox{1\kern -0.27em l}} {\small{1\kern -0.27em l}}{\small{1\kern -0.27em l}}}_{\{ x \le -1.2297\}}\\ &+& \exp(-|x+0.2297|) {\mathchoice {\hbox{1\kern -0.27em l}}{\hbox{1\kern -0.27em l}} {\small{1\kern -0.27em l}}{\small{1\kern -0.27em l}}}_{\{ -1.2297< x \le -0.2297 \}}\\ &+&\exp(-0.4024 \cdot (x+0.2297)) {\mathchoice {\hbox{1\kern -0.27em l}}{\hbox{1\kern -0.27em l}} {\small{1\kern -0.27em l}}{\small{1\kern -0.27em l}}}_{\{ -0.2297 < x \le 2.2552 \}}\\ &+& 1.09848 \cdot (0.4024 x + 0.29245)^{-6} {\mathchoice {\hbox{1\kern -0.27em l}}{\hbox{1\kern -0.27em l}} {\small{1\kern -0.27em l}}{\small{1\kern -0.27em l}}}_{\{ 2.2552< x \}}],\\ g_{2}(x) &=& 0.5962 \, {\mathchoice {\hbox{1\kern -0.27em l}}{\hbox{1\kern -0.27em l}} {\small{1\kern -0.27em l}}{\small{1\kern -0.27em l}}}_{\{ |x| \le 0.81628\}}+ 0.005948 \, {\mathchoice {\hbox{1\kern -0.27em l}}{\hbox{1\kern -0.27em l}} {\small{1\kern -0.27em l}}{\small{1\kern -0.27em l}}}_{\{ 0.81628 < |x| \le 3.05876\}}.\end{array}$$

Both densities are unimodal and coincide in the first four moments, which are $m_{1}= 0$, $m_{2}=0.3275$, $m_{3}=0$, $m_{4}=0.72299$ ($m_{q}(P) = \int w^q \, dP(w)$). The fifth moments, however, could not differ more: While P ₁ has infinite fifth moment, the fifth moment of P ₂ is zero. Density g ₁ is asymmetric, has a sharp cusp at the point −0.2297 and unbounded support. In contrast, g ₂ is symmetric around 0, has a flat density there, has finite support, and possesses all moments. The distribution functions and quantiles differ drastically: We have that $G_{P_{1}}(0.81) = 0.6257$ and $G_{P_{1}}(-0.81) = 0.1098$, while $G_{P_{2}}(0.81) = 0.9807$ and $G_{P_{2}}(-0.81) = 0.0133$. Thus the probability of the interval $[-0.81,0.81]$ is only 51% under P ₁, while it is 96% under P ₂.

Two densities g ₁ and g ₂ with identical first four moments.

The two pertaining distribution functions G ₁ and G ₂.

Summarizing, the moment matching semi-distance is not well suited for scenario approximation, since it is not fine enough to capture the relevant quality of approximation.

The other extreme would be to choose as the generating class ${\mathcal H}$ all measurable functions h such that $|h| \le 1$. This class generates a distance, which is called the variational distance (more precisely twice the variational distance). It is easy to see that if P ₁ resp. P ₂ have densities g ₁ resp. g ₂ w.r.t. λ, then

$$\begin{array}{rcl}&& \sup\left\{ \int h \, {\mathit d} P_{1} - \int h \, {\mathit d} P_{2} : | h | \le 1, h \hbox{ measurable} \right\}\\ &=& \int |g_{1}(x) - g_{2}(x) | \, {\mathit d} \lambda(x)\\ &=& 2 \sup \{ | P_{1}(A) - P_{2}(A) : A \ \hbox{measurable set}\}.\end{array}$$

We call

$${\mathsf d}_{V}(P_{1}, P_{2}) = \sup \{ | P_{1}(A) - P_{2}(A)| : A \ \hbox{ measurable set} \}$$

((15.4))

the variational distance between P ₁ and P ₂.

The variational distance is a very fine distance, too fine for our applications: If P ₁ has a density and P ₂ sits on at most countably many points, then ${\mathsf d}_{V}(P_{1}, P_{2}) = 1$, independently on the number of mass points of P ₂. Thus there is no hope to approximate any continuous distribution by a discrete one w.r.t. the variational distance.

One may, however, restrict the class of sets in (15.4) to a certain subclass. If one takes the class of half-unbounded rectangles in ${\mathbb R}^M$ of the form $(-\infty, t_{1}] \times (-\infty, t_{2}] \times \cdots \times (-\infty, t_{M}]$ one gets the uniform distance, also called Kolmogorov distance

$${\mathsf d}_{U}(P_{1},P_{2}) = \sup \{ | G_{P_{1}}(x) - G_{P_{2}}(x) | : x \in {\mathbb R}^M \},$$

((15.4))

where $G_{P}(t)$ is the distribution function of P,

$$G_{P}(t) = P\{(-\infty, t_{1}] \times \cdots \times (-\infty, t_{M}] \}.$$

The uniform distance appears in the Hlawka–Koksma inequality:

$$\int h(u) \; {\mathit d} P_{1}(u) - \int h(u) \; {\mathit d} P_{2}(u) \le {\mathsf d}_{U}(P_{1},P_{2}) \cdot V(h),$$

((15.6))

where $V(h)$ is the Hardy–Krause variation of h. In dimension $M=1$, V is the usual total variation

$$V(h) = \sup \left\{ \sum_{i} | h(z_{i}) - h(z_{i-1})| : z_{1} < z_{2} < \cdots < z_{n}, n \ \hbox{arbitrary} \right\}.$$

In higher dimensions, let $V^{(M)}(h) = \sup \sum_{J_{1}, \dots, J_{n} \ \hbox{ {\tiny is a partition by rectangles $J_{i}$}}} | \Delta_{J_{i}}(h)|,$ where $\Delta_{J}(h)$ is the sum of values of h at the vertices of J, where adjacent vertices get opposing signs. The Hardy–Krause variation of h is defined as $\sum_{m=1}^M V^{(m)}(h)$. ${\mathsf d}_{U}$ is invariant w.r.t. monotone transformations, i.e., if T is a monotone transformation, then the image measures $P_{i}^T = P_{i} \circ T^{-1}$ satisfy

$${\mathsf d}_{U}(P_{1}^T, P_{2}^T) = {\mathsf d}_{U}(P_{1}, P_{2}).$$

Notice that a unit mass at point 0 and at point $1/n$ are at a distance 1 both in the ${\mathsf d}_{U}$ distance, for any even large n. Thus it may be felt that also this distance is too fine for good approximation results. A minimal requirement of closedness is that integrals of bounded, continuous functions are close and this leads to the notion of weak convergence.

Definition 1.2

(Weak convergence) A sequence of probability measures P _n on ${\mathbb R}^M$ converges weakly to P (in symbol $P_{n} \Rightarrow P$), if

$$\int h \, {\mathit d} P_{n} \to \int h \, {\mathit d} P$$

as $n \to \infty$, for all bounded, continuous functions h. Weak convergence is the most important notion for scenario approximation: We typically aim at constructing scenario models which, for increasing complexity, finally converge weakly to the underlying continuous model.

If a distance ${\mathsf d}$ has the property that

$${\mathsf d}(P_{n},P) \to 0 \quad \hbox{ if and only if } P_{n} \Rightarrow P$$

we say that d metricizes weak convergence.

The following three distances metricize the weak convergence on some subsets of all probability measures on ${\mathbb R}^M$:

• (i) The bounded Lipschitz metric: If ${\mathcal H}$ is the class of bounded functions with Lipschitz constant 1, the following distance is obtained:

  $${\mathsf d}_{\mathrm{BL}}(P_{1}, P_{2}) = \sup \left\{ \int h \; {\mathit d} P_{1} - \int \; h {\mathit d} P_{2}: |h(u)| \le 1, L_{1}(h) \le 1 \right\},$$

  ((15.7))

  where

  $$L_{1}(h) = \inf \{ L: |h(u) - h(v) | \le L \|u - v \| \}.$$

  This distance metricizes weak convergence for all probability measures on ${\mathbb R}^M$.

• (ii) The Kantorovich distance: If one drops the requirement of boundedness of h, one gets the Kantorovich distance

  $${\mathsf d}_{\mathrm{KA}}(P_{1}, P_{2}) = \sup \left\{ \int h \; {\mathit d} P_{1} - \int h \; {\mathit d} P_{2}: L_{1}(h) \le 1 \right\}.$$

  ((15.8))

  This distance metricizes weak convergence on sets of probability measures which possess uniformly a first moment. (A set ${\mathcal P}$ of probability measures has uniformly a first moment, if for every ε there is a constant C _ε such that $\int_{\|x\| > C_\epsilon} \| x \| \, {\mathit d} P(x) < \epsilon$ for all $P \in {\mathcal P}$.) See the review of Gibbs and Su (2002). On the real line, the Kantorovich metric may also be written as

  $$d_{\mathrm{KA}}(P,\tilde{P}) = \int |G_{P}(u) - G_{\tilde{P}}(u)| \; {\mathit d} u = \int |G_{P}^{-1}(u) - G_{\tilde{P}}^{-1}(u)| \; {\mathit d} u,$$

  where $G_{P}^{-1}(u) = \sup \{v: G_{P}(v) \le u \}$ (see Vallander (1973)).

• (iii) The Fortet–Mourier metric: If ${\mathcal H}$ is the class of Lipschitz functions of order q, the Fortet–Mourier distance is obtained:

  $${\mathsf d}_{\mathrm{FM}_{q}}(P_{1}, P_{2}) = \sup \left\{\int h \; {\mathit d} P_{1} - \int \; h {\mathit d} P_{2}: L_{q}(h) \le 1 \right\},$$

  ((15.9))

  where the Lipschitz constant of order q is defined as

  $$L_{q}(h) = \inf \{ L : | h(u) - h(v) | \le L ||u - v|| \max(1,||u||^{q-1}, ||v||^{q-1}) \}.$$

  ((15.10))

Notice that $L_{q}(h) \le L_{q^\prime}(h)$ for $q^\prime \le q$. In particular, $L_{q}(h) \le L_{1}(h)$ for all $q \ge 1$ and therefore

$${\mathsf d}_{\mathrm{FM}_{q}}(P_{1}, P_{2}) \ge {\mathsf d}_{\mathrm{FM}_{q^\prime}}(P_{1},P_{2}) \ge {\mathsf d}_{\mathrm{KA}}(P_{1}, P_{2}).$$

The Fortet–Mourier distance metricizes weak convergence on sets of probability measures possessing uniformly a qth moment. Notice that the function $u \mapsto \|u\|^q$ is q-Lipschitz with Lipschitz constant $L_{q} = q$. On ${\mathbb R}^1$, the Fortet–Mourier distance may be equivalently written as

$${\mathsf d}_{\mathrm{FM}_{q}}(P_{1},P_{2}) = \int \max(1,|u|^{q-1}) |G_{P_{1}}(u) - G_{P_{2}}(u)| \; {\mathit d} u$$

(see Rachev (1991), p. 93). If q = 1, the Fortet–Mourier distance coincides with the Kantorovich distance.

The Kantorovich distance is related to the mass transportation problem (Monge’s problem – Monge (1781), see also Rachev (1991), p. 89) through the following theorem.

Theorem 1.3

(Kantorovich–Rubinstein)

$$\begin{array}{rcl}{\mathsf d}_{\mathrm{KA}}(P_{1}, P_{2}) &=& \inf \{ {\mathbb E}( |X_{1} - X_{2}| ) : \textit{s.t. the joint distribution } (X_{1}, X_{2})\\ && \textit{is arbitrary, but the marginal distributions are fixed}\\ &&\textit{such that} X_{1} \sim P_{1} , X_{2} \sim P_{2} \}\end{array}$$

((15.11))

(see Rachev (1991), theorems 5.3.2 and 6.1.1).

The infimum in (15.11) is attained. The optimal joint distribution $(X_{1}, X_{2})$ describes how masses with distribution P should be transported with minimal effort to yield the new mass distribution $\tilde {P}$. The analogue of the Hlawka–Koksma inequality is here

$$\int | h(u) \; {\mathit d} P_{1}(u) - \int h(u) \; {\mathit d} P_{2}(u) | \le {\mathsf d}_{\mathrm{KA}}(P_{1},P_{2}) \cdot L_{1}(h).$$

((15.12))

The Kantorovich metric can be defined on arbitrary metric spaces R with metric d: If P ₁ and P ₂ are probabilities on this space, then ${\mathsf d}_{\mathrm{KA}}(P_{1}, P_{2};d)$ is defined by

$${\mathsf d}_{\mathrm{KA}}(P_{1}, P_{2};d) = \sup \left\{ \int h \; {\mathit d} P_{1} - \int h \; {\mathit d} P_{2}: |h(u) - h(v) | \le d(u,v) \right\}.$$

((15.13))

Notice that the metric ${\mathsf d}(\cdot,\cdot;d)$ is compatible with the metric d in the following sense: If δ _u resp. δ _v are unit point masses at u resp. v, then

$${\mathsf d}_{\mathrm{KA}}(\delta_{u},\delta_{v};d) = d(u,v).$$

The theorem of Kantorovich–Rubinstein extends to the general case:

$$\begin{array}{rcl}{\mathsf d}_{\mathrm{KA}}(P_{1}, P_{2};d) &=& \inf \{ {\mathbb E}[ d(X_{1},X_{2}) ] : \ \hbox{ where the joint distribution } (X_{1}, X_{2})\\ && \hbox{ is arbitrary, but the marginal distributions are fixed }\\ &&\hbox{ such that } X_{1} \sim P_{1} , X_{2} \sim P_{2} \}.\end{array}$$

((15.14))

A variety of Kantorovich metrics may be defined, if ${\mathbb R}^M$ is endowed with different metrics than the Euclidean one.

2.2 Alternative Metrics on ${\mathbb R}^{M}$

By (15.13), to every metric d on ${\mathbb R}^M$, there corresponds a distance of the Kantorovich type. For instance, let d ₀ be the discrete metric

$$d_{0}(u,v) = \left\{\begin{array}{ll} 1 & \quad \hbox{ if } u \neq v,\\ 0 & \quad \hbox{ if } u = v. \end{array} \right.$$

The set of all Lipschitz functions w.r.t. the discrete metric coincides with the set of all measurable functions h such that $0 \le h \le 1$ or its translates. Consequently the pertaining Kantorovich distance coincides with the variational distance

$${\mathsf d}_{\textrm{KA}}(P_{1},P_{2};d_{0}) = {\mathsf d}_{V}(P_{1}, P_{2}).$$

Alternative metrics on ${\mathbb R}^1$ can, for instance, be generated by nonlinear transform of the axis. Let χ be any bijective monotone transformation, which maps ${\mathbb R}^1$ into ${\mathbb R}^1$. Then $d(u,v):= | \chi(u) - \chi(v)|$ defines a new metric on ${\mathbb R}^1$. Notice that the family functions which are Lipschitz w.r.t the distance d and the Euclidean distance $| u - v|$ may be quite different.

In particular, let us look at the bijective transformations (for $q > 0$)

$$\chi_{q}(u) = \left\{ \begin{array}{ll} u & |u| \le 1\\[3pt] |u|^q \hbox{ sgn}(u) & |u| \ge 1 \end{array} \right. .$$

Notice that $\chi_{q}^{-1}(u) = \chi_{1/q}(u)$. Introduce the metric $d_{\chi_{q}}(u,v) = |\chi_{q}(u) - \chi_{q}(v)|$. We remark that $d_{\chi_{1}}(u,v) = | u - v|$. Denote by ${\mathsf d}_{\mathrm{KA}}(\cdot,\cdot;d_{\chi_{q}})$ the Kantorovich distance which is based on the distance $d_{\chi_{q}}$,

$${\mathsf d}_{\mathrm{KA}}(P_{1}, P_{2}; d_{\chi_{q}}) = \sup \left\{ \int h \; {\mathit d} P_{1} - \int h \; {\mathit d} P_{2}: \| h(u) - h(v) \| \le d_{\chi_{q}}(u,v) \right\}.$$

Let $P^{\chi_{q}}$ be the image measure of P under χ _q , that is $P^{\chi_{q}}$ assigns to a set A the value $P\{ \chi_{1/q}(A)\}$. Notice that $P^{\chi_{q}}$ has distribution function

$$G_{P^{\chi_{q}}}(x) = G_{P}(\chi_{1/q}(x)).$$

This leads to the following identity:

$${\mathsf d}_{\mathrm{KA}}(P_{1},P_{2}; d_{\chi_{q}}) = {\mathsf d}_{\mathrm{KA}}(P_{1}^{\chi_{q}}, P_{2}^{\chi_{q}};| \cdot |).$$

It is possible to relate the Fortet–Mourier distance $d_{M_{q}}$ to the distance ${\mathsf d}_{\mathrm{KA}}(\cdot,\cdot; d_{\chi_{q}})$. To this end, we show first that

$$L_{q}(h \circ \chi_{q}) \le q \cdot L_{1}(h)$$

((15.15))

and

$$L_{1}(h \circ \chi_{1/q}) \le L_{q}(h).$$

((15.16))

If $L_{1}(h) < \infty$, then

$$\begin{array}{rcl}|h(\chi_{q}(u)) - h(\chi_{q}(v))| &\le& L_{1}(h) |\chi_{q}(u) - \chi_{q}(v)|\\ &\le& L_{1}(h) \cdot q \cdot \max(1,|u|^{q-1}, |v|^{q-1}) |u - v|\end{array}$$

which implies (15.15). On the other hand, if $L_{q}(h) < \infty$, then

$$\begin{array}{rcl}&&|h(\chi_{1/q}(u)) - h(\chi_{1/q}(v))|\\ &\le& L_{q}(h) \max(1, |\chi_{1/q}(u)|^{q-1} , |\chi_{1/q}(v)|^{q-1} ) |\chi_{1/q}(u) - \chi_{1/q}(v)|\\ &\le& L_{q}(h) \max(1, \max(|u|,|v|)^{q-1}) \max(1, \max(|u|,|v|)^{(1-q)/q} |u - v|\\ &\le& L_{q}(h) |u - v|\end{array}$$

and therefore (15.16) holds. As a consequence, we get the following relations:

$$\begin{array}{rcl}\frac{1}{q} {\mathsf d}_{\mathrm{KA}}(P_{1},P_{2}; d_{\chi_{q}}) &=& \frac{1}{q} {\mathsf d}_{\mathrm{KA}} (G_{P_{1}} \circ \chi_{1/q}, G_{P_{2}} \circ \chi_{1/q}) \\ &\le& {\mathsf d}_{\mathrm{FM}_{q}}(P_{1},P_{2}) \\ &\le& {\mathsf d}_{\mathrm{KA}}(G_{P_{1}} \circ \chi_{1/q}, G_{P_{2}} \circ \chi_{1/q}) = {\mathsf d}_{\mathrm{KA}}(P_{1},P_{2};d_{\chi_{q}}).\!\!\qquad\qquad\end{array}$$

((15.17))

Thus one sees that it is practically equivalent to measure the distance by the Fortet–Mourier distance of order q or by the Kantorovich distance (i.e., the Fortet–Mourier distance of order 1) but with the real line endowed with the metric $d_{\chi_{q}}$.

2.3 Extending the Kantorovich Distance to the Wasserstein Distance

By the Kantorovich–Rubinstein Theorem, the Kantorovich metric is the optimal cost of a transportation problem. If the cost function is not the distance d itself, but a power d ^r of it, we are led to the Wasserstein metric ${\mathsf d}_{\mathrm{W},r}$.

$$\begin{array}{rcl}{\mathsf d}_{\mathrm{W},r}(P_{1}, P_{2};d)^r &=& \inf \left\{ \int d(x_{1},x_{2})^r \pi({\mathit d} x_{1},{\mathit d} x_{2}) ; \ \hbox{ s.t. the joint probability } \right.\nonumber\\ && \hbox{measure } \pi \ \hbox{ has marginals such that}\nonumber\\ && \left. \pi(A\times {\mathbb R}^M)=P_{1}(A) \hbox{ and } \pi({\mathbb R}^M\times B)=P_{2}(B)\right\}.\end{array}$$

((15.18))

This is a metric for $r\ge 1$. For $r < 1$, the Wasserstein distance is defined as

$$\begin{array}{rcl}{\mathsf d}_{\mathrm{W},r}(P_{1}, P_{2};d) &=& \inf \left\{ \int d(x_{1},x_{2})^r \pi({\mathit d} x_{1},{\mathit d} x_{2}) ; \ \hbox{ where the joint probability } \right.\nonumber\\ && \hbox{measure } \pi \ \hbox{ has marginals such that}\nonumber\\ && \left. \pi(A\times {\mathbb R}^M)=P_{1}(A) \hbox{ and } \pi({\mathbb R}^M\times B)=P_{2}(B)\right\}\end{array}$$

((15.19))

(see Villani (2008)).

2.4 Notational Convention

When there is no doubt about the underlying distance d, we simply write

$${\mathsf d}_{r}(P_{1}, P_{2}) \quad \hbox{ instead of } \quad {\mathsf d}_{W,r}(P_{1},P_{2};d).$$

Recall that in this notation, the Kantorovich distance is ${\mathsf d}_{\mathrm{KA}}(P_{1},P_{2}) = {\mathsf d}_{1}(P_{1},P_{2})$.

2.5 Wasserstein Distance and Kantorovich Distance as Linear Program

To compute the Wasserstein distance for discrete probability distributions amounts to solving a linear program, as we shall outline here:

Consider the discrete measures $P:=\sum_{s}p_{s}\delta_{z_{s}}$ and $Q:=\sum_{t}q_{t}\delta_{z_{t}^{\prime}}$ and – within this setting – the problem

$$\begin{array}{lll} \begin{array}{l} \hbox{ Minimize }\\ \hbox{\quad(in }\pi)\end{array} & \sum\limits_{s,t}\pi_{s,t}c_{s,t}\vspace*{3pt}\\ \hbox{ subject to } & \sum\limits_{t}\pi_{s,t}=p_{s},\vspace*{3pt}\\ & \sum\limits_{s}\pi_{s,t}=q_{t}\mbox{ and} & \pi_{s,t}\ge0,\end{array}$$

((15.20))

where $c_{s,t}:=d\left(z_{s},z_{t}^{\prime}\right)^{r}$ is a matrix derived from the general distance function d. This matrix c represents the weighted costs related to the transportation of masses from z _s to $z_{t}^{\prime}$.

Notice that (15.20) is a general linear program, which is already well defined by specifying the cost matrix $c_{s,t}$ and the probability masses p _s and q _t . So in particular the mass points z _s are not essential to formulate the problem; they may represent abstract objects.

Observe further that

$$\sum_{s,t}\pi_{s,t}=\sum_{s}p_{s}=\sum_{t}q_{t}=1,$$

thus π is a probability measure, representing – due to the constraints – a transport plan from P to Q. The linear program (15.20) thus returns the minimal distance between those measures, and as a minimizing argument the optimal transport plan in particular for transporting masses from object z _s to $z_{t}^{\prime}$.

The linear program (15.20) has a dual with vanishing duality gap. The theorem of Kantorovich–Rubinstein allows to further characterize (in the situation r = 1) the dual program; it amounts to just finding a Lipschitz-1 function h which maximizes the respective expectation:

$$\begin{array}{ll} \begin{array}{l} \hbox{ Maximize }\\ \hbox{\quad(in }h)\end{array} & \sum_{s}p_{s}h_{s}-\sum_{t}q_{t}h_{t},\\ \hbox{ subject to } & h_{s}-h_{t}\le d\left(z_{s},z_{t}\right).\end{array}$$

Due to the vanishing duality gap the relation

$$\sum_{s}p_{s}h_{s}^{*}-\sum_{t}q_{t}h_{t}^{*}=\sum_{s,t}\pi^*_{s,t}c_{s,t}$$

holds true, where h ^c is the optimal Lipschitz-1 function and π ^π the optimal joint measure.

2.6 Bibliographical Remarks

The distance ${\mathsf d}_{\mathrm{KA}}$ was introduced by Kantorovich in 1942 as a distance in general spaces. In 1948, he established the relation of this distance (in ${\mathbb R}^n$) to the mass transportation problem formulated by Gaspard Monge in 1781. In 1969, L. N. Wasserstein – unaware of the work of Kantorovich – reinvented this distance for using it for convergence results of Markov processes and 1 year later R. L. Dobrushin used and generalized this distance and initiated the name Wasserstein distance. S. S. Vallander studied the special case of measures in ${\mathbb R}^1$ in 1974 and this paper made the name Wasserstein metric popular. The distance ${\mathsf d}_{U}$ was introduced by Kolmogorov in 1933. It is often called Kolmogorov distance.

3 Single-Period Discretizations

In this section, we study the discrete approximation problem:

Let a probability measure P on ${\mathbb R}^M$ be given. We want to find a probability measure sitting on at most S points, such that some distance ${\mathsf d}(P, \tilde{P})$ is small.

We say “small” and not “minimal”, since it may be computationally intractable to really find the minimum. Formally, define ${\mathcal P}_{S}$ as the family of all probability measures

$$\tilde{P}=\sum_{s=1}^S p_{s} \delta_{z_{s}}$$

on ${\mathbb R}^M$ sitting on at most S points. Here δ _z denotes the point mass at point z. We try to find a $\tilde{P} \in {\mathcal P}_{S}$ such that

$${\mathsf d}(P, \tilde{P}) \textrm{is close to} \min \{ {\mathsf d}(P,Q) : Q \in {\mathcal P}_{S}\}.$$

There are several methods to attack the problem, which we order in decreasing order of computational effort and as well in decreasing order of approximation quality (see Fig. 15.1):

Fig. 15.1

Methods of scenario generation

While the probability measure P may have a density or may be discrete, the measure $\tilde {P}$ is always characterized by the list of probability masses $p_{s}, s=1, \dots, S$ and the list of mass points $z_{s}, s=1, \dots, S$. The discrete measure $\tilde {P}$ is represented by

$$\tilde{P} = \left[ \begin{array}{cccc} p_{1} & p_{2} & \cdots & p_{S}\\ \hline z_{1} & z_{2} & \cdots & z_{S}.\\ \end{array}\right].$$

The approximation problem depends heavily on the chosen distance d, as will be seen. We treat the optimal quantization problem in Section 15.3.1, the quasi-Monte Carlo technique in Section 15.3.2 and the Monte Carlo technique in Section 15.3.3. Some quantization heuristics are contained in Chapter 3.

3.1 Optimal and Asymptotically Optimal Quantizers

The basic approximation problem, i.e., to approximate a distribution on ${\mathbb R}^M$ by a distribution sitting on at most S points leads to a non-convex optimization problem. To find its global solution is computationally hard. Moreover, no closed-form solution is known, even for the simplest distributions.

Recall the basic problem: Let ${\mathsf d}$ be some distance for probability measures and let ${\mathcal P}_{S}$ be the family of probability distributions sitting on at most S points. For a given probability $P \in {\mathcal P}_{S}$, the main question is to find the quantization error

$$q_{S,{\mathsf d}}(P) = \inf \{ {\mathsf d}(P,Q) : Q \in {\mathcal P}_{S} \}$$

((15.21))

and the optimal quantization set

$${\mathcal Q}_{S,{\mathsf d}}(P) = \arg\min \{ {\mathsf d}(P,Q) : Q \in {\mathcal P}_{S} \}$$

((15.22))

(if it exists).

3.1.1 Optimal Quantizers for Wasserstein Distances ${\mathsf d}_{r}$

Since all elements $\tilde {P}$ of ${\mathcal P}_{S}$ are of the form $\tilde{P} = \sum_{s=1}^S p_{s} \delta_{z_{s}}$, the quantization problem consists essentially of two steps:

• (1) Find the optimal supporting points z _s.

• (2) Given the supporting points z _s, find the probabilities p _s, which minimize

  $${\mathsf d}_{r}\left(P,\sum_{s=1}^S p_{s} \delta_{z_{s}}\right)$$

  ((15.23))

  for the Wasserstein distance.

Recall the Wasserstein ${\mathsf d}_{r}$ distances contain the Kantorovich distance as the special case for r = 1.

We show that the second problem has an easy solution for the chosen distance: Let $z=(z_{1}, \dots, z_{S})$ be the vector of supporting points and suppose that they are all distinct. Introduce the family of Voronoi diagrams ${\mathcal V}(z)$ as the family of all partitions $(A_{1}, \dots, A_{S})$, where A _s are pairwise disjoint and ${\mathbb R}^M = \bigcup_{s=1}^S A_{s}$, such that

$$A_{s} \subseteq \{ y: d(y,z_{s}) = \min_{k} d(y,z_{k})\}.$$

Then the possible optimal probability weights p _s for minimizing ${\mathsf d}_{r}\left(\!P,\sum_{s=1}^S p_{s} \delta_{z_{s}}\right)$ can be found by

$$p = (p_{1}, \dots, p_{S}), \hbox{ where } p_{s} = P(A_{s}); \quad (A_{1}, \dots, A_{S}) \in {\mathcal V}(z).$$

The optimal probability weights are unique, iff

$$P \{ y: d(y,z_{s}) = d(y,z_{k}), \hbox{ for some $s \neq k$} \}= 0.$$

One may also reformulate (15.23) in terms of random variables: Let $X \sim P$ and let $\tilde {X}$ be a random variable which takes only finitely many values $\tilde{X} \in \{z_{1}, \dots, z_{S}\}$, then

$$\begin{array}{rcl}D_{{\mathsf d}_{r}}(z) &:=& \inf \{ {\mathbb E}[ d(X,\tilde{X})^r] : X \sim P, \tilde{X} \in \{z_{1}, \dots, z_{S}\} \}\\ &=& \inf \{ {\mathsf d}_{r}(P, \tilde{P})^r \colon \mathrm{supp}(\tilde{P}) \subseteq \{ z_{1}, \dots, z_{S} \} \}\\ &=& \int \min_{s} d(x,z_{s})^r \, {\mathit d} P(x).\end{array}$$

Unfortunately, the function $z \mapsto D_{{\mathsf d}_{r}}(z)$ is non-convex and typically has multiple local minima. Notice that the quantization error defined in (15.21) satisfies

$$q_{S,{\mathsf d}_{r}}(P) = \min \{ [D_{{\mathsf d}_{r}}(z)]^{1/r} : z = (z_{1}, \dots, z_{S}) \}.$$

Lemma 2.1

The mapping $P \mapsto q_{S,{\mathsf d}_{r}}(P)$ is concave.

Proof

Let $P = \sum_{i=1}^I w_{i} P_{i}$ for some positive weights with $\sum_{i=1}^I w_{i}=1$. Then

$$q_{S,{\mathsf d}_{r}}(P) = \sum_{i=1}^I w_{i} \int \min_{s} [d(x,z_{s})]^r \, \textrm{d} P_{i}(x) \ge \sum_{i=1}^I w_{i} q_{S,{\mathsf d}_{r}}(P_{i}).$$

□

Lemma 2.2

Let $\sum_{i=1}^I S_{i} \le S$ and the weights w _i as above. Then

$$q_{S,{\mathsf d}_{r}}\left(\sum_{i=1}^I w_{i} P_{i}\right) \le \sum_{i=1}^I w_{i} q_{S_{i},{\mathsf d}_{r}}(P_{i}).$$

□

Proof

Let $\tilde{P_{i}}$ such that ${\mathsf d}_{r}(P_{i},\tilde{P}_{i}) = q_{S_{i},{\mathsf d}_{r}}(P)$. Then

$$q_{S,{\mathsf d}_{r}}\left(\sum_{i=1}^I w_{i} P_{i}\right) \le {\mathsf d}_{r}\left(\sum_{i=1}^I w_{i} P_{i}, \sum_{i=1}^I w_{i} \tilde{P}_{i}\right) \le \sum_{i=1}^I w_{i} q_{S_{i},{\mathsf d}_{r}}(P_{i}).$$

For the next lemma, it is necessary to specify the distance d to

$$d_{r}(x,y) = \left[\sum_{m=1}^M |x_{m}^r - y_{m}^r| \right]^{1/r}.$$

Lemma (Product quantizers) Let $\prod_{i=1}^I S_{i} \le S$. Then

$$q_{S,{\mathsf d}_{r}}( \otimes_{i=1}^I P_{i}) \le \sum_{i=1}^I q_{S,{\mathsf d}_{r}}(P_{i}).$$

□

Proof

Let $\tilde{P_{i}} \in {\mathcal P}_{S}$ such that ${\mathsf d}_{r}(P_{i},\tilde{P}_{i}) = q_{S_{i},{\mathsf d}_{r}}(P)$. Then

$$q_{S,{\mathsf d}_{r}}(\otimes_{i=1}^I P_{i}) \le {\mathsf d}_{r}(\otimes_{i=1}^I P_{i}, \otimes_{i=1}^I \tilde{P}_{i}) = \sum_{i=1}^I q_{S_{i},{\mathsf d}_{r}}(P_{i}).$$

3.1.2 Interpretation as Facility Location Problems on ${\mathbb R}$

On ${\mathbb R}^{1}$ one may w.l.o.g. assume that the points z _s are in ascending order $z_{1} \le z_{2} \le \cdots \le z_{S}$. The pertaining Voronoi tessellation then is

$$V_{s} = (b_{s-1}, b_{s}], \qquad s=1, \dots S,$$

with $b_{0} = -\infty$, $b_{S}= + \infty$ and for $1\le s \le S$; the points b _s are chosen such that $d(b_{s},z_{s}) = d(b_{s}, z_{s+1})$, and the optimal masses are then $p_{s} = G(b_{s}) - G(b_{s-1})$. For the Euclidean distance on ${\mathbb R}$, the b _s’s are just the midpoints

$$z_{s} = \frac{1}{2}(b_{s-1} + b_{s}), \qquad s=1, \dots, S.$$

In this case, the Wasserstein distance is

$${\mathsf d}_{r}(P,\tilde{P})^r = \sum_{s=1}^S \int_{\frac{z_{s-1}+z_{s}}{2}} ^{\frac{z_{s}+z_{s+1}}{2}} |u - z_{s}|^r \; {\mathit d} G(u),$$

((15.24))

with $z_{0} = - \infty$ and $z_{S+1}= + \infty$.

While step (2) of (15.23) is easy, step (1) is more involved: Let, for $z_{1} \le z_{2} \le \cdots \le z_{S}$,

$$D(z_{1}, \dots, z_{S}) = \int \min_{s} d(x,z_{s})^r \; {\mathit d} G(x)$$

((15.25))

The global minimum of this function is sought for. Notice that D is non-convex, i.e., the global minimization of D is a hard problem. The function D can be viewed as the travel mean costs of customers distributed along the real line with d.f. G to travel to the nearest location of one of the facilities, placed at $z_{1}, \dots, z_{S}$, if the travel costs from u to v are $d(u,v)^r$.

Facility Location The problem of minimizing the function D in (15.25) is an instance of the classical Weber location problem, which was introduced by A. Weber in 1909 (English translation published 1929 (Weber, 1929)). A recent state-of-the-art overview of the theory and applications was published by Drezner and Hamacher (2002).

Explicit Optimal Solutions Only in exceptional cases explicit solutions of the optimal quantization problems (15.21) resp. (15.22) are known. Here are some examples; for more details, see Graf and Luschgy (2000).

Example

(The Laplace distribution in ${\mathbb R}^1$) For the Euclidean distance on ${\mathbb R}$ and the Laplace distribution with density $f(x) = \frac{1}{2} \exp(-|x|)$, the optimal supporting points for even $S = 2k$ are

$$z_{s} = \left\{ \begin{array}{ll} 2 \log \left( \frac{s}{\sqrt{k^2 + k}} \right), & \quad 1 \le s \le k,\\ \\ 2 \log \left( \frac{\sqrt{k^2 + k}}{S+1-s} \right), & \quad k+1 \le s \le S. \end{array} \right.$$

The quantization error is

$$q_{S,{\mathsf d}_{1}}(P) = \left\{ \begin{array}{ll} \log\left(1+\frac{2}{S}\right), & \quad S \hbox{ even },\\ \frac{2}{S+1}, & \quad S \hbox{ odd. } \end{array} \right.$$

Example

(The Exponential distribution in ${\mathbb R}^1$)

For the Euclidean distance on ${\mathbb R}$ and the Exponential distribution with density $f(x) = \exp( -x) {\mathchoice {\hbox{1\kern -0.27em l}}{\hbox{1\kern -0.27em l}} {\small{1\kern -0.27em l}}{\small{1\kern -0.27em l}}}_{x \ge 0}$, the optimal supporting points are

$$z_{s} = 2 \log \left( \frac{\sqrt{S^2 + S}}{S+1-s} \right); \quad s=1, \dots, S.$$

The quantization error is

$$q_{S,{\mathsf d}_{1}}(P) = \log\left(1+\frac{1}{S}\right).$$

Example

(The uniform distribution in ${\mathbb R}^M$) To discuss the uniform distribution in higher dimension, it is necessary to further specify the distance on the sample space: As distances on ${\mathbb R}^M$ we consider the p-norms $d_{p}(u,v) = \left[ \sum_{m=1}^M |u_{m} - v_{m}|^p \right]^{1/p}$ for $1 \le p < \infty$ resp. $d_\infty(u,v) = \max_{1\le m \le M} |u_{m} - v_{m}|$.

Based on d _p, we consider the Wasserstein distances ${\mathsf d}_{p,r}$

$$\begin{array}{rcl}{\mathsf d}_{p,r}(P_{1}, P_{2})^r &=& \inf \left\{ \int d_{p}(x_{1},x_{2})^r \pi({\mathit d} x_{1},{\mathit d} x_{2}) ; \ \hbox{ where the joint probability }\right.\\ && \hbox{measure } \pi \ \hbox{has marginals such that}\nonumber\\ && \left.\pi(A\times {\mathbb R}^M)=P_{1}(A) \ \hbox{ and } \pi({\mathbb R}^M\times B)=P_{2}(B)\phantom{\inf}\!\!\!\!\!\!\right\}\end{array}.$$

((15.26))

Let $q_{S,{\mathsf d}_{p,r}}^{(M)} := q_{S,{\mathsf d}_{p,r}}({\mathcal U}[0,1]^M)$ be the minimal error of approximation to the uniform distribution on the M-dimensional unit cube $[0,1]^M$. The exact values are only known for

$$q_{1,{\mathsf d}_{p,r}}^{(M)} = \left\{\begin{array}{ll} \frac{M}{(1+r) 2^r}, & \quad 1 \le p < \infty,\\ \\ \frac{M}{(M+r) 2^r}, & \quad p = \infty \end{array} \right.$$

and

$$q_{1,{\mathsf d}_{\infty,r}}^{(M)} = \frac{M}{(M+r) 2^r}.$$

3.1.3 Asymptotically Optimal Quantizers

In most cases, the solutions of (15.21) and (15.22) are unknown and cannot be expressed in an analytic way. Therefore one may ask the simpler “asymptotic” questions:

• What is the rate in which $q_{S,{\mathsf d}_{r}}(P)$ converges to zero as S tends to infinity?

• Is there a constructive way to find a sequence being asymptotically optimal, i.e., a sequence $(P_{S}^+)$ such that

  $$\frac{{\mathsf d}(P,P^+_{S})}{q_{S,{\mathsf d}_{r}}(P)} \to 1$$

  as $S \to \infty$?

To investigate these questions introduce the quantities

$$\begin{array}{rcl}\bar{q}_{{\mathsf d}_{p,r}}^{(M)} &:=& \inf_{S} S^{r/M} q_{S,{\mathsf d}_{p,r}}({\mathcal U}[0,1]^M),\\ \bar{q}_{{\mathsf d}_{p,r}}(P) &:=& \inf_{S} S^{r/M} q_{S,{\mathsf d}_{p,r}}(P),\end{array}$$

((15.27))

where ${\mathcal U}[0,1]^M$ is the uniform distribution on the M-dimensional unit cube $[0,1]^M$.

It deduces from the concavity of $P \mapsto q_{S,{\mathsf d}_{r,p}}(P)$ that the mappings $P \mapsto \bar{q}_{{\mathsf d}_{p,r}}(P)$ are concave as well.

The quantities $\bar{q}_{{\mathsf d}_{p,r}}^{(M)}$ are found to be universal constants; however, they are known in special cases only:

• $\bar{q}_{{\mathsf d}_{p,r}}^{(1)} = \frac{1}{(1+r)2^r}$,

• $\bar{q}_{{\mathsf d}_{\infty,r}}^{(M)} = \frac{M}{(M+r)2^r}.$

The next theorem links a general distribution P with the uniform distribution, providing a relation between $\bar{q}_{{\mathsf d}_{p,r}}(P)$ and $\bar{q}_{{\mathsf d}_{p,r}}^{(M)}$. As for a proof we refer the reader to Graf and Luschgy (2000), theorem 6.2. or Na and Neuhoff (1995).

Theorem

(Zador–Gersho formula) Suppose that P has a density g with $\int |u|^{r+\delta} g(u)\, {\mathit d} u < \infty$ for some $\delta>0$. Then

$$\bar{q}_{{\mathsf d}_{p,r}}(P) = \inf_{S} S^{r/M} q_{S,{\mathsf d}_{p,r}}(P) = \bar{q}_{{\mathsf d}_{p,r}}^{(M)} \cdot \left[ \int_{{\mathbb R}^M} g(x)^{\frac M {M+r}} \, {\mathit d} x \right]^{\frac{M+r} M},$$

((15.28))

where $\bar q_{{\mathsf d}_{p,r}}^{(M)}$ is given by (15.27).

For the real line, this specializes to

$$\bar{q}_{{\mathsf d}_{p,r}}(P) = \frac{1}{(1+r)2^r} \left( \int_{\mathbb R} g(u)^{\frac 1 {1+r}} \, du \right)^{1+r}$$

for all p, since all distances ${\mathsf d}_{p}$ are equal for $M=1$. Specializing further to r = 1, one gets

$$\bar{q}_{d_{p,1}}(P) = \frac{1}{4} \left( \int_{{\mathbb R}} \sqrt{g(u)} \, {\mathit d} u \right)^2.$$

Heuristics The Zador–Gersho formula (15.28), together with identity (15.24) give rise that the optimal, asymptotic point density for z _s is proportional to $g^\frac M{M+r}$. In ${\mathbb R}^1$ again this translates to solving the quantile equations

$$\int_{-\infty}^{z_{s}} g^\frac 1{1+r}(x) \, {\mathit d} x=\frac{2s-1}{2S} \cdot \int_{-\infty}^\infty g^\frac 1{1+r}(x) \, {\mathit d} x$$

for $s=1,2,\dots S$ and then to put

$$p_{s} := \int_\frac{z_{s-1}+z_{s}}2 ^\frac{z_{s}+z_{s+1}}2 g(x)\, {\mathit d} x$$

as above. It can be proved that the points z _s specified accordingly are indeed asymptotically optimal and in practice this has proven to be a very powerful setting.

Example

If P is the univariate normal distribution $N(\mu,\sigma^2)$, then $\bar{q}_{{\mathsf d}_{p,1}}(N(\mu,\sigma) = \sigma \sqrt{\frac{\pi}{2}}$. For the M-dimensional multivariate normal distribution $N(\mu, \Sigma)$ one finds that

$$\bar{q}_{{\mathsf d}_{p,r}}(N(\mu,\Sigma) = \bar{q}_{{\mathsf d}_{p,r}}^{(M)} (2 \pi)^{r/2} \left(\frac{M+r}{M}\right)^{(M+r)/2} (\hbox{det} \Sigma)^{r/(2M)}.$$

3.1.4 Optimal Quantizers for the Uniform (Kolmogorov) Distance

In dimension $M=1$, the solution of the uniform discrete approximation problem is easy: Notice that the uniform distance is invariant w.r.t. monotone transformations, which means that the problem can be mapped to the uniform distribution via the quantile transform and then mapped back.

The uniform distribution ${\mathcal U}[0,1]$ is optimally approximated by

$$\tilde{P} = \left[ \begin{array}{ccccc} 1/S& 1/S & 1/S & \cdots & 1/S\\ \hline\\[-3mm] \frac{1}{2S}& \frac{3}{2S} & \frac{5}{2S} & \cdots & \frac{2S-1}{2S}\\ \end{array}\right]$$

and the distance is

$${\mathsf d}_{U}({\mathcal U}[0,1],\tilde{P}) = 1/S.$$

For an arbitrary P with distribution function G, the optimal approximation is given (by virtue of the quantile transform) by

$$\begin{array}{rcl}z_{s} = G^{-1}\left(\frac{2s-1}{2S}\right), \quad s=1, \dots, S,\\ p_{s} = 1/S, \quad s=1, \dots, S.\end{array}$$

The distance is bounded by $1/S$. If G is continuous, then the distance is exactly equal to $1/S$. In this case, the uniform distance approximation problem leads always to approximating distributions, which put the same mass $1/S$ at all mass points. This implies that the tails of P are not well represented by $\tilde {P}$. This drawback is not present when minimizing the Kantorovich distance.

3.1.5 Heavy Tail Control

Minimizing the Kantorovich distance minimizes the difference in expectation for all Lipschitz functions. However, it may not lead to a good approximation for higher moments or even the variance. If a good approximation of higher moments is also required, the Fortet–Mourier distance may be used.

Another possibility, which seems to be even more adapted to control tails, is to choose the Wasserstein r-distance instead of the Kantorovich distance for some appropriately chosen $r>1$.

To approximate tails and higher moments are necessary for many real-world applications especially in the area of financial management.

Example

Suppose we want to approximate the t-Student distribution P with 2 degrees of freedom, i.e., density $(2+x^2)^{-3/2}$ by a discrete distribution sitting on 5 points. The optimal approximation with the uniform distance is

$$\tilde{P}_{1} = \left[ \begin{array}{ccccc} 0.2 & 0.2 & 0.2 & 0.2 & 0.2\\ \hline -1.8856 & -0.6172 & 0 & 0.6172 & 1.8856\\ \end{array} \right],$$

while minimizing the Kantorovich distance, the approximated distribution is

$$\tilde{P}_{2} = \left[\begin{array}{ccccc} 0.0446 & 0.2601 & 0.3906 & 0.2601 & 0.0446\\ \hline -4.58 & -1.56 & 0 & 1.56 & 4.58 \end{array}\right].$$

These results can be compared visually in Fig. 15.2 where one can see clearly that the minimization of the Kantorovich distance leads to a much better approximation of the tails.

Fig. 15.2

Approximation of the $t(2)$-distribution: uniform (left) and Kantorovich (right)

But even this approximation can be improved by heavy tail control: Applying the stretching function χ ₂ to the t-distribution, one gets the distribution with density (Fig. 15.3)

$$\left\{\begin{array}{ll} (2+x^2)^{-3/2} & \qquad \hbox{ if } |x| \le 1,\\ \frac{1}{2 \sqrt{x}} (2+|x|)^{-3/2} & \qquad \hbox{ if } |x| > 1.\\ \end{array} \right.$$

This distribution has heavier tails than the original t-distribution. We approximate this distribution w.r.t the Kantorovich distance by a 5-point distribution and transform back the obtained mass points using the transformation $\chi_{1/2}$ to get

$$\tilde{P} = \left[ \begin{array}{ccccc} 0.05 & 0.2 & 0.5 & 0.2 & 0.05 \\ \hline -4.8216 & -1.6416 & 0 & 1.6416 & 4.8216 \\ \end{array} \right].$$

Compared to the previous ones, this approximation has a better coverage of the tails. The second moment is better approximated as well.

Fig. 15.3

Approximation of the $t(2)$-distribution: Kantorovich with Euclidean distance (left) and Kantorovich with distorted distance $d_{\chi_{2}}$ (right)

3.2 Quasi-Monte Carlo

As above, let ${\mathcal U}[0,1]^M$ be the uniform distribution on $[0,1]^M$ and let $\tilde{P}_{S} = \frac{1}{S} \sum_{s=1}^S \delta_{z_{s}}$. Then the uniform distance $d_{U}({\mathcal U}[0,1]^M,\tilde{P}_{S})$ is called the star discrepancy $D_{S}^*(z_{1}, \dots, z_{S})$ of $(z_{1}, \dots, z_{S})$

$$D_{S}^*(z_{1}, \dots, z_{S}) = \sup \left\{ \frac{1}{S} \sum_{s=1}^S {\mathchoice {\hbox{1\kern -0.27em l}}{\hbox{1\kern -0.27em l}} {\small{1\kern -0.27em l}}{\small{1\kern -0.27em l}}}_{\{[0,a_{1}]\times \dots \times [0,a_{M}]\} } (z_{s}) - \prod_{m=1}^M a_{m} : 0 < a_{m} \le 1 \right\}.$$

((15.29))

A sequence $z=(z_{1}, z_{2}, \dots)$ in $[0,1]^M$ is called a low-discrepancy sequence , if

$$\limsup_{S \to \infty} \frac{S}{\log(S)^M} D_{S}^*(z_{1}, \dots, z_{S}) < \infty,$$

i.e., if there is a constant C such that for all S,

$$D_{S}^*(z)=D_{S}^*(z_{1}, \dots, z_{S}) \le C \frac{\log(S)^M}{S}.$$

A low-discrepancy sequence allows the approximation of the uniform distribution in such a way that

$$d_{U}({\mathcal U}[0,1]^M,\tilde{P}_{S}) \le C \frac{\log(S)^M}{S}.$$

Low-discrepancy sequences exist. The most prominent ones are as follows:

• The van der Corput sequence (for $M=1$): Fix a prime number p and let, for every s

  $$s = \sum_{k=0}^{L} d_{k}(s) p ^{k}$$

  be the representation of n in the p-adic system. The sequence z _n is defined as

  $$z_{n}^{(p)} = \sum_{k=0}^{L} d_{k}(s) p^{-k-1}.$$

• The Halton sequence (for $M > 1$):

  Let $p_{1}, \ldots, p_{M}$ be different prime numbers. The sequence is

  $$(z_{s}^{(1)}, \dots, z_{s}^{(M)}),$$

  where $z_{s}^{(p_{m})}$ are van der Corput sequences.

• The Hammersley sequence:

  For a given Halton sequence $(z_{s}^{(1)}, \dots, z_{s}^{(M)})$, the Hammersley sequence enlarges it to ${\mathbb R}^{M+1}$ by

  $$(z_{s}^{(1)}, \dots, z_{s}^{(M)}, s/S).$$

• The Faure sequence.

• The Sobol sequence.

• The Niederreiter sequence.

(For a thorough treatment of QMC sequences, see Niederreiter (1992).) The quasi-Monte Carlo method was used in stochastic programming by Pennanen (2009). It is especially good if the objective is the expectation, but less advisable if tail or rare event properties of the distribution enter the objective or the constraints.

3.2.1 Comparing Different Quantizations

We¹ have implemented the following portfolio optimization problem: Maximize the expected average value at risk (${\mbox{{${\mathbb A}$}V{\scriptsize @}R}}$, CVaR) of the portfolio return under the constraint that the expected return exceeds some threshold and a budget constraint. We used historic data of 13 assets. The “true distribution” is their weekly performance for 10 consecutive years. The original data matrix of size $520 \times 13$ was reduced by scenario generation (scenario approximation) to a data matrix of size $50 \times 13$. We calculated the optimal asset allocation for the original problem (1) and for the scenario methods: (2) minimal Kantorovich distance, (3) moment matching, and (4) quasi-Monte Carlo with a Sobol sequence. The Kantorovich distance was superior to all others, see Fig. 15.4.

Fig. 15.4

Asset allocation using different scenario approximation methods. The pie charts show the optimal asset mix

3.3 Monte Carlo

The Monte Carlo approximation is a random approximation, i.e., $\tilde {P}$ is a random measure and the distance ${\mathsf d}(P, \tilde{P})$ is a random variable. This distinguishes the Monte Carlo method from the other methods.

Let $X_{1}, X_{2}, \dots, X_{S}$ be an i.i.d. sequence distributed according to P. Then the Monte Carlo approximation is

$$\tilde{P}_{S} = \frac{1}{S} \sum_{s=1}^S \delta_{X_{s}}.$$

3.3.1 The Uniform Distance of the MC Approximation

Let $X_{1}, X_{2}, \dots$ be an i.i.d. sequence from a uniform [0,1] distribution. Then by the famous Kolmogorov–Smirnov theorem

$$\lim_{S \to \infty} P\{ \sqrt{S} D_{S}^*(X_{1}, \dots, X_{S}) > t \} = 2 \sum_{k=1}^\infty (-1)^{k-1} \exp(-2 k^2 t^2).$$

3.3.2 The Kantorovich Distance of the MC Approximation

Let $X_{1}, X_{2}, \dots$ be an i.i.d. sequence from a distribution with density g. Then

$$\lim_{S \to \infty} P\{ S^{1/M} d_{\mathrm{KA}} (P, \tilde{P}_{S}) \le t \} = \int [1- \exp(-t^M b_{M} g(x))] g(x) \, dx,$$

where $b_{M} = \frac{2 \pi^{M/2}}{M \Gamma(M/2)}$ is the volume of the M-dimensional Euclidean ball (see Graf and Luschgy (2000), theorem 9.1).

4 Distances Between Multi-period Probability Measures

Let P be a distribution on

$${\mathbb R}^{MT} = \underbrace{{\mathbb R}^M \times {\mathbb R}^M \times \cdots \times {\mathbb R}^M}_{T \hbox{ times}}.$$

We interpret the parameter $t=1, \dots T$ as time and the parameter $m=1, \dots M$ as the multivariate dimension of the data.

While the multivariate dimension M does not add to much complexity, the multi-period dimension T is of fundamentally different nature. Time is the most important source of uncertainty and the time evolution gives increasing information. We consider the conditional distributions given the past and formulate scenario approximations in terms of the conditional distributions.

4.1 Distances Between Transition Probabilities

Any probability measure P on ${\mathbb R}^{MT}$ can be dissected into the chain of transition probabilities

$$P = P_{1} \circ P_{2} \circ \cdots \circ P_{T},$$

where P ₁ is the unconditional probability on ${\mathbb R}^M$ for time 1 and P _t is the conditional probability for time t, given the past. We do not assume that P is Markovian, but bear in mind that for Markovian processes, the past reduces to the value one period before.

We will use the following notation: If $u= (u_{1}, \dots, u_{T}) \in {\mathbb R}^{MT}$, with $u_{t} \in {\mathbb R}^M$, then $u^t = (u_{1}, \dots, u_{t})$ denotes the history of u up to time t.

The chain of transition probabilities are defined by the following relation: $P = P_{1} \circ P_{2} \circ \dots \circ P_{T},$ if and only if for all sequence of Borel sets $A_{1}, A_{2}, \cdots, A_{T}$,

$$\begin{array}{rcl}& & P(A_{1} \times \cdots \times A_{T}) \\ &=& \int_{A_{1}} \cdots \int_{A_{T}} P_{T}({\mathit d} u_{T}|u^{T-1}) \cdots P_{3}({\mathit d} u_{3}|u^2) P_{2}({\mathit d} u_{2}|u_{1}) P_{1}({\mathit d} u_{1}).\end{array}$$

We assume that d makes ${\mathbb R}^M$ a complete separable metric space, which implies that the existence of regular conditional probabilities is ensured (see, e.g., Durrett (1996), ch. 4, theorem 1.6): Recall that if R ₁ and R ₂ are metric spaces and ${\mathcal F}_{2}$ is a σ-algebra in R ₂, then a family of regular conditional probabilities is a mapping $(u,A) \mapsto P( A | u)$, where $u \in R_{1}$, $A \in {\mathcal F}_{2}$, which satisfies

• $u \mapsto P(A|u)$ is (Borel) measurable for all $A \in {\mathcal F}_{2}$, and

• $A \mapsto P(A|u)$ is a probability measure on ${\mathcal F}_{2}$ for each $u \in R_{1}$.

We call regular conditional probabilities $P(A|u)$ also transition probabilities.

The notion of probability distances may be extended to transition probabilities: Let P and Q be two transition probabilities on $R_{1} \times {\mathcal F}_{2}$ and let d be some probability distance. Define

$${\mathsf d}(P,Q) : = \sup_{u} {\mathsf d}( P(\cdot | u), Q( \cdot | u)).$$

((15.30))

In this way, all probability distances like d _U , ${\mathsf d}_{\mathrm{KA}}$, ${\mathsf d}_{\mathrm{FM}}$ may be extended to transition probabilities in a natural way.

The next result compares the Wasserstein distance ${\mathsf d}_{r}(P,Q)$ with the distances of the components ${\mathsf d}_{r}(P_{t},Q_{t})$. To this end, introduce the following notation. Let d be some distance on ${\mathbb R}^M$. For a vector $w = (w_{1}, \dots, w_{T})$ of nonnegative weights we introduce the distance $d^{t}(u^t,v^t)^{r}:=\sum_{s=1}^t w_{s} \cdot d(u_{s}, v_{s})^{r}$ on ${\mathbb R}^{tM}$ for all t.

Then the following theorem holds true:

Theorem 3.1

Assume that P and Q are probability measures on ${\mathbb R}^{TM}$, such that for all conditional measures P_t resp. Q_t we have that

$${\mathsf d}_{r}(P_{t+1}[.|u^{t}],{\mathbb Q}_{t+1}[.|v^{t}])\le\tau_{t+1}+K_{t+1}\cdot d^{t}(u^{t},v^{t})$$

((15.31))

for $t=1, \dots, T-1$. Then

$${\mathsf d}_{r}(P^{t+1},Q^{t+1})^r \le w_{t+1} \tau_{t+1} + (1 + w_{t+1} K_{t+1}) {\mathsf d}_{r} (P^t,Q^t)^r$$

((15.32))

and therefore

$${\mathsf d}_{r} (P,Q)^r \le {\mathsf d}_{r}(P_{1}, Q_{1})^r \prod_{s=1}^T (1+w_{s} K_{s})+ \sum_{s=1}^T \tau_{s} w_{s} \prod_{j=1}^s (1+w_{j} K_{j}).$$

((15.32))

Proof

Let π _t denote the optimal joint measure (optimal transportation plan) for ${\mathsf d}_{r}(P^{t},Q^{t})$ and let $\pi_{t+1}[.|u,v]$ denote the optimal joint measure for ${\mathsf d}_{r}(P_{t+1}[.|u], Q_{t+1}[.|v])$ and define the combined measure

$$\pi^{t+1}\left[A_{t}\times B^{t},C_{t}\times D^{t}\right]:=\int_{A_{t}\times C_{t}}\pi_{t+1}\left[B^{t}\times D^{t}|u^{t},v^{t}\right]\pi^{t}\left[du^{t},dv^{t}\right].$$

Then

$$\begin{array}{rcl}{\mathsf d}_{r}(P^{t+1},Q^{t+1})^{r} &\le& \int d^{t+1}(u^{t+1},v^{t+1})^{r} \; \pi^{t+1}\left[\mathrm{d}u^{t+1},\mathrm{d}v^{t+1}\right]\\ &=& \int\left[d^{t}(u^{t},v^{t})^{r}+w_{t+1}d_{t+1}(u_{t+1},v_{t+1})^{r}\right]\\ && \quad\pi_{t}\left[\mathrm{d}u_{t+1},\mathrm{d}v_{t+1}|u^{t},v^{t}\right]\pi^{t}\left[du^{t},dv^{t}\right]\\ &=& \int d^{t}\left(u^{t},v^{t}\right)^{r}\pi^{t}\left[du^{t},dv^{t}\right]+\\ && \quad + w_{t+1} \int\!\!\! d_{t+1}\left(u_{t+1},v_{t+1}\right)^{r}\!\! \; \pi_{t}\left[du_{t+1},dv_{t+1}|u^{t},v^{t}\right]\pi^{t}\!\!\left[du^{t},dv^{t}\right]\\ &=& \int d^{t}\left(u^{t},v^{t}\right)^{r} \; \pi^{t}\left[du^{t},dv^{t}\right]+\\ && \quad+w_{t+1}\int {\mathsf d}_{r}\left(P_{t+1}\left[.|u^{t}\right], Q_{t+1}\left[.|v^{t}\right]\right)^{r} \; \pi^{t}\left[du^{t},dv^{t}\right]\\ &\le& \int d^{t}\left(u^{t},v^{t}\right)^{r} \; \pi^{t}\left[du^{t},dv^{t}\right]+\\ && \quad+w_{t+1}\int\tau_{t+1} + K_{t+1}d^{t}\left(u^{t},v^{t}\right)^{r} \; \pi^{t}\left[du^{t},dv^{t}\right]\\ &=& {\mathsf d}_{r}\left(P^{t},Q^{t}\right)^{r}+w_{t+1}\left(\tau_{t+1} + K_{t+1} {\mathsf d}_{r}\left(P^{t},Q^{t}\right)^{r}\right)\\ &=& w_{t+1}\tau_{t+1}+\left(1+w_{t+1} K_{t+1}\right){\mathsf d}_{r}\left(P^{t},Q^{t}\right)^{r}.\end{array}$$

This demonstrates (15.32). Applying this recursion for all t leads to (15.33). □

Definition 3.2

Let P be a probability on ${\mathbb R}^{MT}$, dissected into transition probabilities $P_{1}, \dots, P_{T}$. We say that P has the $(K_{2}, \dots, K_{T})$-Lipschitz property, if for $t=2, \dots, T$,

$${\mathsf d}_{r}(P_{t}(\cdot|u), P_{t}(\cdot| v)) \le K_{t} d(u,v).$$

Example

(The normal distribution has the Lipschitz property) Consider a normal distribution P on ${\mathbb R}^{m_{1}+m_{2}}$, i.e.,

$$P = \mathcal{N} \left( \left(\begin{array}{c} \mu_{1}\\ \mu_{2} \end{array} \right), \left( \begin{array}{cc} \Sigma_{11} & \Sigma_{12}\\ \Sigma_{12} & \Sigma_{22} \end{array} \right) \right).$$

The conditional distribution, given $u \in {\mathbb R}^{m_{1}}$, is

$$P_{2}( \cdot | u) = \mathcal{N} \left( \mu_{1} - \Sigma_{12} \Sigma_{11}^{-1} (u - \mu_{1}), \Sigma_{22} - \Sigma_{12} \Sigma_{11} \Sigma_{12}^{-1} \right).$$

We claim that

$${\mathsf d}_{\mathrm{KA}}( P_{2}( \cdot | u), P_{2}( \cdot | v)) \le \| \Sigma_{12} \Sigma_{11}^{-1} (u - v) \|.$$

((15.34))

Let $Y \sim \mathcal{N}(0, \Sigma)$ and let $Y_{1} = a_{1} + Y$ and $Y_{2} = a_{2} + Y$. Then $Y_{1} \sim \mathcal{N}(a_{1}, \Sigma)$, $Y_{2} \sim \mathcal{N}(a_{2}, \Sigma)$ and therefore

$${\mathsf d}_{\textrm{KA}}(\mathcal{N}(a_{1}, \Sigma), \mathcal{N}(a_{2}, \Sigma)) \le {\mathbb E}(\| Y_{1} - Y_{2} \|) = \|a_{1} - a_{2} \|.$$

Setting $a_{1}= \mu_{1} - \Sigma_{12} \Sigma_{11}^{-1} (u - \mu_{1})$, $a_{2} = \mu_{1} - \Sigma_{12} \Sigma_{11}^{-1} (v - \mu_{1})$ and $\Sigma = \Sigma_{22} - \Sigma_{12} \Sigma_{11} \Sigma_{12}^{-1}$, the result (15.34) follows.

Corollary 3.3

Condition (15.31) is fulfilled, if the following two conditions are met:

• (i) P has the $(K_{2}, \dots, K_{T})$-Lipschitz property in the sense of Definition 3.2

• (ii) Closeness of all P _t and Q _t in the following sense:

  $${\mathsf d}_{r}(P_{t},Q_{t}) = \sup_{u} {\mathsf d}_{r}(P_{t}( \cdot | u), Q_{t}(\cdot | u) \le \tau_{t}$$

The Lipschitz assumption for P is crucial. Without this condition, no relation between ${\mathsf d}_{r}(P,Q)$ and the ${\mathsf d}_{r}(P_{t},Q_{t})$’s holds. In particular, the following example shows that ${\mathsf d}_{1}(P_{t},Q_{t})$ may be arbitrarily small and yet ${\mathsf d}_{1}(Q,P)$ is far away from zero.

Example

Let $P = P_{1} \circ P_{2}$ be the measure on ${\mathbb R}^2$, such that

$$\begin{array}{rcl}P_{1} &=& {\mathcal U}[0,1],\\ P_{2}( \cdot| u) &=& \left\{ \begin{array}{ll} {\mathcal U}[0,1] & \enskip \hbox{if} \enskip u \in \ensuremath{{\mathbb Q}}, \\ {\mathcal U}[1,2] & \enskip \hbox{if} \enskip u \in {\mathbb R} \setminus \ensuremath{{\mathbb Q}}, \\ \end{array} \right.\end{array}$$

where ${\mathcal U}[a,b]$ denotes the uniform distribution on $[a,b]$. Obviously, P is the uniform distribution on $[0,1] \times [1,2]$. $(P_{1},P_{2})$ has no Lipschitz property. Now, let $Q^{(n)} = Q_{1}^{(n)} \circ Q_{2}^{(n)}$, where

$$\begin{array}{rcl}Q_{1}^{(n)} &=& \sum_{k=1}^n \frac{1}{n} \delta_{k/n},\\ Q_{2}^{(n)}( \cdot | u) &=& \left \{ \begin{array}{ll} \sum\limits_{k=1}^n \frac{1}{n} \delta_{k/n} & \enskip \hbox{if} \enskip u \in \ensuremath{{\mathbb Q}}, \\ \sum\limits_{k=1}^n \frac{1}{n} \delta_{1+k/n} & \enskip \hbox{if} \enskip u \in {\mathbb R} \setminus \ensuremath{{\mathbb Q}}. \end{array} \right.\end{array}$$

Note that $Q^{(n)} = Q_{1}^{(n)} \circ Q_{2}^{(n)}$ converges weakly to the uniform distribution on $[0,1] \times [0,1]$. In particular, it does not converge to P and the distance is ${\mathsf d}_{1}(P,Q^{(n)}) = 1$. However,

$${\mathsf d}_{1}(P_{1}, Q_{1}^{(n)}) = 1/n; \quad {\mathsf d}_{1}(P_{2}, Q_{2}^{(n)}) = 1/n.$$

4.2 Filtrations and Tree Processes

In many stochastic decision problems, a distinction has to be made between the scenario process (which contains decision-relevant values, such as prices, demands, and supplies) and the information which is available. Here is a simple example due to Philippe Artzner.

Example

A fair coin is tossed three times. Situation A: The payoff process $\xi^{(A)}$ is

$$\xi_{1}^{(A)}= 0; \quad \xi_{2}^{(A)} = 0;$$

$$\xi_{3}^{(A)} = \left\{ \begin{array}{ll} 1 & \quad \hbox{if heads is shown at least two times},\\ 0 & \quad \hbox{otherwise.} \end{array} \right.$$

We compare this process to another payoff process (situation B)

$$\xi_{1}^{(B)}= 0, \quad \xi_{2}^{(B)} = 0,$$

$$\xi_{3}^{(B)} = \left\{ \begin{array}{ll} 1 & \quad \hbox{if heads is shown at least the last throw},\\ 0 & \quad \hbox{otherwise}. \end{array} \right.$$

The available information is relevant: It makes a difference, whether we may observe the coin tossing process or not. Suppose that the process is observable. Then, after the second throw, we know the final payoff, if two times the same side appeared. Thus our information is complete although the experiment has not ended yet. Only in case that two different sides appeared, we have to wait until the last throw to get the final information.

Mathematically, the information process is described by a filtration.

Definition 3.4

Let $(\varOmega, {\mathcal F}, P)$ be probability space. A filtration ${\mathcal F}$ on this probability space is an increasing sequence of σ-fields ${\mathcal F}$ where for all t, ${\mathcal F}_{t} \subseteq {\mathcal F}_{t+1} \subseteq {\mathcal F}.$ We may always add the trivial σ-field ${\mathcal F}_{0} = \{ \emptyset, \Omega[t])$ as the zeroth element of a filtration.

A scenario process $\xi = (\xi_{1}, \dots, \xi_{T})$ is adapted to the filtration ${\mathcal F}$, if ξ _t is ${\mathcal F}_{t}$ measurable for $t=1, \dots, T$. If ξ _t is measurable w.r.t. ${\mathcal F}_{t}$, we use the notation

$$\xi_{t} \lhd {\mathcal F}_{t};$$

if the process ξ is adapted to ${\mathcal F}$, we use the similar notation

$${\mathcal F}$$

The general situation is as follows: We separate the information process from the value process. Information is modeled by a filtration ${\mathcal F}$, while the scenario values are modeled by a (real or vector values process) ξ, which is adapted to ${\mathcal F}$. We call a pair ${\mathcal F}$ a process-and-information pair. In general, the filtration ${\mathcal F}$ is larger than the one generated by the process ξ.

Fig. 15.5

The payoff process $\xi^{(A)}$ sitting on the tree (the filtration) generated by the coin process

Fig. 15.6

The payoff process $\xi^{(B)}$ sitting on the tree (the filtration) generated by the coin process

In finite probability spaces, there is a one-to-one correspondence between filtrations and probability trees. A process is adapted to such a filtration, iff it is a function of the nodes of the tree. Figures 15.5 and 15.6 show the tree processes and the adapted scenario process sitting on the tree for Artzner’s example and situations (A) and (B).

4.2.1 Tree Processes

Definition 3.5

A stochastic process $\nu = (\nu_{1}, \dots, \nu_{T})$ is called a tree process, if $\sigma(\nu_{1})$, $\sigma(\nu_{2}), \dots, \sigma(\nu_{T})$ is a filtration. A tree process is characterized by the property that the conditional distribution of $\nu_{1}, \dots, \nu_{t}$ given $\nu_{t+1}$ is degenerated, i.e., concentrated on a point. Notice that any stochastic process $\eta = (\eta_{1}, \dots, \eta_{T})$ can be transformed into a tree process by considering its history process

$$\begin{array}{rcl}\nu_{1} &=& \eta_{1},\\ \nu_{2} &=& (\eta_{1}, \eta_{2}),\\ &\vdots&\\ \nu_{T} &=& (\eta_{1}, \dots, \eta_{T}).\end{array}$$

Let $(\nu_{t})$ be a tree process and let ${\mathcal F}$. It is well known that any process ξ adapted to ${\mathcal F}$ can be written as $\xi_{t} = f_{t}(\nu_{t})$ for some measurable function f _t. Thus a stochastic program may be formulated using the tree process ν and the functions f _t .

Let ν be a tree process according to Definition 3.5. We assume throughout that the state spaces of all tree processes are Polish. In this case, the joint distribution P of $\nu_{1}, \dots, \nu_{T}$ can be factorized into the chain of conditional distributions, which are given as transition kernels, that is

$$\begin{array}{rcl}P_{1}(A) &=& P\{\nu_{1} \in A \},\\ P_{2}(A|u) &=& P\{\nu_{2} \in A | \nu_{1} = u \},\\ &\vdots&\\ P_{t}(A|u_{1}, \dots, u_{t-1}) &=& P\{ \nu_{t} \in A | \nu_{1} = u_{1}, \dots, \nu_{t-1}= u_{t-1} \}.\end{array}$$

Definition 3.6

(Equivalence of tree processes) Let ν resp. $\bar{\nu}$ two tree processes, which are defined on possibly different probability spaces $(\Omega, {\mathcal F}, P)$ resp. $(\bar{\varOmega}, \bar{{\mathcal F}}, \bar{P})$. Let $P_{1}, P_{2}, \dots, P_{T}$ resp. $\bar{P}_{1}, \bar{P}_{2}, \dots, \bar{P}_{T}$ be the pertaining chain of conditional distributions. The two tree processes are equivalent, if the following properties hold: There are bijective functions $k_{1}, \dots, k_{T}$ mapping the state spaces of ν to the state spaces of $\bar{\nu}$, such that the two processes $\nu_{1}, \dots, \nu_{T}$ and $k_{1}^{-1}(\bar{\nu}_{1}), \dots, k_{T}^{-1}(\bar{\nu}_{T})$ coincide in distribution.

Notice that for tree processes defined on the same probability space, one could define equivalence simply as $\nu_{t} = k_{t}(\bar{\nu}_{t})$ a.s. The value of Definition 3.6 is that it extends to tree processes on different probability spaces.

Definition 3.7

(Equivalence of scenario process-and-information pairs) Let $(\xi,\nu)$ be a scenario process-and-information pair, consisting of a scenario process ξ and a tree process, such that $\xi \lhd \sigma(\nu)$. Since $\xi \lhd \sigma(\nu)$, there are measurable functions f _t such that

$$\xi_{t} = f_{t}(\nu_{t}), \qquad t=1, \dots T.$$

Two pairs $(\xi, \nu)$ and $(\bar{\xi}, \bar{\nu})$ are called equivalent, if ν and $\bar{\nu}$ are equivalent in the sense of Definition 3.6 with equivalence mappings k _t such that

$$\bar{\xi_{t}} = f_{t}(k_{t}^{-1}(\xi_{t})) \qquad \hbox{ a.s.}$$

We agree that equivalent process-and-information pairs will be treated as equal. Notice that by drawing a finite tree with some values sitting on its nodes we automatically mean an equivalence class of process-and-information pairs.

Fig. 15.7

Artzner’s example: The tree process is coded by the history of the coin throws (H = head,T = tail), the payoffs are functions of the tree process

Fig. 15.8

A process-and-information pair which is equivalent to Artzner’s example in Fig. 15.4. The coding of the tree process is just by subsequent letters

If two stochastic optimization problems are defined in the same way, but using equivalent process-and-information pairs, then they have equivalent solutions. It is easy to see that an optimal solution of the first problem can be transformed into an optimal solution of the second problem via the equivalence functions k _t .

Figures 15.7 and 15.8 illustrate the concept of equivalence. The reader is invited to find the equivalence functions k _t in this example.

4.2.2 Distances Between Filtrations

In order to measure the distances between two discretizations on the same probability space one could first measure the distance of the respective filtrations. This concept of filtration distance for scenario generation has been developed by Heitsch and Roemisch (2003) and Heitsch et al. (2006).

Let $(\varOmega, \bar{{\mathcal F}},P)$ be a probability space and let ${\mathcal F}$ and $\tilde{{\mathcal F}}$ be two sub-sigma algebras of $\bar{{\mathcal F}}$. Then the Kudo distance between ${\mathcal F}$ and $\tilde{{\mathcal F}}$ is defined as

$${\mathfrak D}({\mathcal F},\tilde{{\mathcal F}}) = \max( \sup \{ \| {\mathchoice {\hbox{1\kern -0.27em l}}{\hbox{1\kern -0.27em l}} {\small{1\kern -0.27em l}}{\small{1\kern -0.27em l}}}_{A} - {\mathbb E}({\mathchoice {\hbox{1\kern -0.27em l}}{\hbox{1\kern -0.27em l}} {\small{1\kern -0.27em l}}{\small{1\kern -0.27em l}}}_{A}|\tilde{{\mathcal F}})\|_{p} : A \in {\mathcal F}\}, \sup \{ \| {\mathchoice {\hbox{1\kern -0.27em l}}{\hbox{1\kern -0.27em l}} {\small{1\kern -0.27em l}}{\small{1\kern -0.27em l}}}_{B} - {\mathbb E}({\mathchoice {\hbox{1\kern -0.27em l}}{\hbox{1\kern -0.27em l}} {\small{1\kern -0.27em l}}{\small{1\kern -0.27em l}}}_{B}|{\mathcal F})\|_{p} : A \in \tilde{{\mathcal F}}\}).$$

((15.35))

The most important case is the distance between a sigma algebra and a sub-sigma algebra of it: If $\tilde{{\mathcal F}} \subseteq {\mathcal F}$, then (15.35) reduces to

$${\mathfrak D}({\mathcal F},\tilde{{\mathcal F}}) = \sup \{ \| {\mathchoice {\hbox{1\kern -0.27em l}}{\hbox{1\kern -0.27em l}} {\small{1\kern -0.27em l}}{\small{1\kern -0.27em l}}}_{A} - {\mathbb E}({\mathchoice {\hbox{1\kern -0.27em l}}{\hbox{1\kern -0.27em l}} {\small{1\kern -0.27em l}}{\small{1\kern -0.27em l}}}_{A}|\tilde{{\mathcal F}})\|_{p} : A \in {\mathcal F}\}.$$

((15.36))

If ${\mathcal F}$ is an infinite filtration, one may ask, whether this filtration converges to a limit, i.e., whether there is a ${\mathcal F}_\infty$, such that

$${\mathfrak D}({\mathcal F}_{t}, {\mathcal F}_\infty) \to 0 \quad \hbox{for} \ t \to \infty.$$

If ${\mathcal F}_\infty$ is the smallest σ-field, which contains all ${\mathcal F}_{t}$, then ${\mathfrak D}({\mathcal F}_{t}, {\mathcal F}_\infty) \to 0$. However, the following example shows that not every discrete increasing filtration converges to the Borel σ-field.

Example

Let ${\mathcal F}$ be the Borel-sigma algebra on [0,1) and let $\tilde{{\mathcal F}}_{n}$ be the sigma algebra generated by the sets $\left[\frac k{2^n},\frac{k+1}{2^n}\right), k=0,\dots, 2^n-1$. Moreover, let $A_{n}=\bigcup_{k=0}^{2^n-1} \left[\frac k {2^n}, \frac{2k+1}{2^{n+1}}\right)$. Then ${\mathbb E}({\mathchoice {\hbox{1\kern -0.27em l}}{\hbox{1\kern -0.27em l}} {\small{1\kern -0.27em l}}{\small{1\kern -0.27em l}}}_{A_{n}} | \tilde{\mathcal F}_{n}) = \frac 1 2$ and $\| {\mathchoice {\hbox{1\kern -0.27em l}}{\hbox{1\kern -0.27em l}} {\small{1\kern -0.27em l}}{\small{1\kern -0.27em l}}}_{A_{n}} - {\mathbb E}({\mathchoice {\hbox{1\kern -0.27em l}}{\hbox{1\kern -0.27em l}} {\small{1\kern -0.27em l}}{\small{1\kern -0.27em l}}}_{A_{n}}|\tilde{{\mathcal F}}_{n})\|_{p} = 1/ 2$ for all n. While one has the intuitive feeling that $\tilde{{\mathcal F}}_{n}$ approaches ${\mathcal F}$, the distance is always $1/2$.

4.3 Nested Distributions

We define a nested distribution as the distribution of a process-and-information pair, which is invariant w.r.t. to equivalence. In the finite case, the nested distribution is the distribution of the scenario tree or better of the class of equivalent scenario trees.

Let d be a metric on ${\mathbb R}^M$, which makes it a complete separable metric space and let ${\mathcal P}_{1}({\mathbb R}^M,d)$ be the family of all Borel probability measures P on $({\mathbb R}^M,d)$ such that

$$\int d(u,u_{0}) \, {\mathit d} P(u) < \infty$$

((15.37))

for some $u_{0} \in {\mathbb R}^M$.

For defining the nested distribution of a scenario process $(\xi_{1}, \dots, \xi_{T})$ with values in ${\mathbb R}^M$, we define the following spaces in a recursive way:

$$\Xi_{1} := {\mathbb R}^M,$$

with distance ${\mathchoice {\hbox{d\kern -0.14em l}}{\hbox{d\kern -0.14em l}} {\small{d\kern -0.14em l}}{\small{d\kern -0.14em l}}}_{1}(u,v) = d(u,v)$:

$$\Xi_{2} := {\mathbb R}^M \times {\mathcal P}_{1}(\Xi_{1})$$

with distance ${\mathchoice {\hbox{d\kern -0.14em l}}{\hbox{d\kern -0.14em l}} {\small{d\kern -0.14em l}}{\small{d\kern -0.14em l}}}_{2}((u,P),(u,Q)) := d(u,v) + {\mathsf d}_{\textrm{KA}}(P,Q;{\mathchoice {\hbox{d\kern -0.14em l}}{\hbox{d\kern -0.14em l}} {\small{d\kern -0.14em l}}{\small{d\kern -0.14em l}}}_{1})$:

$$\Xi_{3} := {\mathbb R}^M \times {\mathcal P}_{1}(\Xi_{2}) = ({\mathbb R}^M \times {\mathcal P}_{1}( {\mathbb R}^M \times {\mathcal P}_{1}({\mathbb R}^M)))$$

with distance ${\mathchoice {\hbox{d\kern -0.14em l}}{\hbox{d\kern -0.14em l}} {\small{d\kern -0.14em l}}{\small{d\kern -0.14em l}}}_{3}((u,{\mathbb P}),(v,\ensuremath{{\mathbb Q}})) := d(u,v) + {\mathsf d}_{\textrm{KA}}({\mathbb P},\ensuremath{{\mathbb Q}};{\mathchoice {\hbox{d\kern -0.14em l}}{\hbox{d\kern -0.14em l}} {\small{d\kern -0.14em l}}{\small{d\kern -0.14em l}}}_{2})$. This construction is iterated until

$$\Xi_{T} = {\mathbb R}^M \times {\mathcal P}_{1}(\Xi_{T-1})$$

with distance ${\mathchoice {\hbox{d\kern -0.14em l}}{\hbox{d\kern -0.14em l}} {\small{d\kern -0.14em l}}{\small{d\kern -0.14em l}}}_{T}((u,{\mathbb P}),(v,\ensuremath{{\mathbb Q}})) := d(u,v) + {\mathsf d}_{\textrm{KA}}({\mathbb P},\ensuremath{{\mathbb Q}};{\mathchoice {\hbox{d\kern -0.14em l}}{\hbox{d\kern -0.14em l}} {\small{d\kern -0.14em l}}{\small{d\kern -0.14em l}}}_{T-1})$.

Definition 3.8

(Nested distribution) A Borel probability distribution ${\mathbb P}$ with finite first moments on $\Xi_ {T}$ is called a nested distribution of depth T; the distance ${\mathchoice {\hbox{d\kern -0.14em l}}{\hbox{d\kern -0.14em l}} {\small{d\kern -0.14em l}}{\small{d\kern -0.14em l}}}_{T}$ is called the nested distance (Pflug, 2009).

In discrete cases, a nested distribution may be represented as a recursive structure: Recall that we represent discrete probabilities by a list of probabilities (in the first row) and the values (in the subsequent rows).

Notice that one value or vector of values may only carry one probability, the following structure on the left does not represent a valid distribution, the structure right is correct:

$${\small \left[ \begin{array}{p{20pt}p{20pt}p{20pt}p{20pt}} 0.1 & 0.2 & 0.4 & 0.3\\ \hline\\[-3mm] 3.0 & 3.0 & 1.0 & 5.0 \end{array} \right] \qquad \left[ \begin{array}{p{20pt}p{20pt}p{20pt}} 0.3 & 0.4 & 0.3\\ \hline\\[-3mm] 3.0 & 1.0 & 5.0 \end{array} \right]. }$$

In the same manner, but in a recursive way, we may now represent a nested distribution as a structure, where some values are distributions themselves:

$${\small \left[ \begin{array}{ccc} 0.2 & 0.3 & 0.5\\ \hline\\ 3.0 & 3.0 & 2.4\\ \left[\begin{array}{p{20pt}p{20pt}p{20pt}} 0.4 & 0.2 & 0.4\\ \hline\\[-3mm]6.0 & 4.7 & 3.3 \end{array}\right] & \left[\begin{array}{c} 1.0\\ \hline\\[-3mm]2.8\end{array}\right] & \left[\begin{array}{p{20pt}p{20pt}} 0.6 & 0.4 \\ \hline\\[-3mm]1.0 & 5.1 \end{array}\right] \end{array} \right]}.$$

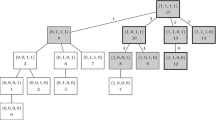
This recursive structure encodes the tree shown in Fig. 15.9.

Fig. 15.9

Example tree

For any nested distribution ${\mathbb P}$, there is an embedded multivariate distribution P. We explain the projection from the nested distribution to the embedded multivariate distribution just for the depth 3, the higher depths being analogous:

Let ${\mathbb P}$ be a nested distribution on Ξ₃, which has components η ₁ (a real random variable) and μ ₂ (a random distribution on Ξ₂, which means that it has in turn components η ₂ (a random variable) and μ ₃, a random distribution on ${\mathbb R}^m$).

Then the pertaining multivariate distribution on ${\mathbb R}^{m} \times {\mathbb R}^m \times {\mathbb R}^m$ is given by

$$P(A_{1} \times A_{2} \times A_{3}) = {\mathbb E}_{\mathbb P}[ {\mathchoice {\hbox{1\kern -0.27em l}}{\hbox{1\kern -0.27em l}} {\small{1\kern -0.27em l}}{\small{1\kern -0.27em l}}}_{\{\eta_{1} \in A_{1}\}} {\mathbb E}_{\mu_{2}}({\mathchoice {\hbox{1\kern -0.27em l}}{\hbox{1\kern -0.27em l}} {\small{1\kern -0.27em l}}{\small{1\kern -0.27em l}}}_{\{\eta_{2} \in A_{2}\}} \mu_{2}(A_{3}))]$$

for A ₁, A ₂, A ₂ Borel sets in ${\mathbb R}^m$.

The mapping from the nested distribution to the embedded distribution is not injective: There may be many different nested distributions which all have the same embedded distribution, see Artzner’s example: $\xi^{(A)}$ and $\xi^{(B)}$ in Figs. 15.5 and 15.6 have different nested distributions, but the same embedded distributions. Here is another example:

Example

Consider again the process-and-information pair (the tree) of Fig. 15.9. The embedded multivariate but non-nested distribution of the scenario process is

$$\left[ \begin{array}{p{20pt}p{20pt}p{20pt}p{20pt}p{20pt}p{20pt}} 0.08 & 0.04 & 0.08 & 0.3 & 0.3 & 0.2\\ \hline\\[-3mm] 3.0 & 3.0 & 3.0 & 3.0 & 2.4 & 2.4\\ 6.0 & 4.7 & 3.3 & 2.8 & 1.0 & 5.1 \end{array} \right].$$

Evidently, this multivariate distribution has lost the information about the nested structure. If one considers the filtration generated by the scenario process itself and forms the pertaining nested distribution, one gets

$$\left[ \begin{array}{cc} 0.5 & 0.5\\ \hline\\[-3mm] 3.0 & 2.4\\ \left[\begin{array}{p{20pt}p{20pt}p{20pt}p{20pt}} 0.16 & 0.08 & 0.16 & 0.6\\ \hline\\[-3mm]6.0 & 4.7 & 3.3 & 2.8\end{array}\right] & \left[\begin{array}{p{20pt}p{20pt}} 0.6 & 0.4 \\ \hline\\[-3mm]1.0 & 5.1 \end{array}\right] \end{array} \right]$$

since in this case the two nodes with value 3.0 have to be identified.

Lemma 3.

Let $(\xi, \nu)$ be equivalent to $(\bar{\xi}, \bar{\nu})$ in the sense of Definition 3.7. Then both pairs generate the same nested distribution.

For a proof see Pflug (2009).

4.3.1 Computing the Nested Distance

Recall that a nested distribution is the distribution of a process-and-information pair, which is invariant w.r.t. equivalence. In the finite case, the nested distribution is the distribution of the scenario tree (or better of the class of equivalent scenario trees), which was defined in a recursive way.

To compute the nested distance of two discrete nested distributions, P and $\tilde {P}$ say, corresponds to computing the distance of two tree processes ν and $\tilde \nu$. We further elaborate the algorithmic approach here, which is inherent is the recursive definition of nested distributions and the nested distance.

To this end recall first that the linear program (15.20) was defined so general, allowing to compute the distance of general objects whenever probabilities p _s , p _t , and the cost matrix $c_{s,t}$ were specified – no further specifications of the samples z are needed. We shall exploit this fact; in the situation we describe here the samples z _s and z _t represent nested distributions with finitely many states, or equivalently entire trees.

Consider the nodes in the corresponding tree: Any node is either a terminal node, or a node with children, or the root node of the respective tree. The following recursive treatment is in line with this structure:

• Recursion start (discrete nested distribution of depth 1) In this situation the nested distributions themselves are elements of the underlying space, $P\in \Xi_{T}$ ($\tilde P\in \Xi_{T}$ resp.), for which we have that

  $${\mathchoice {\hbox{d\kern -0.14em l}}{\hbox{d\kern -0.14em l}} {\small{d\kern -0.14em l}}{\small{d\kern -0.14em l}}}_{T}(P,\tilde P)= d(P,\tilde P)$$

  according to the definition.

  In the notion of trees this situation corresponds to trees which consist of a single node only, which are terminal nodes (leaf nodes).

• Recursive step (discrete nested distribution of depth $t> 1$) In this situation the nested distribution may be dissected in

  $$P_{t}=\left(n_{t}, \sum_{s} p^t_{s} \delta_{z_{s}^{t+1}}\right)\mbox{ and }\tilde P_{t}=\left(\tilde n_{t}, \sum_{\tilde s} \tilde p^t_{\tilde s} \delta_{\tilde z^{t+1}_{\tilde s}}\right),$$

  where $z^{t+1}_{s}\in \Xi_{t+1}$ and $\tilde z^{t+1}_{\tilde s} \in \Xi_{t+1}$.

  We shall assume that ${\mathchoice {\hbox{d\kern -0.14em l}}{\hbox{d\kern -0.14em l}} {\small{d\kern -0.14em l}}{\small{d\kern -0.14em l}}}_{t+1}$ is recursively available, thus define the matrix

  $$c_{s,\tilde s}:= d(n_{t}, \tilde n_{t})+ {\mathchoice {\hbox{d\kern -0.14em l}}{\hbox{d\kern -0.14em l}} {\small{d\kern -0.14em l}}{\small{d\kern -0.14em l}}}_{t+1}\left(z^{t+1}_{s}, \tilde z^{t+1}_{\tilde s} \right)$$

  and apply the linear program (15.20) together with the probabilities $p=(p_{s})_{s}$ and $\tilde p=(\tilde p_{\tilde s})_{\tilde s}$, resulting with the distance ${\mathchoice {\hbox{d\kern -0.14em l}}{\hbox{d\kern -0.14em l}} {\small{d\kern -0.14em l}}{\small{d\kern -0.14em l}}}_{t}(P_{t},\tilde P_{t})$.

  In the notion of trees, again, n _t and $\tilde n_{t}$ represent nodes with children. The children are given by the first components of $z_{s}^{t+1}$ ($\tilde z_{\tilde s}^{t+1}$, resp.); further notice that $(z^{t+1}_{s})_{s}$ are just all subtrees of n _t , all this information is encoded in the nested distribution P _t .

• Recursive end (nested distribution of depth $t= T$) The computation of the distance has already been established in the recursion step.

  Note, that the corresponding trees in this situation represent the entire tree process here.

4.3.2 The Canonical Construction

Suppose that ${\mathbb P}$ and $\tilde{{\mathbb P}}$ are nested distributions of depth T. One may construct the pertaining tree processes in a canonical way: The canonical name of each node is the nested distribution pertaining of the subtree, for which this node is the root. Two valuated trees are equivalent, iff the respective canonical constructions are identical.

Example 3.10

Consider the following nested distribution:

$${\mathbb P}_\epsilon = \left[ \begin{array}{cc} 0.5 & 0.5\\ \hline\\[-3mm] 2 & 2+{\mathbb E}\\ \left[\begin{array}{c} 1.0\\ \hline\\[-3mm] 3\end{array}\right] & \left[\begin{array}{cc} 1.0\\ \hline\\[-3mm] 1\end{array}\right] \end{array} \right].$$

We construct a tree process such that the names of the nodes are the corresponding nested distributions of the subtrees:

The nested distance generates a much finer topology than the distance of the multivariate distributions.

Example

(see Heitsch et al. (2006)) Consider the nested distributions of Example 3.10 and

$${\mathbb P}_{0} = \left[ \begin{array}{c} 1.0\\ \hline\\[-3mm] 2\\ \left[\begin{array}{cc} 0.5 & 0.5\\ \hline\\[-3mm] 3 & 1 \end{array}\right] \end{array} \right]. \vspace*{-6pt}$$

Note that the pertaining multivariate distribution of ${\mathbb P}_\epsilon$ on ${\mathbb R}^2$ converges weakly to the one of ${\mathbb P}_{0}$, if $\epsilon \to 0$. However, the nested distributions do not converge: The nested distance is ${\mathchoice {\hbox{d\kern -0.14em l}}{\hbox{d\kern -0.14em l}} {\small{d\kern -0.14em l}}{\small{d\kern -0.14em l}}}({\mathbb P}_\epsilon, {\mathbb P}_{0}) = 1+\epsilon$ for all ε.

Lemma 3.11

Let ${\mathbb P}$ be a nested distribution, P its multivariate distribution, which is dissected into the chain $P = P_{1} \circ P_{2} \circ \cdots \circ P_{T}$ of conditional distributions. If P has the $(K_{2}, \dots, K_{T})$-Lipschitz property (see Definition 3.2), then

$${\mathchoice {\hbox{d\kern -0.14em l}}{\hbox{d\kern -0.14em l}} {\small{d\kern -0.14em l}}{\small{d\kern -0.14em l}}}({\mathbb P}, \tilde{{\mathbb P}}) \leq \sum_{t=1}^T {\mathsf d}_{1}(P_{t},\tilde{P}_{t}) \prod_{s=t+1}^{T+1} (K_{s} + 1).$$

For a proof see Pflug (2009).

Theorem 3.12

Let ${\mathbb P}$ resp. $\tilde{{\mathbb P}}$ be two nested distributions and let P resp. $\tilde {P}$ be the pertaining multi-period distributions. Then

$${\mathsf d}_{1}(P, \tilde{P}) \le {\mathchoice {\hbox{d\kern -0.14em l}}{\hbox{d\kern -0.14em l}} {\small{d\kern -0.14em l}}{\small{d\kern -0.14em l}}}({\mathbb P}, \tilde{{\mathbb P}}).$$

Thus the mapping, which maps the nested distribution to the embedded multi-period distribution, is Lipschitz(1). The topologies generated by the two distances are not the same: The two trees in Figs. 15.5 resp. 15.6 are at multivariate Kantorovich distance 0, but their nested distance is ${\mathchoice {\hbox{d\kern -0.14em l}}{\hbox{d\kern -0.14em l}} {\small{d\kern -0.14em l}}{\small{d\kern -0.14em l}}}=0.25$.

Proof

To find the Kantorovich distance between P and $\tilde {P}$ one has to find a joint distribution for two random vectors ξ and $\tilde{\xi}$ such that the marginals are P resp. $\tilde {P}$. Among all these joint distributions, the minimum of $d(\xi_{1},\tilde{\xi_{t}}) + \cdots + d(\xi_{T}, \tilde{\xi}_{T})$ equals $d(P,\tilde{P})$. The nested distance appears in a similar manner; the only difference is that for the joint distribution also the conditional marginals should be equal to those of ${\mathbb P}$ resp. $\tilde{{\mathbb P}}$. Therefore, the admissible joint distributions for the nested distance are subsets of the admissible joint distributions for the distance between P and $\tilde {P}$ and this implies the assertion. □

Remark

The advantage of the nested distance is that topologically different scenario trees with completely different values can be compared and their distance can be calculated. Consider the example of Fig. 15.10. The conditional probabilities $P(\cdot | u)$ and $Q(\cdot |v)$ are incomparable, since no values of u coincide with values of v. Moreover, the Lipschitz condition of Definition 3.2 does not make sense for trees and therefore Theorem 3.1 is not applicable. However, the nested distance is well defined for two trees.

Fig. 15.10

Two valuated trees

By calculation, we find the nested distance ${\mathchoice {\hbox{d\kern -0.14em l}}{\hbox{d\kern -0.14em l}} {\small{d\kern -0.14em l}}{\small{d\kern -0.14em l}}} = 1.217$.

Example

Here is an example of the nested distance between a continuous process and a scenario tree process. Let ${\mathbb P}$ be the following continuous nested distribution: $\xi_{1} \sim N(0,1)$ and $\xi_{2}| \xi_{1} \sim N(\xi_{1},1)$. Let $\tilde{{\mathbb P}}$ be the discrete nested distribution

$${\footnotesize \left[ \begin{array}{ccc} 0.30345 & 0.3931 & 0.30345\\ \hline\\[-3mm] -1.029 & 0.0 & 1.029\\ \left[\begin{array}{ccc} 0.30345 & 0.3931 & 0.30345\\ \hline\\[-3mm] -2.058 & -1.029 & 0.0 \end{array}\right]& \left[\begin{array}{ccc} 0.30345 & 0.3931 & 0.30345\\ \hline\\[-3mm] -1.029 & 0.0 & 1.029 \end{array}\right]& \left[\begin{array}{ccc} 0.30345 & 0.3931 & 0.30345\\ \hline\\[-3mm] 0.0 & 1.029 & 2.058 \end{array}\right] \end{array} \right]}$$

Then the nested distance is $d({\mathbb P}, \tilde{{\mathbb P}}) = 0.8215$, which we found by numerical distance calculation.

5 Scenario Tree Construction and Reduction

Suppose that a scenario process $(\xi_{t})$ has been estimated. In this section, we describe how to construct a scenario tree out of it. We begin with considering the case, where the information is the one which is generated by the scenario process and the method is based on the conditional probabilities. Later, we present the case where a tree process representing the information and a scenario process sitting on the tree process has been estimated.

5.1 Methods Based on the Conditional Distance

The most widespread method to construct scenario trees is to construct them recursively from root to leaves. The discretization for the first stage is done as described in Section 15.2. Suppose a chosen value for the first stage is x. Then the reference process $\xi_ {t}$ is conditioned to the set $\{ \omega : |\xi_{1} - x| \le \epsilon \}$, where ε is chosen in such a way that enough trajectories are contained in this set. The successor nodes of x are then chosen as if x were the root and the conditional process were the total process.

The original distributions may either be continuous (e.g., estimated distributions) or more commonly discrete (e.g., simulated with some random generation mechanism which provides some advantages for practical usage). Different solution techniques for continuous as well as discrete approximation have been outlined in Pflug (2001) and Hochreiter and Pflug (2007).

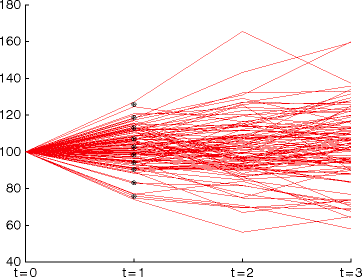
Example

The typical algorithm for finding scenario trees based on the Kantorovich distance can be illustrated by the following pictures.

• Step 1. Estimate the probability model and simulate future trajectories

  

• Step 2. Approximate the data in the first stage by minimal Kantorovich distance

  

• Step 3. For the subsequent stages, use the paths which are close to its predecessor ...

  

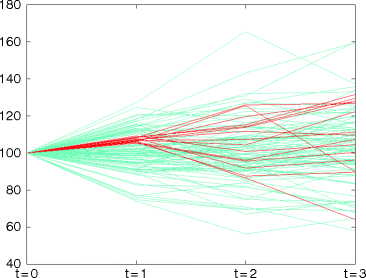
• Step 4. .. and iterate this step through the whole tree.

  

5.2 Methods Based on the Nested Distance

The general scenario tree problem is as follows:

5.2.1 The Scenario Tree Problem

Given a nested distribution ${\mathbb P}$ of depth T, find a valuated tree (with nested distance $\tilde{{\mathbb P}}$) with at most S nodes such that the distance ${\mathchoice {\hbox{d\kern -0.14em l}}{\hbox{d\kern -0.14em l}} {\small{d\kern -0.14em l}}{\small{d\kern -0.14em l}}}({\mathbb P}, \tilde{{\mathbb P}})$ is minimal.

Unfortunately, this problem is such complex, that is, it is impossible to be solved for medium tree sizes. Therefore, some heuristic approximations are needed. A possible method is a stepwise and greedy reduction of a given tree. Two subtrees of the tree may be collapsed, if they are close in terms of the nested distance. Here is an example:

Example

The three subtrees of level 2 of the tree in Fig. 15.9. We calculated their nested distances as follows:

$${\mathchoice {\hbox{d\kern -0.14em l}}{\hbox{d\kern -0.14em l}} {\small{d\kern -0.14em l}}{\small{d\kern -0.14em l}}}\left( \footnotesize \left[ \begin{array}{c} 1.0\\ \hline\\[-3mm] 2.4\\ \left[\begin{array}{cc} 0.4 & 0.6\\ \hline\\[-3mm] 5.1 & 1.0 \end{array}\right] \end{array} \right], \left[ \begin{array}{c} 1.0\\ \hline\\[-3mm] 3.0\\ \left[\begin{array}{c} 1.0\\ \hline\\[-3mm] 2.8\end{array}\right] \end{array} \right] \right) = 2.6,$$

$${\mathchoice {\hbox{d\kern -0.14em l}}{\hbox{d\kern -0.14em l}} {\small{d\kern -0.14em l}}{\small{d\kern -0.14em l}}}\left( \footnotesize \left[ \begin{array}{c} 1.0\\ \hline\\[-3mm] 2.4\\ \left[\begin{array}{cc} 0.4 & 0.6\\ \hline\\[-3mm] 5.1 & 1.0 \end{array}\right] \end{array} \right], \left[\begin{array}{c} 1.0\\ \hline\\[-3mm] 3.0\\ \left[ \begin{array}{ccc} 0.4 & 0.2 & 0.4\\ \hline\\[-3mm] 3.3 & 4.7 & 6.0 \end{array}\right] \end{array} \right] \right ) = 2.62,$$

$${\mathchoice {\hbox{d\kern -0.14em l}}{\hbox{d\kern -0.14em l}} {\small{d\kern -0.14em l}}{\small{d\kern -0.14em l}}}\left( \footnotesize \left[ \begin{array}{c} 1.0\\ \hline\\[-3mm] 2.4\\ \left[\begin{array}{cc} 0.4 & 0.6\\ \hline\\[-3mm] 5.1 & 1.0 \end{array}\right] \end{array} \right], \left[\begin{array}{c} 1.0\\ \hline\\[-3mm] 3.0\\ \left[ \begin{array}{ccc} 0.4 & 0.2 & 0.4\\ \hline\\[-3mm] 3.3 & 4.7 & 6.0 \end{array}\right] \end{array} \right] \right) = 1.86.$$

To calculate a nested distance, we have to solve $\sum_{t=1}^T \#(N_{t}) \cdot \#(\tilde{N}_{t})$ linear optimization problems, where $\#(N_{t})$ is the number of nodes at stage t.

Example

For the valued trees of Fig. 15.11

Fig. 15.11

Distances between nested distributions

we get the following distances:

$$\begin{aligned} {\mathchoice {\hbox{d\kern -0.14em l}}{\hbox{d\kern -0.14em l}} {\small{d\kern -0.14em l}}{\small{d\kern -0.14em l}}}({\mathbb P}^{(1)},{\mathbb P}^{(2)}) & = 3.90; d(P^{(1)},P^{(2)}) = 3.48, \\ {\mathchoice {\hbox{d\kern -0.14em l}}{\hbox{d\kern -0.14em l}} {\small{d\kern -0.14em l}}{\small{d\kern -0.14em l}}}({\mathbb P}^{(1)},{\mathbb P}^{(3)}) & = 2.52; d(P^{(1)},P^{(3)}) = 1.77, \\ {\mathchoice {\hbox{d\kern -0.14em l}}{\hbox{d\kern -0.14em l}} {\small{d\kern -0.14em l}}{\small{d\kern -0.14em l}}}({\mathbb P}^{(2)},{\mathbb P}^{(3)}) & = 3.79; d(P^{(2)},P^{(3)}) = 3.44. \end{aligned}$$

Example

Let ${\mathbb P}$ be the (nested) probability distribution of the pair $\xi=(\xi_{1}, \xi_{2})$ be distributed according to a bivariate normal distribution

$$\left( \begin{array}{c} \xi_{1} \\ \xi_{2} \end{array} \right) = {\Large N} \left( \left( \begin{array}{c} 0 \\ 0 \end{array} \right), \left( \begin{array}{cc} 1 & 1\\ 1 & 2 \end{array} \right) \right).$$

Note that the distribution of $(\xi_{1}, \xi_{2})$ is the same as the distribution of $(\zeta_{1}, \zeta_{1} + \zeta_{2})$, where ζ _i are independently standard normally distributed.

We know that the optimal approximation of a $N(\mu,\sigma^2)$ distribution in the Kantorovich sense by a three-point distribution is

$$\left[ \begin{array}{ccc} 0.30345 & 0.3931 & 0.30345\\ \hline\\[-3mm] \mu-1.029 \sigma & \mu & \mu+ 1.029\sigma\\ \end{array} \right].$$

The distance is 0.3397 σ. Thus the optimal approximation to ξ ₁ is

$$\left[ \begin{array}{ccc} 0.30345 & 0.3931 & 0.30345\\ \hline\\[-3mm] -1.029 & 0.0 & 1.029\\ \end{array} \right]$$

and the conditional distributions given these values are $N(-1.029,1)$, $N(0,1)$, and $N(1.029,1)$. Thus the optimal two-stage approximation is

$$\tilde {\mathcal P}^{(1)}\!\!=\!\!\\[5mm] {\left[ \begin{array}{ccc} 0.30345 & 0.3931 & 0.30345\\ \hline\\[-3mm] -1.029 & 0.0 & 1.029\\ \left[\begin{array}{ccc} 0.30345 & 0.3931 & 0.30345\\ \hline\\[-3mm] -2.058 & -1.029 & 0.0 \end{array}\right]& \left[\begin{array}{ccc} 0.30345 & 0.3931 & 0.30345\\ \hline\\[-3mm] -1.029 & 0.0 & 1.029 \end{array}\right]& \left[\begin{array}{ccc} 0.30345 & 0.3931 & 0.30345\\ \hline\\[-3mm] 0.0 & 1.029 & 2.058 \end{array}\right] \end{array} \right]. }$$

The nested distance is ${\mathchoice {\hbox{d\kern -0.14em l}}{\hbox{d\kern -0.14em l}} {\small{d\kern -0.14em l}}{\small{d\kern -0.14em l}}}({\mathbb P},\tilde{{\mathbb P}}^{(1)}) = 0.76$.

Fig. 15.12

Optimal two stage approximation

Figure 15.12 shows on the left the density of the considered normal model ${\mathbb P}$ and on the right the discrete model $\tilde{{\mathbb P}}^{(1)}$.

For comparison, we have also sampled nine random points from ${\mathbb P}$. Let $\tilde{{\mathbb P}}^{(2)}$ be the empirical distribution of these nine points. Figure 15.13 shows on the right side the randomly sampled discrete model $\tilde{{\mathbb P}}^{(2)}$. The nested distance is ${\mathchoice {\hbox{d\kern -0.14em l}}{\hbox{d\kern -0.14em l}} {\small{d\kern -0.14em l}}{\small{d\kern -0.14em l}}}({\mathbb P},\tilde{{\mathbb P}}^{(2)}) = 1.12$.

Fig. 15.13

Randomly sampled approximation

6 Summary

In this contribution we have outlined some funding components to get stochastic optimization available for computational treatment. At first stage the quantization of probability measures is studied, which is essential to capture the initial problem from a computational perspective. Various distance concepts are available in general, however, only a few of them insure that the quality of the solution of the approximated problem is in line with the initial problem.

This concept then is extended to processes and trees. To quantify the quality of an approximating process, the concept of a nested distance is introduced. Some examples are given to illustrate this promising concept.

The collected ingredients give a directive, how to handle a stochastic optimization problem in general. Moreover – and this is at least as important – they allow to qualify solution statements of any optimization problem, which have stochastic elements incorporated.