Dynamic generation of scenario trees

Abstract

This paper presents new algorithms for the dynamic generation of scenario trees for multistage stochastic optimization. The different methods described are based on random vectors, which are drawn from conditional distributions given the past and on sample trajectories. The structure of the tree is not determined beforehand, but dynamically adapted to meet a distance criterion, which measures the quality of the approximation. The criterion is built on transportation theory, which is extended to stochastic processes.

1 Introduction

Scenario trees are the basic data structure for multistage stochastic optimization problems. They are discretizations of stochastic processes and therefore an approximation to real phenomena. In this paper we describe general algorithms, which approximate the underlying stochastic process with an arbitrary, prescribed precision.

The traditional way from data to tree models is as follows:

• (i) Historical time series data are collected,

• (ii) a parametric model is specified for the probability law which governs the data process,

• (iii) the parameters are estimated on the basis of the observations (and possibly some additional information),

• (iv) future scenarios are generated according to the identified probability laws, and finally

• (v) these scenarios are concentrated in a tree, typically by stepwise reduction.

In the last step a concept of closeness of scenarios and similarity between the simulated paths and the tree has to be used. Some authors use as a criterion for similarity the coincidence of moments (cf. Wallace et al. [13, 14]), others use distance concepts such as the squared norm and a filtration distance (cf. Heitsch and Römisch and others [5, 7–11]).

It has been shown in Pflug and Pichler [26] that an appropriate distance concept for stochastic processes and trees is given by the nested distance (see Definition 20 below). The relevant theorem for multistage stochastic optimization (cited as Theorem 21 below) is extended and simplified for the particular case of pushforward measures (Theorem 16). Based on transportation theory this paper presents in addition theorems which are particularly designed to extract scenario trees by employing techniques, which are adopted from stochastic approximation.

Shapiro [30] mentions that it is standard practice for scenario tree construction to sample at every stage conditionally on the scenarios generated at the previous stage. The trees obtained represent a reference model of the initial stochastic process. The paper [1] by Bally et al. considers Markovian processes as the Brownian diffusion processes and applies optimal quantization to construct a tree reference model for option pricing, while Kuhn [16, 17] considers more general autoregressive processes. Our algorithms follow this idea as well, but in addition we construct scenario trees from observed paths, which may not have a common past.

A related issue is the choice of the tree topology, or the branching structure of the scenario tree: how bushy and how big should the approximating tree be in order not to exceed a given, maximal discretization error? The cited papers do not address this problem. The scenario reduction methods of Heitsch and Römisch are inspired by their work on squared norm and filtration distances, but do not give explicit error bounds.

We propose here a new way from data to tree models as follows:

• (i) as above, historical time series data are collected,

• (ii) a simulator has to be provided, which allows sampling trajectories from all conditional distributions of the estimated data process,

• (iii) a threshold for the maximum discretization error has to be specified, then

• (iv) our algorithms generate a tree with automatically chosen topology and maximal chosen discretization error.

The algorithms apply to stochastic processes with higher dimensional state space too, for which an appropriate distance has to be chosen. This is of relevance and importance in many economic applications.

The presented methods can be applied to approximate stochastic optimization problems with continuous-state scenarios by simpler ones defined on discrete-state scenario trees. Pennanen et al. [12, 21, 22] investigate the convergence of related multistage stochastic programs.

Outline of the paper. The next section (Sect. 2) recalls the notion of transportation distances on probability spaces. Section 3 provides the mathematical basis for algorithms to approximate probability measures. These algorithms are based on stochastic approximation. Section 4 generalizes the results to stochastic processes and gives the related theorems for stochastic programming based on transportation distance. Section 5 introduces the nested distance and generalizes the results from transportation distances to the nested distance. Further, this section explains how scenario trees can be extracted from a set of trajectories of the underlying process. A series of examples demonstrates that it is possible to extract useful scenario trees even from a sample, which is smaller than the nodes of the scenario tree. In Sect. 6 we discuss the relevance of the algorithms and conclude.

2 Approximation of probability measures

It has been elaborated in a sequence of publications that the nested distance is an appropriate concept to provide a distance for stochastic processes, the basic theorem is provided below (Theorem 16). The nested distance is built on the transportation distance (sometimes also Wasserstein, or Katorovich distance), which is a distance for probability measures.

Numerical integration is easily executed for discrete measures. By the Kantorovich–Rubinstein duality theorem (cf. Villani [32], Theorem 1.14]), the Kantorovich distance provides the smallest possible error bound to compare expectations with respect to different measures. The Kantorovich distance, and the more general variant, the Wasserstein distance, are thus the adequate tool to provide adapted, discrete probability measures for numerical integration or expectation. In addition, the distances themselves can be handled numerically.

Having fast computations in mind we are interested in discrete approximating measures, which have as few as possible supporting points. The approach we outline here allows different weights for the supporting scenarios, as this optimal quantization further improves the approximating precision. Respective measures with equally weighted supporting points are, e.g., described in Pagés [20], but the same author provides also optimal quantizers in a series of related papers.

Definition 1

(Transportation distance for probability measures) Assume that $P$ ($\tilde{P}$, resp.) are probability measures on probability spaces $\Xi$ ($\tilde{\Xi }$, resp.), such that for $\xi \in \Xi$ and $\tilde{\xi }\in \tilde{\Xi }$ a distance $\mathsf {d}(\xi ,\tilde{\xi })$ is defined. To the metric $\mathsf {d}$ one may associate the pertaining Wasserstein distance of order $r\ge 1$ of probability measures by

$$\begin{aligned} \mathsf {d}_{r}(P,\tilde{P})\!:=\!\inf \left\{ \left( \iint _{\Xi \times \tilde{\Xi }}\mathsf {d}(\xi ,\tilde{\xi })^{r}\,\pi (d\xi ,d\tilde{\xi })\right) ^{1/r}\left| \begin{array}{l} \pi \text{ is } \text{ a } \text{ probability } \text{ measure } \text{ on } \Xi \times \tilde{\Xi }\\ \text{ with } \text{ marginal } \text{ distributions } P\text { and }\tilde{P} \end{array}\right. \right\} . \end{aligned}$$

(1)

The distance $\mathsf {d}_{1}$ is also called Kantorovich distance.

The methods we develop in what follows consider a special probability measure $\tilde{P}$, which is associated with the initial measure $P$ by a transport map.

Remark 2

The Wasserstein distance introduced here is based on the continuous function (a distance) $\mathsf {d}$. For the theory of more general cost functions we refer, e.g., to Schachermayer et al. [2].

2.1 Transport maps

A particular situation arises if the second probability measure $\tilde{P}$ is a pushforward measure (or image measure) of $P$ for some transport map $T:\,\Xi \rightarrow \tilde{\Xi }$ linking the spaces, $\tilde{P}=P^{T}:=P\circ T^{-1}$. Then an upper bound for the Wasserstein distance is given by

$$\begin{aligned} \mathsf {d}_{r}\bigl (P,P^{T}\bigr )^{r}\le \int _{\Xi }\mathsf {d}\bigl (\xi ,T(\xi )\bigr )^{r}P(d\xi ), \end{aligned}$$

(2)

because the bivariate measure

$$\begin{aligned} \pi _{T}\left( A\times B\right) :=P\left( A\cap T^{-1}(B)\right) \end{aligned}$$

(3)

associated with $T$ has the marginals required in (1).

The situation $\tilde{P}=P\circ T^{-1}$ naturally arises in approximations, where the outcome $\xi$ is approximated by $T(\xi )$. Notice that if $T(\xi )$ is a close approximation of $\xi$, then $\mathsf {d}\bigl (\xi ,T(\xi )\bigr )$ is small and the integral in (2) is small as well, which makes $P^{T}$ an approximation of interest for $P$.

The upper bound (2) is useful in many respects. First, the measure $\pi _{T}$ is computationally much easier to handle than a solution of (1), because the integral in (2) is just over $\Xi$, and not over the product $\Xi \times \tilde{\Xi }$ as in (1). Further, for $r=2$, Brenier’s polar factorization theorem [3, 4] implies that the optimal transport plan $\pi$ solving (1) has the general form (3) for some measure preserving map $T$, such that involving a transport map is not restrictive. Finally, the transport map allows a generalization to stochastic processes which we address in Sect. 4.2.

2.2 Single-period Wasserstein distance minimization

Assume that $P$ and $\tilde{P}$ are probabilities on $\Xi ={\mathbb {R}}^{m}$, which is endowed with the distance

$$\begin{aligned} \mathsf {d}(\xi ,\tilde{\xi }). \end{aligned}$$

To the distance $\mathsf {d}$ one may associate the pertaining Wasserstein-distance according to (1) in Definition 1. Our goal is to approximate $P$ by the “best” discrete multivariate distribution $\tilde{P}$ sitting on $s$ points $z^{(1)},\ldots ,z^{(s)}$ in the sense that the transportation distance $\mathsf {d}_{r}(P,\tilde{P})$ is minimized.

Given a collection of points $Z=\left( z^{(1)},\ldots ,z^{(s)}\right) ,$ which can be collected in a $m\times s$ matrix, introduce the Voronoi partition ${\mathcal {V}}_{Z}=\left\{ V_{Z}^{(i)}:i=1,\ldots ,s\right\}$ of ${\mathbb {R}}^{m}$, where

$$\begin{aligned} V_{Z}^{(i)}=\left\{ \xi \in {\mathbb {R}}{}^{m}\left| \begin{array}{l} \mathsf {d}(\xi ,z^{(i)})=\min _{j}\mathsf {d}(\xi ,z^{(j)}) \text{ and }\\ \mathsf {d}(\xi ,z^{(k)})>\min _{j}\mathsf {d}(\xi ,z^{(j)}) \text{ for } k<i \end{array}\right. \right\} \end{aligned}$$

such that¹

For a given probability $P$ on ${\mathbb {R}}^{m}$ we use the notation $P_{Z}$ for the discrete distribution sitting on the points of the set $Z$ with masses $P\left( V_{Z}^{(i)}\right)$, i.e.,

$$\begin{aligned} P_{Z}=\sum _{i=1}^{s}P\left( V_{Z}^{(i)}\right) \cdot \,\delta _{z^{(i)}}. \end{aligned}$$

Remark 3

Notice that the measure $P_{Z}$ is induced by the plan $T$, $P_{Z}=P^{T}$, where $T:\Xi \rightarrow Z\subset \Xi$ is the transport map

$$\begin{aligned} T(\xi ):=z^{(i)},\text { if }\xi \in V_{Z}^{(i)}. \end{aligned}$$

For a fixed $P$ let

$$\begin{aligned} D(Z):=\int _{\Xi }\min _{i=1,\ldots s}\mathsf {d}\bigl (\xi ,z^{(i)}\bigr )^{r}\,P(d\xi )=\sum _{i=1}^{s}\int _{V_{Z}^{(i)}}\mathsf {d}\bigl (\xi ,z^{(i)}\bigr )^{r}\;P(d\xi ). \end{aligned}$$

(4)

Then

$$\begin{aligned} D(Z)^{1/r}&=\min \left\{ \mathsf {d}_{r}(P,\bar{P}):\,\bar{P}(Z)=1\right\} \nonumber \\&=\min \left\{ \mathsf {d}_{r}(P,\bar{P}):\,\bar{P} \text{ sits } \text{ on } \text{ the } \text{ points } \text{ of } \text{ the } \text{ set } Z\right\} =\mathsf {d}_{r}(P,P_{Z}), \end{aligned}$$

(5)

such that $D(Z)$ measures the quality of the approximation of $P$, which can be achieved by probability measures with supporting points $Z$ (cf. [6], Lemma 3.4]).

2.2.1 Facility location

The approximation problem is thus reduced to finding the best point set $Z$ (the facility location problem) in (4). This problem is an unconstrained, non-convex, high dimensional (as optimal locations consist of $s$ points in ${\mathbb {R}}^{m}$) optimization problem. In addition, the objective is not everywhere differentiable. In general, it is not possible to identify the (a) global solution of the facility location problem, but good locations are often sufficient for applications in stochastic optimization.

In the next section we discuss three algorithms for solving this minimization problem:

• (i) A deterministic iteration procedure, which is applicable, if the necessary integrations with respect to $P$ can be carried out numerically.

• (ii) A stochastic approximation procedure, which is based on a sample from $P$ and which converges to a local minimum of $D$.

• (iii) A branch-and-bound procedure, which is also based on a sample from $P$ and which converges to a global minimum of $D$.

2.2.2 Asymptotics and choice of parameters

Locations, which minimize the objective (5) globally, are called representative points. It is a well-known result established by Dudley (cf. Graf and Luschgy [6]) that $D(Z)^{1/r}$ is asymptotically of order $s^{-1/m}$ independently of $r$. It is desirable to choose $r=1$ or $r$ small, because $\mathsf {d}_{r}(P,\bar{P})\le \mathsf {d}_{r^{\prime }}(P,\bar{P})$ whenever $r\le r^{\prime }$ (a consequence of Hölder’s inequality) to improve the approximation (5).

On the other hand, choosing the Euclidean distance $\mathsf {d}(\cdot ,:):=\left\| \cdot \,-\,:\right\|$ and $r=2$ often simplifies computations significantly. In particular it holds for linear random variables $f$ that ${\mathbb {E}}f={\mathbb {E}}_{P_{Z}}f$, if $P_{Z}=\sum _{i=1}^{s}P\left( V_{Z}^{(i)}\right) \cdot \,\delta _{z^{(i)}}$ and $Z$ is a local minimum of (5) (cf. Graf and Luschgy [6], Remark 4.6]). Hence, (locally) optimal measures are always (even for $s=1$ or $s\le d$) exact for the expectation of linear random variables. In addition, a transportation map is available in the case of $r=2$, cf. Remark 5 below.

However, the choice of the underlying norm and the parameter $r\ge 1$ is often driven by the particular problem at hand, but $r=2$ and the Euclidean norm is the preferable choice for linear problems.

3 Algorithms to approximate probability measures

Before introducing the algorithms we mention the differentiability properties of the mapping $Z\mapsto D(Z)$. This is useful as the first order conditions of optimality for (5) require the derivatives to vanish.

Let $\nabla D(Z)$ be the $m\times s$ matrix with column vector $\nabla _{z^{(i)}}D(Z)$ given by the formal derivative

$$\begin{aligned} \int _{V_{Z}^{(i)}}r\,\mathsf {d}\bigl (\xi ,z^{(i)}\bigr )^{r-1}\cdot \nabla _{\tilde{\xi }}\mathsf {d}\bigl (\xi ,z^{(i)}\bigr )\,P(d\xi ),\qquad i=1,\ldots s \end{aligned}$$

(6)

of (4).

Proposition 4

If $P$ has a density $g$ with respect to the Lebesgue measure, then $Z\mapsto D(Z)$ is differentiable and the derivative is $\nabla D(Z)$.

Proof

Notice first that by convexity of the distance $\mathsf {d}$ the gradient $\nabla _{\tilde{\xi }}\mathsf {d}\bigl (\xi ,z^{(i)}\bigr )$ in the integral (6) is uniquely determined except on a Lebesgue set of measure zero due to Rademacher’s theorem. As $P$ has a Lebesgue density the exception set has measure zero and the integral is well defined. That (6) is indeed the derivative follows by standard means, cf. also Pflug [23], Corollary 3.52, page 184].

3.1 The deterministic iteration

We start with a well known cluster algorithm for partitioning a larger set of points in ${\mathbb {R}}^{m}$ into $s$ clusters. Algorithm 1 is a typical example of an algorithm, which clusters a given set of points into subsets of small intermediate distance. The algorithm can be used to generate representative scenarios. We use it only to find good starting configurations for the subsequent optimization algorithm.

The subsequent single-period algorithm (Algorithm 2, a theory based heuristic) requires integration with respect to $P$, as well as nonlinear optimizations to be carried out numerically. Since this is a difficult task, especially for higher dimensions, we present an alternative algorithm based on stochastic algorithm later.

Remark 5

To compute the argmin in the optimization step (iii) of Algorithm 2 is in general difficult. However, there are two important cases.

• (i) Whenever ${\mathbb {R}}^{m}$ is endowed with the weighted Euclidean metric $\mathsf {d}\left( \xi ,\tilde{\xi }\right) ^{2}=\sum _{j=1}^{m}w_{j}\left| \xi _{j}-\tilde{\xi }_{j}\right| ^{2}$ and the order of the Wasserstein distance is $r=2$, then the argmin is known to be the conditional barycenter, i.e., the conditional expected value

  $$\begin{aligned} z^{(i)}(k+1)=\frac{1}{P\bigl (V_{Z(k)}^{(i)}\bigr )}\int _{V_{Z(k)}^{(i)}}\xi \;P(d\xi ). \end{aligned}$$

  (8)

  This is an explicit formula, which is available in selected situations of practical relevance. Computing (8) instead of (7) may significantly accelerate the algorithm.

• (ii) Whenever ${\mathbb {R}}^{m}$ is endowed with the weighted $\ell ^{1}$-metric $\mathsf {d}\left( \xi ,\tilde{\xi }\right) =\sum _{j=1}^{m}w_{j}\left| \xi _{j}-\tilde{\xi }_{j}\right|$, then $z^{(i)}(k+1)$ in (7) is the componentwise median of the probability $P$ restricted to $V_{Z(k)}^{(i)}$. In general and in contrast to the Euclidean metric, no closed form is available here.

Remark 6

(Initialization) Whenever the probability measure is a measure on ${\mathbb {R}}^{1}$ with cumulative distribution function (cdf) $G$, then the quantiles

$$\begin{aligned} z^{(i)}(0):=G^{-1}\left( \frac{i-1/2}{s}\right) \qquad (i=1,2,\ldots s) \end{aligned}$$

can be chosen as initial points for the Wasserstein distance in (i) of Algorithm 2. These points are optimal for the Kolmogorov distance, that is, they minimize $\sup _{z\in {\mathbb {R}}}\left| P\left( \left( -\infty ,z\right] \right) -\hat{P}_{n}\left( \left( -\infty ,z\right] \right) \right|$ for the measure $P$ and the empirical measure $\hat{P}_{n}=\frac{1}{n}\sum _{i=1}^{n}\delta _{z^{(i)}}$.

For the Wasserstein distance of order $r\ge 1$ even better choices are

$$\begin{aligned} z^{(i)}(0)=G_{r}^{-1}\left( \frac{i-1/2}{s}\right) \qquad (i=1,2,\ldots s), \end{aligned}$$

where $G_{r}$ is the cdf with density $g_{r}\sim g^{1/1+r}$ (provided that a density $g$ is available). This is derived in Graf and Luschgy [6], Theorem 7.5]. Their result is even more general and states that the optimal points $z^{(i)}$ asymptotically follow the density

$$\begin{aligned} g_{r}=\frac{g^{m/(m+r)}}{\int g^{m/(m+r)}}, \end{aligned}$$

(9)

whenever the initial probability measure $P$ on ${\mathbb {R}}^{m}$ has density $g$.

The following proposition addresses the convergence of the deterministic iteration algorithm.

Proposition 7

If $Z(k)$ is the sequence of point sets generated by the deterministic iteration algorithm (Algorithm 2), then

$$\begin{aligned} D\bigl (Z(k+1)\bigr )\le D\bigl (Z(k)\bigr ). \end{aligned}$$

If $D\bigl (Z(k^{*}+1)\bigr )=D\bigl (Z(k^{*})\bigr )$ for some $k^{*}$, then $D\bigl (Z(k)\bigr )=D\bigl (Z(k^{*})\bigr )$ for all $k\ge k^{*}$ and

$$\begin{aligned} \nabla _{z^{(i)}}D\bigl (Z(k^{*})\bigr )=0 \end{aligned}$$

for all $i$.

Proof

Notice that

$$\begin{aligned} D(Z(k))= & {} \int _{\Xi }\min _{j}\,\mathsf {d}(\xi ,z^{(j)})^{r}\;P(d\xi )=\sum _{i=1}^{s}\int _{V_{Z}^{(i)}}\mathsf {d}\bigl (\xi ,z^{(i)}(k)\bigr )^{r}\;P(d\xi )\\\ge & {} \sum _{i=1}^{s}\int _{V_{Z}^{(i)}}\,\mathsf {d}\bigl (\xi ,z^{(i)}(k+1)\bigr )^{r}\;P(d\xi )=\int _{\Xi }\min _{j}\,d\bigl (\xi ,z^{(i)}(k+1)\bigr )^{r}\;P(d\xi )\\= & {} D(Z(k+1)). \end{aligned}$$

If $D(Z(k^{*}+1))=D(Z(k^{*}))$, then necessarily, for all $i$,

$$\begin{aligned} z_{j}^{(i)}(k)\in \mathop {\mathrm{argmin}}\limits _{y}\left\{ \int _{V_{Z(k)}^{(i)}}\mathsf {d}\left( \xi ,y\right) ^{r}\;P(d\xi )\right\} , \end{aligned}$$

which is equivalent to

$$\begin{aligned} \int _{V_{Z}^{(i)}}r\,\mathsf {d}\bigl (\xi ,z^{(i)}\bigr )^{r-1}\cdot \nabla _{\tilde{\xi }}\mathsf {d}\bigl (\xi ,z^{(i)}\bigr )P(d\xi )=0\text { for all }i \end{aligned}$$

by Proposition 4. Hence $\nabla _{Z}D\bigl (Z(k^{*})\bigr )=0$ and evidently, the iteration has reached a fixed point. $\square$

Remark 8

We remark here that the method outlined in Algorithm 2 is related to the k-means method of cluster analysis (see, e.g., McQueen [18]).

3.2 Stochastic approximation

Now we describe how one can avoid the optimization and integration steps of Algorithm 2 by employing stochastic approximation to compute the centers of order $r$. The stochastic approximation algorithm (Algorithm 3) requires that we can sample an independent, identically distributed (i.i.d.) sequence

$$\begin{aligned} \xi (1),\ldots ,\xi (n) \end{aligned}$$

of vectors of arbitrary length $n$, each distributed according to $P$.²

Proposition 9

Suppose that ${\mathfrak {F}}=({\mathcal {F}}_{1},{\mathcal {F}}_{2}\ldots )$ is a filtration and $(Y_{k})$ is a sequence of random variables, which are uniformly bounded from below and adapted to ${\mathfrak {F}}$. In addition, let $(A_{k})$ and $(B_{k})$ be sequences of nonnegative random variables also adapted to ${\mathfrak {F}}$. If $\sum _{k}B_{k}<\infty$ a.s. and the recursion

$$\begin{aligned} {\mathbb {E}}[Y_{k+1}|\,{\mathcal {F}}_{k}]\le Y_{k}-A_{k}+B_{k} \end{aligned}$$

(10)

is satisfied, then $Y_{k}$ converges and $\sum _{k}A_{k}<\infty$ almost surely.

Proof

Let $S_{k}:=\sum _{\ell =1}^{k}B_{\ell }$ and $T_{k}:=\sum _{\ell =1}^{k}A_{\ell }$. Then (10) implies that

$$\begin{aligned} {\mathbb {E}}\left[ Y_{k+1}-S_{k}|{\mathcal {F}}_{k}\right] ={\mathbb {E}}\left[ Y_{k+1}-S_{k-1}|{\mathcal {F}}_{k}\right] -B_{k}\le Y_{k}-S_{k-1}-A_{k}\le Y_{k}-S_{k-1}. \end{aligned}$$

Hence $Y_{k+1}-S_{k}$ is a supermartingale, which is bounded from below and which converges a.s. by the supermartingale convergence theorem (cf. Williams [33], Chapter 11]). Since $S_{k}$ converges by assumption, it follows that $Y_{k}$ converges almost surely. Notice finally that (10) is equivalent to

$$\begin{aligned} {\mathbb {E}}\left[ Y_{k+1}-S_{k}+T_{k}|{\mathcal {F}}_{k}\right] \le Y_{k}-S_{k-1}+T_{k-1}, \end{aligned}$$

and by the same reasoning as above it follows that $Y_{k+1}-S_{k}+T_{k}$ converges a.s., which implies that $T_{k}=\sum _{\ell =1}^{k}A_{\ell }$ converges a.s. $\square$

Proposition 10

Let $F(\cdot )$ be a real function defined on ${\mathbb {R}}^{m}$, which has a Lipschitz-continous derivative $f(\cdot )$. Consider a recursion of the form

$$\begin{aligned} X_{k+1}=X_{k}-a_{k}f(X_{k})+a_{k}R_{k+1} \end{aligned}$$

(11)

with some starting point $X_{0}$, where ${\mathbb {E}}[R_{k+1}|R_{1,}\ldots ,R_{k}]=0$. If $a_{k}\ge 0$, $\sum _{k}a_{k}=\infty$ and $\sum _{k}a_{k}^{2}\Vert R_{k+1}\Vert ^{2}<\infty$ a.s., then $F(X_{k})$ converges. If further $\sum _{k}a_{k}R_{k+1}$ converges a.s., then $f(X_{k})$ converges to zero a.s.

Proof

Let $Y_{k}:=F(X_{k})$ and let $K$ be the Lipschitz constant of $f$. Using the recursion (11) and the mean value theorem, there is a $\theta \in [0,1]$ such that

$$\begin{aligned} F(X_{k+1})&=F(X_{k})+f\bigl (X_{k}+\theta (-a_{k}f(X_{k})+a_{k}R_{k+1})\bigr )^{\top }\cdot (-a_{k}f(X_{k})+a_{k}R_{k+1})\\&\le F(X_{k})+f(X_{k})^{\top }\cdot (-a_{k}f(X_{k})+a_{k}R_{k+1})\\&\quad +K\cdot \left\| -a_{k}f(X_{k})+a_{k}R_{k+1}\right\| ^{2}\\&\le F(X_{k})-a_{k}\left\| f(X_{k})\right\| ^{2}+a_{k}f(X_{k})^{\top }R_{k+1}+2Ka_{k}^{2}\left\| f(X_{k})\right\| ^{2}\\&\quad +2Ka_{k}^{2}\left\| R_{k+1}\right\| ^{2}. \end{aligned}$$

Taking the conditional expectation with respect to $R_{1},\ldots ,R_{k}$ one gets

$$\begin{aligned} {\mathbb {E}}\left[ F(X_{k+1})|R_{1},\ldots ,R_{k}\right]&\le F(X_{k})-a_{k}\left\| f(X_{k})\right\| ^{2}+2Ka_{k}^{2}\left\| f(X_{k})\right\| ^{2}\\&\quad +2Ka_{k}^{2}\left\| R_{k+1}\right\| ^{2}\\&\le F(X_{k})-\frac{a_{k}}{2}\left\| f(X_{k})\right\| ^{2}+2Ka_{k}^{2}\left\| R_{k+1}\right\| ^{2} \end{aligned}$$

for $k$ large enough. Proposition 9, applied for $Y_{k}=F(X_{k}),$ $A_{k}=\frac{a_{k}}{2}\Vert f(X_{k})\Vert ^{2}$ and $B_{k}=2Ka_{k}^{2}\Vert R_{k+1}\Vert ^{2}$, implies now that $F(X_{k})$ converges and

$$\begin{aligned} \sum _{k}a_{k}\Vert f(X_{k})\Vert ^{2}<\infty \;a.s. \end{aligned}$$

(12)

It remains to be shown that $f(X_{k})\rightarrow 0$ a.s. Since $\sum _{k}a_{k}=\infty$, it follows from (12) that $\liminf _{k}\Vert f(X_{k})\Vert =0$ a.s. We argue now pointwise on the set of probability 1, where $\sum _{k}a_{k}\Vert f(X_{k})\Vert ^{2}<\infty$, $\liminf _{k}\Vert f(X_{k})\Vert =0$ and $\sum _{k}a_{k}R_{k}$ converges. Suppose that $\limsup _{k}\Vert f(X_{k})\Vert ^{2}>2\epsilon$. Let $m_{\ell }<n_{\ell }<m_{\ell +1}$ be chosen such that

$$\begin{aligned} \Vert f(X_{k})\Vert ^{2}>\epsilon&\text{ for } m_{\ell }<k\le n_{\ell }\text { and}\nonumber \\ \Vert f(X_{k})\Vert ^{2}\le \epsilon&\text{ for } n_{\ell }<k\le m_{\ell +1}. \end{aligned}$$

(13)

Let $\ell _{0}$ be such large that

$$\begin{aligned} \sum _{k=m_{\ell _{0}}}^{\infty }a_{k}\left\| f(X_{k})\right\| ^{2}\le \frac{\epsilon ^{2}}{2K}\qquad \text{ and } \qquad \left\| \sum _{k=s}^{t}a_{k}R_{k+1}\right\| <\frac{\epsilon }{2}\quad \text{ for } \text{ all } s,t\ge m_{\ell _{0}}. \end{aligned}$$

Then, for $\ell \ge \ell _{0}$ and $m_{\ell }\le k\le n_{\ell }$, by the recursion (11) and (13), as well as the Lipschitz property of $f$,

$$\begin{aligned} \left\| f(X_{i+1})-f(X_{m_{\ell }})\right\|&\le K\Vert X_{i+1}-X_{m_{\ell }}\Vert =K\left\| \sum _{k=m_{\ell }}^{i}a_{k}f(X_{k})+a_{k}R_{k+1}\right\| \\&\le K\sum _{k=m_{\ell }}^{i}a_{k}\Vert f(X_{k})\Vert +K\left\| \sum _{k=m_{\ell }}^{i}a_{k}R_{k+1}\right\| \\&\le \frac{K}{\epsilon }\sum _{k=m_{\ell }}^{i}a_{k}\left\| f(X_{k})\right\| ^{2}+\frac{\epsilon }{2}<\epsilon . \end{aligned}$$

Since $\left\| f\left( X_{m_{\ell }}\right) \right\| \le \epsilon$ it follows that $\lim \sup _{k}\Vert f(X_{k})\Vert \le 2\epsilon$ for every $\epsilon >0$ and this contradiction establishes the result. $\square$

The following result ensures convergence of an algorithm of stochastic approximation type, which is given in Algorithm 3 to compute useful approximating measures.

Theorem 11

Suppose that the step lengths $a_{k}$ in Algorithm 3 satisfy

$$\begin{aligned} a_{k}\ge 0,\,\sum _{k}a_{k}=\infty \text { and }\sum _{k}a_{k}^{2}<\infty . \end{aligned}$$

Suppose further that the assumptions of Proposition 4 are fulfilled. If $Z(k)$ is the sequence of point sets generated by the stochastic approximation algorithm (Algorithm 3), then $D\bigl (Z(k)\bigr )$ converges a.s. and

$$\begin{aligned} \nabla _{Z}D\bigl (Z(k)\bigr )\rightarrow 0\qquad a.s. \end{aligned}$$

as $k\rightarrow \infty$. In particular, if $D(Z)$ has a unique minimizer $Z^{*}$, then

$$\begin{aligned} Z(k)\rightarrow Z^{*}\qquad a.s. \end{aligned}$$

Proof

The matrices $Z(k)$ satisfy the recursion

$$\begin{aligned} Z(k+1)=Z(k)-a_{k}\nabla _{Z}D\bigl (Z(k)\bigr )-a_{k}W(k) \end{aligned}$$

with

$$\begin{aligned} W(k)=\sum _{i=1}^{s}1\!\!1_{V_{Z(k)}^{(i)}}\bigl (\xi (k)\bigr )\cdot&r\,\mathsf {d}\bigl (\xi (k),z^{(i)}(k)\bigr )^{r-1}\cdot \nabla _{\tilde{\xi }}\mathsf {d}\bigl (\xi (k),z^{(i)}(k)\bigr )\\ -\int _{V_{Z(k)}^{(i)}}&r\,\mathsf {d}\bigl (\xi (k),z^{(i)}(k)\bigr )^{r-1}\cdot \nabla _{\tilde{\xi }}\mathsf {d}\bigl (\xi (k),z^{(j)}(k)\bigr )P(d\xi ). \end{aligned}$$

Notice that the vectors $W(k)$ are independent and bounded, ${\mathbb {E}}[W(k)]=0$ and $\sum _{i}a_{i}W(i)$ converges a.s. Proposition 10 applied for $X_{k}=Z(k)$, $F(\cdot )=D(\cdot )$, $f(\cdot )=\nabla _{Z}D(\cdot )$ and $R_{k}=W(k)$ leads to the assertion. $\square$

Remark 12

A good choice for the step sizes $a_{k}$ in Algorithm 3 is

$$\begin{aligned} a_{k}=\frac{C}{(k+30)^{3/4}}. \end{aligned}$$

These step sizes satisfy the requirements $\sum _{k}a_{k}=\infty$, the sequence $a_{k}$ is nonincreasing and $\sum _{k}a_{k}^{2}<\infty$.³

Remark 13

A variant of Algorithm 3 avoids determining the probabilities in the separate step (iv) but counts the probabilities $p_{i}$ on the fly.

3.3 Global approximation

It was mentioned and it is evident that Algorithm 2 converges to a local minimum, which is possibly not a global minimum. There are also algorithms which find the globally optimal discretization. However, these algorithms are so complex that only very small problems, say to find two or three optimal points in ${\mathbb {R}}^{2}$ or ${\mathbb {R}}^{3}$, can be handled effectively. In addition, the probability measure $P$ must have bounded support.

For the sake of completeness we mention such an algorithm which is able to provide a globally best approximating probability measure located on not more than $s$ supporting points. Algorithm 4 produces successive refinements, which converge to a globally optimal approximation of the initial measure $P$.

4 Trees, and their distance to stochastic processes

In this section we give bounds for the objective value of stochastic optimization problems. By generalizing an important result from multistage stochastic optimization we provide bounds first when the law of the underlying process is approximated by a process with a pushforward measure.

The goal is to construct a valuated probability tree, which represents the process $(\xi _{t})_{t=0}^{T}$ in the best possible way. Trees are represented by a tuple consisting of the treestructure (i.e., the predecessor relations), the values of the process sitting on the nodes and the (conditional) probablities sitting on the arcs of the tree. To be more precise, let ${\mathbb {T}}=(n,{\text {pred}},z,Q)$ represent a tree with

• $n$ nodes;

• a function ${\text {pred}}$ mapping $\left\{ 1,2,\ldots ,n\right\}$ to $\left\{ 0,1,2,\ldots ,n\right\}$. ${\text {pred}}(k)=\ell$ means that node $\ell$ is a direct predecessor of node $k$. The root is node 1 and its direct predecessor is formally encoded as 0;

• a valuation $z_{i}\in {\mathbb {R}}^{m}$ of each node $i\in \left\{ 1,2,\ldots ,n\right\}$;

• the conditional probability $Q(i)$ of reaching node $i$ from its direct predecessor; for the root we have $Q(1)=1$.

It is always assumed that these parameters are consistent, i.e., that they form a tree of height $T$, meaning that all leaves of the tree are at the same level $T$. The distance of each node to the root is called the stage of the node. The root is at stage 0 and the leaves of the tree are at stage $T$.

Let $\tilde{\Omega }$ be the set of all leaf nodes, which can be seen as a probability space carrying the unconditional probabilities $P(n)$ to reach the leaf node $n\in \tilde{\Omega }$ from the root. Obviously the unconditional probability $\tilde{P}(i)$ of any node $i$ is the product of the conditional probabilities of all its predecessors (direct and indirect).

Let ${\text {pred}}_{t}(n)$ denote the predecessor of node $n$ at stage $t.$ These mappings induce a filtration $\tilde{{\mathfrak {F}}}=(\tilde{{\mathcal {F}}}_{0},\ldots ,\tilde{{\mathcal {F}}}_{T})$, where $\tilde{{\mathcal {F}}}_{t}$ is the sigma-algebra induced by ${\text {pred}}_{t}$. $\mathcal {\tilde{{\mathcal {F}}}}_{0}$ is the trivial sigma-algebra and $\tilde{{\mathcal {F}}}_{T}$ is the power set of $\tilde{\Omega }$. The process $(\tilde{\xi }_{t})$ takes the values $z_{i}$ for all nodes $i$ at stage $t$ with probability $\tilde{P}(i)$.

On the other hand, also the basic stochastic process $(\xi _{t})$ is defined on a filtered probability space $\bigl (\Omega ,{\mathfrak {F}}=({\mathcal {F}}_{0},\ldots ,{\mathcal {F}}_{T}),P\bigr )$, where ${\mathcal {F}}_{0}$ is the trivial sigma-algebra. Via the two stochastic processes, the basic process $(\xi _{t})$ defined on $\Omega$ and its discretization $(\tilde{\xi }_{t})$ defined on $\tilde{\Omega }$, a distance between $u\in \Omega$ and $v\in \tilde{\Omega }$ is defined by

$$\begin{aligned} \mathsf {d}(u,v)=\sum _{t=1}^{T}\mathsf {d}_{t}\left( \xi _{t}(u),\tilde{\xi }_{t}(v)\right) , \end{aligned}$$

(14)

where $\mathsf {d}_{t}$ are distances on ${\mathbb {R}}^{m_{t}}$ (the state ${\mathbb {R}}^{m_{t}}$ may depend on the stage $t$, but to keep the notation simple we consider only ${\mathbb {R}}^{m}$ processes in what follows, i.e., $m_{t}=m$ for all $t$). To measure the quality of the approximation of the process $(\xi _{t})$ by the tree ${\mathbb {T}}$ one may use the nested distance (see Definition 20 below) or its simpler variant, a stagewise transportation bound.

4.1 Approximation of stochastic processes

Different algorithms have been demonstrated in the previous sections to construct a probability measure $\tilde{P}=\sum _{i=1}^{s}p_{i}\delta _{z_{i}}$ approximating $P$. The approximating measures $\tilde{P}$ presented are all induced by the transport map

$$\begin{aligned} T:\,\Xi\rightarrow & {} Z\\ \xi\mapsto & {} z_{i},\text { if }\xi \in V_{Z}^{(i)}. \end{aligned}$$

It holds moreover that $V_{Z}^{(i)}=\left\{ T=z_{i}\right\}$ (and in particular $P\bigl (V_{Z}^{(i)}\bigr )=P(T=z_{i})$), which shows that the facility location problems can be formulated by involving just transport maps (cf. Remark 3).

In what follows we generalize the concept of transport maps to stochastic processes. We generalize a central theorem in stochastic optimization, which provides a bound in terms for the pushforward measure for transport maps. We demonstrate that an adequately measurable, finitely valued transport map represents a tree. Further, we employ stochastic approximation techniques again to find a useful tree representing a process. The methods allow computing bounds for the corresponding stochastic optimization problem.

4.2 The main theorem of stochastic optimization for pushforward measures

Consider a stochastic process $\xi =(\xi _{t})_{t=0}^{T}$, which is discrete in time. Each component $\xi _{t}:\Omega \rightarrow \Xi _{t}$ has the state space $\Xi _{t}$ (which may be different for varying $t$’s). Further let $\Xi :=\Xi _{0}\times \ldots \Xi _{T}$ and observe that $\Xi _{t}$ is naturally embedded in $\Xi$.

Definition 14

We say that a process $x=(x_{t})_{t=0}^{T}$ (with $x_{t}:\Xi \rightarrow {\mathbb {X}}_{t}$) is nonanticipative with respect to the stochastic process $\xi =(\xi _{t})_{t=0}^{T}$ , if $x_{t}$ is measurable with respect to the sigma algebra $\sigma \bigl (\xi _{0},\ldots \xi _{t}\bigr )$. We write

$$\begin{aligned} x\lhd \sigma (\xi ),\quad&\text { if }x_{t}\text { is measurable with respect to the}\\&\text { sigma algebra }\sigma \bigl (\xi _{0},\ldots \xi _{t}\bigr )\text { for every }t=0,\ldots T. \end{aligned}$$

It follows from the Doob–Dynkin Lemma (cf. Shiryaev [31], Theorem II.4.3]) that a process $x$ is nonanticipative, if there is a measurable function (denoted $x_{t}$ again), such that $x_{t}=x_{t}\left( \xi _{0},\ldots \xi _{t}\right)$, i.e., $x_{t}(\omega )=x_{t}\bigl (\xi _{0}(\omega ),\ldots \xi _{t}(\omega )\bigr )$ for all $t$.

Definition 15

A transport map $T:\,\Xi \rightarrow \tilde{\Xi }$ is nonanticipative if

$$\begin{aligned} T\circ \xi \lhd \sigma (\xi ), \end{aligned}$$

that is, each component $T(\xi )_{t}\in \tilde{\Xi }_{t}$ depends on the vector $(\xi _{0},\ldots \xi _{t})$, but not on $(\xi _{t+1},\ldots \xi _{T})$, i.e, $T(\xi _{0},\ldots \xi _{T})_{t}=T(\xi _{0},\ldots \xi _{t},\xi _{t+1}^{\prime },\ldots \xi _{T}^{\prime })_{t}$ for all $(\xi _{t+1}^{\prime },\ldots \xi _{T}^{\prime })$ and $t=0,\ldots T$.

We consider first the stochastic optimization problem

$$\begin{aligned} \min \left\{ {\mathbb {E}}_{P}\,[Q\left( x,\xi \right) ]:\,x\in {\mathbb {X}},\,x\lhd \sigma (\xi )\right\} , \end{aligned}$$

(15)

where the decision $x$ is measurable with respect to the process $\xi$, $x\lhd \sigma (\xi )$.

The following theorem generalizes an important observation (cf. [26], Theorem 11]) to image measures. This outlines the central role of a nonanticipative transport map in stochastic optimization.

Theorem 16

(Stagewise transportation bound) Let ${\mathbb {X}}$ be convex and the ${\mathbb {R}}$-valued function $\tilde{Q}:{\mathbb {X}}\times \tilde{\Xi }\rightarrow {\mathbb {R}}$ be uniformly convex in $x$, that is,

$$\begin{aligned} \tilde{Q}\bigl ((1-\lambda )x_{0}+\lambda x_{1},\,\tilde{\xi }\bigr )\le (1-\lambda )\tilde{Q}\left( x_{0},\tilde{\xi }\right) +\lambda \tilde{Q}\left( x_{1},\tilde{\xi }\right) \qquad (\tilde{\xi }\in \tilde{\Xi }). \end{aligned}$$

Moreover, let $Q:{\mathbb {X}}\times \Xi \rightarrow {\mathbb {R}}$ be linked with $\tilde{Q}$ by

$$\begin{aligned} \left| Q\bigl (x,\xi \bigr )-\tilde{Q}\left( x,\tilde{\xi }\right) \right| \le c\bigl (\xi ,\tilde{\xi }\bigr )\qquad \text {for all }\xi \in \Xi \text { and }\tilde{\xi }\in \tilde{\Xi }, \end{aligned}$$

(16)

where $c:\Xi \times \tilde{\Xi }\rightarrow {\mathbb {R}}$ is a function (called cost function).

Then for every nonanticipative transport map

$$\begin{aligned} T:\Xi \rightarrow \tilde{\Xi } \end{aligned}$$

it holds that

$$\begin{aligned} \left| \inf _{x\lhd \sigma \left( \xi \right) }{\mathbb {E}}_{P}\,Q\bigl (x(\xi ),\,\xi \bigr )-\inf _{\tilde{x}\lhd \sigma (\tilde{\xi })}{\mathbb {E}}_{P^{T}}\tilde{Q}\left( \tilde{x}\left( \tilde{\xi }\right) ,\tilde{\xi }\right) \right| \le {\mathbb {E}}_{P}\,c\bigl (\xi ,T(\xi )\bigr ). \end{aligned}$$

(17)

Remark 17

Equation (17) relates the problem (15), the central problem of stochastic optimization, with another stochastic optimization problem on the image measure $P^{T}$. The problem on $P^{T}$ may have a different objective ($\tilde{Q}$ instead of $Q$), but it is easier to solve, as it is reduced to the simpler probability space with pushforward measure $P^{T}$ instead of $P$.

The right hand side of (17), ${\mathbb {E}}_{P}\,c\bigl (\xi ,T(\xi )\bigr )$, is notably not a distance, but an expectation of the cost function $c$ in combination with the transport map $T$.

Remark 18

In a typical application of Theorem 16 one has that $\tilde{\Xi }\subset \Xi$ and $\tilde{Q}(\cdot )=Q(\cdot )$. Further, $c\bigl (\xi ,\tilde{\xi }\bigr )=L\cdot \mathsf {d}\bigl (\xi ,\tilde{\xi }\bigr )$, where $\mathsf {d}$ is a distance on $\Xi \times \Xi$ and $L$, by means of (16), is a Lipschitz constant for the objective function $Q$.

Proof of Theorem 16

First, let $\tilde{x}$ be any feasible policy with $\tilde{x}\lhd \sigma (\tilde{\xi })$, that is, $\tilde{x}_{t}=\tilde{x}_{t}\left( \tilde{\xi }_{0},\ldots \tilde{\xi }_{t}\right)$ for all $t$. It follows from the measurability of the transport map $T$ that the derived policy $x:=\tilde{x}\circ T$ is nonanticipative, i.e., $x\lhd \sigma (\xi )$. By relation (16) it holds for the policy $x$ that

$$\begin{aligned} {\mathbb {E}}Q\left( x(\xi ),\xi \right) ={\mathbb {E}}Q\bigl (\tilde{x}(T(\xi )),\xi \bigr )\le {\mathbb {E}}\tilde{Q}\bigl (\tilde{x}(T(\xi )),T(\xi )\bigr )+{\mathbb {E}}c\bigl (\xi ,T(\xi )\bigr ), \end{aligned}$$

and by change of variables thus

$$\begin{aligned} {\mathbb {E}}Q\left( x(\xi ),\xi \right) \le {\mathbb {E}}_{P^{T}}\tilde{Q}\left( \tilde{x}(\tilde{\xi }),\tilde{\xi }\right) +{\mathbb {E}}c\left( \xi ,T(\xi )\right) . \end{aligned}$$

One may pass to the infimum with respect to $\tilde{x}$ and it follows, as $x=\tilde{x}\circ T\lhd \sigma (\xi )$, that

$$\begin{aligned} \inf _{x\lhd \sigma (\xi )}{\mathbb {E}}Q\left( x(\xi ),\xi \right)\le & {} \inf _{\tilde{x}\lhd \sigma (\tilde{\xi })}{\mathbb {E}}_{P^{T}}\tilde{Q}\left( \tilde{x}(\tilde{\xi }),\tilde{\xi }\right) +{\mathbb {E}}c\left( \xi ,T(\xi )\right) . \end{aligned}$$

(18)

For the converse inequality suppose that a policy $x\lhd \sigma (\xi )$ is given. Define

$$\begin{aligned} \tilde{x}:={\mathbb {E}}\left( x|T\right) ,\text { i.e., }\tilde{x}_{t}(\tilde{\xi }):={\mathbb {E}}\left( x_{t}|\,T_{t}(\cdot )=\tilde{\xi }\right) \end{aligned}$$

(Figure 1 visualizes the domain and codomain of this random variable) and note that $\tilde{x}\lhd \sigma (T(\xi ))$ by construction and as $T$ is nonanticipative.

As the function $\tilde{Q}$ is convex it follows from Jensen’s inequality, conditioned on $\left\{ T(\cdot )=\tilde{\xi }\right\}$, that

$$\begin{aligned} \tilde{Q}\left( \tilde{x}\left( \tilde{\xi }\right) ,\tilde{\xi }\right)= & {} \tilde{Q}\left( {\mathbb {E}}\left( x|T\right) \left( \tilde{\xi }\right) ,\tilde{\xi }\right) \\= & {} \tilde{Q}\left( {\mathbb {E}}\left( x(\xi )|\,T(\xi )=\tilde{\xi }\right) ,\tilde{\xi }\right) \\\le & {} {\mathbb {E}}\left( \tilde{Q}\left( x(\xi ),\tilde{\xi }\right) \Bigr |\,T(\xi )=\tilde{\xi }\right) . \end{aligned}$$

By assumption (16) linking $Q$ and $\tilde{Q}$ it holds further that

$$\begin{aligned} \tilde{Q}\left( \tilde{x}\left( \tilde{\xi }\right) ,\tilde{\xi }\right)\le & {} {\mathbb {E}}\left( \tilde{Q}\left( x(\xi ),\tilde{\xi }\right) \Bigr |\,T(\xi )=\tilde{\xi }\right) \\= & {} {\mathbb {E}}\left( \tilde{Q}\bigl (x(\xi ),T(\xi )\bigr )\Bigr |\,T(\xi )=\tilde{\xi }\right) \\\le & {} {\mathbb {E}}\left( Q\bigl (x(\xi ),T(\xi )\bigr )+c\bigl (\xi ,T(\xi )\bigr )\Bigr |\,T(\xi )=\tilde{\xi }\right) \\= & {} {\mathbb {E}}\left( Q\bigl (x(\xi ),T(\xi )\bigr )\Bigr |\,T(\xi )=\tilde{\xi }\right) +{\mathbb {E}}\left( c\bigl (\xi ,T(\xi )\bigr )\Bigr |\,T(\xi )=\tilde{\xi }\right) , \end{aligned}$$

and by taking expectations with respect to the measure $P^{T}$ it follows that

$$\begin{aligned} {\mathbb {E}}_{P^{T}}\tilde{Q}\left( \tilde{x}\left( \tilde{\xi }\right) ,\tilde{\xi }\right) \le {\mathbb {E}}\,Q\bigl (x(\xi ),T(\xi )\bigr )+{\mathbb {E}}\,c\bigl (\xi ,T(\xi )\bigr ). \end{aligned}$$

Recall that $x\lhd \sigma (\xi )$ was arbitrary, by taking the infimum it follows thus that

$$\begin{aligned} \inf _{\tilde{x}\lhd \sigma (T((\xi ))}{\mathbb {E}}_{P^{T}}\tilde{Q}\left( \tilde{x}\left( \tilde{\xi }\right) ,\tilde{\xi }\right) \le \inf _{x\lhd \sigma (\xi )}{\mathbb {E}}\,Q\bigl (x(\xi ),\,\xi \bigr )+{\mathbb {E}}\,c\bigl (\xi ,T(\xi )\bigr ). \end{aligned}$$

Together with (18) this is the assertion. $\square$

Fig. 1

Left the measurable transport map $T$, mapping trajectories $\xi$ to $\tilde{\xi }=T(\xi )$. Right the diagram displays the domain and codomain of the functions involved. The diagram is commutative on average

4.3 Approximation by means of a pushforward measure

In this section we construct a tree by establishing a transport map $T:\Xi \rightarrow \tilde{\Xi }$ with the properties of Definition 15. The algorithm is based on stochastic approximation and extends Algorithm 3, as well as an algorithm contained in Pflug [24]. We do not require more than a sample of trajectories (i.e., scenarios). The scenarios may result from observations or from simulation.

Algorithm 5 is the tree equivalent of Algorithm 3. It uses a sample of trajectories to produce a tree approximating the process $\xi$. The algorithm further provides the estimate ${\mathbb {E}}\,c(\xi ,T(\xi ))$, which describes the quality of the approximation of the tree $T\circ \xi$ in comparison with the original process $\xi$.

Example 19

To demonstrate Algorithm 5 we consider a standard Gaussian random walk in three stages first. The tree with bushiness $\left( 10,5,2\right)$, found after 1000 and 100,000 samples, is displayed in Fig. 2 (left plots). The probability distribution of the leaves is annotated in the plots. The final distribution of the initial process is $N(0,3)$ (Fig. 2a). The Gaussian walk and the tree are at a distance of $\bigl ({\mathbb {E}}\mathsf {d}(\xi ,T(\xi ))^{2}\bigr )^{1/2}\simeq 0.084$, where we have employed the usual Euclidean distance and $r=2$.

Fig. 2

Trees produced by Algorithm 5 after 1000 (Figure 2b) and 100,000 (Fig. 2c) samples. Annotated is a density plot of the probability distribution at the final stage. a 1000 sample paths of the standard Gaussian random walk and the (non-Markovian) running maximum process. b Trees with bushiness $\left( 10,5,2\right)$ and $\left( 3,3,3,2\right)$ approximating the process in Fig. 2a. c The transportation bound to the underlying Gaussian process is $0.084$, the transportation bound to the non-Markovian running maximum process is 0.13

The process which we also consider is the running maximum

$$\begin{aligned} M_{t}:=\max \left\{ \sum _{i=1}^{t^{\prime }}\xi _{i}:\,t^{\prime }\le t\right\} \text { with }\xi _{i}\sim N(0,1)\text { i.i.d}. \end{aligned}$$

(20)

Note, that the running maximum is not a Markovian process. The results of Algorithm 5 are displayed in Fig. 2 (right) for a bushiness of $(3,3,3,2)$. The running maximum process and the tree in Fig. 2c have distance $\bigl ({\mathbb {E}}\,\mathsf {d}(\xi ,T(\xi ))^{2}\bigr )^{1/2}\simeq 0.13$.

5 The nested distance

In the previous section we have proposed an algorithm to construct an approximating tree from observed sample paths by stochastic approximation. It is an essential observation that the algorithm proposed establishes a measure $\tilde{P}$ on the second process which is induced by a nonanticipative transport map $T$, $\tilde{P}=P^{T}$. It is a significant advantage of Theorem 16 that the bound

$$\begin{aligned} {\mathbb {E}}\,c\bigl (\xi ,T(\xi )\bigr ) \end{aligned}$$

(21)

in equation (17) is very cheap to compute (Eq. (19) in Algorithm 5, e.g., provides ${\mathbb {E}}\,c\bigl (\xi ,T(\xi )\bigr )$ as a byproduct). However, the algorithm is not designed for a pre-specified measure $\tilde{P}$ on the second process.

In the general situation the quantity (21) is not symmetric, that is, there does not exist a transportation map $\tilde{T}$, say, such that ${\mathbb {E}}\,c\bigl (\xi ,T(\xi )\bigr )={\mathbb {E}}\,c\bigl (\tilde{T}(\tilde{\xi }),\tilde{\xi })\bigr )$. For this (21) does not extend to a distance of processes, as is the case for the Wasserstein distance for probability measures.

The nested distance was introduced to handle the general situation. In what follows we recall the definition and cite the results, which are essential for tree generation. Then we provide algorithms again to construct approximating trees, which are close in the nested distance.

Definition 20

(The nested distance, cf. [25]) Assume that two probability models

$$\begin{aligned} {\mathbb {P}}=\left( \Omega ,\left( {\mathcal {F}}_{t}\right) ,P,\xi \right) \text { and }\tilde{{\mathbb {P}}}=\left( \tilde{\Omega },\left( \tilde{{\mathcal {F}}}_{t}\right) ,P,\tilde{\xi }\right) \end{aligned}$$

are given, such that for $u\in \Omega$ and $v\in \tilde{\Omega }$ a distance $\mathsf {d}(u,v)$ is defined by (14). The nested distance of order $r\ge 1$ is the optimal value of the optimization problem

$$\begin{aligned} \begin{array}{l} \text {minimize }\\ \text {(in }\pi ) \end{array}&\left( \iint \mathsf {d}\left( u,v\right) ^{r}\pi \left( du,dv\right) \right) ^{1/r}\nonumber \\ \text {subject to }&\pi \left( A\times \tilde{\Omega }\mid {\mathcal {F}}_{t}\otimes \tilde{{\mathcal {F}}}_{t}\right) =P\left( A\mid {\mathcal {F}}_{t}\right) \qquad \left( A\in {\mathcal {F}}_{t},\,t=0,\ldots T\right) \text { and}\nonumber \\&\pi \left( \Omega \times B\mid {\mathcal {F}}_{t}\otimes \tilde{{\mathcal {F}}}_{t}\right) =\tilde{P}\left( B\mid \tilde{{\mathcal {F}}}_{t}\right) \qquad \left( B\in \tilde{{\mathcal {F}}}_{t},\,t=0,\ldots T\right) , \end{aligned}$$

(22)

where the infimum in (22) is among all bivariate probability measures $\pi \in \mathcal {P}\left( \Omega \times \tilde{\Omega }\right)$ which are measures for ${\mathcal {F}}_{T}\otimes \tilde{{\mathcal {F}}}_{T}$. Its optimal value – the nested, or multistage distance – is denoted by

$$\begin{aligned} \mathsf {dl}_{r}\left( {\mathbb {P}},\tilde{{\mathbb {P}}}\right) . \end{aligned}$$

By (14) the distance depends on the image measures induced by $\xi _{t}:\Omega \rightarrow {\mathbb {R}}^{m}$ and $\tilde{\xi }:\tilde{\Omega }\rightarrow {\mathbb {R}}^{m}$ on ${\mathbb {R}}^{m}$.

It can be shown by counterexamples that the optimal measure $\pi$ in (22) cannot be described by a transport map in general.

The following theorem is the counterpart of Theorem 16 for general measures and proved in [26]. However, the nested distance can be applied to reveal the same type of result.

Theorem 21

Let ${\mathbb {P}}=\left( \Omega ,\left( {\mathcal {F}}_{t}\right) ,P,\xi \right)$ and $\tilde{{\mathbb {P}}}=\left( \tilde{\Omega },\left( \tilde{{\mathcal {F}}}_{t}\right) ,P,\tilde{\xi }\right)$ be two probability models. Assume that ${\mathbb {X}}$ is convex and the cost function $Q$ is convex in $x$ for any fixed $\xi$. Moreover let $Q$ be uniformly Hölder continuous in $\xi$ with constant $L_{\beta }$ and exponent $\beta$, that is

$$\begin{aligned} \left| Q(x,\xi )-Q(x,\tilde{\xi })\right| \le L_{\beta }\left( \sum _{t=1}^{T}d_{t}(\xi _{t},\tilde{\xi }_{t})\right) ^{\beta } \end{aligned}$$

for all $x\in {\mathbb {X}}$. Then the optimal value function inherits the Hölder constants with respect to the nested distance,

$$\begin{aligned} \begin{vmatrix}\begin{array}{l} \min \left\{ {\mathbb {E}}_{P}\,[Q\left( x,\xi \right) ]:x\in {\mathbb {X}},\ x\lhd {\mathfrak {F}},\,{\mathbb {P}}=\left( \Omega ,{\mathfrak {F}},P,\xi \right) \right\} \\ \qquad -\min \left\{ {\mathbb {E}}_{\tilde{p}}\,[Q\left( x,\tilde{\xi }\right) ]:x\in {\mathbb {X}},\ x\lhd \tilde{{\mathfrak {F}}},\,\mathbb {\tilde{{\mathbb {P}}}}=\left( \tilde{\Omega },\tilde{{\mathfrak {F}}},\tilde{P},\tilde{\xi }\right) \right\} \end{array}\end{vmatrix}\le L_{\beta }\,\mathsf {dl}_{r}({\mathbb {P}},\tilde{{\mathbb {P}}})^{\beta } \end{aligned}$$

(23)

for any $r\ge 1$. This bound cannot be improved.

The relation between the nested distance and the single period Wasserstein distance. The nested distance $\mathsf {dl}_{r}({\mathbb {P}},\tilde{{\mathbb {P}}})$ can be bounded by the Wasserstein distances of the conditional probabilities as is described in Theorem 23 below. It uses the notion of the $K$-Lipschitz property.

Definition 22

( $K$-Lipschitz property) Let $P$ be a probability on ${\mathbb {R}}^{mT}$, dissected into transition probabilities $P_{1},\ldots ,P_{T}$ on ${\mathbb {R}}^{m}$. We say that $P$ has the $K$ -Lipschitz property for $K=(K_{1},\ldots ,K_{T-1})$, if the transitional probability measures satisfy

$$\begin{aligned} \mathsf {d}_{r}\left( P_{t+1}(\cdot |u^{t}),\,P_{t+1}(\cdot |v^{t})\right) \le K_{t}\,\mathsf {d}\bigl (u^{t},v^{t}\bigr ) \end{aligned}$$

(24)

for all $u^{t},\,v^{t}\in {\mathbb {R}}^{m(t-1)}$ and $t=1,\ldots ,T-1$.

Theorem 23

(Stagewise transportation distance) Suppose that the probability measure $P$ on ${\mathbb {R}}^{mT}$ fulfills a $(K_{1},\ldots ,K_{T-1})$-Lipschitz property and that the conditional distributions of $P$ and $\tilde{P}$ satisfy

$$\begin{aligned} \mathsf {d}_{r}(P_{1},\tilde{P}_{1})\le \epsilon _{1} \end{aligned}$$

and

$$\begin{aligned} \mathsf {d}_{r}\left( P_{t+1}(\cdot |v^{t}),\,\tilde{P}_{t+1}(\cdot |v^{t})\right) \le \epsilon _{t+1}\qquad \text{ for } \text{ all } v^{t}\text { and }t=0,\ldots ,T-1. \end{aligned}$$

(25)

Then the nested distance is bounded by

$$\begin{aligned} \mathsf {dl}_{r}({\mathbb {P}},\tilde{{\mathbb {P}}})\le \sum _{t=1}^{T-1}\epsilon _{t}\cdot \prod _{s=t}^{T}(1+K_{s}). \end{aligned}$$

(26)

Proof

The proof is contained in [19]. $\square$

Remark 24

As variant of the results one may consider distorted distances such as the Fortet–Mourier distance (cf. Rachev [28] or Römisch [29]). Küchler [15] combines a nonanticipativity condition for the approximating process (a pushforward approximation) and a Lipschitz property for the conditional processes (such as (24) in Theorem 23 below) to establish a stability result similar to Theorem 16.

The previous sections address approximations of a probability measure, where the quality of the approximation is measured by the Wasserstein distance. The algorithms described in Sect. 3 can be employed at every node separately to build the tree. To apply the general result (26) it is necessary to condition on the values of the previous nodes (cf. (25)), which have already been fixed in earlier steps of the algorithm. To apply the algorithms described in Sect. 3 in connection with Theorem 23 it is thus necessary that the conditional probability measure is available to compute (25), that is, samples from

$$\begin{aligned} F_{t+1}\left( \cdot |\,\xi _{t},\xi _{t-1},\ldots ,\xi _{0}\right) \end{aligned}$$

can be drawn.

We outline this approach in the next section for a fixed branching structure of the tree, and in the following section with an adaptive branching structure to meet a prescribed approximation quality.

5.1 Fixed branching structure

Algorithm 6 elaborates on generating scenario trees in further detail. The trees are constructed to have $b_{t}$ successor nodes at each node at level $t$, the vector ($b_{1},\ldots b_{T})$ is the bushiness of the tree.

The algorithm based on Theorem 23 described in this and the following section have been implemented in order to demonstrate their behavior by using the following example.

Example 25

Consider the Markovian process

$$\begin{aligned} \xi _{0}=2,\quad \xi _{t+1}=\xi _{t}^{1-\beta _{t}}\cdot e^{\eta _{t}}, \end{aligned}$$

(28)

where $\beta _{0}=0.62$, $\beta _{1}=0.69$, $\beta _{2}=0.73$, $\beta _{3}=0.75$ and $\beta _{4}=0.77$, and

$$\begin{aligned} \eta _{0}\sim \eta _{2}\sim \eta _{4}\sim \mathcal {N}\left( 0,\,0.5\beta _{t}^{2}\right) \text { and }\eta _{0}\sim \eta _{2}\sim \mathcal {N}\left( 0,\,0.2\beta _{t}^{2}\right) . \end{aligned}$$

Notice that the distribution, given the past, is explicitly available by (28), although the conditional variance depends heavily on $t$.

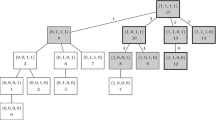
Figure 3 displays some trajectories of the process (28). A binary tree, approximating the process (28), is constructed by use of Algorithm 6. Figure 4 displays the tree structure, as well as the approximating binary tree.

Fig. 3

1000 trajectories of the process (28) in Example 25

Fig. 4

A binary tree generated by Algorithm 6 approximating process (28), Example 25. a The structure of the binary tree. b The approximating process

5.2 Tree, meeting a prescribed approximation precision

Assume that the law of the process to be approximated satisfies the $K$-Lipschitz property introduced in Definition 22. Theorem 23 then can be used to provide an approximation of the initial process in terms of the nested distance up to a prescribed precision. Algorithm 7 outlines this approach. Again, as in the preceding algorithm, it is necessary to have samples of the distribution $F_{t+1}\left( \cdot |\xi _{t},\xi _{t-1},\ldots ,\xi _{0}\right)$ available, given that the past is revealed up to the present stage $t$.

The algorithm is demonstrated again for the process (28) in Example 25. Results are displayed in Fig. 5.

Fig. 5

A tree, dynamically generated by Algorithm 7, approximating the process (28). The maximal stagewise distances were 0.30, 0.15, 0.30, 0.30 and 0.40. The approximating tree process has 390 nodes and 224 leaves. a The branching structure of the tree with bushiness $(3,4,4,2)$. b The approximating process

6 Summary

This paper addresses scenario tree generation, which is of interest in many economic and managerial situations, in particular for stochastic multistage optimization.

It is demonstrated that techniques, which are used to approximate probability measures, can be extended to generate approximating trees, which model stochastic process in finite stages and states.

Various algorithms are shown first to approximate probability measures by discrete measures. These algorithms are combined then at a higher level to provide tree approximations of stochastic processes. The generated trees meet a quality criterion, which is formulated in terms of the nested distance. The nested distance is the essential distance to compare stochastic scenario processes for stochastic optimization.

The algorithms presented require sampling according to probability distributions based on the past evolutions of the process. Several examples and charts demonstrated the quality of the solutions.

Appendix: Conditional method for multivariate distributions

To generate instances from a multivariate distribution (random vectors) with cdf $F\left( z_{1},\ldots z_{m}\right)$ one may employ rejection sampling, or the ratio of uniforms method, or generate the vector component by component by proceeding as follows:

• (i) Generate $Z_{1}$ from $F_{1}\left( z\right)$, where $F_{1}(z_{1})=F\left( z_{1},\infty ,\ldots \infty \right)$ is the first marginal. This can be accomplished by solving

  $$\begin{aligned} U_{1}=F_{1}(Z_{1}) \end{aligned}$$

  (the probability integral transform, where $U_{1}$ is a uniformly distributed random variable) or by rejection sampling;

• (ii) Given the random vector up to dimension $i-1$ one may generate $Z_{i}$ conditionally on $\left( Z_{1},\ldots Z_{i-1}\right)$ by solving

  $$\begin{aligned} U_{i}=F_{i}\left( z_{i}|\,Z_{1},\ldots Z_{i-1}\right) =\frac{F\left( Z_{1}\ldots ,Z_{i-1},x_{i},\infty ,\ldots \infty \right) }{F\left( Z_{1},\ldots Z_{i-1},\infty ,\ldots \infty \right) }, \end{aligned}$$

  where $U_{i}$ is uniformly distributed, and independent from $U_{1},\ldots U_{i-1}$.