The Feed-Forward Chain as a Filter-Amplifier Motif

Abstract

Hudspeth, Magnasco, and collaborators have suggested that the auditory system works by tuning a collection of hair cells near Hopf bifurcation, but each with a different frequency. An incoming sound signal to the cochlea then resonates most strongly with one of these hair cells, which then informs the auditory neuronal system of the frequency of the incoming signal. In this chapter, we discuss two mathematical issues. First, we describe how periodic forcing of systems near a point of Hopf bifurcation is generally more complicated than the description given in these auditory system models. Second, we discuss how the periodic forcing of coupling identical systems whose internal dynamics is each tuned near a point of Hopf bifurcation leads naturally to successive amplification of the incoming signal. We call this coupled system a feed-forward chain and suggest that it is a mathematical candidate for a motif.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

Introduction

In this chapter, we discuss how the periodic forcing of the first node in a chain of coupled identical systems, whose internal dynamics is each tuned near a point of Hopf bifurcation, can lead naturally to successive amplification of the incoming signal. We call this coupled system a feed-forward chain and suggest that it is a mathematical candidate for a motif [1]. Periodic forcing of these chains was considered experimentally by McCullen et al. [26]. That study contained observations concerning the amplitude response of solutions down the chain and the effectiveness of the chain as a filter amplifier. This chapter sheds light on these observations.

Our observations motivate the need for a theory of periodic forcing of systems tuned near a point of Hopf bifurcation. Given such a system with Hopf frequency ω_H, we periodically force this system at frequency ω _f . The response curve is a graph of the amplitude of the resulting solution as a function of ω _f . In this chapter, we show that the response curve will, in general, be asymmetric and may even have regions of multiple responses when ${\omega }_{f} \approx {\omega }_{\mathrm{H}}$.

This second set of results has implication for certain models of the auditory system, in particular, models of the basilar membrane and attached hair bundles. Several authors [5, 6, 7, 21, 23, 27, 28] model the hair bundles by systems of differential equations tuned near a point of Hopf bifurcation; however, in their models they assume precisely the nongeneric condition that leads to a symmetric response curve. Since asymmetric response curves are seen experimentally, these authors then attempt to explain that the asymmetry follows from coupling of the hair bundles. Although this coupling may be reasonable on physiological grounds, our results show that it is not needed if one were only attempting to understand the observed response curve asymmetry.

Sections “Synchrony-Breaking Hopf Bifurcations” and “Periodic Forcing of Feed-Forward Chains” discuss the feed-forward chain and sections “Periodic Forcing near Hopf Bifurcation” and “Cochlear Modeling” discuss periodic forcing of systems near Hopf bifurcation and the auditory system. The remainder of this introduction describes our results in more detail.

The theory of coupled systems of identical differential equations [31, 16, 15] and their bifurcations [12, 24, 8, 11] singles out one three-cell network for both its simplicity and the surprising dynamics it produces via a synchrony-breaking Hopf bifurcation. We have called that network the feed-forward chain and it is pictured in Fig. 1. Note that the arrow from cell 1 to itself represents self-coupling.

The general coupled cell theory [16] associates to the feed-forward chain a class of differential equations of the form

$$\begin{array}{rcl} \dot{{x}}_{1} & =&f({x}_{1},{x}_{1},\lambda ) \\ \dot{{x}}_{2} & =&f({x}_{2},{x}_{1},\lambda ) \\ \dot{{x}}_{3} & =&f({x}_{3},{x}_{2},\lambda )\end{array}$$

(1)

where ${x}_{j} \in {\mathbf{R}}^{k}$ is the vector of state variables of node j, $\lambda\in \mathbf{R}$ is a bifurcation parameter, and $f :{ \mathbf{R}}^{k} \times {\mathbf{R}}^{k} \times \mathbf{R} \rightarrow {\mathbf{R}}^{k}$. We assume that the differential equations f in each cell are identical, and because of this the synchrony subspace S = { x ₁ = x ₂ = x ₃} is a flow-invariant subspace; that is, a solution with initial conditions in S stays in S for all time. Synchronous equilibria can be expected to occur in such systems and without loss of generality we may assume that such an equilibrium is at the origin; that is, we assume f(0, 0, λ) = 0. Because of the self-coupling in cell 1, each cell receives exactly one input and the function f can be the same in each equation in (1).

Fig. 1

The feed-forward chain

Recall that in generic Hopf bifurcation in a system with bifurcation parameter λ, the growth in amplitude of the bifurcating periodic solutions is of order ${\lambda }^{\frac{1} {2} }$. As reviewed in section “Synchrony-Breaking Hopf Bifurcations” synchrony-breaking Hopf bifurcation leads to a family of periodic solutions whose amplitude grows with the unexpectedly large growth rate of ${\lambda }^{\frac{1} {6} }$ [12, 8]. This growth rate suggests that when the feed-forward chain is tuned near a synchrony-breaking Hopf bifurcation, it can serve to amplify periodic signals whose frequency ω _f is near the frequency of Hopf bifurcation ω_H and dampen signals when ω _f is far from ω_H. This filter-amplifier motif-like behavior is described in section “Periodic Forcing near Hopf Bifurcation”.

Experiments by McCullen et al. [26] with a feed-forward chain consisting of (approximately) identical coupled electronic circuits whose cells are decidedly not in normal form but with sinusoidal forcing confirm the band-pass filter role that a feed-forward chain can assume and the expected growth rates of the output. Additionally, simulations, when the system is in Hopf normal form and the forcing is spiking, also confirm the behavior predicted for the simplified setup. These results are discussed in sections “Simulations” and “Experiments” under “Periodic Forcing of Feed-Forward Chains”, and motivate the need for a more general theory of periodic forcing of systems near Hopf bifurcation. We note that the lack of a general theory is more than just a question of mathematical rigor.

Analysis and simulation of periodic forcing of systems near Hopf bifurcation often assume that the forcing is small simple harmonic or sinusoidal forcing $\epsilon {\mathrm{e}}^{\mathrm{i}{\omega }_{f}t}$ and that the system is in the simplest normal form for Hopf bifurcation (namely, the system is in third order truncated normal form and the cubic term is assumed to be real). A supercritical Hopf bifurcation vector field can always be transformed by a smooth change of coordinates to be in normal form to third order and the cubic term itself can be scaled to be − 1 + iγ. Simulations of a system in normal form for Hopf bifurcation, but with γ≠0 show phenomena not present in the simplest case (see “Simulations” under “Periodic Forcing near Hopf Bifurcation”). In particular, the amplitude of the response as a function of ω _f can be asymmetric (if γ≠0) and have a region of multiple solutions (if | γ | is large enough). Asymmetry and multiplicity have been noted by several authors. Bogoliubov and Mitropolsky [3] analyze the sinusoidally forced Duffing equation and find multiplicity as the frequency of the forcing is varied; Jordan and Smith [10] also analyze the forced Duffing equation and find multiplicity as the amplitude of the forcing is varied; and Montgomery et al. [27] see asymmetry in a forced system near Hopf bifurcation.

In section “Asymmetry and Multiplicity in Response Curve” we show that asymmetry in the response curve occurs as ω _f is varied whenever γ≠0 and that there are precisely two kinds of response curves. In Theorem 1 we use singularity theoretic methods to prove that multiple solutions occur in a neighborhood of the Hopf bifurcation precisely when $\vert \gamma \vert> \sqrt{3}$.

Additionally, when ω _f is sufficiently close to ω _H , Kern and Stoop [23] and Eguíluz et al. [7] together show that with a truncated normal form system and harmonic forcing the amplitude of the resulting periodic solution is of order ${\epsilon }^{\frac{1} {3} }$. We make this result more precise in section “Scalings of Solution Amplitudes”. Consequently, in the feed-forward chain the amplitude of the periodic forcing can be expected to grow as ${\epsilon }^{\frac{1} {3} }$ in the second cell and ${\epsilon }^{\frac{1} {9} }$ in the third cell. This expectation is observed in the simulations in section “Simulations” under “Periodic Forcing of Feed-Forward Chains” even when the forcing is spiking. A general theory for the study of periodic solutions occurring in a periodically forced system near a point of Hopf bifurcation is being developed in [34].

The efficiency of band-pass filters is often measured by the Q-factor. We introduce this concept in section “Q-factor” and show, in forced normal form systems, that the Q-factor scales linearly with the Hopf frequency. We verify this point with simulations and note the perhaps surprising observation that spiking forcing seems to lead to higher Q factors than does sinusoidal forcing.

In recent years many proposed models for the auditory system have relied on the periodic forcing of systems near points of Hopf bifurcation, and a general theory for periodic forcing of such systems would have direct application in these models. In particular, Hudspeth and collaborators [18, 19, 6, 7] have considered models for the cochlea that consist of periodically forced components that are tuned near Hopf bifurcation. We discuss these models in section “Cochlear Modeling”. In particular, we note that an asymmetry in the experimentally obtained response curves from cochlea is consistent with what would have been obtained in the models if the cubic term in the Hopf bifurcation was complex. Biophysically based cochlear models are sufficiently complicated that asymmetry could be caused by many factors. To our knowledge, multiple solutions in the cochlear response curve have not been observed; nevertheless, in section “Hopf Models of the Auditory System”, we speculate briefly on the possible meaning of such multiplicity. In section “Two-Frequency Forcing”, we briefly discuss some expectations for two-frequency forcing that are based on simulations.

Synchrony-Breaking Hopf Bifurcations

We begin with a discussion of Hopf bifurcations that can be expected in systems of the form (1). The coordinates in f(u, v, λ) are arranged so that u is the vector of internal cell phase space coordinates and v is the vector of coordinates in the coupling cell. Thus, the k ×k matrix α = f _u (0, 0, 0) is the linearized internal dynamics and the k ×k matrix β = f _v (0, 0, 0) is the linearized coupling matrix. The Jacobian matrix for (1) is

$$J = \left [\begin{array}{ccccccccccccccccccccccccr} \alpha+ \beta& \quad 0 & \quad 0 \\ \beta&\quad \alpha & \quad 0 \\ 0 &\quad \beta&\quad \alpha\end{array} \right ].$$

(2)

Synchrony-breaking bifurcations correspond to bifurcations where the center subspace of J does not intersect the synchrony subspace S. Note that for $y \in {\mathbf{R}}^{k}$

$$J\left [\begin{array}{ccccccccccccccccccccccccr} y\\ y \\ y \end{array} \right ] = \left [\begin{array}{ccccccccccccccccccccccccr} (\alpha+ \beta )y \\ (\alpha+ \beta )y \\ (\alpha+ \beta )y \end{array} \right ].$$

Thus, the matrix of J | S is just α + β and a synchrony-breaking bifurcation occurs if some eigenvalue of J has zero real part and no eigenvalue of α + β has zero real part. We focus on the case where the synchrony-breaking bifurcation occurs from a stable synchronous equilibrium; that is, we assume:

• (H1) All eigenvalues of α + β have negative real part.

The lower diagonal block form of J shows that the remaining eigenvalues of J are precisely the eigenvalues of α repeated twice. The generic existence of double eigenvalues would be a surprise were it not for the the restrictions placed on J by the network architecture pictured in Fig. 1. Synchrony-breaking Hopf bifurcation occurs when

• (H2) α has simple purely imaginary eigenvalues ± ω_Hi, where ω_H > 0, and all other eigenvalues of α have negative real part.

Fig. 2

Periodic solution near a synchrony-breaking Hopf bifurcation in the feed-forward chain. The first coordinate in each cell is plotted. Cell 1 is constant at 0 (dotted curve); cell 2 is the smaller signal (dashed curve); and cell 3 is the larger signal (solid curve) (see Figure 12 in [12])

The real part restriction on the remaining eigenvalues just ensures that bifurcation occurs from a stable equilibrium. In fact, in this chapter, we only consider the case where the internal dynamics in each cell is two-dimensional, that is, we assume k = 2.

It was observed in [12] and proved in [8] that generically synchrony-breaking Hopf bifurcations lead to families of periodic solutions ${x}^{\lambda }(t) = (0,{x}_{2}^{\lambda }(t),{x}_{3}^{\lambda }(t))$, where the cell 2 amplitude $\vert {x}_{2}^{\lambda }\vert$ grows at the expected rate of ${\lambda }^{\frac{1} {2} }$ and the cell 3 amplitude $\vert {x}_{3}^{\lambda }\vert$ grows at the unexpected rate of ${\lambda }^{\frac{1} {6} }$. Thus, near bifurcation, the amplitude of the third cell oscillation is much bigger than the amplitude of the second cell oscillation. An example of a periodic solution obtained by simulation of such a coupled-cell system near a point of synchrony-breaking Hopf bifurcation is given in Fig. 2.

The large growth in cell 3 can be understood as a result of resonance in a nonlinear system. To see this, observe that assumption (H1) implies that x ₁ = 0 is a stable equilibrium for the first equation in (1). Thus, the asymptotic dynamics of the second cell is governed by the system of differential equations

$$\dot{{x}}_{2} = f({x}_{2},0,\lambda ).$$

(3)

Assumption (H2) implies that the system (3) undergoes a standard Hopf bifurcation at λ = 0. In addition, we assume

• (H3) (3) undergoes a generic supercritical Hopf bifurcation at λ = 0.

The consequence of assumption (H3) is that for λ > 0 the system (3) has a unique small amplitude stable periodic solution ${x}_{2}^{\lambda }(t)$ whose amplitude grows at the expected rate ${\lambda }^{\frac{1} {2} }$ and whose frequency is approximately ω_H.

It follows from (H3) that the asymptotic dynamics of the cell 3system of differential equations reduces to the periodically forced system

$$\dot{{x}}_{3} = f({x}_{3},{x}_{2}^{\lambda }(t),\lambda).$$

(4)

Since the system $\dot{{x}}_{3} =f({x}_{3},0,\lambda )$, which is identicalto (3), is operating near a Hopf bifurcation with frequency ω_H and the periodic forcing itself has frequency near ω_H; it follows that (4) is being forced near resonance. Therefore, it is not surprising that the amplitude of cell 3 is greater than that of cell 2. It is not transparent, however, that cell 3 will undergo stable periodic oscillation and that the growth of the amplitude of that periodic solution will be ${\lambda }^{\frac{1} {6} }$. These facts are proved in [12, 8].

Remark 1.

It is natural to ask what happens at synchrony-breaking Hopf bifurcation if extra cells are added to the feed-forward chain. The answer is simple: periodic solutions are found whose cell j amplitude grows at a rate that is the cube root of the growth in the amplitude of cell j − 1; that is, the amplitude of cell 4 grows at the rate ${\lambda }^{ \frac{1} {18} }$, etc.

Remark 2.

It was shown in [12] that the periodic solution in (1), that we have just described can itself undergo a secondary Hopf bifurcation to a quasiperiodic solution (see Fig. 3). This observation leads naturally to questions of frequency locking and Arnold tongues, which are discussed in Broer and Vegter [4].

Periodic Forcing of Feed-Forward Chains

An important characteristic of a network motif is that it performs some function [1]. Numerical simulations and experiments [26] with identical coupled circuits support the notion that the feed-forward chain can act as an efficient filter-amplifier,** and hence be a motif. However, the general theoretical results that support this assertion have been proved only under restrictive assumptions. It this section, we present numerical and experimental evidence in favor of the feed-forward chain being a motif.

Fig. 3

([12, Figure 13]) Quasiperiodic solution near a secondary bifurcation from a periodic solution obtained by synchrony-breaking Hopf bifurcation in (1)

We assume that the feed-forward chain in Fig. 1 is modified so that a small amplitude ε periodic forcing of frequency ω _f is added to the coupling in the first cell (see Fig. 4). We assume further that there is a bifurcation parameter λ for the internal cell dynamics that is tuned near a point of Hopf bifurcation. The question we address is: What are the amplitudes of the responses in cells 2 and 3 as a function of the forcing frequency ω _f ? Due to resonance that response should be large when the forcing frequency is near the Hopf frequency and small otherwise.

Simulations

The general form of the differential equations for the periodically forced feed-forward chain is

$$\begin{array}{rcl} \dot{{x}}_{1} & =&f({x}_{1},{x}_{1} + \epsilon g({\omega }_{f}t),\lambda ) \\ \dot{{x}}_{2} & =&f({x}_{2},{x}_{1},\lambda ) \\ \dot{{x}}_{3} & =&f({x}_{3},{x}_{2},\lambda ) \end{array}$$

(5)

where ${x}_{j} \in {\mathbf{R}}^{k}$ is the phase variable of cell j, $g : \mathbf{R} \rightarrow {\mathbf{R}}^{k}$ is a 2π periodic forcing function, and λ is a bifurcation parameter for a Hopf bifurcation.

Fig. 4

The feed-forward chain

Fig. 5

First coordinate of time series of 2π-periodic forcings. (Left) Simple harmonic forcing $\cos t$. (Right) Spike forcing obtained from the Fitzhugh–Nagumo equations (7).

To proceed with the simulations we need to specify f and g. Specifically, we assume that the cell dynamics satisfy:

• The internal cell phase space is two-dimensional and identified with $\mathbf{C}$,

• The internal cell dynamics is in truncated normal form for Hopf bifurcation,

• The Hopf bifurcation is supercritical so that the origin is stable for λ < 0,

• The cubic term in this normal form is real, and

• The coupling is linear.

In addition, we normalize the cubic term to be − 1 and simplify the coupling to be − y; that is, we assume

$$f(z,y,\lambda ) = (\lambda+ {\omega }_{\mathrm{H}}\mathrm{i} -\vert z{\vert }^{2})z - y$$

(6)

where $z,y \in \mathbf{C}$. We assume that λ < 0 is small so that the internal dynamics is tuned near the point of Hopf bifurcation.

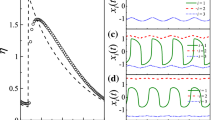
We will perform simulations with two types of forcing: simple harmonic and spiking (see Fig. 5). In simple harmonic forcing g(t) = e^it. In spike forcing g is obtained numerically as a solution to the Fitzhugh–Nagumo equations

$$\begin{array}{rcl} \dot{v}& =&6.4 - 120{m}^{3}h(v - 115) - 36{n}^{4}(v + 12) - 0.3(v - 10.5989), \\ \dot{n}& =&{\alpha }_{n}(1 - n) - {\beta }_{n}n,\end{array}$$

(7)

where

$$\begin{array}{ll@{\quad }l} h = 0.8 - n &m = {\alpha }_{m}/({\alpha }_{m} + {\beta }_{m}) \quad &{\alpha }_{m} = 0.1(25 - v)\mathrm{{e}}^{1-(25-v)/10} \\ {\beta }_{m} = 4\mathrm{{e}}^{-v/18} & {\alpha }_{n} = 0.01(10 - v)\mathrm{{e}}^{1-(10-v)/10}\quad &{\beta }_{n} = 0.125\mathrm{{e}}^{-v/80}\end{array}$$

To obtain g(t) we normalize (v(t), n(t)) so that it has mean zero and diameter 2. The first coordinate of the time series for the spiking forcing is shown in Fig. 5 (right). This time series is compared to simple harmonic forcing in Fig. 5 (left).

Recall that for sufficiently small ε, periodic forcing of amplitude ε, of a system of ODEs near a stable equilibrium, always produces an order ε periodic response. The frequency of the response equals that of the forcing. Hence, (H1) implies that the periodic output x ₁(t) from cell 1 will be of order ε with frequency ω _f .

The periodic output x ₁(t) is fed into cell 2. Although λ < 0 implies that the origin in the cell 2 equation is stable, the fact that λ is near a bifurcation point implies that the rate of attraction of that equilibrium will be small. Thus, only if ε is very small will the periodic output of cell 2 be of order ε.

Fig. 6

Amplitudes of cells 1 (dotted curve), 2 (dashed curve) and 3 (solid curve) as a function of forcing frequency; λ = − 0. 01, ε = 0. 03, ω_H = 1, 0. 7 ≤ ω _f ≤ 1. 3. (Left) simple harmonic forcing; (right) spike forcing

Because of resonance, we expect that the amplitude of x ₂(t) will be large when ω _f is near ω_H. Indeed, Kern and Stoop [23] observe that when the differential equation f is (6) with $\epsilon> \vert \lambda {\vert }^{\frac{3} {2} }$, then the growth of the periodic output will be of order ${\epsilon }^{\frac{1} {3} }$. We revisit this point in section “Periodic Forcing near Hopf Bifurcation” when we discuss some of the theory behind the amplification. Moreover, we can expect the amplitude of x ₃(t) to be even larger in this range; that is, we can expect the amplitude of cell 3 to grow at the rate ${\epsilon }^{\frac{1} {9} }$.

To illustrate these statements we perform the following simulation. Fix ε > 0 and λ < 0, and plot the amplitudes of the periodic states in cells 1, 2, and 3 as a function of the forcing frequency ω _f . The results are given in Fig. 6. Note that the input forcing is amplified when ${\omega }_{f} \approx {\omega }_{\mathrm{H}}$ and that the qualitative results do not depend particularly on the form of g. In particular, note that the response curves are symmetric in ω _f = ω_H.

In Fig. 7, we show the amplitudes of the responses in the three cells as a function of ε, for both harmonic and spiking forcing. In both cases we see a similar pattern of growth rate of amplitude. The amplitude in the first cell grows linearly with ε. In the second cell, as ε increases, the growth rate tends toward “cube root,” that is r ∼ ε^{1 ∕ 3}. Similarly in the third cell, for large enough ε, we see r ∼ ε^{1 ∕ 9}. As ε increases from zero, there is a transition region into these regimes. This appears to occur for different values of ε for the different types of forcing. However, since it is not clear how one should define the “amplitude” of the spiking forcing, and we have arbitrarily chosen to set the diameters of the two forcings equal, this is not unexpected. We investigate the transition region for harmonic forcing more fully in section “Periodic Forcing near Hopf Bifurcation”.

Experiments

McCullen et al. [26] performed experiments on a feed-forward chain of coupled nonlinear modified van der Pol autonomous oscillators. Even though the McCullen experiments were performed with a system that was not in normal form, the results conform well with the simulations. The responses to a simple harmonic forcing with varying frequency are shown in Fig. 8. Note the similarity with the simulation results in Fig. 6. The plot on the right of Fig. 8 shows the expected cube root scaling in the amplitude of cell 3 as a function of the amplitude cell 2.

Fig. 7

Log–log plot of amplitudes of response in cells 1 ( ∘ ), 2 ( ×), and 3 ( + ), as a function of ε, for harmonic forcing and spiking forcing. Also shown are lines of slope 1, 1 ∕ 3, and 1 ∕ 9 (from bottom to top). Parameters are ω _f = ω _H = 1, λ = − 0. 01, (a) 0. 0005 < ε < 0. 36, (b) 0. 0025 < ε < 0. 9

Recall that a band-pass filter allows signals in a certain range of frequencies to pass, whereas signals with frequencies outside this range are attenuated. As we have seen, the feed-forward chain can act as a kind of band-pass filter by exciting small amplitude signals to an amplitude larger than some threshold only if the input frequency is near enough to the Hopf frequency. To determine the frequency of an incoming sound, the human auditory system should have the capability of acting like a band-pass filter. As noted, several authors have suggested that the structure of outer hair cells on the basilar membrane is tuned to be a linear array of coupled cells each tuned near a Hopf bifurcation point but at different frequencies (see “Cochlear Modeling”).

Fig. 8

(Left) [26, Fig. 2]: Cells 2 and 3 amplitudes as a function of forcing frequency in oscillator experiment. (Right) [26, Fig. 5]: Log–log plot of amplitudes of oscillations in cells 2 and 3 as a function of forcing frequency near Hopf bifurcation point

Periodic Forcing near Hopf Bifurcation

In section “Periodic Forcing of Feed-Forward Chains,” we discussed numerical simulations and experiments which suggest that the amplification results for forced feed-forward chains near normal form Hopf bifurcation with sinusoidal forcing appear to hold even when the forcing is not sinusoidal or the system is not in normal form. These observations motivate the need for a general theory of periodic forcing of systems near Hopf bifurcation. In this section, we make a transition from studying feed-forward chains to the simpler situation of periodic forcing of systems near Hopf bifurcation.

In particular we show that when the cubic term in Hopf bifurcation has a sufficiently large complex part, then multiple periodic solutions will occur as ω _f is varied near ω_H. The importance of the complex part of the cubic term in different aspects of forced Hopf bifurcation systems was noted previously by Wang and Young [33]. The existence of regions of multiplicity motivates the need for a general theory of periodic forcing of systems near Hopf bifurcation. A detailed study of these forced systems, based on equivariant singularity theory, is being developed in [34].

Simulations

As in section “Periodic Forcing of Feed-Forward Chains,” we assume that the system we are forcing is in truncated normal form. More precisely, we assume that this system satisfies (B1–B3), but we do not assume that the cubic term is real. We also assume that the forcing is additive so that the equation is

$$\dot{z} = (\lambda+ \mathrm{i}{\omega }_{\mathrm{H}})z + c\vert z{\vert }^{2}z + \epsilon \mathrm{{e}}^{\mathrm{i}{\omega }_{\mathit{f }}t},$$

(8)

where λ < 0 and ε > 0 are small, $c = {c}_{R} + i{c}_{I}$ and ${c}_{R} < 0$. We can rescale z to set c _R = − 1. The scaled equation has the form

$$\dot{z} = (\lambda+ i{\omega }_{\mathrm{H}})z + (-1 + i\gamma )\vert z{\vert }^{2}z + \epsilon \mathrm{{e}}^{\mathrm{i}{\omega }_{f}t},$$

(9)

where $\gamma=-c_I/c_R$.

We show the results of simulation of (9) when γ = 0 (the case that is most often analyzed in the literature) and when γ = 10. Both simulations show amplification of the forcing when ${\omega }_{f} \approx {\omega }_{\mathrm{H}} = 1$. However, when γ≠0, we find that there can be bistability of periodic solutions. Figure 9 (right) shows results of two sets of simulations, with different initial conditions. For a range of ω _f , there are two stable solutions with different amplitude r = | z | .

Asymmetry and Multiplicity in Response Curve

It is well known that the normal form for Hopf bifurcation has phase shift symmetry and hence that the normal form equations can be solved in rotating coordinates. Rotating coordinates can also be used in the forced system. Write (9) in rotating coordinates $z = u\mathrm{{e}}^{i({\omega }_{f}t-\theta )}$, where θ is an arbitrary phase shift, to obtain

$$\dot{u} = (\lambda+ \mathrm{i}\omega )u + (-1 + \mathrm{i}\gamma )\vert u{\vert }^{2}u - \epsilon {\mathrm{e}}^{\mathrm{i}\theta }$$

where ω = ω_H − ω _f . Note that stationary solutions in u, for any θ, correspond to periodic solutions z(t) with frequency ω _f . We set \dot{u} = 0 and solve

$$g(u) \equiv(\lambda+ \mathrm{i}\omega )u + (-1 + \mathrm{i}\gamma )\vert u{\vert }^{2}u = \epsilon {\mathrm{e}}^{\mathrm{i}\theta }$$

(10)

for any u and θ. Note that finding a solution to (10) for some θ is equivalent to finding u such that

$$\vert g(u){\vert }^{2} = {\epsilon }^{2}.$$

(11)

Note also that

$$\vert g(u){\vert }^{2} = ({\lambda }^{2} + {\omega }^{2})\vert u{\vert }^{2} + 2(\omega \gamma- \lambda )\vert u{\vert }^{4} + (1 + {\gamma }^{2})\vert u{\vert }^{6}.$$

That is, | g(u) | ²depends only on | u | ².

Fig. 9

Amplitudes of solutions as function of Hopf frequency of (9), with ω_H = 1, λ = − 0. 0218, ε = 0. 02. (Left) γ = 0. (Right) γ = 10; The $\circ$’s and ×’s indicate two separate sets of simulations with different initial conditions. For 0. 35 < ω _f < 0. 7, there are two stable solutions

Set δ = ε²and R = | u | ². We can write (11) as

$$G(R;\lambda, \omega, \gamma, \delta ) \equiv(1 + {\gamma }^{2}){R}^{3} + 2(\omega \gamma- \lambda ){R}^{2} + ({\lambda }^{2} + {\omega }^{2})R - \delta= 0.$$

(12)

Since G(R; λ, ω, γ, δ) is invariant under the parameter symmetry $(\omega ,\gamma ) \rightarrow (-\omega ,-\gamma )$, we can assume γ ≥ 0. Additionally, if γ = 0, then G(R; λ, ω, γ, δ) is invariant under the parameter symmetry $\omega\rightarrow -\omega$.

Fix λ < 0, δ > 0 and γ ≥ 0. We seek to answer the following question. Determine the bifurcation diagram consisting of solutions R > 0 to (12) as ω varies. Note that variation of ω corresponds to variation of either ω _f or ω_H in the original forced equation (8). In Fig. 10, we plot sample bifurcation diagrams of (12) for three values of γ. We see that as γ is increased, asymmetry occurs in the bifurcation diagram, ultimately leading to multiple solutions.

We use bifurcation theory, in particular hysteresis points, to prove that multiplicity occurs for arbitrarily small λ < 0 and δ > 0. Hysteresis points correspond to points where the bifurcation diagram has a vertical cubic order tangent and such points are defined by

$$G = {G}_{R} = {G}_{\mathit{RR}} = 0\quad \mbox{ and }\quad {G}_{\omega }\neq 0\neq {G}_{\mathit{RRR}}$$

See [13, Proposition 9.1, p. 94]. Multiplicity of solutions occurs if variation of γ leads to a universal unfolding of the hysteresis point. It is shown in [13, Proposition 4.3, p. 136] that γ is a universal unfolding parameter if and only if

$$\det \left (\begin{array}{*{10}c} {G}_{\omega }&{G}_{\omega R} \\ {G}_{\gamma } & {G}_{\gamma R} \end{array} \right )\neq 0.$$

(13)

In this application of singularity theory we will need the following:

$$G = (1 + {\gamma }^{2}){R}^{3} + 2(\omega \gamma-\lambda ){R}^{2} + ({\lambda }^{2} + {\omega }^{2})R - \delta= 0,$$

(14)

$${G}_{R} = 3(1 + {\gamma }^{2}){R}^{2} + 4(\omega \gamma- \lambda)R + ({\lambda }^{2} + {\omega }^{2}) = 0,$$

(15)

$${G}_{\mathit{RR}} = 6(1 + {\gamma }^{2})R + 4(\omega \gamma- \lambda ) = 0,$$

(16)

$${G}_{\mathit{RRR}} = 6(1 + {\gamma }^{2}) > 0$$

(17)

$${G}_{\omega } = 2R(\gamma R + \omega )\neq 0$$

(18)

and

$${G}_{\gamma } = 2{R}^{2}(\gamma R + \omega ),$$

(19)

$${G}_{\gamma } = 2{R}^{2}(\gamma R + \omega ),$$

(20)

$${G}_{\gamma R} = 2R(3\gamma R + 2\omega ).$$

(21)

Fig. 10

Bifurcation diagrams of solutions to (12) for varying γ. As γ is increased, the response curve becomes asymmetric, and as it is increased further, for some values of ω there are multiple solutions. Parameters used are δ = 0. 01, λ = − 0. 109

Note that the determinant in (13) is just ${G}_{\omega }^{2}$, which is nonzero at any hysteresis point. Hence, variation of γ will always lead to a universal unfolding of a hysteresis point and to multiple solutions for fixed ω.

Theorem 1

For every small λ < 0 and δ > 0 there exists a unique hysteresis point of G at R = R _c (δ,λ), ω = ω _c (δ,λ), γ = γ _c (δ,λ). Moreover,

$${\omega }_{c}(\delta ,0) = -\sqrt{3}{(2\delta )}^{\frac{1} {3} }\qquad {\gamma }_{c}(\delta ,0) = \sqrt{3}\qquad {R}_{c}(\delta ,0) ={ \left (\frac{\delta } {4}\right )}^{\frac{1} {3} }.$$

(22)

Proof.

We assert that (14)–(16) define R _c , ω _c , γ _c uniquely in terms of δ and λ. Specifically, we show that

$${R}_{c}(\delta ,\lambda ) ={ \left ( \frac{\delta } {1 + {\gamma }_{c}^{2}}\right )}^{\frac{1} {3} } > 0.$$

(23)

$${\gamma }_{c}(\delta ,\lambda ) = \frac{\lambda+ \sqrt{3}{\omega }_{c}} {{\omega }_{c} -\sqrt{3}\lambda }.$$

(24)

Moreover, let

$$p(\omega ) = {\omega }^{3} -\sqrt{3}\lambda {\omega }^{2} + {\lambda }^{2}\omega-\sqrt{3}{\lambda }^{3}.$$

(25)

Then ω _c (δ, λ) is the unique solution to the equation

$$p({\omega }_{c}) = -6\sqrt{3}\delta.$$

(26)

We can compute these quantities explicitly when λ = 0. Specifically, (26) reduces ω _c ³= − 6\sqrt{3}δ. It is now straightforward to verify (22).

To verify (24) combine (15) and (16) to yield

$$R = -\frac{2(\omega \gamma- \lambda )} {3(1 + {\gamma }^{2})} \quad \mathrm{and}\quad {R}^{2} = \frac{{\lambda }^{2} + {\omega }^{2}} {3(1 + {\gamma }^{2})}.$$

(27)

More precisely, the first equation is obtained by solving G _RR = 0 and the second by solving RG _RR − G _R = 0. Multiplying the first equation in (27) by R and substituting for R ²in the second equation yields

$$2(\omega \gamma- \lambda )R = -({\lambda }^{2} + {\omega }^{2}).$$

(28)

Substituting (28) into (14) yields

$${R}^{3} = \frac{\delta } {1 + {\gamma }^{2}}$$

(29)

thus verifying (23).

We eliminate R from (27) in two ways, obtaining

$$-\frac{8{(\omega \gamma- \lambda )}^{3}} {27{(1 + {\gamma }^{2})}^{2}} = \delta \quad \mbox{ and }\quad \frac{4{(\omega \gamma- \lambda )}^{2}} {3(1 + {\gamma }^{2})} = {\lambda }^{2} + {\omega }^{2}$$

(30)

To verify the first equation in (30), cube the first equation in (27) and use (29) to substitute for R ³. To verify the second equation, square the first equation in (27) and use the second equation in (27) to substitute for R ².

Next we derive (24). Rewrite the second equation in (30) to obtain

$${\omega }^{2}({\gamma }^{2} - 3) - 8\omega \gamma \lambda+ {\lambda }^{2}(1 - 3{\gamma }^{2}) = 0,$$

(31)

which can be factored as

$$\left (\gamma (\omega-\sqrt{3}\lambda ) - (\lambda+ \sqrt{3}\omega )\right )\left (\gamma (\omega+ \sqrt{3}\lambda ) - (\lambda-\sqrt{3}\omega )\right ) = 0.$$

(32)

Thus, potentially, there are two solutions for γ _c ; namely,

$$\gamma= \frac{\lambda+ \sqrt{3}\sigma \omega } {\omega- \sigma \sqrt{3}\lambda },$$

(33)

where σ = ± 1, depending on which bracket is chosen in (32).

Next use (32) to show that

$$\omega \gamma- \lambda= \sqrt{3} \frac{{\lambda }^{2} + {\omega }^{2}} {\sigma \omega-\sqrt{3}\lambda }.$$

(34)

Squaring the second equation in (30) and substituting the first yields

$${({\lambda }^{2} + {\omega }^{2})}^{2} = 6(\omega \gamma- \lambda ) \frac{8{(\omega \gamma- \lambda )}^{3}} {27{(1 + {\gamma }^{2})}^{2}} = -6\delta (\omega \gamma- \lambda ).$$

(35)

Next use (34) to eliminate ωγ − λ. A short calculation leads to

$$({\omega }^{2} + {\lambda }^{2})(\sigma \omega-\sqrt{3}\lambda ) = -6\sqrt{3}\delta.$$

(36)

Since δ > 0, we must have σω − \sqrt{3}λ < 0, or σω < \sqrt{3}λ < 0.

We claim that for γ ≥ 0, we must choose σ = + 1. Since λ < 0 and σω < 0, the numerator of (33) is negative. If σ = − 1, then the denominator of (33) is σ(σω − \sqrt{3}λ) > 0, since $\sigma \omega-\sqrt{3}\lambda< 0$. Hence γ < 0. We thus write σ = + 1 and verify (24).

We claim that given δ and λ there is a unique solution ω to (36). Observe that the cubic polynomial in ω on the left side of (36) is (25). Since

$$p'(\omega ) = {(\sqrt{3}\omega- \lambda )}^{2},$$

(37)

p(ω) is monotonic; and there is a unique solution ω _c , as claimed.

Finally, we must show that ${G}_{\omega }$ is nonzero at R _c , ω _c , γ _c . We do this by showing that

$${\gamma }_{c}(\delta ,\lambda ){R}_{c}(\delta ,\lambda ) + {\omega }_{c}(\delta ,\lambda ) < 0.$$

By cubing the first equation in (30) and dividing by the square of the second equation, we can eliminate the ωγ − λ factor and show that

$$1 + {\gamma }_{c}^{2} = \frac{{({\lambda }^{2} + {\omega }_{ c}^{2})}^{3}} {27{\delta }^{2}}.$$

Using this alongside (29) we write R _c as

$${R}_{c} = \frac{{\delta }^{1/3}} {{(1 + {\gamma }_{c}^{2})}^{1/3}} = {\delta }^{1/3} \frac{3{\delta }^{2/3}} {{\lambda }^{2} + {\omega }_{c}^{2}} = \frac{3\delta } {{\lambda }^{2} + {\omega }_{c}^{2}}.$$

Then use (34) to substitute for γ _c to find

$${R}_{c}{\gamma }_{c} = \frac{3\delta } {{\lambda }^{2} + {\omega }_{c}^{2}} \frac{\lambda+ \sqrt{3}{\omega }_{c}} {{\omega }_{c} -\sqrt{3}\lambda } = -\frac{\lambda+ \sqrt{3}{\omega }_{c}} {2\sqrt{3}} ,$$

where we have used (36) to simplify the denominator. Therefore

$${R}_{c}{\gamma }_{c} + {\omega }_{c} = \frac{\sqrt{3}{\omega }_{c} - \lambda } {2\sqrt{3}} = \frac{1} {2}\left ({\omega }_{c} - \frac{1} {\sqrt{3}}\lambda \right ) < \frac{1} {2}\left ({\omega }_{c} -\sqrt{3}\lambda \right ) < 0,$$

where the penultimate inequality follows because $\frac{1} {\sqrt{3}}\lambda> \sqrt{3}\lambda$.

Scalings of Solution Amplitudes

Kern and Stoop [23] and Eguíluz et. al [7] consider the system (9) with γ = 0, and observe that there are regions of parameter space in which the input signal (forcing) is amplified – that is, the solution $z(t) = r\mathrm{{e}}^{\mathrm{i}(\omega t+\theta )}$ has an amplitude r which scales like ε^{1 ∕ 3}.

Specifically, Eguíluz et. al [7] specialize (9) exactly at the bifurcation point (λ = 0) and show that the solution has an amplitude r ∼ ε^{1 ∕ 3}when ω_H = ω _f . Away from resonance, (ω_H≠ω _f ), they show that for ε small enough (small enough forcing), the response r ∼ ε ∕ | ω_H − ω _f |. Kern and Stoop [23] consider forcing exactly at the Hopf frequency (i.e., ω_H = ω _f ), and show that the solution has an amplitude r ∼ ε^{1 ∕ 3}when λ = 0, and when λ < 0 the amplitude r ∼ ε ∕ | λ | .

In the following, we make precise the meaning of “cube-root growth,” and additionally, do not assume γ = 0. We show that, in some parameter regime, the response r can be bounded between two curves, specifically, that

$${\left ( \frac{\epsilon } {\sqrt{2}}\right )}^{\frac{1} {3} } < r < {\epsilon }^{\frac{1} {3} },$$

that is, r lies between two lines in log–log plots. In Fig. 11, we show the result of numerical simulations of (9) as ε is varied along with the two lines given above. For large enough ε, the response amplitude lies between these lines. Compare also with Fig. 7 – we could perform a similar process here of bounding the amplitudes of response to determine regions of different growth rates.

The width of this region is in some sense arbitrary – choosing a different lower boundary would merely result in different constants in the proof of the lemmas given below. We consider here only the scaling of the amplitude of the maximum response (as a function of ω), but note that our calculations can easily be extended beyond this regime.

Fig. 11

For “cube root growth,” the amplitude r is bounded by two straight lines in a plot of logr vs. logε

For consistency with the previous section, we work with R = r ²and δ = ε²; it is clear that similar relations will hold between R and δ. Recall

$$G(R;\lambda ,\omega ,\gamma ,\delta ) = (1 + {\gamma }^{2}){R}^{3} + 2(\omega \gamma- \lambda ){R}^{2} + ({\lambda }^{2} + {\omega }^{2})R - \delta ,$$

where ω = ω_H − ω _f . The amplitude of solutions is given by G(R; λ, ω, γ, δ) = 0. Consider the amplitude as ω is varied, then the maximum response R occurs when ${G}_{\omega } = 0$, that is, at ω = − γR, which is nonzero for γ≠0. At γ = 0, the response curve is symmetric in ω, and so the maximum must occur at ω = 0.

Write

$$G(R;\lambda ,\omega ,\gamma ,\delta ) = \Gamma (R;\lambda ,\omega ,\gamma ) - \delta ,$$

(38)

so the amplitude squared of the response, R, is related to the amplitude squared of the forcing, δ, by

$$\Gamma (R;\lambda ,\omega ,\gamma ) = \delta.$$

Consider the function Γ(R; λ, ω, γ) evaluated at the value of ω for which the maximum response occurs, that is, compute

$$\Gamma (R;\lambda ,-\gamma R,\gamma ) = {R}^{3} - 2\lambda {R}^{2} + {\lambda }^{2}R,$$

which turns out to be independent of γ, and so write $\mathcal{G}\left (R;\lambda \right ) \equiv\Gamma (R;\lambda ,-\gamma R,\gamma )$. Moreover, since λ < 0, $\mathcal{G}\left (R;\lambda \right )$ is monotonically increasing in R and hence invertible. Therefore, the response curve has a unique maxima for all γ.

Write $\mathcal{H}(\delta ;\lambda ) \equiv \mathcal{G}{\left (R;\lambda \right )}^{-1}$. Then for given δ, λ, the maximum R satisfies $R = \mathcal{H}(\delta ;\lambda )$.

Observe that for | R | small, $\mathcal{G}\left (R;\lambda \right ) \approx {\lambda }^{2}R$, and for | R | large, $\mathcal{G}\left (R;\lambda \right ) \approx {R}^{3}$. Therefore, for | δ | small we expect $R = \mathcal{H}(\delta ;\lambda ) \approx \delta /{\lambda }^{2}$, and for | δ | large, $R = \mathcal{H}(\delta ;\lambda ) \approx {\delta }^{1/3}$. We make these statements precise in the following lemmas.

Lemma 1.

If |λ| < 0.33 δ ^1∕3 , then

$${\left (\frac{\delta } {2}\right )}^{1/3} < \mathcal{H}(\delta ;\lambda ) < {\delta }^{1/3}.$$

Remark 3.

The constant 0. 33 in the statement of Lemma 1 can be replaced by k ₁, the unique positive root of ${y}^{2} + {2}^{2/3}y - {2}^{-2/3} = 0$. The hypothesis in this lemma can then read $\vert \lambda \vert< {k}_{1}{\delta }^{1/3}$. In the proof we use k ₁ rather than 0. 33.

Proof.

Since $\mathcal{G}\left (R;\lambda \right )$ is monotonic increasing, we need to show that

$$\mathcal{G}\left ({\left (\frac{\delta } {2}\right )}^{1/3};\lambda \right ) < \delta< \mathcal{G}\left ({\delta }^{1/3};\lambda \right ).$$

Since λ < 0 and δ > 0 the second inequality follows from

$$\mathcal{G}\left ({\delta }^{1/3};\lambda \right ) = \delta- 2\lambda {\delta }^{2/3} + {\lambda }^{2}{\delta }^{1/3} > \delta.$$

For the first inequality, we have

$$\mathcal{G}\left ({\left (\frac{\delta } {2}\right )}^{1/3};\lambda \right ) = \frac{\delta } {2} - {2}^{1/3}\lambda {\delta }^{2/3} + {\lambda }^{2}\frac{{\delta }^{1/3}} {{2}^{1/3}}.$$

We have assumed $-\lambda< {k}_{1}{\delta }^{1/3}$; so

$$\mathcal{G}\left (\left (\frac{\delta } {2}\right );\lambda \right ) < \frac{\delta } {2} + {2}^{1/3}{k}_{ 1}\delta+ {k}_{1}^{2} \frac{\delta } {{2}^{1/3}} = \frac{1} {{2}^{1/3}}\left ( \frac{1} {{2}^{2/3}} + {2}^{2/3}{k}_{ 1} + {k}_{1}^{2}\right )\delta= \delta ,$$

since ${k}_{1}^{2} + {2}^{2/3}{k}_{1} = {2}^{-2/3}$.

Lemma 2.

If $\vert \lambda \vert> 1.06\;{\delta }^{1/3}$ , then

$$\frac{\delta } {2{\lambda }^{2}} < \mathcal{H}(\delta ;\lambda ) < \frac{\delta } {{\lambda }^{2}}.$$

Remark 4.

The constant 1. 06 in the statement of Lemma 2 can be replaced by k ₂, where y = k ₂ ³is the unique positive root of 4y ²− 4y − 1 = 0. The hypothesis in this lemma can then read $\vert \lambda \vert> {k}_{2}{\delta }^{1/3}$. In the proof we use k ₂ rather than 1. 06.

Proof.

Since $\mathcal{G}\left (R;\lambda \right )$ is monotonic increasing in R, we have to show that

$$\mathcal{G}\left ( \frac{\delta } {2{\lambda }^{2}};\lambda \right ) < \delta< \mathcal{G}\left ( \frac{\delta } {{\lambda }^{2}};\lambda \right ).$$

Since λ < 0 and δ > 0 the second inequality follows from

$$\mathcal{G}\left ( \frac{\delta } {{\lambda }^{2}};\lambda \right ) = \frac{{\delta }^{3}} {{\lambda }^{6}} - 2 \frac{{\delta }^{2}} {{\lambda }^{3}} + \delta> \delta.$$

For the first inequality, we have

$$\mathcal{G}\left ( \frac{\delta } {2{\lambda }^{2}};\lambda \right ) = \frac{{\delta }^{3}} {8{\lambda }^{6}} - \frac{{\delta }^{2}} {2{\lambda }^{3}} + \frac{\delta } {2}.$$

We assumed λ⁶> k ₂ ⁶δ²and − λ³> k ₂ ³δ. So

$$\mathcal{G}\left ( \frac{\delta } {2{\lambda }^{2}};\lambda \right ) < \frac{{\delta }^{3}} {8{k}_{2}^{6}{\delta }^{2}} + \frac{{\delta }^{2}} {2{k}_{2}^{3}\delta } + \frac{\delta } {2} = \frac{1} {8{k}_{2}^{6}}(4{k}_{2}^{6} + 4{k}_{ 2}^{3} + 1)\delta= \delta ,$$

since 4k ₂ ³+ 1 = 4k ₂ ⁶.

Remark 5.

Note that ${k}_{1} \approx 0.33$ and ${k}_{2} \approx 1.06$, so k ₁ < k ₂. It follows that the region of linear amplitude (ε) growth is very small, whereas the region of cube root growth is quite large. In Fig. 12, we illustrate this point by graphing the curves that separate the regions; namely $\epsilon= {(\lambda /{k}_{1})}^{3/2}$ (dashed curve for cube root growth) and $\epsilon= {(\lambda /{k}_{2})}^{3/2}$ (continuous curve for linear growth). Since $\frac{1} {{k}_{2}} < \frac{1} {{k}_{1}}$ the linear and cube root growth regions are disjoint.

Remark 6.

The maximum amplitude r satisfies$\mathcal{G}\left(r^2 ;\lambda\right) = \epsilon^2$, where $\mathcal{G}\left (R;\lambda \right )$ is an increasing function of R. Hence r increases as ε increases. Recall that the maximum r occurs at ω = − γr ². Hence with fixed parameters λ < 0, γ≠0, the forcing frequency for which the maximum amplitude occurs, varies as the amplitude of the forcing (ε) increases.

Remark 7.

It is simple to extend this type of reasoning into regions away from the maximum amplitude of response, to find linear growth rates for ω far from the maximum response. However, the algebra is rather messy and so we do not include the details here.

Q-Factor

Engineers use the Q-factor to measure the efficiency of a band-pass filter. The Q-factor is nondimensional and defined by

$$Q = \frac{{\omega }_{\mathrm{max}}} {\mathrm{d}\omega } ,$$

where ${\omega }_{\mathrm{max}}$ is the forcing frequency at which maximum response amplitude ${r}_{\mathrm{max}}$ occurs, and dω is the width of the amplitude response curve when it has half the maximum height. In Fig. 13, we give a schematic of a response curve and show how Q is calculated.

Fig. 12

Regions of linear and cube root growth in the λ-ε plane

The larger the Q, the better the filter. Quantitatively, there is a curious observation. It can be shown that for our Hopf normal form, Q varies linearly with ω_H. The response curve in ω–r space is defined implicitly by (12) (recall R = r ², δ = ε²). This curve depends only on ω (not on ω _f or ω_H independently). Therefore, as ω_H varies, the curve will be translated, but its shape will not change. Hence the width of the curve, dω, is independent of ω_H.

Fig. 13

Schematic of a response curve as ω _f is varied, for fixed ω_H. The Q-factor is ${\omega }_{\mathrm{max}}/\mathrm{d}\omega$

As shown in section “Scalings of Solution Amplitudes,” the maximum response ${r}_{\mathrm{max}}$ is independent of ω_H. The position of the maximum response is given by $\omega= -\gamma {r}_{\mathrm{max}}^{2}$, or ${\omega }_{f} = {\omega }_{\mathrm{H}} + \gamma {r}_{\mathrm{max}}^{2}$. Hence

$$Q = \frac{{\omega }_{\mathrm{H}} + \gamma {r}_{\mathrm{max}}^{2}} {d\omega }$$

and so depends linearly on ω_H.

In addition, we find from simulations that for any given ω_H the Q-factor of the system is better for spiking forcing than for sinusoidal forcing. Figure 14 shows results of simulations of the three cell feed-forward network from section “Simulations” under “Periodic Forcing of Feed-Forward Chains” using sinusoidal and spiking forcing. From these figures, we see two, perhaps surprising, results. First, that the Q-factor for spiking forcing is almost five times higher than that of sinusoidal forcing. Second, that for both forcings, the Q-factor for cell 3 is less than that of cell 2.

We explain the first observation by the following analogy. Consider the limit of very narrow spiking forcing, on a damped harmonic oscillator, for example, pushing a swing. Resonant amplification can only be achieved if the frequency of the forcing and the oscillations exactly match. If they are slightly off, then the forcing occurs at a time when the swing is not in the correct position and so only a small amplitude solution can occur.

Fig. 14

The figures show the Q factor as ω_H is varied for sinusoidal forcing (left) and spiking forcing (right) for each cell in the feed-forward network from section “Simulations” under “Periodic Forcing of Feed-Forward Chains”. In these simulations λ = − 0. 01 and ε = 0. 08

We further note that although the output from a cell receiving spiking forcing is not sinusoidal, it is closer to sinusoidal than the input. That is, as the signal proceeds along the feed-forward chain, at each cell the output is closer to sinusoidal than the last. Combining this observation with the first explains why the Q-factor of cell 3 should be less than that for cell 2.

Cochlear Modeling

The cochlea in the inner ear is a fluid filled tube divided lengthwise into three chambers. The basilar membrane (BM) divides two of these chambers and is central to auditory perception. Auditory receptor cells, or hair cells, sit on the BM. Hair bundles (cilia) protrude from these cells, and some of the cilia are embedded in the tectorial membrane in the middle chamber. For reviews of the mechanics of the auditory system, see [2, 17, 29].

When a sound wave enters the cochlea, a pressure wave in the fluid perturbs the BM near its base. This initiates a wave along the BM, with varying amplitude, that propagates toward the apex of the cochlea. The envelope of this wave has a maximum amplitude, the position of which depends on the frequency of the input. High frequencies lead to maximum vibrations at the stiffer base of the BM, and low frequencies lead to maximum vibrations at the floppier apex of the BM. As discussed in [22], each point along the BM oscillates at the input frequency. As the sound wave bends the BM, the hair cells convert the mechanical energy into neuronal signals. There is evidence [6, 23, 25] that the oscillations of the hair cells have a natural frequency which varies with the position of the hair cell along the BM.

Experiments have shown that the ear has a sharp frequency tuning mechanism along with a nonlinear amplification system – there is no audible sound soft enough to suggest that the cochlear response is linear. Many authors [5, 6, 7, 21, 23, 27, 28] have suggested that these two phenomena indicate that the auditory system may be tuned near a Hopf bifurcation. Detailed models of parts of the auditory system (Hudspeth and Lewis [18, 19], Choe, Magnasco, and Hudspeth [6]) have been shown to contain Hopf bifurcations for biologically realistic parameter values.

Hopf Models of the Auditory System

Most simplified models model a single hair cell as a forced Hopf oscillator, similar to (9), but with the imaginary part of the cubic term (γ) set equal to zero. As we have shown in section “Periodic Forcing near Hopf Bifurcation”, this assumption leads to nongeneric behavior, in particular, that the response curve is symmetric in ω. In fact, a center manifold reduction of the model of Hudspeth and Lewis [18, 19] by Montgomery et al. [27] finds that γ≠0. Specifically, they find γ = − 1. 07.

Furthermore, the response curve in the auditory system has been shown experimentally (see [29] and references within) to be asymmetric. Two papers [23, 25] have considered the dynamics of an array of Hopf oscillators (rather than the single oscillators studied by most other authors). They achieve the aforementioned asymmetry through couplings between the oscillators via a traveling wave which supplies the forcing terms. This complicates the matter significantly, so that analytical results cannot be obtained.

However, we note that merely having a complex, rather than real, cubic term in the Hopf oscillator model would have a similar effect. The value of γ found by Montgomery et al. [27] is in the regime where we observe asymmetry, but not multiplicity of solutions. Multiple solutions in this model could correspond to perception of a sound of either low or high amplitude for the same input forcing. We have seen no mention of this phenomena in the literature.

Two-Frequency Forcing

It is clear that stimuli received by the auditory system are not single frequency, but contain multiple frequencies. If each hair cell is to be modeled as a Hopf oscillator, we are interested in the effect of multifrequency forcing on an array of Hopf oscillators. We give here some numerical results from an array of N uncoupled Hopf oscillators:

$$\dot{{z}}_{j} = (\lambda+ \mathrm{i}{\omega }_{\mathrm{H}}(j))z + (-1 + \mathrm{i}\gamma )\vert {z}_{j}{\vert }^{2}{z}_{ j} + \epsilon g(t),\quad j = 1,\ldots ,N,$$

(39)

where ω_H(j) = ω₁ + jΔω, for some ω₁, Δω, that is, the Hopf frequency increases linearly along the array of oscillators. Note that all oscillators receive the same forcing.

Fig. 15

The mean amplitude for each of an array of forced Hopf oscillators (39), with forcing given in (40). The phase plane portraits for the outputs of the oscillators with ω_H = 1 and ω_H = 1. 6 are shown in Fig. 16. Remaining parameters are λ = − 0. 01, ε = 0. 05, γ = − 1

Consider forcing which contains two frequency components, for instance:

$$g(t) ={ \mathrm{e}}^{\mathrm{i}t} +{ \mathrm{e}}^{\sqrt{5}\mathrm{i}t}.$$

(40)

In Fig. 15, we plot the mean amplitude of the responses of each oscillator in the array. The response clearly has two peaks, one close to each frequency component of the input.

Note also that the forcing g(t) is quasiperiodic. In those oscillators which have aHopf frequency close to one component of the forcing, only that component isamplified. This results in an output which is close to periodic. InFig. 16 we show the resulting phase plane solutions from two of the Hopfoscillators. The first has ω_H = 1,so the first component of the forcing is amplified, and the solution is close toperiodic. The second hasω_H = 1. 6, which is far fromboth 1 and \sqrt{5}. Hence neither component is amplified and the output isquasiperiodic.

Fig. 16

The phase plane portraits for Hopf oscillators with ω_H = 1 (left) and ω_H = 1. 6 (right), with forcing as given in (40). The left figure is almost periodic, but the right is clearly quasiperiodic. Remaining parameters are λ = − 0. 01, ε = 0. 05, γ = − 1