Keywords

1 Introduction

Trapping is a common source of capture–recapture data, but the spatial component of such data has generally been ignored. By trapping we mean sampling an animal population with traps set for a known time at known points in the habitat, often on a grid. Time is usually divided into discrete intervals (‘occasions’), and new animals may be captured, marked and released on each occasion. By convention, closed-population encounter histories are coded in binary form: on each occasion an individual is either captured (1) or not captured (0) (Otis et al. 1978). A spatial encounter history also records the location of each capture. We are concerned with the estimation of population density using information in the spatial encounter history.

Previous methods for estimating population density D with arrays of traps have used the relation \(\hat D = \hat N / A\), where N is the population size and A is the area occupied by the population. This is the method of choice if the biological population occupies a defined geographic area (e.g. an island) and if every member of the population is at risk of capture. More commonly, the individuals at risk of capture in traps are an ill-defined subset N c of a larger biological population that extends indefinitely beyond the trap array. We may estimate N c empirically from the encounter histories with conventional closed population methods (Otis et al. 1978; Chao and Huggins 2005), but this quantity bears only a vague relationship to the biological parameters of interest (N and D). While we may hypothesize the existence of an ‘effective trapping area’ A c such that \( D = N_c /A_c \), rigorous general methods for estimating A c are lacking (but see White et al. 1982; Jett and Nichols 1987).

A more secure approach is to estimate density directly without recourse to the quantities N c and A c. The feasibility of estimating D directly from trapping data was demonstrated by Efford (2004) and Efford et al. (2004). Their method relied on a simulation of the trapping process. Here we describe a likelihood-based approach that is in some ways more general and flexible. The underlying theory was developed by Borchers and Efford (2007).

The literature on nonspatial capture–recapture has not been concerned with the trapping process although it is an important determinant of capture probability. At the simplest level, increasing the number of traps per home range will increase capture probability; more subtly, per capita capture probability will decline with increasing local density if traps are of a type that ‘fill up’, particularly if they are ‘single-catch’ traps. Such patterns result naturally from suitably formulated spatial trapping models, so long as care is taken to match the model to the process by which data were collected. The focus in Borchers and Efford (2007) was on traps that do not fill up, but which stop an animal from advancing to another trap within the same occasion (we call these ‘multi-catch’ traps). We extend their treatment to allow for other types of trapping process; in particular, we model ‘proximity detectors’ such as automatic cameras and devices that passively collect DNA samples from animals without limiting their movement. As an example, we analyse data from stoats Mustela erminea identified by their microsatellite DNA in hair samples. We also discuss the extension of likelihood-based methods to single-catch traps. In lieu of a likelihood function for single-catch traps, we use simulation to evaluate the performance of the multi-catch density estimator applied to data from single-catch traps.

2 Model

We wish to construct a probability model for encounter histories that include the location of each detection. Our model comprises one submodel for the distribution of animals in a region that includes the traps, and another submodel for the capture process. The capture process submodel gives the probability of catching an individual in a particular trap, given the location of its home range. We introduce these models before proceeding to the likelihood.

2.1 Distribution Submodel

We assume that for the duration of trapping the general location of each individual in the population may be summarised by the coordinates of a point that we call the animal’s home range centre. Later we relate probability of detection to radial distance from this point. The density of the population is equivalent to the intensity of a spatial point process for the home range centres. In this paper we model the distribution with a homogeneous spatial Poisson process; more generally, we could use an inhomogeneous Poisson process (Borchers and Efford 2007).

2.2 Capture Submodel

A spatial model of capture probability must take into account properties of the trap or detector. We distinguish three types of detector:

  • Proximity detector

  • Multi-catch trap

  • Single-catch trap

We order these by increasing complexity in the probability model, rather than novelty. Multi-catch traps were treated by Borchers and Efford (2007), while the likelihood given here for proximity detectors is new.

A proximity detector records the presence of an individual at or near a point, but leaves it free to visit other detectors on the same occasion. Multiple individuals may be recorded at a detector on one occasion (see Discussion for one-shot detectors). Examples are camera traps and passive DNA sampling devices such as sticky hair traps. The probability that a particular individual i with home range centre X(i) is recorded at detector k, located at Y(k), is assumed to be a function of the Euclidean distance d k [X(i)] = |X(i) – Y(k)|, and possibly also of other covariates. Here vector notation (in bold) is used for location, which might otherwise have been represented by Cartesian coordinates (x, y). We assume independence between visits to different detectors. Each occasion-specific entry in an encounter history from an array of K proximity detectors is itself a vector of length K whose elements take the value 1 for detectors at which the individual was recorded at least once and 0 otherwise.

Multi-catch traps differ from proximity detectors in that capture in one trap precludes capture of the same individual in other traps on the same occasion. As with proximity detectors, multiple individuals may be recorded at a trap on one occasion. Mist nets for birds and pitfall traps for lizards are examples of multi-catch traps used in capture–recapture studies. The probability of capture is modified by ‘competition’ among traps for the chance to capture an individual (multiple traps within an individual’s home range may reduce its probability of capture in any particular trap). An additive competing risks hazard formulation is appropriate for trap-specific capture probability (Borchers and Efford 2007). Each occasion-specific entry in an encounter history from an array of K multi-catch traps is a single trap index k where 0 ≤ k ≤ K, and k = 0 indicates no capture.

Single-catch traps are able to catch only one animal at a time, and capture probability is affected by the presence of other individuals that may ‘compete’ for traps. The majority of traps used for capture–recapture of small mammals are of this type. The encounter history has the same form as for multi-catch traps, but different histories may have the same entry on one occasion only if both are zero. Capture of an animal disables a trap and immediately reduces the capture probabilities of neighbouring animals. Simulation of the capture process is straightforward in continuous time, and a capture model may be fitted by inverse prediction (Efford 2004). A likelihood model for single-catch traps is considerably more complicated than for multi-catch traps, and remains to be developed.

3 Likelihood

The probability associated with each capture history may be treated as the product of the probability of catching an individual at least once (p.) and the probability of the observed history given that it includes at least one capture. Each part is conditional on the location of the individual’s home range centre X, but using the distribution submodel we may integrate over possible locations to evaluate the likelihood without knowing X.

We start by defining a spatial analogue of detection probability \(a= \int p.({\bf{X}};\break {\boldsymbol{\uptheta} })\;d{\bf{X}} \), where θ is a vector of detection parameters and a has units of area (the parallel between a and detection probability becomes clear in the next section). For a homogeneous Poisson distribution model, the probability of observing exactly n capture histories is itself Poisson-distributed:

$$ \Pr (n) = {\frac{(Da)^n \exp ( - Da)}{n!}}.$$
((1))

The likelihood given n observed capture histories ω = (ω1,…,ωn) is then

$$ L({\boldsymbol{\uptheta} },D) = \Pr (n) \times \prod\limits_{i = 1}^n {{\frac{\int {\Pr (\omega _i |{\bf{X}};{\boldsymbol{\uptheta}})d{\bf{X}}}}{a}}},$$
((2))

where \( \Pr \{ \omega _i |{\bf{X}};{\boldsymbol{\uptheta} }\} \), the probability of the capture history for a given home range location and model parameters, is defined below. The probability of being caught at least once over S occasions depends on the distances d k (X) to each of the K traps:

$$ p.({\bf{X}};{\boldsymbol{\uptheta} }) = 1 - \prod\nolimits_s {\prod\nolimits_k {\{ 1 - p_s (d_k ({\bf{X}})\;;{\boldsymbol{\uptheta} })\} } } .$$
((3))

Here p s is analogous to the detection function in distance sampling (e.g. Buckland et al. 2001).Footnote 1. Its parameters θ control the overall efficiency of detection and also its spatial scale, which we expect to increase with home range size. Three suitable forms for p s are shown in Table 1. These use the independent parameters g 0 for overall efficiency of detection and σ for spatial scale.Footnote 2

Table 1 Detection functions p s for spatially explicit capture–recapture models. d is the distance between an animal’s home range centre and a detector. The parameter g 0 is common to all functions and represents the probability of detection at a single detector placed in the centre of the home range; values of the spatial scale parameter σ are not comparable between functions
Full size table

The hazard function has an additional shape parameter b (b > 0); when b is fixed at a large value (e.g. 100) the hazard function comes to resemble a step function (p s(d) ≈ 0 for d > σ). Although our experience tends to favour the hazard function, we recommend that a function is selected for each dataset only after comparing the fit of alternatives.

The preceding formulation applies to all three types of detector. Differences arise in the term Pr{ωi |X;θ}. This has the general form

$$\Pr \{ \omega _i |{\bf{X}};{\boldsymbol{\uptheta}}\} = \prod\nolimits_s {\prod\nolimits_k {p_{ks} ^{\delta _{iks} } \;(1 - p_{ \cdot s} )} } ^{1 - \delta _{i \cdot s} },$$
((4))

where p ks is the probability of detection at k on occasion s, δ iks = 1 if individual i was detected at k on occasion s and \( \delta _{i \cdot s} = 1 \) if \( \sum\limits_k {\delta _{iks} } > 0 \) and \( \delta _{i \cdot s} = 0 \) otherwise.

For an array of proximity detectors we use

$$ p_{ks} = p_s (d_k ({\bf{X}})\;;{\boldsymbol{\uptheta} }).$$
((5))

Multi-catch traps ‘compete’ for animals and a competing risks hazard-rate form is appropriate:

$$ p_{ks} = {\frac{h(d_k ({\bf{X}}))}{h.({\bf{X}})}}[1 - e^{ - h.({\bf{X}})} ],$$
((6))

where \( h(d_k ({\bf{X}})) = - \ln \{ 1 - p_s (d_k ({\bf{X}};{\boldsymbol{\uptheta} }))\} \) and \( h.({\bf{X}}) = \sum\nolimits_{k = 1}^K {h(d_k ({\bf{X}}))} \).

4 Estimation

We estimate D and θ by numerically maximising the full likelihood (1) with respect to the parameters. For maximisation we log-transform D and σ, and logit-transform g 0 to keep each within feasible ranges. Each evaluation of the likelihood requires numerical integration over the plane, once for each observed encounter history ω i and once for the null capture history to calculate a. The speed of the algorithm used for integration is therefore critical. We have not obtained satisfactory results with standard algorithms such as the adaptive method of Genz and Malik (1980) used in some packages; our preferred method at present is to sum function values over a grid of points. Integration may be limited to a subset of the plane that contains plausible animal locations X; the estimated density will then apply to that area of habitat. Asymptotic variances may be estimated from the inverse of the information matrix. Confidence limits for \( \hat D \) may be estimated as \( \exp [\ln (\hat D) \pm z_\alpha \hat s_D ] \), where \( \hat s_D \) is the estimated SE of \( \hat D \) on the log scale and z α is the appropriate normal deviate, or by profile likelihood. Software is available (Efford 2007).

An alternative procedure is to maximise the conditional likelihood (the product over capture histories in (1)) to get estimates \( {\hat {\boldsymbol{\uptheta} }} \) and hence \( a({\hat {\boldsymbol{\uptheta} }}) \) , and to estimate \( \hat D = n/\hat a \). This is advantageous when there are individual covariates z i as we can then use the Horvitz-Thompson-like estimator \( \hat D = \sum\nolimits_{i = 1}^n {\hat a({\bf{z}}_i )^{ - 1} } \), which does not require the pdf of covariates to be modelled (Borchers and Efford 2007). Similar methods are used in conventional capture–recapture to estimate population size N from individual detection probabilities p i ( \( \hat N = \sum\nolimits_{i = 1}^n {\hat p_i ^{ - 1} } \)) (Huggins 1989).

5 Extensions

5.1 Modelling Additional Variation in Detection

Our core model accounts for variation in capture probability due to the varying number and location of traps in each animal’s home range. This confers a robustness that is lacking in conventional closed-population analyses of trapping data. Other sources of variation that are addressed in conventional analyses (e.g. Otis et al. 1978; Chao and Huggins 2005) may readily be included (Borchers and Efford 2007). Capture probability p in conventional models is replaced in the spatial model by a vector of at least two parameters, g 0 and σ. Each conventional source of variation in p (i.e. time, response to capture, and individual heterogeneity; Otis et al. 1978) may affect either or both of g 0 and σ. For example, we can fit a model for a change after first capture in either the efficiency of detection (Mb(g 0)) or its spatial scale (Mb(σ)). Individual heterogeneity may be incorporated via mixture models for either parameter (e.g. 2-class finite mixture Mh2(g 0) cf. Pledger 2000). In addition, the spatial model allows for novel sources of variation, such as dependence of capture on the type of trap or on other trap-level covariates describing the habitat at the trap site. Modelling and estimation of additional sources of variation in detection probability requires additional parameters and adjustments to the expression for p ks (Eqs. (5) and (6)). We do not describe these in detail because they follow directly from current practice (Otis et al. 1978; Chao and Huggins 2005).

5.2 Variation Across Space or Time

The purpose of a capture–recapture study will often be to compare density at different places, or at different times. For convenience, we use the word ‘session’ for each sampled population, whether populations are separated by space, time or an attribute such as sex. Our ‘sessions’ have been termed ‘groups’ in other capture–recapture contexts (e.g. Williams et al. 2002, p. 426), and are loosely equivalent to primary sessions in the open-population robust design of Pollock (1982). Even when a separate density is to be estimated for each session, if data are sparse it may be efficient to estimate a common detection function across all sessions. In general, session effects may be treated as constant (pooled across sessions), as fixed effects (e.g. session-specific levels or a trend across sessions) or as random effects (yet to be implemented). Thus the utility of the method is greatly extended by a multi-session model. Alternative models may be compared by standard methods (e.g., Akaike’s Information Criterion or likelihood ratio tests).

Sessions are assumed to be demographically closed (no births, deaths, immigration or emigration), and each encounter history spans only one session. If the same individual is caught in two sessions it is artificially assigned a new identity in the second session. Under these independence assumptions it is appropriate to use a combined multi-session likelihood (the product of within-session likelihoods) to model variation between sessions.

Session-specific parameter values (levels of D and the elements of θ) may be treated as functions of session-level covariates, including time. For each evaluation of the combined likelihood we substitute the current values of D and θ into the within-session likelihood (1), and sum the resulting log-likelihoods across sessions. The combined likelihood is maximised over all parameters, including those of the functions controlling the session-specific D and θ.

6 Example: Stoats Identified by DNA Microsatellites

Stoats Mustela erminea introduced to New Zealand have deleterious effects on populations of native birds, and their ecology and population management are therefore a prime concern for conservation. Capture–recapture with traps is onerous and not always successful because of low capture rates. An alternative to trapping is to register the presence of individuals from DNA in hair or dung. For stoats, a convenient sampling device is a tube with a transverse adhesive-coated rubber band that retains hairs from stoats that pass through (Duckworth et al. 2005). Here we analyse data from a pilot study in Nothofagus fusca forest in the Matakitaki Valley, South Island, New Zealand (172°30'E, 42°00'S). Hair sampling tubes (K = 94) were placed on a 3 ×3 km grid with 500 m spacing between rows and 250 m spacing along rows. Tubes were baited with rabbit meat and checked daily for 7 days, starting 15 December 2001. Stoat hair samples were identified to individual using DNA microsatellites amplified by PCR from follicular tissue.Footnote 3 Six loci were amplified and the mean number of alleles was 7.3 per locus, allowing identification of individuals even in samples for which not all loci could be amplified (27%).

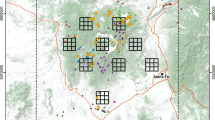
Table 2 Spatial encounter histories of 20 stoats identified by DNA microsatellites in hair samples collected daily on 7 parallel lines of sampling stations A–G; spacing 500 m between lines and 250 m along lines. Matakitaki, South Island, New Zealand, 15–21 December 2001. ‘–’ indicates the stoat was not detected. There were no multiple records (>1 stoat per trap or >1 trap per stoat on any occasion)
Full size table

The dataset included 20 individuals of which 7 were ‘recaptured’ a total of 10 times (Table 2). The largest detected movement (707 m) was small relative to the usual home range size of stoats (the average home-range diameter of stoats in New Zealand is at least 1.3 km; data from King and Murphy 2005, Table 5.5), and individuals appeared to be localised within the grid (Fig. 1). No stoat was detected in more than one tube on the same day, although both the field methodology and the analysis allow for this.

Fig. 1
figure 1

Map of detections of individual stoats in red beech forest, Matakitaki Valley, South Island, New Zealand, 15–21 December 2001. Sampling stations (crosses) were on seven lines A–G; stations spaced 500 m between lines and 250 m along lines, with three additional detectors as shown. The first station on each line was on a forest-pasture edge. Lines are drawn between locations of the same individual on different occasions; locations are shifted slightly from the actual location for clarity

Full size image

We fitted a homogeneous Poisson density by maximising the full likelihood. For numerical integration we evaluated the function at 1024 evenly-distributed points in a rectangular area extending 1000 m beyond the grid. Modelling of even a single-session dataset such as this requires multiple choices: among forms for the detection function p s , and among models for variation in the parameters of p s in relation to previous capture and random individual variation. We did not collect data on occasion-, trap- or individual covariates (we note that sex determined from DNA would be a potentially useful covariate of g 0 and σ in this sexually dimorphic species).

Strictly territorial animals may have a ‘hard’ edge to their range that is best represented by a step function (p s (d) = 0 for d > range radius), but zero values for p s can cause problems when maximising the likelihood. Instead, we used the hazard function to emulate a step function by setting b = 100. Density estimates and confidence intervals were not noticeably affected by the form used for p s (halfnormal, hazard or negative exponential; Fig. 2), and asymptotic intervals resembled profile likelihood intervals (Table 3). We also fitted models with additional parameters allowing for a response to previous capture (Mb(g 0), np = 4) or random individual variation using a 2-class finite mixture (Mh2(g 0), Mh2(σ), np = 6), but these barely increased the maximised log likelihood (ΔLL < 0.05) and were clearly inferior by AIC.

Fig. 2
figure 2

Detection functions p s (d) fitted to stoat data from proximity detectors in the Matakitaki Valley, New Zealand, where d is the distance between an animal’s home range centre and a detector. Density estimates (Table 3) were stable despite the considerable variation in the fitted detection functions

Full size image
Table 3 Comparison of models for density and spatial detection of stoats, fitted to data from hair samples collected in the Matakitaki valley, South Island, New Zealand, December 2001. LL = maximised log-likelihood, np = number of parameters. See Section 4 for calculation of asymptotic confidence intervals
Full size table

7 Single-Catch Traps

Single-catch traps are used very widely in studies of small mammals, and biologists will ask whether such data may be analysed with the methods described here. Competition for single-catch traps breaches the model assumption that animals are caught independently. We expect any resulting bias to be small when trap saturation (the proportion of traps occupied) is low. Trap saturation will be higher when population density is high, the intervals between trap checks are longer, traps are highly attractive or the animals are inherently very trappable.

With high trap saturation we would intuitively expect density estimates from single-catch trap data analysed with multi-catch models to be biased downwards. We conducted simulations to test this prediction for a scenario in which 100 traps on a square grid with spacing c were operated for 5 occasions. Notional home range centres were placed at expected density D in a rectangular area extending 4c beyond the traps. Three distributions were compared. In the first (‘Poisson’), centres were placed at random uniformly and independently across the area. For the second distribution (‘clustered’), centres followed a Neyman-Scott distribution in which the foci of clusters were from a spatial Poisson process with intensity D/μ, and μ range centres were located around each focus according to a bivariate normal distribution with scale σc; the clustering parameters were set to μ = 5 and σc = c. For the third distribution (‘inhomogeneous Poisson’), centres were placed independently, but with a linear gradient in expected density from east to west, from zero at –4c from the western-most traps to 2D at +4c from the eastern-most traps (the gradient over the traps themselves was from 0.47D to 1.53D). Detection was simulated with a halfnormal function (g 0 = 0.2, σ = c) using the algorithm in Efford (2004, Appendix) to allow for competition between traps for animals and between animals for traps. Simulated average densities spanned the range 0.0625σ–2– 2σ–2; 100 replicate simulations were performed for each level of density. For estimation, a halfnormal detection function was fitted by maximising the conditional likelihood for multi-catch traps (see Eqs.(2), (3), (4), (6)). Trap saturation was measured by the proportion of traps occupied at the end of each occasion. Relative bias is estimated by\( RB(\hat \nu ) = {\frac{\hat \nu - \nu }{\nu} } \), where υ represents any of the parameters D, g 0 and σ.

Our simulations detected no bias in \( \hat D \) for a Poisson distribution, even when 86% of traps were occupied (Table 4). Clustering of home range centres caused no detectable bias in\( \hat D \) at any level of trap saturation (Table 4b). The simulated gradient in density had a detectable effect only at the highest level of trap saturation, when the density estimates showed a 5% negative bias (Table 4c). These results are surprising. We note that \( \hat \sigma \) also remains unbiased at high levels of trap saturation, whereas \( \hat g_0 \) becomes negatively biased. We infer that competition for traps causes a spatially homogeneous reduction in capture probability under the conditions of these simulations, and that this is adequately modelled by a multi-catch likelihood with lower g 0. We tentatively conclude that the associated estimator for D may be sufficiently robust to use for single-catch traps without further development. Extreme trap saturation should be avoided by increasing the density of traps or the frequency of trap checking, if only because the additional captures will increase precision.

Table 4 Simulation of bias in density and detection parameters estimated by spatially explicit capture recapture when data are from single-catch traps and the fitted model assumes multi-catch traps. Simulations used one of three alternative distributions for animal range centers. Results are mean ± SE over 100 replicates. Density is expressed in terms of σ (1.0 σ–2 × 16 is equal to 6.25 ha–1 when σ = 10 m, and 0.0625 ha–1 when σ = 100 m). Trap saturation is the proportion of occupied traps at the end of each occasion
Full size table

8 Discussion

Many general benefits accrue from the estimation of density in a likelihood-based framework (Borchers and Efford 2007). Attention is shifted from the artificial parameters N c and A c to the ecologically significant parameter D. The model may be applied to any configuration of detectors, and is not restricted to compact arrays such as trapping grids (Efford et al. 2005). Differences between individuals in capture probability due to spatial location can be modelled with these methods and so do not result in unmodelled heterogeneity, the bane of conventional population estimation (there may of course be other sources of unmodelled heterogeneity). Hypotheses for variation in density over time or space may be evaluated using nested models and likelihood ratio tests. The fitted model describes the detection process and may be used in simulations to evaluate the effect of altering the study design, for example by changing the number and placement of traps.

To these general benefits we now add the ability to adapt the analysis for specific types of detector, for greater realism in modelling the detection process. In the case of proximity detectors, the model embraces the possibility of detecting an individual at multiple points on one occasion. Our results support the tentative use of a multi-catch model with data from single-catch traps if the goal is unbiased estimation of density. However, estimates of the detection parameter g 0 by this method are highly biased by trap saturation, and the method of simulation and inverse prediction (Efford 2004) should be used to fit the full process model to data from single-catch traps if it is intended to use the process estimates in simulations.

Our stoat example establishes the feasibility of applying spatially explicit capture-recapture methods to quite small data sets. Precision increases with the number of recaptures (Efford et al. 2004; M. G. Efford unpubl.), and it is generally desirable to obtain at least 20 recaptures. There was a promising robustness to the choice of detection function. Robustness of density estimates to the shape of the fitted detection function (step function vs halfnormal) was also found in simulations using inverse prediction (Efford 2004). Passive DNA sampling (e.g. Woods et al. 1999; Mills et al. 2000; Boulanger and McLellan 2001; Boulanger et al. 2004) and camera traps (e.g. Karanth and Nichols 1998; Trolle and Kéry 2003; Soisalo and Cavalcanti 2006) are used increasingly for mobile and difficult-to-trap animals such as carnivores. We expect our likelihood for proximity detectors to be widely applicable, assuming reliable identification of individuals.

The three detector types introduced so far do not exhaust the possibilities. A ‘one-shot’ proximity detector would become disabled once it detected an animal, but would not prevent the animal from finding another detector. Examples are a camera that does not reset itself, or hair sampling for DNA by some method that blocks collection of more than one sample per site per occasion (this might be desirable if sample mixing degrades the accuracy of identification). While there is no competition among detectors for animals, there is a sense in which animals ‘compete’ for access to ‘one-shot’ detectors. Equation (6) may possibly be adapted to allow for this by recasting it in terms of a trap-specific hazard rate.

A more difficult issue arises if the laboratory protocol is to reject all mixed DNA samples because individuals cannot be distinguished with confidence. Censoring mixed samples effectively creates a new type of detector (one which works only if fewer than two animals use it). At present we lack a satisfactory model for p ks with this detector, as with single-catch traps. Field methods should be adapted to minimise the frequency of mixed samples (e.g. by frequent checking of devices). For analysis, we advise the use of simulation-based methods (e.g. Efford 2004) or cautious application of the proximity detector or multi-catch likelihoods; simulations should be used to check that the bias in the estimates is small relative to sampling error.

Other types of single-catch and multi-catch detector may remove animals permanently from the population. Used alone, these are not useful for fitting movement-based models such as we describe, because in the absence of recaptures we have no information on the scale of movements. However, such detectors may in principle be used in composite arrays with other detectors described here.