Magnetic Tweezers for Single-Molecule Experiments

Abstract

Over the last decade, single-molecule techniques have proven their wide applicability in the study of processive motor proteins and other enzymes, yielding insight into their kinetics and mechanochemistry. In the context of force spectroscopy of protein–nucleic acid interactions, optical tweezers, magnetic tweezers, and atomic force microscopy have made important contributions. Advantages of magnetic tweezers include particularly straightforward control of the supercoiled state of DNA, facile extension to parallel measurement of multiple molecules and to integration with fluorescence measurements, and the simplicity and robustness of the experimental configuration. This chapter reviews the principles behind magnetic tweezers and their experimental implementation and points out recent improvements. It also describes several types of experiments that can be performed using magnetic tweezers.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

13.1 Introduction

Nucleic acids (i.e., DNA and RNA) can exist in different structural forms that perform various functions in vivo. For example, double-stranded DNA (dsDNA) is mostly responsible for the storage of genetic information. Alternatively, single-stranded DNA (ssDNA) acts as an intermediate in biologically relevant processes such as DNA replication and recombination, as well as in the storage of viral genetic information [1–3]. RNA, which is predominately present in a single-stranded form (ssRNA), takes part in processes as diverse as transcription, protein translation, and gene regulation, and also acts as a carrier of genetic information in ssRNA viruses [4]. Its double-stranded counterpart (dsRNA) is present as a biological intermediate (e.g., in RNA silencing) and as a carrier of genetic information in dsRNA viruses [5–7].

The different structural forms adopted by nucleic acids have a number of consequences. For instance, the predominately double-stranded nature of DNA leads to the structural complexity of supercoiling: If torsion is applied to dsDNA, the molecule, provided that it is torsionally constrained, can acquire additional twist or form looped structures. This additional intertwining of the strands in dsDNA poses a number of topological problems during fundamental processes such as cell cycle progression and cell division [8]. In addition, the structural forms of nucleic acids are not necessarily static structures but are instead constantly being converted from one to the other by cellular signals such as protein binding or enzyme activity.

Of interest, the mechanical properties of the various structural forms of nucleic acids (e.g., persistence length) change in response to their interconversion or protein binding and enzyme activity. Magnetic tweezers (MT) can probe these mechanical properties very sensitively and thus enable real-time detection of changes in nucleic acid state [9]. In addition, MT provide a way to perform force-dependence measurements at forces as low as ∼10 fN, which is lower than what is possible with other single-molecule techniques. Furthermore, MTs have the ability to control the degree of supercoiling, making it a technique of choice for studying supercoiling-dependent processes such as prokaryotic DNA condensation and regulation of dsDNA supercoiling by topoisomerases.

Although MTs have predominantly been used as an experimental tool to investigate biological processes involving nucleic acids, they have also been successfully applied in studies of the mechanical properties of proteins [10–14], as well as of the mechanical response of cells [11,15–18]. This chapter discusses the MT experimental configuration, then describes current challenges from a nucleic acid perspective, and finally considers examples of MT studies of the mechanical properties of proteins.

13.2 Experimental Design of the Magnetic Tweezers

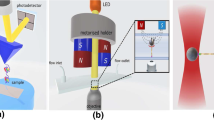
Figure 13.1 shows a schematic picture of a typical MT experimental configuration. At the heart of the experimental configuration is a flow cell: A nucleic acid is tethered in this flow cell between a glass surface and a paramagnetic bead (references to a “bead” in the remainder of the chapter imply this paramagnetic bead unless otherwise specified) by means of noncovalent bonds that can resist forces on the order of ∼100 pN [19–23]. Alternatively, the nucleic acid can also be suspended between a surface-immobilized nonmagnetic bead and a tethered bead [24,25]. Above the flow cell, a pair of permanent magnets or an electromagnet is suspended, exposing the flow cell to a magnetic field B [26]. The magnetic field exerts an upward stretching force F on the bead given by

$$\overrightarrow {\textbf{F}} = \frac{1}{2}\overrightarrow \nabla \left( {\overrightarrow {\textbf{m}} \cdot \overrightarrow {\textbf{B}} } \right)$$

((13.1))

where $\overrightarrow {\textbf{m}}$ is the induced magnetic moment of the bead in an external magnetic field, $\overrightarrow {\textbf{B}}$. The bead and the nucleic acid experience a constant F because the length scale of the motion of the tethered bead (typically micrometers) is small compared to the length scale of changes in the magnetic field B (typically millimeters; Section 13.7). The force F can be decreased or increased by moving the permanent magnets either up or down as the local magnetic field gradient is decreased or increased, respectively. MTs can apply a wide range of forces between ∼10 fN and ∼100 pN. At forces less than ∼10 fN, the bead is very close to the surface, where the interactions with the surface become dominant over the applied force. On the other hand, at forces greater than ∼100 pN, the majority of bonds that are used to tether the molecule to the surface are not stable.

Figure 13.1.

Schematic representation of a magnetic tweezers (MT) experimental configuration. A flow cell is built up from two microscope cover slips separated at the edges by a thin layer of parafilm approximately ∼0.2 mm thin. In the top cover slip, two holes are drilled that are connected to an inlet and an outlet reservoir, allowing solutions to be flushed in and out of the cell using a pump. Polymers are attached to the bottom surface at one end and to a paramagnetic bead at the other end. A reference bead is located in the vicinity of the tethered paramagnetic bead and is fixed to the bottom cover slip surface. Above the cell, a parallel light source is located, as well as a pair of permanent magnets, that can be translated and rotated, making it possible to vary force and torque on the paramagnetic bead. There are two possible magnet configurations: horizontal and vertical. Below the bottom cover slip, an objective is located that is connected to a charge-coupled device (CCD) camera that records the image from the objective focal plane. A controller containing a piezoelectric crystal can adjust vertical position of the objective’s focal plane. LED, light-emitting diode.

An external magnetic field will induce a major component of the magnetic moment to align in the direction of $\overrightarrow {\textbf{B}}$. Due to a slight anisotropy in the magnetization of the bead, a minor component of the magnetic moment,$\overrightarrow {\textbf{m}}_{\textbf{0}}$, is initially not aligned with $\overrightarrow {\textbf{B}}$. This generates a torque, $\overrightarrow {\boldsymbol{\Gamma }}$, on the bead:

$$\overrightarrow {{\boldsymbol\Gamma }} = {\overrightarrow{\textbf{m}}}_{\textbf{0}} \times {\overrightarrow{\textbf{B}}}$$

((13.2))

Rotating the magnets results in a rotation of the bead because the torque applied by the nucleic acid on the bead is negligible compared to the torque imposed by the magnetic field.

In the most common optical configuration, the bead is illuminated by parallel light placed above the flow cell and the magnet (Figure 13.1). The interference of the illuminating light with the light scattered by the bead produces concentric diffraction rings in the focal plane of the objective placed below the flow cell. The image of the diffraction pattern is recorded through an objective with a charge-coupled device (CCD) camera and analyzed with a computer (see Section 13.3). Furthermore, MT applications have been developed in which the nucleic acid is suspended between two beads rather than a bead and a glass surface [24,25]. In these applications, one bead is magnetic and the other is nonmagnetic and immobilized on a solid support, with the objective positioned perpendicular rather then parallel to the tethered nucleic acid [24,25].

13.3 Image Analysis

An MT experiment enables a real-time measurement of the vertical extension of the nucleic acid, l, as well as computation of the applied force, F. To extract these parameters from the acquired data, image analysis of the diffraction pattern recorded by the CCD is required. To monitor l, a method first designed by Gosse and Croquette is used, in which the objective’s focal plane (OFP) is accurately shifted in the vertical direction while the diffraction rings of the bead attached to the nucleic acid are imaged (Figure 13.2A–D) [9]. In this manner, a calibration profile can be generated correlating the diffraction pattern of the bead to the distance between the bead and the OFP (Figure 13.2E). When this calibration profile is interpolated, the vertical displacements of the bead can be measured with an accuracy of up to ∼10 nm [9]. If one then measures a similar calibration profile for a reference bead fixed to the surface in the proximity of the tethered bead, a distance between the surface and OFP can be determined. Finally, the difference between the two measured distances yields l. The measurement of the calibration profile of the reference bead also allows one to perform a differential measurement between the tethered bead and the reference bead, minimizing the effect of drift between the objective and the sample holder (i.e., flow cell). To compute the applied force, both the mean vertical extension of the nucleic acid and the bead’s in-plane fluctuations are required (see Section 13.4). The latter are computed via cross-correlation analysis of the intensity profiles displayed by a bead at subsequent time intervals [27,28]. As in the case of tracking the vertical position, in-plane tracking can be carried out at subpixel resolution to an accuracy of a few nanometers [9].

Figure 13.2.

Generation of a calibration profile in the z direction for a bead in magnetic tweezers. A 10 × 10 μm image of the diffraction pattern of a reference bead with a diameter of ∼3 μm at different positions of the objective’s focal plane (OFP). First, the OFP is positioned close to the bead (A). Next, the OFP is moved away from the bead, and the images of the diffraction rings are recorded at successive positions of the OFP (B–D). If the bead is illuminated with a parallel light source, the diffraction pattern of the bead will always be identical when the objective is focused at the same relative distance from the bead. By recording the size and intensity of the diffraction rings at different positions of the OFP a calibration profile can be made (E), which can be used to measure vertical relative displacements of the bead with an accuracy of ∼10 nm, limited by the resolution of the piezo that controls the position of OFP.

13.4 Determination of the Applied Force

The applied force can be determined from the fluctuations of the in-plane position of the bead, provided that we know the extension of the nucleic acid, l (Figure 13.3) [9,29]. Two forces act on the bead: (1) the applied magnetic force (referred to as the “applied force” in the remainder of the chapter) and (2) the restoring force exerted by the nucleic acid. The total potential energy of the system E_p thus equals

$${\textrm{E}}_{\textrm{p}} {\textrm{ }} = {\textrm{ E}}_{{\textrm{NA}}} {\textrm{ }} + {\textrm{ E}}_{{\textrm{mag}}} = {\textrm{A}}(l){\textrm{ }} - {\textrm{ }}Fz$$

((13.3))

where A(l) is the mechanical energy stored in the nucleic acid, which depends on the end-to-end extension of the nucleic acid l, and F is the applied force acting on the bead. In equilibrium, where the position of the bead $(x,y,z) = (0,0,l) = \overrightarrow {{\textbf{r}}_{\textbf{0}} }$, all partial derivatives of the total potential energy are equal to zero. The potential gradient in the z direction can thus be expressed as

$$\frac{{\partial {\textrm{E}}_{\textrm{p}} }}{{\partial z}} = \frac{{\partial {\textrm{A}}(l)}}{{\partial z}} - F = \frac{{\partial {\textrm{A}}(l)}}{{\partial l}} - F = 0$$

((13.4))

resulting in F = ∂A/∂l. Brownian motion constantly forces the system out of its equilibrium position (indicated by the dotted outline of the bead in Figure 13.3). A Taylor expansion around the equilibrium position yields to leading order:

$$\frac{{\partial ^2 {\textrm{E}}_{\textrm{p}} }}{{\partial x^2 }} = \frac{{\partial ^2 {\textrm{E}}_{\textrm{p}} }}{{\partial y^2 }} = \frac{F}{l}$$

((13.5))

$$\frac{{\partial ^2 {\textrm{E}}_{\textrm{p}} }}{{\partial z^2 }} = \frac{{\partial F}}{{\partial l}}$$

((13.6))

yielding an expression for the total potential energy around the equilibrium position:

$${\textrm{E}}_{\textrm{p}} (\overrightarrow {{\textbf{r}})} \approx {\textrm{E}}_{\textrm{p}} (\overrightarrow {{\textbf{r}}_{\textbf{0}} )} + \frac{1}{2}\left( {\frac{F}{l}} \right)\delta x^2 + \frac{1}{2}\left( {\frac{F}{l}} \right)\delta y^2 + \frac{1}{2}\left( {\frac{{\partial F}}{{\partial l}}} \right)\delta z^2 $$

((13.7))

Setting the potential energy in equilibrium position to zero, we can approximate the contribution of the displacement in the direction of the magnetic field (i.e., the x direction) to the average potential energy by the expression

$$\left\langle{\textrm{E}}_{\textrm{p}}\right\rangle = \frac{1}{2}\frac{F}{l}\left\langle {\delta x^2 } \right\rangle $$

((13.8))

where F/l represents an effective trap stiffness in the x direction, k _x ; and $\left\langle {\delta x^2 } \right\rangle$ is equal to the variance of the bead excursions in the x direction around its equilibrium position at $x_0 = 0$:

$${\mathop{\textrm var}} \, \delta x \equiv \left\langle {\delta x^2 } \right\rangle - \left\langle {\delta x} \right\rangle ^2 = \left\langle {\delta x^2 } \right\rangle $$

((13.9))

By the equipartition theorem, the energy of this degree of freedom equals ½k _B T. Rearranging terms, this yields a simple expression for the applied force,

$$F = \frac{{k_{\textrm{B}} Tl}}{{\left\langle {\delta x^2 } \right\rangle }}$$

((13.10))

By measuring the extension of the molecule l and the variance of the bead excursions $\left\langle {\delta x^2 } \right\rangle$ in real space, one can thus evaluate the applied force from Eq. (13.10). Figure 13.4 shows an example of the determination of $\left\langle {\delta x^2 } \right\rangle$ and the subsequent calculation of the applied force using Eq. (13.10). A comparison of the bead excursions measured at two different forces confirms that the excursions of the bead center in the (x, y) plane indeed decrease with an increase in the applied force as predicted by Eq. (13.10) (Figure 13.4A). The actual value $\left\langle {\delta x^2 } \right\rangle$ is obtained, however, from the statistical analysis of x position of the bead as a function of time (Figure 13.4B). Subsequently, $\left\langle {\delta x^2 } \right\rangle$ and l can then be used to compute the applied force (Figure 13.4C). In practice, the use of Eq. (13.10) is limited to a certain force range. In particular, at forces greater than ∼1 pN the measurement of $\left\langle {\delta x^2 } \right\rangle$ in real space shows a systematic error that can be corrected in Fourier space as described in the next section.

Figure 13.3.

A schematic representation of a tethered bead with a reference bead fixed to the bottom cover slide. The paramagnetic bead (orange) is tethered by a nucleic acid polymer to a surface. In the magnetic field gradient the paramagnetic bead experiences a vertical stretching force F. The paramagnetic bead is constantly displaced from its equilibrium position (vertical dashed line) by Brownian motion of the solvent molecules. The displacements of the tethered paramagnetic bead δx are measured relative to a nonmagnetic reference bead that is fixed close to the surface (gray) to compensate for sample drift.

Figure 13.4.

Measuring the applied force using the fluctuations in bead excursions in real space. A. The excursions of the bead center in the (x, y) plane for low force (red) and higher force (green). The data points for the low force have been offset for better representation. B. The bead excursion in the x dimension in time (the low-force measurement from panel A is shown), with a histogram on the right, including a Gaussian fit to the histogram. C. The computed variance of the bead excursions (not obtained from a fit to the Gaussian) for a variety of magnet positions (red solid circles), as well as the calculated corresponding forces (blue solid squares).

13.4.1 Calculation of the Applied Force—Analysis of the Brownian Motion of the Bead in Real and Fourier Space

Although it is possible to calculate the applied force using Eq. (13.10) in real space, the computation of $\left\langle {\delta x^2 } \right\rangle$ is typically performed in Fourier space because it allows for a more accurate determination. Namely, by decomposing the fluctuations in bead excursions into their spectral components, one can, for instance, compute corrections for the sample drift and the finite integration time of the CCD camera; these necessary corrections become larger as the applied force increases (see the discussion on the correction for the camera integration time in Section 13.4.2).

In Fourier space, $\left\langle {\delta x^2 } \right\rangle$ can be calculated by integrating the power spectrum of the bead motion:

$$\left\langle {\delta x^2 } \right\rangle = \frac{1}{{{\textrm{2}}\pi }}\int {{\textrm{P(}}\omega {\textrm{)}}d\omega } $$

((13.11))

where P(ω) is the power spectrum [30]. To derive the theoretical power spectrum P(ω) of the motion of the bead in the x direction, we consider the equation of motion of the bead:

$$m\frac{{\partial ^2 {\textrm{x}}(t)}}{{\partial t^2 }} = - {\textrm{6}}\pi R\eta \frac{{\partial {\textrm{x}}(t)}}{{\partial t}} - k_x {\textrm{x}}(t) + {\textrm{f}}_{\textrm{L}} {\textrm{(}}t{\textrm{)}}$$

((13.12))

where m is the mass of the bead, x(t) is the bead position in time, η is the viscosity of the buffer, R is the radius of the bead, k _x , = F/l (Eq. 13.8), and f_L is a Langevin force at a given bandwidth caused by Brownian fluctuations of the bead. Taking the Fourier transform of Eq. (13.12) gives

$${\textrm{X(}}\omega {\textrm{)}} = \frac{{{\textrm{F}}_{\textrm{L}} {\textrm{(}}\omega {\textrm{)}}}}{{ - m\omega ^2 + {\textrm{6}}\pi i\eta R\omega + k_x }}$$

((13.13))

where $i = \sqrt { - 1}$. Here $F_{\textrm{L}} (\omega ) = 2\sqrt {6k_{\textrm{B}} T\pi \eta R}$ represents the square root of the power spectrum density of f_L [31]. With typical values for m and R of the bead equal to 10⁻¹⁵ kg and 10⁻⁶ m, respectively, along with η = 10⁻³, k _x = 10⁻⁹ N/m, and ω = (k _x /m)^½ ∼ 1 kHz, the inertial term mω² is significant only at frequencies ω > ∼6πηR/m ∼ 30 MHz. Because the sampling frequency of the camera is considerably smaller (typically ∼100 Hz), the inertial term can be neglected in both Eqs. (13.12) and (13.13). Defining ω _c = k _x /6πηR and assuming F_L(ω) to be constant, we find that the square of Eq. (13.13) yields the theoretical power spectrum:

$${\textrm{P(}}\omega {\textrm{)}} = \left| {{\textrm{X}}^{\textrm{2}} {\textrm{(}}\omega {\textrm{)}}} \right| = \frac{{{\textrm{F}}^{\textrm{2}} {\textrm{(}}\omega {\textrm{)}}}}{{\left( {1 + \dfrac{{i\omega }}{{\omega _c }}} \right)^2 k_x ^2 }} = \frac{{2k_B T6\pi \eta R}}{{\left( {1 + \left( {\dfrac{\omega }{{\omega _c }}} \right)^2 } \right)\pi k_x ^2 }}$$

((13.14))

Equation (13.14) is a Lorentzian, and by fitting the experimental power spectrum to Eq. (13.14) we obtain ω _c , which can be used to calculate k _x and subsequently the applied force F. Alternatively, the applied force can be calculated using $\left\langle {\delta x^2 } \right\rangle$ [Eq. (13.10)], which is determined by integration of the experimental power spectrum over all frequencies:

$$\left\langle {\delta x^2 } \right\rangle = \int\limits_0^\infty {\frac{{24\pi k_{\textrm{B}} TR}}{{\pi k_x^2 }}} \frac{1}{{1 + (\omega /\omega _c )^2 }}d\omega $$

((13.15))

Experimentally, the integral in Eq. (13.15) is determined within a finite signal bandwidth at the high-frequency limit at half of the sampling frequency f _s and at low frequency at the inverse of the data acquisition time f _L = T _a ⁻¹. Equation (13.15) can thus be used, provided that f _L << f _c << f _s /2, where f _c is the cutoff frequency of the system and f _c = ω _c /2π [9]; otherwise one does not have a statistically accurate determination.

Let us now compare the evaluations of the applied force in the real space and in Fourier space. The experimentally derived power spectra for the same two forces as employed in Figure 13.4A are shown in Figure 13.5A. The integration of the experimental power spectra (Figure 13.5B) yields corresponding variances that are in turn used to calculate the applied forces (Figure 13.5C). It is clear from the Figure 13.5C that the forces calculated in real space (red triangles in Figure 13.5C) overestimate the applied force, particularly at high forces, where larger excursions due to rapid fluctuations tend to be averaged out.

Figure 13.5.

Measuring applied force in Fourier space. A. The spectra of the one-dimensional fluctuations for the same two forces as shown in Figure 13.4A. The spectrum is relatively flat until the cutoff frequency f _c (see text), after which they decay with 1/f ². Note qualitatively here that f _c increases with applied force. B. The integral of the spectra shown in panel A; the variance of the bead excursions can be obtained by integrating the spectra. Note that the variance decreases with increasing applied force. C. A comparison between the force measurement in real space (red solid triangles) and Fourier space (blue solid circles). In the low-force regime (less than ∼1 pN), the two methods yield similar results. Only at higher forces, where the fluctuations of the bead are fast, does one run into the problem of underestimating the variance of the bead fluctuations, leading to an overestimation of the applied force.

13.4.2 Correction for the Camera Integration Time

The calculation of the variance of the bead excursions necessary for the determination of the applied force requires a measurement of an accurate position of the bead. The systems commonly used to detect the image of the bead (e.g., a CCD camera) record the image for a finite time interval to acquire sufficient signal. Consequently, the acquired image does not reflect an instantaneous position x but instead a “blurred” average of instantaneous positions x _m explored by the bead during the finite time interval [9,30]. The correction for the camera integration time is derived below and follows that by Wong and Halvorsen [30].

In the case of a rectangular integration time window, the relation between the average x _m and x at time t can be obtained by convolving the true trajectory in x with a rectangular function [30]:

$$x_m (t) = \int\limits_{t - W}^t {x(t^{\prime}){\textrm{H(}}t - t^{\prime})} {\textrm{ }}dt^{\prime}$$

((13.16))

where ${\textrm{H(}}t{\textrm{)}}$ is defined as

$${\textrm{H(}}t{\textrm{)}} = \left\{ \begin{array}{l} \dfrac{1}{W}\begin{array}{*{20}c} {} \\ {} \\ \end{array}0 < t \le W \\ 0\begin{array}{*{20}c} {} \\ {} \\ \end{array}\begin{array}{*{20}c} {} \\ {} \\ \end{array}Elsewhere \\ \end{array} \right.$$

((13.17))

where W is the integration time of the camera. Consequently, the true trajectory taken by the particle in the x direction cannot be extracted from a measurement with a finite integration time. However, assuming the bead is undergoing Brownian motion within a harmonic potential, variances in x _m and x can nonetheless be calculated, provided respective power spectra are known. The var(x) can be calculated using Eq. (13.15), and var(x _m ) can be expressed using the definition of variance in Eqs. (13.9) and (13.16) as

$${\mathop{\textrm var}} (x_m ) = \frac{1}{{2\pi }}\int {{\textrm{P(}}\omega {\textrm{)P}}_{\textrm{H}} {\textrm{(}}\omega {\textrm{)}}d\omega } $$

((13.18))

If the power spectrum of the moving rectangular integration window is written as [30]

$${\textrm{P}}_{\textrm{H}} = \left( {\frac{{\sin (\omega W/2)}}{{\omega W/2}}} \right)^2 $$

((13.19))

then Eq. (13.18) can be integrated to yield an expression for the variance in the measured position var(x _m ):

$${\mathop{\textrm var}} (x_m ) = \frac{{2k_{\textrm{B}} T}}{{k_x }}\left[ {\frac{\tau }{W} - \frac{{\tau ^2 }}{{W^2 }}\left( {1 - e^{ - W/\tau } } \right)} \right]$$

((13.20))

where τ = 1/ω _c . The var(x _m ) can be expressed in terms of var(x):

$${\mathop{\textrm var}} (x_m ) = {\mathop{\textrm var}} (x)\left( {\frac{2}{\alpha } - \frac{2}{{\alpha ^2 }}\left( {1 - e^{ - \alpha } } \right)} \right)$$

((13.21))

where α is a dimensionless exposure time W/τ. The expression in large parentheses on the right-hand side of Eq. (13.21) is referred to as the motion blur correction function [30]. This correction function has been experimentally verified over a range of parameters by Wong and Halvorsen [30].

The experimentally measured quantity var(x _m ) is thus expressed in terms of the quantity one would like to know, var(x), and the parameter α, which is a function of ω _c . An iterative procedure can be used to determine the value of var(x). One starts with the experimental power spectrum P_m(ω), undoes the effect of the camera windowing according to Eqs. (13.18) and (13.19), and finally fits the underlying spectrum P(ω) according to Eq. (13.14) to obtain a value for ω _c . This procedure is repeated until the fitting error is below a minimally acceptable value, at which point var(x) can be correctly computed from the fitted P(ω) using Eq. (13.15). This value for var(x) should comply with Eq. (13.21).

13.5 Nucleic Acids under Force and Torque

As described in Section 13.2, by controlling the distance between the magnets and the flow cell, one can control the force applied to the tethered bead. By rotating the magnets, one can apply a torque to the bead. The response of nucleic acids to such forces and torques can be analyzed using simple models of polymer physics. This section briefly reviews the behavior of DNA and RNA under applied force and torque.

If the bead in question is tethered to the surface by an unnicked, double-stranded nucleic acid molecule that is attached via multiple bonds at each end, the molecule is torsionally constrained and rotating the magnets will twist the DNA or RNA. In contrast, if the nucleic acid molecule that tethers the bead to the surface is attached only via a single bond at either end or if the molecule has a single or multiple nicks or is (partly) single-stranded, the molecule will swivel around the single bond(s) and remain torsionally unconstrained, even if the magnets are rotated.

The force–extension behavior of torsionally unconstrained double-stranded DNA molecules for forces less that 5–10 pN is well described by the worm-like chain (WLC) model (Figure 13.6A) [32–36]. The WLC model is a simple polymer model that treats the DNA as a homogeneous, isotropic polymer with a bending stiffness. It has two free parameters—the contour length L _c and the persistence length L _p. The length L _c is the total contour of the DNA, which is typically close to the crystallographic length, which is equal to 3.4 Å per base pair. L _p is the decay length of bending fluctuations, that is, the length scale over which the DNA undergoes significant bending [37]. Under typical experimental conditions (∼10–100 mM monovalent salt), L _p is approximately equal to 50 nm, and its value decreases slightly with increasing ionic strength. The WLC model was shown to also provide an accurate description of the force–extension behavior of double-stranded RNA, with L _p of 64 nm [38]. For forces >5–10 pN, enthalpic stretching of the DNA becomes significant and can be incorporated into the WLC model by adding an elastic stretching term [34]. At forces greater than 50–60 pN, DNA undergoes an overstretching transition [39,40].

Figure 13.6.

Behavior of double-stranded DNA under applied forces and torques. A. Force–extension curves of single 21-kbp DNA molecules. Symbols represent force measurements obtained from analysis of the spectrum of the bead fluctuations as described in Section 13.4. Solid lines are from fits of the worm-like chain (WLC) equation described in Section 13.5. The four different colors correspond to independent measurements with different magnet configurations, described in more detail in Section 13.7. The fits of the WLC equation gave contour lengths of 7.1 ± 0.2 μm and persistence lengths of 47 ± 3 nm (mean and standard deviation, respectively). B. DNA extension as a function of magnet rotations for a torsionally constrained 21-kbp DNA molecule at forces of 0.25 pN (black), 1 pN (brown), and 5 pN (light brown). At low forces (<1 pN) the formation of plectonemic supercoils is symmetric for positive and negative coiling. At higher forces, plectonemic supercoils are formed under positive torque, but the DNA denatures locally when a negative turn is applied, as can be seen from the asymmetry of the curves at 1 and 5 pN. The points at which the buckling transition into the plectonemic regime occurs at positive torques are denoted by errors. The slopes in the plectonemic regime (solid lines) give the change in extension per turn, Δz. C. Change in DNA extension per turn, Δz, deduced from the slopes of rotation curves (as in panel B). Black symbols show the results of magnetic tweezers measurements from our lab. Red symbols are the data of Forth et al. obtained using optical torque tweezers [42]. The green solid line shows the prediction of the simple model derived in the text. The blue solid line is the prediction of the Marko model, with a plectoneme helicity of 24 nm.

White showed that for torsionally constrained DNA the linking number Lk is a topological invariant [41]:

$$Lk = Tw + Wr = {\textrm{const}}$$

((13.22))

Tw is the twist of the double helix, defined as the number helical turns in the double helix of DNA. For torsionally relaxed DNA the natural twist Tw ₀ of DNA is equal to the number of base pairs divided by the helical turn (10.5 bp per turn). The writhe Wr is the number of times the axis of the double helix crosses itself. In the absence of external constraints, the writhe is zero, Wr ₀ = 0. A molecule is said to be supercoiled when its linking number is different from Lk ₀ = Tw ₀ + Wr ₀ . A useful quantity in this context is the supercoil density σ:

$$\sigma = \frac{{Lk - Lk_0 }}{{Lk_0 }}$$

((13.23))

Rotating the bead attached to a torsionally constrained nucleic acid changes Lk, as shown in Figure 13.6B. Starting from a torsionally relaxed molecule, the change in linking number is initially absorbed by elastic twist deformations and increases Tw of the molecule, whereas Wr remains unchanged. In this regime, the torque Γ increases linearly with the number of turns N:

$$\Gamma = C\frac{{2\pi N}}{{L_{\textrm{c}} }}$$

((13.24))

where C is the torsional modulus; C ≈ 90k _B T for DNA [43,44]. If one continues to rotate the magnets, the molecule undergoes a buckling transition when the energy stored in the elastic twisting deformation is reduced by forming a loop (see the arrows in Figure 13.6B). Further rotations past the buckling transition do not increase Tw but instead increase Wr as plectonemic supercoils are formed. A simple model for the buckling torque Γ_B and the size of the plectonemes can be derived by assuming a loop of size R [42,43]. At Γ_B, the work done by one more turn is 2πΓ_B and equals the work required to form a loop of size R:

$${\textrm{E}}_R = 2\pi RF + \frac{{\pi L_{\textrm{p}} k_{\textrm{B}} T}}{R}$$

((13.25))

where the first term corresponds to the work done against the external (magnetic) force F and the second term is the work required to bend a stiff polymer into a loop of radius R. By minimizing E _R with respect to R, one finds for Γ_B and for the change in extension per superhelical turn (Δz) [43,44]

$$\Gamma _{\textrm{B}} = \sqrt {2L_{\textrm{p}} k_{\textrm{B}} TF} {\textrm{ and }}\Delta {\textrm{z = }}2\pi R = \pi \sqrt {\frac{{2L_{\textrm{p}} k_{\textrm{B}} T}}{F}} $$

((13.26))

This simple model qualitatively yields the right trends. In particular it predicts an increase in Γ_B and a decrease in the shortening of the DNA per turn with increasing applied force. However, it fails to quantitatively match the experimental data, in particular at low forces (Figure 13.6C). To describe the elastic response of twisted DNA more accurately, a number of models have been developed. Recently, Marko derived an analytical model that includes an additional parameter—the twist stiffness of the plectonemic state [45]. The Marko model provides additional physical insight and improves the fit to the experimental data in the force range >1 pN. However, it asymptotically approaches the result of the simple model at low forces and fails to accurately match the experimental data below ∼1 pN (Figure 13.6C). In addition, neither model explicitly accounts for the effect of ionic strength. Experimentally, increasing the ionic strength of the solution decreases Δz at constant force, which is qualitatively expected because increased electrostatic screening makes smaller plectonemic loops energetically less costly. Neukirch and coworkers derived a theoretical framework for obtaining the effective plectoneme radius from experimental data [46,47]. Another description of DNA under force and torque is the rod-like chain (RLC) model, an extension of the WLC model that considers twisting rigidity and twist–stretch coupling. The RLC model appears to yield an accurate description of twisted DNA under low forces; however, it can only be solved numerically [48–50].

13.6 Current Capabilities in Terms of Temporal and Spatial Resolution: Practical Limitations

The foregoing considerations described the experimental configuration of the MT and explained how it can be used to apply forces and torques to nucleic acids. Particularly in applications to nucleic acid–protein interactions, it is of interest to know with what resolution in both space and time one can monitor the molecule.

Assuming that one measure long enough (i.e., longer than 1/f _c ) to probe the full excursion probability distribution, one can obtain an unbiased and infinitely small spatial resolution by measuring an infinite number of time points. For a measurement of N data points, the accuracy with which one measures the x, y, or z position is given by the standard error of the mean (S_E):

$${\textrm{S}}_{\textrm{E}} = \frac{{{\textrm{SD}}}}{{\sqrt N }}$$

((13.27))

In other words, measuring faster will only lead to an increase in spatial resolution when the sampling takes place longer than 1/f _c , and thus f _c sets the temporal resolution. For example, with an acquisition frequency of 60 Hz, one obtains a spatial resolution of ∼30% in 200 ms, or 3% in 17 sec at 2 pN. According to Eq. (13.8), the MT trap stiffness decreases inversely with the length of the nucleic acid. A reduction in trap stiffness with nucleic acid length leads to a reduced $f_c$. MTs typically have a lower temporal (and in practice thus a lower spatial) resolution than other force-spectroscopy techniques such as atomic force microscopy and optical tweezers [26,51]. To a certain extent, this may be compensated by running experiments with short molecules at high forces, although the degree to which this is possible depends on the biological question being addressed. Nevertheless, the typical spatial resolution of MTs is between 2 and 10 nm, and their resolution is usually between 10^–2 and 10⁻⁴ sec.

13.7 Optimization of the Magnet Geometry

Section 13.4 described how the applied force can be calibrated from the motion of the bead using the equipartition theorem. This section discusses how the applied force from a pair of permanent magnets can be calculated from basic physics principles, without requiring measurement of any bead fluctuations. Being able to compute the magnetic force from first principles provides a consistency check on the calibration from the fluctuations in the in-plane position of the bead. More importantly, it provides physical insight and allows the design of magnet geometries for particular experimental specifications without the need to build and test a large number of magnet configurations.

The magnetic force exerted on a bead is given by the negative gradient of the magnetic energy [Eq. (13.1)]. To compute the force exerted by a given magnet configuration on a bead, both $\overrightarrow {\textbf{B}}$ and $\nabla \overrightarrow {\textbf{B}}$ at the position of the bead, as well as the value of $\overrightarrow {\textbf{m}}$ for a given external magnetic field, have to be determined. Two complementary strategies can be used to compute $\overrightarrow {\textbf{B}}$ for a given magnet configuration [52]. For simple symmetric geometries and in the absence of an iron yoke or other complicating factors, it is possible to compute the magnetic field from first principles using the Biot–Savart law [53]. In this case, the magnets are replaced by current loops using the method of equivalent sources and integrating their contributions to the magnetic field at any point in space. This approach is semianalytical: Only the one-dimensional integral derived from the Biot–Savart law needs to be evaluated numerically. The only property of the magnets (apart from their geometry) required for the calculation is their remnant field, which is available from the manufacturer’s specifications. Alternatively, the remanent field can be determined from a direct measurement of the surface field by using a Hall probe.

An alternative strategy to evaluating the magnetic field of arbitrary magnet geometries is to solve the magnetostatic problem using a three-dimensional (3D) finite-element partial differential equation solver. The Multiphysics AC/DC module from COMSOL has been used to build complete 3D models of several magnet geometries and to solve the magnetostatics problem numerically [52]. The finite-element approach can be applied to more complicated geometries. In addition, material properties of components of the setup, for example, an iron yoke or iron tips, can be included in the model.

To quantitatively assess the accuracy of magnet simulations, the magnetic field of a pair of permanent magnets has been measured using a Hall probe [52]. Figure 13.7A shows the magnetic field as a function of distance to the center of the magnet pair for a gap size (i.e., the distance between the magnets) of 1 mm and vertical (red and brown) and horizontal (light and dark blue) magnet alignments (see Figure 13.1 for a definition of the magnet alignments). Data are shown for the absence (red and light blue) and presence (brown and dark blue) of an iron yoke (Figure 13.7A). The semianalytical calculations (black dashed lines) are in excellent agreement with the results of the 3D finite-element modeling (solid lines) for the geometries without added iron yokes (Figure 13.7A). For the case of added iron yokes, only the finite-element solution was obtained. In addition, the theoretical predictions are in good agreement with experimentally measured values for the magnetic field (symbols in Figure 13.7A). Similar agreement for other gap sizes has been obtained. It should be emphasized that the lines in Figure 13.7 are direct predictions from magnetostatic theory, without any free fitting parameters. The data suggest that it is possible to accurately model the magnetic field of a pair of magnets from first principles.

Figure 13.7.

Calculations of magnetic fields and forces from first principles. A. Magnetic fields as a function of distances from the center of magnet pairs in the vertical (brown, red) and horizontal (light blue, dark blue) configuration. Data points are from measurements with a Hall probe in the absence (red, light blue) and presence (brown, dark blue) of an iron yoke. Solid lines show the results of corresponding calculations using a three-dimensional (3D) finite-element solver, and black dashed lines show the results of semianalytical calculations (Section 13.7). The inset shows the magnetization of MyOne beads from Invitrogen as a function of the external magnetic field as reported by the vendor. B. Magnet forces exerted on a 1-μm MyOne bead by the magnet configurations described in Figure 13.1 (with the same color code as in panel A). Symbols represent experimental results determined from the analysis of the bead’s fluctuations. Lines are predictions from 3D finite-element simulations (solid lines) and the semianalytical theory (black dashed lines). The region that is experimentally inaccessible due to the finite thickness of the magnets and the flow cell is shown as a shaded region in the plot. Force–extension curves for these data are shown in Figure 13.6A, using the same color code as here.

To compute the force exerted on a bead, knowledge of m in response to an external B is required. For beads commonly used in MT experiments, m is approximately described by the Langevin function [26], and these data are available from the literature (for Dynabeads MyOne beads from Invitrogen see Ref. 54 and the manufacturer’s Web site; for MagSense 1-μm beads see the technical support at the manufacturer’s Web site). The inset of Figure 13.7A shows m for MyOne beads as a function of the external B. Two regimes can be distinguished: For external B less than ∼50 mT, m increases approximately linearly with the external B, and, as a result, F will grow as $\nabla B^2$. For B greater than ∼100 mT, m saturates and is approximately constant. In this regime, F will be proportional to $\nabla B$. In typical MT configurations, B spans both the linear and saturation regimes, and, therefore, it is crucial to take into account the full magnetization behavior in the force calculation.

Figure 13.7B shows force measurements for the different magnet geometries considered in the foregoing using DNA-tethered MyOne beads. The theoretical predictions from semianalytical theory (dashed line) and from the 3D finite-element simulations (solid lines) are in good agreement with the direct measurements of the force from the observed fluctuations in the bead in-plane position (symbols; analyzed in Section 13.4). Several interesting observations can be made. For the horizontal magnet configuration and in the absence of an iron yoke (light blue lines), the force becomes negative, that is, the bead is pushed toward the surface. Experimentally, one cannot measure negative forces using the strategy outlined in Section 13.4; therefore only positive (i.e., pulling) forces are shown in Figure 13.7B. Adding an iron yoke to the setup suppresses the negative-force region for the horizontal configuration (dark blue curves). Of interest, addition of an iron yoke increases the maximum force that can be applied in either configuration only slightly.

The applied force decreases much faster with increasing distance to the magnets in the horizontal configuration than in the vertical configuration. For applications that require measurements at very low forces (<0.1 pN; Figure 13.6A), a horizontal magnet configuration is therefore desirable. For the horizontal configuration, reducing the gap size between the magnets does not significantly increase the maximum force that can be applied because the maximum of the force occurs at a position inside the gap between the magnets that is not experimentally accessible. In contrast, for the vertical magnet configuration, decreasing the gap size can significantly increase the maximum applicable force. For applications that benefit from large applied forces, a horizontal magnet configuration with a small gap size and a thin flow cell are therefore recommended. In addition, the choice of beads can be optimized for particular applications. For example, to maximize the forces that can be applied, large beads with a high magnetization per volume are desirable.

13.8 Flow Cells for Magnetic Tweezers

MT measurements require specially designed reaction chambers or flow cells. A flow cell must satisfy several criteria to be suitable for MT measurements. First, the walls of the flow cell have to be transparent for the light used to visualize the beads (e.g., quartz glass slides). Second, a flow cell requires an inlet and an outlet to enable an exchange of buffers during an experiment. Third, the inner surface of the flow cell opposite to the magnet must provide attachment points for the nucleic acid conjugated to the bead (Figure 13.1). Finally, the remainder of the inner surface not covered by the attachment points has to be passivated to prevent any nonspecific interactions that may interfere with the measurement of the extension of the nucleic acid or of the applied force (e.g., sticking of the nucleic acid and/or bead to the inner surface). The following paragraphs review the current strategies for nucleic acid labeling to suspend the nucleic acids between the bead and the glass surface, as well as ways to passivate the inner glass surface.

13.8.1 Strategies for Tethering Nucleic Acids to the Flow Cell and the Bead

To suspend a nucleic acid between the attachment point on the inner surface of the flow cell and the bead, the two extremities of the nucleic acid have to be specifically labeled with two different labels. The labels have to provide bonds that can resist the applied forces. The inner surface and bead are thus usually coated with either antidigoxigenin or streptavidin, whereas the corresponding extremities of the nucleic acid are labeled with their binding partners, digoxigenin or biotin, respectively [55]. The fluorescein–antifluorescein binding pair has also been used in MT and tethered particle motion (TPM) applications, with fluorescein placed on the nucleic acid end and antifluorescein adsorbed on the inner surface of the flow cell or attached to the bead [56,57]. Considering the stability of the fluorescein–antifluorescein binding pair against forces typically applied in MT studies, it is a viable alternative to the two standard binding pairs mentioned previously.

Labeling of nucleic acids can be carried out in several ways: (1) Generation of labeled DNA and RNA fragments by polymerase chain reaction (PCR) or in vitro run-off transcription, respectively, followed by their ligation to the corresponding nucleic acid terminus using DNA or RNA ligase [58,59]; (2) Chemical modifications of the nucleic acid ends [56,60–62]; (3) enzymatic extension of the nucleic acid ends with modified nucleotides using PolyA polymerase (pAP), terminal deoxynucleotidyl transferase (TdT), or T4 RNA ligase 1 (T4 RNL 1) [63–65]; or (4) hybridization of a labeled RNA or DNA strands that are complementary to the ends of the nucleic acid [38,58,59,66,67]. The choice of optimal labeling protocol for a particular application will primarily depend on the nature of the nucleic acid (i.e., DNA vs. RNA, and single- vs. double-stranded nucleic acid) [55]. Although ligation-based protocols have been applied with great success in DNA-related studies [55,68–70], the other protocols listed have been developed primarily for RNA-based applications due to the limited selection of molecular biology tools that can be used in the synthesis of RNA molecules. Finally, application of a torque in the MT requires a torsionally constrained double-stranded nucleic acid, which is most conveniently obtained by introducing multiple labels at each end of the nucleic acid using PCR and in vitro run-off transcription of corresponding DNA and RNA, respectively [38,58,68].

13.8.2 Inner Surface Passivation Techniques

Ideally, a nucleic acid molecule should be suspended between the inner surface and the bead in the absence of any interfering interaction among the nucleic acid, bead, and the inner surface. However, most of the reaction buffers used in in vitro biological reactions contain components that promote interaction of the nucleic acid and/or the bead with the flow cell surface (e.g., Mg²⁺) [71,72]. These interactions affect the measured extension of the nucleic acid, as well as the fluctuations of the bead, which prevents an accurate determination of the applied force and mechanical properties of the system under investigation. Thus, to prevent these interactions, the inner surface of the flow cell has to be passivated after the adsorption of the attachment points for the nucleic acid (e.g., antidigoxigenin, biotin, or fluorescein).

The most common way to passivate a flow cell surface is by adsorbing inert proteins (e.g., bovine serum albumin [BSA]) or polypeptides (e.g., poly-l-glutamic acid [PGA]) to the part of the surface not occupied by the nucleic acid attachment points [38,68,73]. Although both the passivating material and the nucleic acid attachment points can be adsorbed to bare glass with reasonable efficiency, an intermediate polystyrene layer has been commonly used to enhance their adsorption [38,68]. Alternatively, a monolayer composed of poly(ethylene glycol) (PEG) and biotinylated PEG has been successfully used to reduced nonspecific interactions between the inner surface and the components of the system [74] (for the properties of the PEGylated glass surface see Ref. 75). In addition, the authors’ lab has used nitrocellulose-based passivation of the flow cell surface [76], which is characterized by its ease of preparation and high density of nucleic acid tethers.

13.8.3 Considerations When Working with RNA

There are several reasons why MT experiments on RNA have been few and far between. First, during every step of MT experiments, RNA systems require special considerations not necessary in the case of DNA. For example, due to the lack of a molecular biology toolbox comparable to that for DNA, a combination of molecular biology and chemical techniques is required to assemble a viable RNA construct (for a comprehensive review of available techniques and protocols, see Ref. 55). Furthermore, a major obstacle to a wider application of MT to RNA-related research is the instability of RNA under in vitro conditions. As is widely acknowledged, there are two principal reasons why RNA is less stable than its deoxyribose counterpart, DNA: (1) the abundance of RNA-degrading enzymes—RNases—in the environment [77], and (2) RNA’s chemical instability due to the presence of 2^′-hydoxyl groups, which can serve as nucleophiles to attack their proximal phosphorous atoms, leading to a nucleophilic substitution and resulting in a cleavage of the phosphodiester bond [78]. Nevertheless, there are measures that can enhance RNA stability and enable a successful RNA MT study [38].

Whereas RNases are active under a wide range of conditions, the RNA phosphodiester bond cleavage by 2^′-hydoxyl group requires elevated temperatures and the presence of divalent ions as catalysts [79–82]. RNase nuclease activity in the MT can be inhibited by the use of both RNase-free reagents and commercially available RNase inhibitors. Alternatively, the cleavage of the phosphodiester bond by the 2^′-hydorxyl group can be considerably inhibited by the use of chelating agents that bind divalent ions (e.g., ethylenediaminetetraacetic acid or sodium citrate). In addition, the use of inert surfaces such as PEGylated glass slides further increases the stability of RNA constructs in the MT.

13.9 Use of Magnetic Tweezers in Biological Experiments: Examples

Having detailed the MT experimental configuration in the preceding sections, this section considers three different examples of experiments in which DNA–protein interactions have been monitored using MT. The first two examples depend on the unique ability of MT to easily control and monitor the degree of supercoiling in a single molecule of DNA. The ease with which this can be done has allowed researchers to probe the mechanical properties of supercoiled DNA and to study the activity of topoisomerases (Example 1) (Figure 13.8). It will also be shown how MT can be used to probe restriction enzymes, RNA polymerases, and translocases, whose primary function is not in supercoil regulation but whose activities can be monitored indirectly via the degree of supercoiling induced (Example 2) (Figure 13.9). In addition, it is shown how MT can be used to study processive translocating enzymes such as DNA helicases (Example 3) (Figure 13.10). Finally, recent MT studies on purely protein-based systems are reviewed (Example 4).

Figure 13.10.

Unwinding of a DNA helix by bacteriophage T4 helicase (gp41). A. Experimental configuration for studying gp41 unwinding of a DNA duplex, where the DNA hairpin is suspended between the glass surface and the bead. B. In the presence of gp41, the DNA hairpin is unwound, resulting in the lengthening of the DNA, followed by shortening as a consequence of rehybridization of the complementary strands back into a DNA hairpin. The initial increase and subsequent decrease in DNA extension results in the observed spikes. The majority of spikes correspond to the unwinding of the entire DNA hairpin (an example is indicated with a blue arrow). Occasionally, partial unwinding events can be observed as indicated by lower spikes (green arrow). (Adapted from Lionnet et al. [90]. Copyright 2007 National Academy of Sciences, USA.)

Figure 13.8.

Examples of magnetic tweezers studies of supercoil dynamics and removal. A. The dynamics of a supercoiled DNA molecule bound to a bead can be addressed in two ways. First, combined magnetic and optical tweezers were used as shown in the inset. The laser beam used to trap the bead is represented in pink. Alternatively, supercoils were removed in the presence of a nicking enzyme. The traces shown here were obtained with the combined tweezers setup for two different values of the magnetic force: 2.2 pN (inverted red triangles) and 4.1 pN (black squares). These traces monitor the end-to-end extension of the DNA molecule, which increases after release of the optical trap at t = 0 until it reaches its steady-state value under the magnetic force. The solid lines represent the quasistatic model that was used by the researchers to successfully describe the dynamics. B. Supercoil removal by topoisomerase IB. Topoisomerase IB first binds double-stranded DNA (dsDNA) (step I in the inset), cleaves one strand of the dsDNA, which allows the release of the supercoils (step II in the inset), and finally ligates the cleaved strand to yield back the intact dsDNA (step III in the inset). On supercoil release, the measured extension, z, increases.

Figure 13.9.

The experimental strategy employed to observe DNA untwisting by RNA polymerase (RNAP). A torsionally constrained molecule is held in molecular tweezers. Unwinding of DNA by RNAP will induce negative twist, which in a torsionally constrained molecule must be compensated by positive writhe. If the DNA prior to the unwinding by RNAP contains positive writhe, the activity of the RNAP will serve to further increase the writhe. This will lead to an observable decrease in the end-to-end extension of the DNA molecule (top). If the DNA prior to the unwinding by RNAP contains negative writhe, the activity of the RNAP will serve to make the overall degree of writhe less negative. Consequently, this will lead to an observable increase in the end-to-end extension of the DNA molecule, as indicated (bottom). (From Revyakin et al. [86]. Reprinted with permission from AAAS. American Association for the Advancement of Science.]

13.9.1 Example 1: Supercoils Dynamics, and Supercoil Removal

During cell division, the genetic material is copied, and the enzymes responsible for this must be able to access the base sequences. This is only possible if the portion of DNA to be replicated is unwound. Such DNA unwinding, which takes place during both replication and transcription, gives rise to supercoils in the DNA. The degree of supercoiling must be carefully regulated to avoid impeding the motion of the molecular machinery because supercoils can give rise to torsional forces in the DNA, the magnitude of which increases the more the DNA is unwound. In the context of DNA replication, such forces can delay the process of cell division and under certain conditions even arrest it [83].

A number of processes, both mechanical and biochemical, are involved in supercoil regulation. In this context, MT can be used to probe the dynamics of supercoiled DNA to assess its precise role in such regulation. For instance, diffusing supercoils of opposite sign might annihilate on a circular plasmid, provided their drag is low enough to allow their rapid diffusion. MT can also be used to probe enzymes called topoisomerases that control DNA supercoiling. These enzymes serve to reduce the torsional forces and to unknot DNA. They are grouped into two classes, types I and II. Type I topoisomerases are characterized by their ability to cleave a single strand of duplex DNA, whereas type II topoisomerases cleave both strands of duplex DNA.

Two distinct methods have been used to examine the dynamics of supercoiled DNA. In the first method, the force on a supercoiled DNA molecule was rapidly increased, leading to a conversion of the plectonemic supercoils to DNA twist (Figure 13.8A, inset). To achieve rapid force switching in practice, MTs were supplemented with an optical trap to keep DNA under low tension while the magnets were translated to increase the force. Subsequently shutting off the laser trap led to motion of the bead back to its equilibrium position under the high magnetic force established. In the second method, supercoil removal dynamics were probed by incubating the supercoiled DNA in the presence of a nicking enzyme that relaxes the torsional constraint by nicking the DNA [84]. Both experiments on plectoneme dynamics could be described in a satisfying way with a simple theoretical model assuming fast internal DNA dynamics (data for the force switching experiment are shown in Figure 13.8A). Surprisingly, the relaxation of plectonemic structures that occurred during these experiments did not significantly slow down DNA dynamics [84]. This study of the dynamics of bare DNA has provided a solid baseline to which the dynamics of supercoiled DNA in the presence of proteins should be compared.

To illustrate the use of MT in probing topoisomerase activity, consider the enzyme topoisomerase IB, a eukaryotic enzyme that releases the torsion built up in a supercoiled DNA. The enzyme releases the torsion from the DNA by surrounding the dsDNA like a clamp and temporarily cleaving one of the two strands. The accumulated torsional forces in the DNA are then spun out around the intact strand. After a number of turns, the topoisomerase IB again firmly grabs the spinning DNA and neatly ligates the broken strands back together (Figure 13.8B, inset). Using single-molecule techniques, Koster et al. could follow single topoisomerase IB enzymes over time as they acted on single DNA molecules [68]. Because the supercoils are removed from the DNA as soon as the topoisomerase cuts through one of the two DNA strands, they were able to determine the exact number of turns removed by the topoisomerase between “cutting” and “sealing” (Figure 13.8B). In addition, various parameters, such as the torque dependence of the average number of turns removed and the degree of friction of the rotating DNA in a cavity of the enzyme, could be measured. The experimental evidence for the existence of friction relied on a comparison with a control experiment in which supercoil relaxation was carried out by a nicking enzyme, as described previously, because such an enzyme does not impose noticeable friction following cleavage.

13.9.2 Example 2: DNA Scrunching by RNA Polymerase

In the previous example, changes in supercoil density were shown to yield kinetic information on enzymes whose primary role involves supercoil removal. However, the precise analysis of supercoils in the magnetic tweezers can also yield information on enzymes whose primary role is quite different. An example of this is the detection by Strick and colleagues of DNA scrunching by RNA polymerase during abortive initiation [85,86]. In this experiment, a single DNA molecule that included a unique promoter for Escherichia coli RNA polymerase (RNAP) was prepared in the MT. As shown in Figure 13.9, the molecule can be prepared in either a positively or a negatively supercoiled state. RNAP will start unwinding the DNA, but as the DNA molecule is torsionally constrained, the linking number cannot be altered. Any negative twist induced through DNA unwinding by RNAP must therefore be compensated by positive writhe. If the DNA is initially positively supercoiled, the compensation by positive writhe will decrease the end-to-end extension of the DNA molecule, whereas if the DNA is initially negatively supercoiled, the compensation by positive writhe will increase the end-to-end extension of the DNA molecule (Figure 13.9). In this manner, the researchers could measure the degree of unwinding by the RNA polymerase in several states (open complex, initially transcribing complex, etc.). For instance, the ability to measure the small differences in the change of DNA length during abortive initiation in a positively versus a negatively supercoiled state, equal to Δl _u = (Δl _obs,neg – Δl _obs,pos)/2, where l _obs,neg is the length change of the DNA during abortive initiation at negative supercoiling and Δl _obs,pos is the corresponding length change at positive supercoiling, proved the existence of DNA scrunching by RNAP in this phase of its cycle.

13.9.3 Example 3: DNA Helicase Activity

It has been shown how a knowledge of the behavior of supercoiled DNA in the tweezer can permit sensitive detection of enzymatic activity. MTs are by no means limited to the detection of enzymes that act on supercoils, either directly or indirectly. Indeed, they have also been used to monitor replication by DNA polymerases, unwinding by DNA helicases, and looping by GalR, among others [87–89]. This subsection briefly describes how MTs can be used to study DNA helicase activity.

As a helicase unwinds duplex DNA or RNA into two separated single strands, its motion can be monitored in several ways. One manner is to take advantage of different force–extension relations for single- and double-stranded nucleic acids (i.e., different persistence lengths and contour lengths per nucleotide). Under a fixed force, these varying stiffnesses result in altered end-to-end lengths monitored in the MT, depending on whether the nucleic acid is predominantly single or double stranded [40]. Such discrimination has been used to monitor the activity of DNA helicases [88]. An alternative technique to monitor helicase activity, first introduced by the Bustamante group, is to monitor DNA unzipping of a single hairpin [59]. Here, the signal-to-noise ratio is higher because it is not a length differential between single- and double-stranded nucleic acids that contributes to the signal, but rather the entire length revealed by the appearance of additional single-stranded DNA under tension. Unzipping of a 231-bp hairpin by bacteriophage T4 helicase (gp41), leading to lengthening of the DNA during unzipping and shortening during subsequent rehybridization, is shown in the context of MT in Figure 13.10 [90]. From such time traces, one can readily deduce the velocity and the processivity distribution, as well as the force dependence of helicase activity, very precisely, which places stringent constraints on potential helicase mechanisms.

13.9.4 Example 4: MT Applications in Protein Science

Recently MTs have been applied to nucleic acids–free protein systems [10–14]. Lee et al. developed an immunoassay using MTs that enabled antigen detection with two-orders-of-magnitude-higher sensitivity than conventional solid surface phase immunoassay techniques due to the increase in the signal-to-noise ratio in the case of MTs [14]. In addition, MTs have been used to measure the lengths and dissociation rates of bonds between phage-displayed peptides and their protein targets [13]. This work was later expanded with studies of antigen–antibody interactions [12]. Finally, MTs were used to measure the stiffness of protein assemblies, as well as the bond strengths stabilizing these assemblies [10, 11].

13.10 Outlook

Single-molecule MT techniques have been applied to many biological problems with considerable success. Although they were applied initially to study DNA supercoiling and its biological regulation, MTs have also been used to study other important systems involving nucleic acids and proteins, such as nucleic acid helicase and polymerases. There are several technical and biological challenges that remain to be solved. First, the accuracy of spatial tracking should continue to be improved, and the MT should be extended to directly measure the applied torque. Second, developing the instrumentation and software to enable high-speed parallel measurements of several beads (i.e., several single molecules) will prove beneficial in studying biological processes with low initiation rates [91]. Furthermore, combing MT with other single-molecule techniques such as fluorescence resonance energy transfer or optical tweezers should expand the versatility of the technique, enabling studies of multicomponent processes. Finally, extending the abilities of current MTs to investigate nucleic acid–dependent metabolism in living cells, in which various proteins are bound to DNA under “truly” in vivo conditions, should further diversify the experimental questions that can be addressed by this technique.