Modelling Human Heat Transfer and Temperature Regulation

Abstract

In recent years there has been a growing demand from research, military and the industry for robust, reliable models predicting human thermophysiological responses. This chapter discusses the various aspects of- and approaches to- modelling human heat transfer and thermoregulation including the passive and the active system, numerical tissue heat transfer, environmental heat exchange, and clothing. Attention is also paid to advanced modelling topics such as model personalisation to predict responses of individuals, and methods for coupling with other simulation models and measurement systems. Several application examples of coupled systems are illustrated including numerical and physical simulation systems and a system for non-invasive assessment of internal temperature using signals from wearable sensors. The predictive performance of the model is discussed based on validation examples covering different exposure scenarios, personal characteristics, physical activities and in conjunction with non-invasive determination of rectal temperature with measured skin temperatures as model input. It is concluded that the model is a robust predictor of human thermophysiological responses, and, the proposed numerical simulation approach to non-invasive assessment of body core temperature, a reliable method applicable to a broad range of exposure conditions, personal characteristics, exercise intensities and types of clothing.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

In recent years there has been a steadily growing demand for robust and reliable computer models predicting human thermophysiological and perceptual responses in industrial, civilian, and military settings. Computer simulation, in general, has become a widely used technology which enabled systematic analysis of complex physical, chemical, biological and engineering problems becoming thus an attractive, cost-effective alternative to expensive experimental trials.

Aspects of human heat transfer, temperature regulation and occupant comfort play an essential role in several disciplines. Expansion of human endeavour in hostile and extreme environments, tightening of industrial health and safety standards are two areas of importance. Related modelling research into human performance, tolerance limits, thermal acceptability or occupant comfort has implications for military applications, in the car and aerospace industries, meteorology, clinical, textile and clothing research, as well as medical engineering.

Diverse industrial applications require detailed analysis of the complex environmental heat transfer processes involving human occupancy in order to design safe, comfortable and energy-efficient buildings, cars, or industrial environments [7, 20]. Ongoing research efforts address e.g. the development of ‘physiologically intelligent’ thermal manikins for clothing research [55, 56], methods for assessing the impact of outdoor weather conditions on humans in meteorology [4, 5, 24], development of simulation systems to predict patients’ responses during open-heart surgery or other clinical treatments [11, 62]. Non-invasive determination of the body core temperature is a further area with implications for the development of intelligent personal protective, monitoring and heat stress warning systems for military and civilian applications [22, 23].

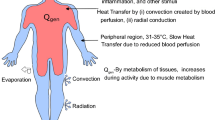
To adequately quantify the thermal influences to which man is exposed in different environmental settings, the specific behaviour of the human thermal and regulatory system has to be considered. Within the human body, metabolic heat is generated. This heat is distributed over body regions by blood circulation, is stored within tissues and carried by conduction to the body surface, where, insulated by clothing, heat is lost to the environment by convection, radiation, and evaporation or conduction. Humans keep their internal temperature at fairly constant levels by autonomous regulatory responses of the central nervous system including adjustments to skin blood flow, increase of metabolic heat production in muscles by shivering in the cold, or evaporation of sweating in warm and hot conditions. In addition, the perceptual responses of thermal comfort and sensation enable humans to react consciously by behavioural action which is often the far more efficient way to regulate body temperatures compared to autonomous thermoregulation.

Following general human heat balance considerations, diverse two-node models of human thermoregulation emerged some of which found widespread use [1, 25, 26, 36]. In the past decades, also more sophisticated, multi-segmental, models have been developed (e.g. [17–24, 37, 64, 65, 68]). Compared to two-node models which predict overall physiological responses, the latter simulate the human body in greater detail predicting also local temperature and regulatory responses. Heat transfer phenomena within tissues (including blood circulation) are modelled explicitly and also the specific role of extremities in human thermoregulation can be considered. Environmental heat losses are modelled in more detail taking into account typical asymmetries such as non-uniform distribution of skin temperatures, regulatory responses, non-uniform clothing and local environmental conditions.

One of the multi-segmental models of human heat transfer and thermoregulation that has gained popularity over the past decade is the Fiala thermal Physiology and Comfort (FPC) model. The stimulus for developing the original model [17–19] was the desire to make fundamental physiological concepts and models available to engineers and researchers working in other disciplines (for a review see e.g. [21]). The FPC model is a numerical framework of models which—linked together—predict human temperature and regulatory [18, 57], as well as overall and local perceptual (thermal sensation, thermal comfort) responses [15, 19] to steady-state and transient environment and personal conditions.

The model contains two interacting systems of human thermoregulation: the controlling active system and the controlled passive system. The passive system model simulates the physical human body and the heat and mass transfer processes which occur within the body and at its surface. The active system model simulates the human thermoregulatory system predicting responses of the central nervous system and local autonomic thermoregulation.

Diverse versions of the original ‘Fiala model’ are currently in use adopted by companies and institutions based on originally published material [17–19]. Model applications include the automotive sector, meteorology, architecture, textile and clothing research, research into health and safety in extreme conditions, diverse clinical and medical engineering applications (for a summary see e.g. [21]). The revised FPC-model was further developed and extended, beyond others, to (i) better represent average-population humans (ii) consider inter-individual variability to enable simulation of individuals, (iii) facilitate flexible coupling with other simulation models, systems or devices and (iv) predict global and local perceptual (thermal sensation and comfort) responses to transient and asymmetric exposure scenarios.

This chapter deals with the various aspects of modelling human heat transfer and temperature regulation based on approaches and algorithms implemented in the FPC model. Treated topics include numerical modelling of heat and mass transport within tissues, advanced modelling of human environmental heat exchange and modelling the active system. Tackled are furthermore endeavours to modelling individuals as are methods to facilitate flexible coupling with other models, sensors and devices. Examples of existing coupled systems are presented. Finally, several validation examples are discussed including the results of a study in which the rectal temperature of exercising subjects wearing protective clothing was determined non-invasively based on measured skin temperatures and metabolic rates.

2 Modelling the Passive System

2.1 Body Construction

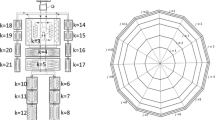
The passive system is modelled as a composite of cylindrical and spherical (head) body elements built of concentric tissue layers (section A-A″ in Fig. 1) with skin represented as inner cutaneous layer (incorporating the cutaneous plexus) and outer skin. The latter contains sweat glands but no thermally significant blood vessels [17, 24]. As indicated in Fig. 1, body elements are also subdivided into sectors to enable adequate simulation of asymmetric exposure scenarios.

Fig. 1

Schematic diagram of the passive system model including body subdivisions, components of the environmental heat exchange, and a crosssection through the upper leg (right)

The reference FPC passive system model resembles an average-population person based on analysis of anthropometric field surveys [22] which included older [50, 51] as well as recent, large-scale, studies [29, 53]. Thereby, the original (left-right symmetry) model consisting of 12 compartments [17] was refined to simulate the human body in greater detail consisting of 20 body elements. This so called ‘reference’ human anthropometry model is an average, i.e. ‘50-percentile’ (35 years old, unisex) 169.7 cm tall person weighting 71.4 kg (24.8 kg/m² body mass index). It features a skin surface area of 1.83 m², body fat content of 22.6 %, and an average body density of 1.05 g/cm³ [22]. The unisex anthropometry represents the average of a 50-percentile male and female person according to the above surveys which agree well also with other published data [52]. It was defined to (i) obtain a common basis for simulating individuals (see further below) and (ii) provide a well-defined reference model for simulating average-population responses in cases when no subject details are available or of interest.

The resultant anthropometric characteristics of the reference person are compared—in terms of relative body element lengths—with the corresponding field survey data and data employed in a biomechanical model of Daanen and Heerlen [8], in Table 1. The results agree with field survey data within 0.7 % deviation for main body parts. Larger discrepancies result for hands and feet as the incorporated thermal models required additional factors to be considered in order to simulate these body parts adequately in thermophysiological terms [17]. Larger discrepancies result also for data used by Daanen and Heerlen due to the inherent differences in the definition of individual body parts in the thermal (FPC) and biomechanical models.

Table 1 Comparison of relative body part lengths of the reference anthropometry model with the published data

2.2 Scalable Anthropometry Model

The scalable anthropometry model was designed to be an easy-to-use model which, despite the complexity of the subject area, would only require the basic four individual parameters as model input, i.e. body height, weight, age, and gender. The scaling procedure employs the above reference human anthropometry model as a basis upon which the personal anthropometric characteristics of the person to be simulated are modelled. The individual parameters are then used to perform calculations of the overall and local body characteristics as indicated in Fig. 2.

Fig. 2

Schematic diagram of the calculation process constituting the scalable FPC human anthropometry model

To simulate an individual, body elements of the Reference Model are ‘scaled’ based on the four overall input parameters characterizing a person.

Results of anthropometric surveys indicate that the dimensions of individual body parts do not change uniformly as the stature varies. Tall subjects, for example, tend to feature longer extremities in proportion to the body height than smaller subjects. In the model, the length of arms and legs is derived from the gender-specific length of the tibia, femur, humerus and ulna bones calculated as [51]:

$$ L = a_{1} H\,{ + }\,a_{0} $$

(1)

where L is the length of the bone in cm, H body height in cm, and a ₁ and a ₀ are the corresponding regression coefficients [50]. The remaining (cylindrical) body parts are scaled proportionally to changes in the body height while the trunk is sized to retain the body height of the simulated person.

The predicted length of the main body sections are compared with measurements obtained from the CEASAR anthropometric survey [9, 59] for male subjects grouped in ten height categories ranging from 155 to 202 cm average height in Fig. 3. The predicted dimensions reproduce measured data within an overall average relative error of 1.8 %. The largest average relative error of 3.6 % resulted for upper legs. For lower legs, the crotch height, and the trunk the error was 1.1, 1.8 and 1.4 %, respectively. A similar level of accuracy was obtained also for upper extremities with 1.5 and 2.2 % average relative error for lower and upper arms, respectively [22].

Fig. 3

Comparison of predicted body part lengths forming the stature with data obtained for male subjects from the CEASAR Project [9, 59] for 10 body height categories [22]

2.3 Body Composition

Body composition is another factor to consider in order to adequately represent a human in thermal simulations. The reference person was defined to represent an ‘average’ human with respect to the body dimensions, fat content, average tissue density, skin surface area, basal metabolic rate, cardiac output, as well as the overall body weight and body weight distribution. The relative weights of different body compartments, provided as percentages of the total body weight, are compared with the corresponding measured data in Fig. 4.

Fig. 4

Comparison of relative body part weights: model (reference person) versus measured data [8, 50]

To simulate a person, not only his/her body dimensions but also the overall and local body properties have to be ‘individualized’ to fit the personal characteristics [22]. Thereby, the overall body fat content is either direct model input or is calculated according to Han and Lean [30] using the body mass index and the age of the simulated person:

$$ {\text{BF}} = c_{bf,b} \cdot {\text{BMI + }}c_{bf,a} \cdot {\text{age}} + c_{bf,0} $$

(2)

where BF is the body fat content in %, BMI body mass index in kg/m²; and age in years. The coefficients c _bf,b , c _bf,a , and c _bf,0 with 1.330, 0.236 and −20.20 for males and 1.210, 0.262 and −6.70 for females, respectively, indicate significant differences in the body fat content among sexes [30].

Especially in males a notable portion of body fat may be retained as abdominal subcutaneous adipose tissue (ASAT) and visceral adipose tissue (VAT). VAT is determined based on Kuk et al. [44] who investigated the influence of the personal factors age and sex on VAT and ASAT in 483 young and older male and female subjects covering a wide range of body compositions. Taking into account the dependency of the waist circumference on the overall body fat content and age according to Han and Lean [30] the amount of the visceral adipose tissue is obtained as:

$$ {\text{VAT}} = {\text{BF}}\left( {c_{vat,bf0} { + }c_{vat,bfa} \,{\text{age}}} \right) + c_{vat,aa} \,{\text{age}}^{2} + c_{vat,a} \,{\text{ age}} + c_{vat,0} $$

(3)

where VAT is visceral fat tissue in kg and BF body fat content in % body weight. The coefficients c _vat,bf0, c _vat,bfa , c _vat,aa , c _vat,a , and c _vat,0 are gender specific with 0.459, 0.003, 0.0003, −0.071 and 12.892 for males and −0.005, 0.003, 0.0008, −0.076 and 0.529 for females, respectively.

The abdominal subcutaneous fat content is calculated similarly based on experimental results of Kuk et al. [44] and Han and Lean [30]:

$$ {\text{ASAT}} = c_{as,b} \,{\text{BF}} + c_{as,a} \,{\text{age}} + c_{as,0} $$

(4)

where ASAT is the amount of abdominal subcutaneous fat in kg. The coefficients c _as,b , c _as,a and c _as,0 are 0.194, 0.020, and −1.400 for males and 0.251, 0.055 and −3.387 for females, respectively.

An iterative procedure distributes the overall quantities to obtain local adipose and fat-free mass portions by scaling the thickness of local subcutaneous fat tissue layers relative to the corresponding proportions of the reference model. This approach recognizes that while the largest portion of the body fat is contained in central body parts, the remainder is distributed with decreasing share over proximal limbs towards the outer extremities and the head [13].

The individualized properties are ‘mapped’ onto individual body elements of the reference model resulting in an updated numerical representation of the human body in the model. As illustrated in Fig. 5, the model’s resultant total body fat content after iterative scaling and integration reproduces experimentally based values [30] with and average error of 0.56 % for a wide range of body height and fat content combinations.

Fig. 5

Comparison of model’s body fat content with experimentally derived data as a function of body height and body weight obtained for male (35 years old) subjects [22, 30]

It should be noted that the scaling processes not only changes the anthropometric and morphological body characteristics but indirectly changes also other important body properties including e.g. the basal metabolic rate and skin surface area. According to WHO [67], the basal metabolic rate of males and females varies in proportion to body weight though with significant differences among sexes. The scalable model reproduces the WHO formula model within 5 % relative error for both sexes. The overall skin surface area affects the heat exchange with the environment and thus has important implications also for temperature regulation. The total skin surface area which results from the above scaling processes is compared with the Dubois body surface area [12] for different combinations of body height and weight in Fig. 6. It reproduces the Dubois formula with an average error of 0.010 ± 0.008 m².

Fig. 6

Model’s total skin surface area as a function of body height and weight obtained for male (35 years old) subjects compared with experimentally based data [12, 22]

2.4 Tissue Heat Transfer

Pennes formulated the so called bioheat equation to describe the dynamic heat transfer processes that occur within living tissues [54]. Extended for heat dissipation in spheres in the model (head), the differential equation can be written as:

$$ \rho c {\frac{\partial T}{\partial t}} = k \left( { \frac{{\mathop \partial \nolimits^{2} T}}{{\partial r^{2} }} + {\frac{\omega }{r}} \,{\frac{\partial T}{\partial r}} } \right) + \mathop q\nolimits_{m} + c_{bl} \,\mathop \rho \nolimits_{bl} w_{bl} \left( {T_{bla} - T} \right) $$

(5)

where ρ, c, and k are tissue density (kg m⁻³), heat capacitance (J kg⁻¹ K⁻¹) and conductivity (W m⁻¹ K⁻¹), respectively. T is the tissue temperature (°C), t time (s), r radius (m); ω a geometry factor (ω = 1: polar, ω = 2: spherical co-ordinates), q _m metabolic heat generation (W m⁻³), ρ _bl blood density (kg m⁻³), w _bl blood perfusion rate (m³ s⁻¹ m⁻³), c _bl heat capacitance of blood (J kg⁻¹ K⁻¹), and T_bla (°C) arterial blood temperature.

In the numerical model, tissue layers are discretized as nodes using a numerical form of the bioheat equation that employs a finite-difference (Crank-Nicholson) scheme [17]. Applied to a tissue node n (with n − 1 and n + 1 being the preceding and succeeding adjacent nodes, respectively) and separating the (unknown) ‘future’ temperature terms (t + 1) the numerical form of the general bioheat equation yields:

$$ \begin{aligned} & \left[ {\mathop \gamma \nolimits_{n} - 1} \right] \mathop T\nolimits_{ n - 1}^{ (\,t + 1)} + \left[ { {\frac{{\mathop \zeta \nolimits_{n} }}{{\Delta t}}} + 2 + \mathop \delta \nolimits_{n} \mathop \beta \nolimits_{n}^{ (\,t + 1)} } \right] \mathop T\nolimits_{n}^{ (\,t + 1)} - \left[ { 1 + \mathop \gamma \nolimits_{n} } \right] \mathop T\nolimits_{ n + 1}^{ (\,t + 1)} - \mathop \delta \nolimits_{n} \mathop \beta \nolimits_{n}^{ (\,t + 1)} \mathop T\nolimits_{ bla}^{ (\,t + 1)} \\ & = \left[ {1 - \mathop \gamma \nolimits_{n} } \right] \mathop T\nolimits_{n - 1}^{ (t)} + \left[ { {\frac{{\mathop \zeta \nolimits_{n} }}{{\Delta t}}} - 2 - \mathop \delta \nolimits_{n} \mathop \beta \nolimits_{n}^{(t)} } \right] \mathop T\nolimits_{n}^{ (t)} \\ & \quad + \left[ { 1 + \mathop \gamma \nolimits_{n} } \right] \mathop T\nolimits_{n + 1}^{ (t)} + \mathop \delta \nolimits_{n} \left[ {\mathop q\nolimits_{m,n}^{(\,t + 1)} + \mathop q\nolimits_{m,n}^{(t)} } \right] + \mathop \delta \nolimits_{n} \mathop \beta \nolimits_{n}^{ (t)} \mathop T\nolimits_{bla}^{(t)} \\ \end{aligned} $$

(6)

where

$$ \mathop \gamma \nolimits_{n (cyl.)} = {\frac{{\Delta r_{n} }}{{2 r_{n} }}}; \mathop \gamma \nolimits_{n\,\,(sph.)} = {\frac{{\Delta r_{n} }}{{r_{n} }}}; \mathop \zeta \nolimits_{n} = 2\Delta r_{n}^{2} {\frac{{\mathop \rho \nolimits_{n} \mathop c\nolimits_{n} }}{{\mathop k\nolimits_{n} }}};\mathop \delta \nolimits_{n} = {\frac{{\Delta r_{n}^{2} }}{{\mathop k\nolimits_{n} }}}. $$

(7)

The time step Δt (s) approximates the differential dt, and β _n (Wm⁻³K⁻¹) represents a time-dependent calorimetric equivalent of the nodal blood flow rate:

$$ \beta_{n} = \rho_{bl} \,c_{bl} \,w_{bl,\,n} $$

(8)

Applying Eq. 6 to each tissue node of the numerical model with the corresponding material properties, nodal heat generation and blood perfusion rates, constitutes a system of coupled linear equations which is to be solved for each time and iteration step of a simulation [17]. Solving the whole body matrix for the (undressed) reference person exposed to thermo-neutral, steady state (still air) environmental conditions of 30 °C, 50 % RH results in a mean skin temperature of 34.3 °C and body core temperatures of 37.0 °C in the head core (hypothalamus) and 36.9 °C in the abdomen core (rectum). The resultant overall physiological data replicate a reclining subject with an overall basal body metabolism of 75.5 W, basal evaporation (i.e. moisture diffusion) rate from the skin of 19 W, and basal cardiac output of 4.9 L min⁻¹ [22].

The q _m -term in Eq. 6 is a sum of the local tissue’s thermo-neutral basal metabolic rate, q _m,0 (W m⁻³) and any additional heat gain, Δq _m  (W m⁻³):

$$ \mathop q\nolimits_{m} = \mathop q\nolimits_{m,0} +\Delta \mathop q\nolimits_{m} $$

(9)

Δq _m includes variations in basal metabolism due to changes in tissue temperature from the local setpoint, T ₀ , which refers to the above conditions of thermal neutrality. In muscles, additional heat may be generated by exercise, q _m,w , or by regulatory shivering, q _m,sh , as local portions of the respective overall quantities:

$$ \Delta \mathop q\nolimits_{m} = \mathop q\nolimits_{ m,0} \left( {\mathop 2\nolimits^{{\,\frac{{T - T_{0} }}{ 10}}} - \,1} \right) + \mathop q\nolimits_{ m,w} + \mathop q\nolimits_{ m,sh} $$

(10)

Similarly to q _m , local tissue blood perfusion rates, w _bl , are defined as a sum of the thermo-neutral basal rate β _m,bas,0 (Wm⁻³K⁻¹) and variations Δβ _bl (Wm⁻³K⁻¹):

$$ \beta_{bl} = \beta_{bl,0} +\Delta \beta_{bl} $$

(11)

the latter being proportional to changes in the local metabolic rate: Δβ _bl  = 0.932Δq _m [64]. The largely variable blood flows within the cutaneous plexus are subject to central nervous system regulation as described further below.

Blood circulation plays a dominant role in the human heat transfer. In the passive system model, each body element is supplied with arterial blood from the central pool (heart). Before perfusing local tissues, blood is ‘conditioned’ by counter-current blood streams of adjacent veins. Arterial blood at local arterial temperatures perfuses then tissues exchanging heat in the capillary beds where, according to Eq. 5, it reaches equilibrium with local tissues. Depleted blood is then collected in veins being rewarmed by counter-current heat exchange with adjacent arteries as it flows back to the central pool. Finally, venous blood from the whole body is mixed in the central blood pool perfusing the lung to constitute a new central blood pool temperature.

The blood perfusion term in Eq. 5 only accounts for heat exchange with tissues in the capillary bed. In the model also counter-current heat exchange between pairs of adjacent arteries and veins is considered [17]. The net heat exchange between adjacent vessels, Q _x (W) is expressed as [28]:

$$ \mathop Q\nolimits_{x} = h_{x} \left( { T_{bla} - T_{blv} } \right) $$

(12)

where h _x (WK⁻¹) is the counter-current heat exchange coefficient [24]. These coefficients are equal to zero in central body parts and are >0 in extremities. In the individualized model they vary with the length of individual extremities.

Considering the counter-current heat exchange between adjacent vessels, the heat loss from an artery equals the heat gain of the adjacent vein. Assuming mass-continuity in blood vessels, the decrease in arterial blood temperature, T _blp  − T _bla is thus equal to the rise of venous blood temperature, T _blvx  − T _blv , after passing the counter-current heat exchanger [17]:

$$ \sum\limits_{i}^{nodes} {\beta_{i} \,V_{i} } \,\left( {T_{blp} - T_{bla} } \right) = \sum\limits_{i}^{nodes} {\beta_{i} \,V_{i} \,} \left( {T_{blvx} - T_{blv} } \right) $$

(13)

where T _blp (°C) is the central blood pool temperature, V _i (m³) tissue nodal volume, and T _blv (°C) and T _blvx (°C) is the body element’s venous temperature before and after passing the counter-current heat exchanger, respectively. Since the bioheat Eq. 5 assumes capillary blood to reach equilibrium with the surrounding tissues, T _blv yields:

$$ T_{blv} \, = {\frac{{\sum\nolimits_{i}^{nodes} {T_{i} \,\beta_{i} \,V_{i} } }}{{\sum\nolimits_{i}^{nodes} {\beta_{i} \,V} }}} $$

(14)

With the above equations the local arterial blood temperature, T _bla , (°C) of a body element can be calculated as:

$$ T_{bla} = {\frac{{T_{blp} \,\sum\nolimits_{i}^{nodes} {\beta_{i} \,V_{i} } }}{{h_{x} + \sum\nolimits_{i}^{nodes} {\beta_{i} \,V_{i} } }}} + {\frac{{ \frac{{h_{x} }}{{\rho_{bl} \,c_{bl} }}\,\sum\nolimits_{i}^{nodes} {T_{i} \,\beta_{i} \,V_{i} } }}{{\sum\nolimits_{i}^{nodes} {\beta_{i} \,V_{i} } \left( {h_{x} + \sum\nolimits_{i}^{nodes} {\beta_{i} \,V_{i} } } \right)}}} $$

(15)

The blood pool temperature, T _blp , is a function of local tissue temperatures from all body parts:

$$ \mathop T\nolimits_{blp} = \frac{{\sum\nolimits_{k}^{b.elem.} {\left( {\frac{{\sum\nolimits_{i}^{nodes} {\beta_{k,i} \,V_{k,i} } }}{{h_{x,k} + \sum\nolimits_{i}^{nodes} {\beta_{k,i} \,V_{k,i} } \sum\nolimits_{{}}^{{}} {} }} \times \sum\nolimits_{i}^{nodes} {T_{k,i} \,\beta_{k,i} \,V_{k,i} } } \right)} }}{{\sum\nolimits_{k}^{b.elem.} {\left[ {{\frac{{\left( {\sum\nolimits_{i}^{nodes} {\beta_{k,i} \,V_{k,i} } } \right)^{2} }}{{h_{x,k} + \sum\nolimits_{i}^{nodes} {\beta_{k,i} \,V_{k,i} } }}} } \right]} }} $$

(16)

3 Modelling the Active System

3.1 Concept and Model Definition

The active system is a cybernetic model of human thermoregulation that simulates the four essential responses of the central nervous system: production of sweat moisture, Sw, increase of metabolic heat generation in muscles due to shivering, Sh, and changes in cutaneous blood flows due to peripheral vasodilatation, Dl, and vasoconstriction, Cs. The implemented concept adopts principles of a set-point temperature based control system that has been formulated and implemented previously in other models (e.g. [25, 26, 64]). Set-point based systems define regulatory stimuli generating afferent signals as ‘error’ signals, i.e. the difference between a variable of the actual thermal state, x (e.g. temperature) and the corresponding setpoint that refers to conditions of thermal neutrality (see Sect. 2.4), x ₀ :

$$ \Delta x = x - x_{0} $$

(17)

Rather than using postulative methods, meta-regression analysis was employed to define a statistically founded reference active system [18] for simulating responses of an ‘average’ person. Thereby, published experimental studies were simulated and measured regulatory responses were correlated with predicted afferent signals to (i) investigate their involvement and responsibility in each response based on their statistical significance and to (ii) formulate the governing regulatory equations. Considered were established signals associated with skin temperatures (ΔT _skm ), head core (hypothalamus) temperatures (ΔT _hy ), rates of change of skin temperature (dT _skm /dt) as well as theoretical signals associated e.g. with muscle temperatures or skin heat fluxes (Δq _skm ,), Fig. 7.

Fig. 7

Example of linear regression lines as functions of different afferent signals to predict the shivering response observed in semi-nude reclining subjects (exp.) suddenly exposed to a cold environment of 5 °C. Adopted from [18] with permission

Overall, the regression studies confirmed the body core (hypothalamus) temperature, T _hy , and (mean) skin temperature, T _skm , to be the main driving impulses for human thermoregulatory action. A further signal, i.e. rate of change of the skin temperature, dT _skm /dt, weighted by the error signal associated with the skin temperature, was identified as the driving impulse that governs the dynamics of regulatory responses during rapid skin cooling such as the typical shivering ‘overshoot’ (e.g. Fig. 7). A schematic diagram of the reference active system model is provided in Fig. 8.

Fig. 8

Schematic diagram of the reference active system model. Left responses of local autonomic control; right responses of the central nervous system regulation accounting for overall changes in muscle metabolism by Shivering, Sh, (and the corresponding changes in muscle blood flow), skin moisture excretion by sweating, Sw, and skin blood flow by peripheral vasodilatation, Dl, and constriction, Cs. The model uses temperatures of the skin (T _sk ) and of head core (T _hy ) as well as the rate of change of skin temperature as input signals into the regulatory centre. Setpoint temperatures T _sk,0 , T ₀ and T _hy,0 refer to the nude reclining body’s thermo-neutral state at 30 °C operative temperature

The analysed conditions included 26 different experiments covering exposures to steady state and transient environments ranging from cold, over moderate to heat stress conditions and physical activities from reclining to intense exercise [18]. The results obtained for all exposures were then subjected to meta-regression analysis to study the consistency and functional dependencies of the linear regression coefficients on the subjects’ thermal state. The coefficients for individual responses are plotted together with the respective fitting non-linear functions in Fig. 9.

Fig. 9

Dependency of linear regression coefficients b obtained for different exposures on skin and head core temperature levels, i.e. error signals ΔT _sk and ΔT _hy obtained for the Sh-, Sw-, Dl-, and Cs-response, and the corresponding fitting functions (adopted from [18] with permission)

With the dynamic term for skin cooling, i.e. negative rates of change of skin temperature, $dT^{-}_{skm} /dt$, and (the statistically significant) temperature error signal from the head core included, the control equation for shivering, Sh (W), yields:

$$ \begin{aligned} Sh & = 10 \left[ {\,{ \tan }h \left( {0.48\Delta T_{skm} + 3.62} \right) - 1} \right]\Delta T_{skm} - \,27.9\Delta T_{hy} \\ & \quad + 1.7\Delta T_{skm} \times {\tfrac{{\mathop {dT}\nolimits_{skm}^{ - } }}{dt}} - 28.6 \\ \end{aligned} $$

(18)

The Sh–response is limited to a maximum of 350 W in the model [18]. The response is compensated by any extra metabolism due to exercise, q _m,w , and is distributed over body regions using distributions coefficients, c _sh [18].

The overall sweat excretion rate, Sw (g min⁻¹), is predicted as:

$$ \begin{aligned} Sw & = \left[ {0.8 { \tan }h \left( {0.59\,\Delta T_{skm} - 0.19} \right) + 1.2} \right]\,\Delta T_{skm} \\ & \quad + \left[ {5.7 { \tan }h \left( {1.98\Delta T_{hy} - 1.03} \right) + 6.3} \right]\,\Delta T_{hy} \\ \end{aligned} $$

(19)

An upper limit for Sw of 30 g min⁻¹ applies as a typical maximum rate for an average person [18] in the reference active system model. The resultant, local sweat rates, dm _sw /dt (g/min), are obtained as portions of Sw distributed over body parts using coefficients, c _sw [24], and being weighted by local influences of the Q10-effect due to local skin temperatures deviations from setpoints, T _sk,0 [18, 48] and local skin wettedness, f _wsk [6, 49]:

$$ {\frac{{dm_{sw} }}{dt}}\,\, = \,\mathop c\nolimits_{sw} f_{wsk} \,Sw \times 2^{{\frac{{T_{sk} - T_{sk,0} }}{10}}} $$

(20)

No statistically significant effect of the body core temperature was found in the response of peripheral vasoconstriction, Cs [−]. The control equation thus only includes static and dynamic afferent signals associated with the skin temperature:

$$ Cs = 35 \left[ {{ \tan }h\left( {0.34\Delta T_{skm} + 1.07} \right) - 1} \right]\Delta T_{skm} + 6.8\Delta T_{skm} {\tfrac{{\mathop {dT}\nolimits_{skm}^{ - } }}{dt}} $$

(21)

In contrast to constriction, vasodilatation, Dl (W K⁻¹), is regulated by statistically significant afferent signals associated with both the skin and body core temperature in the model:

$$ Dl = 21 \left[ {{ \tan }h\left( {0.79\Delta T_{skm} - 0.70} \right) + 1} \right]\Delta T_{skm} + 32 \left[ {{ \tan }h\left( {3.29\Delta T_{hy} - 1.46} \right) + 1} \right]\Delta T_{hy} $$

(22)

The resultant local blood perfusion rates, w _bl , within the skin are obtained as local portions c _dl and c _cs [24] of the overall vasomotor responses also being modulated by local skin temperatures:

$$ \beta_{sk} = \frac{{\beta_{sk,0} + c_{dl} \,Dl}}{{1 + c_{cs} Cs \cdot e^{ - Dl/80} }} \times 2^{{{^{{\frac{{T_{sk} \, - \,T_{sk,0} }}{10}}} }}} $$

(23)

Literature indicates a maximum skin blood flow that varies with the type and level of exercise [61]. In the model, the maximum overall skin blood flow, B _sk,max (W K⁻¹), decreases in proportion with any overall increase in muscle blood flow, ΔB _msc (W K⁻¹) [18]:

$$ B_{sk,\hbox{max} } = 386.2 - 0.32 \times\Delta B_{msc} $$

(24)

If the sum of all local blood flows in the skin as prescribed by Eq. 23 exceeds B _sk,max at any exercise condition then the local rates are trimmed in proportion to B _sk,max in the model.

3.2 Personalized Thermoregulation

Human thermoregulatory responses are known to be affected by personal characteristics such as gender, age, physical fitness, anthropometry and body composition, acclimatisation, etc. Of the various personal characteristics there are four main factors which affect the human individual heat stress response [33]: aerobic fitness, acclimatization, and anthropometric and morphological properties of the body. Other factors including age and gender lose their influence when ‘correcting’ observed responses for the effect of the maximum aerobic power, VO _2,max, and the body fat content [33].

Of the four main personal factors the individualized passive system described above implicitly accounts for the effect of a person’s anthropometry and morphology including related factors involved in the environmental heat exchange, e.g. skin surface area, bodily thermal insulation (fat content), heat capacity (body mass), and the body surface-to-volume ratio.

The individual heat stress response model of Havenith [34] was adapted for use with the FPC-model to account for the effect of the remaining two personal factors, i.e. the aerobic fitness and acclimatization status. Personal parameters that directly and indirectly affect responses of the active system model are depicted in Fig. 10.

Fig. 10

Personal factors used as ‘direct’ and ‘indirect’ (passive system variations) input into the active system model to simulate responses of individuals

The approach is based on the assumption that individual variations in thermoregulatory responses are associated with a shift of the setpoint of the body core temperature, i.e. hypothalamus temperature in the FPC-model, ∆T _hy,set (°C):

$$ T_{hy,set} = T_{hy,set,0} -\Delta T_{hy,set} $$

(25)

where T _hy,set (°C) is the adapted setpoint temperature, and T _hy,set,0 (°C) the setpoint temperature of the reference active system simulating an ‘average’ person. According to Havenith [34] the shift is a function of the physical fitness, fit, and the acclimatization status, F _ac :

$$ \Delta T_{hy,set} = 0.1 \times \frac{fit}{10} + 0.25 \times F_{ac} $$

(26)

The personal fitness, fit, is dealt with in terms of the individual maximum aerobic power, VO _2,max (ml kg⁻¹min⁻¹) as direct model input. The difference between the individual and the average maximum aerobic power of an average-fit person, i.e. 40 ml kg⁻¹min⁻¹, is used as a measure of the individual fitness, fit:

$$ fit = VO_{2,\hbox{max} } - 40 $$

(27)

where VO _2,max may vary between 20 ≤ VO _2,max ≤60 ml kg⁻¹min⁻¹ for unfit and trained individuals, respectively [34]. Quantities exceeding these limits are trimmed accordingly in the model.

The acclimatization status, F _ac , is a function of the number of acclimatization days, n _d :

$$ F_{ac} = 1 - \exp ( - 0.3\,n_{d} ) $$

(28)

Thereby the number of acclimatization days, which is another direct input parameter, varies between 0 ≤ n _d ≤14 days in the model [34].

The central effector outputs for sweating, Sw, and vasodilatation, Dl, are computed as in the reference model by Eqs. 19 and 22, respectively, but using modified afferent signals from the head core, i.e. ∆T _hy = T _hy  − T _hy,set with T _hy being the actual head core temperature and T _hy,set the corresponding modified setpoint temperature, Eq. 25. If both fit and F _ac are zero also ∆T _hy,set is zero and the original setpoint temperature of 37.0 °C applies. However, any shift ∆T _hy,set  > 0 causes a shift of the onset of sweating and skin blood flow towards lower body core temperatures and vice versa.

In addition to the shift of the body core temperature setpoint due to acclimatization and physical fitness, the gain factor, g_sw, influences the sweating response in the individualized model:

$$ g_{sw} = \left( {1 + 0.35 \times \frac{fit}{20}} \right) \times \left( { 1 { + 0} . 1 5\times F_{ac} } \right) $$

(29)

g_sw modulates the sweating response, Sw, predicted by Eq. 19 to obtain the individualized response, Sw _ind (g min⁻¹):

$$ Sw_{ind} = Sw \times g_{sw} $$

(30)

The reference upper limit for sweating, Sw _max, of 30 g min⁻¹ is also subject to personal variations which is accomplished using the factor f _sw,max:

$$ f_{sw,\hbox{max} } = 1 + 0.25 \times \frac{fit}{20} + 0. 2 5\times F_{ac} $$

(31)

with f _sw,max the individual maximum sweat rate, Sw _max,ind (g min⁻¹) yields:

$$ Sw_{\hbox{max} ,ind} = Sw_{\hbox{max} } \times f_{sw,\hbox{max} } $$

(32)

In the model the maximum overall skin blood flow, B _sk,max, is not constant but varies with the intensity of exercise. The individualized maximum is derived from B _sk,max using the factor f _Bsk,max which is a function of the aerobic fitness and acclimatization status:

$$ f_{Bsk,\hbox{max} } = 1 + 0.25 \times \frac{fit}{60} + \, 0. 2 5\times F_{ac} $$

(33)

For any activity level, the individualized overall maximum skin blood flow, B _sk,max,ind (W K⁻¹) then yields:

$$ B_{sk,\hbox{max} ,ind} = B_{sk,\hbox{max} } \times f_{Bsk,\hbox{max} } $$

(34)

4 Human Environmental Heat Exchange

4.1 Heat Exchange Components

Humans exchange heat with the environment by surface convection, evaporation of sweating, thermal radiation with enclosing surfaces, short wave irradiation from high intensity sources, or conduction with surfaces in direct contact with the body. Part of bodily heat is also lost to the ambient air by respiration from within the lungs and nasal cavity. The surface heat losses may vary considerably over body regions due to inhomogeneous thermoregulatory responses, non-uniform clothing or asymmetric environmental conditions. Multi-segmental models are capable of accounting for such typical human inhomogeneities by establishing local heat and mass balances at surface sectors of individual body elements. Thereby, the net heat exchange between a body sector and the environment is a sum of the individual heat exchange components:

$$ \mathop q\nolimits_{bs} = \mathop q\nolimits_{c} + \mathop q\nolimits_{e} + \mathop q\nolimits_{r} + \mathop q\nolimits_{rs} $$

(35)

where q _bs (Wm⁻²) is the total heat loss from a body sector, q _c (Wm⁻²) heat loss by convection, q _e (Wm⁻²) sweat moisture evaporation and skin moisture diffusion, q _r (Wm⁻²) long wave radiation, q _rs (Wm⁻²) short wave irradiation. If the body surface is in direct contact with another surface, then q _bs equals to the rate of heat that is transferred by conduction from the interface to the material in contact with the human body, q _cn (Wm⁻²).

Convective heat losses, q _c (W m⁻²), are calculated using local surface temperatures of body sectors, T _bs (°C), the corresponding local air temperatures, T _a (°C), and convective heat transfer coefficients, h _c (W m⁻²K⁻¹):

$$ \mathop q\nolimits_{c} = h_{c} \left( {T_{bs} - T_{a} } \right) $$

(36)

In the FPC-model, h _c are obtained for individual body sectors considering both free and forced convection. The coefficients are thus a function of the temperature difference between the sector surface and air, as well as the local air speed, v _a (m/s):

$$ h_{c} = \left[ {a\,\left( {T_{bs} - T_{a} } \right)^{{{\raise0.5ex\hbox{$\scriptstyle 1$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 2$}}}} + bv_{a} + c} \right]\,^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} $$

(37)

where a, b and c are regression coefficients fitting experimental observations. Basis for h _c are measurements of local heat losses from heated full-scale manikins with realistic skin temperature distributions [24]. For special-purpose applications such as face cooling effects in windy outdoor climate conditions or water immersions dedicated local convection coefficients are computed for exposed or immersed body parts within the model [3, 40, 66].

Sweat moisture may or may not evaporate from the skin depending on the evaporative potential between the skin and the air, p _sk  − p _a (Pa), and the local evaporative resistance of the clothing, R _ecl (W m⁻²K⁻¹). Therefore, evaporation of sweating is not considered a direct response of the human thermoregulatory system in the FPC-model; rather the regional portion of regulatory sweat moisture secretion dm _sw /dt (kg s⁻¹ m⁻²) is used to constitute the latent heat balance for each skin sector:

$$ \frac{{p_{sk} - p_{a} }}{{R_{ecl} }} = {\frac{{\mathop p\nolimits_{ss} - \mathop p\nolimits_{sk} }}{{\mathop R\nolimits_{esk} }}} + \lambda_{{{\text{H}}_{2} {\text{O}}}} {\frac{{dm_{sw} }}{dt}} $$

(38)

where p _sk , p _a and p _ss (Pa) are partial water vapour pressures at the skin surface, of the air, and the saturated value within the skin (location of sweat glands), respectively [17]; $\lambda_{{{\text{H}}_{2} {\text{O}}}}$ (J kg⁻¹) is the (temperature dependent) heat of vaporisation of water [60], and R _sk,e (kg s⁻¹ m⁻²) the moisture permeability of the outer skin [17]. The maximum possible skin evaporation rate is reached when p _sk rises to the saturation level. Excessive sweating, dm _ac /dt (kg s⁻¹ m⁻²), then cannot evaporate may accumulate at the skin:

$$ {\frac{{dm_{ac} }}{dt}} = {\frac{{dm_{sw} }}{dt}} - {\frac{{p_{sk} - p_{a} }}{{R_{ecl} \,\lambda_{{H_{2} O}} }}}. $$

(39)

The accumulation capacity, however, is not unlimited. According to Jones et al. [39], quantities exceeding 35 g m⁻² drip off.

The local long wave radiative heat loss from body sector surfaces can be expressed, in analogy to surface convection, as:

$$ \mathop q\nolimits_{r} = h_{r} \left( {T_{bs} - T_{env} } \right) $$

(40)

where h _r (W m⁻² K⁻¹) is the radiative heat transfer coefficient:

$$ h_{r\,} = \sigma \varepsilon_{bs\,} \varepsilon_{en} \,\phi_{bs - en} \,\left( {T_{bs}^{2} + T_{en}^{2} } \right)\,\left( {T_{bs}^{{}} + T_{en}^{{}} } \right) $$

(41)

with σ = 5.67 × 10⁻⁸ W m⁻² K⁻⁴ being the Stefan-Boltzmann constant, ε _bs and ε _en emissivity of the sector surface and the environment, respectively, φ _bs-en view factor between the body sector and the enclosure ‘seen’ by that sector. T _bs and T _en (K) are surface temperatures of the body sector and of the corresponding radiant enclosure, respectively. The view factors φ _bs−en of individual body sectors [22] with respect to the entire enclosure ‘seen’ are based on numerical radiation simulations of projected area factors, f _p , calculated using detailed 3D human geometry models [41].

Simulation of the human radiative heat exchange in asymmetric environments (e.g. exposures to proximal cold surfaces, Fig. 11, right) uses f _p -factor-based calculations of view factors, φ _bs−en , between individual body sectors and surfaces of the envelope, A _w . This approach employs the concept of directional mean surface temperatures of the enclosure, T _en , to enable fast and accurate simulations. The geometry configuration parameters involved in the calculation of view factors between a body sector and a surface of the envelope, is depicted in Fig. 11, left.

Fig. 11

Geometry-related parameters used to calculate view factors between body sectors and a wall surface, A _w (left). Regional body cooling due to asymmetric thermal radiation exchange with a proximal cold surface (right). Adopted from [41] with permission

The short wave radiation q _rs (W m⁻²) absorbed by a body sector is given by:

$$ \mathop q\nolimits_{rs} = \alpha_{bs\,} \,f_{p} \,I_{s} $$

(42)

where α _bs is the short-wave absorptivity of the body surface which depends on the colour of skin or the material covering the sector, I _s (Wm⁻²) is the incident short-wave (e.g. direct or diffuse solar) radiation, and f _p the sector’s corresponding projected area factor. The local human f _p -factors were modelled for both direct and diffuse radiation using detailed 3D human geometry and radiation models [42, 43] as a function of the azimuth and altitude angles (direct radiation, Fig. 12) and the ground albedo (diffuse radiation).

Fig. 12

Variation range of altitude (β) and azimuth (α) angles studied in the numerical radiation simulations (left); example of resultant local projected area factor curves: posterior thorax (right). Adopted from [42] with permission

Respiration heat losses typically only represent a small fraction of the heat loss humans release from their body surface to the environment. According to Fanger [16], the latent part of the respiratory heat loss, E _rsp (W), is a function of the pulmonary ventilation rate which depends on the whole body metabolism, Q _m (W), the latent heat of vaporisation of water, and the difference between the humidity ratio of the exhaled and inhaled air which depends on air temperature, T _a (°C), and the partial vapour pressure of the ambient air, p _a (Pa). An explicite inclusion of T _a in the formula and re-arranging yields:

$$ E_{rsp} = 3.233 \times 10^{ - 3} Q_{m} \left( { 27.7 - 0.065\, T_{a} - 0.00491\,\mathop p\nolimits_{a} } \right) $$

(43)

Since the enthalpy of the exhaled air depends to a certain degree upon the condition of the inhaled air, E _rsp appears as a function of both T _a and p _a. The inclusion of T _a allows E _rsp to be calculated for a wide range of ambient air conditions.

The dry respiratory heat loss by convection due to the difference between the temperature of the exhaled and inhaled air is a function of the pulmonary ventilation rate, and the temperature and vapour pressure of the ambient air, T_a and p_a, respectively [16]:

$$ C_{rsp} = 1.44 \times 10^{ - 3} Q_{m} \left( { 32.6 - 0.934\,\,T_{a} + 1.96\, \times 10^{ - 4} \mathop p\nolimits_{a} } \right) $$

(44)

The total respiratory heat losses E _rsp  + C _rsp is distributed over compartments of the pulmonary tract [17].

4.2 Clothing

Current clothing standards define ‘global’ thermal and evaporative resistances of garments, I _cl (m² K W⁻¹) and R _e,cl (m² Pa W⁻¹), for the human body as a whole [14]. As this global insulation approach assumes all body parts (incl. head, face, hands, etc.) being covered by a (fictitious) uniform layer of clothing it appears inappropriate for use with multi-segmental models. To adequately model the local heat and mass transport processes the non-uniformity of clothing has to be considered using the actual, i.e. local, insulation properties of clothing at individual body parts.

The FPC-model is used in conjunction with a ‘local’ clothing model that predicts the required local resistances of garments from measured resistances of textile fabrics [46, 47]. The model simulates the local (steady state) heat and mass transfer processes within cloth composites considering also radiation effects and the insulation of any air trapped between clothing layers based on an approach by McCullough et al. [47]. The local clothing model employs an iteration algorithm to fine-tune predicted resultant local resistances of garments and clothing ensembles to ensure agreement with the overall resistances as measured in thermal manikin experiments.

Within the physiological model the resultant total local sensible thermal resistance R _lT (m² K W⁻¹) of a multi-layered composite covering a body sector is calculated as:

$$ R_{lT} = \mathop \sum \limits_{i = 1}^{{}} R{}_{lcl,i} + \frac{1}{{f_{lcl} \left( {h_{c} + h_{r} } \right)}} $$

(45)

where R _lcl,i (m² K W⁻¹) is the local thermal resistance of the i-th clothing item covering that body part, h _c and h _r (W m⁻² K⁻¹) are local surface coefficients for convection and long wave radiation heat exchange as defined above, and f _lcl [−] is the local clothing area factor defined as a quotient of radii of the outmost clothing layer, r _cl (m), and the skin, r _sk (m):

$$ f_{lcl} = \frac{{r_{cl} }}{{ r_{sk} }} $$

(46)

The corresponding total local evaporative resistance, R _e,lT (m² Pa W⁻¹), is obtained from local evaporative resistances, R _e,lcl,i (m² Pa W⁻¹), of individual clothing layers applied to the body sector as:

$$ R_{e,lT} = \mathop \sum \limits_{i = 1}^{m} R{}_{e,lcl,i} + \frac{1}{{f_{lcl} \,h_{e} }} $$

(47)

where

$$ h_{e} = L_{a} \times h_{c} $$

(48)

with h _e (W m⁻² Pa⁻¹) being the local evaporative heat transfer coefficient and L _a the Lewis constant for air, L _a = 0.0165 K Pa⁻¹ [27].

The incorporated clothing model offers options for considering additional phenomena and effects such as wind penetration, the impact of walking and the clothing habits of the population (Fig. 13) as discussed elsewhere [35].

Fig. 13

Resultant global thermal clothing insulation values as a function of the ambient temperature reflecting the clothing habits of different European countries. Reproduced from [35] with permission

5 Coupled Simulation and Measurement Systems

Mathematical models of human thermoregulation typically incorporate simplified calculations of the human environmental heat exchange as an integral part of the simulation process. In reality, however, these processes as well as the environmental conditions themselves may be very complex so they either have to be measured directly or simulated using sophisticated numerical models of conjugate heat transfer.

From the mathematical point of view, the heat exchange with the environment represents a type of boundary conditions at the body surface that principally may be replaced by alternative formulations using e.g. measured or predicted surface heat fluxes or surface temperatures as model input. These quantitates too contain all the information that is required and is sufficient to fully describe the boundary conditions of an exposure for thermophysiological simulations.

As illustrated in Fig. 14, the FPC-model accepts the traditional definition of boundary conditions (Standard Model Input), i.e. environmental conditions with implicit calculations of environmental heat losses, as well as alternative definitions (Extended Model Input) using e.g. real-time measured skin temperatures, predicted heat fluxes, etc. as model input [22]. Thereby the extended model enables the type of boundary conditions to be defined flexibly for different body regions, body elements or individual sectors of the passive system.

Fig. 14

Schematic diagram of the ‘individualized’ FPC-model extended for use with different types of boundary conditions at the body/skin surface (e.g. skin temperatures, Tsk, clothing temperatures, Tcl, or skin heat fluxes, qsk) and personal states (e.g. heard rate, HR, oxygen consumption, VO₂, breathing rate, BR, etc.) for easy and flexible coupling with other simulation tools or measurement systems

Various industrial applications require detailed analysis of the complex environmental heat transfer processes involving human occupancy. Numerical simulation systems have thus been developed which couple the model e.g. with dynamic thermal simulation of vehicles [20, 21], numerical radiation scenario models [69], behavioural clothing models [35], temperature regulation during cardiac surgery [62], or sophisticated Computational Fluid Dynamics (CFD) simulation to aid the design of comfortable and energy-efficient cars and buildings [7, 45]; for further examples see e.g. [21].

With the extended definition of boundary conditions the FPC-model enables an easy and flexible coupling and integration with other simulation tools. In the examples illustrated in Fig. 15, detailed 3D human geometry models were used to facilitate the bi-directional data exchange between CFD and physiological models. In the coupling process CFD provided the environmental boundary conditions at surfaces of the simulated person needed for thermophysiological simulation while the physiological model delivered the required boundary conditions for CFD simulation. In the current FPC-model version users can set-up the coupling with CFD (or other tools) flexibly without the need to modify the source code of the models.

Fig. 15

Examples of 3D geometry models used for detailed human environmental heat transfer analysis: air flow and temperature distribution around a thermoregulated human body using coupled CFD-FPC-model simulation. Reproduced from [45] with permission

Coupled systems may also involve physical models such as thermal manikins. Accurate numerical simulations generally require detailed knowledge of scene-specific factors and parameters of the human environmental heat exchange. This information may be readily available for well-controlled laboratory conditions but difficult to obtain for human exposures in the field. Combined hardware-software solutions may thus be superior when predicting human responses to the complex conditions of uncontrolled real-world exposure scenarios.

As an example, the system illustrated in Fig. 16 uses the FPC-model to provide a heated sweating cylinder Torso with ‘thermophysiological intelligence’ [55, 56]. This ‘human simulator’ device measures the net surface heat fluxes which result from the complex heat and mass transfer processes taking place within clothing systems thus enabling measurement of clothing properties under physiologically realistic conditions.

Fig. 16

Scheme of data exchange in the single-sector thermophysiological ‘human simulator’ [55], reproduced with permission, graphs on the left reproduced by permission of IOP Publishing. All rights reserved © Institute of Physics and Engineering in Medicine

Other examples include ‘intelligent’ measurement systems which deploy numerical simulation of human heat transfer to postprocess and interpret measured data. An example of such a system is the development of a non-invasive monitoring and warning system (MWS) that uses wearable sensors to determine internal temperature and heat stress levels of people working in hot industrial environments [22, 23]. MWS can measure skin/clothing temperatures, Fig. 16, providing the required boundary conditions at the body surface of the wearer. This information is used by the FPC-model to assess the body core temperature of people exposed to different environmental and personal conditions. Body core temperatures are determined non-invasively by means of numerical simulation—but without the need for detailed knowledge of scene-specific factors and parameters. Validation examples of predicted rectal temperatures using the personalized model are provided further below (Fig. 17).

Fig. 17

Peripheral sensor set-up of a monitoring and warning system for non-invasive body core temperature assessment in individuals exposed to different environmental and personal conditions and wearing different types of (protective) clothing systems

6 Predicting Human Thermophysiological Responses

In the past, the standard model was subject to various general as well as application-specific validation studies. The tests included climate chamber experiments with exposures to wide-ranging steady state and transient environmental and personal conditions [18], diverse indoor climate conditions with/without asymmetric radiation in cars and buildings [19, 20, 42, 43], exposures to heat stress conditions of subjects wearing protective clothing [22, 23, 58], etc. A large-scale, international study also addressed field surveys and exposures to uncontrolled outdoor climates including weather extremes [57].

Fig. 18 compares measured and predicted responses of semi-nude subjects exposed for one hour to different steady-state ambient temperatures ranging from 5 and 48 °C [18]. The experimental results collected from several climate chamber experiments are provided as averages with the corresponding standard deviations (SD).

Fig. 18

Mean skin temperature, body core temperature and thermoregulatory responses as measured and predicted over wide-ranging steady state environmental conditions. Reproduced from [18] with permission

The dynamic behaviour of the model was examined extensively for different types of transient exposure conditions. Comparisons of predicted body temperature and regulatory responses with experimental data obtained using the standard model for sudden changes in environmental temperatures from neutral to hot and from hot to cold and back again are illustrated in Fig. 19.

Fig. 19

Body temperature and thermoregulatory responses as measured and predicted for step changes in room temperature into a hot environment of Ta = 43 °C (left) and from a hot environment of 43 °C to a cold environment of 17 °C and back again (right). Reproduced from [18] with permission

Also the individualized FPC-model was subjected to several validation tests [22, 23]. In one test, unacclimatized semi-nude male subjects featuring different personal characteristics and fitness levels [38, 57] were exposed to steady indoor climate conditions of 28 °C ambient temperature (T_a = T_wall), va = 3.8 m/s air speed, 50 % relative humidity while exercising on a treadmill at levels up to 13 met (90 % VO_2,max). The following validation tests focused on the performance of the individualized model to predict body core (rectal) temperature responses [22]. In the simulations, information on personal characteristics including stature, body weight, gender and age, as well as information on fitness and acclimatization levels were used as input into the model along with environmental conditions and exercise intensity.

In Fig. 20 predicted rectal temperatures are compared with measured data for average-fit, semi-nude male subjects exercising at an intensity level of 8.9 met. To simulate group-average responses the model was run with the following data representing averages of eight subjects: stature = 1.81 m, weight = 74.1 kg (BMI = 22.6 kg/m²), age = 33.4 years, unacclimatized, ‘standard’ fitness (s.fit.M). Rectal temperature predicted using this configuration agreed with measured responses within a root mean square deviation [2], rmsd, of <0.1 °C. For comparison also rectal temperatures predicted using the Reference Model (ref.M) and an unfit female (u.fit.F) are plotted in Fig. 20. The role of aerobic fitness and body composition (sex) on predicted rectal temperatures is apparent from the results obtained for a standard-fit male and unfit female both featuring the above group-average body height and weight. Substantial discrepancies from measured rectal temperatures resulted for the simulated female indicating the significance of the physical fitness and body composition under conditions of intense exercise.

Fig. 20

Average rectal temperature responses of semi-nude male standard-fit subjects (n = 8) exercising at 8.9 met with s.fit.M: standard-fit male (VO_2,max =40 ml kg⁻¹min⁻¹), ref.M: reference model (40 ml kg⁻¹min⁻¹), u.fit.F: unfit female (20 ml kg⁻¹min⁻¹), exp.: experiment

The above example studied average-group responses. Rectal temperatures predicted for two individual athletes are compared with measured temperatures in Fig. 21. The left-hand diagram refers to the smallest and lightest subject of the athlete group who was 19 years old, 1.72 m tall, and weighed 62.7 kg (BMI = 21.2 kg/m²). The right-hand diagram of Fig. 21 depicts the response of the tallest and heaviest athlete in the trials with a body height of 1.84 m, and weight of 79.7 kg (BMI = 23.5 kg/m²), aged 20 years. The simulations (fit.M) reproduced measured rectal temperatures (exe.) by rms-deviations of <0.2 and <0.1 °C, respectively.

Fig. 21

Comparison of predicted and measured rectal temperatures of single male athletes: (i) response of the smallest and lightest athlete in the group exercising at 13.2 met (left) and (ii) group tallest and heaviest athlete exercising at 11.5 met (right) with fit.M: fit male (VO_2,max = 60 ml kg⁻¹min⁻¹), s.fit.M: standard-fit male (40 ml kg⁻¹min⁻¹), exp.: experiment

For comparison also rectal temperature predicted for a standard-fit male (s.fit.M) is plotted in Fig. 21, left. The predicted rectal temperature reached 41 °C at the end of the exposure, again underlining the need to consider physical fitness in conditions of very high-intensity exercise, i.e. 13.2 met in this case.

In Fig. 22, two different types of boundary conditions (BC) at the skin were used to predict body core temperatures of semi-nude sedentary subjects exposed to step changes in air temperatures of 29-38-28 °C [22, 32]. In the ‘classic’ BC-type mode (‘input: Env.C.’) rectal temperature was predicted by the FPC-model simulating a standard person from measured climatic conditions (and metabolic rates) as model input calculating the subjects’ dry and latent heat losses to the environment. In the alternative BC-type mode (‘in: Tsk,m’ in Fig. 22) observed mean skin temperatures and metabolic rates were used as model input avoiding so calculations of environmental heat losses. In both cases rectal temperature was predicted with an error of less than 0.2 °C rmsd; though the alternative method better reproduced measured data.

Fig. 22

Exposure of sedentary (act = 1.0 met) semi-nude (Icl = 0.1 clo) subjects (n = 3) to sudden changes in environmental temperature (T_wall = Ta), from neutral (29 °C) to warm (38 °C) and back to neutral (28.0 °C), v_a = 0.1m/s, and RH = 40-33-41 % [32]. Rectal temperature was predicted using two definitions of boundary condition at the skin: classic (input: Evn.C.) and alternative (in: Tsk,m) method using environmental conditions and mean skin temperature, respectively, as model input (see text for more detail)

The results obtained for a 22-43-22 °C scenario are plotted in Fig. 23 [22, 63]. Except for the initial period, both the level and the dynamics of the measured response were reproduced well by the alternative method using measured skin temperature as model input (note: in the classic Env.C.-method skin temperature, Fig. 23 left, was predicted as a result of calculated environmental heat losses). In both cases rectal temperature was predicted within 0.2 °C rmsd.

Fig. 23

Exposure of sedentary (act = 1.0 met) semi-nude (Icl = 0.1 clo) subjects (n = 3) to sudden changes in environmental temperature (T_wall = T_a), from cool (22 °C) to hot (44 °C) and back to cool (23 °C), v_a = 0.1 m/s, and RH = 40 % [63]. Rectal temperature was predicted using two definitions of boundary condition at the skin: classic (input: Evn.C.) and alternative (in: Tsk,m) method using environmental conditions and mean skin temperature, respectively, as model input (see text for more detail)

The performance of the individualized model predicting body core temperature from measured skin temperatures was tested for subjects wearing permeable and impermeable protective clothing [23]. In the climate chamber trials subjects were undergoing periods of rest and exercise under different combinations of environmental and clothing conditions [10]. Although the multi-segmental FPC-model accepts individual local skin temperatures, mean skin temperatures were used as model input in this study. In the base-case simulation series (Tsk,m), the mean skin temperature was calculated as a weighted average of measured local skin temperatures using a nine-point relationship [31]. In the second simulation series (Tsk,c) local skin temperatures solely from the central body parts (five-point average) were used. The third simulation series (Ehx) was conducted for comparison calculating environmental heat losses from measured climatic conditions and thermophysical clothing properties. In all simulations, experimental metabolic rates were used as an additional model input as were personal body characteristics aerobic fitness and the acclimatisation status of the subjects.

A comparison of predicted and measured responses for subjects wearing impermeable coveralls exposed to moderate environmental conditions of 25.7 °C air temperature is provided in Fig. 24. Using the Tsk,m-method rectal temperature was predicted within the range of experimental standard deviation throughout the exposure. The Tsk,c-method overestimated the (nine-point) mean skin temperature by about 1 °C. As a result, rectal temperature was overpredicted slightly at the end of the exposure although the method still delivered a comparable accuracy, rmsd <0.1 °C. No substantial differences from experimental observations resulted also for rectal temperatures predicted using the Ehx-method with rmsd <0.2 °C.

Fig. 24

Responses of subjects (n = 13) wearing an impermeable suit exposed for 110 min to a moderate environment of 25.7 °C air temperature (50 % RH, 0.3 m/s air speed). The predicted group-average rectal temperature (Tre) and total body weight loss (Msw) were predicted from different configuration of skin temperature sensors (Tsk,m and Tsk,c) and environmnetal conditions (Env) as input boundary conditions (see text)

Predicted and measured group-average responses obtained for a hot environment of 40.4 °C with subjects wearing impermeable clothing are plotted in Fig. 25. The inability of the subjects to evaporate sweating caused a notable increase of the heat stress level associated with a rise of the mean skin temperature, rectal temperature, and total body moisture losses by 0.8, 0.3 °C and 0.1 L, respectively. Under such uncompensable heat stress conditions only the Tsk,m- and Tsk,c-mode methods predicted rectal temperature within the range of the experimental standard deviation with rmsd <0.15 °C. The Ehx-mode method obviously overestimated the cooling effect of sweat evaporation causing rectal temperature to be under-predicted by up to −0.6 °C with a rmsd >0.4 °C.

Fig. 25

Responses of subjects (n = 14) wearing an impermeable suit exposed for 100 min to a hot environment of 40.4 °C air temperature (23.4 % RH, 0.4 m/s). The predicted group-average rectal temperature (Tre) and total body weight loss (Msw) were predicted from different configuration of skin temperature sensors (Tsk,m and Tsk,c) and environmnetal conditions (Env) as input boundary conditions

The impact of an additional thermal load of 600 W/m² due to (simulated) direct solar radiation incident on the back of the subjects wearing permeable clothing is apparent from Fig. 26. Also under these asymmetric radiation conditions the Tsk,m- and Tsk,c-methods reproduced experimental observations of the rectal temperature within 0.1 °C rmsd. The Ehx-method required preliminary simulations of the 3D-radiation scene and the amount of radiation incident on irradiated body parts. With this information the Ehx-method predicted the rectal temperature with rmsd <0.2 °C.

Fig. 26

Responses of subjects (n = 17) wearing a permeable suit exposed for 110 min to hot environmental conditions of 40.8 °C air temperature and 600 W/m² direct short wave radiation (22.8 % RH, 0.3 m/s). The predicted group-average rectal temperature (Tre) and total body weight loss (Msw) were predicted from different configuration of skin temperature sensors (Tsk,m and Tsk,c) and environmental conditions (Env) as input boundary conditions

7 Summary and Conclusions

This chapter dealt with aspects of modelling the human heat transfer and thermoregulatory system. Approaches to simulate the passive system included modelling the human body based on results of anthropometric field surveys, and heat and mass transfer processes that occur inside the body and at its surface. The statistically founded active system was formulated by means of meta-regression analysis of thermoregulatory responses observed in published experimental studies collected to cover a wide range of exposure conditions. The set-point based feedback active system uses afferent signals associated with temperatures of the skin and head core, and the rate of change of skin temperature to predict the responses of sweating, shivering and peripheral vasomotion to static and dynamic thermal stimuli.

The passive and active system models were extended to simulate individuals. The personalized models account for variations in anthropometric and morphological body properties, aerobic fitness, acclimatization status and their effect on human thermophysiological responses using readily-available personal data as model input. The individualized FPC-model accepts different types of boundary conditions at the surface of the simulated person. This way an easy and flexible coupling with other simulation models or measurement systems is possible. The model can so be ‘connected’ e.g. to different wearable sensors to assess, non-invasively, internal temperatures of people in real-life exposure settings.

The model was validated against experimental data in diverse general as well as application-specific validation studies. Validation tests discussed in this chapter included responses to wide-ranging steady state and transient environmental conditions, and responses of sedentary and exercising subjects wearing different types of clothing and featuring different personal characteristics.

The tests also included non-invasive assessments of the rectal temperature using measured skin temperatures and metabolic rates as model input. The numerical simulation approach proved to be a robust predictor of the body core temperature under a broad range of exposure scenarios. Rectal temperatures were predicted with a rms-deviation of <0.2 °C for individuals and <0.15 °C for group-average responses irrespective of the test environmental conditions, exercise intensities, type of (permeable/impermeable) clothing, and presence or absence of high intensity radiation sources. It is concluded that—unlike empirical data-driven algorithms—this first-principles numerical approach is applicable beyond the range of experimental data used to develop it including different exposure circumstances, personal characteristics, exercise levels or types of clothing.