Keywords

1 Introduction

Commonly, the noises in most of geophysical time series are described as a power-law process (Agnew 1992) with the power spectrum equal to:

$$ {P}_x(f)={P}_0{\left(\frac{f}{f_0}\right)}^{\kappa } $$
(1)

where f is the spatial or temporal frequency, P 0 and f 0 are the normalising constants and κ is the spectral index of noise (Mandelbrot and Van Ness 1968). Agnew (1992) described that the spectral indices for the geophysical processes often fall between −3 and −1. The integer values of indices indicate special types of noises: “κ = −2” represents random-walk process which is related to the monument instability of the GPS antennae (Johnson and Agnew 1995; Williams et al. 2004; Klos et al. 2014); “κ = −1” stands for the flicker noise process (Mandelbrot 1983) that is recognized in most of GNSS time series (Mao et al. 1999; Williams et al. 2004; Bogusz and Kontny 2011); “κ = 0” corresponds to the white noise which is not correlated in time.

Any of the topocentric component is thought to follow the sum of:

$$\setcounter{equation}{1}\begin{array}{lll}x(t)&=&{x}_0+{\textit{v}}_x\cdot t+{\displaystyle \sum_{i=1}^n\left[{A}_i\cdot \sin \left({\omega}_i\cdot t+{\varphi}_i\right)\right]}\nonumber\\&& +{O}_x+{\displaystyle \sum_{j=1}^m{p}_j\cdot {x}_j^{\it off}}+{\varepsilon}_x(t) \end{array}$$
(2)

where x 0 is the initial value, v x is the velocity, A, ω, ϕ are the amplitude, angular velocity and phase shift of the i-th periodic component of a time series, O x stands for any known outliers, x off for offsets, p is the Heaviside step function, ε x is the noise. The noises in geophysical time series are correlated in time. This correlation has a great impact on any linear parameters that are estimated from these time series (Williams 2003).

The outliers detection and their removal plays a significant role in the interpretation of the GNSS data. The disputable issue here is the criterion. The most common criteria that depend on the time series character are the removal of values greater than 3 or 5 times the standard deviation. Bergstrand et al. (2007) estimated the noises in the GPS time series after removal of the outliers with 5σ criterion what was stated to be more conservative approach than the 3σ one, used for instance by Johansson et al. (2002). Dong et al. (2006) used the method of discarding the residuals exceeding the constant values of 100, 100 and 300 mm for east, north and vertical components, respectively, to remove the outliers before performing the Principal Component Analysis (PCA). It is worth to note that sigma-based methods correspond strictly to the normal distribution of data. However, what about data that are not normally distributed? Having the above in mind, we decided to investigate the influence that the outliers removal method may have on the time series characteristic using skewness, kurtosis (derived from the moments of data probability density function – PDF) and noise analysis (with Maximum Likelihood Estimation). We took 12 extremely spread EPN time series and removed the outliers with three chosen criterions. At the beginning, the commonly used 3 and 5 times of standard deviations were applied that assume data normal distribution. Then, the Median Absolute Deviation criterion was used. Our main goal of this research was to show how the proper removal of outliers affects estimation of kurtosis and skewness and therefore our understanding of the nature of the data. As shown previously by Peinke et al. (2004) or Sura and Gille (2003), the geophysical phenomena are not necessarily Gaussian. The deviations from Gaussianity can have an impact on the real dynamics. On the other hand, Sura and Gille (2010) stated that the skewness is positive if the additive and multiplicative noises are positively correlated and the skewness is negative if the noise terms are negatively correlated.

2 Data Processing and Methods

The time series used in the following research were obtained within the reprocessing project (“repro-1”) according to the EPN guidelines (Bruyninx et al. 1996) using Bernese 5.0 software (Dach et al. 2007). It was performed at the Military University of Technology in the Centre of Applied Geomatics that is one of the 16 independent Local Analysis Centres (MUT LAC). The coordinates in the ITRF2005 reference frame (Altamimi et al. 2007) were obtained as the result. The set of 12 stations with the greatest number of outliers was selected to the research. The white and power-law noise were assumed to be present in the time series before the Maximum Likelihood Estimation (MLE) with CATS software (Williams 2008). The MLE method follows the equation of:

$$\begin{array} {lll}{\it lik}\left(\widehat{{\textit v}},C\right)&=&\frac{1}{{\left(2\cdot \pi \right)}^{N/2}\cdot {\left( \det C\right)}^{1/2}}\cdot\nonumber\\ &&\exp \left(-0.5\cdot {\widehat{{\textit v}}}^T\cdot {C}^{-1}\cdot \widehat{{\textit v}}\right) \end{array}$$
(3)

The power-law noise is characterized by spectral index κ and the amplitude A. The MLE method has been already successfully used to evaluate noises in many researches, described e.g. in the papers by Beavan (2005), Bergstrand et al. (2007), Teferle et al. (2008), Bos et al. (2008).

3 Outliers Removal in the Noise Analysis

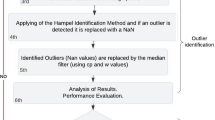
Three methods of outliers removal were tested in this research. The first and the second one removed the outliers greater than 3 and 5 times the standard deviation of time series (referred to as: 3 sigma (3σ), 5 sigma (5σ)), respectively. The third one focused on the Median Absolute Deviation – MAD (Mosteller and Tukey 1977; Sachs 1984), of time series. No interpolation of removed data was performed. The advantage of MAD method is being much more robust for outliers than sigma-based methods. The ‘robust’ is being used throughout the paper when describing the MAD method. We mean here that the data median value makes MAD not to be as sensitive to outliers as the sigma-based criterions are. The MAD is calculated from:

$$ {\it MAD}= {\it median}\left(\left|{X}_i- {\it median}(X)\right|\right) $$
(4)

To use the MAD value in a similar way as the standard deviation for the normal distribution, we multiply it by 1.4826 (Ruppert 2011). Later in this paper, whenever we use MAD it is actually \( 3\cdot 1.4826\cdot \mathrm{M} AD \), what makes the values of median absolute deviation close to 3 times the standard deviation, but never equal to. Twelve extremely noisy EPN stations (BISK, BOLG, CNIV, BZRG, HERS, MDVO, MEDI, MOPI, NYIR, SNEC, ZWEN, SFER) were chosen to investigate how the outliers influence noise estimation (Figs. 1 and 2).

Fig. 1
figure 1

The time series (in the ITRF2005) with the highest amount of outliers taken for the removal analyses. For shorter time series, all data were analyzed, for longer ones – only the data in the black boxes were considered. Some of the time series are quite consistent and there are just few of outliers. For others, all data are spread (SNEC, ZWEN) and noise estimation can be disturbed by them

Full size image
Fig. 2
figure 2

The removed values with 3σ, 5σ and MAD criteria for SFER station, here – Up component was presented, data in the ITRF2005

Full size image

The number of outliers removed from the twelve of the analyzed stations reaches the greatest value of 4% for ZWEN station with the 3 sigma criterion, whereas it is larger than 15% for MAD for the same station (Fig. 3). The MLE was performed after outliers removal with 3σ, 5σ, MAD assuming the white plus power-law noises. As the result, the spectral indices and noise amplitudes with uncertainties were obtained (Fig. 4a–c).

Fig. 3
figure 3

The percentage of outliers removed from the analysed time series using the 3σ, 5σ and MAD criteria. The results are presented for topocentric components in the North, East, Up order

Full size image
Fig. 4
figure 4

The spectral indices (a), noise amplitudes (with one sigma error bars) (b) and their uncertainties (one sigma error bars, presented apart from noise amplitudes) (c) estimated for all of analyzed stations using the MLE method. The amplitudes are presented in \( mm\cdot y{r}^{\kappa /4} \). The results are presented with respect to the analyzed stations. The blue colour indicates no removal of outliers, green stands for the 5σ criterion, red for 3σ, and yellow for MAD. In all cases no interpolation of removed data was performed

Full size image

The spectral indices for twelve of analyzed stations range between −2 and 0. The noise amplitudes for stations with spread time series reach quite odd and unrealistic values (HERS, SNEC, SFER). The noise amplitude uncertainties in case of no removal of outliers are too large and unacceptable. All stations prove the necessity of outliers removal. The disputable issue here is the criterion. No removal or 5σ criterion brings unacceptable results for stations with just a few of outliers (BISK; BOLG; CNIV; BZRG; HERS – the North and East components; MDVO; MEDI; MOPI; NYIR; ZWEN). The noise amplitudes obtained after 3σ or MAD criterion are smaller than \( 10\ mm\cdot y{r}^{\kappa /4} \) and quite close to each other at the same time for the consistent time series. The situation changes in case of spread time series. Here, the MAD criterion results in smaller noise amplitudes and uncertainties as well. The most interesting time series with extremely spread values for both horizontal and vertical changes comes definitely from the SNEC station. The spectral index for SNEC was estimated as close to random-walk what may be interpreted as changes related to the monument instability. As stated by King and Williams (2009) random-walk amplitudes for well monumented stations are probably no higher than \( 0.5\ mm\cdot y{r}^{-0.5} \). The SNEC station with such a spread time series reaches the highest noise amplitude. It is still too large even after MAD outliers removal. Now, the BZRG station with quite consistent time series with two periods of strong reflexes from trend. No removal of outliers, 5σ and 3σ criteria result in similar values of amplitudes, while the MAD criterion results in smaller and interpretable noise parameters. It causes the reduction of amplitudes to around \( 10\ mm\cdot y{r}^{\kappa /4} \) with the increment of spectral index to -1 for the Up component. Bearing in mind, that the type and amplitude of noise takes part in estimation of the linear parameters from the time series, one has to understand the values he obtains. Sometimes they do not strictly reflect the existence of the noise, but they can simply be the effect of the wrong or even lack of data pre-analysis.

4 The Probability Analysis

The probability analysis was conducted beyond the noise analysis. The point is whether treating the time series as normally distributed for the GNSS time series and therefore using the 3σ criterion for outliers removal is appropriate or some robust method (here MAD) should be used. The analysis was performed by estimation of moments of the data’s probability density function (PDF) that are the skewness and kurtosis. Their advantage in this study, however, is high sensitiveness to outliers.

Fig. 5
figure 5

The values of skewness and kurtosis (with no removal, 5σ, 3σ and MAD criteria) for analyzed stations for the North, East and Up components, data in the ITRF2005

Full size image

The asymmetry of PDF’s shape can be described by the skewness:

$$ S=\frac{E{\left(x-\overline{x}\right)}^3}{\sigma^3} $$
(5)

where \( \overline{x} \) is the mode of x, σ is the standard deviation of the data and E is the expected value. If the classic Gaussian distribution is considered, its skewness is equal to zero. If not, the distribution is skewed right for values greater than zero or skewed left for values below zero. The standard error of skewness (SES) can be computed by (Cramer 1977):

$$ {\it SES}=\sqrt{\frac{6n\left(n-1\right)}{\left(n-2\right)\left(n+1\right)\left(n+3\right)}} $$
(6)

where n is the number of data in the time series. In this paper, \( {\it SES}=\pm 0.06 \). The value of \( 3\times {\it SES}=\pm 0.18 \) was assumed here as the boundary value for normal distribution.

The kurtosis is a measure of the probability distribution “peakedness” of a real-valued random variable. The kurtosis is computed by the formula:

$$ K=\frac{E{\left(x-\overline{x}\right)}^4}{\sigma^4} $$
(7)

If the kurtosis is equal to 3 we deal with the normal distribution. High kurtosis means that the peak near the mean is distinct, and probability distribution decline rather rapidly. The standard error of kurtosis can be estimated by (Cramer 1977):

$$ {\it SEK}=\sqrt{\frac{n^2-1}{\left(n-3\right)\left(n+5\right)}} $$
(8)

where n is the number of data in the time series. Here, \( {\it SEK}=\pm 0.12 \) and \( 3\times {\it SEK}=\pm 0.36 \) were assumed as the boundary values for the normal distribution. The skewness and kurtosis put together can indicate the normally distributed time series.

Firstly, the skewness and kurtosis were calculated for data with no removal of outliers. Then, for the 5σ, 3σ and MAD criterion. The usage of 5σ brought the unexpectedly good betterment in the analyzed values (even though there were just few values exceeding this limit), what proved that the skewness and kurtosis are really sensitive to outliers (Fig. 5). The differences in the skewness values after removal of outliers with 3σ and MAD criteria are mostly within 3 times of SES for the horizontal components what proves that the use of removal criterion does not change the probability distribution. Three stations (HERS, SNEC, SFER) in case of the Up component show quite large differences between skewness after 3σ and MAD. The differences between the kurtosis values after 3σ and MAD removal in most cases fall into 3 times the SEK. However, the differences are greater for few stations: HERS (the East and Up components), MDVO (the East component), SNEC (the East and Up components), SFER (the North and Up components). One of the kurtosis interpretations is the precision of data gathered. If kurtosis is high, precision is also high – the peak near the mean is very distinct (but only if the skewness is equal to 0). In case of the inappropriate criterion of outliers removal and no analyses of skewness, remaining outliers can have a significant impact on kurtosis values and therefore lead to falsified conclusions. The example of data stated as highly precised (without analysing its skewness) is presented in the Fig. 6. However, it is well known that high values of kurtosis can also mean heavy tails, which is exactly what would be expected if outliers are present. Thus, the large value of kurtosis obtained without outliers removal is entirely expected. Therefore the data pre-analysis is so essential before any further estimations.

Fig. 6
figure 6

The probability density function for the SNEC station – the Up component with no removal (left) and after MAD (right) outliers removal

Full size image

5 Discussion and Conclusions

Our main goal in this research is to show how the proper removal of outliers affects the estimation of kurtosis and skewness and therefore our understanding of the nature of the data. The pre-analysis of data that includes outliers removal has to be well-chosen to the type of time series. The commonly used 3σ criterion seems to fail in case of spread GNSS time series, due to the fact that the standard deviation is calculated from the whole data set. Otherwise, the MAD criterion seems to be more appropriate for outliers removal, since it is calculated from the median value and therefore is much more robust for outliers than sigma-based methods. The obvious issue is that the outliers have to be removed, while further analyses that are to be conducted could be really sensitive to them. As showed in this research, although the MLE method resulted in quite consistent spectral indices, the amplitudes of noises were unacceptable in a few cases. They did not even differ in the range of their uncertainties, what may result in the variety of wrong interpretations. To show how the outliers can affect any further estimations, the probability analysis was performed, since skewness and kurtosis are highly sensitive to outliers. We showed that the wrongly-chosen criterion leads to the misinterpretation on the time series distribution and also data precision. A few of differences of skewness and kurtosis showed in this research were higher than the set value of 3 times the SEK and SES. It proved that sometimes the use of 3σ criterion is not proper enough to remove outliers since the analyzed time series do not strictly reflect the normal distribution. On the basis of the results, the usage of the MAD criterion is recommended for the GNSS data. Its advantages over commonly used sigma-based criteria are quite obvious, according to the presented paper. Being less sensitive to outliers, it removes greater number of them, providing in this way better interpretation of real effects. The presented paper discusses the univariate time series. In the future, authors plan to expand the work for multivariate cases as in Feng (2012).