Introduction

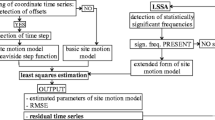
The Create and Analyze Time Series (CATS) software uses least squares to fit a multi-parameter model to a time series while concurrently analyzing the residuals to assess the type and magnitude of the stochastic noise. The program solves for all parameters in a two-part procedure; the linear function which includes an intercept, a slope, the possibility of abrupt steps (as from earthquakes or equipment changes) and any known periodicities (for example annual and semi-annual terms), while the non-linear part allows the parameters and amplitudes of several specific noise models to be estimated. There are currently three methods implemented in CATS for assessing the noise content; maximum likelihood estimation (MLE) (e.g. Langbein and Johnson 1997), spectral estimation (via Whittle’s approximate MLE in the frequency domain, Beran 1994), and an empirical method based on the work described in Williams (2003). There is also one other option, weighted least squares, where all of the noise parameters are pre-defined and not estimated. The principal method, and the one that most users have downloaded the software for, is MLE and it is the implementation of this method that will be described in greater detail below.

Maximum likelihood estimation

The origins of the MLE algorithms come from a set of MATLAB routines produced by H. Johnson. When it became apparent that the routines were becoming too slow and there was a need for a package that is independent of commercial software, the routines were consolidated and re-written in C. The background to this method, in the context of geodetic observations, can be found in the following papers, Langbein and Johnson (1997), Zhang et al. (1997), Mao et al. (1999), Williams (2003), Williams et al. (2004) and Langbein (2004). A short overview and some notes specific to CATS are given below.

To estimate the noise components and the parameters from the linear function the likelihood, l, that these values have occurred for a given set of observations, x, is maximized. Assuming a Gaussian distribution, the likelihood is

$$ l{\left( {x,C} \right)} = \frac{1} {{{\left( {2\pi } \right)}^{{\raise0.5ex\hbox{$\scriptstyle N$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 2$}}} {\left( {\det C} \right)}^{{\raise0.5ex\hbox{$\scriptstyle 1$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 2$}}} }}\exp {\left( { - 0.5\hat{v}^{{\text{T}}} C^{{ - 1}} \hat{v}} \right)} $$
(1)

where det is the determinant of a matrix, C is the covariance matrix representing the assumed noise in the data, N is the number of epochs and \( \hat{v} \) are the postfit residuals to the linear function using weighted least squares with the same covariance matrix C. For greater numerical stability, we maximize (or minimize the negative of) the logarithm of the likelihood,

$$ \ln {\left[ {l{\left( {x,C} \right)}} \right]} = - \frac{1} {2}{\left[ {\ln {\left( {\det C} \right)} + \hat{v}^{{\text{T}}} C^{{ - 1}} \hat{v} + N\ln {\left( {2\pi } \right)}} \right]} $$
(2)

since the maximum is unaffected by monotonic transformations. The algorithm of choice for solving the maximum likelihood problem is the Nelder–Mead uphill simplex (see for example, Press et al. 1992). It is a straightforward method to program, only requires function evaluations and not derivatives, and can cope with any combination of noise model parameters given to it. However the drawback is its lack of efficiency in the number of function evaluations used. The algorithms used in CATS have been optimized in two broad categories to improve the computational speed: a single dimension reduction in the estimation of amplitudes and nested maximization algorithms. This is achieved without the use of approximations.

Nested maximization

Very often one may wish to estimate parameters of the stochastic model other than just the noise amplitude: for instance, estimating the spectral index, κ, in power-law noise models, or the cross-over parameter, β, in first-order Gauss–Markov noise. These parameters could simply be added as extra dimensions in a general uphill simplex together with the set of noise amplitudes. However there is a good reason for not doing this. At most iterations the uphill simplex may choose a new value for one of these parameters and therefore a new unit covariance matrix has to be created. It appears better to split the maximization up into two parts. One part, let’s call it the inner maximization, simply estimates the noise amplitudes for fixed noise model parameters. An outer maximization is then used to estimate the other noise model parameters. This results in far fewer calls to the routines dealing with the covariance matrices (creation, inversion and determinant estimation) and is likely to be more stable numerically.

Single dimension reduction in estimating noise amplitudes

In reality the desired covariance matrix can be any combination of different stochastic models, that is

$$ C = {\sum\limits_{i = 1}^m {\sigma ^{2}_{i} J_{i} } } $$
(3)

where there are m different unit covariance matrices. For a fixed set of J i the MLE is often thought to be an m-dimensional problem. However, it can be shown to be m - 1 dimensional. If the covariance matrix consists of one noise source then we have

$$ C = \sigma ^{2} J $$
(4)

and the MLE can be re-written as

$$ \ln {\left[ {l{\left( {x,\sigma } \right)}} \right]} = - \frac{1} {2}{\left[ {2N\ln {\left( \sigma \right)} + \ln {\left( {\det J} \right)} + \frac{{\hat{v}^{{\text{T}}} J^{{ - 1}} \hat{v}}} {{\sigma ^{2} }} + N\ln {\left( {2\pi } \right)}} \right]}. $$
(5)

Now, in least squares we find that the residuals \( \hat{v} \) and the estimated parameters (but not their uncertainties) are invariant to a scale change in the covariance matrix. Therefore we can differentiate the log likelihood equation with respect to σ and find the value of σ that gives us the maximum likelihood is

$$ \sigma = {\sqrt {\frac{{\hat{v}^{{\text{T}}} J^{{ - 1}} \hat{v}}} {N}} }. $$
(6)

So in this case the maximum log-likelihood can be found explicitly. By association then a two-dimensional covariance matrix should only need a one-dimensional numerical maximization. Instead of two noise amplitudes σ1 and σ2 we can transform these to two alternative variables namely an angle, ϕ and a scalar r such that

$$ \begin{aligned}{} \sigma _{1} = & r\cos \phi \\ \sigma _{2} = & r\sin \phi \\ \end{aligned} $$
(7)

For a given angle we can compute a “unit” covariance matrix containing the correct ratios of the two, that is

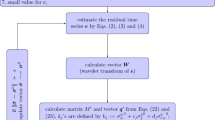
$$ C_{{unit}} = r^{2} {\left( {\cos ^{2} {\left( \phi \right)}J_{1} + \sin ^{2} {\left( \phi \right)}J_{2} } \right)} $$
(8)

which is similar in form to the one-dimensional covariance matrix. This reconfiguration can be extended to any number of dimensions. For a given angle, ϕ we can explicitly solve for r and therefore only need to maximize the log-likelihood numerically as a function of the angle, thereby reducing the dimensionality by one. Typically, this results in far fewer steps than the equivalent m-dimensional maximization. An example of this is illustrated in Fig. 1. There is additional dividend to casting the problem this way: like the one-dimensional problem, the estimated parameters and residuals are invariant to the scale change r therefore ensuring a reduction in the number of times the weighted least squares (and therefore the inverse of the full covariance) is calculated. In the case of a two-dimensional noise model the noise amplitudes can be solved using the one-dimensional, Brent algorithm (Press et al. 1992), which is more efficient than the uphill simplex in one dimension.

Fig. 1
figure 1

Log-likelihood estimates for the north component of GPS site BRST. a Log-likelihood values greater than 2130 plotted in amplitude space, that is, as a function of flicker noise and white noise amplitude. Black triangles indicate the path of the uphill simplex from σ1 = 1; σ2 = 1. White dots are the predictions from the 1D brent maximizations. White line is the exact maximum at all possible angles. b as a except in ϕ and r space. c The results of the 1d (Brent) maximization which calculates the maximum log likelihood value as a function of ϕ

Full size image

Noise models available

Currently CATS can produce a covariance matrix for the following noise models

  • White noise.

  • Power-law noise (also known as fractionally integrated noise, see Hosking 1981). This includes flicker noise and random walk noise by fixing the spectral index.

  • First-order Gauss Markov (FOGM) noise (equivalent to autoregressive AR(1) noise).

  • Band-pass noise (See Langbein 2004).

  • Generalized Gauss Markov noise (See Langbein 2004).

  • Variable white noise (i.e. using the formal errors).

  • Step-variable white noise (i.e. a change in the scale of white noise between two epochs, must be used with at least one other noise model).

  • Time-variable white noise (i.e. an exponential decay in the scale of the white noise).

Spectral estimation

An alternative method to maximum likelihood estimation is to estimate the stochastic noise components from the power spectrum of the time series (Langbein and Johnson 1997; Zhang et al. 1997; Mao et al. 1999). In CATS the power spectrum is created using the FFT, if the data is free from gaps and outliers, or the Scargle periodogram (Scargle 1982) otherwise. The stochastic noise components are estimated using Whittle’s approximate MLE in the frequency domain (Beran 1994). As for MLE method, the spectral estimation is solved using nested maximization routines together with the scale and angle approach. The positive aspect of spectral estimation is that it is, in general, much faster than MLE. However the negative aspects outweigh this positive. There are a limited number of noise models compared to MLE: for instance variable white noise cannot be distinguished from white noise in a power spectrum. Spectral estimation doesn’t implicitly estimate the parameters and uncertainties of the functional model: it simply uses least squares to create the residuals from which the power spectrum is created. The power spectrum is largely invariant to the subtle changes in the residuals brought upon by changes in the stochastic noise model. If the parameters and uncertainties of the functional model are required they can be estimated using the weighted least squares option afterwards. Finally spectral estimation is widely perceived to be less precise than the MLE method (Langbein and Johnson 1997; Pilgrim and Kaplan 1998; Mao et al. 1999).

Empirical estimation

A final fast method is offered in CATS, based on the empirical equations derived in Williams (2003). These are very limited in scope, only dealing with the case of power-law plus white noise, where the spectral index is fixed. This method has similar negative aspects to spectral estimation and is simply offered as an alternative where estimates for large networks are required on a regular basis and where the power-law plus white noise model is considered adequate.

Input files

There are currently two accepted formats for input; a CATS file for GPS-like time series and a PSMSL (Permanent Service for Mean Sea Level) file for sea-level time series. In the future, other formats may become available. Users are free to suggest new formats (writing the code would be even better; see read_series.c in the lib directory for examples).

CATS file description

The data file is fairly free format consisting of two parts: header information and the time series. The header information is basically a list of parameters relevant to the GPS site the time series comes from. The header information (plus any line you want to eliminate from the processing) starts with a # symbol. The only header information relevant to CATS is the list of offsets. The data set consists of seven columns (no particular format) corresponding to, in order, time (in decimal years) north, east, up, north error, east error, up error. The positions are, by default, assumed to be in meters, however this can be altered as an option. The individual formal errors are only used in the MLE estimation to define a variable white noise component. An example of a file following this format is given in Table 1.

Table 1 Example of a CATS time series file
Full size table

If there any known discontinuities or offsets in the time series then these are specified in the header of the file in the following format

# offset decimal_date component_code where the decimal_date is the time the offset occurred and the component_code is an integer describing which of the three directional components the offset should be applied to. The component code is expressed in a manner similar to file permissions on a Linux-style system. The component code is the sum of the components in which the offsets appears with the values north (4), east (2) and vertical (1). This gives an exclusive number between 0 and 7 for all combinations of affected components. For example for an offset occurring in the north and up components the component code is 5. For all components the value is 7. The offsets need not be in chronological order nor do you even have to ensure that they are within the time span of the data set. The program will sort the offsets correctly when processing the file.

PSMSL description

This type of data file is, again, very simplistic and is described on the Permanent Service for Mean Sea Level web site (see Links section at end of paper). It basically consists of two main columns. Column one is the time stamp and column two is the data. The third column in this type of file indicates the number of days of data missing in the month. CATS only uses data from months where there are no missing data. An example of a data file is given in Table 2.

Table 2 Example of a PSMSL time series file
Full size table

This file format has been adapted so that it can read in offsets and ignore lines that begin with the # symbol the same way as for the CATS format.

CATS installation

CATS is available at http://www.pol.ac.uk/home/staff/?user=WillSimoCats as either a GCC compiled binary for Linux, a Portland compiled binary (also for Linux but generally faster) or as source code using a gzipped tar file. If you download the binaries we also recommend that you download the source code since the documentation and some example time series files are included in the tar file. The software has been compiled on many different Linux distributions, SUN workstations and on Windows-based PCs using CYGWIN.

To compile the source code the user must have some familiarity with makefiles and the Unix make utility. The majority of the mathematical computations are performed using the clapack and blas libraries so they need to be preinstalled on your system and the paths to the appropriate directories changed in the make.inc file. Since there is a large computational burden in CATS it is important to make sure that the clapack and blas libraries are optimized for your system. In addition we recommend that your system has at least 1 Gb of RAM to cope with large time series.

CATS usage

The program is command-line orientated (with long and short options), so it does not require any other files except for the input time series file in order to run. The documentation that comes with the software goes into explicit detail about each option for CATS. The options can be divided into three categories: stochastic model, functional model and other. The stochastic model is defined using the model option and can be used as many times as required on the command line. For instance, the options for a flicker noise plus white noise model would look like

--model pl:k-1 -–model wh:

where pl: stands for power-law and wh: stands for white noise. The second part of the pl: option, k, sets the spectral index to -1 (flicker noise). If a spectral index is not specified then the program will solve for this parameter.

The functional model is already predefined as having a slope, an intercept and any offsets that are found in the time series file. If you wish to solve for the amplitude and phase of any periodic signals then this can be achieved using the sinusoid switch. This switch can also be used as many times as required on the command line. If you do not require the program to estimate a trend in the data, then this option can be switched off using notrend.

Some other options of note are method which defines which estimation method to use, verbose which outputs extra information and output which forces the results to be printed to a file instead of the screen.

Typical CATS output

Output from the software is either to the screen (stdout) or to a file named using the output option. The output for the north component of the file vyas.neu (included with the software) using the command

cats --model pl:k-1 --model wh: --columns 4 --sinusoid 1y --verbose --output vyas.fn_wh_mle vyas.neu

is shown in Fig. 2.

Fig. 2
figure 2

Output from the CATS program with the verbose option on. Only the parameters for the North component of the time series were computed

Full size image

The first block of lines provide a brief summary of the command issued, the software version and some information on the user and the machine the program was executed on. The second block, if the verbose option is included, provides a summary of the data set used. The program attempts to guess at the probable sampling frequency of the time series (most often 1 day). This is required because the power-law and first-order Gauss Markov covariance matrices are scaled by the sampling interval (Williams 2003). If the data sampling is particularly uneven then there is an option to create the power-law or FOGM covariance matrix via a different method that scales the matrix by the individual sampling intervals (Williams 2003).

The lines containing actual results are preceded with a + symbol, followed by NORT, EAST, VERT or PSMSL and are generally self-evident. MLE is the calculated, maximum log-likelihood value, INTER is the intercept at t 0 which is defined as the start of the first year of data (for example, if the time series starts at 1995.5 then t 0 will be 1995.0). Quoted uncertainties are one sigma and are calculated using the Fisher Information matrix (Fisher 1925). The uncertainties for the functional parameters are correct (with respect to the stochastic model) and, from recent tests, appear to be realistic for the noise amplitudes. Unfortunately in this version the uncertainties for stochastic model parameters other than amplitudes are not estimated because of the extra computational burden. Uncertainties for these parameters are printed as NaN or zero depending on the machines architecture. Another feature that is obviously lacking in this version is more detail in the labeling for the offset and periodic parameters. However, they are in order, as used in the command line for the case of the periodic parameters and in chronological order for the offsets.

For the example shown in Fig. 2 the amplitudes of a white plus flicker noise model are estimated. Since this is a one-dimensional maximization problem and a special class of model where one of the components is white (whereby we can calculate the determinant using a different method) the software uses the Brent maximization (see for example, Press et al. 1992) instead of the uphill simplex. The steps of this algorithm are seen above the results as a series of angles and next choice of angles. The software also calculates the two end-members of the noise spectrum: white only and colored noise only to ensure the correct answer should the angle get close to 0 or 90.

Future

CATS will continue to evolve with time. There is already a development version (4.0.0) available that is, in places, very different to this stable version. The following are the most obvious changes: a new program, CHEETAH, that uses the fast error analysis method described in Bos et al. (2007); incorporation of the ATLAS linear algebra routines; capability for process threading; the ability to read a file containing the functional model so that more complex functions can be used; estimating the uncertainties of all the estimated parameters (in CHEETAH).

Links

Table 3  
Full size table