A Velocity Controller for Quadrotors Based on Reinforcement Learning

Abstract

UAVs based on PID controllers are having increasing difficulties in handling complex tasks. Whereas, reinforcement learning-based high-dimensional models provide an important entry point for flight control to handle complex and high-dimensional tasks. In this paper, a neural network controller training framework for outer-loop control is proposed, which is used as a base platform for velocity controller training. Also, a reinforcement learning-based quadrotor neural network speed controller is proposed which maps the state of the UAV to the throttle commands of the rotor for stable control of speed. In addition, this paper employs the idea of curriculum learning to help the UAV adapt to a larger speed tracking range and improve its overall performance. We demonstrate the performance of the trained neural network controller by comparing it with a conventional PI controller in simulations, achieving improvements in both steady-state response time and tracking performance.

1 Introduction

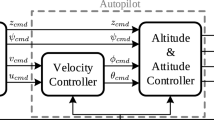
Unmanned Aerial Vehicles are extensively utilized in military exploration, agriculture, transportation, and other fields due to their agile maneuverability. In these complex application scenarios, precise execution of position commands is crucial, leading to an increasing demand for advanced intelligence in UAV flight controllers. Traditional UAV controllers typically consist of an outer-loop position control loop and an inner-loop attitude control loop. The outer-loop position control loop generates attitude and thrust commands to track specific trajectories or speeds, while the inner-loop attitude control loop generates actuation commands to the rotors to accurately track the target attitude state. However, these conventional controller architectures face several challenges: (1) classical PID control algorithms are commonly used for tracking expected values in both loops. Although PID control can be effective, it relies on small angle assumptions that approximate the nonlinear dynamics of UAV as linear. Additionally, the process of simultaneously adjusting PID parameters is also can be complex and challenging to generalize. (2) Differences in the modal periods of the two control loops result in delays between control signals and longer periods for upper-level position control. Recent research has shown that intelligent control algorithms based on reinforcement learning offer a promising solution to these challenges.

For attitude loop control, using reinforcement learning, an optimal attitude control strategy for UAVs can be achieved without assuming aircraft dynamics, ensuring that UAVs maintain good attitude stability despite unknown dynamics or unexpected conditions. Deep reinforcement learning uses neural network models instead of traditional control strategies. It has the advantage that Deep Reinforcement Learning (DRL) has the ability to adapt to any non-linear input/output mapping. Training data is collected iteratively in a simulation environment to adapt the neural network model to the ideal controller distribution. In [5], a simulation platform for reinforcement learning attitude controllers is built, which simulates a realistic UAV maneuvering dynamics model and motor model, and on which the Proximal Policy Optimization (PPO) algorithm-based attitude controller is trained. Adversarial reinforcement learning algorithms were proposed by [15] to enhance the capabilities of Sim2Real and based on [5] the attitude controller was migrated to a real environment for deployment, on top of which [10] proposed domain randomisation and course adversarial reinforcement learning to further improve the robustness of the attitude controller.

For position loop control, which is more challenging due to the incorporation of UAV’s high-level dynamics attributes, Neural network controllers have been applied to solve specific problems. For instance, [12] addresses the accurate landing of quadrotors and introduces neural network controllers for quadrotor landing. In [7], a deep Q-network hierarchy is designed for the autonomous landing of a quadrotor in various simulated environments, demonstrating superior performance compared to human-controlled aerial vehicles in the presence of environmental disturbances. [11] applies the Deep Deterministic Policy Gradient (DDPG) algorithm for outer-loop control of aircraft landing and showcases the capability and potential of the reinforcement learning approach, validating its robustness under diverse wind disturbance conditions. In [14], a simulation platform for a hybrid UAV velocity controller is developed, and a velocity control strategy is trained on this platform for the hybrid UAV model. While [4] proposes a reinforcement learning-based position controller, it only addresses recovery from an arbitrary initial state to a stationary state, limiting its applicability to all cases of UAV position control.

In this work, a simulation platform for training a quadrotor velocity controller based on the gym-pybullet-drone project [6] was proposed. On top of this, a DRL-based quadrotor velocity controller was proposed, which maps the target speed and the quadrotor’s state as inputs directly to the rotor commands. A PPO-based reinforcement learning strategy is used to train the controller, and a curriculum learning approach is added on top of this to extend further the velocity tracking range and robustness of the controller.

2 Background

2.1 Reinforcement Learning

The RL-based algorithm learns the optimal strategy by allowing agents to interact with the environment continuously so as to maximize returns or to achieve specific goals [1]. The interaction process between an agent and the environment is modeled as a Markov Decision Process (MDP). Namely, at a certain time t, an agent obtains the state value $S_t$ from the environment, takes the corresponding action $A_t$ according to the current state value, changes the environment, and obtains the state value $S_{t+1}$ at the next time. The state transition is defined as a probability of transition to state $s'$. Assume that the current state and action are denoted as s and a, respectively. Then, the probability of transition to state $s'$ can be expressed as $p_r\{S_{t+1}=s'|S_t=s,A_t=a\}$. The behavior of an agent is defined by its policy, which is essentially a mapping of actions to be taken for a specific state, as shown in Fig. 1.

Fig. 1.

Schematic diagram of the RL framework

2.2 Curriculum Learning

Curriculum learning, introduced by [3] in 2009, is regarded as a training strategy and has been widely referenced in the field of machine learning. It aims to mimic the human learning process by initially training on simple tasks and gradually increasing the training difficulty, enabling the model to accomplish more challenging tasks. Through curriculum learning, the intelligent agent can organize a systematic exploration of the state space to address the issue of sparse rewards and accelerate the convergence rate of the model. Therefore, we incorporate the concept of curriculum learning into the training process to further enhance the convergence efficiency and control effectiveness of the model.

3 Simulation Platform

3.1 Framework

We have designed the training framework shown in Fig. 2 as the basis for this work, which is suitable for training not only velocity controllers but also supports the training of inner and outer loop controllers such as attitude and position. In each interaction, the Pybullet physics engine will give a 12-dimensional variable O representing the state of the UAV, including the position, attitude angle, angular velocity, and linear velocity of the quadrotor, which can be expressed as

$$\begin{aligned} O = [x,y,z,\varphi ,\theta ,\psi ,v_x,v_y,v_z,\omega _x,\omega _y,\omega _z] \end{aligned}$$

(1)

Then, the input state S(t) of the neural network controller was calculated based on the state of the UAV and the target state given by the environment. Based on S(t) the neural network controller selects an optimal action A(t) based on its own policy distribution, which corresponds to the throttle commands of the four motors, denoted as

$$\begin{aligned} A(t) = [\sigma _1,\sigma _2,\sigma _3,\sigma _4], \sigma _i \in [0,1] \end{aligned}$$

(2)

Subsequently, the throttle commands are then fed into the rotor model to compute the revolutions per minute (RPM) of the propellers. These RPMs are further supplied as inputs to the quadrotor’s rigid body force model, yielding the total thrust and torques in the body frame. Finally, the total thrust and torques will be fed into the physics engine to calculate the quadrotor’s state at the subsequent time step. The state variables, along with the rewards computed based on these states, are fed as input into the neural network controller.

The above process constitutes a single simulation step for the controller, with the neural network controller’s objective being the attainment of the optimal execution strategy by maximizing long-term rewards.

Fig. 2.

Controller training Framework

3.2 Rotor Model

The RPM of the four rotors of a quadrotor is commonly controlled by a throttle command, denoted as $\sigma \in [0,1]$. It takes a certain amount of time for the rotor to reach a steady-state speed, which is referred to as the rotor’s dynamic response time, denoted as $T_m$. The dynamic response process of a rotor can be approximated as a first-order low-pass filter, represented by:

$$\begin{aligned} T_m\frac{d\varpi (t)}{t}+\varpi (t)=C_m\sigma (t)+\varpi _0 \end{aligned}$$

(3)

$C_m$ is the revolution rate of a rotor. $\varpi _0$ denotes the rotor revolution when the throttle command is 0. Equation (1) can be further represented as:

$$\begin{aligned} \dot{\varpi }(t) = \frac{d\varpi (t)}{dt} =\frac{1}{T_m}(C_m\sigma (t)+\varpi _m-\varpi (t)) \end{aligned}$$

(4)

$\dot{\varpi }(t)$ denotes the change rate of rotor revolution. Finally, the rotor revolution in the next timestep can be represented as:

$$\begin{aligned} \varpi (t+1)=\dot{\varpi }(t)*d_t+\varpi (t) \end{aligned}$$

(5)

$d_t$ denotes the simulation timestep of the physical engine, and $T_m$ denotes the response time of the rotor.

3.3 Quadrotor Model

Depending on the rotational speed of the rotor, we can obtain the total thrust and the corresponding torque for each axis:

$$\begin{aligned} \left[ \begin{array}{c} f \\ \tau _{y} \\ \tau _{y} \\ \tau _{z} \end{array}\right] =\left[ \begin{array}{cccc} c_{T} &{} c_{T} &{} c_{T} &{} c_{T} \\ -\frac{\sqrt{2}}{2} d c_{T} &{} \frac{\sqrt{2}}{2} d c_{T} &{} \frac{\sqrt{2}}{2} d c_{T} &{} -\frac{\sqrt{2}}{2} d c_{T} \\ \frac{\sqrt{2}}{2} d c_{T} &{} -\frac{\sqrt{2}}{2} d c_{T} &{} \frac{\sqrt{2}}{2} d c_{T} &{} -\frac{\sqrt{2}}{2} d c_{T} \\ c_{M} &{} c_{M} &{} c_{M} &{} c_{M} \end{array}\right] \left[ \begin{array}{c} w_{1}^{2} \\ w_{2}^{2} \\ w_{3}^{2} \\ w_{4}^{2} \end{array}\right] \end{aligned}$$

(6)

where $c_T$ and $c_M$ denote the drag force factor and torque factor, which depend mainly on the geometry of the propeller. And $w_i$ denotes the RPM of the propellers.

3.4 Dynamic Model

The quadrotor is considered as a rigid body and its total thrust is always parallel to the z-axis of the body frame. We can calculate the positional and rotational dynamics of the quadrotor based on the total thrust and torques on the three axes in the body frame obtained in (6).

$$\begin{aligned} \left\{ \begin{array}{lr} \dot{{\textbf {p}}}^e = {\textbf {v}}^e \\ \dot{{\textbf {v}}}^e = g{\textbf {e}}_3 - \frac{f}{m}{} {\textbf {R}}^w_be_3 \end{array} \right. \end{aligned}$$

(7)

where p denotes position, v denotes velocity, the right superscript w denotes the world frame, and the right superscript b denotes the body frame. $R_b^e$ denotes the rotation matrix from the body frame to the world frame, f denotes the total thrust, m denotes the quadrotor mass, g denotes the gravitational acceleration, and $e_3$ is the unit vector of the z-axis in the world frame.

Its attitude model can be written as:

$$\begin{aligned} \left\{ \begin{array}{lr} \boldsymbol{\dot{\varTheta }}=\boldsymbol{R}^w_b \cdot \boldsymbol{\omega }^b \\ J\dot{\boldsymbol{\omega }}^b=-\boldsymbol{\omega }^b\times J \boldsymbol{\omega }^b + \boldsymbol{G}_a + \boldsymbol{\tau } \end{array} \right. \end{aligned}$$

(8)

where $\boldsymbol{\dot{\varTheta }}$ denotes the Euler angle change rate in the world frame, $\boldsymbol{\omega }^b$ denotes the angular velocity in the body frame, J denotes the inertia matrix, $\boldsymbol{G_a}$ denotes the gyroscopic moment, and $\boldsymbol{\tau }$ denotes the torque in the three axes. After calculating the corresponding angular velocity, linear velocity, and linear acceleration, we integrate them in a simple discrete form in (9) and thus obtain the twelve-dimensional variables of the quadrotor UAV.

$$\begin{aligned} \left\{ \begin{array}{lr} \boldsymbol{v}_i = \boldsymbol{v}_{i-1} + d_t \cdot \dot{\boldsymbol{v}}_{i} \\ \boldsymbol{p}_i = \boldsymbol{p}_{i-1} + d_t \cdot \boldsymbol{v}_{i} \\ \boldsymbol{\varTheta } = \boldsymbol{\varTheta } + d_t \cdot \dot{\boldsymbol{\varTheta }} \end{array} \right. \end{aligned}$$

(9)

4 Neural Network Velocity Controller

4.1 Network Structure

Based on Sect. 3, a neural network velocity controller was trained using the PPO algorithm. The controller adopts the network structure of the classical PPO algorithm, shown in Fig. 3. The input $S(t)\in R^{12}$ to the network comes from the state of the quadrotor and the target velocity, which can be represented as:

$$\begin{aligned} S(t)=[\varphi ,\theta ,\psi ,\alpha ,\beta ,\gamma ,P_{v_x},P_{v_y},P_{v_z}, I_{v_x},I_{v_y},I_{v_z}] \in R^{12} \end{aligned}$$

(10)

where $[\varphi ,\theta ,\psi ]$ respectively denote the quadrotor’s roll, pitch, and yaw angles. $[\alpha ,\beta ,\gamma ]$ respectively denote the angular velocity of the three axes in the body frame of the quadrotor. $[P_{v_x},P_{v_y},P_{v_z}]$ denote the proportional term for the difference between the line velocity of the quadrotor and the desired velocity. $[I_{v_x},I_{v_y},I_{v_z}]$ denote the integral term. The output of the network is the throttle commands $\sigma _i$ for the four rotors.

Given that the model of the controller does not incorporate temporal networks like RNN or LSTM, the incorporation of an integration module will enhance the tracking performance of the controller [14]. Therefore, an integral module is incorporated into the model, and its discrete form is shown below:

$$\begin{aligned} I_n = \eta I_{n-1} + D_n \end{aligned}$$

(11)

where $D_n$ denotes the velocity error sum in the current timestep. $I_{n-1}$ denotes cumulative velocity integral in the last timestep. And $\eta$ is the constant decay coefficient.

Fig. 3.

Neural Network Controller

4.2 Reward Function

The reward function consists of the following components: (1)Survival reward $g_s$, which is used to keep the flight stable at the beginning. (2)Velocity error penalty $g_v$, which is used to ensure the quadrotor tracks the desired velocity as closely as possible. (3)Angular velocity penalty $g_\omega$, which is used to ensure that the quadrotor remains as stable as possible during the tracking and to prevent constant oscillations.

$$\begin{aligned} R(t) = g_s -w_vg_v - w_\omega g_\omega \end{aligned}$$

(12)

where $w_v$,$w_\omega$ are the corresponding weights and $g_s$ is defined as a constant.

4.3 Normalization

Normalization is a significant part of the training process, as there are gaps in the magnitudes of the original inputs. If normalization is not performed, the training process will not converge and result in the accumulative reward oscillating repeatedly. To address this issue, a normalization step for the state variables of the quadrotor is adopted.

In our approach, we normalize the state quantities of the UAV by constraining the velocity and desired velocity within the range of [−3, 3] and the angular velocity within the range of [−50, 50]. Subsequently, we apply a max-min normalization to ensure that all the state variables fall within a consistent range.

By performing input normalization, we aim to mitigate the adverse effects of input disparities and facilitate the training process of the controller. This normalization step helps to establish a more stable and effective learning environment, allowing the controller to converge toward optimal performance.

4.4 Training Setup

We implemented the PPO algorithm using Python and based on the Stable Baselines3 library [8]. The training process consists of two phases. In the first phase, the quadrotor is initialized with a random attitude (pitch and roll angles randomly selected from the range of $[-\pi /2,\pi /2]$ rad/s) and a random target velocity along each axis (with single-axis velocities randomly selected from the range of $[-1,1]$ m/s). At each time step, the controller executes motor commands within the range of [0,1] and receives a reward based on the current state. When any of the pitch, roll, and angular velocities exceeds the predefined threshold, it indicates that the quadrotor has lost stability and is no longer in a controlled state. In such cases, the early termination is considered.

The simulation operates at a frequency of 240 Hz, and a total of eight million steps are trained in this phase. In the second phase, we fine-tune the model trained in the first phase by increasing the task difficulty. The target speed range is expanded to a single-axis target speed within the range of [−3,3] m/s, allowing for a larger speed range. We train a total of two million steps in this stage.

Fig. 4.

The mean reward during the training process

The average reward curve for each episode during the final convergence is illustrated in Fig. 4. It’s worth noting that at the beginning of the second stage, there is a significant drop in the reward. This reduction is due to the larger speed variation range, which results in a higher penalty term for tracking speeds, impacting the overall reward.

In order to enhance the robustness of the controller in real-world control scenarios, we incorporated noise during the training process [10, 15, 16]. Specifically, we added Gaussian noise with a mean of 0 and a variance of 0.1 to several state variables, including velocity, angular velocity, and attitude of the UAV, during the training phase. The inclusion of noise helps the controller to adapt and handle variations and uncertainties that may arise during actual control tasks, thereby improving its overall robustness.

5 Result

Since in practice quadrotors do not have an accurate estimation of acceleration, conventional PID controllers generally rely on proportional and integral terms in the velocity loop. A comparative analysis is conducted between our controller and the PI controller. It is worth noting that the NN controller also relies explicitly only on the proportional and integral terms as input, and its knowledge of the derivative terms will probably come from its derivation of the pose. Moreover, it is important to consider that the velocity control loop exhibits a longer steady-state response time delay in comparison to the attitude control loop, typically ranging from 0.5 to 1 s, depending on the tracked speed.

Fig. 5.

Comparison of two controllers in the simulation of velocity tracking

To evaluate their performance, both the NN Controller and PI Controller are initialized from a static state and tasked with tracking four velocity changes within 12 s. The velocities are randomly altered every 3 s, with the third change being of greater magnitude. The step response performance of the controllers with different algorithm implementations under the interference of random noise is illustrated in Fig. 5. Intuitively, the NN Controller has an advantage in response latency and exhibits a smoother response curve when tracking larger velocity changes (6–9 s) in comparison to the PI Controller.

In order to effectively evaluate the tracking performance and emphasize the impact of high errors, we utilize the root mean square error (RMSE) as a performance metric. The RMSE amplifies errors and provides a more comprehensive measure of the actual tracking error. The formula of RMSE is as follows:

$$\begin{aligned} RMSE(x,y,f)=\sqrt{\frac{1}{m}\sum _{i=1}^{m}[f(x_i)-y_i]^2} \end{aligned}$$

(13)

The results of the RMSE are presented in the table, clearly demonstrating that our algorithm outperforms the PI controller in terms of smaller RMSE values across all three axes. This indicates that our algorithm excels in velocity tracking for the flight task, achieving superior performance.

Table 1. The RMSE of PI Controller and NN Controller

6 Conclusion

In this paper, we propose a simulation framework used to train the neural network controller for quadrotors and a novel neural network velocity controller for quadrotors based on the PPO algorithm. Additionally, we extend the tracking speed range of the controller by incorporating the concept of curriculum learning. The obtained controller demonstrates stable tracking control of the quadrotor’s upper velocity, exhibiting comparable or superior tracking performance compared to the conventional PI controller.

In our future work, we aim to further enhance the algorithm model to improve the tracking performance of the controller. Additionally, we plan to incorporate control of the yaw angle of the quadrotor. Furthermore, we intend to deploy the developed controller to real aircraft and utilize it as the underlying controller for path planning. By pursuing these avenues, we anticipate achieving significant advancements in the tracking capabilities of the controller, expanding its potential applications, and enhancing its performance in real-world scenarios.