Chaos and Multistability in Fractional Order Power System: Dynamic Analysis and Implications

Abstract

This paper presents a comprehensive study about the dynamic behavior of a fractional ordered three-machine infinite bus (TMIB) power system model using Grunwald–Letnikov’s method. The study investigates nonlinear behaviors including chaos, coexisting behavior and multistability behaviors, using nonlinear tools such as phase portraits, bifurcation analysis, Lyapunov exponents and Lyapunov dimensions. The results demonstrate that the TMIB system exhibits chaos behavior, which is resulting instability in rotor angle through multiscroll chaotic attractors. Furthermore, it is found that the presence of coexisting attractors and multistability leads to undesired state switching and pose a potential threat to the stability of the TMIB power system. These findings provide valuable insights into the nonlinear behavior of TMIB power system via varying fractional order range and can be used to develop effective countermeasures to address potential stability issues arise in TMIB and similar modern power systems. The simulation is conducted in MATLAB, and the obtained results illustrate the efficacy of the work.

1 Introduction

A multimachine power system is a complex electrical power system consisting of multiple interconnected synchronous generators, transmission lines, transformers, and loads [1]. It is a vital component of the modern electric power grid and is used to supply electrical energy to homes, businesses, and industries. The behavior of a multimachine power system is highly nonlinear and dynamic, making its analysis and control a challenging task [2].

Previous studies have investigated the chaos and bifurcation behavior of different power system models [3,4,5,6]. The SMIB system has been specifically studied for its nonlinear complex dynamic motions, including period-doubling bifurcations (PDB), chaotic movements, and unbounded motions [7, 8]. Furthermore, the SMIB power system’s qualitative behavior has been investigated through the imposition of a periodic load disturbance [9]. In addition, the presence of white Gaussian noise in a system can affect its dynamical behaviors, with higher intensity of random noise potentially leading to increased chaos and instability [10, 11]. Besides single machine models, there have also been studies on multimachine power system models. The Melnikov method has been used to investigate chaos in rotor dynamics of power systems [12]. Specifically, a special case of the conservative swing equation based on a three-machine system was analyzed. The rotor dynamics of this three-machine swing equation were studied using qualitative and quantitative tools to examine its chaotic behavior. State feedback and dither signal control were also applied to transform the chaotic oscillation into a periodic oscillation [13, 14].

Multistability is a common phenomenon in complex systems, such as biological, physical, and engineering systems, and can have important implications for their behavior and stability [15, 16]. Multistability is a property of a system that can exhibit multiple stable equilibrium states or attractors. This means that the system can maintain different stable states depending on its initial conditions, and small changes or perturbations may cause it to transition from one stable state to another [2, 17]. In recent years, the analysis of chaos and multistability behavior has become increasingly popular, including its fractional order counterpart. Fractional calculus, which is a generalization of traditional calculus, has emerged as a powerful tool for modeling and analyzing the dynamics of systems [18]. It has gained attention in various fields due to its ability to capture nonlocal and memory-dependent behavior, making it suitable for describing complex systems with long-range interactions [19]. The application of fractional calculus to the study of chaos and multistability behavior has provided new insights and perspectives, leading to a deeper understanding of the underlying dynamics of complex systems [20, 21]. Despite the existence of multiple power systems in which chaos and bifurcation behavior have been discussed, the phenomenon of multistability in power system models has received limited attention. Although there have been recent studies on multistability in certain power system models [2, 17], the fractional order counterparts of such models have not yet been explored in the literature. Therefore, the investigation of the fractional order counterpart of power system models exhibiting multistability is a significant research direction that needs to be addressed. Motivated by the above literature, this paper focuses on fractional order model of TMIB power system. The contribution and novelty of this work are listed as follow:

• 1. A TMIB power system model is derived from the conventional N-machine power system model, and its fractional order analysis is carried out using Grunwald–Letnikov’s (GL) method.

• 2. The TMIB power system model shows the rotor angle instability by multiscroll chaotic attractors.

• 3. The TMIB power system model reveals the presence of multistability (coexistence of attractors) behavior.

The rest of the paper is organized as follows: In Sect. 2, the mathematical model of fractional order TMIB power system is described. In Sect. 3, different nonlinear dynamic behaviors, including chaos, bifurcation, and multistability, in the fractional order range are discussed. Finally, in Sect. 4, the conclusions and future scope of the work are presented.

2 Mathematical Modeling of TMIB Power System

The n-machine system [12], is the basic for the classical model of the electrical network. The system comprises n internal machine nodes (1 to n) working in parallel mode, with reference node 0 acting as a neutral node. During stability analysis, the voltages $E_1, E_2, E_3, \ldots E_n$ are assumed to remain constant throughout the transient period. The rotor angles for the n-machine system are represented by $\delta _1, \delta _2, \delta _3, \ldots \delta _n$, while $r_1, r_2, r_3, \ldots r_n$ and $x'_{d1}, x'_{d2}, x'_{d3}, \ldots x'_{dn}$ denote the resistance and sub-transient reactance of the n generators. The current output from each generator unit is represented by $I_1, I_2, I_3, \ldots I_n$.

The expression for the electrical power output of the $i{\mathrm{{th}}}$ machine in the network is given as:

$$\begin{aligned} P_{ei} = E^2_{i}G_{ii}+ \sum _{\begin{array}{c} j=1 \\ j\ne i \end{array}}^nE_i~E_j ~Y_{ij}~\mathrm{{cos}} (\theta _{ij}-\delta _i +\delta _j) \end{aligned}$$

(1)

Here, $Y_{ii}$ and $Y_{ij}$ represent the self admittance or driving point admittance at node i and mutual admittance between nodes i and j, respectively. This can be further written as in term of conductance (G) and susceptance (B) as: $Y_{ii}=G_{ii}+B_{ii}$ and $Y_{ij}=G_{ij}+B_{ij}$.

$$\begin{aligned} P_{ei} = E^2_{i}G_{ii}+ \sum _{\begin{array}{c} j=1 \ j\ne i \end{array}}^nE_iE_j ~[B_{ij}~\mathrm{{sin}} (\delta _i -\delta _j) +G_{ij}\mathrm{{cos}} (\delta _i -\delta _j)] \end{aligned}$$

(2)

Assuming the resistance of the transmission line is negligible and can be modeled as a pure reactive component, the expression for the electromagnetic output power is simplified as:

$$\begin{aligned} P_{ei} = E^2_{i}G_{ii}+ \sum _{\begin{array}{c} j=1 \ j\ne i \end{array}}^nE_iE_j ~B_{ij}~\mathrm{{sin}} (\delta _i -\delta _j) \end{aligned}$$

(3)

The equation of motion for a multimachine system can be expressed as:

$$\begin{aligned} \dot{\delta _i}=\omega _i \end{aligned}$$

(4)

$$\begin{aligned} \frac{2H_i}{\omega _s} \dot{\omega _i}+ D_i\omega _i= Pm_i- Pe_i \end{aligned}$$

(5)

By utilizing Eqs. (3) and (5), we can derive the following Eq. (6):

$$\begin{aligned} \frac{2H_i}{\omega _s}\dot{\omega _i} = -D_i\omega _i+Pm_i- E^2_{i}G_{ii} - \sum _{\begin{array}{c} j=1 \\ j\ne i \end{array}}^nE_i~E_j ~B_{ij}~sin (\delta _i -\delta _j) \end{aligned}$$

(6)

where $\omega _s$ represents for synchronous speed, $\omega _i$ for the deviation between the rotor angle velocity and synchronous speed for the $i{\mathrm{{th}}}$ bus, $H_{i}$ for the inertia of the $i{\mathrm{{th}}}$ machine, $P_{mi}$ and $P_{ei}$ for the mechanical input power and electromagnetic output power respectively of the $i\mathrm{{th}}$ machine.$D_i$ represents the damping coefficient of the $i\mathrm{{th}}$ machine. To simplify the system parameters, we can define $\frac{2H_i}{\omega _s}$ as $M_i$, $P_{mi}-E^{2}{i}G{ii}$ as $P_{i}$, and $E_j ~B_{ij}$ as $T_{ij}$.

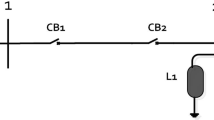
Assuming that an infinite bus node connects the three generators, shown in Fig. 1, a simplified swing equation for the TMIB power system that describes the generator rotors can be written by using Eq. (6).

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{\delta _i}=\omega _i,\\ \dot{\omega _i} =\frac{1}{M_i} [-D_i\omega _i+P_i - E_i~ \sum _{\begin{array}{c} j=1 \\ j\ne i \end{array}}^nT_{ij}~\mathrm{{sin}} (\delta _i -\delta _j)-E_i~V_B~B_{iB}~\mathrm{{sin}} (\delta _i -\delta _B)] \end{array}\right. } \end{aligned}$$

(7)

where i=1,2,3, $V_B$ and $\delta _B$ are the infinite bus voltage and phase angle. $B_{iB}$ represents the admittance between the $i\mathrm{{th}}$ machine and infinite bus bar.

Fig. 1

Three-machine infinite bus (TMIB) power system (7)

2.1 Fractional Order Model of TMIB Power System

Although there are several available methods for fractional order computations, previous studies have primarily utilized the Caputo method for numerical solutions of fractional order systems. However, research has shown that the GL method [22] provides better smoothness in coefficients for solving fractional order systems. Therefore, we utilize the GL method to solve the fractional order multimachine power system model.

The fractional order equation has limits of a and t and is represented by the equation ${ }{a} D_{t}^{q} f(t)$, where q is the fractional order of the differential equation. The calculation involves the use of the generalized difference $\Delta _{h}^{q} f(t)$, where h represents the step size. The GL derivative can be defined as:

$$\begin{aligned} { }_{a} D_{t}^{q} f(t)=\lim _{h \rightarrow 0}\left\{ \frac{1}{h^{q}} \sum _{m=0}^{\left[ \frac{t-a}{h}\right] }(-1)^{m}\left( \begin{array}{l}q \\ m\end{array}\right) f(t-m h)\right\} =\lim _{h \rightarrow 0}\left\{ \frac{1}{h^{\alpha }} \Delta _{h}^{q} f(t)\right\} \end{aligned}$$

(8)

To perform numerical calculations, the equation mentioned above can be modified as follows:

$$\begin{aligned} { }_{(t-L)} D_{t}^{q} f(t)=\lim _{h \rightarrow 0}\left\{ h^{-q} \sum _{m=0}^{N(t)} \beta _{j}(f(t-m h)\right\} . \end{aligned}$$

(9)

To simulate the fractional order TMIB system using the GL method, we utilize the discretization method described in previous studies . Since the required memory for calculating binomial coefficients is theoretically infinite, we truncate the number of samples to make the calculation feasible. The discretization method is as follows:

$$\begin{aligned} \begin{aligned} & \delta _i\left( t_{k}\right) =A\left( \delta _i\left( t_{k-1}\right) , \mathrm {\omega _i}\left( t_{k-1}\right) \right) h^{q_{\delta _i}}-\sum _{m=1}^{N} \beta _{m}^{q_{\delta _i}} \delta _i\left( t_{k-m}\right) \\ & \omega _i\left( t_{k}\right) =B\left( \delta _i\left( t_{k-1}\right) , \textrm{y}\left( t_{k-1}\right) \right) h^{q_{\omega _i}}-\sum _{m=1}^{N} \beta _{m}^{q_{\omega _i}} \omega _i\left( t_{k-m}\right) \end{aligned} \end{aligned}$$

(10)

In the above equation, $\beta$ denotes the binomial coefficients. The value of N is determined based on the available memory. Specifically, if the available memory is not fully utilized, N is set to the truncation window size L. Otherwise, N is set to k to make the most of the available memory elements. We can define the fractional order TMIB power system derived using Eq. (7) as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} D^{q_{\delta _i}}\delta _i=\omega _i,\\ D^{q_{\omega _i}}\omega _i =\frac{1}{M_i} [-D_i\omega _i+P_i - E_i~ \sum _{\begin{array}{c} j=1 \\ j\ne i \end{array}}^nT_{ij}~\mathrm{{sin}} (\delta _i -\delta _j)-E_i~V_B~B_{iB}~\mathrm{{sin}} (\delta _i -\delta _B)] \end{array}\right. }\nonumber \\ \end{aligned}$$

(11)

The discrete version of the fractional order TMIB power system can be expressed as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} \delta _i(t_k)=(\omega _{i_{t_{k-1}}})h^{q_{\delta _i}}-\sum _{m=1}^{N} \beta _{m}^{q_{\delta _i}} x\left( t_{k-m}\right) ,\\ \omega _i(t_k) =[\frac{1}{M_i} \{-D_i\omega _{i_{t_{k-1}}}+P_i - E_i~ \sum _{\begin{array}{c} j=1 \\ j\ne i \end{array}}^nT_{ij}~\mathrm{{sin}} (\delta _{i_{t_{k-1}}} -\delta _j)\\ ~~~~~~~~~ -E_i~V_B~B_{iB}~\mathrm{{sin}} (\delta _{i_{t_{k-1}}} -\delta _B)\}] h^{q_{\omega _i}}-\sum _{m=1}^{N}\beta _{m}^{q_{\omega _i}} x\left( t_{k-m}\right) \end{array}\right. } \end{aligned}$$

(12)

The value of N is taken as the truncation window size L and as k when all the available memory elements are used. Calculation parameters for analysis of fractional order TMIB power system are given as: $D_1=0.003$, $D_2=0.0045$, $D_3=0.003$, $M_1=0.01$, $M_2=0.015$, $M_3=0.01$, $P_1=0.3$, $P_2=0.4$, $P_3=0.3$, $T_{12}=T_{21}=0.1$, $T_{13}=T_{31}=0.6$, $T_{23}=T_{32}=1$, $B_{1B}=2$, $B_{2B}=1.5$, $B_{3B}=2$, $E_1=1$, $E_2=1$, $E_3=1$, $V_B=1$, and $\delta _B=0$. To investigate the various dynamic behaviors within the fractional order range, the value of the fractional order parameter q is varied.

3 Nonlinear Dynamic Behavior of Fractional Order TMIB Power System

In this section, we analyzed the different dynamic behaviors of the TMIB power system by varying the order of differential equation and studying its behavior using both qualitative and quantitative analysis tools.

Fig. 2

Bifurcation diagram of TMIB power system (11) when the order $q\in [0.9, 1]$

3.1 Dynamic Response at Varied Fractional Order (q)

Bifurcation analysis is a crucial qualitative tool used to analyze the nonlinear behavior of the system under parameter perturbations. This analysis provides information about the topological changes in the system’s behavior when it experiences small or smooth parameter variations. Nonlinear behaviors are observed using bifurcation diagram while keeping all parameter values constant and by varying the fractional order derivative within the range $q\in [0.9, 1]$. Different transitions in the dynamic behavior are observed in the bifurcation diagram as shown in Fig. 2. To further analyze these behavior the dynamic response in the phase plane is plotted at specific values to the corresponding bifurcation diagram shown in Fig. 3. Lyapunov exponents also correspond the phase plane behavior at different value of fractional order q listed the Table . At $q=0.93$, by observing bifurcation plot, phase portrait, and the nature of maximum positive Lyapunov exponents (MLE) is negative, confirm the period-1 behavior. Similarly at $q=0.965$, the system displays a period-2 behavior. However, at $q=0.982$, the system exhibits aperiodic behavior, can be observed from the bifurcation plot and phase plane analysis. The Lyapunov exponents have been calculated and the nature of MLE confirms the chaos behavior. Further, dissipativity and Lyapunov dimension analysis are performed. Dissipativity analysis is an essential measure for understanding the converging and diverging nature of dynamical system. It provides a way to quantify the energy flow of a system and identify critical parameters that affect the system dynamics. A dynamical system is dissipative if the sum of all Lyapunov exponents is negative, i.e., $\sum _{i=1}^{n} \lambda _i < 0$, where $\lambda _i$ are the individual Lyapunov exponents of the system, and n is the state space dimension. The dissipativity, at $q=0.982$, is calculated as the sum of Lyapunov exponents ($L_1+L_2+L_3+L_4+L_5+L_6)=-1.4680$. The $-ve$ value indicates that the system is dissipative in nature. Lyapunov dimension or Kaplan–Yorke dimension is calculated using the following formula as:

$$\begin{aligned} D_{KY} = \lim _{\epsilon \rightarrow 0} \left[ \sum _{i=1}^{k} \lambda _i + \frac{1}{|\lambda _{k+1}|} \sum _{i=k+1}^{n} |\lambda _i| \right] \end{aligned}$$

where $\lambda _i$ denotes the i-th Lyapunov exponent, k is the largest index such that the sum of the first k exponents is non-positive, and n is the total number of Lyapunov exponents. The Kaplan–Yorke dimension is obtained as $D_{KY} = 2.699$ using calculated Lyapunov exponents at $q=0.982$ which implies that the system has fractal nature and has complex attractor with a dimension between 2 and 3. At the value of fractional order $q=0.997$, the phenomenon of chaos breaking has observed, where the MLE is positive, resulting in rotor angle instability with the emergence of multiscroll chaotic attractors. The time series and phase portrait behavior of the rotor angle and angular velocity for each machine are shown in Fig. 4, under multiscroll chaotic attractors.

Fig. 3

Phase plane behavior (transients are removed) correspond to the bifurcation diagram of fractional order multimachine power system (11) at four different value of fractional order q

Fig. 4

Time series and phase plane behavior of fractional order multimachine power system (11), reflects angle instability through multiscroll chaotic attractors at $q=0.997$

Obtain nonlinear behavior through the bifurcation and Lyapunov exponents in fractional order range which can be effectively applied to parameter tuning in the stability analysis of multimachine power systems experiencing chaotic behavior. Overall, fractional calculus combined with nonlinear theories is used to study chaos and chaos breaking behavior in multimachine power systems, which may provide helpful insights to aid in the development of counter measures to ensuring its stability and reliability.

3.2 Coexistence of Attractor and Multistability Analysis

In the previous subsection, we analyzed the TMIB power system for a range of fractional orders. Now, we fixed the order of the differential equation at $q=0.997$ and varied the damping coefficient parameter $d_1=\frac{D_1}{M_1}$ while keeping all other parameters constant at their previously defined fixed values. The bifurcation diagram, shown in Fig. 5, displays the various dynamic behaviors, including PDB route to chaos, observed when the damping coefficient $d_1$ is varied within the range of [0, 0.6]. The bifurcation diagram presented in Fig. 5 not only illustrates the dynamic behavior of the TMIB power system with varying damping coefficient $d_1$, but also shows the coexistence phenomenon at three distinct initial conditions. These initial conditions are $[\delta _1(0), \omega _1(0), \delta _2(0), \omega _2(0), \delta _3(0), \omega _3(0))] = [\delta _1(0), 0, 3, 0, 4, 0]$ where the value of $[\delta _1(0)]$ is considered as 2, 3, 4, and represented via black, red, blue colors in throughout analysis.

Fig. 5

Coexisting bifurcation behavior of fractional order multimachine power system (11) at three initial conditions [2, 0, 3, 0, 4, 0], [3, 0, 3, 0, 4, 0], [4, 0, 3, 0, 4, 0]; depicted via colors, respectively

Fig. 6

Multistability (coexistence of attractors) in the fractional order multimachine power system (11), at three initial conditions depicted with different colours. a Phase plane and time series behavior of machine-2, exhibiting the coexistence of three chaotic attractors at $d_1=0.15$. b Coexistence of two chaotic and one multiscroll chaotic attractor of machine-2 at $d_1=0.14$. c Coexistence of one chaotic attractor with two multiscroll chaotic attractors of machine-2 at $d_1=0.137$

Fig. 6 displays the multistability behavior of the TMIB power system (11) at machine-1 in terms of its phase plane and time series response. The figure shows the response of the rotor angle and angular velocity of machine-1 at three different initial conditions for three distinct values of the parameter $d_1$. Specifically, Fig. 6a corresponds to $d_1=0.15$, and it depicts the coexistence of three chaotic attractors at the given initial conditions. Figure 6b corresponds to $d_1=0.14$, and it depicts the coexistence of two chaotic attractors and one multiscroll chaotic attractor. Fig. 6c corresponds to $d_1=0.137$, shows the coexistence of three multiscroll chaotic attractor.

The multistability behavior of the TMIB power system (11) at machine-1 is depicted in Fig. 6, in terms of its phase plane and time series response. This Fig. 6 depicts the response of machine-1’s rotor angle and angular velocity under three different initial conditions for three different values of the parameter $d_1$. Figure 6a, corresponds to $d_1=0.15$ and displays the presence of three chaotic attractors under the specified initial conditions. The coexistence of two chaotic attractors and one multiscroll chaotic attractor is depicted in Fig. 6b, which corresponds to $d_1=0.14$. The presence of three multiscroll chaotic attractors is shown in Fig. 6c, which corresponds to $d_1=0.137$.

The multistability exhibited by the TMIB power system is concerning due to its potential for unpredictable and uncontrolled behavior. Multistability can increase the risk of cascading failures in power systems. If one component of the system fails, the system may shift to a different stable state, leading to further failures and potentially a complete system collapse.

4 Conclusion

The paper presents a TMIB power system model which is derived from the classical N-Machine model power system, and applies Grunwald–Letnikov’s method to perform a fractional order analysis. The study reveals interesting behaviors, such as period-1, period-2, chaos, and angle instability by multiscroll chaotic attractor under specific parameter values and fractional order q, using both qualitative and quantitative analysis tools. Furthermore, coexisting behavior and multistability are also observed through the use of coexisting bifurcation diagram, phase plane, and time series analysis. However, this study highlights the presence of chaos and multistability in the fractional order TMIB power system, and it is concerning due to its potential for unpredictable and uncontrolled behavior, which can result in power outages, equipment damage, and safety hazards. Therefore, it is critical to manage and control the effects of chaos and multistability in practical applications such as power systems to ensure their safe and reliable operation.