Active Disturbance Rejection Control of a SEPIC Converter

Abstract

Single-ended primary inductor converter(SEPIC) is a high-gain buck-boost converter, but its controller’s design is a challenging task as it is a fourth-order nonlinear system. This paper proposes an active disturbance rejection control (ADRC)-based controller for a SEPIC converter with high switching frequency. ADRC is an advanced control technique that does not rely on the exact information of the system as all the external and internal disturbances are estimated as separate variables and are canceled directly by the effect of the controller. Simulation results suggest that the proposed ADRC technique gives good setpoint tracking and robustness toward disturbances like input voltage fluctuations and load variations. The performance parameters have been calculated and analyzed to conclude that the proposed method has stable and robust performance.

1 Introduction

The extraction of energy from renewable sources like solar and wind requires a DC-to-DC converter. Other applications for DC-to-DC converters are in DC motor drives personal communication equipment and power Computers, etc. [18]. DC-to-DC converters are of three types based on the transformer action, i.e., buck, boost, and buck-boost. Based on the requirement of output voltage with respect to the input, each of the converters has specific uses. Buck-boost converter topologies like cuk converter, zeta converter converters are suited for solar energy generation systems, where the input voltage keeps on fluctuating depending on the intensity of sunlight [5, 14, 23]. However, the low energy conversion efficiency, due to the hard-switched states, inverted output, and low voltage gain are the drawbacks of the Cuk and Zeta and some other buck-boost converters [21].

The above-noted problems can be handled by the use of single-ended primary inductor converter (SEPIC) converters [3]. These converters are suitable for off-grid solar power plants due to the possibility of connecting it to the various batteries and PV applications, where they can match the characteristics of current and voltage [3, 10, 22]. SEPIC converter is a fourth-order nonlinear system whose behavior depends on operating conditions like input voltage, duty cycle, and load variations. It requires an advanced control technique to meet goals of guaranteed stability, good set-point tracking, efficient and fast attenuation of the load disturbance and satisfactory robustness toward parametric variations. Various nonlinear control methods such as back-stepping and passivity-based control[2], fuzzy logic-based control [6], sliding mode control [9, 20] have been reported in the literature for controlling SEPIC converters. Sliding mode control is known for better robustness; however, methods proposed in [9, 20] resulted in slow response, and they also failed to reject disturbances of large magnitudes. Authors have designed indirect sliding mode control for the SEPIC using the current mode control in [16]. The output response is satisfactory in the above-cited work however the tuning method looks lengthy and complex. They have not suggested any explicit formulae for calculating the input current reference. It is observed that there is a need for a simple and efficient control strategy for the SEPIC converter as it has a wide range of applications. The two degree of freedom internal model control (TDF-IMC) [15] has been recently reported in the literature for the boost converter. It is a plant model-dependent scheme consisting of three control blocks which are tuned using two design parameters. ADRC control technique is a robust control technique, and it doesn’t require the exact knowledge of the system to be controlled [4, 13, 24]. ADRC method draws attention owing to its excellent performance in satisfying the aforementioned control objectives [1]. Up to the best of the authors’ knowledge, the ADRC method has not been implemented on the SEPIC converter.

Further, it is important to mention here that larger values of the components such as capacitors and inductors of SEPIC cause significant power losses. At higher switching frequencies, these components’ size reduces and also the loading effect of external filter components decreases which results in a faster dynamic response. However, designing a converter at higher frequencies such as in the MHz range limits its operating voltage range as the voltage stresses across the switches and diodes are also increased [11]. Therefore, operational voltage ranges at very high frequencies may not be suitable for power converters applications. Thus, for a wide range of operations, a switching frequency close to a few hundred kHz is commonly used.

In the present work, active disturbance rejection control (ADRC) is proposed for the SEPIC converter with high switching frequency. For the effective application of this controller, the order of the converter is reduced to the second-order system using a balanced reduction technique based on the calculation of the Hankel singular value. The tuning parameter has been decided on the basis of the bandwidth parametrization technique described in [8]. Also, the suitable values of the tuning parameters are selected according to the suitable value of maximum sensitivity. The designed controller has been verified using simulation results. The controller provides good setpoint tracking and disturbance rejection proving its stability robustness. The robustness of the closed-loop system has been proved on the basis of lower values of settling time, overshoot/undershoot voltage, peak inductor current, and integral square error (IAE).

This paper is divided into seven subsections. Section 2 describes the modeling and design of the SEPIC converter. Section 3 explains the complete design of the ADRC controller for the SEPIC converter. Simulation results are presented in Sect. 4. Finally, the conclusion is derived in Sect. 5.

2 SEPIC Converter

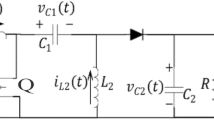
Single-ended primary inductor converter (SEPIC) is a buck-boost converter with noninverted output. It has also the unique property of isolating the input–output circuit when no gating signal is provided to the switch. The circuit diagram of the SEPIC is shown in Fig. 1. It consists of a primary inductor ($L_1$), a coupling capacitor ($C_1$), a secondary inductor ($L_2$), a switch (Q), a diode (D) and an output capacitor ($C_2$). The circuit works as a boost converter if the duty cycle (D) is greater than 0.5 and as a buck converter if the duty cycle is less than 0.5. The output and inputs are equal when the duty cycle is exactly 0.5. Practically the voltage drops of the diode and MOSFET affect the output voltage. The gate terminal of the switch is provided a pulse width modulated (PWM) generated according to the duty cycle. Hence, the operation of the SEPIC can be divided into two modes as described further.

Fig. 1

Schematic diagram of SEPIC converter

2.1 Switch on Mode

The circuit diagram resembling this mode is shown in Fig. 2. When the switch is ON, it acts like a short circuit and the diode is reverse-biased. Inductor ($L_1$) charges through the source, while the capacitor supplies the stored energy to the load maintaining the output voltage ($V_0$) to be constant. Also, the inductor ($L_2$) is charged by the capacitor ($C_1$).

Fig. 2

Schematic diagram of SEPIC converter in switch ON mode

The differential equations corresponding to this mode is:

$$\begin{aligned} \frac{{\text {d}{i_{{L_1}}}}}{{\text {d}t}} = \frac{{{v_s}}}{{{L_1}}} \end{aligned}$$

(1)

$$\begin{aligned} \frac{{\text {d}{i_{{L_2}}}}}{{\text {d}t}} = \frac{{{v_{{c_1}}}}}{{{L_2}}} \end{aligned}$$

(2)

$$\begin{aligned} \frac{{\text {d}{v_{{c_1}}}}}{{\text {d}t}} = - \frac{{{i_{{L_2}}}}}{{{C_1}}} \end{aligned}$$

(3)

$$\begin{aligned} \frac{{\text {d}{v_{{c_2}}}}}{{\text {d}t}} = - \frac{{{v_{{c_2}}}}}{{{C_2}R}} \end{aligned}$$

(4)

The equations in matrix form can be written as:

$$\begin{aligned} \left[ {\begin{array}{*{20}{c}} {{{\dot{i}}_{{L_1}}}}\\ {{{\dot{i}}_{{L_2}}}}\\ {{{\dot{v}}_{{c_1}}}}\\ {{{\dot{v}}_{{c_2}}}} \end{array}} \right] &= \left[ {\begin{array}{*{20}{c}} 0&{}0&{}0&{}0\\ 0&{}0&{}1/L_2&{}0\\ 0&{}- 1/C_1&{}0&{}0\\ 0&{}0&{}0&{}- 1/R C_2\\ \end{array}} \right] \left[ {\begin{array}{*{20}{c}} {{i_{{L_1}}}}\\ {{i_{{L_2}}}}\\ {{v_{{c_1}}}}\\ {{v_{{c_2}}}} \end{array}} \right] \nonumber \\ &+\left[ {\begin{array}{*{20}{c}} 1/L_1\\ 0\\ 0\\ 0 \end{array}} \right] \left[ {{v_s}} \right] \end{aligned}$$

(5)

2.2 Switch OFF Mode

When the switch is turned off by the means of the PWM signal, then $L_1$ and $L_2$ supplies the stored energy toward the load end thereby charging the capacitors $C_1$ and $c_2$. The output voltage is still maintained constant when a constant duty ratio is used for the generation of the PWM signals. The circuit diagram defining this mode is shown in Fig. 3.

Fig. 3

Schematic diagram of SEPIC converter in switch OFF mode

The differential equations describing this mode are:

$$\begin{aligned} \frac{{\text {d}{i_{{L_1}}}}}{{\text {d}t}} = \frac{{{v_s}}}{{{L_1}}} - \frac{{{v_{{c_1}}}}}{{{L_1}}} - \frac{{{v_{{c_2}}}}}{{{L_1}}} \end{aligned}$$

(6)

$$\begin{aligned} \frac{{\text {d}{i_{{L_2}}}}}{{\text {d}t}} = \frac{{{v_{{c_2}}}}}{{{L_2}}} \end{aligned}$$

(7)

$$\begin{aligned} \frac{{\text {d}{v_{{c_1}}}}}{{\text {d}t}} = \frac{{{i_{{L_1}}}}}{{{C_1}}} \end{aligned}$$

(8)

$$\begin{aligned} \frac{{\text {d}{v_{{c_2}}}}}{{\text {d}t}} = \frac{{({i_{{L_1}}} + {i_{{L_2}}})}}{{{C_2}}} - \frac{{{v_{{c_2}}}}}{{{C_2}R}} \end{aligned}$$

(9)

These equations can again be written as:

$$\begin{aligned} \left[ {\begin{array}{*{20}{c}} {{{\dot{i}}_{{L_1}}}}\\ {{{\dot{i}}_{{L_2}}}}\\ {{{\dot{v}}_{{c_1}}}}\\ {{{\dot{v}}_{{c_2}}}} \end{array}} \right] &= \left[ {\begin{array}{*{20}{c}} 0&{}0&{}- 1/L_1&{}- 1/L_1\\ 0&{}0&{}0&{}/- 1/L_2\\ 1/C_1&{}0&{}0&{}0\\ 1/C_2&{}1/C_2/C_2&{}0&{}- 1/RC_2\\ \end{array}} \right] \left[ {\begin{array}{*{20}{c}} {{i_{{L_1}}}}\\ {{i_{{L_2}}}}\\ {{v_{{c_1}}}}\\ {{v_{{c_2}}}} \end{array}} \right] \nonumber \\ &+\left[ {\begin{array}{*{20}{c}} 1/L_1\\ 0\\ 0\\ 0 \end{array}} \right] \left[ {{v_s}} \right] \end{aligned}$$

(10)

The differential equations obtained in ON and OFF modes are combined by multiplying D and $(1-D)$ respectively using the state-space averaging technique to get the matrices of A, B, C, and D as:

$$\begin{aligned} A = D{A_1} + (1 - D){A_2} \end{aligned}$$

(11)

$$\begin{aligned} B = D{B_1} + (1 - D){B_2} \end{aligned}$$

(12)

Now the combined equations in matrix form can be written as:

$$\begin{aligned} \left[ {\begin{array}{*{20}{c}} {{{\dot{i}}_{{L_1}}}}\\ {{{\dot{i}}_{{L_2}}}}\\ {{{\dot{v}}_{{c_1}}}}\\ {{{\dot{v}}_{{c_2}}}} \end{array}} \right] = &\left[ {\begin{array}{*{20}{c}} 0&{}0&{}- D'/L_1&{}- D'/L_1\\ 0&{}0&{}D/L_2&{}- D'/L_2\\ D'/C_1&{}- D/C_1&{}0&{}0\\ D'/C_2&{}D'/C_2&{}0&{}- 1/ RC_2\\ \end{array}} \right] \nonumber \\ &\times \left[ {\begin{array}{*{20}{c}} {{i_{{L_1}}}}\\ {{i_{{L_2}}}}\\ {{v_{{c_1}}}}\\ {{v_{{c_2}}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} 1/L_1\\ 0\\ 0\\ 0 \end{array}} \right] \left[ {{v_s}} \right] \end{aligned}$$

(13)

where $D' = 1 - D$.

The calculation of the transfer function between the output voltage and duty cycle can be performed by using small signal analysis(SSA). Hence, after performing the SSA, the following state-space equations are obtained:

$$\begin{aligned} \begin{aligned} \left[ {\begin{array}{*{20}{c}} {{{\dot{\hat{i}}}_{{L_1}}}}\\ {{{\dot{\hat{i}}}_{{L_2}}}}\\ {{{\dot{\hat{v}}}_{{c_1}}}}\\ {{{\dot{\hat{v}}}_{{c_2}}}} \end{array}} \right] =& \left[ {\begin{array}{*{20}{c}} 0&{}0&{}{\frac{{ - D'}}{{{L_1}}}}&{}{\frac{{ - D'}}{{{L_1}}}}\\ 0&{}0&{}{\frac{D}{{{L_2}}}}&{}{\frac{{ - D'}}{{{L_2}}}}\\ {\frac{{D'}}{{{C_1}}}}&{}{\frac{{ - D}}{{{C_1}}}}&{}0&{}0\\ {\frac{{D'}}{{{C_2}}}}&{}{\frac{{D'}}{{{C_2}}}}&{}0&{}{\frac{{ - 1}}{{R{C_2}}}} \end{array}} \right] \left[ {\begin{array}{*{20}{c}} {{{\hat{i}}_{{L_1}}}}\\ {{{\hat{i}}_{{L_2}}}}\\ {{{\hat{v}}_{{c_1}}}}\\ {{{\hat{v}}_{{c_2}}}} \end{array}} \right] + \\ &\left[ {\begin{array}{*{20}{c}} {\frac{{({V_{{c_1}}} + {V_{{c_2}}})}}{{{L_1}}}}\\ {\frac{{({V_{{c_1}}} + {V_{{c_2}}})}}{{{L_1}}}}\\ {\frac{{ - ({I_{{L_1}}} + {I_{{L_2}}})}}{{{C_2}}}}\\ {\frac{{ - ({I_{{L_1}}} + {I_{{L_2}}})}}{{{C_2}}}} \end{array}} \right] \left[ {\hat{d}} \right] + \left[ {\begin{array}{*{20}{c}} {\frac{1}{{{L_1}}}}\\ 0\\ 0\\ 0 \end{array}} \right] \left[ {{{\hat{v}}_s}} \right] \end{aligned} \end{aligned}$$

(14)

and ${{\hat{v}}_0} = \left[ {\begin{array}{*{20}{c}} 0&0&0&1 \end{array}} \right] \left[ {\begin{array}{*{20}{c}} {{{\hat{i}}_{{L_1}}}}\\ {{{\hat{i}}_{{L_2}}}}\\ {{{\hat{v}}_{{c_1}}}}\\ {{{\hat{v}}_{{c_2}}}} \end{array}} \right]$

Using the above state-space equations, and neglecting any parasitic resistances, the transfer function is calculated as:

$$\begin{aligned} \frac{{{v_0}(s)}}{{d(s)}} \approx \frac{{\left( {1 - s\frac{{{L_1}}}{R}\frac{{{D^2}}}{{{{D'}^2}}}} \right) \left( {1 - s\frac{{{C_1}({L_1} + {L_2})R}}{{{L_1}}}\frac{{{{D'}^2}}}{{{D^2}}} + {s^2}\frac{{{L_2}{C_1}}}{D}} \right) }}{{{{D'}^2}\left( {1 + \frac{s}{{{\omega _{01}}{Q_1}}} + \frac{{{s^2}}}{{{{({\omega _{01}})}^2}}}} \right) \left( {1 + \frac{s}{{{\omega _{02}}{Q_2}}} + \frac{{{s^2}}}{{{{({\omega _{02}})}^2}}}} \right) }} \end{aligned}$$

(15)

where

$$\begin{aligned} {\omega _{01}} = \frac{1}{{\sqrt{{L_1}\left( {{C_2}\frac{{{D^2}}}{{{{D'}^2}}} + {C_1}} \right) + {L_2}({C_1} + {C_2})} }} \end{aligned}$$

(16)

$$\begin{aligned} {\omega _{02}} = \sqrt{\frac{1}{{{L_2}\frac{{{C_1}}}{{{D^2}}}\left\| {\frac{{{C_2}}}{{{{D'}^2}}}} \right. }} + \frac{1}{{{L_1}{C_1}\left\| {{C_2}} \right. }}} \end{aligned}$$

(17)

$$\begin{aligned} {Q_1} = \frac{R}{{{\omega _{01}}\left( {{L_1}\frac{{{D^2}}}{{{{D'}^2}}} + {L_2}} \right) }} \end{aligned}$$

(18)

$$\begin{aligned} {Q_2} = \frac{R}{{{\omega _{02}}\left( {{L_1} + {L_2}} \right) \frac{{\omega _{01}^2}}{{\omega _{02}^2}}}} \end{aligned}$$

(19)

The design of the converter is dependent on the frequency of operation at which the switch operates. The higher switching frequency (${{f_{s}}}$) allows the selection of reactive components like capacitors and inductors with smaller sizes. In this work, the operating switching frequency of the PWM signal selected is 100 kHz. The selected values of the circuit elements in the present work are listed in Table 1.

Table 1 Specifications of SEPIC converter

Substituting the calculated values for the components in equation (13), the transfer function of the original system is calculated as:

$$\begin{aligned} {G_p}(s) = \frac{{ - 980{s^3} + 1.9 \times {{10}^8}{s^2} - 6 \times {{10}^{10}}s + 9.6 \times {{10}^{15}}}}{{{s^4} + 20{s^3} + 5.3 \times {{10}^7}{s^2} + 1 \times {{10}^9}s + 3.2 \times {{10}^{13}}}} \end{aligned}$$

(20)

2.3 Reduced Order Model of SEPIC Converter

Being a fourth-order nonminimum phase system, the application of some of the advanced controlling techniques on SEPIC converter leads to complex equations and sluggish response. Hence, a need for the reduction of the order of the system arises. In this work, ADRC control method has been proposed for the converter. The controller design based on the fourth-order system induces greater phase lag that deteriorates the performance of the controller in the case of the transients. To overcome the above-said difficulties and to apply the ADRC method, this converter is reduced to a second-order system. The order of the system is reduced on the basis of a balanced reduction method on the calculations of Hankel singular values. Firstly, a balanced reduction of the system is done to isolate the states whose contribution to the input–output response is negligible[17]. After the reduction of the system, Hankel singular values are calculated which has N small entries. A scientist named Hermann Hankel designed a method to obtain Hankel singular values based on the controllability Gramian, and the observability Gramian[19]. Actually, Hankel singular values provide a measure of energy for each state in a system. Hankel singular values are calculated as the square roots, of the eigenvalues. They are the basis for balanced model reduction, in which high-energy states are retained while low-energy states are discarded. The second-order reduced transfer function is obtained as:

$$\begin{aligned} {G_\textrm{pr}}(s) = \frac{{299.9{s^2} + 146.5\,s + 1.56 \times {{10}^{10}}}}{{{s^2} + 0.009676\,s + 5.203 \times {{10}^7}}} \end{aligned}$$

(21)

The reduced model retains the important features of the original model as its bode plot resembles the original system. The bode plot for these two systems is shown in Fig. 4.

Fig. 4

Schematic block diagram of an ADRC controller

3 Design of ADRC Controller for SEPIC Converter

In the ADRC method, the disturbances whether known or unknown are initially clubbed together in a single variable and further they are estimated in a certain way with the help of an observer. The estimated disturbance is then suppressed with the action of the controller. The block diagram depicting the structure of the ADRC controller is shown by Fig. 4. ${b_o}$ is defined as the gain of the system, u is considered as the control input and the system’s output is denoted by y. Also, ${k_p}$ is the controller’s gain, ${\tilde{y}}$ is the estimated output, ${\tilde{f}}$ is the estimated value of disturbance and $\varphi$ is the external disturbance. The SEPIC converter’s reduced order transfer function model is characterized by Eq. (21). By taking the inverse Laplace transform of this transfer function, we get the dynamics of the SEPIC converter in the time domain in the form of a differential equation that relates the output with the input using the following relation:

$$\begin{aligned} \ddot{y}=( - {a_0}y - {a_1}\dot{y} +\delta {b_o}u - {b_1}\dot{u} + \delta {b_o}u + \delta (t)) + {b_o}u =f\left( {y,\dot{y},u,\dot{u},w,\delta } \right) + {b_o}u \end{aligned}$$

(22)

where $f\left( {y,\dot{y},u,\dot{u},w,\delta } \right)$ has been considered as a generalized form of disturbance comprising of all the internal a well as the external disturbances. Since the system has been reduced to second order hence by the application of basic rules of ADRC method, a third-order observer is designed. The first two states in the observer are formed using the system dynamics while the third state in particular represents the cumulative disturbance. The estimated third state from the observer is canceled by the proper selection of the controller.

Let ${x_0} = y,{x_1} = \dot{y},{x_2} = h(.),$ and ${{\dot{x}}_2} = {m}$ where h(.) is differentiable and m is bounded. Using these assumptions, the state-space model for the system can be derived as:

$$\begin{aligned} \begin{array}{l} \dot{x}(t) = Ax(t) + Bu(t) + H{m}\\ y = Cx(t) \end{array} \end{aligned}$$

(23)

where

$\dot{x}(t) = \left[ {\begin{array}{*{20}{c}} {{{\dot{x}}_0}(t)}\\ {{{\dot{x}}_1}(t)}\\ {{{\dot{x}}_2}(t)} \end{array}} \right]$, $A = \left[ {\begin{array}{*{20}{c}} 0&{}1&{}0\\ 0&{}0&{}1\\ 0&{}0&{}0 \end{array}} \right]$, $B = \left[ {\begin{array}{*{20}{c}} 0\\ {{b_0}}\\ 0 \end{array}} \right]$, $C = \left[ {\begin{array}{*{20}{c}} 1&0&0 \end{array}} \right]$ and $H = \left[ {\begin{array}{*{20}{c}} 0\\ 0\\ 1 \end{array}} \right]$

The above state-space model can be used to design an ESO for the system given by:

$$\begin{aligned} \begin{array}{l} \dot{z} = Az + Bu + L(y - \hat{y}),\\ \hat{y} = Cz \end{array} \end{aligned}$$

(24)

where $z(t) = {\left[ {\begin{array}{*{20}{c}} {{z_0}}&{{z_1}}&{{z_2}} \end{array}} \right] ^T}$ is the estimated states and $L = {\left[ {\begin{array}{*{20}{c}} {{\beta _0}}&{{\beta _1}}&{{\beta _2}} \end{array}} \right] ^T}$ is the gain of the observer. A PD controller of the following form is considered:

$$\begin{aligned} {u_0}(t) = {k_1}(r - {z_1}) - {k_2}{z_2} \end{aligned}$$

(25)

The third state of the observer is rejected by the final control law given by:

$$\begin{aligned} u(t) = \frac{{{u_0}(t) - {z_3}}}{{{b_o}}} \end{aligned}$$

(26)

where $k_p = \left[ {\begin{array}{*{20}{c}} {{k_1}}&{{k_2}}&1 \end{array}} \right]$ is the controller’s gain.

The previous works in [7, 12] have proposed some techniques for the selection of bandwidths of the observer ${(\omega _0)}$ and controller ${(\omega _c)}$. The characteristics equation of the controller is compared with the second-order equation tuned in the form of the controller’s bandwidth($\omega _c$) that configures the controller’s gain as:

$$\begin{aligned} \lambda (s) = {s^2} + {k_1}s + {k_2} = {(s + {\omega _c})^2} \end{aligned}$$

(27)

From this, the controller’s bandwidth is calculated as:

${k_1} = 2{\omega _c},{k_2} = \omega _c^2$

Similarly, the characteristics equation of the observer is compared with the third-order equation tuned in the form of the observer’s bandwidth(${\omega _0}$).

$$\begin{aligned} \psi (s) = {s^3} + {\beta _0}{s^2} + {\beta _1}s + {\beta _2} = {(s + {\omega _0})^3} \end{aligned}$$

(28)

From this equation observer’s bandwidth is calculated as:

${\beta _0} = 3{\omega _0}$ , ${\beta _1} = 3\omega _0^2$ and ${\beta _2} = \omega _0^3$.

The values of ${\omega _c}$ and ${\omega _0}$ are selected as 900 rad/sec and 12600 rad/sec respectively based on the calculation of maximum sensitivity as 1.4.

4 Simulation Results

The circuit for the converter along with the controller was designed in the MATLAB/Simulink environment. The simulation results have been plotted for all three possible cases, i.e., for variation in set point voltage, variation in input voltage, and variation in load resistances. The performance parameters consisting of settling time, overshoot/undershoot, peak inductor current, and integral square error (IAE) has been calculated in each of these cases and listed in Table 2.

Table 2 Performance parameters of the proposed method

4.1 Servo Performance

In this case, the reference tracking capability of the controller is studied. Figures 5 and 6 depict the output voltages, the inductor currents, and the load currents obtained through simulation in boost and buck modes respectively. For the boost mode of operation, the input voltage is fixed to 30 V, while the load resistance is set to 100 $\Omega$. At the time $t=0.2$ s, the reference is step changed from 48 to 60 V, and again back to 48 V at time $t=0.3$ s. In the buck mode, the input voltage is set to 60 V, and at time $t=0.2$ s, the reference voltage is decreased from 48 to 30 V and again to 48 V at time $t=0.3$ s. The performance parameters have been listed in Table 2. From this, it is observed that the settling time is around 0.01 s when the reference is increased, while the curve settles at around 0.03 s when the reference is decreased.

Fig. 5

Responses for change in reference in boost mode

Fig. 6

Responses for change in reference in buck mode

4.2 Regulatory Performance for Variation in Input Voltage

In this case, the effect of varying input was studied by keeping the load resistance and reference voltage fixed to 100 $\Omega$ and 48 V respectively. Firstly, the input voltage was changed from 30 to 60 V (boost-buck mode) at time $t= 0.2$ s, and again from 60 to 30 V (buck-boost mode) at time $t= 0.3$ s, keeping the reference constant at 48 V. Figure 7 shows the simulation results under the assumed conditions. Also, the performance parameters are listed in Table 2. It is observed that the output voltage remains settled at 60V with very little overshoot/undershoot at the input voltage transition phase thereby proving a faster disturbance rejection capability.

Fig. 7

Responses for change in input voltage

4.3 Regulatory Performance for Variation in Load Resistance

Here the reference voltage was set to 48 V for observing the effect of varying load. In the buck mode of operation, the input voltage was adjusted to 60 V and the load resistance was varied from 100 to 50 $\Omega$ at time $t=0.1$ s and then back to 100 $\Omega$ at time $t=0.15$ s. For analyzing the boost mode of operation, the input voltage was fixed to 30 V, and at time $t=0.1$ s, load resistance was varied from 100 $\Omega$ to 50 $\Omega$ and back to 100 $\Omega$ at time $t= 0.15$ s. The corresponding responses are shown in Figs. 8 and 9, and the performance parameters are listed in Table 2. It can be analyzed that a small overshoot/undershoot of around 0.2 V is present. Also, the settling time of around 0.005 s was seen. The load voltage remains settled at the reference voltage, while the load current and primary inductor current changed instantly due to the change in the load as the power demand increased/decreased with increasing/decreasing load resistance.

Fig. 8

Responses for change in load resistance in boost mode

Fig. 9

Responses for change in load resistance in buck mode

5 Conclusion

In the present work, active disturbance rejection control (ADRC) is proposed for the SEPIC converter with high switching frequency. Higher switching frequency has allowed the selection of components with lower sizes. An ADRC-based control structure has been proposed for this converter which is derived based on the reduced order model of the SEPIC converter obtained through a balanced reduction technique. The suggested ADRC method results in outstanding performance and satisfactory robustness toward varying input voltages and loading conditions. This SEPIC converter along with suggested ADRC control may be used to achieve constant DC voltage from renewable energy sources like solar PV panels and windmill in varying environmental conditions.