Keywords

1 Introduction

With the rapid development of information technology, the integration of cyber system and physical system has become an inevitable trend in recent years, thus the cyber-physical system (CPS) has emerged. With the characteristics of high flexibility and easy scalability, CPS enables the aggregation of system information and real-time data sharing [1]. Their deployment in critical infrastructures has shown the potential to revolutionize the world, such as smart grids [2], digital manufacturing [3], healthcare [4] and so on. In most of these applications, the information is delivered over a wireless channel. However, the attacks become easier to implement in the process of transmitting information through the wireless channel [5, 6].

There are many types of common cyber attacks in CPS, such as deception attacks [7], replay attacks [8], denial-of-service (DoS) attacks [9,10,11] and so on. Among them, DoS attacks are easier and less costly to execute. In order to analyze the damage caused by DoS attacks on CPS, many scholars employ state estimation based on Kalman filter to evaluate the operation of CPS [12, 13]. In [12], distributed Kalman filter is designed to address event-triggered distributed state estimation problems. In [13], two Kalman filter-based algorithms are presented for detection of attacked sensors. Thus, in this paper, the state estimation algorithm based on Kalman filter is conceived to assess the state of CPS under DoS attacks.

In CPS, the defender and the attacker can be considered as a two-player game. The interactive decision process between a system with countermeasures and an attacker is studied under the framework of game theory in [14, 15]. In the game, the Nash equilibrium is used to find the point of convergence so that an optimal strategy can be determined. In [16], the Nash equilibrium algorithm is investigated as a means to enable each player to dictate their individual strategies and attain maximum benefit. Owing to the game theory is excellent at solving complex problems, a system model under the DoS attacks is constructed based on the game theory to solve for the optimal strategy.

Nowadays, reinforcement learning is rapidly spreading to a variety of domains. The long-term vision of the reinforcement learning algorithm allows it to be ideal for gaming between sensors and attackers in a CPS. For example, the literature [17] from the perspective of two reinforcement learning algorithms analyzes the security problem for the state estimation of CPS, both of which obtain the corresponding optimal policies. In [18], the distributed reinforcement learning algorithms for local information based sensors and attackers are proposed to find their Nash equilibrium policy, respectively. In this paper, we introduce reinforcement learning algorithms into the secure state estimation to solve the game problem between sensors and attackers.

Based on the above discussion, this paper presents a novel state estimation method based on reinforcement learning for a multi-sensor CPS under DoS attacks. Different from other papers, the main contributions of the paper are as follows: (i) The existing achievements of the single-sensor CPS are not guaranteed to meet with the needs in realistic scenarios, thus the CPS secure issue is extended to the multi-sensor CPS to explore the optimal policy selection problem of sensors and attackers under DoS attacks. (ii) Different from other works that passively describe the state of a system after DoS attacks, we positively analyze the optimal policy selection of sensors and attackers in a multi-sensor CPS. (iii) To further release the restriction on the set of states, the state space is unrestricted in order to comprehensively describe the state transition of the constructed markov chain in this paper. Besides, the complexity of the algorithm is decreased by introducing a penalty in the reward function.

The remainder of the paper is organized as follows. Section 2 portrays the system model for multi-sensor CPS under DoS attacks as well as the state estimation based on Kalman filter, and illustrates the state estimation processes. In Sect. 3, the secure state estimation algorithm based on reinforcement learning for multi-sensor CPS in confronting DoS attacks is proposed. The simulation results for a 3-sensor CPS in Sect. 4 demonstrate the effectiveness of the algorithm, and conclusions are drawn in Sect. 5.

2 Problem Formulation and Preliminaries

2.1 System Model

Fig. 1.
figure 1

The single-target multi-sensor system model under DoS attacks

Full size image

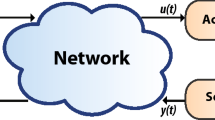
Consider a CPS with n sensors and a remote estimator as shown in Fig. 1, where different sensors work together to monitor a specified CPS. At time k, the expression of sensor m under DoS attacks can be given by:

$$\begin{aligned} \left\{ \begin{array}{l} x(k+1)=A x(k)+B w(k) \\ y_{m}(k)=C x(k)+ v_{m}(k), \end{array}\right. \end{aligned}$$
(1)

where \(k \in \mathbb {Z}\) indicates the discrete time step. \(x(k) \in \mathbb {R}^{d_{x}}\) refers to the state vector of the system and \(y_{m}(k) \in \mathbb {R}^{d_{y_{m}}}\) is the sensor measurement vector by sensor m at time k. \(w(k) \in \mathbb {R} ^{d_{w}}\) and \(v_{m}(k) \in \mathbb {R} ^{d_{v_{m}}}\) represent the process and measurement noises with zero mean, and their covariance matrices are Q(k) and \(R_{m}(k)\), respectively. A, B, and C are coefficient matrices with corresponding dimensions.

As seen the system model in Fig. 1, data measured by n sensors is transmitted to the remote estimator via a wireless channel. Each sensor \(m \in \{1,2,...,n\}\) has the option of secure transmission \(p_{k}=1\) or insecure transmission \(p_{k}=0\) in the channel. In the channel between the sensor and the remote estimator, the attackers has two actions that can be chosen respectively denoted as \(q_{k}=1\) and \(q_{k}=0\). The former indicates that the attackers launch DoS attacks on the communication channel, while the latter on the contrary. At time k, the state estimation based on the packet from sensor m denoted by \(\bar{x}(k)\). The symbol \( \eta _k \) indicates whether the packet is successfully received by the remote estimator. We denote \(\eta _k\) to indicate whether packet is lost at time k, which can be expressed as

$$\begin{aligned} \eta _k=\left\{ \begin{array}{ll} 1, &{} p_k=0,q_k=1 \\ 0, &{} p_k=0,q_k=0 \\ 0, &{} p_k=1,q_k=1 \\ 0, &{} p_k=1,q_k=0 . \end{array}\right. \end{aligned}$$
(2)

2.2 State Estimation Based on Kalman Filter

State estimation is performed employing a local Kalman filter to recursively update the system state. For each sensor m, the initial state x(0) is a zero-mean Gaussian random vector with non-negative covariance. At each time k, the Kalman filter is run to obtain the minimum mean-squared error (MMSE) \(\hat{x}(k)\) of the state vector x(k) based on the measured data. The MMSE estimate of sensor m is denoted by:

$$\begin{aligned} \hat{x}_{m}(k)=\textbf{E}\left[ x(k) \mid y_{m}(1), \ldots , y_{m}(k)\right] , \end{aligned}$$
(3)

with its corresponding estimation error covariance

$$\begin{aligned} P_{m}(k)=\textbf{E}\big [\left( x(k)-\hat{x}_{m}(k)\right) \left( x(k)-\hat{x}_{m}(k)\right) ^{T} \mid y_{m}(1), \ldots , y_{m}(k)\big ]. \end{aligned}$$
(4)

According to the Kalman filter equations, \(\hat{x}_{m}(k)\) and \(P_{m}(k)\) are updated recursively. For simplicity, the Lyapunov and Riccati operators h and \(\tilde{g}_{m}\) are defined as

$$\begin{aligned} \begin{array}{l} h(X) \triangleq \ A X A^T+Q \\ \tilde{g}_{m}(X) \triangleq \ X-X C^T\left[ C X C^T+R_{m}\right] ^{-1} C X . \end{array} \end{aligned}$$
(5)

Then the recursive updating equation of Kalman filter can be expressed as follows:

$$\begin{aligned} \begin{array}{l} \hat{x}_{m}(k \mid k-1)=A \hat{x}_{m}(k-1) \\ P_{m}(k \mid k-1)=h\left( P_{m}(k-1)\right) \\ K_{m}(k)=P_{m}(k \mid k-1) C^{T}\left[ C P_{m}(k \mid k-1) C^{T}+R_{m}\right] ^{-1} \\ \hat{x}_{m}(k)=\hat{x}_{m}(k \mid k-1)+K_{m}(k)\left( y_{m}(k)-C \hat{x}_{m}(k \mid k-1)\right) \\ P_{m}(k)=\tilde{g}_{m}\left( P_{m}(k \mid k-1)\right) . \end{array} \end{aligned}$$
(6)

2.3 State Estimation Process

The remote estimator performs state estimation based on the packet from the sensor m. In this paper, we define \(\bar{x}(k)\) and P(k) to denote the state estimation of remote estimator and the corresponding error covariance respectively. To simplify the game as well as the reinforcement learning algorithm, we assume that the error covariance matrix has converged to the steady state, i.e., \(P(k)=\bar{P}_m\).

The estimation process can be formulated as follows: if the local estimation arrives, the estimator synchronizes its own estimate with it; otherwise, the estimator predicts \(\bar{x}(k)\) according to the optimal estimate from the previous time step, i.e.,

$$\begin{aligned} \bar{x}(k)=\left\{ \begin{array}{ll} A \bar{x}(k-1), &{} \eta _k = 1\\ \hat{x}_m(k), &{} \eta _k = 0, \end{array}\right. \end{aligned}$$
(7)

with the corresponding estimation error covariance

$$\begin{aligned} P(k)=\left\{ \begin{array}{ll} h(P(k-1)), &{} \eta _k = 1\\ \bar{P}_m, &{} \eta _k = 0. \end{array}\right. \end{aligned}$$
(8)

In order to elaborate the changing process of the error covariance P(k), an interval is defined as \(\tau _k \triangleq \ k-\max _{0 \le l \le k}\left\{ l: \eta _l=1\right\} \), which is obtained by the time interval between the current time k and the time l when the packet is last received. When no packet loss occurs, \(\tau _{k}\) recursively increases by 1, otherwise \(\tau _{k}\) is updated to 0, that is,

$$\begin{aligned} \tau _{k}=\left\{ \begin{array}{ll} 0, &{} \eta _{k}=1 \\ \tau _{k-1}+1, &{} \eta _{k}=0. \end{array}\right. \end{aligned}$$
(9)

The estimation error covariance based on the time interval \(\tau _k\) can be derived from (8) and (9) as

$$\begin{aligned} P(k) = h^{\tau _k}( \bar{P}_m). \end{aligned}$$
(10)

Here, we assume that the packet successfully arrives at the remote estimator at the beginning of transmission, so \(\tau _0 = 0\). Therefore, the initial value of the estimation error covariance is \(P(0) = \bar{P}_m\).

In this paper, a Markov chain is introduced to represent the stochastic process of transition among states. On the basis of Markov property, the probability distribution of the next state can only be determined by the current state, independent of the state of the previous time series. Figure 2 represents the Markov chain of state transition with two sensors as an example.

Fig. 2.
figure 2

The transition of Markov chain P(k)

Full size image

3 Secure State Estimation Based on Reinforcement Learning

Reinforcement learning is an important research branch of machine learning algorithms, which focuses on learning through the interaction process between agents and their environment to achieve their own goals. As a value-based algorithm in reinforcement learning methods, the Q-learning algorithm constructs a Q-table of states and actions to store the expectation of gain as Q-value at each time. The Q-value is continuously updated during the learning process, and the action that obtains the greatest gain is selected based on the Q-table.

The goal of reinforcement learning is to find the optimal policy for a given Markov decision process (MDP). The MDP considers agents interacting with the environment by actions to obtain rewards. To more briefly describe the interaction, the MDP can be represented by a five-tuple: \(MDP::= \langle \mathcal {S},\mathcal {A},\mathcal {P}_{sa},\gamma ,\mathcal {R}\rangle \) [19], where \(\mathcal {S}\) and \(\mathcal {A}\) refer to the finite set of states and actions, respectively. \(\mathcal {P}_{sa}\) denotes the set of state transition probabilities, indicating the probability of taking a certain action at a state and transferring to the next state. \(\gamma \) represents a discount factor for the decision process and \(\mathcal {R}\) refers to the reward obtained at that moment given the current state and action. In this paper, an MDP is established to describe the interaction decision-making of the system defender and attacker, as depicted in detail below.

  1. a)

    State: In a CPS, there are n sensors, corresponding to n initial states. Whenever a packet is lost, a new state is generated.

  2. b)

    Action: The action combinations are defined as \(a_k=(n_k,p_k,q_k)\), where \(n_k\) represents the selected sensor serial number, \(p_k\) represents whether to spend cost to transmit, and \(q_k\) represents whether the attacker initiates DoS attacks.

  3. c)

    State transition: Consider the state of system as \(s_k=P(k)\). Since packet loss may or may not occur, a corresponding transition will take place between the states, which is detailed described in the Sect. 2.3.

  4. d)

    Discount factor: In order to achieve better algorithmic performance, a discount factor \(\gamma \) is introduced in the calculation of the cumulative reward, which locates in the interval of [0, 1].

  5. e)

    Reward function: The costs and actions are taken into account in the reward function, as the cost settings of both attacker and defender and the actions of them affect the gains of both players. In addition, a penalty is added to the reward function to avoid infinite traversal of states. Thus, the reward function at time k can be obtained as

    $$\begin{aligned} r_{k}=Tr\left( s_{k}\right) +c_m p_k-c_a q_k+ heaviside(s_k-h^i(P))*t, \end{aligned}$$
    (11)

where t is the added penalty, and i is set as the number of packet loss occurrences as the condition for adding the penalty.

Remark 1

The system defender and the attacker have opposite objectives of minimizing the reward and maximizing the reward, respectively. For the attacker, it theoretically contributes to its reward maximization objective and makes it easier to launch DoS attacks. However, this is not the case in the actual operation of the algorithm. This is because the inhibitory effect of the cost of spending on the attacks partially offsets the promotional effect of a larger reward on the attacks, and in general the attacks are not facilitated.

For an MDP involving system defender and attacker, a Q-learning based algorithm is proposed to solve the optimal decision-making problem for the two players. The steps of the algorithm are as follows.

  • a) Initialization

    Based on the input set of steady-state error covariance matrix and the number of sensors n, a set of states \(S=\{\bar{P_1},\bar{P_2},\cdots ,\bar{P_n}\}\) can be obtained.

Lemma 1

For a system with finite actions and finite states, reinforcement learning uses the optimal action-value function to guide the agent to make decisions. Suppose the state of the system is \(s_k\) and action \(a_k\) is taken, the optimal action-value function can be expressed as

$$\begin{aligned} Q_{\star }\left( s_{k}, a_{k}\right) =\max _{\pi } Q_{\pi }\left( s_{k}, a_{k}\right) , \quad \forall s_{k} \in \mathcal {S}, \quad a_{k} \in \mathcal {A}. \end{aligned}$$

According to Lemma 1, the size of the Q-value table is determined by the number of states and actions, so a Q-value table with n rows and 4n columns is initialized, where the initial value of the table is set to u.

  • b) Sensor and action selection

    At each moment, the system randomly selects actions with the probability of \(\varepsilon \) or selects the optimal action with the probability of \(1-\varepsilon \) according to the minimum-maximum principle.

  • c) Observation of rewards and states

    After the actions of the sensor and the attacker are determined, the reward obtained at the current moment is also available. The reward is observed at each moment according to (11).

  • d) Updating the Q-value table

    Before updating the Q-value table at each moment, we determine whether there is a corresponding row in the Q-value table of the next state. Then, the corresponding value in the Q-value table is updated according to the following formula.

    $$\begin{aligned} \begin{aligned} \widetilde{Q}_{k+1}&(s,n,p,q)=\left( 1-\alpha _{k}\right) \tilde{Q}_{k}(s,n,p,q) \\ &+\alpha _{k}\left( r_{k}+\rho \max _{q_{k+1}} \min _{p_{k+1}} \widetilde{Q}_{k}(s,n,p,q)\right) . \end{aligned} \end{aligned}$$
    (12)

  • e) Obtaining the Nash equilibrium strategy

    When the loop satisfies the termination condition, it means that the Q-value table has reached convergence. That is, the optimum Q-value table \(\widetilde{Q}_{\star }(s,n,p,q)\) can be obtained.

4 Simulations and Experiments

Consider a CPS with three sensors and a remote state estimator. The system parameters are given as follows:

$$ \textbf{A}= \begin{bmatrix} 1 &{} 0.5 \\ 0 &{} 1 \end{bmatrix}, \textbf{C}= \begin{bmatrix} 1 & 0 \end{bmatrix}, \textbf{Q}= \begin{bmatrix} 0.8 &{} 0 \\ 0 &{} 0.8 \end{bmatrix}. $$

The three sensors have different measurement accuracy and their noise measurement covariance matrices are respectively \({R_1}=0.08\), \({R_2}=0.4\) and \({R_3}=0.8\). Running the Kalman filter, the steady state error covariance matrices of the three sensors are obtained as

$$ \mathbf {\bar{P}_1}= \begin{bmatrix} 0.0758 &{} 0.0577 \\ 0.0577 &{} 2.1043 \end{bmatrix}, \mathbf {\bar{P}_2}= \begin{bmatrix} 0.3314 &{} 0.2343 \\ 0.2343 &{} 2.2627 \end{bmatrix}, \mathbf {\bar{P}_3}= \begin{bmatrix} 0.6 &{} 0.4 \\ 0.4 &{} 2.4 \end{bmatrix}, $$

where traces \(Tr(\bar{P}_1)\), \(Tr(\bar{P}_2)\) and \(Tr(\bar{P}_3)\) respectively are 2.1801, 2.5941 and 3.

In the game between defender and attacker in a multi-sensor CPS, the defender can choose whether to spend a certain cost on defense depending on the situation. The defense cost of the three sensors decreases sequentially with cost values of \({c_1}=10.7\), \({c_2}=9.2\) and \({c_3}=6.6\). The cost for attackers to launch DoS attacks in the system model is set to \({c_a}=1.5\).

In the MDP corresponding to this simulation experiment, there are three initial states \(\bar{P}_1\), \(\bar{P}_2\) and \(\bar{P}_3\). A new state is generated only when a new packet loss condition occurs. According to the reward setting in (11), when two consecutive packet losses occur, a penalty of \(t=10\) is added to the reward function. When the number of sensors in a multi-sensor system is determined, the number of action combinations \(a_k=(n_k,p_k,q_k)\) is also determined.

Table 1. \(\widetilde{Q}^*(s,n,p,q)\) matrix for convergence of multi-sensor system
Full size table

After the secure state estimation algorithm based on reinforcement learning is executed for 5000 iterations, the converged system contains 11 states, which are \(\bar{P}_1,\bar{P}_2,\bar{P}_3,h(\bar{P}_1),h(\bar{P}_2),h(\bar{P}_3),h^2(\bar{P}_1),h^2(\bar{P}_2),h^2(\bar{P}_3),h^3(\bar{P}_2),h^3(\bar{P}_3)\). To facilitate the presentation, some of the states such as \(\bar{P}_1,\bar{P}_2,\bar{P}_3,h(\bar{P}_2),h(\bar{P}_3),h(\bar{P}_1)\) are extracted as shown in Table 1. The action combination in the Table 1 is \(a =(n,p,q)\), denotes serial number of the selected sensor, the sensor and attacker action selection. Each value in Table 1 represents the convergent value of the corresponding state action pair \(\widetilde{Q}(s,n,p,q)\).

Fig. 3.
figure 3

Learning process \(\widetilde{Q}(s,n,p,q)\) for multi-sensor system

Full size image

Taking the initial state of the three sensors as an example, the learning process of \(\widetilde{Q}(s,n,p,q)\) is plotted in Fig. 3. According to the Fig. 3, it can be concluded that with the continuous iterations of the reinforcement learning algorithm, the attacker and defender gradually converge to the Nash equilibrium solution \(\widetilde{Q}^*(s,n,p,q)\) eventually. In the first 500 iterations, the algorithm follows the \(\varepsilon -greedy\) strategy in the trial-and-error exploration phase, and the elements of the Q-table are monotonically non-increasing. Through iterations learning of \(500-5000\), the elements of the Q-table can converge to a stable value.

Table 2. Nash equilibrium strategy for multi-sensor systems (n, p) and q
Full size table

By solving the convergent values in the Q-value table adopting a linear programming approach, the Nash equilibrium strategy of the game can be obtained, as shown in Table 2. The defender’s strategy consists of choosing the serial number of the sensor and whether to defend, i.e., (n, p). The attacker’s strategy is whether to launch DoS attacks, i.e., q. For example, in state \(s=h(\bar{P}_1)\), the Nash equilibrium strategies of the defender and the attacker are (1, 0) and 1 respectively. This means that sensor 1 is chosen in this state and no defense is taken, meanwhile the attacker chooses to launch DoS attacks in this case.

5 Conclusion

This paper studies the optimal policy selection problem for sensors and attackers in CPS with multiple sensors under DoS attacks. In order to solve the strategy selection problem, we propose a state estimation method based on reinforcement learning to evaluate the damage caused by DoS attacks. Initially, an MDP is constructed for a CPS containing multiple sensors to describe the interaction decision-making of the sensors and attackers. Then, a reinforcement learning algorithm is introduced to the proposed secure state estimation algorithm to dynamically adjust the strategy since it has advantages in interacting with unknown environments. In order to optimize the strategy, game theory is introduced to discuss the interaction process between sensors and attackers. During the interaction, there is no restriction imposed on the set of states in order to fully explore the transfer of states. Besides, a penalty is introduced to the reward function to ensure the algorithm’s feasibility. Finally, the simulation results of the CPS containing three sensors show that the proposed algorithm can effectively optimize the policy selection of sensors and attackers in the CPS. In the future, the algorithm proposed in this paper is extended to deal with the case of multi-channel multi-sensor CPS against DoS attacks to maximize resource utilisation.