The Geometric Modelling and Linearization of Small-Scale Wind Turbine Blades for Optimized Renewable Energy

Abstract

The modelling of blade geometry is the first step to be taken before the boundary element momentum theory (BEMT) analysis can be conducted on the wind turbine (WT). Yet it is a crucial step in establishing the best aerodynamic achievement the WT can give. In this paper, the power coefficient of a WT utilizing different blade geometries are determined and compared using the BEMT method. The blade geometries are obtained from the proposed formulas in literature and from the recommended polynomials that are based on experimental works. All blades are analyzed using the extended BEMT that includes the tip loss effect, the axial induction correction factor, $a$ and the stall effect. At the same time, the obtained tapered blade usually varies in its chord length and twist angle in a nonlinear manner with respect to radius of the blade. As this may cause manufacturing difficulty of the blade and increasing the wind turbine manufacturing cost, the best nonlinear distribution based on the BEMT analysis conducted has been linearized through a process of linearization. A comparison is made on the aerodynamic performances of the WT for the linearized and nonlinear blades. The study shows that the geometry of the blade is better with the use of the empirical formula that gives high power at higher tip speed ratio (TSR) while having lower axial thrust. Furthermore, comparing the linear and nonlinear blade, it can be concluded that linearizing the chord length and twist angle is a good practice because with its simpler construction, the maximum power of 200 W that was produced is at par with the nonlinear one, while the axial thrust is much lower at 125N when compared with 225N in the case of nonlinear blade.

1 Introduction

In today’s world, with the rapid growing and evolving of technology, the environmental issues have become one of the top priorities to be considered, especially in areas of green manufacturing processes [1, 2], failure of structures [3, 4] and design of materials [5, 6] and renewable energy [7, 8]. Following this, wind energy has developed into one key green energy source throughout the world in an effort to replace the carbon-based energies [9]. At the same time, research on the small-scale wind turbine (SSWT) that works in low wind speed regions has been gradually broadened in catching up with its widely used large counterpart [10]. In the analysis part, the blade element momentum theory (BEMT) has been widely adopted in the field of wind turbine design due to its simplicity and accuracy. In conducting the BEMT analysis, one early step is to assign dimensions of chord length and twist angle along the blade length before shape optimization process can be conducted to determine the designed aerodynamic performance values of the wind turbine. These chord length and twist angle values can be drawn from formulas such as proposed in literature [11,12,13,14,15]. Going through the iteration process in the BEMT analysis, the blade has been proven suitable to be tapered and twisted, especially for low wind speed applications [11, 16, 17] so that the maximum coefficient of power, ${C}_{P}$ can be reached. The purpose of twisting the blade is to adjust the wind direction such that the angle of attack (AOA) is always closed to the critical AOA, ${\alpha }_{\mathrm{cr}}$ where glide ratio, $L/D$ is maximum. In addition, a blade is tapered to reduce drag and bending stress so that the blade is stronger and lighter, where the later effect can also improve the starting capability of the wind turbine.

Improvements made by tapering and twisting have been demonstrated by many researchers [18,19,20]. In a comparison study made between experimental [21] and numerical work, blades with and without tapering and twisting were compared, [18] where tapered and twisted blade showed 50% of ${C}_{P}$ improvement. NACA4418 airfoil was used by Hsiao et al. [19] to study aerodynamic performance of blades with and without tapering and twisting, using the extended BEMT method, computational fluid dynamic (CFD) method and experiment. It was verified that the best blade in having the consistently highest ${C}_{P}$ for over an extensive span of tip speed ratio (TSR) was the blade having tapering and twisting.

The tapering and twisting of the blades however, come with disadvantages as well. Both actions have caused the distribution of the chord length and the twist angle throughout the length of the blade to become nonlinear. The nonlinear distribution will lead to the increase in difficulty in fabrication, increase in cost of material and reduce in accuracy of the turbine blade. In a research study [22], it was indicated that the nonlinear distribution obtained after the shape optimization process did not guarantee better performance compared with the linearized one. In this study, a new approach was applied in a SSWT design in relation to linearize the blade geometry. Based on the optimization method, the best linear blade’s geometry was decided among the 589 combinations of chord and twist angle that provided the best annual energy production. The results demonstrated that the linearized distribution gave some improved performances of the WT as shown in Fig. 1.

Fig. 1

Output power of preliminary and optimal blades [22]

Tahani et al. [23] made tangent line crossing that passes through every point on the preliminary lines in order to linearize the blade geometry. The line that gave the lowest decrease in ${C}_{P}$, applying the BEMT method was decided as the best linearized line. The smallest decrease in ${C}_{P}$ was determined through this method when measured up to the previous work [22, 24]. Rahgozar et al. [25] studied optimization power maximization and starting time minimization by combining linear and nonlinear distribution of chord length and angle of twist. The linear distribution was determined to enhance power. The starting time of the WT was improved by the nonlinear distribution.

Abdelsalam et al. [26] compared experimentally the ${C}_{P}$ of a SSWT equipped with linear and nonlinear distribution of the blade geometry. Only one airfoil was used, i.e. the RISØ-A-24 profile. The linearized blades were found to have volume reduction of 26% while having ${C}_{P}$ closed to the nonlinear blades. Further, the starting ability of the linearized blade was improved.

It can be observed from literature review that the BEMT study on a certain blade geometry is common. However, comparison studies between several of these geometric modelling of the blade that will show the effectiveness of each model, to our knowledge are rare. Similarly, it can be said that only few studies have been conducted to compare the aerodynamic performances of wind turbine operating with nonlinear and linear distributions of the chord length and the twist angle. This is however important in designing such blades that give the maximum power and power coefficient. As such, in this study, a comparison is made on the aerodynamic performances of a SSWT having chord length and twist angle with four different distributions. The best geometric distribution in terms of the resulting aerodynamic performances is then linearized through optimization method. Following that, a comparison is made between the nonlinear and linear distributions of the blade dimensions. The airfoil, SG6043, has been chosen for this study for having the highest $L/D$ compared with several well-known airfoils for SSWT applications. The aerodynamic analysis was conducted using the extended BEMT method applying the Prandtl’s tip loss factor, the axial induction correction factor, $a$ and the high AOA in post-stall region to uncover the best WT performances between the geometric dimensions of the blade and also between the linear and nonlinear distributions.

This paper starts with the discussion on the importance of selecting the geometry of the blades and its linearization that ends with the objective of the paper. Following that, the methodology used for this study that includes the elaboration on formulas used for determining blade geometries, the discussion on the method of linearization and the BEMT analysis of the blades. Following that, the results on the best geometry, the linearization of the best blades and the comparison on the aerodynamic performances of the linear and nonlinear blades are given. Finally, the conclusion of the paper is given along with the future work to be conducted.

2 Methodology

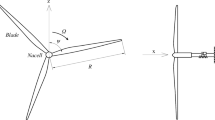
The specifications of the WT, profile and blade are presented in this section. Furthermore, the formulas for chord lengths and twist angles are given. The simplified version of the BEMT is explained where the method is extended to include the Prantdl’s factor of tip loss, thrust influence due to elevated axial induction factor, $a$ and the interpolated ${C}_{L}$ and ${C}_{D}$ at high AOAs. This study is on the SSWT with two number of blades, i.e. $N$ = 2. The radius of rotor is 1.5 m. The wind speed and tip speed ratio (TSR) are varied to find both minimum values that meet the minimum requirement of power, $P$ required per household which is about 600 W [27].

2.1 The Airfoil

Referring to Fig. 2, the profile applied here is the SG6043. The SG6043 airfoil is recognized to have high maximum glide ratio, maximum $L/D$ which is the most critical factor to obtain the best power coefficient, ${C}_{P}$ and power, $P$.

Fig. 2

SG6043 airfoil

2.2 The Formulas for Chord Length and Twist Angle

Table 1 gives the formulae for chord length and twist angle that are available in literature. Four Eqs. (1–4) are estimated based on AOAs, while the last equation is obtained from fitting the experiment data.

Table 1 Chord length formulae

The empirical formulas for chord length and twist angle as applied by Anderson [18] are

$$c\left( r \right) = 5 * \left( {0.162 - r/R * \left( {0.585 - r/R * \left( {1.033 - r/R * \left( {0.876 - r/R * 0.284} \right)} \right)} \right)} \right)/3$$

(1)

$$\theta \left( r \right) = \left\{ {\begin{array}{*{20}l} {54.17 - \frac{r}{R}\left( {307.43 - \frac{r}{R} * \left( {719.55 - \frac{r}{R} * \left( {785.97 - \frac{r}{R} * 326.67} \right)} \right)} \right) } \hfill & {\frac{r}{R} < 0.7} \hfill \\ {5.32 - \frac{r}{R}\left( {7.06} \right)} \hfill & {\frac{r}{R} \ge 0.7} \hfill \\ \end{array} } \right.$$

(2)

2.3 The Linearization of the Geometric Distribution

The linearization process in this study follows the work of Liu et al. [21]. The chord length and twist angle values are fixed at the tip of the blade. The end values at the root of the blade are changed according to the following equations to give huge numbers of linearized spreadings of the length and angle to choose from.

$${c}_{i,n}={c}_{t,o}+\left(0.7{c}_{r,0}-{c}_{t,0}\right)\frac{(n-1)}{N}\frac{{r}_{i}}{R} \quad n=\mathrm{1,2},\dots ,N+1$$

(3)

$${\theta }_{i,n}={\theta }_{t,o}+\left(0.7{\theta }_{r,0}-{\theta }_{t,0}\right)\frac{(n-1)}{N}\frac{{r}_{i}}{R}\quad n=\mathrm{1,2},\dots ,N+1$$

(4)

For reasonable varying steps of the twist angle and chord length of about 1° and 0.025 m, respectively, the number of divisions $n$ in this study are taken as 18 and 30 for chord length and twist angle linearization, respectively. For each linear distribution, the optimization is conducted by calculating for the blade geometry the annual energy production (AEP), where the distribution with the highest AEP will be taken as the best distribution. With air density ($\rho$), the transmission efficiency ($\eta$), swept area ($A$), rotor power coefficient of the wind turbine (${C}_{\mathrm{PR}}$) and the wind speed Rayleigh distribution (${f}_{\mathrm{Raleigh}})$, the AEP can be calculated as

$$E=8760\times \frac{1}{2}\eta \rho A \int\limits_{{v}_{c\mathrm{in}}}^{{v}_{\mathrm{cout}}}{v}^{3}{C}_{\mathrm{PR}}(v)\times {f}_{\mathrm{Raleigh}}\left(v\right)\mathrm{d}v$$

(5)

where $\eta$ is the transmission efficiency (in percentage) of both mechanical and electronic systems of the wind turbine, $\rho$ is the air density, $A$ is the swept area of the wind turbine rotor and ${C}_{\mathrm{PR}}$ is the rotor power coefficient of the wind turbine derived from the BEMT as a function of velocity, $v$.

2.4 The BEMT

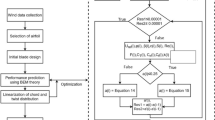
In the BEMT analysis, iterations are necessary to determine the axial and tangential induction factors $a$ and $a^{\prime}$, respectively. After making assumptions of these two values in the first iteration, $a$ and $a^{\prime}$ can be calculated using the following formulae in the following iterations until the values converged.

$$a=\frac{1}{\frac{4{F\mathrm{sin}}^{2}\phi }{\sigma {C}_{a}}+1}$$

(6)

$$a^{\prime}=\frac{1}{\frac{4F\mathrm{sin}\phi \mathrm{cos}\phi }{\sigma {C}_{t}}+1}$$

(7)

where $\phi$ and $\sigma$ are the flow angle and the solidity of the wind turbine, respectively and ${C}_{a}$ and ${C}_{t}$ are the axial and tangential force coefficients. Furthermore, $F$ is the Prantdl’s tip loss factor that is the first correction made to the BEMT. $F$ is defined as

$$F=\frac{2}{\pi }{\mathrm{cos}}^{-1}\left[\mathrm{exp}\left(-\frac{0.5B(r-R)}{r\mathrm{sin}\phi }\right)\right]$$

(8)

The second correction factor is the effect of low axial thrust, ${F}_{a}$ at high value of $a$. While there are several corrective models, in this study, the model of Glauert’s, such as in the following is used. Defining the two parameters ${Y}_{1}$ and ${Y}_{2}$:

$${Y}_{1}=\frac{{4F\mathrm{sin}}^{2}\phi }{{\sigma C}_{a}}$$

(9)

$${Y}_{2}=\frac{4F\mathrm{sin}\phi \mathrm{cos}\phi }{{\sigma C}_{d}}$$

(10)

The new induction factor, ${a}_{n}$ is then set to be:

$${a}_{n}=\left\{ \begin{array}{c}\frac{2+{Y}_{1}-\sqrt{4{Y}_{1}\left(1-F\right)+{Y}_{1}^{2}}}{2\left(1+F{Y}_{1}\right)}\,\,\,{Y}_{1}\ge 2 \\ \frac{\left(2+{Y}_{1}{c}_{t}-\sqrt{\left({\left({Y}_{1}{c}_{t}+2\right)}^{2}-4\left(1-\frac{1}{9}F{Y}_{1}\right)\right)}\right)}{2}\,\,\, { Y}_{1}<2\end{array}\right.$$

(11)

And the new radial induction factor,

$${a}^{\prime}=\frac{1}{\frac{{\left(1-aF\right)Y}_{2}}{\left(1-a\right)}-1}.$$

(12)

The BEMT analysis in this study is conducted using MATLAB’s codes following the paper’s work steps that can be easily understood from the flowchart in Fig. 3.

Fig. 3

Flowchart of the work

3 Results and Discussions

In this section, the differences in the chord length and twist angles among different blades are given. With this, the BEMT analysis is conducted on the blades to determine and compare the power coefficient and power of each blade. The best model is selected to go through linearization process of the chord length and angle of twist distributions. It is followed by the comparison on the aerodynamic performances between the blade with nonlinear and its linearized distributions.

3.1 The Chord Length and Twist Angle Distributions

Based on the given formulae in Table 1, the plots of the chord length and twist angle against blade’s radius are shown in Fig. 4 which correspond to the five geometric formulae, including one that is based on empirical relationship [14]. All formulas give parallel distribution throughout the length except for the Burton’s twist angle distribution. It can be seen that different formulae provide different sizes of chord length and twist angle, where the Manwell’s formula without considering the wake rotation gives the highest values of twist angle and chord length throughout the blade length.

Fig. 4

a Twist angle and b Chord length along the blade radius

3.2 The Aerodynamic Performances for Different Blade Geometries

The aerodynamic performances of the five wind turbines correspond to five different blade’s chord length, and twist distributions are given. Figure 5 shows the plots of power versus tip speed ratio, TSR. It shows the typical plot of the achievement criteria having a maximum value at a certain TSR value, where the Schmitz and Manwell 1 plots are almost identical. Note that due to convergence problem, the plot for Manwell 1 is only up to TSR = 8. The Schmitz’s, Manwell 1’s and Anderson’s plots show almost the same value of maximum power, except that in the Anderson’s plot, maximum $P$ occurs at higher TSR.

Fig. 5

Glide ratio against the AOA for modified airfoils

Figure 6 shows the comparison of thrust plots for the blades that correspond to the applied formulas. It shows that the Anderson’s formula gives such lower values of thrust throughout the TSR. Recall that the Anderson’s formula has given almost similar maximum $P$ and ${C}_{P}$ to Schmitz’s and Manwell 1’s formulae which occur at higher TSR. With these advantages, the Anderson’s blade is taken to the next step of linearization of the chord length and twist angle distributions.

Fig. 6

Plots of thrust, ${F}_{a}$ against TSR

3.3 The Linearization of the Distributions

Here, the distributions provided by Anderson’s empirical formulae have been chosen to be linearized. Based on Eqs. (3) and (4), the value of $n$ chosen here is 15 and 25 for chord length and twist angle, respectively. Figure 7a shows all the 15 possible linear distributions along with the nonlinear distributions of the chord length, while similar plots of 25 linear distribution for twist angle can be seen in Fig. 7b. In the following optimization process, the BEMT analysis has been conducted on turbine blades, each having combination of 15 chord length and 25 twist angle distributions that makes it all 375 possible combinations of twist angle and chord length.

Fig. 7

Linearization of the a Chord length b Twist angle distribution

Figure 8 shows the plot of power that corresponds to all combinations of chord lengths and twist angles. The dimensions of the chord length and twist angles are referring to the values at the roots of the blades. It shows that as the chord length is increased in sizes, the power and power coefficient performances are increased as well. However, the effect of the twist angle can be seen to give maximum power for the blade having root’s twist angle of 7.6°. As such, the optimal values of chord length and twist angles are the chord length with linear distribution of n = 15 and the twist angle with linear distribution of n = 10.

Fig. 8

Power against the linearized twist angle distribution

The BEMT analysis has been conducted on the blade equipped with the chosen linear distributions of the chord length and twist angle. Comparison is made between the performances of the blades with linear and nonlinear (Anderson’s) distributions of chord length and twist angle. Figure 9 shows the plots of power and thrust versus TSR for blades having linear and nonlinear chord length and twist angle distribution. It shows that with the simplified linear distributions, the linear blade gives almost the same maximum power as the nonlinear blade as shown in Fig. 9a. Furthermore, Fig. 9b shows one desired result of the linear distribution blade that shows lower values of thrust load, ${F}_{a}$.

Fig. 9

Performance comparison for linear and nonlinear distribution: a Power b Thrust

4 Conclusion

A study has been conducted on comparing for the best nonlinear distribution of the chord length and twist angle that gives the best aerodynamic performance of the blade. This best distribution is then linearized to study the effect of the linearization on the performances of the blades. It was found that the distribution given by empirical formulas gives the highest power and power coefficient at high TSR and at the same time gives the lowest axial thrust force. Furthermore, by linearizing this distribution, the more simplified blade design with cheaper manufacturing cost has been determined that gives similar power to the nonlinear blades while it produces much less maximum thrust force of about 125N when compared with 225N for its nonlinear counterpart. The logical next course of action is to determine the best blade geometry through the available optimization methods, such as genetic algorithm (GA) and particle swarm optimization (PSO) to apply a more systematic way in finding the best blade geometry.