Modeling and Control of BLDC Motor for Scaled Autonomous Vehicle Application

Abstract

This paper includes a brief study of a BLDC motor considering it an important actuator in new autonomous applications. It can be a sample in treating such actuators from a low level till reaching a controlled closed-loop system. The BLDC motor with the presence of ESC (Electronic Speed Controller) is modeled as a DC motor. Experimental results with gray-box identification techniques were used to validate this assumption. Robust $\mathcal {H}_\infty$ controller is implemented and compared with the conventional PI controller. To improve the controlled system loop an observer is designed and implemented in real-time. It works on the fusion of multiple sensors available on the platform. The targeted actuator is identified and controlled as a part of controlling and developing remote-control (RC) vehicles found in GiPSA-LAB. The main contribution of this paper is to propose a strategy that helps treat the BLDC motors used in scaled autonomous vehicles and pave the way for designing vehicle longitudinal controllers.

This work has been supported by GiPSA-LAB, safe team. Special thanks to the engineering team in the LAB.

1 Introduction

As one of the most important mechatronics components, DC motors come to the scene of interest of researchers as it plays an important role in the dynamic system. DC motors can be used as main components in applications related to autonomous vehicles [1, 2], autonomous aerial vehicles [3], industrial robotics [4], and other electro-mechanical applications. These applications consider the motor as the main actuator that affects the behavior of the system. Mainly the actuators of the mentioned systems are related to BLDC motor types.

Based on what is mentioned, designing a good controller is a challenge in this field. BLDC motors can be affected by measurement noises and manufacturing uncertainty. To obtain a closed loop, that can track desired references, it is obvious that we need a controller to guarantee system stability and required performances. A fuzzy PID controller is presented by [5] and compare the results with the conventional PID controller. Also [6], proposes a self-tuning fuzzy PID controller targeting autonomous vehicles application. The aim of it is to control the speed of the tire of an electric vehicle based on Pacejka’s model. A state of art on different control techniques is presented by [7] and presents modeling techniques and all mechanical and electrical components of BLDC motors. In [3] an adaptive closed-loop controller is used to control actuators of aerial vehicles. The supposed algorithm is proved experimentally to be robust in the scene of parameter uncertainties.

The work presented in this paper forms part of a larger project set to build a full autonomous scaled vehicle platform. The vehicle contains three main actuators, two BLDC motors actuate the longitudinal dynamics of the vehicle while a servo motor acts on the lateral dynamics. The angular speed of the motor is transferred to the angular speed of the vehicle’s tire, and then it can be translated to transnational velocity depending on the radius of the tire. The envisioned full autonomous scheme is represented in Fig. 1, shown in green the actuators targeted by this paper. All implementation algorithms and experimental tests were done in the ROS2 framework.

The paper presents a robust controller for the used BLDC motors. The used platform is presented in the first section. Then modeling and identification of the used BLDC are presented in the second section. In the third section a presentation of the theory and development of robust controller based on $\mathcal {H}_\infty$ approach. An observer is designed and implemented in real-time to reduce measurement noises. Experimental results and comparisons between the conventional PI controller and the robust controller are presented in the last section.

Fig. 1

Vehicle control scheme

2 GiPSA-LAB Platform

The platform found in GiPSA-LAB consists of having the targeted car, a motion-capturing system, and a PC where ROS is running and sending the command input to the Arduino positioned in the vehicle using wireless connections. The full platform is shown in Fig. 2. However, it is important to mention that the capturing system (vicon tracker) is not used in the objective of this paper.

Fig. 2

GiPSA-LAB platform

Fig. 3

RC car back view

Fig. 4

RC car front view

The RC car is equipped with two BLDC motors and one servo motor that allow both longitudinal and heading motions, respectively Figs. 3 and 4. This vehicle is equipped with different sensors (battery voltage and current, wheel encoders). The PC runs the control algorithms at specified frequencies and sends PWM signals to the Arduino RP, which transmits the signal as the voltage input to the actuator (Table 1).

As mentioned before, the ROS2 framework is used to consist of this development. It is considered an open source that helps researchers and engineers solving complex problems. ROS contains different nodes that can interact and send messages with different structure types using topics. The nodes are running python3 codes at different frequencies. One important thing is containing a ROS bag where all the measured and sent data are collected. This file is treated on Matlab to be able to get clean synchronized data that help in the identification and designing controllers. A joystick is connected also to the platform, and it is used to do different test tasks either by sending a PWM command directly to the Arduino or by generating the desired reference to be tracked by the actuators.

Table 1 RC car components

To convert between the input voltage and the PWM signal commanded (1) is used.

$$\begin{aligned} V = V_{battery} \times PWM \end{aligned}$$

(1)

Encoder sensors were used to estimate the shaft position of the motor, knowing the time between the signals, it is obvious to estimate the velocity of the output rotor using (2)

$$\begin{aligned} \dot{\theta }_{k} = \frac{2\pi }{8\times Ts}(ttr_{k}-ttr_{k-1}) \end{aligned}$$

(2)

where $ttr_K$ represents the number of counted ticks at instant k, $T_s$ corresponds to the working time or frequency of the sensor, and the number 8 is related to the pulse signals read by the sensor at each rotation. It should be mentioned that this velocity estimation produces a noisy signal due to the poor resolution from the encoders. To solve this issue an observer that can estimate a better signal of motor angular velocity is required.

The key system of the scaled autonomous vehicle involved in this work is the actuator component. The BLDC motor used scheme is shown in Fig. 5. We count with a voltage and current sensor for the battery, meaning that the independent current that each motor consumes is not known. To control each BLDC motor, we count with a dedicated ESC which receives a PWM signal from the Arduino board, controlling then the voltage applied to the motor. The last pair of sensors available, are a hall-effect encoder sensor which is used to derive the angular velocity for each motor.

Fig. 5

BLDC schemes

3 Physical Modeling and System Identification

3.1 Physical Modeling

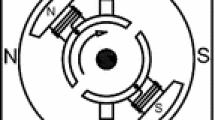
As mentioned in the previous section, the motor scheme contains an ESC that controls the speed of the motor. However, the system can be modeled as a DC motor from a perspective point of matching input voltage to the output $\dot{\theta }$. The assumed DC scheme is represented in Fig. 6. DC motors consist of having internal inductance coils L, resistors R, inertial rotating rotor J, b motor viscous friction constant, and a stator with magnets to generate an electromagnetic field. Applying Newton’s second law and Kirchhoff’s voltage law Eq. (3) is derived where $\tau = K_{\tau }i$, and $e = K_e\dot{\theta }$, with the assumption that $K_{\tau } = K_e = K$. $K_e$ and $K_\tau$ correspond to the emf and motor torque constants.

$$\begin{aligned} \begin{aligned} & J\ddot{\theta } + b\dot{\theta } = Ki \\ & L\frac{di}{dt} + Ri = V - K\dot{\theta } \end{aligned} \end{aligned}$$

(3)

A linear second-order state-space (4) is constructed based on the results given by (3).The input of the the system is voltage V, and the output is the angular speed of the rotor of the motor $\dot{\theta }$. Indeed, the voltage input affects the current i passing through the coil in the motor which affects the rotor angular speed.

$$\begin{aligned} \begin{aligned} & \frac{d}{dt}\begin{bmatrix} \dot{\theta }\\ i \end{bmatrix} = \begin{bmatrix} -\frac{b}{J} &{} \frac{K}{J} \\ -\frac{K}{L} &{} -\frac{R}{L} \end{bmatrix} \begin{bmatrix} \dot{\theta }\\ i \end{bmatrix} + \begin{bmatrix} 0 \\ \frac{1}{L} \end{bmatrix}V\\ \end{aligned} \end{aligned}$$

(4)

The motor used contains four poles that generate an electromagnetic field that forces the motor rotor to rotate. The ROS2 master can interact with the used microprocessor by sending a PWM signal as a calculated control input.

Fig. 6

DC scheme [8]

3.2 Open Loop Identification

An important prerequisite for control design is having a good model that can describe the behavior of the system. Benefiting from the mathematical model of the BLDC motor (4) it is possible to undergo parameter estimation for b, K, J, R, L parameters using Gray-box identification.

Experimental Setup

An open loop identification test is done on the motor by giving varying PWM amplitude signals. It is worth mentioning that the generated input PWM is considered to be persistently exciting input where it triggers all BLDC targeted frequencies. The signals were generated using the connected JOYSTICK. ROS framework connects the JOYSTICK with the Arduino RP placed on the vehicle and sends it the PWM signals by wireless connection. The measured data can be collected easily as a ‘CSV’ file thanks to ROSbag and plotjuggler. Plotjuggler is used to plot the collected data after each experiment. It is very important to analyse the collected data set just after finishing each experiment.

Numerical Identification

After treating and filtering the collected data using MATLAB, an optimization problem is used to solve Eq. (5) where y represents the real measured data representing the states of the motor, and $\hat{y}(\hat{\phi })$ represents the simulated states of the model. It is important to mention that while identifying the system constraints on the estimated current were included. This constraints can ensure having feasible solutions while solving an optimization problem. The results of the identification appear in Fig. 7 and Table 2. It is shown that the input delay occurs between 9 and 13 sampling times in the system. The RMSE is calculated to be 0.268.

$$\begin{aligned} \min _{\hat{\Phi }} {\Vert y - \hat{y}(\hat{\phi }) \Vert }_2 \quad \text {Where}\quad \hat{\Phi } = [J, b, K, L, R] \end{aligned}$$

(5)

Fig. 7

Motor model identification

Table 2 Motor parameter estimation results

3.3 Validation

Before designing the controller, a validation of the identified model is performed. Using the previously estimated parameters, and undergoing a new experiment, Fig. 8 represents the validation results. The simulated model fits the real data in both current and angular speed measurements. It is worth mentioning that the validation process is done using data sets resulting from different experiments. These sets are collected by either triggering the dynamic behavior of the motor or by trying to perform it stabilized. The represented results are a sample that verifies the model for different objectives.

Fig. 8

Motor-estimated model validation

4 Observer and Control Design

4.1 Sensor Fusion Observer

As seen from Figs. 7 and 8, the available angular speed measurement for the motor speed has a quite high noise to signal ratio due to the low resolution on the motor encoders. However, given that the identified model matches very well the system behaviour, a solution is to use a state observer to filter out the signal noise. One possibility is to have an independent pair of observers for each motor. This design would impose a direct trade-off between confidence on the measurement and confidence on the motor identified model. Another approach is to use the available current measurement coming out from the battery.

As seen in Fig. 5, this sensor can not distinguish the exact current going to each independent motor. However, this measurement can be described mathematically as:

$$\begin{aligned} i_{bat}(t)=i_1(t)+i_2(t) \end{aligned}$$

(6)

Were $i_{bat}(t)$ is the current measured for the battery current sensor and $i_{1,2}(t)$ are the current states of motor 1 and 2 respectively. Using this information we propose an extended BLDC Model for the purpose of observer design which fuses the information from the two available motors in the scaled vehicle. This extended model is given by:

$$\begin{aligned} \frac{d}{dt}\bar{x} = \bar{A}\bar{x}+\bar{B}\bar{V} = \left[ \begin{array}{cc} A &{} 0\\ 0 &{} A \end{array}\right] \bar{x} + \left[ \begin{array}{cc}B &{} 0\\ 0 &{} B\end{array} \right] [V_1,\,V_2]^T \end{aligned}$$

(7)

$$\begin{aligned} \bar{y} = \bar{C}\bar{x} = \left[ \begin{array}{cccc} 1 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 1 &{} 0\\ 0 &{} 1 &{} 0 &{} 1\end{array}\right] \bar{x} \end{aligned}$$

(8)

with the extended state vector given by:

$$\begin{aligned} \bar{x} = [\dot{\theta }_1\, i_1\,\dot{\theta }_2\, i_2]^T \end{aligned}$$

(9)

Note that the state matrices A and B in Eq. 7 are those identified from the DC motor model (4). Also note that each motor is assumed to share the same parameter values.

Employing this extended model we make use of a classical Luenberg Observer in order to estimate all states from the motors.

$$\begin{aligned} \dot{\hat{x}}(t) = \bar{A} \hat{\bar{x}}(t)+\bar{B} \bar{V}(t)+L(\bar{y}(t)- \bar{C}\hat{\bar{x}}(t)) \end{aligned}$$

(10)

The design of the observer gain $L\in \mathbb {R}^{4\times 3}$ is accomplished by means of pole placement using Matlab function place and using the observer error closed loop dynamics:

$$\begin{aligned} \dot{e}(t) = (\bar{A} - L \bar{C})e(t) \end{aligned}$$

(11)

In the rest of the section we describe the control techniques applied for motor control using the information computed by the observer. In contrast to the observer, however, the control of each motor will be carried out independently.

4.2 PI Controller

Based on the estimated model of the BLDC motor a PI controller is tuned to control the input voltage of the motor. According to the tuned terms $K_p = 0.16$ and $K_I = 1.1$ can solve the tracking problem. However, since this controller can go to exceed feasible issues, a saturation function is used to bound the input voltage. The used control scheme is represented in Fig. 9.

Fig. 9

PI BLDC control simulation architecture

4.3 $\mathcal {H}_\infty$ Controller

An $\mathcal {H}_\infty$ control problem formulation is represented in this part as shown by [9]. The target system to be controlled is represented in Fig. 10 by G(s). Two weighting functions $W_e$ and $W_u$ act as tuning constraints for the built controller K(s). The scheme in Fig. 10 is converted to the scheme LFT shown in Fig. 11.

Fig. 10

$\mathcal {H}_\infty$ control architecture

Fig. 11

Generalized plant P

The generalized plant P aims to characterize the controlled output with the external input and build a controller that minimizes the $\mathcal {L}_2$ induced gain from the external input $\omega$ to the controlled output e. In other words, the controller must minimize the impact of the reference and the assumed disturbances and noises with respect to the output of the defined weighting functions. Problem $\mathcal {H}_\infty$ is formulated by (12).

$$\begin{aligned} {\Vert e \Vert }_2 \le \gamma {\Vert \omega \Vert }_2 \quad \text {,}\quad {\Vert T_{ew}\Vert }_\infty = \begin{Vmatrix} W_eS \\ W_uKS \end{Vmatrix} \le \gamma \end{aligned}$$

(12)

$$\begin{aligned} T=\frac{GK}{1-GK} \quad \text {,}\quad S =1-\frac{GK}{1-GK} \quad \text {,}\quad SG = S\times G \quad \text {,}\quad KS = K\times S \end{aligned}$$

(13)

S denotes the sensitivity function that indicates the effect of noise on the closed loop $T_{yr}$, and KS designates the controlled sensitivity function that demonstrates the consequences of external input on controlled input u. It is possible to formulate a controller giving $\gamma _{\text {min}}$ regarding the sensitivity functions under defined templates. It is solved by operating the algebraic Riccati approach or using the LMI method (Zhou, Skogestad, & Postlewaite). The weighting functions are defined as $W_e$ and $W_u$ (14) used in designing templates for S and KS, respectively.

$$\begin{aligned} \frac{1}{W_e} = \frac{s+\omega _b \epsilon _e}{\frac{s}{M_s}+\omega _b} \quad \text { and }\quad \frac{1}{W_u}=\frac{\epsilon _u s + \omega _bc}{s+\frac{\omega _bc}{M_u}} \end{aligned}$$

(14)

The weighting function is tuned according to the required performance, where:

• $M_s$: Robustness required with max module margin.

• $\omega _b$: Tracking speed and rejecting disturbances.

• $\epsilon _e$: Steady-state tracking error.

• $M_u$: Actuator constraints based on $\frac{\Delta u}{\Delta r}$.

• $\omega _{bc}$: Actuator Bandwidth.

• $\epsilon _u$: Attenuate noises on controlled input.

The plant P can be written in another form shown in (15).

$$\begin{aligned} \begin{aligned} & \dot{x} = Ax + B_1\omega + B_2u \\ & e = C_1x + D_{11}\omega +D_{12}u \\ & y = C_2x + D_{21}\omega +D_{22}u \\ \end{aligned} \end{aligned}$$

(15)

$x \in \mathbb {R}^n$, the union of the plant states and the weighing function states, $\omega \in \mathbb {R}^{n_\omega }$, the defined external inputs to P, $u \in \mathbb {R}^{n_u}$, the controlled input, $e \in \mathbb {R}^{n_e}$, the controlled outputs, $y \in \mathbb {R}^{n_y}$, the measured outputs of the system. $W_e$ is used to obtain a minimum overshoot and steady-state error, while $W_u$ is used to limit controlled input ($V_{in})$ and avoid saturation [10]. The weighting function is defined as follows and parameters are defined and tuned according to Table 3 to obtain the required performances.

Table 3 BLDC $\mathcal {H}_\infty$ weighting parameters

The generalized plant P of order 3 including a second-order and first-order system. The architecture used to build the controller is represented in (10). The controller K(s) is designed using the Robust Matlab Toolbox. It is important to mention that optimal calculated $\gamma$ is increased by $30\%$ to ensure the numerical stability of the controller while discretization and implementation. The frequency analysis of the closed-loop system using the $\mathcal {H}_\infty$ approach is shown in Fig. 12. The system is under the defined template in all frequency ranges, has a good steady-state error, and rejects noises at high frequencies.

Fig. 12

BLDC closed-loop frequency analysis

5 Experimental Implementation

The developed control algorithms have been implemented on the scaled RC car. However, before implementation, different simulation iterations have been done to tune the defined controllers as mentioned previously. In the same step, the designed observer is implemented so that the closed-loop is defined by the feedback of the filtered measured data. It has been implemented with a sampling frequency of 50 Hz. As mentioned before the controllers were designed and tuned offline using MATLAB. Python3 programming was used to implement the controllers in real time.

5.1 PI Experimental

Conventional PI control implementation results are shown in Fig. 13. The controlled output appears to follow the reference with a good steady state error thanks to the integrated part of the controller. However, the rising time is large causing slow variation in the dynamics of the controller. This slowness in variation can affect the response of the longitudinal dynamics of the vehicle causing crashes in some maneuvers. The output feedback is filtered using the implemented observer. It is regarded that this controller affects the attenuation of the observer being noisier.

Fig. 13

PI BLDC implementation results

5.2 $\mathcal {H}_\infty$ Control Implementation

Benefiting from the identified model the weighting matrices have been tuned to track the reference. Experimental results are shown in Fig. 14. The $\mathcal {H}_\infty$ controller appears to track the required reference with a small overshoot and steady-state error. However, it is obvious that the rising time is small causing fast dynamic variations, thanks to the weighing template “$\frac{1}{We}$”. In addition, the used observer appears to be smooth in filtering the noises showing noise attenuation in high frequencies. It is worth mentioning that the controller is not saturating while tracking the desired reference.

Fig. 14

$\mathcal {H}_\infty$ BLDC implementation results

6 Conclusion

In this paper, we represent the physical model of a BLDC motor as a DC motor with the presence of ESC. The targeted controller is mainly used in electrical RC cars used to develop autonomous vehicle algorithms. An identification algorithm based on gray-box techniques is used to identify the parameters of the model. The identification method is validated by expiremental data. The data were collected from noisy sensors due to derivation term, however, the method used was able to give a feasible physical value of the motor parameters. PI and $\mathcal {H}_\infty$ control algorithms were introduced and implemented in real-time. A comparison between these two methods shows that the robust $\mathcal {H}_\infty$ controller is better at attenuating noises than the PI controller. The PI controller is easier in tuning and in implementing in real-time, however, the performance of the $\mathcal {H}_\infty$ controller appears to be better in terms of tracking and rising time. Also, the designed observer appears to work greatly in attenuating noises when implemented in the closed loop with the robust controller. The proposed work is validated experimentally and theoretically to be used in treating BLDC motors , specially that used for scaled autonomous vehicle applications.

Future work may be comparing different control strategies for the motor with the presence of the longitudinal controller of the vehicle. A study of sensor fault diagnosis can be done in the presence of different type sensors.