Prevention of Expansion Shock by the Control of Numerical Dissipation of Upwind Schemes

Abstract

This paper is concerned with the prevention of expansion shock given by some upwind schemes. Upwind schemes for the Euler equations of gas dynamics, be it flux vector splitting (FVS) or flux difference splitting (FDS), have many attractive shock-capturing properties. However, some of these schemes are known to give expansion shock, thus violating the so-called entropy condition. It is not very easy to say whether a particular upwind scheme violates the entropy condition, as lack of evidence cannot be taken as a rigorous proof for satisfaction of the condition. For some schemes that are known to violate the entropy condition, a number of entropy fixes based on the flux function have been suggested in the literature. Here we propose a more general method of fixing the problem by controlling numerical dissipation of the schemes.

1 Introduction

Euler equations are frequently solved in the context of many aerospace design problems. These equations govern the dynamics of inviscid compressible flows. The unsteady Euler equations demand the design of a stable, robust and accurate scheme that works for a variety of challenging situations. The Euler equations allow discontinuous solutions in the forms of shocks, contact discontinuities, slip surfaces and expansion waves with sonic points [1]. The addition of artificial viscosity for the purpose of capturing shocks was first pioneered by von Neumann and Richtmyer [2]. With further research in this field, it became clear that the addition of explicit numerical diffusion is essential for numerical stability in case of central discretization of the flux terms. Pure central differencing of the Euler fluxes leads to instabilities because the direction of wave propagation is not respected, upwind schemes on the other hand are so designed as to respect the direction of signal propagation and hence they are generally stable because the strategy itself used to construct the schemes. They also provide better nonlinear stability near shocks. The FVS scheme of van Leer [3] is known to be highly robust but has high numerical diffusion which leads to smearing of discontinuities. Gudonov’s scheme [4] laid the foundation for a variety of upwind schemes, the primary drawback of which was that it was computationally expensive as it involves an exact Riemann solver. The expansion shock phenomenon suffered by the Steger and Warming Scheme [5], the first major FVS scheme, was remedied by the dissipative van Leer scheme. Later, the quest for better accuracy gave rise to a number of FVS and FDS upwind schemes. A few important ones are Roe’s FDS scheme [6], Liou and Steffen’s AUSM scheme [7], Edward’s LDFSS Scheme [8], Zha-Bilgen’s scheme [9], Jameson’s CUSP scheme [10], etc. Majority of these schemes have relatively low dissipation and the ability to capture shocks accurately. However, the question whether these schemes satisfy the entropy condition has received less attention. Merely not giving an expansion shock in a particular test problem is not a definitive proof of satisfying the entropy condition. However, if a scheme is seen to give expansion shock in a certain test case, we can justifiably say that it violates the entropy condition. In this paper, we experiment with two such schemes, namely, Roe’s scheme and Zha-Bilgen scheme. Through a test case designed by Zha [11], we first demonstrate that for the quasi-one-dimensional nozzle flow through a convergent-divergent nozzle, both these schemes give expansion shocks at the throat, thus violating the entropy condition. Roe’s FDS scheme is an important event in the development of approximate Riemann solvers as a natural progression to the Gudonov’s scheme which involves an exact Riemann solver. Although, it provides high accuracy for a range of problems, Roe’s FDS scheme suffers from limitations such as computational cost [7], carbuncle phenomenon and expansion shock [12]. Being a remarkable scheme with low dissipation, the Roe’s scheme has received considerable attention from researchers and several so-called entropy fixes have been suggested [13,14,15]. We also demonstrate that one such entropy fix, namely, Hyman and Harten’s [14] entropy fix rids the scheme of its entropy condition violation at the throat. It has been widely demonstrated that the entropy fixes cures Roe’s scheme also of the strong-shock carbuncle phenomenon. Thus, the Roe’s scheme gives a very accurate and powerful method when acting in conjunction with various entropy fixes.

In this paper, we observe that all these entropy fixes are based on the modification of the Roe’s flux function and the strategy cannot be seamlessly extended to other schemes that violate the entropy condition. Not denying the effectiveness of these entropy fixes for the Roe’s scheme, we ask ourselves—‘Is it possible to adopt a general strategy that provides a common cure to all entropy condition violating upwind schemes’? The answer seems to be ‘yes’, and that is the problem we address in this paper. We first demonstrate that by adopting this general strategy the expansion shock given by the Roe’s scheme can be eliminated as effectively as the entropy fixes found in literature. We then experiment with the other upwind scheme of Zha-Bilgen that violates the entropy condition. We first demonstrate that this scheme also gives an expansion shock at the nozzle throat and then go to show that the common strategy we propose remedies the problem effectively for this scheme as well. This, we feel justifies the claim that our strategy is likely to work with all entropy condition violating upwind schemes. The cure for entropy condition violation we propose has its roots in the dissipation regulation (DR-LLF) of a central scheme proposed in [1]. It has already been observed that an upwind flux function can be first cast in the form of a central flux function plus some dissipation term. The diffusion regulation strategy proposed in the DR scheme can be easily applied to the dissipation term inherently associated with an upwind scheme. In the next section, we explain the methodology adopted and then substantiate our claims with numerical results. It may be noted that we solve the nozzle flow problem using the quasi-one-dimensional (quasi-1D) version of the Euler equations using finite volume discretization.

2 Problem Definition and Numerical Procedure

2.1 Geometry

The Sod’s problem [16] is a classic-bench-marking problem often used to test the performance of numerical schemes for hyperbolic conservation laws. Figure 1 shows a shock tube of length $L = 15$ m, in the middle there exists a diaphragm separating two gases of different pressures and densities into two sections, the driver with higher pressure and driven section with lower pressure. Initially, the gases on both sides of the diaphragm are at rest. Once the diaphragm is broken at $t = 0$ it leads to flow in the tube; the Mach number variation is studied numerically vs. analytically for validation. There are two problems, namely Sod’s first and second problem. For the first problem the pressures in the driver and driven section are 1000 and 100 kPa, respectively while the densities are 1 and 0.125 kg/m³. For the Sod’s second problem the pressures in the driver and driven section are1000 and 10 kPa, respectively while the densities are 1 and 0.01 kg/m³. For both the cases the gases are at rest initially.

Fig. 1

Schematic of Sod’s shock tube problem

The geometry of the nozzle chosen for analysis is a converging–diverging nozzle designed and tested at NASA Langley Research Centre namely nozzle A2. The geometry is formed to be a converging and diverging section with slope angles of $\theta$ and $\beta ,$ respectively. The sections are connected via a circular-arc as shown in Fig. 1. The geometry is symmetric in nature. The mathematical equations describing the geometry [7] are given below:

$$ y = x \tan \theta + h_{\text{t}} , \quad 0 \le x \le L_1 $$

(1)

$$ y = - \sqrt {{r_{\text{c}}^2 - \left( {x - x_{\text{c}} } \right)^2 }} + y_{\text{c}} , \quad L_1 \le x \le L_2 $$

(2)

$$ y = \left( {x - x_{\text{t}} } \right)\tan \beta + y_{\text{t}} ,\quad L_2 \le x \le L_3 $$

(3)

In the above equations, θ = −22.33°, β = 1.21°, L₁ = 4.74 cm, L₂ = 5.84 cm, L₃ = 11.56 cm, x_c = 5.7814 cm, y_c = 4.11 cm, r_c = 2.74 cm, $x_{\text{t}} = 5.84$ cm, $y_{\text{t}} = 1.37$ cm. The minimum area of the nozzle is located at $x_{\text{c}}$ where $y_{\text{t}}$ is the throat radius (Fig. 2).

Fig. 2

A2 nozzle NASA

2.2 Governing Equations

In case of the quasi-1D nozzle problem, the physics is governed by the Euler equation. In the Cartesian coordinates it is expressed as:

$$ \frac{\partial U}{{\partial t}} + \frac{\partial F}{{\partial x}} - H = 0, $$

(4)

where,

$$ U = AQ, F = AE. $$

Here, U is the vector of conserved variables and F is the flux vector.

$$ Q = \left[ {\begin{array}{*{20}c} \rho \\ {\rho u} \\ e \\ \end{array} } \right],\quad E = \left[ {\begin{array}{*{20}c} {\rho u} \\ {\rho u^2 + p} \\ {\left( {e + p} \right)u} \\ \end{array} } \right],\quad H = \frac{{{\text{d}}A}}{{{\text{d}}x}}\left[ {\begin{array}{*{20}c} 0 \\ p \\ 0 \\ \end{array} } \right]. $$

Additionally, as we have three governing equations and four unknown’s density, momentum, energy and also the pressure term. To close this system, we use the below equation.

$$ p = \left( {\gamma - 1} \right)\left( {e - \frac{1}{2}\rho u^2 } \right) $$

(5)

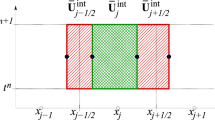
In the above equation, ρ is the density, u is the velocity in the x-direction, p is the static pressure, e is the total energy, i.e. the sum of internal and kinetic energy per unit volume and A is the cross-sectional area of the nozzle (Fig. 3).

Fig. 3

Computational 1D finite volumes with cell interface

We use the finite volume method (FVM) formulations to discretize the above governing equations and obtain the following formulation for cell ‘I’ and time level ‘n’.

$$ Q_i^{n + 1} = Q_i^n - \Delta t\left( {\frac{1}{\Delta xA_i }\left( {F_{i + \frac{1}{2}} - F_{i - \frac{1}{2}} } \right) - \left( {\frac{H_i }{{A_i }}} \right)} \right)^n $$

(6)

It is to be noted that the same formulations are applicable to the Sod’s shock tube problem with $A_i = 1$ and H_i = 0.

2.3 Artificial-Viscosity Form of Central Schemes

It is known that central discretization of the flux terms for the Euler equations which are hyperbolic in nature leads to numerical instabilities. The stabilization is achieved by the explicit addition of a numerical diffusion term. Hence, we solve a modified Euler’s equation which contains second-order derivatives which exhibit viscous-like effects. The presence of excessive numerical diffusion smears out the discontinuities and therefore it becomes critical to control the diffusion term by the introduction of a diffusion regulation parameter. The flux expression in general can be derived as follows:

$$ \frac{\partial U}{{\partial t}} + c\frac{\partial F}{{\partial x}} = 0. $$

(7)

In the above equation, c is the speed of wave propagation. Since, the direction of signal propagation is important for the discretization of the flux terms, we express c as the algebraic sum of two parts as shown in Eq. 6.

$$ c = \frac{c + \left| c \right|}{2} + \frac{c - \left| c \right|}{2} $$

(8)

In the above equation, it is to be noted that if the magnitude of c is positive, the second term becomes zero, while in case c is negative, the first term becomes zero.

$$ \frac{\partial U}{{\partial t}} + \frac{c + \left| c \right|}{2}\frac{\partial F}{{\partial x}} + \frac{c - \left| c \right|}{2}\frac{\partial F}{{\partial x}} = 0 $$

(9)

Now, the upwind scheme can be applied appropriately to each of the flux term. Expressing the flux terms as shown below allows us to apply upwind differencing without concern about the direction of wave propagation.

$$ \frac{{U^{n + 1} - U^n }}{\Delta t} + \left( {\frac{c + \left| c \right|}{2}} \right)\frac{{F_i - F_{i - 1} }}{\Delta x} + \left( {\frac{c - \left| c \right|}{2}} \right)\frac{{F_{i + 1} - F_i }}{\Delta x} = 0 $$

Finally, the flux terms can be collected to express the above as the sum of a central scheme and an additional diffusion term.

$$ U^{n + 1} = U^n - \frac{\Delta t}{{2\Delta x}}\left\{ {c\left( {F_{i + 1} - F_{i - 1} } \right)} \right\} + D, $$

(10)

where D is the numerical diffusive flux given by

$$ D = \left| c \right|\frac{\Delta t}{{2\Delta x}}\left( {F_{i + 1} - 2F_i + F_{i - 1} } \right) . $$

(11)

In the above equation, the diffusive flux term is regulated by the introduction of the diffusion regulation parameter $\Phi$ [1], this parameter is set based on the jump in Mach number across the cell interface and its magnitude in comparison with a parameter δ [1], the recommended value of which is 0.5.

$$ U^{n + 1} = U^n - \frac{\Delta t}{{2\Delta x}}\left\{ {c\left( {F_{i + 1} - F_{i - 1} } \right)} \right\} - {\Phi }D $$

(12)

2.4 Numerical Procedure

In case of the Sod’s shock tube problem, the pressure, velocities and densities are known throughout the domain at the initial condition. The properties in the tube are uniform with a single discontinuity, therefore, it can be classified as a Riemann problem, the analytical solution to which is well-known [1]. It is to be noted that most of the analytical calculations needed are trivial, but numerical techniques need to be employed to find the pressure ratios across the shock as there is no straightforward way to solve the implicit equation relating the pressures $p_1$ and $p_2$ as shown in Eq. 13.

$$ \frac{p_4 }{{p_1 }} = \frac{p_2 }{{p_1 }}\left[ {1 + \frac{\gamma - 1}{{2a_4 }}\left\{ {u_4 - u_1 - \frac{a_1 }{\gamma }\frac{{\frac{p_2 }{{p_2 }} - 1}}{{\sqrt {{\frac{\gamma - 1}{{2\gamma }}\left( {\frac{p_2 }{{p_2 }} - 1} \right) + 1}} }}} \right\}} \right]^{\frac{ - 2\gamma }{{\gamma - 1}}} , $$

(13)

where $a$ is the speed of sound and the subscripts denote the corresponding region in the shock tube in Fig. 1.

For the nozzle problem, we assume that the inlet of the nozzle is connected to an infinite reservoir, for which the pressure and temperature are taken as the reservoir conditions of 101,325 Pa and 300 K, respectively. For the entry boundary condition for isentropic transonic flow, we apply the method of characteristics for specifying the correct number of boundary conditions, i.e. the inlet and outlet boundary conditions needed are specified based on the number of characteristics entering and leaving the corresponding boundary. The number of variables at the inlet is specified equal to the number of characteristics entering through the same, whereas, the number of variables to be extrapolated from the interior of the domain is equal to the number of characteristics leaving the domain.

In the quasi-1D nozzle problem, there are three characteristic waves crossing any point in the domain simultaneously. For the case considered, two characteristics enter and one leaves the computational domain. Therefore, we fix two variables at the inlet and extrapolate one from the interior. In the outlet for the supersonic case, three characteristics leave the domain. So, all the variables are extrapolated from within the computational domain.

The numerical formulation is done using FVM, while the two schemes chosen for study are the Roe and Zha-Bilgen scheme. For the purposes of comparison with the analytical case, the area-Mach number relation [17] mentioned in Eq. 14 is solved using Newton–Raphson method.

$$ \left( {\frac{A}{{A_{\text{t}} }}} \right)^2 = \frac{1}{M^2 }\left[ {\frac{2}{\gamma + 1}\left( {1 + \frac{\gamma - 1}{2}M^2 } \right)} \right]^{\frac{{\left( {\gamma + 1} \right)}}{{\left( {\gamma - 1} \right)}}} , $$

(14)

where $A_{\text{t}}$ is the area at the throat of the nozzle.

For the numerical solutions, we use a uniform structured 1D grid. The Roe’s scheme involves solving the approximate Riemann problem for every grid point. The Zha-Bilgen scheme on the other hand involves splitting the fluxes into a convective and pressure parts.

2.5 Grid Independence Test

The grid independence test is performed on the Sod’s second problem for a variety of grid sizes. We observe that the numerical results for $N = 200$ has reasonable accuracy. Here, for the purpose of resolving the entropy violation we choose lesser number of grid points. Although, choosing a large number of points may give better agreement with the analytical results, it also reduces the jump at the sonic point thus making it more difficult to identify and resolve the same (Fig. 4).

Fig. 4

Comparison of results for various grid sizes

2.6 Code Validation

The FVM formulations of the Zha-Bilgen and Roe’s schemes are validated by comparing with the well-known Sod’s shock tube problem [16] along with its analytical solution. For the shock tube problem, the time step at which the plots were verified is $t = 0.005$ s and the chosen value of Courant–Friedrichs–Lewy (CFL) number is 0.1. Additionally, it is also demonstrated that the analytical solution of the quasi-1D nozzle problem is in good agreement with the Roe’s scheme when the well-known Hyman and Harten Fix is applied to the same as shown in Fig. 6.

We observe in the Fig. 5 that the numerical results are in good agreement with the analytical solution. Next, the code of the quasi-1D nozzle problem is also validated by plotting the analytical results along with the Roe’s scheme with the incorporation of a well-known entropy fix name.

Fig. 5

Comparison with analytical results of Sod’s first shock tube problem

Fig. 6

Demonstration of Hyman and Harten’s entropy fix for Roe’s scheme

In the Fig. 6 for the plot without the fix, we observe that the Roe scheme exhibits a strong-shock at the throat of the nozzle. We choose one of the many well-known existing entropy fixes for the Roe scheme, namely Hyman and Harten Fix [14]. As expected this rids the scheme of its entropy violation condition and no jump is visible in the throat region.

3 Results and Discussion

The numerical computations are performed on a structured 1D mesh using the FVM formulations using an in-house code written in C language. Firstly, Sod’s second shock tube problem is implemented as it is expected that both the Zha-Bilgen as well as the Roe’s scheme will produce a jump near the sonic region.

It can be observed from Fig. 7 that there is a jump in the expansion front near the sonic region where Mach number is equal to one. The results of the same is shown in Fig. 7.

Fig. 7

Entropy violation for Roe and Zha-Bilgen schemes: shock tube problem

It can be seen in the Fig. 7 that the violation of the entropy condition which caused a jump has been resolved upon incorporating the diffusion regulation parameter and setting the value optimally so as to minimize smearing, while simultaneously resolving the jump near the sonic point. It is also worth noting that reducing the dissipation regulation parameter any further would cause the schemes to become unstable (Fig. 8).

Fig. 8

Entropy violation fix for Roe and Zha-Bilgen schemes using dissipation regulation

Secondly, the quasi-1D nozzle problem is addressed. For transonic flow, we observe a jump near the throat, i.e. the sonic point. For the isentropic transonic case, it is expected that the velocity or Mach number will gradually increase from subsonic to supersonic speeds without any jumps. However, at the sonic point the Zha-Bilgen and Roe’s scheme is expected to show a jump in the throat near the sonic region due to the violation of the entropy condition as shown below in Fig. 9.

Fig. 9

Entropy violation for Roe and Zha-Bilgen schemes: nozzle problem

Finally, the present problem which involves the control of the diffusion regulation parameter to resolve the entropy violation is explored.

In the Fig. 10, a minimal amount of dissipation is added so as to handle the existing issues with minimal smearing of the results as diffusion inherently smooths out discontinuities and imparts stability to the numerical calculations.

Fig. 10

Entropy violation fix for Roe and Zha-Bilgen schemes using dissipation regulation

4 Conclusions

A number of upwind schemes are seen to give expansion shocks in some flow situations involving the Euler equations, which is a direct violation of physical laws. As the Euler equations are frequently used in the aerodynamic design of various objects such as wings, eliminating these nonphysical solutions is an extremely important CFD activity. This work proposes a general remedy to the problem of expansion shock demonstrated by some upwind schemes. To substantiate our claim, we take two well-known schemes that are known to violate the entropy condition, namely the Roe’s scheme and the Zha-Bilgen scheme. We use these schemes to solve the quasi-1D Euler equations that govern the transonic flow in a convergent-divergent nozzle. As expected both these schemes give expansion shocks at the nozzle throat, where the flow turns supersonic from subsonic, thus violating the entropy condition. A number of entropy fixes have been proposed for the Roe’s scheme, we use one of these to show that it remedies the problem of expansion shock at the throat. However, we observe that this remedy is not general in nature and is largely scheme-dependent. This motivates us to find a general cure for all upwind schemes that violate the entropy condition. This general strategy consists in first casting the upwind scheme in the form of a central-plus-dissipation scheme, and then regulating the diffusion proposed in a scheme named DR-LLF [1] scheme. Our numerical results clearly demonstrate that the expansion shock given by both Roe’s and Zha-Bilgen schemes are completely eliminated by suitably adjusting the diffusion regulation parameter. In the case of Roe’s scheme, the entropy fix proposed earlier and our diffusion regulation strategy are seen to be equally effective. In the case of Zha-Bilgen scheme our diffusion regulation strategy is highly effective in eliminating the expansion shock at the throat. As the method proposed in this work is likely to remedy the problem of entropy condition violation exhibited by any upwind scheme, the framework is very general. In this paper, we present case studies involving only two upwind schemes. Work is in progress to determine which other upwind schemes violate the entropy condition and then examine how our general cure remedies the problem.