Keywords

1 Introduction

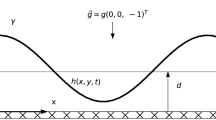
It is possible to create well-controlled waves in a finite size container by pushing the container in the direction perpendicular to the liquid surface. In both the gravity and capillary limits, these waves—also referred to as Faraday waves—that are subharmonically excited (wave frequency equal to half the driving frequency) have been thoroughly researched. Understanding the physical behaviour of surface standing waves, such as capillary or gravity waves, begins with understanding the dispersion relationship, also known as the Kelvin relation for waves on fluid surfaces. Gravitational and capillary forces are combined in this relation, demonstrating that surface tension and gravity dominate waves at the surface of fluids [1,2,3,4,5,6]. The dispersion relation for finite depth of the container is given by:

$$\omega^{2} = \left[ {\left( {g k_{w } + \left( {\frac{\sigma }{\rho } } \right) k_{w }^{3} } \right) {\text{tanh}}\left( {k_{w } h} \right)} \right]$$
(1)

Equation (1) describes the dispersion relation for the capillary gravity wave for finite depth, considering both gravity and surface tension forces.

The fluid depth can be considered infinite when tan(kwh) is approximately equal to 1. The dispersion relation for capillary and gravity waves for infinite depth is given by Eq. (2)

$$\omega^{2} = \left[ {\left( {g k_{w } + \left( {\frac{\sigma }{\rho } } \right) k_{w }^{3} } \right)} \right]$$
(2)

To obtain the dispersion relation purely for capillary waves, we have to neglect the first term of the right-hand side of the Eq. (2), and for gravity waves, we have to disregard the second term of the right-hand side of the Eq. (2).

The dispersion relation for the capillary and gravity waves is given by Eq. (3) and Eq. (4), respectively. Dispersion relation for capillary waves:

$$\omega^{2} = \left( {\frac{\sigma }{\rho } } \right) k_{w }^{3}$$
(3)

Dispersion relation for gravity waves:

$$\omega^{2} = g k_{w }$$
(4)

The waves with a wavelength of a few millimetres and wave vectors of a thousand per meter are known as capillary waves. The amplitude of these waves is very small (approximately 0.1 to 1 µm). In capillary waves, the main dominant force is the surface tension, which brings back the liquid’s disturbed surface to the equilibrium position [7,8,9,10,11]. On the other hand, high wavelength and relatively small wave vector waves onto the surface of rivers and oceans are known as gravity waves. Since the propagation of these waves is caused mainly by gravity, they are called gravity waves. As the name implies, gravity is the main restoring force in gravity waves, just like surface tension is in capillary waves [12, 13].

The crossover wave frequency [14] from gravity waves to capillary waves is given by Eq. (5).

$$\omega_{{o_{t} }} = \left( {\frac{{4 g^{3} \rho }}{\sigma }} \right)^{1/4}$$
(5)

The above equation purely depends on the fluid properties. In their study, Puthenveettil and Hopfinger [14] demonstrated that FC-72 liquid has the highest cross-over wave frequency from gravity to capillary waves, followed by Glycerine–water solution and water. Dense material will result in a smaller surface tension value, thus resulting in a larger cross-over wave frequency. For parametric instability in the capillary, unbounded, and infinite fluid depth limits, the driving threshold acceleration is given by

$$a_{c} = 8\left( {\frac{\sigma }{\rho } } \right)^{1/3} \nu \omega^{5/3}$$
(6)

The Faraday critical acceleration is directly proportional to driving frequency and increases as frequency increases. To obtain the Faraday wave frequency, multiply the driving frequency by a factor of 0.5. Capillary and decay lengths are the two significant parameters that characterize surface waves. The capillary length, also known as the capillary constant, relates gravity to surface tension and is mathematically expressed as the reciprocal of the wave vector at which surface and gravitational potential energies are equal. In finite-size containers, the decay length is essential in producing surface waves. The sidewall effects of the container are felt with decay length. Like capillary length, it also relates gravity to surface tension [15, 16]. If the radius of the container (R) is greater than the decay length, then sidewall boundary effects can be neglected: the system is then considered a’large system’ [16, 17]. The decay length of surface standing waves can be mathematically expressed:

$$l_{d = } \frac{\sigma }{{4\nu \omega { }\rho }} = \frac{\sigma }{{8\nu \omega_{0 } \rho }}$$
(7)

The pattern evolution of Faraday waves is complicated above the stability limit. In large systems, Binks et al. [18] demonstrated that the around the instability threshold, theories that suggest three-wave resonant interactions have successfully matched experiments [19, 20]. There is no general theory for pattern evolution in small systems with significant side boundary effects. Ciliberto and Gollub [21] proposed that the evolution of wave patterns can be due to mode competition in small systems. Although the study of pattern formation in the case of water, as well as silicon oil, has been thoroughly studied by many researchers over the past decades. Even though the pattern generation in Newtonian liquids like Kerosene oil and water-glycerine mixture has not been explored in detail. In this chapter, we examined the pattern formation on liquid surfaces in the presence of excited surface waves at different driving frequencies.

2 Methodology

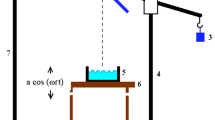
A circular aluminium tray with a diameter of 14 cm and a depth of 6 cm, filled with the test fluid and mounted on a vibrating device, was used as the experimental set-up schematically shown in Fig. 1. In the present case, we used a loudspeaker to meet the requirement of surface vibration. The loudspeaker (8 inches in size) is connected to the amplifier via a frequency generator, which is further connected to the main power supply. The frequency generator was only used to drive the electrical loudspeaker in the vertical direction. The acceleration of the circular bath is given by a(t) = \(A\omega^{2} {\text{sin}}\left( {\omega t} \right)\), where A is the shaker amplitude. The vibration exciter received a clean sinusoidal signal through electrical isolation from the signal generator and amplifier.

Fig. 1
An illustration presents an experimental setup in which an aluminum circular container placed over the vibrating shaker observes the liquid pattern emitted by the L E D light panel. The vibrating shaker is connected to an amplifier, which is connected to a function generator.

A schematic illustration of the experimental setup. A container is mounted on the vibrating shaker (loudspeaker), which only vibrates in the vertical direction. The liquid of interest is filled inside the container to observe the pattern at a different frequency. The vibrating shaker is connected to the function generator through an amplifier

Full size image

The loudspeaker was mounted on a wooden frame and bolted together to reduce any vibrational effect from the earth’s surface. The circular container is placed directly onto the loudspeaker and fixed from the side to prevent its lateral displacement. The working area was illuminated by the two LED light sources mounted directly from the top of the container and inclined at a 45-degree angle. An image of the generated pattern was captured using a Nikon D-750 DSLR camera at 60 frames per second. Image-J software was used for the post-processing of the recorded pattern, and MATLAB was used to plot the data obtained from the image processing.

Adequate precautions were taken to avoid contamination in the fluids. Water, water-glycerine mixture, kerosene oil, and silicon oil were used in the study as the test fluids. The relevant properties of the test fluids are summarized in Table 1. Kerosene and silicone oil has a low surface tension in the air, which makes them less susceptible to contamination than water and water-glycerine mixtures. Silicon, as well as kerosene oil, was taken from sealed containers hand handled carefully to avoid contamination. The experiments were conducted over a short duration, and the test fluids were not left exposed to the atmosphere for extended periods. We approximated the system to have an infinite depth for the current configuration because tanh(kh) = 1 for these fluids.

Table 1 Physical properties of liquids at 20 ℃
Full size table

3 Results and Discussion

One of the primary objectives of the present study is to investigate the pattern generation in different liquids inside the circular container over the vertical vibrating surface experimentally. We used water, silicon oil, kerosene oil, and water–glycerine mixture as test fluids. A separate container of equal size is used for viscous and non-viscous liquids. The container contains the desired liquid up to a certain depth placed over the vibrating shaker operated at different frequencies.

First, we explain the pattern formation in water followed by silicon oil, kerosene oil, and water-glycerine mixture.

The pattern formation over the water surface at different frequency are illustrated in Fig. 2. The corresponding physical parameters responsible for pattern generation are tabulated in Table 2. The hollow patterns form onto the water surface at a low value of driving frequency.

Fig. 2
Four sets of images in sequence display the formation of various water patterns at different frequencies.

An image sequence represents the pattern formation on the water surface at a different driving frequency. a 20 Hz, b 40 Hz, c 60 Hz, d 80 Hz

Full size image
Table 2 Represents the value of physical parameters obtained from the experimental observation at different driving frequencies for water
Full size table

Furthermore, these hollow patterns will change into a small benzene-like structure as the value of the driving frequency increases from 20 to 80 Hz. The literature shows that the Faraday critical acceleration, which is one of the prime parameters responsible for pattern generation, is the function of driving frequency that increases as frequency increases. For water, the Faraday critical acceleration (ac) lies in the range of 0.60 to 6.11 m/s2 as the excitation frequency of the container varies in the range of 20 Hz to 80 Hz.

The variation in Faraday critical acceleration with driving frequency is graphically represented in Fig. 6a. The experimental study reveals that at low driving frequency, there is no significant variation encountered in the value of ac. However, the value of ac drastically increases as ω increases beyond 200 rad/s. Furthermore, the study is also conducted to obtain the value of the decay length of water, which is also a significant parameter responsible for the pattern generation, lies in the range of 0.1432 to 0.0358 m for a given frequency range and decreases as the driving frequency increases. The variation in decay length with driving frequency is shown in Fig. 6b.

The study is also conducted to determine the wavelength of the generated pattern in water at different driving frequencies. The wavelength of the water waves decreases from 0.016 to 0.0065 m (shown in Fig. 6c), Whereas the corresponding wave vector, which is inversely related to the wavelength of the waves, increases from 379.88 m−1 to 957.26 m−1 (shown in Fig. 6d) as the driving frequency increases. We further investigate the impact of higher frequency over the pattern formation on water. When the driving frequency increases beyond 80 Hz, we find a circular pattern on the water surface. The formation of Faraday circular waves on the water surface at 100 Hz frequency is shown in Fig. 3.

Fig. 3
A set of eight images displays circular wave patterns formed on the surface of the water in circular containers.

Faraday circular wave formation over the water surface at 100 Hz frequency. The first row represents our experimental observation and the second row represents the result of Puthenveettil, and Hopfinger [14] from their experiment

Full size image

In the same way, we did before, to explain the pattern formation over the water surface, we will now describe the pattern generation on the silicon oil surface in detail. Here, we examine the pattern formation for the same driving frequency range (20 Hz to 80 Hz). At low driving frequency (up to 125.66 rad/s), a bigger benzene-like structure (shown in the first row of Fig. 4) is formed on the surface of silicon oil, whereas these bigger patterns will change into a small size as the driving frequency increases from 125.66 rad/s to 502.65 rad/s.

Fig. 4
Four sets of image sequences a to d display the silicon oil patterns at various frequencies, which are indicated by lighter and darker shades. Images e and f display the silicon oil patterns at 20 and 80 hertz, respectively.

An image sequence represents the pattern formation in silicon oil at a different frequency. a 20 Hz, b 40 Hz, c 60 Hz, d 80 Hz, e, and f represents the result of Puthenveettil and Hopfinger [14] from their experiment at 20 Hz and 80 Hz, respectively

Full size image

In this chapter, the pattern formed at 20 Hz and 80 Hz driving frequency is similar to the pattern created by Puthenveettil, and Hopfinger [14] at the same driving frequency. Like in water, in the case of silicon oil, the Faraday critical acceleration increases (from 1.45 to 14.71 m/s2), and the decay length decreases (from 0.041 to 0.010) with increases in the driving frequency. The variation in the physical parameters with driving frequency and effect of Faraday wave frequency on wavelength as well as wave vector in cases of silicon oil is shown in Fig. 6. The physical parameters for silicon oil are tabulated in Table 3. Additionally, the variation in the wavelength obtained from experimental and theoretical studies with Faraday wave frequency is shown in Fig. 8b. Furthermore, we also experimentally investigate the pattern formation on the surface of Kerosene oil at the same driving frequency (20 Hz to 80 Hz). The evolution of the pattern formed onto the kerosene oil surface as driving frequency increases is illustrated in Fig. 5. Here, we also found that the Faraday critical acceleration increases and decay length decreases (graphically shown in Fig. 6) as the value of driving frequency increases (refer Table 4).

Fig. 5
Four sets of image sequences a to d display different wave patterns formed on the surface of the water at various frequencies, which are indicated by lighter shades.

An image sequence represents the pattern formation on the kerosene oil surface at a different driving frequency. a 20 Hz, b 40 Hz, c 60 Hz, d 80 Hz

Full size image
Fig. 6
4 multi-line graphs. Graphs A and B plot Faraday critical acceleration and decay length versus driving frequency. Graphs C and D plot wavelength and wave vector versus Faraday wave frequency. The lines are plotted for water, silicon oil, kerosene oil, and water and glycerine. A and D depict an increasing trend, while B and C depict a downward trend.

A graphical representation of the variation of physical parameters with driving frequency and Faraday wave frequency. a Faraday critical acceleration versus driving frequency. b Decay length versus driving frequency. c Wavelength versus Faraday wave frequency. d Wave vector versus Faraday wave frequency

Full size image
Table 3 Represents the value of physical parameters obtained from the experimental observation at different driving frequencies for silicon oil
Full size table
Table 4 Represents the value of physical parameters obtained from the experimental observation at different driving frequencies for kerosene oil
Full size table

The parameters responsible for the pattern generation in kerosene oil are tabulated in Table 4. The comparison of experimental and theoretical wavelength variation with ω0 in the case of kerosene oil is graphically illustrated in Fig. 8c. In the last of this experimental investigation, we also like to examine the pattern generation when the water’s viscosity increases by adding a small amount of glycerine (30 mL). The evolution of the pattern generation with an increase in the driving frequency for the water-glycerine mixture is experimentally shown in Fig. 7.

Fig. 7
Four sets of image sequences a to d display the formation of various wave patterns for the water-glycerine mixture at different frequencies.

An image sequence represents the pattern formation in the water-glycerine mixture at a different frequency. a 20 Hz, b 40 Hz, c 60 Hz, d 80 Hz

Full size image
Fig. 8
4 line graphs a to d plot wavelength versus Faraday wave frequency. The lines are plotted for theoretical and experimental wavelengths. All the graphs depict a downward trend.

The variation in experimental and theoretical wavelength for different liquids with Faraday wave frequency (ω0) is represented graphically. a water, b silicon oil, c kerosene oil, and d water-glycerine mixture

Full size image

The pattern formed in the case of the water-glycerine mixture is similar to the water. The only difference is that the hallow pattern present in the case of water at low driving frequency is completely eliminated by adding glycerine into the water. At all driving frequencies, we found the benzene like structure over the surface of the water-glycerine mixture. The effect of driving frequency over the ac and ld as well as variation of λ and kw with ω0 are graphically represented in Fig. 6. Furthermore, the variation in experimental as well as theoretical λ and kw with ω0 is illustrated in Fig. 8d.

4 Conclusions

In this chapter, we presented the simple and cost-effective method of surface vibration to investigate the pattern formation over the surface of viscous (oils) and non-viscous (water) liquids under a wide range of driving frequencies. According to the study, the patterns generated over the water and silicon oil surface for a particular value of the forcing frequency and show excellent agreement with the patterns obtained in the literature. Furthermore, the physical parameters responsible for the pattern generation have also been investigated in detail. The experimental results show that the value of Faraday critical acceleration and decay length of the pattern formation increases and decreases, respectively, as the value of driving frequency increases. For the given driving frequency range, the experimental study found that the Faraday critical acceleration and decay length are maximum for silicon oil and water, respectively. Additionally, the study emphasizes the well-known Mathieu equation to determine the wavelength and wave vector of the generated pattern. The study shows that the wavelength of the generated pattern is maximum in the case of water, whereas minimum in the case of kerosene oil for a given range of frequency. Similarly, the wave vector is found to be maximum in the case of kerosene oil and minimum in the case of water. The pattern obtained over the surface of the water and the water-glycerine mixture is observed to be the same.