Robust Design Optimization of Telecommunication Tower Under Extreme Load in Dual Response Surface Method

Abstract

Application of robust design optimization (RDO) technique to ensure least deviation of structural performance is getting popular in recent years. However, RDO is generally executed in probabilistic domain. But, in many cases, such as for tall telecommunication tower under wind, most of the parameters like widths and thicknesses of angle sections, wind speed, drag and lift coefficients, do not bear any defined probability density function. Only their ranges of variations are known to an engineer. Hence, these parameters can be more rationally modeled as uncertain-but-bounded (UBB). Though, there is significant attention on RDO of structures with UBB parameters under static load, study of UBB-based RDO under uncertain dynamic load is scarce. Also, usual convex hyper-ellipsoidal programming-based RDO for UBB parameters cannot be readily applied to the present problem due to unavailability of explicit functional form of constraints. Another issue is the record-to-record variations of wind load time-histories, which are generally observed even for the same set-up of characterizing parameters. To circumvent these problems, the present study proposes a dual response surface method (RSM)-based RDO procedure using convex programming, which generates explicit functional forms of mean and standard deviation of the constraints, and considers record-to-record variation of wind load, as well. By virtue of dual RSM, the method becomes computationally efficient, as well. The RDO results obtained by the proposed approach are observed to track robust and economic solution. The results are compared with the conventional RDO approach to establish its improvements over the proposed approach.

1 Introduction

It is well established now that optimization disregarding uncertainty may lead to unsafe design leading to catastrophic failure consequences. This is due to the undesirable deviation of structural performance caused by uncertainty. To minimize such unwanted deviation, and also to maintain economy of structural cost, a suitable scheme of uncertainty-based-optimization is needed. In fact, in mechanical and production engineering, to yield the best quality products by ensuring minimum undesirable deviation from their design performances in the presence of uncertainty, a technique popularly known as robust design optimization (RDO) is used [1,2,3,4]. An RDO simultaneously minimizes the dispersion of structural performance under uncertainty and cost. Besides production engineering, the application of RDO is also becoming popular in aircraft engineering to design aeroplane wings, ensuring minimum chance of flutter and resonance under extremely uncertain wind turbulence [5]. In the last decade, RDO has also paved its path in structural engineering to ensure minimum deviation of structural performance (thus the minimum chance of failure), maintaining simultaneously the budget under extremely uncertain loads [1, 6]. The present paper focuses on the RDO of a telecommunication tower structure as substantial deviations of structural performance for such a structure is highly anticipated when subjected to extremely uncertain wind environment.

In this regard, it is worth mentioning that a reliability-based design optimization (RBDO) is the most popular approach to uncertainty-based-optimization. The RBDO brings specified reliability of structure by yielding a design which has reliability index more than a user-specified target reliability index value [7, 8]. But, there are two major drawbacks of RBDO. Firstly, the system may still be sensitive to input parameter variation due to uncertainty, leading to large undesirable deviations, even though the target reliability index criteria are satisfied. Secondly, the RBDO is only applicable when sufficient statistical data, such as mean, standard deviation, and probability density function (PDF), is available for all the parameters. The RBDO is fully hinged on the reliability index calculation, which cannot be done unless one has the mean, standard deviation, or PDF information about the uncertain parameters.

In fact, most often, sufficient realistic statistical data of involved system parameters like load, temperature difference, etc., are not available to characterize an uncertain system and construct probability density function to conduct a reliability analysis. Instead, only a range of variation of the parameters due to uncertainty is available, by which parameters can be treated as uncertain-but-bounded (UBB) type. Dynamic wind load is an extremely stochastic phenomenon characterized by many uncertain parameters. Lift coefficient, drag coefficient, wind speed, gradient height, the Power law exponent, dead load of antenna, dimensions and thicknesses of the tower members—for all these parameters a definite mean, standard deviation or PDF is not available. Only a set of upper and lower bounds can be constituted based on the findings of the previous researchers or from experience. The dynamic wind load signatures vary significantly over time and show different fluctuating behaviour at different realizations even for same set of input parameters [9, 10] Thus, it is more logical to set lower and upper bounds of the parameters so that all possible variations within that range can be suitably considered.

Thus, it is clear that the RBDO cannot be applied with UBB parameters as reliability calculation is impossible under the above-mentioned circumstances. However, the RDO, since it does not depend on the reliability information, and works fine with UBB parameters (as noted for seismic load in [3]), is an elegant approach in this regard. Also, the RDO makes the structural performance least sensitive to uncertainty effects. Thereby, the drawbacks of the RBDO mentioned above gets circumvented. Thus, the present paper focuses on the RDO of tower structure under UBB-type uncertainty.

The RDO with UBB parameters is generally executed using a first-order perturbation approach [11], which is only valid for the low level of uncertainty. Also, this approach often leads to uneconomic and very conservative design since it is based on worst-case propagation of uncertainty [12]. In this regard, the convex programming (CP) approach [13] is gaining increasing attention, where the UBB parameters constitute a convex set. In the CP, the design parameters are so selected that provides a so-called ‘safety measure’ more than the target one [13]. It may be noted here that the term ‘safety measure’ is not the same as the ‘reliability index’ used for probabilistic parameters. Rather, it is a term that denotes the largest variation of the UBB parameters that the system can withstand.

The state-of-the-art on mathematical formulation of RDO with probabilistic parameters is quite advanced [7]. Available techniques enable one to formulate RDO problem in presence of higher uncertainty level, mixed probability distribution and correlation. In this regard, there is enough scope to explore RDO formulation with UBB parameters. Ben-Tal and Nemirovski [6] detailed the concept of convex modelling to treat UBB uncertainty. Since then, researchers have tried various extension of the convex modelling to effectively solve RDO problem. Au et al. [6] proposed an unsatisfactory degree function following the concept of Physical Programming to express the feasibility of constraints under undesirable variation of UBB parameters. Wang et al. [14] applied convex modelling for optimization of a simple semi-active tuned mass damper system. Chen et al. [13] presented hyper-ellipsoidal CP approach for RDO of structural system, where the authors proposed a sub-optimization scheme to efficiently yield RDO solution. Meng et al. [15] proposed a super-parametric approach of convex modelling which is a general case of ellipsoidal model. In this regard, the theoretical review of Jiang et al. [16] on probability-interval hybrid uncertainty analysis for structures with both aleatory and epistemic uncertainties is of worth mentioning. In this paper, the wind effect is simulated by generating the artificial wind field while using weighted amplitude wave superposition technique. In this regard, Kaimal’s power spectral density function (PSDF) [17] is used. This approach of artificial wind force generation has been successfully used in wind fragility analysis of structures [1, 18]. One can also obtain wind force distribution over height, space and time by using wind tunnel experiments or by computational fluid dynamics. But, such approaches will require execution of a large number of experimentations (or computer simulations) and thus it takes high simulation time to generate the random wind field. Hence, in the present study, random wind field is simulated by numerically generating artificial wind force time-histories considering uncertainty in related parameters.

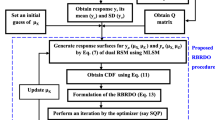
It is now well conceived that RDO under stochastic dynamic load becomes extensively onerous in context of computational time and hazards by conventional direct Monte Carlo simulation based approach [19, 20]. To circumvent this, use of response surface method (RSM) is quite popular [2]. The usual RSM yields an explicit equation for mean value of response as functions of input parameters. Once the explicit equation of response quantity under interest becomes available, the RDO problem can be easily cast and solved as one does for simple structural systems [13]. However, such single level RSM is not sufficient to capture the highly stochastic nature of extreme wind, as this approach does not focus on the performance dispersion values. In fact, under extremely uncertain wind load, the wind force time-history signatures vary even for the same set up of wind speed, wind incidence angle and other parameters of wind. Due to this reason, the record-to-record variation of wind force time-history cannot be considered using a single RSM [1]. In this regard, Datta et al. [9] adopted a dual RSM concept, where this variation time-history signatures are taken into account through another response surface, which is for standard deviation of response. By this approach, for the same set up of input parameters, a number of wind speed time-histories are generated. So, at each design of experiment (DOE) point, it will create two response surfaces, one for the mean response and another for the standard deviation (SD) of the response. It is quite clear that the application of single RSM in RDO may be erroneous as it does not consider the record-to-record variation of wind speed time-histories. However, work on Datta et al. [9] was confined for probabilistic parameters only and attains its limitation for UBB parameters. Thus, this present work is more general as it considers UBB parameters as well. In doing so, the CP-based RDO formulation is posed in dual RSM framework, which is not attempted earlier in the existing literature.

Thus, the unique contribution of this paper is to propose a new RDO formulation with UBB parameters under dual RSM, which is hinged on the concept of imposing the record-to-record variation of wind speed time-histories. The improvement by the proposed approach is elucidated by optimizing a steel telecommunication tower problem, and the results are compared with the existing formulations of CP.

2 Conventional CP Based RDO

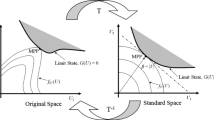
The concept of CP is first described with the help of Fig. 1. Let us suppose that, U₁ and U₂ are two UBB parameters which can be represented by a general ellipse defined by their ranges Ū₁ and Ū₂ shown in Fig. 1. Since, these have dimensions; it will be quite advantageous to transform the system in non-dimensional space. It is done by changing the scale of U_i^L (lower bound) to U_i^U (upper bound) to (− 1) (lower bound) to (+ 1) (upper bound). Thereby, the ellipse becomes a circle as shown in Fig. 2. Thus, by this normalization, the UBB parameters are transformed from U space to u space. It can be written that $U_i = \bar{U}_{\text{i}} + \left( {u_t + \Delta U_i } \right)$, where $\bar{U}_i = \frac{{\left( {U_i^L + U_i^U } \right)}}{2}$ and $\Delta U_i = \max \left( {\left| {U_i^U - \bar{U}} \right|,\left| {\bar{U} - U_i^L } \right|} \right)$ ${\overline{\text{U}}}_{\text{t}} = \frac{{\left( {U_i^L + U_i^U } \right)}}{2}$. By this operation, the variation of the interval variables will lie in the interval [− 1, 1].

Fig. 1

Convex ellipsoidal space

Fig. 2

Unit radius circle case

Now, the structure is said to be in reliable state if the constraint function g(u) < 0. On the other hand, g(u) > 0 indicates the failure of the structure. g(u) = 0 defines the critical condition or limiting state of the structures. These conditions are depicted in Fig. 3. The safety region and the failure region are indicated by yellow and blue fill, respectively, in Fig. 3. In this figure, η defines the safety of the structures. Higher the values of η, more will be the tolerance of the structures to uncertainty, and hence, more will be the robustness. Chen et al. [13] formulated robust optimization problem such as to make η more than a target value η_target (shown in Fig. 3). In this proposition, the original unit circle is allowed to increase in size whose radius depicts the uncertainty. η = 1 presents the case of highest variation of UBB parameters i.e. $\Delta U_i = 1.0$. η_target is generally taken as 1.0. But, by proper selection of design variables (DVs), if it becomes possible to achieve η > 1, the design is said to be more robust since it can endure substantial amount of undesirable variations which is unprecedented. But, in this case, for η < 1, the curve touches or becomes inside the circle which implies the failure of the system. At η = 1, the curve cuts the unit circle tangentially that implies the critical state of the structures.

Fig. 3

Concept of η

Chen et al. [13] proposed a two-step optimization process for the RDO. The main Optimization problem is to find the DVs X as,

$$ \begin{aligned} & {\text{find X such as to minimize}}\;f(X,U) \\ & {\text{such that}},g_j (X,U) \le 0,\forall j \in M,X \in \left[ {X^L ,X^U } \right] \\ \end{aligned} $$

(1)

A sub-optimization problem is defined at each update of X to find out the maximum deviation of UBB parameters U that the system can tolerate. This optimization formulation finds U, such as to,

$$ \begin{aligned} & {\text{minimize}}\;g_j (X,U),\forall j \in n \\ & {\text{such that}},n_j = \max \left( {\left| {u_1 } \right|,\left| {u_2 } \right|, \ldots ,\left| {u_m } \right|} \right) \ge \eta_{{\text{target}}} \\ \end{aligned} $$

(2)

The constraint function is minimized in the sub-optimization problem to find the most probable failure point or the set-up of U for which g(U) is just critical or becomes an active constraint.

3 Dual RSM

Let us suppose the response Y_a is to be considered by the RSM for the a-th wind force time-histories. Consider, u_i^(m) as the m-th observation of the i-th input variable, u_i, in the DOE space whereas Y_l^(m) is the output response of m-th DOE point under a-th wind force time histories. The relationship between the predicted response (Ŷ) and the input variables (U) can be expressed by the quadratic polynomial form as:

$$ \hat{Y} = \beta_0 + \sum_{i = 1}^n {\beta_i u_i } + \sum_{i = 1}^n {\sum_{j = 1}^n {\beta_{ij} u_i u_j } } $$

(3)

where, n is the total number of variables and u = [x z]. The parameters, β₀, β_i and β_ij are the unknown coefficients which are obtained by the least-squares method. Based on the obtained response values at all the DOE points, the relationship between structural response and input random variables can be put into the matrix form as follows:

$$ {\hat{\text{Y}}} = {\text{Q}}{{\upbeta }} $$

(4)

where Q is known as the design matrix. The unknown polynomial coefficient vector (β) is to be obtained by minimising an error, Δ_y, which is defined as:

$$\begin{aligned} \Delta _{\text{y}} & = \sum_{{\text{i}} = 1}^{\text{m}} {\left( {{\text{Y}}_{\text{i}} - {{\upbeta }}_0 - \sum_{{\text{i}} = 1}^{\text{n}} {{{\upbeta }}_{\text{i}} {{\text{u}}_{\text{i}}^{({\text{m}})}} } - \sum_{{\text{i}} = 1}^{\text{n}} {\sum_{{\text{j}} = 1}^{\text{n}} {{{\upbeta }}_{{\text{ij}}} {{\text{u}}_{\text{i}}^{({\text{m}})}} {{\text{u}}_{\text{j}}^{({\text{m}})}} } } } \right)^2 } \\ & = \left( {{\text{Y}} - {{\hat{\text{Y}}}}} \right)^{\text{T}} \left( {{\text{Y}} - {{\hat{\text{Y}}}}} \right) = \left( {{\text{Y}} - {\text{Q}}{{\upbeta }}} \right)^{\text{T}} \left( {{\text{Y}} - {\text{Q}}{{\upbeta }}} \right) \\ \end{aligned} $$

(5)

The least-squares estimate of β is then obtained as:

$$ {{\upbeta }} = \left[ {{\text{Q}}^{\text{T}} {\text{Q}}} \right]^{ - 1} {\text{Q}}^{\text{T}} {\text{Y}} $$

(6)

Once β is obtained by the Eq. (5), Ŷ can easily obtained for any set of input variables by using Eq. (3). Now stochasticity due to the wind analysis is obtained by using the wind force time-histories to consider the record-to-record variations. In case of the dual RSM, at first for each DOE point (each DOE point corresponds to a particular wind speed), a number of wind speed time-histories are generated. Then, the mean and SD of response are obtained for each DOE point. This process is to be repeated for all the DOE points (which include a set of different wind speeds). Due to this, two vectors, viz. a mean vector and a SD vector, of the desired responses ‘Ŷ’ are generated. Then the response surface for mean and SD are obtained for the considered responses as,

$$ \hat{Y}_{{\upmu }} = g_1 (U)\;{\text{and}}\;\hat{Y}_{{\upsigma }} = g_2 (U) $$

(7)

4 Generation of Wind Load

In general, the along-wind component of wind force acting at ith level at height z from the ground can be written as [9]:

$$ F_D \left( {z,t} \right) = \frac{1}{2}\rho \left[ {V(z,t)} \right]^2 C_D A_i $$

(8)

In above Eq. (8), A_i is the tributary area of the node under consideration. C_D is the drag coefficient, which is invariant over height. In the present study, the value of C_D is obtained from IS 875(III) (2015) [21] since the structure considered is regular in shape and size. It may be noted that under dynamic condition and due to various uncertainty effects the drag coefficient may vary. Thus, C_D is considered as a UBB parameter (see Table 2). The wind speed, V(z, t) is composed of time-invariant mean component $\bar{V}(z)$, and a fluctuating component v(t), known as gust. i.e.,

$$ V(z,t) = \overline{V}(z) + v(t). $$

(9)

The mean wind speed profile is expressed by the Power law [22] as:

$$ {\mathop V\limits^{\_\_}} \left( z \right) = V_G \left( {{z / {z_G }}} \right)^{1 / \varsigma } $$

(10)

where, V_G is the gradient wind speed, z_G is the gradient height, and ζ is the exponential coefficient. The values of z_G and ζ depend on ground surface roughness and terrain categories. z_G and ζ values are taken as 270 m and 7 as per ANSI (1982) [23] for terrain category 2 in the present study. In fact, these parameters are also uncertain with no definite distribution. Hence, in the present study these parameters are taken as UBB parameters. Their ranges are provided in Table 2. In the numerical study, z_G = 270 m and ζ = 7 have been considered.

In this study, the gust component is generated by using Kaimal’s PSDF [17] which can be expressed as:

$$ S_u (\Omega ,z) = {{50u_*^2 z} / {\left\{ {\pi \overline{V}(z)\left[ {1 + 50\left( {{{\left| \Omega \right|z} / {2\pi \overline{V}(z)}}} \right)} \right]^{5/3} } \right\}}} $$

(11)

where Ω(=2пf) is the frequency in rad/s, and f is in Hz. The shear velocity u_* is computed by logarithmic law of mean velocity as,

$$ u_* = {{\kappa {\mathop V\limits^{\_\_}} } / {\ln \left( {{z / {z_o }}} \right)}} $$

(12)

in which, κ is the von Karman constant, taken as 0.4, and z_o is the roughness length of the surface which depends on the surface properties only and can be taken as 0.01 for smooth surface.

It is important to note here that for telecommunication tower like structures, the effect of vortex shedding must have to be considered in addition to the along-wind effect. The time-varying vortex shedding force can be expressed as [9],

$$ F_L \left( {z,t} \right) = \frac{1}{2}\rho \left[ {V\left( {z,t} \right)} \right]^2 C_L \left( {z,t} \right)A_i $$

(13)

In above Eq. (10), the stochastic lift force co-efficient, $C_L \left( {z,t} \right)$ is obtained by weighted aptitude wave superposition technique with the PSDF of $C_L \left( {z,t} \right)$ as [24],

$$ {{S_{C_L } \left( {z,\omega } \right)} / {\sigma_{C_L }^2 \left( z \right) = \left\{ {{{\left( {{1 / {\omega_0 }}} \right)} / {2\sqrt {\pi } \beta \left( z \right)}}} \right\}}}exp\left\{ { - {{\left[ {1 - {\omega / {\omega_0 }}} \right]^2 } / {\beta^2 \left( z \right)}}} \right\} $$

(14)

where $\omega_0 = 2\pi f_0$ is the vortex shedding frequency and $f_0 = S_t {{{\text{V}}\left( {\text{z}} \right)} / {D\left( Z \right)}}$. S_t is the Strouhal number, assumed as 0.20 (for D × V < 6 m²/s) and 0.25 (for D × V ≥ 6 m²/s) [21]. β(z) is the band-width parameter of the PSDF assumed as 0.25. $\sigma_{C_L } \left( z \right)$ is the standard deviation of C_L which is assumed as invariant over height and taken as 0.4. D(z) is the outside width of the tower at height z from the ground level. Finally, the along-wind force and across-wind force are combined as,

$$ F\left( {z,t} \right) = \sqrt {{\left\{ {F_D \left( {z,t} \right)^2 + F_L \left( {z,t} \right)^2 } \right\}}} $$

(15)

Note that As per Eq. (8), the along-wind component of wind force depends on the drag coefficient (C_D) and from Eq. (13) the across-wind component depends upon the lift force coefficient (C_L). The C_D values are more near the ground surface and decrease as the elevation increases; but, the C_L values increase as the elevation increases. Accordingly, for realizing drag forces and lift forces by Eqs. (8) and (13), at first, using the uniform design method, the values of C_D and C_L are realized and sorted in descending and ascending order, respectively. Then, these sorted values of C_D and C_L are assigned with increasing heights. As a result, at higher elevation, lower C_D and higher C_L got assigned in the design of DOE, and vice-versa. Since, the whole RDO approach is based on these DOE, this issue is taken care of right at the wind field simulation stage.

It may be further noted here that overturning moment may be also checked to ensure stability and design of foundations. Though, in this study, dimensioning of main members due to stress constraints under extremely uncertain wind load is of main concern, the methodology can be easily applied for checking stability of the tower against overturning. In such a case, in addition to tensile stress and compressive stress in tower members, the overturning moment should be also included as one of the response quantity. It will vary over time and should be obtained as, $M\left( t \right) = \sum_i {F_i \left( t \right)} \times z_i$ where, $F_i$ is the wind force at i-th elevation from ground level at height $z_i$ and obtained through Eq. (15).

5 Dual RSM Based Proposed RDO

As mentioned, the conventional CP based RDO is one of the most viable alternative when dealing with the uncertain parameters. But, one of the important disadvantages for the conventional CP based approach of RDO is that, it is proven incompetent when it comes to consider the random fluctuations in case of stochastic dynamic loadings such as earthquake load, blast load, wind load etc. as the approach only consider only the mean in terms of constraint function. Thus, the proposed dual RSM based modified CP approach may seem to be a potential choice as it not only takes up the record to record variation of stochastic load, but also reduces the constraint boundary. The proposed approach considers the mean as well as the standard deviation in the constraint function and is given as follows:

$$ \begin{aligned} & {\text{Find}}\;{\bf{X}}\;{\text{such}}\;{\text{as}}\;{\text{to}}, \\ & {\text{Minimize}},f(X,U) \\ & {\text{Subject}}\;{\text{to}},\begin{array}{*{20}l} {\overline{g_j }(X,U) + k*\Delta \overline{g_j }(X,U) \le 0,} \hfill & {{\text{if}}\;\overline{g_j }(X,U) \le 0} \hfill \\ {\overline{g_j }(X,U) - k*\Delta \overline{g_j }(X,U) \le 0,} \hfill & {{\text{if}}\;\overline{g_j }(X,U) \ge 0} \hfill \\ \end{array} ,j = 1,2, \ldots M,X_L \le X + \Delta X \le X_U \\ \end{aligned} $$

(16)

where $\overline{g_j }(X,U)$ and $\Delta \overline{g_j }(X,U)$ are the RS meta-models of mean and standard deviation of constraints, respectively and k is the penalty factor.

$$ \begin{aligned} & {\text{Minimize}},a_j = \overline{g_j }(X,U),\quad j = 1,2, \ldots {\text{M}}, \\ & {\text{Such}}\;{\text{that}},\eta_j = \max \left( {\left| {u_1 } \right|,\left| {u_2 } \right|, \ldots ,\left| {u_n } \right|} \right) \ge \eta_{{\text{target}}} \\ \end{aligned} $$

(17)

6 Numerical Study

A 80 m tall steel telecommunication tower is modeled to analyze the efficiency of the present RDO. The tower is made up of angle sections, and square in plan. The tower consists of 16 panels at each face. The top five panels are straight with panel-height of 2 m. Thereafter, the batter starts at a slope of 6.85 degree from the vertical. The supports are fixed. The telecommunication tower carries the weight of the antennas and equipment for the functioning of the telecom services. These loads are equally shared between the topmost nodes. The modeling and analysis of the tower are done in STAAD.Pro software. A linear elastic analysis is performed.

To ensure stability, it is customary to design the leg members such that the lower legs have greater thickness and widths compared to upper leg members. To effectively economize the tower, the tower members are grouped in five categories, shown in Table 1 and Fig. 4. A deterministic design is first carried out following IS:875(III) (2015) considering wind load along with gust. The optimal sections obtained are shown in Table 1. The modulus of elasticity (E) and density ($\rho$) of the steel are taken as 2 × 10⁵ N/mm² and 7850 kg/m³, respectively. The deterministic optimization is posed to minimize material cost of tower subjected to stress constraints.

Table 1 Geometry and properties of telecommunication tower

Table 2 Details of the UBB parameters

Fig. 4

Telecommunication tower members: a Group 1, b Group 2, c Group 3, d Group 4, and e Group 5

The major impact on the cost of a telecommunication tower is weight of the tower. Due to this significance of the weight, the objective function is chosen as to minimize the weight of the tower (W):

$$ W = \sum {\rho .L_i .A_i } $$

(18)

where $\rho$ the unit weight of steel, $L_i$ and $A_i$ is the length and area of the i-th member of the tower, respectively. The constraints are framed to limit the maximum tensile and compressive stress in each group within allowable tensile stress or compressive stress. The allowable stresses are calculated using IS: 802 (I) (1992) [25]. The maximum slenderness ratios of tower members are also constrained by allowable slenderness ratio as per IS: 802 (I) (1992) [25]. The design variables are the widths and thicknesses of angle sections of the five groups (i.e. total 10 design variables for the five groups). All the design variables are taken as UBB parameters. The basic wind speed, dead weight of antenna, etc., C_D, C_L, z_G, ζ are all taken as UBB parameters. The dead weight of antenna and associated attachments are taken as UBB parameters. This is taken uncertain as these antennas may be changed in future based on availability of more technologically advanced systems, which may have different weights. ${\mathop V\limits^{\_\_}}$, that is the time-invariant component of wind speed at 10 m elevation, is taken as UBB parameter. ${\mathop V\limits^{\_\_}} \left( z \right)$ can be found in Eq. (9).The ranges and the nominal values of the UBB parameters are listed in Table 2.

Now, the DOE space is constituted by the UD scheme [26] with these UBB parameters. To consider the record-to-record variation of stochastic wind load, a suite of 10 wind load time-histories is generated at each set up of the DOE points. The variations of the mean along wind drag force and lift force over height are presented in Fig. 5. Both the forces increase over height. Drag force is observed to be more than the lift force here.

Fig. 5

Variation of along and across wind force component for varying height of the tower

The response quantities (maximum tensile stresses and compressive stresses for all the groups here) are obtained for these wind load time-histories at each DOE point using linear elastic time-history analysis in STAAD.Pro. Mean and SD of each response quantity at each DOE point are then obtained. These data are in-turn used to generate the dual response surfaces ($\hat{Y}_\mu$ and $\hat{Y}_\sigma$) for each response quantity through Eq. (7). The RDO is posed using Eqs. (16) and (17) using the CP and solved by the sequential quadratic programming method in MATLAB.

The RDO results by the formulation of CP [13] and the proposed RDO over the conventional formulation of [13] are presented in Figs. 6 and 7 for varying range of uncertainty level of the UBB parameters. Value of η is considered as 1.0 to develop these figures. Figure 6 is plotted by varying all the UBB parameters, simultaneously; whereas, in Fig. 7, the optimal weight is plotted for increasing uncertainty range of wind speed only. These plots are so done to envisage the effect of uncertainty of wind with respect to combined effect of uncertainty in all the UBB parameters. Here, uncertainty range is defined by $\Delta U_i$ of Sect. 2. By comparing Figs. 6 and 7, it can be observed that the increase in robust optimal weight due to all UBB parameters uncertainty with respect to uncertainty due to wind is only 12% to 20%. Thus, wind speed constitutes the major source of uncertainty in this system.

Fig. 6

Optimal weight of the tower for varying dispersion of UBB parameters

Fig. 7

Optimal weight of the tower for varying dispersion of wind speed

In Fig. 7, the robust optimal weight is further plotted for η equals to 1.0, 2.0, and 3.0. As expected, that the highest values of optimal weights are required for η = 3.0, that is when the system demands more tolerance to uncertainty. The safety circle of Fig. 3 in such a case can grow to a larger extent without failure. However, even though there is a trend of optimal weight increment for higher η, in the present case, the difference between the RDO results for η equals to 1.0, 2.0, and 3.0, is marginal, especially for the proposed CP case. This may be due to the fact, that higher growing of the safety circle than that achieved at η equals to 1.0, is not possible, owing to the random fluctuations of wind load. In fact, the safety circle cannot grow indefinitely in size denoting an indefinite tolerance to uncertainty. This issue has been correctly identified through the proposed dual RSM-based CP formulation, which considers more detailed uncertainty description of wind load time-histories.

It can be observed from Figs. 6, 7 and 8 that the proposed RDO approach requires lesser optimal weight than the existing approaches in the most cases. However, when uncertainty range is higher, the proposed RDO approach requires marginally higher optimal weight (1–5%) than the existing approaches. The higher optimal weight requirement may be due to consideration of detailed uncertainty description of wind load through dual RSM to make the system insensitive to undesirable variation of UBB parameters.

Fig. 8

Optimal weight of the tower for varying η

7 Conclusions

An improved RDO formulation with UBB parameter is proposed using CP, where the robustness of the system is imposed through a dual RSM-based metamodelling approach. The improvement by the proposed approach is elucidated by optimizing weight of a telecommunication tower subjected to axial stress and slenderness ratio constraints. It has been observed that even at the same set-up of hazard parameters, wind speed time-histories vary significantly due to the effect of randomness in the wind field. In such situations, the conventional single RSM-based approach is inadequate as it considers only one sample of wind speed time-history, neglecting record-to-record variation. On the other hand, sufficient wind speed time-history records are taken in dual RSM for capturing the variation of wind speed in a more detailed way. As a result, the proposed RDO approach yields optimal solution with a detailed consideration of wind uncertainty. The proposed approach yields lesser optimal weight in most of the cases. Thus, the proposed approach is cost-economic as well. In some cases, the proposed approach demands marginally higher optimal weight than the usual CP-based RDO. However, irrespective of whether the proposed RDO will yield lesser optimal weight or marginally higher optimal weight, the main merit of the proposed approach is incorporation of uncertainty in a more detailed way through UBB parameter modeling and the convex programming in the dual RSM framework. The proposed approach yields optimal results in a computationally efficient way. The proposed RDO, though have been presently applied on wind-excited steel tower, can be applied to other structures under various other uncertain loads, as well. This is under consideration at this stage.