Universe with Power Law Expansion

Abstract

This paper presents Inflationary scenarios in $f(R, T)$ gravity using power law, with scalar curvature $R$ and energy momentum tensor trace $T$. Power law expansion of scale factor is used to determine precise solutions to field equations (FE) of Bianchi type-I (BT-I) model. Expansion rate of universe changes with time, fluctuating between an infinite pace at starting and a fixed rate at later epochs. The current model’s energy conditions have been established, and the results show that it is consistent with the data. The strong energy condition (SEC) is failed which implies the accelerated phase of the universe. The model’s geometrical and the physical behaviours have been discussed.

1 Introduction

Notion of inflation was established in the study of the very early cosmos to solve numerous cosmological problems such as flatness problem, entropy problem, horizon problem, monopole problem, and so on. Even though there are numerous competing solutions to the above-mentioned difficulties of hot Big Bang (BB) model, we don’t possess a fully functional inflationary model (IM). If an IM can reheat the cosmos, it is termed a feasible IM. When the inflationary phase has finished, reheating begins, raising the temperature of a very cold cosmos, making this period extremely important for our universe. No feasible model could tackle the challenges of hot BB model and the graceful exit issue of old IM until 1982.

An IM was proposed by Linde [1] known as the “New” IM. This IM provided answers to the difficulties of a hot BB and elegant exit. In contrast to the old IM, which showed the cosmos to be inhomogeneous, the new IM depicts it as homogeneous. The Cosmic Microwave Background power spectrum has recently been observed to be identical to the order of $1{0}^{-5}$ [2, 3] demonstrating greater success for the new IM than the old IM. Many model observations show that the cosmos is presently going through a period of accelerated expansion. Following the discovery that cosmic expansion is speeding up [4, 5] subsequent Balloon-born experiments such as Boomergang [6] and Maxima [7] have identified the anisotropic spectrum of the CMBR observation of a flat universe. This evidence suggests that present mainstream model of cosmology is influenced by dark energy, an unclustered fluid with a huge -ve pressure that is reason for the universe’s expansion. Spergel et al. [8] also discovered that the cosmos is spatially flat, which accounts for 70% of dark energy. Alternative theories to be found such as $f(R)$ gravity [9,10,11,12,13,14] and $f(T)$ gravity [15, 16]. The Einstein-Hilbert (E–H) action has demonstrated the modifications of general relativity. Harko et al. [17] proved the greatest continuation of E–H action by adopting gravitational Lagrangian in the form of an arbitrary function of the $R$ and matter Lagrangian$Lm$. $f(R,T)$ gravity is a generalised form of $f(R)$ gravity [17]. Trace dependency must be caused by exotic imperfect fluid or quantum processes. They showed three different variations of arbitrary function$f(R,T)$. Ibotombi et al. [18, 19] provided power law and exponential law based on bulk viscous cosmological models in Lyra’s manifold and scale covariant theory of gravity. Adhav [20] studied the anisotropic perfect fluid cosmological model within the context of this theory and Ahmed et al. [21] explored the BT-V model for particular form$f(R,T)=f1(R)+f2(T)$, where they took cosmological constant $\Lambda$ as a function of $T$. Sahoo et al. [22] investigated Locally Rotationally Symmetric BT-I model in the context of this theory with variable $\Lambda$(T) and got many surprising solutions. Sahoo et al. [23] examined the physical and geometrical solutions to the variable deceleration parameter in anisotropic cosmological models under this theory. Singh et al. [24] studied power law inflation on Lyra’s manifold with an anisotropic fluid and discovered that cosmos is non-isotropic at the beginning of universe and becomes isotropic afterwards. Singh et al. [25] examined the dynamical properties of non-isotropic dark energy in gravity theory and discovered that values of matter and dark energy densities ${\Omega }_{m}$ and ${\Omega }_{\Lambda }$ are in complete conciliation with WMAP statistics over the previous five years. For the very first time in this gravity theory, S. Bhattacharjee et al. [26] offered a modelling of inflationary scenarios. Singh [27] looked into the theory in a 5D universe and established that dark energy is important in the Kaluza–Klein world as wet dark fluid, as well as the fact that anisotropic and new isotropic models of the Kaluza–Klein universe can be developed. Another work by Singh [28] examined dark energy in the context of this modified theory from Locally Rotationally Symmetric BT-I metric.

Current work was motivated by the previous work in order to investigate power law inflation in $f(R,T)$ theory and organised as follows: We derived FE of this theory in Sect. 2. In Sect. 3 model with power law has been discussed. Energy conditions and model’s observational parameters with power law are then discussed. The energy conditions and other model observational parameters are then discussed in Sect. 4. We examine our findings and concluded in Sect. 5.

1.1 $f(R,T)$Gravity and Its FE

Anisotropic Locally Rotationally Symmetric BT-I model is defined by the metric as in an orthogonal frame.

$${\text{d}}s^{2} = {\text{d}}t^{2} - A^{2} {\text{d}}x^{2} - B^{2} \left( {{\text{d}}y^{2} + {\text{d}}z^{2} } \right)$$

(1)

The cosmic scale factors are denoted by $A$ and $B$. This metric exhibits symmetry about $z$-axis and has a symmetric plane in conjunction with $xy$-plane. Tensor of matter’s energy momentum is given as

$$T_{j}^{i} = {\text{diagonal}}\left[ {\rho , - \rho_{x} , - \rho_{y} , - \rho_{z} } \right].$$

(2)

And can be parametrized as

$$\begin{aligned} T_{j}^{i} & = {\text{diagonal}}\left[ {\rho , - p_{x} , - p_{y} , - p_{z} } \right] \\ & = {\text{diagonal}}\left[ {1, - \omega_{x} , - \omega_{y} , - \omega_{z} } \right]\rho \\ & = {\text{diagonal}}\left[ {1, - \omega , - \left( {\omega + \delta } \right), - \left( {\omega + \delta } \right)} \right]\rho \\ \end{aligned}$$

(3)

Energy density is denoted by$\rho$, and the symbols $p_{x}$. , $p_{y}$, and $p_{z}$ respectively, stand for pressures across the $x$, $y,$. and $z$ axes. $\omega_{x}$, $\omega_{y}$, and $\omega_{z} ,$ respectively, are fluid’s directional EoS parameters along $x$, $y$, and $z$ axes. By establishing $\omega_{x} = \omega_{y} = \omega_{z}$, we can now parameterize the deviation from isotropy. The divergence from $\omega$ on the $y$ and $z$ axes is the skewness term $\delta$, which is introduced after that. $\delta$ and $\omega$ ain’t necessary constants in this case, and they can be considered as functions of $t$ (cosmic time). FE of this theory are determined using E–H variational principle. For this theory, Harko et al. [17] utilise subsequent action

$$\begin{aligned} S & = \frac{1}{16\pi }\smallint f(R,T)\sqrt { - g} d^{4} x + \smallint L_{m} \sqrt { - g} d^{4} x \\ & = \smallint \sqrt { - g} \left( {\frac{1}{16}f\left( {R,T} \right) + L_{m} } \right)d^{4} x \\ \end{aligned}$$

(4)

with $T$ as trace of energy momentum tensor $T_{ij}$, $R$ as scalar curvature, $L_{m}$ is matter Lagrangian density and $g$ denotes metric determinant. Taking $f\left( {R,T} \right) = R + 2f\left( T \right)$, we vary action into Eq. (4) w.r.t $g_{ij}$, and obtain the FE of the theory as

$$R_{ij} - \frac{1}{2}g_{ij} R = 8\pi GT_{ij} + 2f_{T} T_{ij} + \left[ {2pf_{T} + f\left( T \right)} \right]g_{ij}$$

(5)

here $G$ denotes gravitational constant, $R_{ij}$ is Ricci scalar, and $g_{ij} u^{i} u^{j} = 1$. We let function $f\left( T \right) = \mu T$ with $\mu$ as constant, then for metric (1), obtain the FE as

$$\left( {\frac{{\dot{B}}}{B}} \right)^{2} + 2\left( {\frac{{\dot{A}\dot{B}}}{AB}} \right) = - \rho \left[ {8\pi G + 2\mu + 1 - 3\omega - 2\delta } \right] - 2\mu p$$

(6)

$$\left( {\frac{{\dot{B}}}{B}} \right)^{2} + 2\frac{{\ddot{B}}}{B} = \rho \left[ {\left( {8\pi G + 2\mu } \right)\left( \omega \right) - \left( {1 - 3\omega - 2\delta } \right)} \right] - 2\mu p$$

(7)

$$\frac{{\ddot{A}}}{A} + \frac{{\ddot{B}}}{B} + \frac{{\dot{A}\dot{B}}}{AB} = \rho \left[ {\left( {8\pi G + 2\mu } \right)\left( {\omega + \delta } \right) - \left( {1 - 3\omega - 2\delta } \right)} \right] - 2\mu p$$

(8)

here the overhead indicates the differentiation w.r.t $t$. Spatial volume $\left( V \right)$ can be calculated as follows:

$$\begin{aligned} V & = a^{3} = AB^{2} \\ a & = (AB^{2} )^{\frac{1}{3}} \\ \end{aligned}$$

(9)

$a$ stands for the universe’s scalar factor.

The following formula is used to compute average Hubble constant or parameter $\left( H \right)$:

$$H = \frac{{\dot{a}}}{a} = \frac{1}{3}\left( {\frac{{\dot{A}}}{A} + 2\frac{{\dot{B}}}{B}} \right)$$

(10)

In x, y, and z axes’ directions, directional H can be described as

$$\begin{aligned} H_{x} & = \frac{{\dot{A}}}{A}, \\ H_{y} & = H_{z} = \frac{{\dot{B}}}{B} \\ \end{aligned}$$

(11)

The shear term $\sigma^{2}$ and the expansion term $\theta$ are provided by

$$\theta = \frac{{\dot{A}}}{A} + 2\frac{{\dot{B}}}{B}$$

(12)

and

$$\sigma^{2} = \frac{1}{2}\left[ {\Sigma H_{i}^{2} - 3H^{2} } \right]$$

(13)

When we deduct (7) from (8), we obtain

$$\frac{{\text{d}}}{{{\text{d}}t}}\left( {\frac{{\dot{A}}}{A} - \frac{{\dot{B}}}{B}} \right) + \left( {\frac{{\dot{A}}}{A} - \frac{{\dot{B}}}{B}} \right)\frac{{\dot{V}}}{V} = - \left( {8\pi G + 2\mu } \right)\delta \rho$$

(14)

When we integrate the equation above, we get

$$\frac{{\dot{A}}}{A} - \frac{{\dot{B}}}{B} = \frac{\lambda }{V}\exp \smallint \frac{{\left( {8\pi G + 2\mu } \right)}}{{\left( {\frac{{\dot{B}}}{B} - \frac{{\dot{A}}}{A}} \right)}}\rho \delta {\text{d}}t$$

(15)

where the integrating constant is $\lambda$. We assume the following form to determine the exact solution to Eq. (15):

$$\frac{\rho \delta }{{\frac{{\dot{B}}}{B} - \frac{{\dot{A}}}{A}}} = \frac{1}{t}$$

(16)

from (15) and (16), we achieve

$$\frac{{\dot{A}}}{A} - \frac{{\dot{B}}}{B} = \frac{\lambda }{V}t^{{\left( {8\pi G + 2\mu } \right)}}$$

(17)

2 Model with Power Law

To thoroughly solve FE of $f\left( {R,T} \right)$, we assumed the following Power Law. $a = a_{0} t^{n}$ so using value of $a$ in (9), we get

$$\begin{aligned} V & = a^{3} \\ & = AB^{2} \\ & = a_{0}^{3} t^{3n} \\ \end{aligned}$$

(18)

where $a_{0} > 0$ and $n \ge 0$ are constants. Using (18) in (17) and on integrating, it gives

$$A = BC_{1} \exp \left[ {\frac{{\lambda t^{{\left( {8\pi G + 2\mu - 3n + 1} \right)}} }}{{a_{0}^{3} \left( {8\pi + 2\mu - 3n + 1} \right)}}} \right]$$

(19)

where integration constant is $C_{1}$. From above expression of $A$ and $B$, we see that their rates of expansion are different in the different directions. Using (18) and (19), we now get $A$ and $B$ as follows:

$$A = a_{0} t^{n} C_{1}^{\frac{2}{3}} \exp \left[ {\frac{{2\lambda t^{{\left( {8\pi G + 2\mu - 3n + 1} \right)}} }}{{3a_{0}^{3} \left( {8\pi G + 2\mu - 3n + 1} \right)}}} \right]$$

(20)

$$B = \frac{{a_{0} t^{n} }}{{C_{1}^{\frac{1}{3}} }}\exp \left[ {\frac{{ - \lambda t^{{\left( {8\pi G + 2\mu - 3n + 1} \right)}} }}{{3a_{0}^{3} \left( {8\pi G + 2\mu - 3n + 1} \right)}}} \right]$$

(21)

here integration constant is $C_{1}$. The following are the directional H for this model:

$$H_{x} = \frac{{\dot{A}}}{A}\,{\text{and}}\,H_{y} = \frac{{\dot{B}}}{B}.$$

On solving we get,

$$H_{x} = \frac{n}{t} + \frac{{2\lambda t^{{\left( {8\pi G + 2\mu - 3n + 1} \right)}} }}{{3a_{0}^{3} }}$$

(22)

and

$$H_{y} = \frac{n}{t} - \frac{{\lambda t^{{\left( {8\pi G + 2\mu - 3n + 1} \right)}} }}{{3a_{0}^{3} }}$$

(23)

$$\begin{aligned} H & = \frac{1}{3}\left( {\frac{{\dot{A}}}{A} + \frac{{2\dot{B}}}{B}} \right) \\ & = \frac{1}{3}\left[ {H_{x} + 2H_{y} } \right] \\ \end{aligned}$$

(24)

$$= \frac{n}{t}$$

(25)

For $n > 0$, $a > 0$, $H$ remains positive. This demonstrates that universe is expanding as it evolves. This observation is in accordance with latest observational data. The scalar expansion is denoted by the symbol $\theta$ where $\theta = 3H$. So,

$$\begin{aligned} \theta & = \left( {\frac{{\dot{A}}}{A} + \frac{{2\dot{B}}}{B}} \right) \\ & = \frac{3n}{t} \\ \end{aligned}$$

(26)

It suggests that in the beginning, the universe expands at an unlimited rate and then expands and returns into the phase of initial singularity in later periods. The shear scalar $\sigma^{2}$ is written like this:

$$\begin{aligned} \sigma^{2} & = \frac{1}{2}\left[ {\Sigma H_{i}^{2} - 3H^{2} } \right] \\ & = \frac{1}{2}\left[ {H_{x}^{2} + 2H_{y}^{2} - 3H^{2} } \right] \\ \end{aligned}$$

(27)

Now in our model we are using the condition,

$$\omega + \delta = 0$$

(28)

Now using above condition and Eq. (22) and (23) in (6), (7), and (8), we get

$$\rho = \frac{ - 1}{{\left( {8\pi G + 2\mu } \right)}}\left[ {\frac{2n}{{t^{2} }} - \frac{{\lambda t^{{\left( {8\pi G + 2\mu - 3n - 1} \right)}} \left( {8\pi G + 2\mu } \right)}}{{3a_{0}^{3} }} - 6\left( {\frac{{\lambda t^{{\left( {8\pi G + 2\mu - 3n} \right)}} }}{{3a_{0}^{3} }}} \right)^{2} } \right]$$

(29)

$$p = \frac{ - 1}{{8\pi G + 2\mu }}\left[ {\frac{{\lambda t^{{\left( {8\pi G + 2\mu - 3n - 1} \right)}} \left[ {9n + 3\left( {8\pi G + 2\mu - 3n} \right)} \right]}}{{3a_{0}^{3} }}} \right]$$

(30)

Now using the relations of equation of state, $\omega = \frac{p}{\rho }$ using this on dividing $p$ by $\rho$ we get our $\omega$ as

$$\omega = \frac{{\left[ {\frac{{\lambda t^{{\left( {8\pi G + 2\mu - 3n - 1} \right)}} \left[ {9n + 3\left( {8\pi G + 2\mu - 3n} \right)} \right]}}{{3a_{0}^{3} }}} \right]}}{{\left[ {\frac{2n}{{t^{2} }} - \frac{{\lambda t^{{\left( {8\pi G + 2\mu - 3n - 1} \right)}} \left( {8\pi G + 2\mu } \right)}}{{3a_{0}^{3} }} - 6\left( {\frac{{\lambda t^{{\left( {8\pi G + 2\mu - 3n} \right)}} }}{{3a_{0}^{3} }}} \right)^{2} } \right]}}$$

(31)

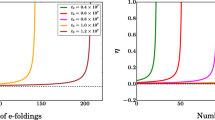
From this mathematical expression, we see that plot of $\omega$ shifts from +ve quadrant to −ve quadrant. Thus shifting from deceleration to acceleration phase of universe is witnessed in this model. There are numerous options for obtaining values for $a_{0}$, $\lambda$, $\mu$, and $n$. Finding suitable values for these parameters is all that is required to develop physically viable cosmological models. In Fig. 1, time variation of directional parameters are plotted and are decreasing functions of time in positive domain. Plot of energy density versus time is displayed in Fig. 2 and is decreasing as the universe evolves. Pressure $\left( p \right)$ with time is shown in Fig. 3 and is always negative which implies universe’s expansion. We see plot of EOS parameter against time in Fig. 4 and there is the phase transition of deceleration to acceleration.

Fig. 1

Time variation of $H_{x}$, $H_{y} ,$ and $H$ for $n = 0.5$, $\lambda = 1$, $\mu = 0.01$, $8\pi G = 0.5$,$a_{0} = 0.9$

Fig. 2

Time ($t$) versus Density ($\rho$) for $n = 0.5$, $\lambda = 1$, $\mu = 0.1$, $8\pi G = 0.1, a_{0} = 0.8$

Fig. 3

Time ($t$) versus Pressure ($p$) for $n = 0.5$, $\lambda = 1$, $\mu = 0.01$, $8\pi G = 0.5$, $a_{0} = 0.9$

Fig. 4

EOS Parameter ($\omega$) versus time ($t$) for $n = 0.5$, $\lambda = 1$, $\mu = 0.01$, $8\pi G = 0.5$, $a_{0} = 0.9$

3 Energy Conditions and Some Observational Parameters

$a\left( t \right) = \frac{1}{1 + z}$ is the observational setup, and the time-redshift relationship is stated as

$$t = \frac{n}{\alpha }W\left[ {\frac{\alpha }{n}\left( {\frac{1}{{a_{0} \left( {1 + z} \right)}}} \right)^{{^{\frac{1}{n}} }} } \right]$$

(32)

The Lambert W function, commonly called the product logarithm or omega function, is denoted by W. Using the above relationship, Redshift can be used to represent the parameters of the derived model. This kind of relationship is useful for putting the model to the test with real-world data. In general relativity, energy conditions are classified into four types: weak (WEC), null (NEC), strong (SEC), and dominant (DEC) and respectively defined by

$${\text{NEC}} \Leftarrow \rho + p \ge 0$$

(33)

$${\text{WEC}} \Leftarrow {\text{NEC }}\;{\text{and}}\;\rho \ge 0$$

(34)

$${\text{SEC}} \Leftarrow \rho + 3p \ge 0$$

(35)

$${\text{DEC}} \Leftarrow \rho - p \ge 0$$

(36)

The density remains positive, as shown in Fig. 2 at both early and late times. NEC $> 0$, WEK $> 0$, DEC $> 0,$ and SEC $< 0$ were found in Figs. 5, 6, and 7. SEC is failed, whereas NEC, DEC, and WEC are all fulfilled.

Fig. 5

3D plot of EC ($\rho + p$) versus time ($t$) for $n = 0.5$, $\lambda = 1$, $\mu = 0.1$, $8\pi G = 0.1$, $a_{0} = 0.15$

Fig. 6

3D plot of EC ($\rho + 3p$) versus time ($t$) for $n = 0.5$, $\lambda = 1$, $\mu = 0.1$, $8\pi G = 0.1$, $a_{0} = 0.2$

Fig. 7

3D plot of EC ($\rho - p$) versus time ($t$) for $n = 0.5$, $\lambda = 1$, $8\pi G = 0.1,$ $\mu = 0.1$, $a_{0} = 0.15$

4 Conclusion

We explored a generalised method of finding the exact solutions of Locally Rotationally Symmetric BT-I space time in this theory by using power law cosmology. Here, we assume $f\left( {R,T} \right) = 2\mu T + R$. In figures, energy density of universe is decreasing as ages of universe progress, and it demonstrates a positive condition that favours observation. Pressure is always negative. In Figs. 1 and 2, the parameters $p$ and $\rho$ becomes infinite at $t \to 0$ which suggests that universe starts from Big Bang and these parameters becomes extremely small at $t \to \infty$ which are consistent with observations. The derived model shows the characteristics of dark energy model as $\omega$ approaches to $- 1$ with the evolution of time which is in agreement with present universe that is assumed to be dominated by dark energy. WEC, SEC, DEC, and NEC of model are found to be satisfied. The present model may be able to highlight behaviours of universe from the anisotropic behaviours at early universe to accelerated expansion at late epoch. Although this model is simple, this investigation may lead to the cosmologists for further research in modified cosmology.