Abstract
The notion of path connectedness is more intuitive than connectedness. It appears before connectedness, even in history. Motivated by that, we start this chapter with path connectedness and its relationship with continuity; through which we deduce the Intermediate Value Theorem. Then we discuss connectedness and its characterizations, followed by a section on components; which provides insights into connected components and path components. Finally, we present some miscellaneous topics such as local connectedness, quasi-components, and totally disconnected spaces.
Access provided by Autonomous University of Puebla. Download chapter PDF
6.1 Path Connectedness
Path connectedness is natural for subsets of \(\mathbb {R}^m.\) Analogously, it can be extended to arbitrary metric spaces. First, we introduce the notion of a path.
Definition 6.1
Let X be a metric space and \(x,y\in X.\) A path from x to y, in X, is defined to be the range of a continuous function \(f:[0,1]\longrightarrow X\) such that \(f(0)=x\) and \(f(1)=y.\)
Therefore, a subset \(\gamma \) of X is said to be a path in X if there exists a continuous function \(f:[0,1]\longrightarrow X\) with range \(\gamma .\) Alternate terms for path are curve and arc.
Definition 6.2
A metric space X is said to be path connected if any two points inside X can be joined by a curve, inside X.
Further a nonempty subset S of a metric space X is said to be path connected if it is a path connected subspace of X.
Examples 6.3
Let X be a metric space. The following are immediate:
-
(a)
Every singleton subset of X is path connected.
-
(b)
Every curve in X is path connected.
-
(c)
Every open ball in \(\mathbb {R}^2\) is path connected.
-
(d)
If A and B are non-disjoint path connected subsets of X, then so is \(A\cup B.\)
Recall that a subset I of \(\mathbb {R}\) is defined to be an intervalif I contains all reals between any two points of I (see Definition 1.1).
Proposition 6.4
Every nonempty interval is path connected.
Proof
Let I be a nonempty interval and \(a,b\in I.\) Define \(g:[0,1]\longrightarrow I\) as
Then g is path in I from a to b. Hence, I is path connected. \(\square \)
Remarks 6.5
-
(a)
Unless specified, all the sets of this chapter will be taken as nonempty subsets of an arbitrary metric space.
-
(b)
If A and B are disjoint sets, we shall write
 instead of \(A\bigcup B,\) which would intrinsically convey that the sets A and B are disjoint.
instead of \(A\bigcup B,\) which would intrinsically convey that the sets A and B are disjoint. -
(c)
It is a standard practice to take arbitrary compact intervals in Definition 6.1, instead of \([0,1].\) Due to the natural bijection between any two non-degenerate compact intervals, our choice of the unit interval has no loss of generality.
The following lemma opens up a world of abstraction.
Lemma 6.6
Let I be an interval. Then I is not a disjoint union of two nonempty sets, closed in I.
Proof
Suppose  for some nonempty disjoint sets A and B, closed in I. Pick any \(a\in A\) and \(b\in B.\) Without loss of generality, suppose that \(a<b.\)
for some nonempty disjoint sets A and B, closed in I. Pick any \(a\in A\) and \(b\in B.\) Without loss of generality, suppose that \(a<b.\)
Then \(A_1:=A\cap [a,b]\) and \(B_1:=B\cap [a,b]\) are nonempty disjoint sets, closed in \([a,b]\) such that  . Let \(c:=\sup A_1.\) The definition of c and the fact that
. Let \(c:=\sup A_1.\) The definition of c and the fact that  is an interval implies that
is an interval implies that
Therefore, c is an adherent point of both \(A_1\) and \(B_1,\) which are closed in \([a,b].\) Also, \(c\in [a,b].\) Hence, \(c\in A_1\cap B_1=\emptyset ,\) a contradiction. \(\square \)
Theorem 6.7
Let X be a path connected metric space. Then X is not a disjoint union of two nonempty closed subsets of X.
Proof
Suppose there are disjoint nonempty closed sets A and B such that  . Pick any \(a\in A\) and \(b\in B.\) Let \(f:[0,1]\longrightarrow X\) be a continuous map with \(f(0)=a\) and \(f(1)=b.\)
. Pick any \(a\in A\) and \(b\in B.\) Let \(f:[0,1]\longrightarrow X\) be a continuous map with \(f(0)=a\) and \(f(1)=b.\)
Then \(f^{-1}(A)\) and \(f^{-1}(B)\) are closed subsets of [0, 1], containing 0 and 1, respectively. Since A and B are disjoint, so are \(f^{-1}(A)\) and \(f^{-1}(B).\) Moreover,  implies that
implies that  a contradiction to Lemma 6.6. \(\square \)
a contradiction to Lemma 6.6. \(\square \)
Now we prove that the only path-connected subsets of \(\mathbb {R}\) are nonempty intervals.
Theorem 6.8
Let \(\emptyset \ne I\subset \mathbb {R}.\) Then I is path connected if and only if I is an interval.
Proof
The converse holds by Proposition 6.4. Assume that there exists a path connected subset I of \(\mathbb {R}\) which is not an interval. Then there are \(a,b\in I\) and \(c\in \mathbb {R}\setminus I\) such that \(a<c<b.\)
Since I is path connected, there exists a continuous function \(f:[0,1]\longrightarrow I\) such that \(f(0)=a\) and \(f(1)=b.\) Let
Note that \(a\in A, b\in B\) and \(A\cup B=f^{-1}(I)=[0,1].\) Since f is continuous, A and B are closed in [0, 1]. Since \(c\notin I,\) we have \(c\notin f([0,1])\) and therefore, \(A\cap B=\emptyset .\) Hence, A and B are nonempty disjoint sets, closed in \([0,1]\) with union \([0,1],\) a contradiction to Lemma 6.6. \(\square \)
Next, we shall discuss the relationship between continuity and path connectedness. We shall present various consequences and generalizations of the Intermediate Value Theorem, which is also known as the Intermediate Value Property of continuous real functions. A few other generalizations will follow in the next section of this chapter.
First, we establish that continuous image of a path connected space is path connected.
Theorem 6.9
Let X, Y be metric spaces such that X is path connected and \(f:X\longrightarrow Y\) be a continuous function. Then f(X) is a path connected subspace of Y.
Proof
Let \(y_1,y_2\in f(X).\) Then \(y_1=f(x_1)\) and \(y_2=f(x_2)\text { for some }x_1, x_2\in X.\) Since X is path connected, there exists a continuous function \(\phi :[0,1]\longrightarrow X\) such that \(\phi (0)=x_1\) and \(\phi (1)=x_2.\) Then \(f\circ \phi :[0,1]\longrightarrow f(X)\) is a continuous function with \((f\circ \phi )(0)=y_1\) and \((f\circ \phi )(1)=y_2.\) Hence, f(X) is a path connected subset of Y. \(\square \)
Corollary 6.10
Let X be a path connected metric space, \(f:X\longrightarrow \mathbb {R}\) be a continuous function and \(a,b\in X\) be such that \(f(a)<f(b).\) Then for every \(l\in (f(a),f(b)),\) there exists some \(c\in X\) such that \(f(c)=l.\)
Proof
By Theorems 6.8 and 6.9, f(X) is a path connected subset of \(\mathbb {R}\) and hence an interval. Therefore, \(f(X) \supset [f(a),f(b)],\) which contains l. Hence, \(f(c)=l,\) for some \(c\in X.\) \(\square \)
As an application of the above corollary, we now show that the continuous injective real valued maps on intervals are strictly monotone with strictly monotone inverses on their range.
Example 6.11
Let I be an interval and \(f:I\longrightarrow \mathbb {R}\) be a continuous injective map. Then f is strictly monotone with strictly monotone inverse on f(I).
Proof
Let \(E:=\{(x,y)\in I^2: x<y\}.\) Define \(g:E\longrightarrow \mathbb {R}\) as \(g(x,y)=f(x)-f(y).\) Note that E is path connected. Since g is continuous, g(E) is also path connected.
If f is not strictly monotone, then g takes positive and negative values on E. Therefore, there exist \((x,y)\in E\) such that \(g(x,y)=0.\) This contradicts the fact that f is injective.
Hence, f is strictly monotone on I. It can be shown that \(f^{-1}:f(I)\longrightarrow I\) is also strictly monotone, which we leave to the readers. \(\square \)
Theorem 6.12
(Intermediate Value Theorem) Let \(a<b\) be reals and \(f:[a,b]\longrightarrow \mathbb {R}\) be a continuous function. Then f maps intervals onto intervals. In other words, if \(f(a)<l<f(b),\) then \(f(c)=l\text { for some }c\in (a,b).\)
Proof
By Theorem 6.8, \([a,b]\) is path connected. Now apply Corollary 6.10. \(\square \)
The converse is not true. However, it holds under some additional hypotheses (see Exercise 6.13) A few immediate consequences of the Intermediate Value Theorem are presented below. The first one is a fixed point theorem.
Example 6.13
Let \(f:[0,1]\longrightarrow [0,1]\) be a continuous function. Then there exists some \(x\in [0,1]\) such that \(f(x)=x.\)
Proof
Let \(g(x):=f(x)-x.\) If \(g(0)= 0\) or \(g(1)=1,\) we are done. Otherwise \(g(0)> 0\) and \(g(1)< 0.\) Since g is continuous on \([0,1],\) the result follows by Intermediate Value Theorem. \(\square \)
Example 6.14
Let \(S^1\) denote the unit circle in \(\mathbb {R}^2\) and \(f:S^1\longrightarrow \mathbb {R}\) be continuous. Then there exists some \(z\in S^1\) such that \(f(z)=f(-z).\) (There are two antipodal points on the equator of the earth at which the temperatures are exactly the same.)
Proof
Consider the functions \(g:S^1\longrightarrow \mathbb {R}\) and \(h:[0,1]\longrightarrow S^1\) defined as
Since g and h are continuous, so is their composition \(g\circ h:[0,1]\longrightarrow \mathbb {R}.\) Note that \(h(0)=(1,0)=-h(1/2).\) Therefore,
If \((g\circ h)(0)=0,\) then take \(z=h(0).\) Otherwise \((g\circ h)(0)\) and \((g\circ h)(1/2)\) are of opposite signs. By Intermediate Value Theorem, there exists \(c\in (0,1/2)\) such that \((g\circ h)(c)=0.\) Then \(z=h(c)\) satisfies our requirements. \(\square \)
Proposition 6.15
[4, Theorem 2] Let \(f:\mathbb {R}\longrightarrow \mathbb {R}.\) Then f is continuous if and only if f maps intervals onto intervals, and compact sets onto compact sets.
Proof
The necessity follows by Theorems 5.31 and 6.12. For the converse, assume that f maps intervals onto intervals and compact sets onto compact sets, but is not continuous at some \(x\in \mathbb {R}.\) Then there exists some \(\epsilon >0\) and a sequence \(\{y_n\}\) of real numbers such that
Then for each \(n\in \mathbb {N},\) either \(f(y_n)\ge f(x)+\epsilon \) or \(f(y_n)\le f(x)-\epsilon .\) Since f maps intervals onto intervals, one can choose a real \(x_n\) between x and \(y_n\) such that
Write \(X:=\{x_n:n\in \mathbb {N}\}\cup \{x\}.\) Since \(x_n\longrightarrow x,\) X is a closed and bounded subset of \(\mathbb {R}\) and hence compact. By hypothesis, f(X) is also compact. Also, (6.1) ensures that either \(f(x)+\epsilon /2\) or \(f(x)-\epsilon /2\) is an adherent point of f(X), but not in f(X), a contradiction. \(\square \)
Alternative proofs of the Intermediate Value Theorem (6.12) will be suggested in Exercise 6.14.
History Notes 6.16
The first proof of the Intermediate Value Theorem appeared in a 60 pages book by Bolzano in 1817. In 1821, Cauchy provided its modern formulation (see [4, p. 847]).
Exercise 6.1
Show that every curve is a path connected compact set, given by a uniformly continuous map.
Exercise 6.2
Can a metric space have a path connected finite subset, with exactly two points?
Exercise 6.3
Characterize the set of continuous functions from \(\mathbb {R}\) into \(\mathbb {Z}.\)
Exercise 6.4
Let \(f:[0,2]\longrightarrow \mathbb {R}\) be a continuous function with \(f(0)=f(2).\) Prove that there exists some \(x\in [0,1]\) such that \(f(x)=f(x+1).\)
Exercise 6.5
Does there exist any normed linear space which is not path connected?
Exercise 6.6
Let \(f:\mathbb {R}\longrightarrow \mathbb {R}\) be a continuous function such that f(O) is an open set, for every open set O. Prove that f is strictly monotone.
Exercise 6.7
Does there exist any \(p>0\) such that the square root of the arithmetic mean of the \(p^{th}\) powers of 2, 3 and 4 is \(\pi ?\)
Exercise 6.8
Does there exist a continuous bijection from \([0,1]^2\) onto \([0,1],\) or from \((0,1)^2\) onto (0, 1)?
Exercise 6.9
Let \(f:[0,1)\cup [3,4]\longrightarrow \mathbb {R}\) be a strictly increasing function such that the range of f is connected. Prove that f is a continuous function.
Exercise 6.10
If a, b, c are distinct reals, then what is the number of distinct real roots of the equation \((x-a)^3+(x-b)^3+(x-c)^3=0?\)
Exercise 6.11
Let \(n\in \mathbb {N},\) and \( a_1,\dots , a_{n-1}\in \mathbb {R}\) such that the polynomial given by \(p(x):=x^n+a_{n-1}x^{n-1}+\dots +a_1 x-1 \) has no roots in \(\{z\in \mathbb {C}:|z|<1\}\) and it satisfies \(p(-1)=0.\) Prove or disprove:
-
(a)
\(p(1)=0.\)
-
(b)
\(p(2)>0.\)
-
(c)
\(\displaystyle \lim _{x\rightarrow \infty } p(x)=\infty .\)
-
(d)
\(p(3)=0.\)
Exercise 6.12
Let \(\{(X_i,\rho _i):i=1,\dots n\}\) be a finite collection of path connected metric spaces and \(\rho \) be the metric on the Cartesian product \(X:= \prod _{i=1}^n X_i\) defined as in Exercise 2.24. Is \((X,\rho )\) a path connected metric space?
Exercise 6.13
Let \(f:\mathbb {R}\longrightarrow \mathbb {R}\) such that f maps intervals onto intervals.
-
(a)
Is it necessary that f is continuous?
-
(b)
If \(f^{-1}(\{r\})\) is closed for every \(r\in \mathbb {Q},\) prove that f is continuous.
Exercise 6.14
Write alternate proofs for the Intermediate Value Theorem (6.12) using (a) the least upper bound property of \(\mathbb {R}\) and (b) Heine-Borel Theorem (5.14) for \(\mathbb {R}.\)
Exercise 6.15
Write an alternate proof of Lemma 6.6, using relative open sets only.
6.2 Connected Sets
Motivated by Theorem 6.7, we now present the notion of connectedness.
Definition 6.17
A metric space X is said to be connected if it is not a union of two nonempty disjoint sets, closed in X.
A nonempty subset Y of a metric space X is said to be connected if Y is a connected subspace of X. Otherwise, Y is called disconnected.
It is evident from the definition that a metric space X is connected if and only if X is not a union of two nonempty disjoint sets, open in X.
Examples 6.18
-
(a)
In any metric space, the singleton sets are connected.
-
(b)
In \(\mathbb {R},\) no finite set having more than one point is connected.
-
(c)
By Lemma 6.6, every nonempty interval of reals is connected.
-
(d)
By Theorem 6.7, every path connected metric space is connected.
In this chapter, we will provide several examples of connected metric spaces that are not path connected. However, for subspaces of \(\mathbb {R},\) these two notions are equivalent.
Theorem 6.19
Let \(\emptyset \ne I\subset \mathbb {R}.\) Then the following are equivalent:
-
(a)
I is an interval.
-
(b)
I is path connected.
-
(c)
I is connected.
Proof
The implications \((a) \iff (b)\) and \((b)\Rightarrow (c)\) hold by Theorems 6.8 and 6.7, respectively. To prove that \((c)\Rightarrow (a),\) assume that I is not an interval. Then there are \(a<c<b\) such that \(a,b\in I,\) but \(c\notin I.\) So I is a disjoint union of the nonempty sets \(I\cap (-\infty , c)\) and \(I\cap (c,+\infty ),\) which are open in I. Hence, I is not connected. \(\square \)
Just like path connected spaces, the continuous image of a connected space is connected.
Theorem 6.20
Let X, Y be metric spaces such that X is connected and \(f:X\longrightarrow Y\) be a continuous function. Then f(X) is a connected subspace of Y.
Proof
Suppose that the result is not true. Then there exists continuous function f on a connected metric space X into another metric space Y such that f(X) is not connected. Then  for some nonempty disjoint sets \(O_1\) and \(O_2,\) open in f(X).
for some nonempty disjoint sets \(O_1\) and \(O_2,\) open in f(X).
Then we obtain  as a disjoint union. Since f is continuous, both \(f^{-1}(O_1)\) and \(f^{-1}(O_2)\) are open inside X. Since X is connected, either \(f^{-1}(O_1)=\emptyset \) or \(f^{-1}(O_2)=\emptyset .\) So either \(O_1=f(\emptyset )=\emptyset \) or \(O_2=f(\emptyset )=\emptyset ,\) a contradiction. \(\square \)
as a disjoint union. Since f is continuous, both \(f^{-1}(O_1)\) and \(f^{-1}(O_2)\) are open inside X. Since X is connected, either \(f^{-1}(O_1)=\emptyset \) or \(f^{-1}(O_2)=\emptyset .\) So either \(O_1=f(\emptyset )=\emptyset \) or \(O_2=f(\emptyset )=\emptyset ,\) a contradiction. \(\square \)
Corollary 6.21
Let X be a connected metric space, \(f:X\longrightarrow \mathbb {R}\) be a continuous function and \(a,b\in X\) be such that \(f(a)<f(b).\) Then for every \(l\in (f(a),f(b)),\) there exists some \(c\in X\) such that \(f(c)=l.\)
Proof
Applying Theorems 6.20 and 6.19, f(X) is a connected subset of \(\mathbb {R}\) and hence an interval. Therefore, \( l\in [f(a),f(b)]\subset f(X).\) Hence, \(f(c)=l,\) for some \(c\in X.\) \(\square \)
Now we present a property of connected spaces which is not shared by path connected spaces, in general. Therefore, it serves as our main motivation to construct examples of connected sets which are not path connected.
Theorem 6.22
If A is a connected subset of a metric space X, then any set B such that \(A\subset B \subset \overline{A},\) is connected.
Proof
Let  where \(B_1\) and \(B_2\) are disjoint sets, closed in B. Then
where \(B_1\) and \(B_2\) are disjoint sets, closed in B. Then

is a union of disjoint sets, closed in A. Since A is connected, either \(A\cap B_1=\emptyset \) or \(A\cap B_2=\emptyset .\) Without loss of generality, assume that \(A\cap B_1=\emptyset .\) That is \(A\subset B_2.\)
For \(E\subset B,\) let \(\widehat{E}\) denote the closure of E in the subspace B. Then \(\widehat{A}=\overline{A}\cap B=B,\) which implies \( B = \widehat{A} \subset \widehat{B_2}=B_2,\) as \(B_2\) is closed in B. Therefore, \(B_1=\emptyset .\) Hence, B is connected. \(\square \)
Example 6.23
The topologist’s sine curve \(T_s,\) defined as under, is connected but not path connected.

Note that the set
is path connected and hence a connected subspace of \(\mathbb {R}^2.\)
Also, note that \(\overline{T}=T_s.\) Applying Theorem 6.22, the space \(T_s\) is connected.
It can also be verified that there is no path from (0, 0) to \((1,\sin 1),\) in \(T_s.\)
Example 6.24
Let X denote the subspace of \(\mathbb {R}^2\) given by the union of an infinite spiral and the unit circle as under:

By Theorem 6.22, X is connected. However, X is not path connected.
It can be shown that there exists no path joining (1, 0) and \((2\cos 1, 2\sin 1),\) inside this space.
A few other examples of connected but not path connected metric spaces will be presented Example 6.38 and Exercise 6.22.
Definition 6.25
Let X be a metric space and \(A,B\subset X.\) Then A and B are said to be separated if
Separated sets are always disjoint. However, the intervals (0, 1) and (1, 2) are separated in \(\mathbb {R},\) while [0, 1] and (1, 2) are not. The converse holds under some additional hypotheses.
Proposition 6.26
Let A and B be two disjoint subsets of a metric space.
-
(a)
If both A and B are closed, then these are separated.
-
(b)
If both A and B are open, then these are separated.
Proof
-
(a)
This part is trivial, as then \(A\cap \overline{B}=A\cap {B}=\emptyset \) and \(\overline{A}\cap {B}=A\cap {B}=\emptyset \)
-
(b)
Assume that there are open disjoint sets A and B which are not separated. Then either \(A\cap \overline{B}\ne \emptyset \) or \(\overline{A}\cap {B}\ne \emptyset .\) Without loss of generality, suppose that \(A\cap \overline{B}\ne \emptyset .\) Pick any \(x\in A\cap \overline{B}\ne \emptyset .\) Since A is open, there exists some \(r>0\) such that \(B(x;r)\subset A.\) Since \(x\in \overline{B},\) we have \(B(x;r) \cap B\ne \emptyset .\) This implies that \( A\cap B\ne \emptyset ,\) a contradiction. \(\square \)
Proposition 6.27
Let X be a metric space such that  for some separated sets A and B. Then both A and B are open (and hence closed) in X.
for some separated sets A and B. Then both A and B are open (and hence closed) in X.
Proof
If either \(A=\emptyset \) or \(B=\emptyset ,\) the result is obvious. Assume otherwise. If \(x\in A,\) then \(x\notin \overline{B}.\) So there exists some \(r>0\) such that \(B(x;r)\cap B=\emptyset .\) Since \(X=A\cup B,\) we obtain \(B(x;r)\subset A.\) Hence, A is open. Similarly, B is open in X. \(\square \)
Sets which are open as well as closed, are also known as clopen sets. Further, if X is a union of two nonempty disjoint clopen sets A and B, we say that A|Bis a separation of X or that  is a separation of X.
is a separation of X.
Now we present a few characterizations of disconnected spaces. Note that these characterizations correspond to characterizations of connected sets.
Theorem 6.28
If X is a metric space, then the following are equivalent:
-
(a)
X is a union of two nonempty disjoint sets, open in X.
-
(b)
X is a union of two nonempty disjoint sets, closed in X.
-
(c)
X is a union of two nonempty separated sets.
-
(d)
X contains a proper clopen subset.
-
(e)
There exists a continuous surjective map \(f:X\longrightarrow \{0,1\}.\)
Proof
The equivalence (\((a)\iff (b)\)) is immediate from the definition of closed sets. The implications (\((b)\Rightarrow (c)\)) and (\((a)\Rightarrow (c)\)) follow from Proposition 6.26. Finally, (\((c)\Rightarrow (b)\)) and (\((c)\Rightarrow (a)\)) are evident from Proposition 6.27.
To prove (\((b)\iff (d)\)), assume that X is union of two nonempty disjoint closed sets A and B. Then \(A=X\setminus B\) is an open subset of X, which is a proper subset of X as both A and B are nonempty. Conversely, if X contains a proper subset A which is both open as well as closed, then for \(B:=X\setminus A,\) the second assertion holds.
To prove (\((b)\iff (e)\)), assume that X is union of two nonempty disjoint closed sets A and B. Define f to be 0 on A, and 1 on B. It can be shown that f is a continuous surjective map from X onto \(\{0,1\}.\) Conversely, assume that there exists a continuous surjective map \(f:X\longrightarrow \{0,1\}.\) Then the disjoint sets \(A:=f^{-1}(\{0\})\) and \(B:=f^{-1}(\{1\})\) serve our purpose. \(\square \)
Theorem 6.29
Let X be a compact and connected metric space such that \(X\setminus \{x\}\) is disconnected, for some \(x\in X.\) Then there exist two different elements \(x_1,x_2\in X\) such that both \(X\setminus \{x_1\}\) and \(X\setminus \{x_2\}\) are connected.
The above result is immediate when X is a subspace of \(\mathbb {R}.\) Its general proof is out of the scope of this textbook. Interested readers are referred to [4, p. 89, Theorem 6.6].
Metric spaces which are compact as well as connected are also known as continuum (see [4]). Further, a point x of a connected metric space X is known as a cut point, if \(X\setminus \{x\}\) is disconnected. Hence, the above theorem concisely states the following:
If a continuum has a cut point, then it has at least two non-cut points.
Exercise 6.16
Prove that any curve in a metric space is a connected set.
Exercise 6.17
Does there exist a subset of \(\mathbb {Q}\) which is both open and closed in \(\mathbb {Q}?\)
Exercise 6.18
Is finite intersection of connected subsets of a metric space always connected?
Exercise 6.19
Does there exist a connected subset whose interior is not connected?
Exercise 6.20
Prove or disprove:
-
(a)
The interior of every path connected set is path connected.
-
(b)
The interior of every connected set is path connected.
Exercise 6.21
Can you replace the word ‘connected’ with ‘path connected’ in Theorem 6.22?
Exercise 6.22
Show that the infinite broom space, given by
is connected but not a path connected subspace of \(\mathbb {R}^2.\)
Exercise 6.23
If X is a metric space, prove that the following are equivalent:
-
(a)
X is not a union of two nonempty disjoint sets, open in X.
-
(b)
X is not a union of two nonempty disjoint sets, closed in X.
-
(c)
X is not a union of two nonempty separated sets.
-
(d)
X does not contain any proper clopen subset.
-
(e)
There exists no continuous surjective map \(f:X\longrightarrow \{0,1\}.\)
Exercise 6.24
Write a proof of Theorem 6.29 if X is a subspace of \(\mathbb {R}.\)
Exercise 6.25
In discrete metric spaces, prove that disjoint sets are separated.
Exercise 6.26
Let A be a subset of a metric space X. If A is connected, prove that so is \(\overline{A}.\) Is the converse true? Justify your answer.
Exercise 6.27
Let A, B be separated subsets of a metric space and \(C\subset A\) and \(D\subset B.\) Prove that C and D are also separated.
Exercise 6.28
Let X be a metric space. Prove that
-
(a)
singletons subsets of X are connected,
-
(b)
the only finite connected subsets of X are singletons and
-
(c)
if X is discrete, then only singletons are connected.
Exercise 6.29
Let X be a metric space and \(A, B\subset X\) such that\(dist(A,B):=\inf \{d(a,b):a\in A, b\in B\}>0.\) Prove that A and B are separated sets. Is the converse true?
Exercise 6.30
Let X be a metric space with two nonempty subsets A and B satisfying \(dist(A,B)>0\) and \(X=A\cup B.\) Prove that both A and B are open as well as closed in X and thence conclude that X is not a connected metric space.
Exercise 6.31
Let \(A\subset \mathbb {C}\) such that \( A\notin \{\emptyset , \mathbb {C}\}.\) Prove that A is not clopen in \(\mathbb {C}.\)
Exercise 6.32
Let A and B be closed subsets of a metric space such that both \(A\cup B\) and \(A\cap B\) are connected. Prove that both A and B are connected.
Exercise 6.33
Let \(E\subset Y\subset X.\) Prove or disprove: E is connected in X if and only if E is connected in Y.
Exercise 6.34
What difference does it make if we define empty sets to be connected or path connected?
Exercise 6.35
Let \(A\subset B\subset C\subset X.\) Prove or disprove: If A and C are connected, then so is B.
Exercise 6.36
Deduce Intermediate Value Theorem (6.12) from Theorem 6.20.
Exercise 6.37
Prove that a metric space X is disconnected if and only if there exists a continuous surjective function \(f:X\longrightarrow \{0,1\}.\)
Exercise 6.38
Prove that a metric space X is disconnected if and only if there exists a continuous function \(f:X\longrightarrow \mathbb {R}\) such that \(f^{-1}(\{0\})=\emptyset ,\) while both of the sets \(f^{-1}(0,+\infty )\) and \(f^{-1}(-\infty , 0)\) are nonempty.
Exercise 6.39
Let X denote the space of functions from \([0,1]\) into itself, under uniform norm \(\Vert .\Vert _\infty \) and let A be any connected subset of X. Prove that for every \(x\in [0,1],\) the set \(\{a(x):a\in A\}\) is either an interval or a singleton set.
Exercise 6.40
Show that the subspace \(\big \{f\in C[0,1]:\int _0^1f \ne 0\big \}\) of C[0, 1], under uniform norm \(\Vert .\Vert _\infty ,\) is disconnected.
Exercise 6.41
Under uniform norm, is C[0, 1] connected?
Exercise 6.42
Does there exist any \(p\in [1, \infty ] \) for which the sequence space \( \ell ^p\) is connected?
Exercise 6.43
Obtain the set of non-cut points of the Topologist’s Sine Curve of Example 6.23.
Exercise 6.44
Does there exist a continuum having no non-cut point?
Exercise 6.45
Does there exist a continuum having
-
(a)
no cut point?
-
(b)
exactly one cut point?
-
(c)
exactly n cut points, for every \(n\in \mathbb {N}\setminus \{1\}?\)
-
(d)
infinitely many cut points?
Exercise 6.46
Does there exist a continuum having
-
(a)
exactly one non-cut point?
-
(b)
exactly n non-cut points, for every \(n\in \mathbb {N}\setminus \{1\}?\)
-
(c)
infinitely many non-cut points?
6.3 Components
Definition 6.30
Let X be a metric space and \(\emptyset \ne Y\subset X.\) Then Y is said to be a connected component of X if Y is a maximal connected subset of X, that is
-
(a)
Y is a connected subset of X and
-
(b)
if \(\widehat{Y}\) is a connected subset X with \(\widehat{Y}\supset Y,\) then \(\widehat{Y}=Y.\)
Analogously, we define path components or path connected components of a metric space, by replacing the term ‘connected’ with ‘path connected’, in the above definition.
Most of the significant fundamental results about (path) connected components emerge from the following theorem.
Theorem 6.31
Let \(\Omega \) be any nonempty collection of (path) connected subsets of a metric space X, containing a common point. Then \(\bigcup _{E\in \Omega }E\) is also (path) connected.
Proof
Let \(a\in X\) such that \(a\in E\text { for all }E\in \Omega \) and write \(A:=\bigcup _{E\in \Omega }E.\)
-
(a)
Proof for path connectedness: Pick any \(x,y\in A.\) Then there exist \(E_x, E_y\in \Omega \) such that \(x\in E_x\) and \(y\in E_y.\) Since \(E_x\) and \(E_y\) are path connected, there are continuous functions \(f_x:[0,1]\longrightarrow E_x\) and \(f_y:[0,1]\longrightarrow E_y\) such that \(f_x(0)=x, f_x(1)=a=f_y(0)\) and \(f_y(1)=y.\) Define \(f:[0,1]\longrightarrow E_x\cup E_y \) such that
$$\begin{aligned} f(x):=\left\{ \begin{array}{lll} &{} f_x(2t) &{}; t\in [0,1/2],\\ &{} f_y(2t-1) &{}; t\in (1/2,1]. \end{array}\right. \end{aligned}$$Then \(f:[0,1]\longrightarrow A\) is a continuous function such that \(f(0)=x\) and \(f(1)=y.\) Hence, A is path connected.
-
(b)
Proof for connectedness: Assume that A is a disjoint union of sets \(A_1\) and \(A_2,\) closed in A. Since \(a\in A,\) without loss of generality we assume that \(a\in A_1.\) Pick any \( E \in \Omega .\) Then

Note that \(E\cap A_1\) and \(E\cap A_2\) are closed in E. Since \(E \text{ is } \text{ connected } \text{ and } a\in E\cap A_1,\) we obtain \(E\cap A_2=\emptyset .\) Therefore, \(E= E\cap A_1,\) which implies that \(E\subset A_1.\) Since \(E\in \Omega \) was arbitrary, we obtain \(A\subset A_1\) and thus \(A_2=\emptyset .\) Hence, A is connected. \(\square \)
Theorem 6.32
Let \(X\) be any metric space.
-
(a)
Any two connected components of X are either identical or disjoint.
-
(b)
Every element of X belongs to a connected component of X.
-
(c)
Every connected subset of X, is a subset of a connected component of X.
-
(d)
X is a disjoint union of its connected components.
Each of the above assertions is true for path connected components.
Proof
We establish the result only for connected components. The proofs for path connected components are analogous.
-
(a)
Let A and B be two connected components of X. If \(A\cap B\ne \emptyset ,\) by Theorem 6.31, \(A\cup B\) is connected. Since \(A\subset A\cup B,\) we have \(A\cup B=A.\) Similarly, \(A\cup B=B.\) Hence, \(A=B.\)
-
(b)
Let \(a\in X\) and \(\Omega :=\{A:a\in A\subset X, A \text{ is } \text{ connected }\}.\) By Theorem 6.31, \(T=\bigcup _{A\in \Omega }A\) is connected. It can be shown that T is the required component.
-
(c)
Let S be a connected subset of X. Pick any \(s\in S.\) As in (b), for \(\Omega :=\{A:s\in A\subset X, A \text{ is } \text{ connected }\},\) the set \(T=\bigcup _{A\in \Omega }A\) is the connected component of X containing s. Since \(S\in \Omega ,\) we obtain \(S\subset T.\)
-
(d)
Follows from (a) and (b). \(\square \)
Proposition 6.33
Let \(n\in \mathbb {N}, U\) be an open subset of \(\mathbb {R}^n\) and A be a connected component of the subspace U of \(\mathbb {R}^n.\) Then A is a clopen subset of U.
Proof
If \(a\in A(\subset U),\) there exists some \(\epsilon >0\) such that \(B:=B(a; \epsilon )\subset U.\) Since \(a\in A\cap B,\) we obtain \(A\cap B\ne \emptyset .\) By Theorem 6.31, \(A\cup B\) is connected. So it is contained in a connected component of U. Since A is a connected component of U, we have \(A=A\cup B.\) Therefore, \(B\subset A.\) Hence, A is open.
Further by Theorem 6.22, \(\overline{A}\cap U\) is a connected subset of the subspace U and it contains A. Consequently, \(\overline{A}\cap U=A.\) Hence, A is closed in U. \(\square \)
Another important result on connected components will be discussed in Theorem 7.18. Below we provide one last consequence of Theorem 6.31.
Lemma 6.34
If X and Y are (path) connected metric spaces, then so is \(X\times Y. \)
Proof
We prove the result for connectedness, as the case of path connectedness is analogous.
If X and Y are connected, then so are the ‘horizontal’ and ‘vertical’ slices in \(X\times Y,\) respectively, given by \(X\times y:=X\times \{y\}\) and \(x\times Y:=\{x\}\times Y\) for all \(x\in X\) and \(y\in Y.\) Fix any \(a\in X\) and \(b\in Y.\) Define
Since both \(X\times b\) and \(x\times Y\) contain a common point (x, b), by Theorem 6.31, each \(T_x\) is connected. Further note that \(\bigcup _{x\in X} T_x= X\times Y\) and each \(T_x\) contains a common point (a, b). Again by Theorem 6.31, the space \(X\times Y\) is connected. \(\square \)
Theorem 6.35
If \(X_1, \dots , X_n\) are (path) connected metric spaces, then so is the product space is \(\prod _{i=1}^n X_i.\)
Proof
Apply induction on n. The result is trivial for \(n=1\) and true for \(n=2\) by Lemma 6.34. Assume the result for some \(n\ge 2.\) We establish it for \(n+1.\)
Let \(X_1, \dots , X_{n+1}\) be (path) connected metric spaces. By induction hypothesis, so are the spaces \(\prod _{i=1}^n X_i\) and \((\prod _{i=1}^n X_i)\times X_{n+1}.\) Define \(f:(\prod _{i=1}^n X_i)\times X_{n+1}\longrightarrow \prod _{i=1}^{n+1} X_i\) as
It can be shown that f is a surjective map, continuous with respect to the usual product topologies. Hence, \( \prod _{i=1}^{n+1} X_i =f\big ( (\prod _{i=1}^n X_i)\times X_{n+1}\big )\) is (path) connected. \(\square \)
Let \(GL_n(\mathbb {K})\) denote the collection of \(n\times n\) invertible matrices over a field \(\mathbb {K}.\) Consider \(GL_n(\mathbb {K})\) as a subspace of \(\mathbb {K}^{n^2},\) equipped with the Euclidean metric in \(n^2 \) dimensions.
Example 6.36
\(GL_n(\mathbb {C})\) is path connected, while its subspace \(GL_n(\mathbb {R})\) is not even connected.
Proof
For \(M\in GL_n(\mathbb {C}),\) let det(M) denote the determinant of M. The space \(GL_n(\mathbb {R})\) is not connected, as the image of \(GL_n(\mathbb {R})\) under the continuous map \(M\longmapsto det(M)\) is not connected.
Let A be an arbitrary element of \(GL_n(\mathbb {C})\) and I denote the \(n\times n\) identity matrix. It is enough to prove that there exists a path from A to I inside \(GL_n(\mathbb {C}).\)
Let \(P(z):=det(A+z(I-A))\text { for all }z\in \mathbb {C}.\) Then P(z) is a polynomial over \(\mathbb {C}\) and hence has finitely many zeros. Thus, there exists a path from 0 to 1 in \(\mathbb {C}\) which lies inside \(\{z\in \mathbb {C}:P(z)\ne 0\},\) except possibly for the initial and terminating points 0 and 1. That is, there exists a continuous map h on \([0,1]\) such that \(h(0)=0, h(1)=1\) and \(P(h(t))\ne 0\text { for all }t\in [0,1].\)
If \(H(t):=A+h(t)(I-A)\text { for all }t\in [0,1],\) then H is a continuous map from \([0,1]\) into \(GL_n(\mathbb {C})\) with \(H(0)=A\) and \(H(1)=I.\) Hence the result. \(\square \)
In Sect. 7.2, we shall come across some other interesting facts about connected components.
Exercise 6.47
Prove that every path component of a space is its connected component. Is the converse true?
Exercise 6.48
Let X be metric space with exactly two connected components. How many subsets of X are both open as well as closed?
Exercise 6.49
Let X be metric space with exactly n connected components. How many subsets of X are both open as well as closed?
Exercise 6.50
Let X be a metric space such that every two points of X are contained in some (path) connected subset of X. Prove that X is (path) connected.
Exercise 6.51
Let \(\Omega \) be a collection of connected subsets of a metric space X such that \(A\cap B\ne \emptyset \text { for all }A, B\in \Omega .\) Prove that \(\bigcup _{A\in \Omega } A\) is a connected subset of X.
Exercise 6.52
Let \(k\in \mathbb {N}\) and \(\{A_1,\dots , A_k\}\) be connected sets such that \(A_n\cap A_{n+1}\ne \emptyset \text { for all }n=1,\dots k-1.\) Prove that \(\bigcup _{n=1}^k A_n\) is a connected set.
Exercise 6.53
Let \(\{A_n\}\) be a sequence of connected sets such that \(A_n\cap A_{n+1}\ne \emptyset \text { for all }n\in \mathbb {N}.\) Prove that \(\bigcup _{n=1}^\infty A_n\) is also a connected set.
Exercise 6.54
If X has only finitely many connected components, prove that every connected component of X is clopen.
Exercise 6.55
If A and B are (path) connected subsets of \(\mathbb {R}^2,\) is \(A+B\) also (path) connected?
Exercise 6.56
Let X be a metric space. Define \(x\sim y\iff x\text { and }y\) lie in some connected subset of X. Prove that \(\sim \) is an equivalence relation on X and the equivalence classes of this relation are precisely the connected components of X. State and prove analogous results for path components.
Exercise 6.57
Let X be the metric space of \(2\times 2\) invertible matrices over \(\mathbb {R},\) equipped with the Euclidean metric in four dimensions. Which of the following spaces can be obtained as images of continuous maps on X?
-
(a)
The usual space of real numbers \(\mathbb {R}?\)
-
(b)
The subspace \(\{(x,1/x):x\ne 0\}\) of \(\mathbb {R}^2?\)
-
(c)
The subspace \(\mathbb {R}^2\setminus \{(x,1/x):x\ne 0\}\) of \(\mathbb {R}^2?\)
-
(d)
The circle \(\{(x,y)\in \mathbb {R}^2:x^2+y^2 = 1\}?\)
-
(e)
The closed disk \(\{(x,y)\in \mathbb {R}^2:x^2+y^2\le 1\}?\)
6.4 Miscellaneous
We wind up this chapter by discussing locally (path) connected sets, convex sets, and totally disconnected sets. We shall also explore their relationship with the notions presented earlier in this chapter.
6.4.1 Locally Connected and Locally Path Connected Spaces
A metric space X is said to be locally (path) connected if for all \(x\in X,\) every neighborhood of x contains a (path) connected neighborhood of x.
Since every path connected set is connected, it is immediate that every locally path connected space is also locally connected.
A natural question that arises here is whether local properties imply global properties or conversely. The answers are all negative.
There are locally path connected spaces, which are not path connected or even connected.
Examples 6.37
-
(a)
\((0,1)\cup (2,3)\) is locally connected, but not connected.
-
(b)
Let X be a discrete metric space with at least two elements. Then every singleton subset of X is path connected. Hence, X is locally path connected, but not connected.
The converse is also false. That is, there are connected spaces, which are not locally connected.
Examples 6.38
The comb space, as under, is path connected but not locally connected.

Further, the deleted comb space defined as
is not path connected, as there is no path from (0, 0) to (0, 1) inside \( Comb_0.\) Further, \(C:=Comb_0\setminus \{(0,0),(0,1)\}\) is path connected and hence connected. Since \(C\subset Comb_0\subset \overline{C},\) by Theorem 6.22, \(Comb_0\) is connected.
Example 6.39
The Topologist’s Sine Curve, \(T_s\) of Example 6.23, is connected but not locally connected. Note that (0, 1) has no connected neighborhood in \({T_s}.\)
There are path connected spaces, which are not even locally connected.
Example 6.40
Let X denote the union of Topologist’s Sine Curve \(T_s\) and a curve \(\gamma \) from (0, 0) to \((1,\sin 1)\) such that \(\gamma \) does not meet \(T_s\) at any other point, except (0, 0) and \((1,\sin 1).\) Then X is path connected but not locally path connected or even locally connected.
6.4.2 Path Connectedness in Locally Path Connected Spaces
Recall that every path connected space is connected and the converse holds for subspaces of \(\mathbb {R}.\) In Examples 6.23, 6.24 and 6.38, we have seen that the converses are false, in general.
However, for open subsets of locally connected spaces, the converse holds. In normed spaces, this holds with stronger consequences. Instead of general paths, we get polygonal paths, in that case. In case of finite-dimensional Euclidean spaces, the results become further stronger. First we present the notion of polygonal lines or polygonal paths in normed linear spaces.
Definitions 6.41
Let X be a normed linear space.
-
(a)
If \(x_1, x_2\in X,\) the line segment from \(x_1\) to \(x_2\) is defined as
$$\begin{aligned}{}[x_1,x_2]:=\{(1-t)x_1+tx_2:0\le t\le 1\}. \end{aligned}$$ -
(b)
Let \(x_1, \dots , x_n\) be any finite number of elements in X, then the union of line segments \([x_1,x_2],\dots ,[x_{n-1},x_n]\) is denoted by \([x_1,\dots ,x_n],\) and is called a polygonal path.
-
(c)
A subset S of X is said to be convex if \([a,b]\subset S\text { for all }a,b\in S.\)
Examples 6.42
-
(a)
Every interval is convex.
-
(b)
The set \(\mathbb {C}\setminus \{0\}\) is not convex.
-
(c)
No finite subset of \(\mathbb {R}^n\) is convex.
-
(d)
Every rectangular (triangular) region in \(\mathbb {R}^2\) is a convex set.
Proposition 6.43
In normed linear spaces, every ball is a convex set.
Proof
Let \((X,\Vert .\Vert )\) be a normed linear space, \(x\in X\) and \(r>0.\) Write \(B:=B(x;r).\) Pick any \(x_1,x_2\in B.\) To see that \([x_1,x_2]\subset B,\) pick any \(y\in [x_1,x_2].\) Then \(y=tx_1+(1-t)x_2\text { for some }t\in [0,1].\) Applying triangle inequality, we obtain
Therefore, \(y\in B.\) Hence, B is convex. \(\square \)
Theorem 6.44
Let O be an open connected subset of a locally path connected space X. Then O is path connected.
Proof
Let \(x\in O\) be arbitrary. Let \(O_1\) denote the collection of those \(y\in O\) for which there exists a path from x to y, inside O. Write \(O_2:=O\setminus O_1.\) We claim that \(O_1\) and \(O_2\) are open in X, and hence in O.
Let \(y_1\in O_1.\) Then \(y_1\in O.\) Since O is open and X is locally path connected, there exists a path connected neighborhood \(U_1\) of \(y_1\) such that \(U_1\subset O.\)
Since \(y_1\in O,\) there exists a path \(P_1\) inside O, from x to \(y_1.\) As \(P_1\) and U contain a common point x, applying Theorem 6.31, \(P_1\cup U_1\) is path connected. Hence, for every \(z_1\in U_1,\) there exists a path from x to \(z_1,\) inside O. Therefore, \(U_1\subset O_1,\) which proves that \(O_1\) is an open set.
Now, let \(y_2\in O_2.\) Then \(y_2\in O.\) As above there exists a path connected neighborhood \(U_2\) of \(y_2\) such that \(U_2\subset O.\) We shall prove that \(U_2\subset O_2,\) which will conclude that \(O_2\) is open.
If possible, let \(z_2\in U_2\setminus O_2.\) Then \(z_2\in O_1.\) Let \(P_2\) be a path from x to \(z_2,\) inside O. As above \(P_2\cup U_2\) path connected. Thus, there exists a path from x to \(y_2,\) inside O. Hence, \(y_2\in O_1,\) a contradiction.
Therefore, both \(O_1\) and \(O_2\) are open in X and hence also open in the open set O. The connectedness of O ensures that either \(O_1=\emptyset \) or \(O_2=\emptyset .\) Since \(x\in O_1,\) we obtain \(O_2=\emptyset .\) Hence, \(O=O_1\) and the result follows. \(\square \)
Note that Proposition 6.43 ensures that every normed linear space is locally path connected. Therefore, every open connected subset of a normed linear space is path connected. The following are stronger results, for particular cases.
Corollaries 6.45
Let O be an open connected subset of a normed linear space X.
-
(a)
Then any two elements of O can be joined by a polygonal path, inside O.
-
(b)
If \(X=\mathbb {R}^m\text { for some }m\in \mathbb {N},\) then any two elements of O can be joined by a polygonal path consisting of line segments parallel to the axes, inside O.
Proof
-
(a)
Let \(x\in O\) be arbitrary and \(O_1\) be the set of \(y\in O\) which are connected to x through a polygonal path inside O.
The proof is analogous to Theorem 6.44. The only difference is that here we take \(U_1\) and \(U_2\) to be some open balls in X and use the fact that if \(P_1\) is a polygonal path from x to \(y_1\) inside O, then \(P_1\cup [y_1,z_1]\) is a polygonal path from x to \(z_1.\)
-
(b)
Let \(x\in O\) be arbitrary and \(O_1\) be the set of \(y\in O\) which are connected to x through a polygonal path, with line segments parallel to the axes, inside O.
The proof is analogous to part (a). Use the fact that any two points in a ball \(B\subset \mathbb {R}^m\) can be joined by a polygonal path inside B, having line segments parallel to the axes. \(\square \)
6.4.3 Quasi-components
Let X be a metric space and \(x\in X.\) The quasi-component of x in X is defined to be the intersection of all clopen subsets X, containing x. For this section, let \(C_x\) and \(Q_x\) denote the connected component and the quasi-component of x in X, respectively.
Theorem 6.46
Let X be a metric space and \(x\in X.\) Then \(C_x\subset Q_x.\)
Proof
Suppose there exists some \(y\in C_x\setminus Q_x.\) Then there exists a clopen set A containing x such that \(y\notin A.\) Then  is a separation of \(C_x,\) a contradiction. \(\square \)
is a separation of \(C_x,\) a contradiction. \(\square \)
The opposite inclusion holds for compact metric spaces. That requires the following lemmas.
Lemma 6.47
Let A and B be disjoint compact subsets of a metric space X. Then there exist disjoint open subsets U and V of X such that \(U\supset A\) and \(V\supset B.\)
Proof
Let \(\delta :=\inf \{d(a,b):a\in A,b\in B\}.\) Since A and B are compact and disjoint, one can conclude that \(\delta >0.\) Let
It can be shown that U and V satisfy our requirements. \(\square \)
Lemma 6.48
Let X be a compact metric space, O be an open subset of X and \(\mathcal {F}\) be a collection of closed subsets of X such that \(\bigcap _{F\in \mathcal {F}}F\subset O.\) Then there exist finitely many \(F_1,\dots , F_n\in \mathcal {F}\) such that \(\bigcap _{i=1}^n F_i\subset O.\)
Proof
Since \(X\setminus O\) is a closed subset of the compact space X, it is a compact subset of X. The given hypothesis implies that \(X\setminus O\subset \bigcup _{F\in \mathcal {F}}(X\setminus F).\) The compactness of \(X\setminus O\) implies that there are finitely many \(F_1,\dots , F_n\in \mathcal {F}\) such that \(X\setminus O\subset \bigcup _{i=1}^n(X\setminus F_i).\) \(\square \)
Theorem 6.49
Let X be a compact metric space and \(x\in X.\) Then \(C_x=Q_x.\)
Proof
By Theorem 6.46, we have \(C_x\subset Q_x.\) Since \(C_x\) is the largest connected set containing x and \(C_x\subset Q_x,\) to prove that \(C_x\supset Q_x,\) it is enough to prove that \(Q_x\) is a connected set.
If possible, let  be a separation of \(Q_x.\) Without loss of generality, assume that \(x\in A.\) Since by definition \(Q_x\) is closed in X, the sets A and B are also closed in X. Since X is compact, A and B are also compact subsets of X.
be a separation of \(Q_x.\) Without loss of generality, assume that \(x\in A.\) Since by definition \(Q_x\) is closed in X, the sets A and B are also closed in X. Since X is compact, A and B are also compact subsets of X.
Applying Lemma 6.47, there are disjoint open subsets U and V of X such that \(U\supset A\) and \(V\supset B.\) Applying Lemma 6.48, there are finitely many clopen subsets \(D_1,\dots , D_n\) of X such that  . Write \(D:=\bigcap _{i=1}^n D_i.\) Then D is a clopen subset of X such that
. Write \(D:=\bigcap _{i=1}^n D_i.\) Then D is a clopen subset of X such that  .
.
Let \(E:=D\cap U.\) Then E is open and \(x\in E,\) as \(x\in A\subset U.\) Also, \(E:= D\cap (X\setminus V)\) is closed. By definition \(Q_x\subset E.\) Consequently, \(B=Q_x\cap V\subset E\cap V=\emptyset .\) Hence the result. \(\square \)
6.4.4 Totally Disconnected Sets
Definition 6.50
A subset A of a metric space is said to be totally disconnected if no two points of A lie in a connected subset of A.
In other words, A is totally disconnected if and only if singletons are its only connected subsets if and only if all singletons subsets are its connected components.
Examples 6.51
Finite metric spaces, all discrete metric spaces, the set of natural numbers, and the set of rational numbers are all totally disconnected spaces.
Definition 6.52
A complex number is said to be algebraic if it is a root of some polynomial over integers. Non-algebraic complex numbers are known as transcendental numbers.
The numbers e and \(\pi \) are two standard examples of transcendental numbers. In Example 7.15, we establish an abundance of transcendental numbers besides the algebraic ones.
Example 6.53
The set of real algebraic numbers is totally disconnected.
Proof
Let \(\mathbb {A}\) be the set of real algebraic numbers. To the contrary, assume that \(\mathbb {A}\) is not totally disconnected. Then \(\mathbb {A}\) has a connected component E containing two distinct reals, say \(x<y.\) Pick any \(r\in \mathbb {Q}\) such that \(\pi \in (x+r,y+r).\) Then we have \(\pi -r\in (x,y).\)
By suitably modifying the polynomials satisfied by the algebraic numbers x and y, one can prove that \(\pi -r\) is not an algebraic number.
Note that the sets \(\{x\in E:x<\pi -r\}\) and \(\{x\in E:x>\pi -r\}\) are nonempty and form a separation of E. This is impossible, as E is a connected set. Hence the result. \(\square \)
Theorem 6.54
Let X be a compact metric space. Then X is totally disconnected if and only if for every \(x\in X\) and \(r>0\) there exists some clopen set A such that \(x\in A\subset B(x;r).\)
Proof
The converse follows from the definition of totally disconnected sets. For the necessity part, let X be totally disconnected, \(x\in X,\) \(r>0\) and \(B:=B(x;r).\)
By Theorem 6.49, \(Q_x=C_x=\{x\}\subset B.\) Applying Lemma 6.48, there are finitely many clopen subsets \(A_1,\dots , A_n\) of X such that \(x\in \bigcap _{i=1}^n A_i\subset B.\) Write \(A:=\bigcap _{i=1}^n A_i.\) Then A is a clopen subset of X and \(x\in A\subset B.\) Hence the result. \(\square \)
Corollary 6.55
Let X be a totally disconnectedcompact metric space, \(K\subset O\subset X\) such that K is compact and O is open in X. Then X has a clopen subset A such that \(K\subset A\subset O.\)
Proof
For every \(x\in K,\) there exists some \(r_x>0\) such that \(B(x;r_x)\subset O.\) Applying Theorem 6.54, one can choose clopen sets \(A_x \) such that \(x\in A_x\subset B(x;r_x)\text { for all }x\in K.\) Since K is compact and \(K\subset \bigcup _{x\in K}A_x,\) there are finitely many \(x_1,\dots , x_n\in K\) such that \(K\subset \bigcup _{i=1}^n A_{x_1}.\) Then \(A:= \bigcup _{i=1}^n A_{x_i}\) meets our requirements. \(\square \)
Notes and Remarks 6.56
-
(a)
It is possible to have three disjoint connected open sets in the plane which have the same boundary. For example, see Lakes of Wada [4, p. 138].
-
(b)
In Sect. 10.5.3, we shall discuss a connected space, which is not path connected, known as the Cantor’s leaky tent. It is such a connected metric space, which becomes totally disconnected after the removal of a particular point.
-
(c)
Let X, Y be compact metric spaces and let \(f:X\longrightarrow Y.\) We state two characterizations of continuity. Readers interested in details are referred to [5].
-
(i)
f is continuous if and only if f maps compact sets onto compact sets, and \(f^{-1}(y)\) is a closed set, for every \(y\in Y.\)
-
(ii)
If X is locally connected, then f is continuous if and only if f maps compact sets onto compact sets, and connected sets onto connected sets.
-
(i)
Exercise 6.58
Let \(D:=\{z\in \mathbb {C}:|z|<1\}\) and \(f:D\longrightarrow \mathbb {R}^3\) be a continuous function. How many subsets of f(D) are both open as well as closed?
Exercise 6.59
Complete the details in the proof of Corollaries 6.45.
Exercise 6.60
Let X be a normed linear space. Prove the following:
-
(a)
Every convex subset of a normed linear space is path connected.
-
(b)
X is convex, and hence path connected.
-
(c)
The converse of (a) does not hold.
Exercise 6.61
Prove that every discrete metric space is totally disconnected.
Exercise 6.62
Prove that both \(\mathbb {Q}\) and \(\mathbb {R}\setminus \mathbb {Q}\) are totally disconnected sets.
Exercise 6.63
After replacing \(\sin \frac{1}{x}\) with \(x\sin \frac{1}{x}\) in Example 6.23, does the resulting space become locally connected or path connected?
Exercise 6.64
Let A be a connected component of a locally connected metric space X. Prove that A is clopen in X.
Exercise 6.65
If E is a convex subset of a normed linear space, prove that so are the sets \(E^o\) and \(\overline{E}.\)
Exercise 6.66
If E is a convex subset of a normed linear space such that \(E^o\ne \emptyset ,\) prove that \(\overline{E}=\overline{E^o}.\)
Exercise 6.67
Let X be a metric space in which every open ball is a closed subset of X. Prove that X is totally disconnected.
Exercise 6.68
Let X be a metric space. Prove that the following are equivalent:
-
(a)
Quasi-components of X are singletons.
-
(b)
For any \(x,y\in X,\) there exist disjoint clopen neighborhoods \(U_x\) and \(U_y\) of x and y, respectively, such that
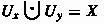 . (Such an X is called a totally separated space.)
. (Such an X is called a totally separated space.)
Exercise 6.69
Prove that every totally separated space is totally disconnected. Is the converse true?
Exercise 6.70
If d is an ultrametric on X, prove that (X, d) is totally separated.
Exercise 6.71
Let X be a totally disconnected compact metric space. Prove that for every \(n\in \mathbb {N},\) there exists a finite open cover \(\mathcal {U}_n\) of X with disjoint sets, each having diameter \(<2^{-n}.\)
Exercise 6.72
Prove that a metric space X is locally connected if and only if for every open set O of X, each connected component of O is open in X.
Exercise 6.73
Prove that a metric space X is locally path connected if and only if for every open set O of X, each path component of O is open in X.
Exercise 6.74
Let X be a metric space. Prove that each path component of X lies in a connected component of X.
Exercise 6.75
If X is locally path connected, then prove that has same collection of path components and connected components.
Exercise 6.76
Let X be a metric space and \(x\in X.\) Let \(P_x, C_x\) and \( Q_x\) denote, respectively, the path component, connected component and the quasi-component of x. Prove that \(P_x\subset C_x\subset Q_x.\) If X is locally path connected, then prove that \(P_x = C_x = Q_x.\)
Exercise 6.77
A metric space X is said to be weakly locally connected at \(x\in X\) if every neighborhood U of x contains a connected subspace S of X that contains a neighborhood of x. Prove that if X is weakly connected at each of its points, then X is locally connected. Is the converse true?
Exercise 6.78
State and prove the result analogous to Exercise 6.56 for quasi-components.
6.5 Hints and Solutions to Selected Exercises
-
6.2
No. Suppose that\(a\ne b\) and \(\{a,b\}\) be a path connected subset of a space X. Then there exists a continuous map \(f:[0,1]\longrightarrow \{a,b\}\) such that \(f(0)=a\) and \(f(1)=b.\) Thus, \(A:=f^{-1}({a})\) and \(B:=f^{-1}({b})\) are nonempty disjoint closed subsets of \([0,1]\) with union \([0,1],\) a contradiction to Lemma 6.6.
-
6.4
Apply Intermediate Value Theorem (6.12) on \(x\longmapsto f(x)-f(x+1)\) on \([0,1].\)
-
6.7
Yes. Apply Intermediate Value Theorem (6.12) on \(f(p):=\sqrt{(2^p+3^p+4^p)/3}.\)
-
6.8
No. Let \(f:[0,1]^2\longrightarrow [0,1]\) be a continuous bijection and x, y, z be any three elements from \([0,1]^2.\) Since \([0,1]^2\setminus \{x,y,z\}\) is path connected, so is its image under f. That is, \([0,1]\setminus \{f(x),f(y),f(z)\}\) is a path connected subset of \([0,1],\) a contradiction to Theorem 6.9. Similarly, the second part.
-
6.10
One. Let f(x) denote the given cubic. Since f is a real polynomial of odd degree, it must have at least one real root. If it has two distinct roots, then \(f'\) must have a root between those. This is impossible as f(x) is a sum of squares of reals and a, b, c are all distinct.
-
6.11
First three options are correct and the last one is false. Note that (c) is trivial. Let \(-1,\alpha _1,\dots , \alpha _{n-1}\) be all the roots of p, counting multiplicities. Equating coefficients from \(p(x)= (x+1)\prod _{i=1}^{n-1} (x-\alpha _i),\) we obtain
$$\begin{aligned} \prod _{i=1}^{n-1} \alpha _i=(-1)^n, \text{ which } \text{ implies } \prod _{i=1}^{n-1} |\alpha _i|=1. \end{aligned}$$(6.2)If \(\alpha \) is a non-real root of p, then by hypothesis, \(\overline{\alpha }\) is also a root of p and \(|\alpha |\ge 1.\) Thus, \(\alpha \overline{\alpha }\ge 1.\) Now (6.2) implies that \(|\alpha |=1,\) that is \(\alpha \overline{\alpha }=1,\) for every non-real root of p. Similarly, since p has no real root in \((-1,1),\) again (6.2) implies p has no real root in \(\mathbb {R}\setminus [-1,1].\) This concludes that (d) is false. Also, (b) is true, because if (b) is false then p will have a root in \([2,\infty ),\) a contradiction. By now we have established that all the roots of p lie on \(\{z\in \mathbb {C}:|z|=1\}.\) If 1 is not a root of p, then the representation \((x+1)\prod _{i=1}^{n-1} (x-\alpha _i)\) of p will either have linear factors \((x+1)\) or pairs of complex conjugates \(\alpha ,\overline{\alpha }\) such that \(\alpha \overline{\alpha }=1.\) Therefore, the constant term in this product must be 1, a contradiction. Hence, (a) is also true.
-
6.13
-
(a)
No. For example, consider the function f as in Exercise 1.100.
-
(b)
Assume that f is not continuous. Then there exists \(x_n\longrightarrow x_0\) such that
 . Without loss of generality, we can suppose that there is a rational number r and a subsequence \(\{x_{n_k}\}\) of \(\{x_n\}\) such that \(f(x_0)>r>f(x_{n_k})\text { for all }k\in \mathbb {N}.\) By hypothesis, one can choose \(t_k\) between \(x_0\) and \(x_{n_k}\) such that \(f(t_k)=r\text { for all }k\in \mathbb {N}.\) Then \(t_k\longrightarrow x_0.\) Since \(\{t_k\}\) is a sequence in the closed set \(f^{-1}(\{r\}),\) we conclude that its limit \(x_0\) also belongs to this set. Hence, \(f(x_0)=r,\) a contradiction.
. Without loss of generality, we can suppose that there is a rational number r and a subsequence \(\{x_{n_k}\}\) of \(\{x_n\}\) such that \(f(x_0)>r>f(x_{n_k})\text { for all }k\in \mathbb {N}.\) By hypothesis, one can choose \(t_k\) between \(x_0\) and \(x_{n_k}\) such that \(f(t_k)=r\text { for all }k\in \mathbb {N}.\) Then \(t_k\longrightarrow x_0.\) Since \(\{t_k\}\) is a sequence in the closed set \(f^{-1}(\{r\}),\) we conclude that its limit \(x_0\) also belongs to this set. Hence, \(f(x_0)=r,\) a contradiction.
-
(a)
-
6.14
Let f, a, b and l be as in Theorem 6.12.
-
(a)
Write \(S:=\{t\in [a,b]:f(t)<l\}.\) Then S is a nonempty subset of \([a,b],\) containing a, and bounded above by b. Let \(c:=\sup S.\) Since the function f is continuous at a and b, with \(f(a)<l\) and \(f(b)>l,\) we obtain \(a<c<b.\) We claim that \(f(c)=l.\) If \(f(c)<l,\) then the continuity of f at c implies that there exists some \(\delta >0\) such that \((c-\delta ,c+\delta )\subset [a,b]\) and \(f(x)<l\text { for all }x\in (c-\delta ,c+\delta ).\) Therefore, \( c+\delta /2\in S,\) a contradiction as \(c=\sup S.\) Similarly, if \(f(c)>l,\) there also exists \(\delta >0\) such that \((c-\delta ,c+\delta )\subset [a,b]\) and \(f(x)>l\text { for all }x\in (c-\delta ,c+\delta ).\) Then \( (c-\delta ,c+\delta )\cap S=\emptyset \) which implies that \(c\ne \sup S,\) a contradiction.
-
(b)
Assume that \(f(t)\ne l\text { for all }t\in [a,b].\) For \(t\in [a,b],\) if \(f(t)>l,\) choose \(\delta _t>0\) such that \(f(x)>l\text { for all }x\in (t-\delta _t,t+\delta _t)\cap [a,b].\) Otherwise, choose \(\delta _t>0\) such that \(f(x)<l\text { for all }x\in (t-\delta _t,t+\delta _t)\cap [a,b]\). By compactness of \([a,b],\) there are finitely many \(t_1,\dots , t_n\in [a,b]\) such that \([a,b]\subset \bigcup _{i=1}^n(t_i-\delta _{t_i},{t_i}+\delta _{t_i}).\) Since \(f(a)<l,\) it leads to \(f(b)<l,\) a contradiction.
-
(a)
-
6.15
Assume that
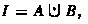 for some disjoint nonempty sets A and B, open in I. Pick any \(a\in A\) and \(b\in B.\) Without loss of generality, suppose \(a<b\). Write \(S_1:=[a,b]\cap A.\) Since \(S_1\) contains a and is bounded above by b, it has a supremum. Let \(s_1:=\sup S_1.\) Then \(s_1\le b.\) We claim that \(s_1<b.\) If \(s_1=b,\) then \(I\cap (s_1-\delta , s_1+\delta )\subset B,\) for some \(\delta >0,\) as B is open in I. This implies that \((s_1-\delta , s_1+\delta )\cap A=\emptyset .\) Therefore, \(s_1=\sup S_1\le s_1-\delta ,\) a contradiction. Hence, \(s_1<b.\) Write \(S_2:=[s_1,b]\cap B\) and \(s_2:= \inf S_2.\) Then \(s_1\le s_2.\) As above, one can show that \(s_1<s_2.\) Let \(s_3\in (s_1,s_2).\) Since \(s_2=\inf S_2,\) we have \(s_3\notin B.\) Similarly, \(s_1=\sup S_1\) implies that \(s_3\notin A.\) Therefore, I is not an interval, as \(s_3\in I\setminus A\cup B.\)
for some disjoint nonempty sets A and B, open in I. Pick any \(a\in A\) and \(b\in B.\) Without loss of generality, suppose \(a<b\). Write \(S_1:=[a,b]\cap A.\) Since \(S_1\) contains a and is bounded above by b, it has a supremum. Let \(s_1:=\sup S_1.\) Then \(s_1\le b.\) We claim that \(s_1<b.\) If \(s_1=b,\) then \(I\cap (s_1-\delta , s_1+\delta )\subset B,\) for some \(\delta >0,\) as B is open in I. This implies that \((s_1-\delta , s_1+\delta )\cap A=\emptyset .\) Therefore, \(s_1=\sup S_1\le s_1-\delta ,\) a contradiction. Hence, \(s_1<b.\) Write \(S_2:=[s_1,b]\cap B\) and \(s_2:= \inf S_2.\) Then \(s_1\le s_2.\) As above, one can show that \(s_1<s_2.\) Let \(s_3\in (s_1,s_2).\) Since \(s_2=\inf S_2,\) we have \(s_3\notin B.\) Similarly, \(s_1=\sup S_1\) implies that \(s_3\notin A.\) Therefore, I is not an interval, as \(s_3\in I\setminus A\cup B.\) -
6.18
No. Take the intersection of the x-axis and the unit circle, in \(\mathbb {R}^2.\) Then both A and B are connected, while \(A\cap B=\{(0,0),(0,1)\}\) is not.
-
6.19
Yes. E.g. consider \(\mathbb {R}^2\setminus \{(x,0):x\in \mathbb {Q}\}\) in \(\mathbb {R}^2.\)
-
6.20
Both assertions are false. E.g., consider the subspace \(\{(x,y)\in \mathbb {R}^2:xy\ge 0\}\) of \(\mathbb {R}^2,\) which is a path connected set while the interior is neither connected nor path connected.
-
6.26
Apply Theorem 6.22. For the converse, take \(A:=[-1,0)\cup (0,1].\)
-
6.29
Let \(\delta := dist(A,B).\) If \({A}\cap \overline{B}\ne \emptyset ,\) then there exists some \(x\in {A}\cap \overline{B}.\) By hypothesis \(B(x;\delta /2)\cap B=\emptyset .\) Therefore, \(x\notin \overline{B},\) a contradiction. For the converse, take \(A=(0,1)\) and \(B=(1,\infty )\) in reals with usual topology.
-
6.32
Let
 be a separation of A. Then
be a separation of A. Then  is a separation of \(A\cap B.\) Since \(A\cap B\) is connected, one of these must be empty. Suppose \(A_1\cap B=\emptyset .\) Then
is a separation of \(A\cap B.\) Since \(A\cap B\) is connected, one of these must be empty. Suppose \(A_1\cap B=\emptyset .\) Then  . Since \(A\cup B\) is connected, either \(A_1=\emptyset \) or \(A_2\cup B= \emptyset ,\) that is, either \(A_1=\emptyset \) or \(A_2= \emptyset .\) Hence, A is connected. Similarly, B is connected.
. Since \(A\cup B\) is connected, either \(A_1=\emptyset \) or \(A_2\cup B= \emptyset ,\) that is, either \(A_1=\emptyset \) or \(A_2= \emptyset .\) Hence, A is connected. Similarly, B is connected. -
6.39
Fix \(x\in [0,1].\) Define \(\phi _x:A\longrightarrow [0,1]\) as \(\phi _x(a):=a(x) \text { for all }a\in A.\) Then \(\phi _x\) is a continuous map, as \(|\phi _x(a)-\phi _x(b)|=|a(x)-b(x)|\le \Vert a-b\Vert _\infty .\) Since A is connected, \(\phi _x(A)=\{a(x):a\in A\}\) is a connected subset of \([0,1].\)
-
6.40
Define \(\phi :C[0,1]\longrightarrow \mathbb {R}\) as \(\phi (f):=\int _0^1 f \text { for all }f\in C[0,1].\) Then \(\phi \) is continuous, as \( |\phi (f)-\phi (g)|\le \int _0^1\big |f-g\big | \le \Vert f-g\Vert _\infty .\) Hence,
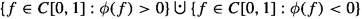
is a separation of \((C[0,1],\Vert .\Vert _\infty ).\)
-
6.44
No. Apply Theorem 6.29.
-
6.50
Apply Theorem 6.31.
-
6.51
Let \(\mathcal {A}:= \bigcup _{A\in \Omega } A\) and fix any \(A_0\in \Omega .\) Let T be the connected component of \(\mathcal {A},\) containing \(A_0.\) For any \(A\in \Omega , \) we have \(A_0\cap A\ne \emptyset \text { which implies }A_0\cup A\subset T\text { for all }\alpha \in \wedge .\) Therefore, \( \bigcup _{A \in \Omega }A\subset T \text { which implies }T= \bigcup _{A\in \Omega }A.\)
-
6.52
The result holds by induction on Theorem 6.31.
-
6.53
Write \(A:=\bigcup _{n=1}^\infty A_n.\) Suppose that A is not connected. Then there exist nonempty disjoint sets \(E_1\) and \(E_2,\) open in A such that
 . We claim that for every \(n\in \mathbb {N},\) either \(A\subset E_1\) or \(A\subset E_2.\) To show this, suppose that there exists some \(n\in \mathbb {N}\) such that \(A\cap E_1\ne \emptyset \) and \(A\cap E_2\ne \emptyset .\) Then \(A_n\) is not connected, as
. We claim that for every \(n\in \mathbb {N},\) either \(A\subset E_1\) or \(A\subset E_2.\) To show this, suppose that there exists some \(n\in \mathbb {N}\) such that \(A\cap E_1\ne \emptyset \) and \(A\cap E_2\ne \emptyset .\) Then \(A_n\) is not connected, as 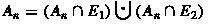 and both \(A_n \cap E_1\) and \(A_n \cap E_2\) are open in \(A_n.\) This establishes our claim. Hence, either \(A_1\subset E_1\) or \(A_1\subset E_2.\) Without loss of generality, suppose that \(A_1\subset \!\!E_1.\) Since \(A_1\cap A_2\ne , \) we have \(A_2 \subset \!\!E_1.\) Inducting like this, we obtain \(A_n\subset E_1\text { for all }n\in \mathbb {N}.\) Hence, \(A\subset \!\!E_1\) and thus \(E_2=\emptyset ,\) a contradiction. This proves the result.
and both \(A_n \cap E_1\) and \(A_n \cap E_2\) are open in \(A_n.\) This establishes our claim. Hence, either \(A_1\subset E_1\) or \(A_1\subset E_2.\) Without loss of generality, suppose that \(A_1\subset \!\!E_1.\) Since \(A_1\cap A_2\ne , \) we have \(A_2 \subset \!\!E_1.\) Inducting like this, we obtain \(A_n\subset E_1\text { for all }n\in \mathbb {N}.\) Hence, \(A\subset \!\!E_1\) and thus \(E_2=\emptyset ,\) a contradiction. This proves the result. -
6.54
Let \(A_1,\dots , A_n\) be the only connected components of X. By Theorem 6.22, each \(A_i\) is closed. By Theorem 6.32, X is a disjoint union of \(A_1,\dots , A_n.\) Then \(A_i=X\setminus \bigcup _{j\ne i}A_j,\) for all i. Hence, each \(A_i\) is open.
-
6.55
Yes. Because \(A\times B\) is a (path) connected subset of \(\mathbb {R}^2\times \mathbb {R}^2 \) and the map \((a,b)\longrightarrow a+b\) from \(A\times B\) onto \( A+B\) is continuous.
-
6.64
Applying Theorem 6.22, A is closed. Let \(a\in A\) and \(N_a\) be a connected neighborhood of a. By Theorem 6.31, \(A\cup N_a\) is a connected subset of X. Since A is a maximal connected set, we obtain \(A\cup N_a=A\) and hence \( N_a\subset A.\) Consequently, A is open.
-
6.65
Assume that E is convex. Let \(t\in (0,1).\) Since E is convex, \(tE^o+(1-y)E^o\subset E.\) By previous part, \(tE^o+(1-y)E^o\) is an open subset of E. Hence, \(tE^o+(1-y)E^o\subset E^o,\) that is, \(E^o\) is convex. To show that \(\overline{E}\) is convex, let \(x,y\in \overline{E}.\) Then there are sequences \(\{x_n\}\) and \(\{y_n\}\) in E, convergent to x and y, respectively. Hence, \(tx+(1-t)y=\lim _{n\rightarrow \infty }(tx_n+(1-t)y_n) \in \overline{E},\) as E is convex. Hence, \(\overline{E}\) is convex.
-
6.66
Let X be the given normed linear space. Clearly, \(\overline{E^o}\subset \overline{E}.\) To prove that \(\overline{E^o}\supset \overline{E},\) it is enough to show that \(\overline{E^o}\supset {E}.\) Since \(E^o\ne \emptyset ,\) let \(a\in E^o.\) Then \(B(a;r)\subset E\text { for all }r>0.\) That is, \(a+ry\in E \text { for all }y\in X\) such that \(\Vert y\Vert \le 1.\) Let \(x\in E\) and \(x_t:=ta+(1-t)x.\) We claim that \(B(x_t;tr)\subset E.\) Let \(y\in X\) such that \(\Vert y\Vert \le 1.\) Then \(x_t+try=t(a+ry)+(1-t)x\in E,\) as E is convex. This proves our claim. Hence, \(x_t\in E^o.\) Hence, \(x=\lim _{t\rightarrow 0}x_t \in E^o.\)
-
6.67
Let \(x\in X\) and A be the connected component of X containing x. We claim that \(A=\{x\}.\) If not, then pick any \(y\in A\setminus \{x\}.\) Let
$$\begin{aligned} \delta :=d(x,y), B_x:= B\bigg (x;\frac{\delta }{2}\bigg )\text { and }B_y:=B\bigg (x;\frac{\delta }{2}\bigg ). \end{aligned}$$By hypothesis, both \(B_x\) and \(B_y\) are clopen in X. Therefore, \(A \cap B_x\) and \(A \cap B_y\) are clopen and nonempty in the connected subspace A, a contradiction.
-
6.69
Apply Theorem 6.46. A counter example will be provided in Exercise 10.81.
-
6.70
Let \(x,y \in X\) such that \(x\ne y\) and \(r:=d(x,y).\) By Exercise 3.65(a), both B(x; r) and \(X\setminus B(x;r) \) are disjoint clopen subsets of X containing x and y, respectively.
-
6.71
Fix \(n\in \mathbb {N}.\) Since X is totally disconnected and compact, by Theorem 6.54, it has a finite cover \(\{O_1,\dots , O_n\}\) consisting of clopen sets with diameter \(<2^{-n}.\) Define \(U_i:=O_i\setminus \bigcup _{j<i}O_j\text { for all }i.\) Then each \(U_i\) is open and has diameter \(<2^{-n}.\) The result follows, as we have \(\bigcup _i U_i=\bigcup _i O_i.\)
-
6.72
(\(\Rightarrow \)) Let O be an open subset of X and U be a connected component of O. Let \(x\in U.\) Since X is locally connected, there exists a connected neighborhood \(B_x\) of x such that \(B_x\subset O.\) Since U is a connected component of O, containing x, we obtain \(B_x\subset U.\) Hence, U is open in X. (\(\Leftarrow \)) Let \(x\in X\) and U be any neighborhood of x. Then there exists an open set O such that \(x\in O\subset U.\) Let \(C_x\) be the connected component of x relative to O. By hypothesis, \(C_x\) is open in X. The result follows as \(x\in C_x\subset O\subset U.\)
-
6.73
Analogous to Exercise 6.72.
-
6.75
Let C be a connected component of X. Let \(x\in C\) and P be the path component of x, inside X. Since P is connected, we obtain \(P\subset C.\) We claim that \(P=C.\) Suppose that \(Q:=C\setminus P\ne \emptyset .\) For each \(q\in Q,\) let \(P_q\) be the path component of q. Then each such \(P_q\) is connected and hence a subset of C. Consequently, Q is a union of path components of X. Applying Exercise 6.73, the union of all these path components, that is Q, is open in X. Similarly, the path component P is open in X. Since
 is connected, either \(P=\emptyset \) or \(Q=\emptyset .\) But \(x\in P.\) Therefore, \(Q=\emptyset .\) Hence, \(P=C.\)
is connected, either \(P=\emptyset \) or \(Q=\emptyset .\) But \(x\in P.\) Therefore, \(Q=\emptyset .\) Hence, \(P=C.\)
References
D.J. Velleman, Characterizing Continuity. Amer. Math. Monthly 104(4), 318–322 (1997)
W. Felscher, Bolzano, Cauchy, Epsilon, Delta. Amer. Math. Monthly 107(9), 844–862 (2000)
S.B. Nadler Jr., Continuum Theory: An Introduction (Marcel Dekker Inc, New York, 1992)
B. R. Gelbaum, J. M. H. Olmsted, Counterexamples in Analysis. Dover Publications, (2003)
E.R. McMillan, On continuity conditions for functions. Pacific J. Math. 32, 479–494 (1970)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Copyright information
© 2023 The Author(s), under exclusive license to Springer Nature Singapore Pte Ltd.
About this chapter
Cite this chapter
Kainth, S.P.S. (2023). Connectedness. In: A Comprehensive Textbook on Metric Spaces. Springer, Singapore. https://doi.org/10.1007/978-981-99-2738-8_6
Download citation
DOI: https://doi.org/10.1007/978-981-99-2738-8_6
Published:
Publisher Name: Springer, Singapore
Print ISBN: 978-981-99-2737-1
Online ISBN: 978-981-99-2738-8
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


 instead of
instead of 
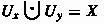 . (Such an X is called a totally separated space.)
. (Such an X is called a totally separated space.)
 . Without loss of generality, we can suppose that there is a rational number r and a subsequence
. Without loss of generality, we can suppose that there is a rational number r and a subsequence 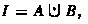 for some disjoint nonempty sets A and B, open in I. Pick any
for some disjoint nonempty sets A and B, open in I. Pick any  be a separation of A. Then
be a separation of A. Then  is a separation of
is a separation of  . Since
. Since 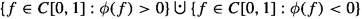
 . We claim that for every
. We claim that for every 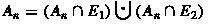 and both
and both  is connected, either
is connected, either