A Pro Rata Definition of the Fractional-Order Derivative

Abstract

In this paper a novel definition of the fractional-order derivative operator will be introduced. This operator will be called “pro rata” due to its ratio form as well as its geometric behavior that it is proportional to the fractional-order value. Some properties and theorems will be investigated. As an inverse of the fractional-order derivative operator, the integral of fractional order will be introduced. Some illustrative examples will be given.

1 Introduction

Non-integer calculus is the calculus of differentiation and integration of arbitrary orders (real or complex), called fractional-order derivatives and integrals, which generalizes the concept of differentiation and fold integration of integer-order [19, 21]. The history of non-integer calculus set out approximately in the meanwhile when the traditional calculus was recognized. It was early reported in a letter between the mathematical geniuses Leibniz and L’Hôpital in 1695, where the semiderivative’s idea was proposed. From that time forward, a lot of well-known physicists and mathematicians have mainly investigated fractional-order derivatives and integrals in a purely mathematical context, without its real applications, the basic concepts being connected with the names of Grunwald, Letnikov, Riemann, Abel, Liouville, and many more. But over the past few decades, it was turned out that the non-integer calculus has gained much attention as a result of its common appearance in different implementations in the scopes of engineering, electrical networks, fluid mechanics, diffusive transport, control theory, optics and signal processing, etc. [1,2,3,4,5, 7, 8, 16, 26, 27]. It should be noted that in current literature the terms “derivative” is used for positive orders and “integral” (for negative orders).

In the scope of mathematics, there exist several definitions of fractional-order differentiation and integration in the literature presently, involving Caputo [9, 10], Riemann-Liouville [11, 20], Crünwald-Letnikov [14], Riesz [24, 25], Weyl [6, 24, 25], Jumarie [15], Hadamard [24, 25]. The most famous definition that has been popularized is due to Riemann and Liouville, which depends in its construction on the nth-Cauchy’s integral formula that relies only on a straightforward integration. The definition is obtained as follow: Let $a, T, \alpha \in \mathbb {R}$ such that $a < T$, $n = \max \{0, [\alpha ] + 1\}$ and f(t) be an integrable function on (a, T). For $n > 0$, if f(t) is n-times differentiable function on (a, T) except on a set of measure zero, then for $t\in (a, T)$

$$\begin{aligned} ^{R}D^{\alpha }_{a}f(t) =\frac{1}{\varGamma (n-\alpha )}\, \frac{d^{n}}{dt^{n}}\, \int _{a}^{t}\frac{f(x)}{(t-x)^{\alpha -n+1}}\,dx= \frac{d^{n}}{dt^{n}}\bigg [ \,^{R}I_{a}^{n-\alpha } f(t) \bigg ] \end{aligned}$$

(1)

where $I_{a}^{\alpha }$ is the fractional integral operator of order $\alpha >0$. In particular, this operator can be outlined as the convolution integral of the function $t^{\alpha -1}$ and the function f itself, i.e.,

$$\begin{aligned} ^{R}I_{a}^{\alpha } f(t)= \frac{1}{\varGamma (\alpha )} \int _{a}^{t}(t-x)^{\alpha -1} f(x)\, dx \end{aligned}$$

(2)

where $\varGamma (\cdot )$ is the gamma function, which is defined by

$$\begin{aligned} \varGamma (z)=\int _{0}^{\infty }e^{-t}t^{z-1}dt, \quad \mathfrak {R}e(z)>0. \end{aligned}$$

(3)

In fact, formula (2) is a generalized formulation of the following Cauchy’s formula for repeated integration of a continuous function f on $\mathbb {R}$, if $\alpha \in \mathbb {N}$ and $(n-1)!$ is replaced by its generalization $\varGamma (\alpha )$, see [22]:

$$\begin{aligned} \int _{a}^{s}\int _{a}^{s_{1}}\int _{a}^{s_{2}} \dots \int _{a}^{s_{n-1}}f(s_{n})ds_{n}ds_{n-1}\dots ds_{2}ds_{1}= \frac{1}{(n-1)!}\int _{a}^{s}(s-t)^{n-1}f(t)dt, \end{aligned}$$

(4)

for $n\in \mathbb {N}$, $a,s\in \mathbb {R},\, s>a$.

On the other hand, if $\alpha =k$ with $k\in \mathbb {N}$, then we have $n=k+1$ and also we get

$$\begin{aligned} ^{R}D^{k}_{a}f(t) =\frac{1}{\varGamma (1)}\, \frac{d^{k+1}}{dt^{k+1}}\, \int _{a}^{t}f(x)\,dx =\, \frac{d^{k}f(t)}{dt^{k}}. \end{aligned}$$

(5)

A useful alternative operator for the fractional-order Riemann-Liouville derivative operator was introduced originally by Caputo in 1967. This operator was then approved by Mainardi and Caputo in 1971 to be called later on by the fractional-order Caputo derivative operator. The definition of this operator can be defined as

$$\begin{aligned} ^{C}D^{\alpha }_{a}f(t) =\frac{1}{\varGamma (n-\alpha )}\, \int _{a}^{t}\frac{f^{(n)}(x)}{(t-x)^{\alpha -n+1}}\,dx, \quad n-1<\alpha <n \end{aligned}$$

(6)

It is clear that the fractional-order Caputo derivative operator is more limiting than the fractional-order Riemann-Liouville derivative operator. This is because it needs the existence of the nth-derivative of the function under consideration. At the same time, it is worth noting that the functions that not having the 1st-order derivative could have, in view of Riemann-Liouville sense, derivatives of fractional-order values less than one. In addition, it should be also noted that the fractional-order derivative of an arbitrary function does not need to be a continuous function at the origin and it does not need to be differentiable too.

However, the Caputo operator has confirmed its ability to greatly match with observational data that is typically used to describe the performance of several engineering and applied science problems. It is very important to point out that the Riemann-Liouville definition has certain drawbacks and limitations, especially in describing several real-life applications. This actually backs the fact that asserts these applications need certain definitions of the fractional-order derivative that can allow the usage of initial conditions that are physically interpretable. For instance, the fractional-order Riemann-Liouville derivative operator of a constant function does not equal zero. Besides, the fractional-order derivative of a given function will have a singularity at the origin, whenever it is constant at the origin. In this regard, it has been shown that the Caputo operator is highly advantageous for such tasks. In particular, such operator has an ability of using the initial conditions reported for the problems formulated by using certain differential equations of fractional order. Moreover, the fractional-order derivative of a constant function is zero by using this operator.

To this point, we have introduced two expressions of the fractional-order derivative operators. Actually, the existence of several expressions of the identical notion raises the query, are these definitions equivalent? The brief reply to this query in general is no, although the differentiation and integration operators are interchanged in the corresponding definitions of the Caputo fractional derivative and Riemann-Liouville fractional derivative. More particularly, it can be noted that, with the help of using Riemann-Liouville operator, the function at hand is first integrated $n-\alpha$-times and then differentiated n-times. On the other hand, with the help of using the Caputo operator, the same function is first differentiated n-times and then integrated $n-\alpha$-times. In general, the two aforesaid definitions cannot be coincided. That is

$$\begin{aligned} ^{R}D^{\alpha }f\ne \,^{C}D^{\alpha }f. \end{aligned}$$

(7)

However, it was shown in [13] that the above two definitions can be coincided if and only if the function f(x) together with its first $n-1$-derivatives vanish at $x=0$. More precisely, for $t>0$, $n-1<\alpha <n$, and $n\in \mathbb {N}$, we have

$$\begin{aligned} ^{C}D^{\alpha }f(t)= \,^{R}D^{\alpha }f(t) - \sum _{k=0}^{n-1} \frac{t^{k-\alpha }}{\varGamma (k+1-\alpha )} \, f^{(k)}(0). \end{aligned}$$

(8)

Proposition 1

Let $n-1<\alpha <n$, $n\in \mathbb {N}$, $\alpha \in \mathbb {R}$ and f(t) be a function such that $^{C}D^{\alpha }f(t)$ exists. Then the following properties for the Caputo fractional derivatives hold:

$$\begin{aligned} \lim _{\alpha \rightarrow n^-}\, ^{C}D^{\alpha }f(t)= & {} f^{(n)}(t), \end{aligned}$$

(9)

$$\begin{aligned} \lim _{\alpha \rightarrow {n-1}^+}\, ^{C}D^{\alpha }f(t)= & {} f^{(n-1)}(t)-f^{(n-1)}(0). \end{aligned}$$

(10)

In the same regard, it should be mentioned here that there is another operator for computing the fractional-order derivatives. This operator is called the Crünwald-Letnikov operator. It can be obtained under the assumption that assumes the function f(t) must be n-times continuously differentiable on [a, t]. However, the Crünwald-Letnikov operator can be defined as follows:

$$\begin{aligned} ^{G}D^{\alpha }_{a}f(t) = \sum _{k=0}^{n-1}\frac{f^{(k)}(a)}{\varGamma (-\alpha +k+1)}(t-a)^{-\alpha +k}+\frac{1}{\varGamma (n-\alpha )}\, \int _{a}^{t}\frac{f^{(n)}(x)}{(t-x)^{\alpha -n+1}}\,dx \end{aligned}$$

(11)

Therefore, by considering a category of functions f(t), possessing n-continuous derivatives for $t\ge 0$, as well as by means of carrying out some differentiations and frequent integrations by parts, the Riemann-Liouville operator can be inferred by the Crünwald-Letnikov operator.

It should be mentioned that all the definitions of fractional derivatives above satisfy the linearity property, that is

$$\begin{aligned} D^{\alpha }(\mu f(x)+\lambda g(x))=\mu D^{\alpha }f(x)+\lambda D^{\alpha }g(x). \end{aligned}$$

(12)

Recently in 2014 in [18], a novel straightforward fractional-order derivative definition called the conformable fractional derivative was proposed. This definition agrees with the traditional definitions of Riemann-Liouville and Caputo in dealing with polynomials. In particular, if $f:[0,\infty )\rightarrow \mathbb {R}$, then the conformable fractional derivative of order $\alpha$ of the function f can be outlined as follows:

$$\begin{aligned} T_{\alpha }f(t):=\lim _{\epsilon \rightarrow 0}\frac{f(t+\epsilon t^{1-\alpha })-f(t)}{\epsilon }, \quad \text {for\,all}\,t>0,\; \alpha \in (0,1). \end{aligned}$$

(13)

If f is $\alpha$-differentiable in some (0, a), $a>0$, and $\lim \limits _{t\rightarrow 0^{+}} f^{(\alpha )}(t)$ exists, then the fractional derivative at 0 is defined by $f^{(\alpha )}(0)=\lim \limits _{t\rightarrow 0^{+}} f^{(\alpha )}(t)$. The authors in [18] proved some properties for the above definition. For example, they proved that if f is differentiable, then $T_{\alpha }(f)(t)= t^{1-\alpha }\, f'(t)$. However, the zero-order derivative of a function does not return the function, i.e., $T_{0}f(t)\ne f(t)$, see [17, 23]. Besides, the derivative reported in (13) does not verify the index law; $T_{\alpha }T_{\beta }f(t)\ne T_{\alpha +\beta }f(t)$ for general $\alpha$ and $\beta$, and it does not verify the generalized Leibniz rule. However, it verifies the product rule,

$$\begin{aligned} T_{\alpha }(fg) = fT_{\alpha }(g) + gT_{\alpha }(f). \end{aligned}$$

(14)

Furthermore, the definition given in (13) satisfies the interpolation property. In other words, for $0<\alpha <1$, we have

$$\begin{aligned} \lim _{\alpha \rightarrow 1^{-}}{T_{\alpha } }f(t)=\frac{df}{dt}, \quad \lim _{\alpha \rightarrow 0^{+}}{T_{\alpha } }f(t)=t\frac{df}{dt}. \end{aligned}$$

(15)

For $n-1<\alpha <n$:

$$\begin{aligned} \lim _{\alpha \rightarrow n^{-}}{T_{\alpha } }f(t)=\frac{d^{n}f}{dt^n}, \quad \lim _{\alpha \rightarrow {n-1}^{+}}{T_{\alpha } }f(t)=t \frac{d^{n}f}{dt^n}, \end{aligned}$$

(16)

In addition, the author in [18] proved similar results to the classical Mean Value Theorem and Rolle’s Theorem.

The organization of this article is arranged in the following manner: In the next section, we propose a new definition of the derivative of order $\alpha$ where $\alpha \in [0,1]$, and a general definition of derivatives of higher order, then we prove some important properties. In Sect. 3, we introduce a generalized definition of the integral of order $\alpha$. We conclude the paper with some remarks in Sect. 4.

2 Fractional Derivative

In this section, we give our new definition of the derivative of order $\alpha$ of a continuous function f at a point x and prove several results that are close to those found in classical calculus.

Definition 1

Let f(x) be a continuous function on the interval $(x-\epsilon ,x+\epsilon )$ where $\epsilon >0$. The derivative of order $\alpha \in [0,1]$ is defined by

$$\begin{aligned} D^{\alpha }f(x)=\frac{d^{\alpha }f}{dx^{\alpha }}= \lim _{h\rightarrow 0} \frac{\alpha f(x+h)+[(1-\alpha )h-\alpha ] f(x)}{h} \end{aligned}$$

(17)

If the derivative of f of order $\alpha$ exists, then we will say that f is $\alpha$-differentiable. Notice that if a function f(x) is differentiable on an interval [a, b] then the derivative $D^{\alpha }f$ is defined. This leads to the following theorem.

Theorem 1

Let f(x) be a continuous function on the interval [a, b]. If $0<\alpha \le 1$ and $x\in [a,b]$, then $D^{\alpha }f(x)$ exists if and only if $f'(x)$ exists. Consequently,

$$\begin{aligned} D^{\alpha }f(x)=(1-\alpha )f(x) + \alpha f'(x), \quad 0<\alpha <1. \end{aligned}$$

(18)

Proof

Let $x\in [a,b]$. First assume that $D^{\alpha }f(x)$ exists, hence the limit in (17) exists, and

$$\begin{aligned} \alpha \, \lim _{h\rightarrow 0} \frac{f(x+h)-f(x)}{h}+(1-\alpha )f(x)= D^{\alpha } f(x) \end{aligned}$$

(19)

hence,

$$\begin{aligned} \lim _{h\rightarrow 0} \frac{f(x+h)-f(x)}{h}=\frac{\alpha -1}{\alpha }f(x)+\frac{1}{\alpha } D^{\alpha } f(x). \end{aligned}$$

(20)

This implies that

$$\begin{aligned} f'(x)=\frac{\alpha -1}{\alpha }f(x)+\frac{1}{\alpha } D^{\alpha } f(x) \end{aligned}$$

(21)

exist. Conversely, assume that

$$\begin{aligned} f'(x)= \lim _{h\rightarrow 0} \frac{f(x+h)-f(x)}{h} \end{aligned}$$

(22)

exists, then

$$\begin{aligned} \lim _{h\rightarrow 0} \frac{f(x+h)-f(x)}{h}+(1-\alpha )f(x) = \lim _{h\rightarrow 0} \frac{\alpha f(x+h)+[(1-\alpha )h-\alpha ] f(x)}{h} \end{aligned}$$

(23)

exists.

It follows that, if a function f is $\alpha$-differentiable, $\alpha \in (0,1]$ at $x_{o}\in (a,b)$, then f is continuous at $x_{o}$.

Example 1

Using formula (18) we can compute the derivative of order $\alpha$ of some functions, for example:

• 1. Let $f(x)=c$, the constant function. Then $D^{\alpha }(f)=(1-\alpha )c$.

• 2. Let $f(x)=Ax+B$. Then $D^{\alpha }(f)=(1-\alpha )(Ax+B)+\alpha A$.

• 3. Let $f(x)=x^{p}$. Then $D^{\alpha }(f)=(1-\alpha )x^{p}+\alpha p x^{p-1}$.

• 4. Let $f(x)=e^{x}$. Then $D^{\alpha }(f)=e^{x}$.

For higher order derivatives case we can generalize the definition to the following:

Definition 2

Let n be a positive integer and $\alpha \in [n,n+1]$. If f(x) is an $n+1$ differentiable on [a, b], then

$$\begin{aligned} \begin{aligned} D^{\alpha }f&= \lim _{h\rightarrow 0} \frac{1}{h}\left( (n+1-\alpha ) \left( f^{(n-1)}(x+h)-f^{(n-1)}(x)\right) \right. \\&+(\alpha -n)\left. \left( f^{(n)}(x+h)-f^{(n)}(x)\right) \right) . \end{aligned} \end{aligned}$$

(24)

Similar argument used in Theorem 1 shows that

$$\begin{aligned} D^{\alpha }f =\frac{d^{\alpha }f}{dx^{\alpha }}= (n+1-\alpha )\frac{d^{n}f}{dx^{n}}+(\alpha -n)\frac{d^{n+1}f}{dx^{n+1}}. \end{aligned}$$

(25)

We notice from Definition 2 of the fractional derivative of order $\alpha$ that when the parameter $\alpha$ varies from the integer n to the integer $n+1$ then the fractional derivative of order $\alpha$ varies continuously from the $n^th$ derivative to the $(n)^{th}$ derivative with

$$\begin{aligned} \lim _{\alpha \rightarrow n^{+}} D^{\alpha }f=\frac{d^n f}{dx^n} \quad \text {and}\quad \lim _{\alpha \rightarrow n+1^{-}} D^{\alpha }f=\frac{d^{n+1} f}{dx^{n+1}} \end{aligned}$$

and hence

$$\begin{aligned} \lim _{\alpha \rightarrow n} D^{\alpha }f=\frac{d^n f}{dx^n}. \end{aligned}$$

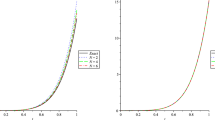
This desired property is not confirmed in many other definitions of the fractional derivative. For the illustration of this property see Fig. 1.

It can be shown that in the case of $\alpha$ is an integer, this definition reduces to the standard definition of the $n^{th}$-derivative of f(x). This shows that our definition of the derivative of order $\alpha$ is a generalization of the integer-order derivative. Now we are going to obtain some general properties of our new definition of the derivative of order $\alpha$. First, the linearity of the differential operator $D^{\alpha }$ is ensured by the following theorem:

Theorem 2

Let n be a non-negative integer and $\alpha \in [n,n+1]$. If f(x) and g(x) are two functions such that both $D^{\alpha }f$ and $D^{\alpha }g$ exists. Then the derivative of order $\alpha$ is a linear operator, i.e.,

$$\begin{aligned} D^{\alpha }\left( \lambda f(x)+\mu g(x)\right) =\lambda D^{\alpha }f(x) +\mu D^{\alpha }g(x), \end{aligned}$$

(26)

for any constants $\lambda ,\,\mu$.

Proof

The proof follows directly from Eq. (25) and the linearity of the limit.

This definition of the derivatives of order $\alpha$ carries with it some important properties, that will show importance when solving equations involving integrals and derivatives of general order.

Proposition 2

(The Product Rule of Fractional Derivative)

• 1. If $0\le \alpha \le 1$, and f, g are two differentiable functions, then

  $$\begin{aligned} D^{\alpha }(fg)= \alpha \left( fg'+f'g\right) + (1-\alpha )fg. \end{aligned}$$

  (27)

• 2. Let n be a non-negative integer. If $n\le \alpha \le n+1$, and f, g are two $(n+1)$-differentiable functions, then

  $$\begin{aligned} D^{\alpha }(fg)= (\alpha -n) \sum _{k=0}^{n+1}\left( D^{k}f\right) \,\left( D^{n+1-k}g\right) + (n+1-\alpha ) \sum _{k=0}^{n}\left( D^{k}f\right) \,\left( D^{n-k}g\right) . \end{aligned}$$

  (28)

Proposition 3

(The Iterated Fractional Derivative) Let n be a non-negative integer, and $n\le \alpha \le n+1$. We denote the $2^{nd}$-iterated fractional derivative $D^{\alpha }D^{\alpha }f$ by $(D^{\alpha })^{2}f$. Then

$$\begin{aligned} (D^{\alpha })^{2}f =(\alpha -n)^{2}f^{(2n+2)} + 2(\alpha -n)(n+1-\alpha )f^{(2n+1)} + (n+1-\alpha )^{2}f^{(2n)}. \end{aligned}$$

(29)

In general, for a positive integer k, we write $(D^{\alpha })^{k}f=D^{\alpha }D^{\alpha }\dots D^{\alpha } f$, k times, then the kth-iterated derivative of f is given by

$$\begin{aligned} (D^{\alpha })^{k}f=\sum _{j=0}^{k} \left( \begin{array}{c} k \\ j \\ \end{array} \right) (\alpha -n)^{j} (n+1-\alpha )^{k-j} \, f^{(kn+j)}. \end{aligned}$$

(30)

The following theorem shows that the derivative of order $\alpha$ defined in (24) is commutative.

Theorem 3

Let n, m be two non-negative integers, and f be an $(n+m+2)$ differentiable function on (a, b). If $\alpha \in [n,n+1]$ and $\beta \in [m,m+1]$, then

$$\begin{aligned} D^{\alpha }D^{\beta }f(x)=D^{\beta } D^{\alpha } f(x), \quad \forall x\in (a,b). \end{aligned}$$

(31)

Proof

To begin with, let $x\in (a,b)$, if we apply (25) twice we get

$$\begin{aligned} D^{\alpha }\left( D^{\beta }f(x)\right)= & {} D^{\alpha }\left( (\beta -m)f^{(m+1)}(x)+ (m+1-\beta )f^{(m)(x)} \right) \\= & {} (\alpha -n)(\beta -m)f^{(n+m+2)}(x)\\&\;+(\alpha -n)(m+1-\beta )f^{(n+m+1)}(x)\\&\;+ (n+1-\alpha )(\beta -m)f^{(n+m+1)}(x)\\ {}&\;+(n+1-\alpha )(m+1-\beta )f^{(n+m)}(x). \end{aligned}$$

Similarly,

$$\begin{aligned} D^{\beta }\left( D^{\alpha }f(x)\right)= & {} D^{\beta }\left( (\alpha -n)f^{(n+1)}(x)+ (n+1-\alpha )f^{(n)(x)} \right) \\= & {} (\beta -m)(\alpha -n)f^{(n+m+2)}(x)\\&\;+(\beta -m)(n+1-\alpha )f^{(n+m+1)}(x)\\&\;+ (m+1-\beta )(\alpha -n)f^{(n+m+1)}(x)\\&\;+(m+1-\beta )(n+1-\alpha )f^{(n+m)}(x). \end{aligned}$$

Hence, $D^{\alpha }D^{\beta }f(x)=D^{\beta } D^{\alpha } f(x)$, for any $x\in (a,b)$.

We noticed that the definition (18) is equivalent to the classical definition of the first derivative of a function f. This suggests that there are corresponding results similar to the classical Rolle’s theorem and the Mean Value theorem for the derivative of order $\alpha$ definition, as we prove in the next theorems.

Theorem 4

(Rolle’s Theorem for Derivative of Order $\alpha$) Let $f:[a,b]\rightarrow \mathbb {R}$ be a continuous function on [a, b] and $\alpha$-differentiable on (a, b) for some $\alpha \in [0,1]$. If $f(a)=f(b)$, then there exists $c\in (a,b)$ such that

$$\begin{aligned} D^{\alpha }f(c)=(1-\alpha )f(c). \end{aligned}$$

(32)

Proof

Since f is $\alpha$-differentiable for $\alpha \in [0,1]$ then f is differentiable on (a, b). Hence, by the classical Rolle’s theorem, there exists $c\in (a,b)$ such that $f'(c)=0$. Consequently, by Eq. (18),

$$\begin{aligned} D^{\alpha }f(c)=\alpha f'(c)+(1-\alpha )f(c)= (1-\alpha )f(c), \quad 0<\alpha <1 \end{aligned}$$

(33)

completing the proof.

The following result is a direct consequence of the ordinary mean value theorem.

Theorem 5

(Mean Value Theorem for Derivative of order $\alpha$) Let $f:[a,b]\rightarrow \mathbb {R}$ be a continuous function on [a, b] and differentiable on (a, b). Then there exists $c\in (a,b)$ such that

$$\begin{aligned} D^{\alpha }f(c)=\alpha \, \left( \frac{f(b)-f(a)}{b-a}\right) + (1-\alpha )f(c), \quad 0<\alpha <1. \end{aligned}$$

(34)

Proof

The asserted conclusion follows directly by applying Eq. (18).

The following theorem is a general version of Rolle’s theorem for the derivative of order $\alpha$.

Theorem 6

(Generalized Rolle’s Theorem for Derivative) Let $f:[a,b]\rightarrow \mathbb {R}$ be a continuous function on [a, b] and n times differentiable on (a, b). If $f(x)=0$ at the $n+1$ distinct points $\{x_{i}\}_{i=0}^{n}$ such that $a\le x_{0}< x_{1}< \dots < x_{n}\le b$, then there exists $c\in (x_{0},x_{n})$, and hence in (a, b), such that

$$\begin{aligned} D^{\alpha }f(c)=(n-\alpha )f^{(n-1)}(c), \end{aligned}$$

(35)

for any $\alpha \in [n-1,n]$.

Proof

Since f is n-times differentiable on (a, b) then by the ordinary generalized Rolle’s theorem [12, p. 549], there exists $c\in (a,b)$ with $f^{(n)}(c)=0$. If $n-1<\alpha <n$, then by (25) we have

$$\begin{aligned} D^{\alpha }f(c)=(\alpha -n+1)f^{(n)}(c)+ (n-\alpha )f^{(n-1)}(c) , \quad n-1<\alpha <n \end{aligned}$$

(36)

simple computations leads to (35).

Proposition 4

If f is n-differentiable at a point $x=c$, for some positive integer n, and

$$\begin{aligned} f(c)=f'(c)=f''(c)=\dots =f^{(n)}(c), \end{aligned}$$

(37)

then $D^{\alpha }f(c)=f(c)$ for any $\alpha \in [0,n]$.

Proposition 5

If f is differentiable on [a, b], and $f(x)\in [c,d]$, $f'(x)\in [c,d]$, for all $x\in [a,b]$, then $D^{\alpha }f(x)\in [c,d]$ for all $x\in [a,b]$ and $\alpha \in [0,1]$.

The following propositions give some geometric representations of the derivative of order $\alpha$ defined in the Definition 1.

Proposition 6

Let f be differentiable on [a, b].

• (a) If $f(x)\le f'(x)$ for all $x\in [a,b]$, then $f(x)\le D^{\alpha }f(x) \le f'(x)$ for all $x\in [a,b]$, $\alpha \in [0,1]$,

• (b) If $f'(x)\le f(x)$ for all $x\in [a,b]$, then $f'(x)\le D^{\alpha }f(x) \le f(x)$ for all $x\in [a,b]$, $\alpha \in [0,1]$.

We note that proposition 6 stated that the graph of $D^\alpha f(t)$ for $0<\alpha <1$ always lies between the functions f(t) and $f'(t)$, for example, the fractional derivative using our definition for $f(t)=\frac{1}{2} \sin (t^2)$ for different values of $\alpha$ is shown in Fig. 1.

Fig. 1

The graph of $D^\alpha f(t)$ where $f(t)=\frac{1}{2} \sin (t^2)$ for $\alpha =$ 0, 0.2, 0.5, 0.7, and 1

Proposition 7

If f is twice differentiable on [a, b] and f and $f'$ are increasing (decreasing) on [a, b], then the graph of $D^{\alpha }f$ is increasing (decreasing) on [a, b], for all $\alpha \in [0,1]$.

Proposition 8

If f is $3^{rd}$-differentiable on [a, b] and f and $f'$ are concave up (concave down) on [a, b], then the graph of $D^{\alpha }f$ is concave up (concave down) on [a, b], for all $\alpha \in (0,1)$.

Proposition 9

For $\alpha \in [0,1]$,

$$\begin{aligned} (1-\alpha )\bigg ( \text {Area\; between} \; f(x)\; \text {and}\;D^{\alpha }f(x)\bigg )=\alpha \bigg (\text {area\; between}\; f'(x) \; \text {and} \; D^{\alpha }f(x)\bigg ). \end{aligned}$$

(38)

Proof

The area between f(x) and $D^{\alpha }f(x)$ over an interval I is given by

$$\begin{aligned} \int _{I}|D^{\alpha }f(x)-f(x)|\,dx= \int _{I}|((1-\alpha )f(x)+\alpha f'(x)) -f(x)|\,dx=\alpha \int _{I}|f(x)-f'(x)|\,dx. \end{aligned}$$

(39)

Similar computations gives that the area between $f'(x)$ and $D^{\alpha }f(x)$ over the interval I is $(1-\alpha ) \int \limits _{I}|f(x)-f'(x)|\,dx$, the conclusion follows immediately.

Recall that a continuously differentiable function is monotone in some interval [a, b] if and only if its first derivative does not change its sign there. We now state general results involving derivatives of order $\alpha$ holds, the proofs are based on the standard definition of limits and the fact that $f'(x)=\lim \limits _{\alpha \rightarrow 1^{-}}D^{\alpha }f(x)$.

Proposition 10

Let $f\in C^{1}[a,b]$.

• 1. If there exists $\alpha _{o}\in [0,1)$ such that $D^{\alpha }f(x)>0$ for all $x\in [a,b]$ and every $\alpha \in (\alpha _{0},1)$, then f is increasing on [a, b]. ,

• 2. If there exists $\alpha _{o}\in [0,1)$ such that $D^{\alpha }f(x)<0$ for all $x\in [a,b]$ and every $\alpha \in (\alpha _{0},1)$, then f is decreasing on [a, b].

Proposition 11

Let $f\in C^{1}[a,b]$.

• 1. If f is increasing on [a, b] then for $x\in [a,b]$ there exists $\alpha _{x}\in (0,1)$ such that $D^{\alpha }f(x)\ge 0$ for all $\alpha \in (\alpha _{x},1)$.

• 2. If f is decreasing on [a, b] then for $x\in [a,b]$ there exists $\alpha _{x}\in (0,1)$ such that $D^{\alpha }f(x)\le 0$ for all $\alpha \in (\alpha _{x},1)$.

Proposition 12

If for all $x\in [a,b]$, $D^{\alpha }f(x)= 0$ and $D^{\beta }f(x)= 0$ for some $\alpha , \,\beta \in [0,1]$ with $\alpha \ne \beta$, then $f(x)=0$ for all $x\in [a,b]$.

Proposition 13

If $\alpha \in (0,1)$ then the Laplace transform of f(x) is given by

$$\begin{aligned} \mathcal {L}\{D^{\alpha }f\}= & {} \mathcal {L}\{(1-\alpha )f+\alpha f'\}\end{aligned}$$

(40)

$$\begin{aligned}= & {} (\alpha (s-1)+1)F(s) -f(0), \end{aligned}$$

(41)

where F(s) is the Laplace transform of f, and for $\alpha \in (n,n+1)$, the Laplace transform of f(x) is given by

$$\begin{aligned} \mathcal {L}\{D^{\alpha }f\}= & {} (n+1-\alpha ) \left( s^{n}F(s)- \sum _{k=0}^{n-1} s^{n-k}\, f^{(k)}(0)\right) \\&\; \quad + (\alpha -n) \left( s^{n+1}F(s)- \sum _{k=0}^{n} s^{n+1-k}\, f^{(k)}(0)\right) . \end{aligned}$$

3 Integral of Order $\alpha$

Now we introduce a generalized definition of the integral of order $\alpha$ as follows:

Definition 3

Let f(t) be a function defined on [a, x]. If $0<\alpha \le 1$, then the integral of order $\alpha$ of f is defined by

$$\begin{aligned} I^{\alpha }_{a}f(x)=\frac{1}{\alpha }\int _{a}^{x} \exp \left[ \left( \frac{1-\alpha }{\alpha }\right) (t-x) \right] f(t)\,dt. \end{aligned}$$

(42)

Observe that the integral of a continuous function f is an anti-derivative of f. We prove this property in the next theorem.

Theorem 7

Let f be a continuous function such that $I^{\alpha }_{a}f(x)$ exists $\alpha \in (0,1]$. Then

$$\begin{aligned} D^{\alpha }I^{\alpha }_{a}f(x)=f(x), \quad x\ge a. \end{aligned}$$

Proof

Since f is continuous, then $I^{\alpha }_{a}f$ is differentiable, hence, By (18) we have

$$\begin{aligned} D^{\alpha }(I^{\alpha }_{a}f)=\alpha \frac{d(I^{\alpha }_{a}f)}{dx}+(1-\alpha )(I^{\alpha }_{a}f)=f(x), \end{aligned}$$

(43)

solving we get

$$\begin{aligned} I^{\alpha }_{a}f= \frac{1}{\alpha }\int _{a}^{x} \exp \left[ \left( \frac{1-\alpha }{\alpha }\right) (t-x)\right] f(t)\,dt + c\exp \left[ \left( \frac{1-\alpha }{\alpha }\right) x\right] , \end{aligned}$$

(44)

where c is an arbitrary constant. Setting the constant c to be zero we get (42), with $D^{\alpha }I^{\alpha }f(x)=f(x)$.

Definition 3 can be generalized for the integral of higher order as follows:

Definition 4

Let f(t) be a function defined on [a, x]. If $n<\alpha \le n+1$, then the integral of order $\alpha$ of f is defined by

$$\begin{aligned} I^{\alpha }_{a}f(x)= \frac{1}{(n-1)!(\alpha -n)} \int _{a}^{x}(x-s)^{n-1}\int _{a}^{s} \exp \left[ \left( \frac{n+1-\alpha }{\alpha -n}\right) (t-s)\right] f(t)\,dt\,ds. \end{aligned}$$

(45)

Similar argument used in the proof of Theorem (7) can be used to show that the definition above satisfies the property $D^{\alpha }I^{\alpha }_{a}f(x)=f(x)$ for all $x\ge a$. Indeed, consider

$$\begin{aligned} (\alpha -n) \frac{d^{n+1}(I^{\alpha }_{a}f)}{dx^{n+1}}+(n+1-\alpha )\frac{d^{n}(I^{\alpha }_{a}f)}{dx^{n}}=f(x), \end{aligned}$$

(46)

equivalently,

$$\begin{aligned} (\alpha -n) \frac{d}{dx}\left( \frac{d^{n}(I^{\alpha }_{a}f)}{dx^{n}}\right) +(n+1-\alpha )\frac{d^{n}(I^{\alpha }_{a}f)}{dx^{n}}=f(x). \end{aligned}$$

(47)

Solving, we get

$$\begin{aligned} \frac{d^{n}(I^{\alpha }_{a}f)}{dx^{n}}= \frac{1}{\alpha -n} \int _{a}^{x} \exp \left[ \left( \frac{n+1-\alpha }{\alpha -n}\right) (t-x)\right] f(t)\,dt+ c \exp \left( \frac{n+1-\alpha }{\alpha -n}\, x\right) , \end{aligned}$$

(48)

where c is an arbitrary constant. Integrating the last expression n-times, and setting the arbitrary constants to be zero, we obtain (45).

Theorem 8

Let f be $\alpha$-function for $\alpha \in (0,1)$. Then for all $x>a$ we have

$$\begin{aligned} I^{\alpha }_{a}\left( D^{\alpha }f(x)\right) =f(x)- f(a)\,\exp \left[ \left( \frac{\alpha -1}{\alpha }\right) (x-a)\right] . \end{aligned}$$

Note that Theorems 7 and 8 show that the derivative of order $\alpha$ and the integral of order $\alpha$ of a function f on [a, b] are inverse of each other provided that $f(a)=0$.

4 Illustrative Examples

Example 2

$D^\alpha (e^x)=e^x$ for any $\alpha >0$. This desired property cannot be satisfied with other definitions.

Example 3

Consider the following initial value problem: $D^{1/2}y=1$, $y(0)=1$.

This equation can be reduced to: $\frac{dy}{dx}+y=2, y(0)=1$, which has the solution: $y=2-e^x$.

Example 4

Consider the following differential equation: $D^{3/2}y-D^{1/2}y=0$.

This equation can be reduced to: $\frac{d^2y}{dx^2}-y=0$. The initial value problem has the general solution: $y=c_1 e^x+c_2 e^{-x}$.

5 Conclusion

In this work, a novel definition of the fractional-order derivative operator has been presented. It has been found that the proposed definition is an extension of the classical operator. The following properties have been inferred:

• 1. For n is a non-negative integer and $n<\alpha <n+1$ we have: $D^\alpha f=(n+1-\alpha ) \frac{d^n f}{dx^n }+(\alpha -n)\frac{d^{n+1} f}{dx^{n+1} }$

• 2. $\lim _{\alpha \rightarrow n}{D^\alpha f}=\frac{df^n}{dx^n}$

• 3. Sum rule.

• 4. Product rules.

• 5. Commutative rule.

It is clear that solving fractional differential equations with the pro rata definition is easier than solving such equations with some other definitions. The computing of Laplace transforms and other transforms is also easier than computing them with some other definitions. The fractional-order integral operator has been also defined.