Energy Harvesting Study of Piezoelectric Vibration Harvester with Double Parallel Slender Structure

Abstract

In this paper, we use a cantilevered double parallel slender structure single deformation piezoelectric energy harvester as a model and combine it with the Lamb-Oseen vortex model, where the effect from fluid vortices is used as an external load, and a metal sheet is attached to the free end of the energy harvester for capturing the shear force generated by wind-generated vortices on the double beams model. The closed-form solution of the bending forced vibration of the piezoelectric energy harvester is solved by establishing the relevant model and deriving the equations. Euler- Bernoulli beam assumptions are used to develop a coupled electromechanical model for the harvester with an intermediate spring layer and a transverse damping is considered, and Green's functions and Laplace transform techniques are used to solve the vibration equations for the coupled piezoelectric vibration system. By solving for the voltage as a function of Green's functions and using Matlab software, we can obtain the functional relationship between the voltage of the harvester and the elastic coefficient of the interlayer and the position of the metal plate setting.

1 Modeling of Piezoelectric Energy Harvester with Cantilevered Double Straight Beams

1.1 Mechanical Equilibrium Control Equations with Electrically Coupled Effects

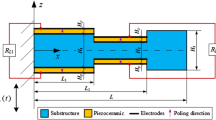
This paper investigates a cantilevered double-beam single-deformation piezoelectric energy harvester, which is subjected to external irregularly distributed loads $P_{1} ,P_{2}$. As shown in Fig. 1, the energy harvester is based on a homogeneous Eulerian beam model, which consists of a combination of an upper piezoelectric layer and a lower structural layer of the beam system, and the length of the piezoelectric beams are assumed to be $L$.

Fig. 1.

Cantilevered double beams single deformation piezoelectric energy harvester

Fig. 2.

Cross-section of piezoelectric energy harvester

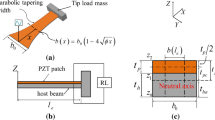
Figure 2 shows a cross-section of a single-deformation piezoelectric energy harvester, where: $b_{s}$ is the width of the beam structural layer; $b_{p}$ is the width of the piezoelectric layer; $h_{s}$ is the width of the beam structural layer; $h_{p}$ is the thickness of the piezoelectric layer; $h_{a}$ is the distance from the neutral axis (NA) to the lowermost surface of the beam structural layer; $h_{b}$ is the distance from the neutral axis (NA) to the bottom of the piezoelectric layer, and $h_{c}$ is the distance from the neutral axis (NA) to the top surface of the piezoelectric layer.

When we consider an air damping coefficient $c_{a}$, the vibration control equations for a double beams system can be written as [1,2,3]:

$$ \frac{{\partial^{2} M_{1} (x,t)}}{{x^{2} }} + c_{a} \frac{{\partial w_{rel1} (x,t)}}{\partial t} + m\frac{{\partial^{2} w_{rel1} (x,t)}}{{\partial t^{2} }} + K(w_{1} - w_{2} ) = P_{1} $$

(1)

$$ \frac{{\partial^{2} M_{2} (x,t)}}{{x^{2} }} + c_{a} \frac{{\partial w_{rel2} (x,t)}}{\partial t} + m\frac{{\partial^{2} w_{rel2} (x,t)}}{{\partial t^{2} }} + K(w_{2} - w_{1} ) = P_{2} $$

(2)

where $\partial w_{rel} (x,t)$ is the transverse deflection of the beam, $M(x,t)$ is the internal bending moment of the beam, $c_{a}$ is the viscous air damping coefficient, and $m$ is the mass per unit length of the beam.

In order to obtain an expression for the internal bending moment $M(x,t)$ of the beams, we can utilize the intrinsic relationship between the piezoelectric layer and the structural layer of the beams [4], and brought into the Eqs. (1)(2):

$$ \begin{gathered} (EI)_{eff} \frac{{\partial^{4} w_{rel1} (x,t)}}{{\partial x^{4} }} + c_{a} \frac{{\partial w_{rel1} (x,t)}}{\partial t} + m\frac{{\partial^{2} w_{rel1} (x,t)}}{{\partial t^{2} }} + K(w_{1} - w_{2} ) \hfill \\ + \vartheta v_{1} (t)\left[ {\frac{{d\delta (x - x_{1} )}}{dx} - \frac{{d\delta (x - x_{2} )}}{dx}} \right] = P_{1} \hfill \\ \end{gathered} $$

(3)

$$ \begin{gathered} (EI)_{eff} \frac{{\partial^{4} w_{rel2} (x,t)}}{{\partial x^{4} }} + c_{a} \frac{{\partial w_{rel2} (x,t)}}{\partial t} + m\frac{{\partial^{2} w_{rel2} (x,t)}}{{\partial t^{2} }} + K(w_{2} - w_{1} ) \hfill \\ + \vartheta v_{2} (t)\left[ {\frac{{d\delta (x - x_{1} )}}{dx} - \frac{{d\delta (x - x_{2} )}}{dx}} \right] = P_{2} \hfill \\ \end{gathered} $$

(4)

where: $\delta (x)$ is the Dirac function, $(EI)_{eff}$ is the bending stiffness of the composite cross-section, $\vartheta$ is the coupling coefficient, they can be expressed as:

$$ (EI)_{eff} = \frac{{E_{s} b_{s} (h_{b}^{3} - h_{a}^{3} ) + E_{p} b_{p} (h_{c}^{3} - h_{b}^{3} )}}{3} $$

(5)

$$ \vartheta = - \frac{{E_{p} b_{p} d_{31} }}{{2h_{p} }}(h_{c}^{2} - h_{b}^{2} ) $$

(6)

1.2 Control Equations for Circuits with Mechanical Coupling Effects

Equations (3)(4) are the vibration control equations for the double beams system under electrical coupling, we utilize the following piezoelectric intrinsic relations [4]:

$$ D_{y} (x,t) = d_{31} E_{p} \varepsilon_{xx} (x,t) - \varepsilon_{33}^{s} \frac{v(t)}{{h_{p} }} $$

(7)

where $D_{y} (x,t)$ is the potential shift parallel to the beam thickness direction, $\varepsilon_{33}^{s}$ is the dielectric constant, and $\varepsilon_{xx} (x,t)$ is the average bending strain.

The bending deformation of the structure will generate a potential shift in the piezoelectric layer, which will be collected by the electrodes, and the charge can be obtained by integrating the potential shift over the electrode region $q(t)$.Since the current $i_{i} (t)$ is related to the capacitance, the voltage across the resistor can be expressed as [4]:

$$ v_{i} (t) = R_{li} i_{i} (t) = - R_{li} \left[ {\int_{{x_{1} }}^{{x_{2} }} {d_{31} E_{p} h_{pc} b_{p} \frac{{\partial^{2} w_{reli} (x,t)}}{{\partial x^{2} \partial t}}dx - \frac{{\varepsilon_{33}^{s} b_{p} (x_{2} - x_{1} )}}{{h_{p} }}\frac{{dv_{i} (t)}}{dt}} } \right] $$

(8)

2 Green's Function Solutions for Piezoelectric Vibrations of Double Straight Beams

2.1 Vibration and Piezoelectric Equations Solving

Assuming that the external transverse loads are time-harmonic loads, we can let the deflections and voltages take a similar form to the following, separating the time parameters from the displacements:

$$ p_{i} (x,t) = P_{i} (x)e^{i\Omega t} ,w(x,t) = W(x)e^{i\Omega t} ,v(t) = Ve^{i\Omega t} $$

(9)

Substitution of Eq. (9) into Eqs. (3) (4) and (8):

$$ W_{1}^{\prime \prime \prime \prime } + a_{2} W_{1} + a_{4} W_{2} = b_{2} P_{1} (x) - b_{3} V_{1} [\delta^{\prime}(x - x_{1} ) - \delta^{\prime}(x - x_{2} )] $$

(10)

$$ W_{2}^{\prime \prime \prime \prime } + c_{2} W_{2} + c_{4} W_{1} = d_{2} P_{2} (x) - d_{3} V_{2} [\delta^{\prime}(x - x_{1} ) - \delta^{\prime}(x - x_{2} )] $$

(11)

$$ \frac{{i\Omega C_{p} R_{l} + 1}}{{R_{l} }}V_{i} = - i\Omega \beta \int_{{x_{1} }}^{{x_{2} }} {W_{i}^{\prime \prime } } (x)dx $$

(12)

where:

$$ \begin{gathered} a_{2} = \frac{{i\Omega c_{a} - \mu_{1} \Omega^{2} + K}}{{E_{1} I_{1} }},a_{4} = - \frac{K}{{E_{1} I_{1} }},b_{2} = \frac{1}{{E_{1} I_{1} }},b_{3} = \frac{\vartheta }{{E_{1} I_{1} }} \hfill \\ c_{2} = \frac{{i\Omega c_{a} - \mu_{2} \Omega^{2} + K}}{{E_{2} I_{2} }},c_{4} = - \frac{K}{{E_{2} I_{2} }},d_{2} = \frac{1}{{E_{2} I_{2} }},d_{3} = \frac{\vartheta }{{E_{2} I_{2} }} \hfill \\ \end{gathered} $$

(13)

For a linear system, the principle of superposition should be satisfied. Therefore, the dynamic response of a double-beam system subjected to loads $P_{1} (x)$ and $P_{2} (x)$ is the sum of the responses of the systems subjected to $P_{1} (x)$ and $P_{2} (x)$ respectively. This shows that the solution of Eqs. (10) and (11) is the sum of the solutions of the following four cases.

Case 1:

$$ W_{1}^{\prime \prime \prime\prime } + a_{2} W_{1} + a_{4} W_{2} = b_{2} \delta (x - x_{0} ) $$

(14)

$$ W_{2}^{\prime \prime \prime \prime } + c_{2} W_{2} + c_{4} W_{1} = 0 $$

(15)

where $\delta ( \cdot )$ is the Dirac delta function [5, 6] and $x_{0}$ denotes the location where the unit harmonic load acts. Laplace transformations of Eqs. (14), (15):

$$ \begin{gathered} Q(s)\overline{W}_{1} (s) = (s^{4} + c_{2} )(s^{3} W_{1} (0) + s^{2} W_{1}^{\prime } (0) + sW_{1}^{\prime \prime } (0) + W_{1}^{\prime \prime \prime } (0) + b_{2} e^{{ - sx_{0} }} ) \hfill \\ - a_{4} (s^{3} W_{2} (0) + s^{2} W_{2}^{\prime } (0) + sW_{2}^{\prime \prime } (0) + W_{2}^{\prime \prime \prime } (0)) \hfill \\ \end{gathered} $$

(16)

$$ \begin{gathered} Q(s)\overline{W}_{2} (s) = (s^{4} + a_{2} )(s^{3} W_{2} (0) + s^{2} W_{2}^{\prime } (0) + sW_{2}^{\prime \prime } (0) + W_{2}^{\prime\prime\prime } (0)) \hfill \\ - c_{4} (s^{3} W_{1} (0) + s^{2} W_{1}^{\prime } (0) + sW_{1}^{\prime \prime } (0) + W_{1}^{\prime \prime \prime } (0) + b_{2} e^{{ - sx_{0} }} ) \hfill \\ \end{gathered} $$

(17)

$$ Q(s) = (s^{4} + a_{2} )(s^{4} + c_{2} ) - a_{4} c_{4} $$

(18)

Divide $Q(s)$ to the right end of the equations and perform an inverse transformation of $\overline{W}_{1} (s)$ and $\overline{W}_{2} (s)$:

$$ \begin{gathered} G_{11} (x,x_{0} ) = H(x - x_{0} )\phi_{11} (x - x_{0} ) + \phi_{21} (x)W_{1} (0) + \phi_{31} (x)W^{\prime}_{1} (0) + \phi_{41} (x)W_{1}^{\prime\prime } (0) \hfill \\ + \phi_{51} (x)W_{1}^{\prime \prime\prime } (0) + \phi_{61} (x)W_{2} (0) + \phi_{71} (x)W_{2}^{\prime } (0) + \phi_{81} (x)W_{2}^{\prime\prime } (0) + \phi_{91} (x)W_{2}^{\prime\prime\prime } (0) \hfill \\ \end{gathered} $$

(19)

$$ \begin{gathered} G_{12} (x,x_{0} ) = H(x - x_{0} )\phi_{12} (x - x_{0} ) + \phi_{22} (x)W_{1} (0) + \phi_{32} (x)W_{1}^{\prime } (0) + \phi_{42} (x)W_{1}^{\prime\prime } (0) \hfill \\ + \phi_{52} (x)W_{1}^{\prime\prime\prime } (0) + \phi_{62} (x)W_{2} (0) + \phi_{72} (x)W^{\prime}_{2} (0) + \phi_{82} (x)W_{2}^{\prime\prime } (0) + \phi_{92} (x)W_{2}^{\prime\prime\prime } (0) \hfill \\ \end{gathered} $$

(20)

The expression of $\varphi$ are displayed in Appendix A. Using the boundary conditions at $x = 0$, The terms in the Green's functions with a coefficient of 0 can be removed:

$$ \begin{gathered} G_{11} (x,x_{0} ) = H(x - x_{0} )\phi_{11} (x - x_{0} ) + \phi_{41} (x)W_{1}^{\prime\prime } (0) \hfill \\ + \phi_{51} (x)W_{1}^{\prime \prime \prime } (0) + \phi_{81} (x)W_{2}^{\prime \prime } (0) + \phi_{91} (x)W_{2}^{\prime \prime\prime } (0) \hfill \\ \end{gathered} $$

(21)

$$ \begin{gathered} G_{12} (x,x_{0} ) = H(x - x_{0} )\phi_{12} (x - x_{0} ) + \phi_{42} (x)W_{1}^{\prime\prime } (0) \hfill \\ + \phi_{52} (x)W_{1}^{\prime\prime\prime } (0) + \phi_{82} (x)W_{2}^{\prime\prime } (0) + \phi_{92} (x)W_{2}^{\prime\prime\prime } (0) \hfill \\ \end{gathered} $$

(22)

Using the boundary conditions at the end of $x = L$, we can derive the second and third order derivatives of the above equations to obtain the following matrix equation:

$$ \left[ {\begin{array}{*{20}c} {\phi^{\prime\prime}_{41} (L)} & {\phi^{\prime\prime}_{51} (L)} & {\phi^{\prime\prime}_{81} (L)} & {\phi^{\prime\prime}_{91} (L)} \\ {\phi^{\prime\prime\prime}_{41} (L)} & {\phi^{\prime\prime\prime}_{51} (L)} & {\phi^{\prime\prime\prime}_{81} (L)} & {\phi^{\prime\prime\prime}_{91} (L)} \\ {\phi^{\prime\prime}_{42} (L)} & {\phi^{\prime\prime}_{52} (L)} & {\phi^{\prime\prime}_{82} (L)} & {\phi^{\prime\prime}_{92} (L)} \\ {\phi^{\prime\prime\prime}_{42} (L)} & {\phi^{\prime\prime\prime}_{51} (L)} & {\phi^{\prime\prime\prime}_{82} (L)} & {\phi^{\prime\prime\prime}_{92} (L)} \\ \end{array} } \right] \cdot \left[ {\begin{array}{*{20}c} {W_{1\prime \prime } (0)} \\ {W_{1}^{\prime \prime \prime } (0)} \\ {W_{2}^{\prime \prime } (0)} \\ {W_{2}^{\prime \prime \prime } (0)} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} { - \phi^{\prime\prime}_{11} (L - x_{0} )} \\ { - \phi^{\prime\prime\prime}_{11} (L - x_{0} )} \\ { - \phi^{\prime\prime}_{12} (L - x_{0} )} \\ { - \phi^{\prime\prime\prime}_{12} (L - x_{0} )} \\ \end{array} } \right] $$

(23)

Case 2:

The Green's functions for case 2 can be obtained by solving the following equations:

$$ W_{1}^{\prime \prime \prime \prime } + a_{2} W_{1} + a_{4} W_{2} = 0 $$

(24)

$$ W_{2}^{\prime \prime \prime \prime } + c_{2} W_{2} + c_{4} W_{1} = d_{2} \delta (x - x_{0} ) $$

(25)

The solution process is similar to case 1, its Green's functions are expressed as:

$$ \begin{gathered} G_{21} (x,x_{0} ) = H(x - x_{0} )\overline{\phi }_{11} (x - x_{0} ) + \phi_{41} (x)W_{1}^{\prime \prime } (0) \hfill \\ + \phi_{51} (x)W_{1}^{\prime \prime \prime } (0) + \phi_{81} (x)W_{2}^{\prime \prime } (0) + \phi_{91} (x)W_{2}^{\prime \prime \prime } (0) \hfill \\ \end{gathered} $$

(26)

$$ \begin{gathered} G_{22} (x,x_{0} ) = H(x - x_{0} )\overline{\phi }_{12} (x - x_{0} ) + \phi_{42} (x)W_{1}^{\prime \prime } (0) \hfill \\ + \phi_{52} (x)W_{1}^{\prime \prime \prime } (0) + \phi_{82} (x)W_{2}^{\prime \prime } (0) + \phi_{92} (x)W_{2}^{\prime \prime \prime } (0) \hfill \\ \end{gathered} $$

(27)

The expression of $\overline{\varphi }$ are displayed in Appendix A. According to the superposition principle, the displacement solution can be expressed as:

$$ \left[ \begin{gathered} W_{11} (x) \hfill \\ W_{21} (x) \hfill \\ \end{gathered} \right] = \int_{0}^{L} {\left[ \begin{gathered} G_{11} (x;\xi ) \hfill \\ G_{12} (x;\xi ) \hfill \\ \end{gathered} \right]} P_{1} (\xi ) + \left[ \begin{gathered} G_{21} (x;\xi ) \hfill \\ G_{22} (x;\xi ) \hfill \\ \end{gathered} \right]P_{2} (\xi )d\xi $$

(28)

Case 3:

The Green's functions for case 3 can be obtained by solving the following equations:

$$ W_{1}^{\prime \prime \prime \prime } + a_{2} W_{1} + a_{4} W_{2} = b_{3} V_{1} \delta^{\prime}(x - x_{0} ) $$

(29)

$$ W_{2}^{\prime \prime \prime \prime } + c_{2} W_{2} + c_{4} W_{1} = 0 $$

(30)

The Green's functions can be solved in a similar way:

$$ \begin{gathered} G_{31} (x,x_{0} ) = V_{1} H(x - x_{0} )\overline{\overline{\phi }}_{11} (x - x_{0} ) + \phi_{41} (x)W_{1}^{\prime \prime } (0) \hfill \\ + \phi_{51} (x)W_{1}^{\prime \prime \prime } (0) + \phi_{81} (x)W_{2}^{\prime \prime } (0) + \phi_{91} (x)W_{2}^{\prime \prime \prime } (0) \hfill \\ \end{gathered} $$

(31)

$$ \begin{gathered} G_{32} (x,x_{0} ) = V_{1} H(x - x_{0} )\overline{\overline{\phi }}_{12} (x - x_{0} ) + \phi_{42} (x)W_{1}^{\prime \prime } (0) \hfill \\ + \phi_{52} (x)W_{1}^{\prime \prime \prime } (0) + \phi_{82} (x)W_{2}^{\prime \prime } (0) + \phi_{92} (x)W_{2}^{\prime \prime \prime } (0) \hfill \\ \end{gathered} $$

(32)

The expression of $\overline{\overline{\varphi }}$ are displayed in Appendix A.

Case 4:

The Green's functions for case 4 can be obtained by solving the following equations:

$$ W_{1}^{\prime \prime \prime \prime } + a_{2} W_{1} + a_{4} W_{2} = 0 $$

(33)

$$ W_{2}^{\prime \prime \prime \prime } + c_{2} W_{2} + c_{4} W_{1} = d_{3} V_{2} \delta^{\prime}(x - x_{0} ) $$

(34)

The Green's functions can be solved in a similar way:

$$ \begin{gathered} G_{41} (x,x_{0} ) = V_{2} H(x - x_{0} )\hat{\phi }_{11} (x - x_{0} ) + \phi_{41} (x)W_{1}^{\prime \prime } (0) \hfill \\ + \phi_{51} (x)W_{1}^{\prime \prime \prime } (0) + \phi_{81} (x)W_{2}^{\prime \prime } (0) + \phi_{91} (x)W_{2}^{\prime \prime \prime } (0) \hfill \\ \end{gathered} $$

(35)

$$ \begin{gathered} G_{42} (x,x_{0} ) = V_{2} H(x - x_{0} )\hat{\phi }_{12} (x - x_{0} ) + \phi_{42} (x)W_{1}^{\prime \prime } (0) \hfill \\ + \phi_{52} (x)W_{1}^{\prime \prime \prime } (0) + \phi_{82} (x)W_{2}^{\prime \prime } (0) + \phi_{92} (x)W_{2}^{\prime \prime \prime } (0) \hfill \\ \end{gathered} $$

(36)

The expressions of $\hat{\varphi }$ are displayed in Appendix A. According to the superposition principle, the displacements $W_{12}$ and $W_{22}$ can be expressed by the Green's functions $G_{31}$, $G_{32}$, $G_{41}$, $G_{42}$ and can be expressed as the following volume integrals.

$$ \begin{gathered} \left[ \begin{gathered} W_{12} (x) \hfill \\ W_{22} (x) \hfill \\ \end{gathered} \right] = \int_{0}^{L} {\left[ \begin{gathered} G_{31} (x;\xi ) \hfill \\ G_{32} (x;\xi ) \hfill \\ \end{gathered} \right]} [\delta (\xi - x_{2} ) - \delta (\xi - x_{1} )] \hfill \\ + \left[ \begin{gathered} G_{41} (x;\xi ) \hfill \\ G_{42} (x;\xi ) \hfill \\ \end{gathered} \right][\delta (\xi - x_{2} ) - \delta (\xi - x_{1} )]d\xi \hfill \\ \end{gathered} $$

(37)

2.2 Decoupling of Electromechanical Eulerian Double Beams Systems

According to the principle of superposition of linear systems, the steady state displacement $W_{1}$ can be divided into $W_{11} ,W_{12}$ two parts; similarly $W_{2}$ can be divided into $W_{21} ,W_{22}$ two parts. So, the expressions for $W_{1}$ and $W_{2}$ are:

$$ \begin{gathered} W_{1} = W_{11} + W_{12} = \int_{0}^{L} {G_{11} (x;\xi )} P_{1} (\xi ) + G_{21} (x;\xi )P_{2} (\xi )d\xi \hfill \\ + \int_{0}^{L} {G_{31} (x;\xi )} [\delta (\xi - x_{2} ) - \delta (\xi - x_{1} )] + G_{41} (x;\xi )[\delta (\xi - x_{2} ) - \delta (\xi - x_{1} )]d\xi \hfill \\ \end{gathered} $$

(38)

$$ \begin{gathered} W_{2} = W_{21} + W_{22} = \int_{0}^{L} {G_{12} (x;\xi )} P_{1} (\xi ) + G_{22} (x;\xi )P_{2} (\xi )d\xi \hfill \\ + \int_{0}^{L} {G_{32} (x;\xi )} [\delta (\xi - x_{2} ) - \delta (\xi - x_{1} )] + G_{42} (x;\xi )[\delta (\xi - x_{2} ) - \delta (\xi - x_{1} )]d\xi \hfill \\ \end{gathered} $$

(39)

Substituting Eqs. (38) (39) into Eq. (8) yields a functional relationship between the voltage and the Green's functions for the four cases:

$$ \begin{gathered} m_{1} V_{1} = m_{2} + m_{3} V_{2} \hfill \\ n_{1} V_{2} = n_{2} + n_{3} V_{1} \hfill \\ \end{gathered} $$

(40)

$$ \begin{gathered} m_{1} = \left( {\frac{{i\Omega C_{p} R_{l} + 1}}{{R_{l} }}} \right) + i\Omega \beta \int\limits_{{x_{1} }}^{{x_{2} }} {\overline{G}^{\prime\prime}_{31} (x;x_{2} )} - \overline{G}^{\prime\prime}_{31} (x;x_{1} )dx \hfill \\ m_{2} = - i\Omega \beta \int\limits_{{x_{1} }}^{{x_{2} }} {\left[ {\int_{0}^{L} {G_{11} (x;\xi )} P_{1} (\xi ) + G_{21} (x;\xi )P_{2} (\xi )d\xi } \right]}^{\prime \prime } dx \hfill \\ m_{3} = - i\Omega \beta \int\limits_{{x_{1} }}^{{x_{2} }} {\overline{G}^{\prime\prime}_{41} (x;x_{2} )} - \overline{G}^{\prime\prime}_{41} (x;x_{1} )dx \hfill \\ n_{1} = \left( {\frac{{i\Omega C_{p} R_{l} + 1}}{{R_{l} }}} \right) + i\Omega \beta \int\limits_{{x_{1} }}^{{x_{2} }} {\overline{G}^{\prime\prime}_{42} (x;x_{2} )} - \overline{G}^{\prime\prime}_{42} (x;x_{1} )dx \hfill \\ n_{2} = - i\Omega \beta \int\limits_{{x_{1} }}^{{x_{2} }} {\left[ {\int_{0}^{L} {G_{12} (x;\xi )} P_{1} (\xi ) + G_{22} (x;\xi )P_{2} (\xi )d\xi } \right]}^{\prime \prime } dx \hfill \\ n_{3} = - i\Omega \beta \int\limits_{{x_{1} }}^{{x_{2} }} {\overline{G}^{\prime\prime}_{32} (x;x_{2} )} - \overline{G}^{\prime\prime}_{32} (x;x_{1} )dx \hfill \\ \end{gathered} $$

(41)

The expressions for voltage we can easily derive from the algebraic Eq. (40) through the linear expressions for voltage $V_{1}$ and voltage $V_{2}$:

$$ V_{1} = \frac{{m_{2} n_{1} + m_{3} n_{2} }}{{m_{1} n_{1} - m_{3} n_{3} }},V_{2} = \frac{{m_{1} n_{2} + m_{2} n_{3} }}{{m_{1} n_{1} - m_{3} n_{3} }} $$

(42)

3 Eddy-Current Induced Vibration of Piezoelectric Energy Harvester

Fig. 3.

Schematic diagram of a piezoelectric energy harvester subjected to vortex shedding aerodynamic loads

As shown in Fig. 3, vortex shedding will generate aerodynamic loads. The Lamb-Oseen vortex model [7], which is used in this system, produces a vertical load that can be expressed as [8]:

$$ F_{v} = - \frac{1}{2}W_{f} \rho_{a} \int_{0}^{{L_{f} }} {(v_{c} \Phi r - \frac{{\Phi^{2} r^{2} }}{4})} dx $$

(43)

where $\rho_{a}$ is the air density; $W_{f}$ and $L_{f}$ are the width and length of the sheet, respectively; $D$ is the diameter of the solid cylinder, which is an immovable obstacle; $U_{0}$ is the mean fluid velocity; $r = ((x - x_{c} )^{2} + y_{c}^{2} )^{0.5}$ is the distance from the point $A(x,0)$ on the sheet to the center $C(x_{c} ,y_{c} )$ of the vortex, where $(x_{c} ,y_{c} )$ is the position and $v_{c}$ is the velocity of the center of the vortex; and the vortex strength $\Phi$ is:

$$ \Phi = (\Gamma_{0} /4\pi v_{e} t)exp( - r_{0}^{2} /4v_{e} t) $$

(44)

where $\Gamma_{0} = (U_{0} D)/2S_{t}$ is the initial velocity cycle, $S_{t}$ is the Strouhal number related to the Reynolds number, $r_{0}$ is the radius of the rigid vortex core [8], $v_{e}$ is the equivalent dissipation factor of the vortex, $t = d_{r} /U_{0}$, $d_{r}$ is the relative distance between the vortex center and the plate. In this study, the Reynolds number of $S_{t} = 0.21$ ranges from 10³ to 10⁵, corresponds to a flow rate of 0.05 to 5 m/s. In addition, $U_{0}$ can be expressed by the velocity $v_{c}$ [8].

When the vortex center is located at $y_{c} = 1.3 \times {D \mathord{\left/ {\vphantom {D 2}} \right. \kern-0pt} 2}$, the vortex coming off the cylinder is stable. When the vortex moves to the middle of the thin lobe, the equivalent harmonic force $F_{v}$ reaches its maximum value, i.e. $x_{c} = {{L_{f} } \mathord{\left/ {\vphantom {{L_{f} } 2}} \right. \kern-0pt} 2}$, $d_{r} = d$. Therefore, the expression of $F_{\max }$ [8]:

$$ F_{\max } = - \frac{1}{2}W_{f} \rho_{a} \int_{0}^{{L_{f} }} {\{ \Phi v_{c} } \sqrt {(x - \frac{{L_{f} }}{2})^{2} + (\frac{1.3D}{2})^{2} } - \frac{{\Phi^{2} }}{4}[(x - \frac{{L_{f} }}{2})^{2} + (\frac{1.3D}{2})^{2} ]\} dx $$

(45)

Substituting into Eq. (42) gives the expression for the voltage:

$$ \begin{gathered} V_{1} = - \frac{{i\Omega \beta \int\limits_{{x_{1} }}^{{x_{2} }} {\left[ {G^{\prime\prime}_{11} (x;L)\lambda F_{\max } + G^{\prime\prime}_{21} (x;L)(1 - \lambda )F_{\max } } \right]} dx \times n_{1} }}{{m_{1} n_{1} - m_{3} n_{3} }} \hfill \\ - \frac{{m_{3} \times i\Omega \beta \int\limits_{{x_{1} }}^{{x_{2} }} {\left[ {G^{\prime\prime}_{12} (x;L)\lambda F_{\max } + G^{\prime\prime}_{22} (x;L)(1 - \lambda )F_{\max } } \right]} dx}}{{m_{1} n_{1} - m_{3} n_{3} }} \hfill \\ \end{gathered} $$

(46)

$$ \begin{gathered} V_{2} = - \frac{{m_{1} \times i\Omega \beta \int\limits_{{x_{1} }}^{{x_{2} }} {\left[ {G^{\prime\prime}_{12} (x;L)\lambda F_{\max } + G^{\prime\prime}_{22} (x;L)(1 - \lambda )F_{\max } } \right]} dx}}{{m_{1} n_{1} - m_{3} n_{3} }} \hfill \\ - \frac{{i\Omega \beta \int\limits_{{x_{1} }}^{{x_{2} }} {\left[ {G^{\prime\prime}_{11} (x;L)\lambda F_{\max } + G^{\prime\prime}_{21} (x;L)(1 - \lambda )F_{\max } } \right]} dx \times n_{3} }}{{m_{1} n_{1} - m_{3} n_{3} }} \hfill \\ \end{gathered} $$

(47)

$$ V = V_{1} + V_{2} $$

(48)

4 Numerical Analysis

Through the computational derivation of the theory, we can get the expression of the voltage generated by the base model under vortex-induced vibration. In the following, we will explore the effects of different external excitation distributions and elasticity coefficients of springs on the voltage by setting up two sub-models without changing the boundary conditions and Green's functions, respectively.

4.1 Effect of External Excitation Distribution on Voltage

Since the position of the metal sheet in this model can be moved up and down, thus the magnitude of the external excitation force received by the two beams in the vibration model of the cantilevered double beams system can be changed, as shown in Fig. 4. We modeled the data by Matlab software, and after numerical analysis, we can get the magnitude of the voltage collected by the piezoelectric trap in different cases. As shown in Figs. 5, 6, 7.

Fig. 4.

Schematic diagram of piezoelectric energy harvester subjected to vortex shedding aerodynamic loads (without considering the spring layer)

In this model $\lambda$ is the external excitation distribution coefficient. Therefore the external excitation forces on the two beams are $F_{v1} = \lambda F_{v}$ and $F_{v2} = \left( {1 - \lambda } \right)F_{v}$ respectively.

Fig. 5.

Variation of V1 with aerodynamic load excitation frequency for different lambda

Fig. 6.

Variation of V2 with aerodynamic load excitation frequency for different lambda

Fig. 7.

Variation of piezoelectric energy harvester Voltage with Lambda when $\Omega = 2661$

Figures 5 and 6 show us the relationship between the voltage of the piezoelectric energy harvester and the frequency of the external excitation force, respectively. Since the physical properties of the two beams are set up the same way, the two beams produce peak voltages at the same frequency of the external excitation force, which is 3388 Hz as well as 9317 Hz. When we change the Lambda (i.e., we change the magnitude of the external excitation force applied to the two beams), the performance of the piezoelectric energy harvester's power generation changed, but it did not affect the frequency magnitude of the external excitation force corresponding to the peak voltage.

From Fig. 7, it can be seen that the voltage of the piezoelectric energy harvester varies linearly with the magnitude of the external excitation force for a certain frequency of the external excitation force, and the sum of the voltages generated by the two beams is a constant value.

4.2 Influence of the Elasticity Coefficient of the Middle Layer on the Voltage of a Piezoelectric Energy Harvester

In this model, as shown in Fig. 8. The two piezoelectric energy harvesters have a spring layer with an elasticity coefficient of $K$ between them. An external excitation force of magnitude both $0.5F_{v}$ is transmitted to the piezoelectric energy harvesters by setting two identical metal sheets mounted on the cantilever end of each of the two beams. Thus, the relationship between the elasticity coefficient of the middle layer and the voltage of the piezoelectric energy harvester is explored, as shown in Fig. 9.

Fig. 8.

Schematic of a piezoelectric energy harvester with an intermediate layer subject to vortex shedding aerodynamic loading

Fig. 9.

Variation of piezoelectric energy harvester voltage with elasticity coefficient of the middle layer, $\Omega$ = 2661.

Figure 9 shows the change rule of piezoelectric energy harvester voltage with the elasticity coefficient of the intermediate layer K when $\Omega$ = 2661. From this figure, it can be seen that: the power generation is highest when the intermediate layer is not added; when the elasticity coefficient is in the range of 0–0.7, the power generation efficiency of the double-beam system is fluctuating; when the elasticity coefficient is greater than 0.7, the constraint capacity of the double-beam system is strong, and the voltage fluctuates in a small range but the overall are smaller than the voltage of not adding the spring layer The voltage of the double-cantilever beams system fluctuates in a small range, but is generally smaller than that without the spring layer. Thus, the addition of an intermediate spring layer to the energy harvester of the double cantilever beams has an inhibiting effect on the power generation efficiency, and when the elasticity coefficient is too large, the generated voltage will gradually converge to a constant value.

5 Conclusions

In this paper, we build a double parallel cantilever energy harvesting system by using the vortex excitation force generated by vortex shedding as the external load. We discuss the effects of different sizes of external loads on the power generation efficiency of the dual-beam system; we also explore the effects on the voltage magnitude with the addition of an intermediate spring layer. The following are the main conclusions of this paper.

• (1) The voltage of each beam of the energy harvester of the double-parallel structure varies linearly with the magnitude of the external excitation force, but does not affect the frequency of the external excitation force corresponding to the peak voltage.

• (2) The addition of an intermediate layer will reduce the power generation efficiency of the double-parallel cantilever energy harvester to a certain extent, and the voltage will be bullied to fluctuate; when the elasticity coefficient of the intermediate layer is large, the voltage is suppressed and tends to be constant.

Appendix A

$$ \overline{\phi }_{11}^{(k)} (x) = - \sum\limits_{i = 1}^{8} {s_{i}^{k} A_{i} } (x)a_{4} d_{2} ;\overline{\phi }_{12}^{(k)} (x) = \sum\limits_{i = 1}^{8} {s_{i}^{k} A_{i} } (x)(s_{i}^{4} + a_{2} )d_{2} $$

$$ \overline{\overline{\phi }}_{11} (x) = \sum\limits_{i = 1}^{8} {A_{i} } (x)(s_{i}^{4} + c_{2} )b_{3} s_{i} ;\overline{\overline{\phi }}_{12} (x) = - \sum\limits_{i = 1}^{8} {A_{i} } (x)c_{4} b_{3} s_{i} $$

$$ \hat{\phi }_{11} (x) = - \sum\limits_{i = 1}^{8} {A_{i} } (x)a_{4} d_{3} s_{i} ;\hat{\phi }_{12} (x) = \sum\limits_{i = 1}^{8} {A_{i} } (x)(s_{i}^{4} + a_{2} )d_{3} s_{i} $$

$$ \begin{gathered} \phi_{11} (x) = \sum\limits_{i = 1}^{8} {A_{i} } (x)(s_{i}^{4} + c_{2} )b_{2} ,\phi_{21} (x) = \sum\limits_{i = 1}^{8} {A_{i} } (x)(s_{i}^{4} + c_{2} )s_{i}^{3} \hfill \\ \phi_{31} (x) = \sum\limits_{i = 1}^{8} {A_{i} } (x)(s_{i}^{4} + c_{2} )s_{i}^{2} ,\phi_{41} (x) = \sum\limits_{i = 1}^{8} {A_{i} } (x)(s_{i}^{4} + c_{2} )s_{i} \hfill \\ \phi_{51} (x) = \sum\limits_{i = 1}^{8} {A_{i} } (x)(s_{i}^{4} + c_{2} ),\phi_{61} (x) = - \sum\limits_{i = 1}^{8} {A_{i} } (x)a_{4} s_{i}^{3} \hfill \\ \phi_{71} (x) = - \sum\limits_{i = 1}^{8} {A_{i} } (x)a_{4} s_{i}^{2} ,\phi_{81} (x) = - \sum\limits_{i = 1}^{8} {A_{i} } (x)a_{4} s_{i} \hfill \\ \phi_{91} (x) = - \sum\limits_{i = 1}^{8} {A_{i} } (x)a_{4} \hfill \\ \end{gathered} $$

$$ \begin{gathered} \phi_{12} (x) = - \sum\limits_{i = 1}^{8} {A_{i} } (x)c_{4} b_{2} ,\phi_{22} (x) = - \sum\limits_{i = 1}^{8} {A_{i} } (x)c_{4} s_{i}^{3} \hfill \\ \phi_{32} (x) = - \sum\limits_{i = 1}^{8} {A_{i} } (x)c_{4} s_{i}^{2} ,\phi_{42} (x) = - \sum\limits_{i = 1}^{8} {A_{i} } (x)c_{4} s_{i} \hfill \\ \phi_{52} (x) = - \sum\limits_{i = 1}^{8} {A_{i} } (x)c_{4} ,\phi_{62} (x) = \sum\limits_{i = 1}^{8} {A_{i} } (x)(s_{i}^{4} + a_{2} )s_{i}^{3} \hfill \\ \phi_{72} (x) = \sum\limits_{i = 1}^{8} {A_{i} } (x)(s_{i}^{4} + a_{2} )s_{i}^{2} ,\phi_{82} (x) = \sum\limits_{i = 1}^{8} {A_{i} } (x)(s_{i}^{4} + a_{2} )s_{i} \hfill \\ \phi_{92} (x) = \sum\limits_{i = 1}^{8} {A_{i} } (x)(s_{i}^{4} + a_{2} ) \hfill \\ \end{gathered} $$

$$ A_{i} (x) = \frac{{e^{{s_{i} x}} }}{{(s_{i} - s_{1} )..(s_{i} - s_{i - 1} )(s_{i} - s_{i + 1} )..(s_{i} - s_{8} )}}(i = 1\sim 8) $$