Keywords

1 Introduction

Extensive harmful vibration in mechanical, aerospace and civil engineering fields requires effective solutions for elimination. The linear dynamic vibration absorber (DVA), also called the tuned mass damper (TMD), was proposed and used to mitigate vibration at the fundamental frequency of the main structure [1]. To improve the robustness of the DVA and broaden the frequency band of the vibration attenuation, researchers have developed the nonlinear dynamic vibration absorber (NDVA) [2,3,4,5]. Vakakis [6] first named a kind of NDVA with strong nonlinear stiffness and the targeted energy transfer mechanism as the nonlinear energy sink (NES). Specifically, the nonlinear stiffness indicates that the NES has non-constant natural frequencies. Therefore, transient resonance capture can be generated in the 1:1 resonant manifold of the system, resulting in an irreversible energy transfer phenomenon [7, 8]. Ding and Chen [9] reviewed NES research comprehensively and summarized several important designs for optimal damping effects and NES shortcoming offset. The significant advantage of NES is reflected in the increased energy absorption efficiency of the attached elements to the primary system [10]. Similarly, in the field of energy harvesting, there is a concern about how to improve the efficiency of energy conversion.

Energy harvesting technology is now extensively employed in mechanical vibration devices for converting vibration energy to electrical energy. Conversion can be achieved by piezoelectric, electromagnetic and triboelectric components. Similar to the development of DVA, research into vibration energy harvesters have also evolved from linear to nonlinear structures. In order to introduce nonlinear characteristics, structural design combined with permanent magnets has been of widespread interest of scholars [11,12,13]. Yang et al. [14] proposed a harvester with bistable and tri-stable nonlinear enhancement mechanisms by adding four external magnets to a conventional tri-magnet electromagnetic energy harvester. Gao et al. [15] presented a multi-stable electromagnetic energy harvester by symmetrically arranging the eight external magnets on two planes. The results indicated that multi-stable configurations could increase the output current. A comprehensive investigation of the nonlinear dynamics of the bistable harvester by Jung et al. [16] revealed that promoting inter-well oscillations and exploiting high amplitude characteristics are critical points in favor of energy harvesting.

In recent years there have been exploratory investigations on simultaneous vibration absorption and energy harvesting [17,18,19,20,21,22]. Pennisi et al. [23] utilized magnetic forces to counteract the linear term of the elastic force and consequently achieved a pure cubic NES. In parallel, an electromagnetic transducer was employed to convert the energy absorbed by the NES into electrical energy. Huang and Yang [24] investigated the energy trapping and harvesting performance of a multi-stable dynamic absorber from the perspective of energy shunting. Rezaei et al. [25] investigated simultaneous energy harvesting and vibration suppression utilizing a tunable bi-stable magneto-piezoelastic absorber (BPMA). The results indicated that the performance of the BMPA in energy harvesting and vibration mitigation was significantly improved due to the chaotic, strongly modulated response. Following this research, the complex dynamic behavior of the tri-stable magneto-piezoelastic absorber (TPMA) was further explored [26]. Although the feasibility of simultaneous vibration absorption and energy harvesting has been theoretically demonstrated, there is still a research gap in such dual-function absorber for cantilever beam vertical vibration attenuation.

This paper proposes a novel tri-magnet bistable electromagnetic vibration absorber (BEVA) for simultaneous vibration absorbing and energy harvesting. The symmetrical bistable potential well in the direction of gravity is achieved by the magnetic interaction of the ring magnet and the cylindrical magnet. This paper is structured as follows. Section 2 describes the equivalent model of the cantilever beam with BEVA attached at the free end and the design of a symmetrical bistable potential well. In Sect. 3, the energy dissipation mechanism of the system is analyzed based on simulation results. Section 4 draws conclusions.

2 Mathematical Modelling

2.1 Equivalent Modeling of the Cantilever Beam with BEVA

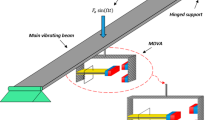
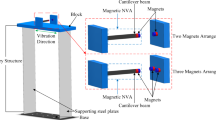
The equivalent model of the cantilever beam with BEVA structure is obtained in this section by exploiting the extended Hamilton’s principle. As shown in Fig. 1(a), the considered system is composed of a cantilever beam with the BEVA rigidly attached at the end. Figure 1(b) shows a cross-sectional diagram of the BEVA. This structure consists of a cylindrical levitating magnet, two ring magnets, a Teflon tube, and two coils. The levitating magnet can move axially inside the tube. When the cantilever beam is excited, part of the energy is transferred to the levitating magnet and dissipated by electromagnetic damping and dry friction. The extended Hamilton’s principle can be stated as:

$$\delta {\int }_{t1}^{t2}\left(T-U\right){\text{dt}}+{\int }_{t1}^{t2}\delta {W}_{nc}{\text{dt}}=0$$
(1)

here, δ is the variational operator, T is the system total kinetic energy, U is the total potential energy, Wnc represents the work done by non-conservative forces, and t1-t2 is an arbitrary time span.

Fig. 1.
figure 1

(a) Schematic diagram of the cantilever beam with BEVA, (b) Cross-sectional diagram of the BEVA, (c) Illustration of the parameter configuration of the BEVA.

Full size image

The total kinetic energy of the understudied system can be expressed as:

$$\begin{aligned} T = & {T}_{1}+{T}_{2}+{T}_{3} \\ = & \frac{1}{2}{\int }_{0}^{{l}_{c}}\rho A{\left(\dot{w}+{\dot{y}}_{b}\right)}^{2}ds+\frac{1}{2}{M}_{t}{\left(\dot{w}{\left. \right|}_{{l}_{c}}+{\dot{y}}_{b}\right)}^{2}+\frac{1}{2}{I}_{t}{\left({\dot{w}}^{\mathrm{^{\prime}}}{\left. \right|}_{{l}_{c}}\right)}^{2}\\ & +\frac{1}{2}m\left[{\left(\dot{w}{\left. \right|}_{{l}_{c}}+{\dot{y}}_{b}+{\dot{y}}_{m}\right)}^{2}+{\left({\dot{y}}_{m}{w}^{\mathrm{^{\prime}}}{\left. \right|}_{{l}_{c}}\right)}^{2}\right]\\ \end{aligned}$$
(2)

In Eq. (2), \({T}_{1},{T}_{2}\) and \({T}_{3}\) represent the kinetic energy of the cantilever beam, the kinetic energy of the BEVA external structure, and the kinetic energy of the levitating magnet, respectively. \(\rho , A\) and \({l}_{c}\) are the density, cross-sectional area and length of the cantilever beam. \(s\) is the arclength of the beam. \(w, {y}_{b}\) and \({y}_{m}\) represent the lateral deflection of the beam relative to the base, the displacement of the base and the displacement of the levitating magnet in the local coordinate system \((\overline{x }, \overline{y })\), respectively. The local system is related to the rotation of the free end of the beam, as shown in Fig. 1(a). Moreover, \({M}_{t}, {I}_{t}\) denotes the mass and rotational inertia of the external structure of the absorber, respectively. \(m\) is the mass of the levitating magnet. The over-dot denotes partial differentiation with respect to time, and the over-prime shows differentiation to the undeformed length.

The total potential energy of the coupled system can also be represented as:

$$ \begin{aligned} U = & U_{1} + U_{2} + U_{3} \\ = & \frac{1}{2}EI\mathop \smallint \limits_{0}^{{l_{c} }} w^{{''2}} ds + \mathop \smallint \limits_{0}^{{l_{c} }} \rho Ag\left( {w + y_{b} } \right)ds + M_{t} g\left( {w{\text{|}}l_{c} + y_{b} } \right) \\ &+ mg\left( {w{\text{|}}l_{c} + y_{b} + y_{m} } \right) + \smallint F_{{mag}} \left( {y_{m} } \right)dy_{m} \\ \end{aligned} $$
(3)

In Eq. (3), \({U}_{1},{U}_{2}\) and \({U}_{3}\) represent the elastic potential energy of the cantilever beam, total gravitational potential energy of the system, and magnetic potential energy of the levitating magnet. Here, \(g\) is the gravitational acceleration, and \({F}_{mag}({y}_{m})\) indicates the magnetic force of the levitating magnet subjected to the ring magnets at both ends.

Next, the virtual work done by non-conservative forces consists of three parts, namely, the virtual work done by the mechanical viscous damping \({c}_{1}\) of cantilever beam, the electromagnetic damping \({c}_{e}\) of the BEVA, and the dry friction \({F}_{fric}\) of the BEVA. Thus, the virtual work can be expressed as:

$$\delta {W}_{nc}=-{\int }_{0}^{{l}_{c}}{c}_{1}\dot{w}\delta wds-{c}_{e}\left({y}_{m}\right){\dot{y}}_{m}\delta {y}_{m}-{F}_{fric}\frac{{\dot{y}}_{m}}{\left|{\dot{y}}_{m}\right|}\delta {y}_{m}$$
(4)

Substituting Eqs. (2), (3), and (5) into Eq. (1), the coupled nonlinear governing equations of the system are obtained as follows:

$$ \begin{gathered} \rho A\ddot{w} + \delta \left( {s - l_{c} } \right)m\ddot{w}\left. \right|_{{l_{c} }} + \delta \left( {s - l_{c} } \right)m\ddot{y}_{m} + \delta ^{\prime}\left( {s - l_{c} } \right)m\dot{y}_{m} ^{2} w^{\prime}\left. \right|_{{l_{c} }} + c_{1} \dot{w} + EIw^{{{\text{''''}}}} \hfill \\ + \rho Ag + \delta \left( {s - l_{c} } \right)(M_{t} + m)g = - \left[ {\rho A + \delta \left( {s - l_{c} } \right)(M_{t} + m)} \right]\ddot{y}_{b} \hfill \\ \end{gathered} $$
(5)
$$ \begin{gathered} m\left[ {1 + \left( {w^{\prime}\left. \right|_{{l_{c} }} } \right)^{2} } \right]\ddot{y}_{m} + m\ddot{w}\left. \right|_{{l_{c} }} + 2m\left[ {w^{\prime}\left. \right|_{{l_{c} }} \dot{w}^{{\text{'}}} \left. \right|_{{l_{c} }} } \right]\dot{y}_{m} + c_{e} \left( {y_{m} } \right)\dot{y}_{m} \hfill \\ + F_{{fric}} \frac{{\dot{y}_{m} }}{{\left| {\dot{y}_{m} } \right|}} + F_{{mag}} \left( {y_{m} } \right) + mg = - m\ddot{y}_{b} \hfill \\ \end{gathered} $$
(6)

The reduced-order model of partial differential equations (PDEs) are obtained by utilizing the Galerkin discretization. The following ordinary differential equations (ODEs) governing the system are obtained as:

$$ \begin{gathered} \ddot{q}_{n} + 2\zeta _{n} \omega _{n} \dot{q}_{n} + \omega _{n}^{2} q_{n} + \mathop \sum \nolimits_{{i = 1}}^{\infty } A_{{ni}} \ddot{q}_{i} + \mathop \sum \nolimits_{{i = 1}}^{\infty } B_{{ni}} q_{i} \dot{x}^{2} + C_{n} \ddot{x} + D_{n} g = \hfill \\ - D_{n} \ddot{y}_{b}| m\ddot{y}_{m} + m\mathop \sum \limits_{{i,j}}^{\infty } E_{{ij}} q_{i} q_{j} \ddot{y}_{m} + 2m\mathop \sum \limits_{{i,j}}^{\infty } E_{{ij}} q_{i} \dot{q}_{j} \dot{y}_{m} + m\mathop \sum \limits_{{i = 1}}^{\infty } \varphi _{i} \left( {l_{c} } \right)\ddot{q}_{i} + c_{e} \left( {y_{m} } \right)\dot{y}_{m} \hfill \\ + F_{{fric}} \frac{{\dot{y}_{m} }}{{\left| {\dot{y}_{m} } \right|}} + F_{{mag}} \left( {y_{m} } \right) + mg = - m\ddot{y}_{b} \hfill \\ \end{gathered} $$
(7)

where the coefficients are defined as:

$$ A_{ni} = m\varphi_{n} \left( {l_{c} } \right)\varphi_{i} \left( {l_{c} } \right) $$
$$ B_{ni} = - m\varphi_{n}{\prime} \left( {l_{c} } \right)\varphi_{i}{\prime} \left( {l_{c} } \right) $$
$$ C_{n} = m\varphi_{n} \left( {l_{c} } \right) $$
$$ D_{n} = \mathop \smallint \limits_{0}^{{l_{c} }} \rho A\varphi_{n} \left( s \right)ds + \left( {M_{t} + m} \right)\varphi_{n} \left( {l_{c} } \right) $$
$$ E_{ij} = \varphi_{i}{\prime} \left( {l_{c} } \right)\varphi_{j}{\prime} \left( {l_{c} } \right) $$

2.2 Design of the Symmetric Bistable Potential Wells

The interaction force between magnets can be calculated by the magnetic dipole model [27]. In this paper, the magnetization direction of each magnet is axial, and the equivalent magnetic charge is uniformly distributed on the end faces of each magnet. As shown in Fig. 1(c), the local coordinate system is established. The magnetic force on the levitating magnet can be expressed as the superposition of the interactions between all equivalent magnetic charge surfaces [28]:

$$\begin{gathered} {F}_{mag}\left({y}_{m}\right)={F}_{13}\left(\frac{d}{2}-\frac{{h}_{lev}}{2}+{h}_{bot}+{y}_{m}\right)-{F}_{14}\left(\frac{d}{2}+\frac{{h}_{lev}}{2}+{h}_{bot}+{y}_{m}\right)\hfill \\ -{F}_{23}\left(\frac{d}{2}-\frac{{h}_{lev}}{2}+{y}_{m}\right)+{F}_{24}\left(\frac{d}{2}+\frac{{h}_{lev}}{2}+{y}_{m}\right)\hfill \\-{F}_{53}\left(\frac{d}{2}+\frac{{h}_{lev}}{2}-{y}_{m}\right)+{F}_{54}\left(\frac{d}{2}-\frac{{h}_{lev}}{2}-{y}_{m}\right)\hfill \\+{F}_{63}\left(\frac{d}{2}+\frac{{h}_{lev}}{2}+{h}_{top}-{y}_{m}\right)-{F}_{64}\left(\frac{d}{2}-\frac{{h}_{lev}}{2}+{h}_{top}-{y}_{m}\right) \end{gathered}$$
(8)

where \({F}_{ij}, {F}_{kj}\) (i = 1, 2, j = 3, 4, k = 5, 6) denotes the interaction force between different equivalent magnetic charge surfaces. i, j and k denote the end surfaces of the bottom magnet, the levitating magnet and the top magnet, respectively. Here, the magnetic force between surface-i and the surface-j can be expressed as:

$${F}_{ij}\left({d}_{ij}\right)=\underset{0}{\overset{2\pi }{\int }}\underset{{r}_{bot}}{\overset{{R}_{bot}}{\int }}\underset{0}{\overset{2\pi }{\int }}\underset{0}{\overset{{R}_{lev}}{\int }}\frac{{\mu }_{0}{M}_{bot}{M}_{lev}}{4\pi }\frac{{d}_{ij}pq}{{\left[{\left(pcos\alpha -qcos\beta \right)}^{2}+{\left(psin\alpha -qsin\beta \right)}^{2}+{{d}_{ij}}^{2}\right]}^\frac{3}{2}}dq\; d\beta \;dp\; d\alpha $$
(9)

where \({d}_{ij}\) is the distance between the two surfaces, \({\mu }_{0}\) is the permeability of vacuum.

As shown in Fig. 1(c), for the BEVA in the local coordinate system, the relative potential energy of the levitating magnet is defined as follows:

$${U}_{r}=\int mgd{y}_{m}-\int {F}_{mag}\left({y}_{m}\right)d{y}_{m}$$
(10)

here, the first integral describes part of the gravitational potential energy of the levitating magnet.

The bistable nonlinear mechanism has been investigated using the single-sided bipolarity of the ring magnet in the previous study [28, 29]. To avoid undesirable effects of the levitating magnet on the primary structure, a smaller-sized levitating magnet has been chosen in this paper. The magnets and other relevant parameters of the BEVA are listed in Table 1. As depicted in Fig. 2, the relative potential energy for different ring magnet spacings (\(d\)) are plotted. When the spacing decreases, the potential wells on both sides gradually move closer to each other, and the potential barrier between them gets lower, which means that the levitating magnet is more susceptible to inter-well oscillations. As the spacing decreases, the bistable system will degrade to a monostable system. A fixed spacing \((d=39\,{\mathrm{mm}})\) was selected for the BEVA because the depths of the potential wells on both sides are equal at this point.

Fig. 2.
figure 2

The relative potential energy for different ring magnet spacings.

Full size image
Table 1. Properties of the BEVA.
Full size table

2.3 Calculation of Electromagnetic Damping

As shown in Fig. 1(c), two coils are attached axially symmetrically to the top (\(\overline{y }={d}_{coil}\)) and bottom (\(\overline{y }=-{d}_{coil}\)) of the tube. This electromagnetic structure is utilized to convert vibration energy into electricity while providing a damping force to impede the movement of the levitating magnet. From the Faraday law of electromagnetic induction, the voltage induced in the top coil can be written as:

$${U}_{v-top}=-\frac{d{\varphi }_{top}}{dt}=-\frac{d{\varphi }_{top}}{d{y}_{m}}\frac{d{y}_{m}}{d{\text{t}}}$$
(11)

where \({\varphi }_{top}\) is the total magnetic flux through the top coil.

According to the charge model, the magnetic field due to the levitating magnet is given as B [27], which is varied with \({y}_{m}\). In reference to Fig. 1 (c), the magnetic flux emanating from the levitating magnet through all turns of the top coil is expressed as:

$${\varphi }_{top}\left({y}_{m}\right)={\sum}_{1}^{N}\iint B({y}_{m})dxdy$$
(12)

where B is projection of the B onto the \(\overline{y }\) axis. Similarly, for the bottom coil, we obtain \({\varphi }_{bot}\left({y}_{m}\right)\) and \({U}_{v-bot}\). When the device is excited, the magnetic fluxes of the upper and lower coils normally change. Assuming the top and bottom coils are connected and winded in the same directions. The total voltage generated in coils is given as:

$${U}_{v}={U}_{v-top}+{U}_{v-bot}$$
(13)

According to the principle of energy conversion, the generated electric power is equal to the mechanical power dissipated by the electromagnetic damping force, i.e.

$${c}_{e}({y}_{m}){{\dot{y}}_{m}}^{2}=\frac{{U}_{v}^{2}}{{R}_{l}+{R}_{c}}$$
(14)

The above equations give the electromagnetic damping coefficient as:

$${c}_{e}({y}_{m})=\frac{{\left(\frac{d{\varphi }_{top}}{d{y}_{m}}+\frac{d{\varphi }_{bot}}{d{y}_{m}}\right)}^{2}}{{R}_{l}+{R}_{c}}$$
(15)

And it must be mentioned that the coil inductance has a negligible effect at low frequency vibrations.

3 Results and Discussions

3.1 Parameter identification and verification

In this section, the electromechanical equations of motion derived in the previous section are validated. For this purpose, the structural parameters of the system are obtained experimentally and compared with the simulation results. First, the dry friction of the BEVA is obtained through parameter identification methods based on the experimental frequency response. Then the mechanical damping ratio of the cantilever beam is identified from the transient response. Finally, the transient electromechanical response of the system, which is simulated using the identified parameters, is compared with the experimental results.

Fig. 3.
figure 3

(a) Experimental system for BEVA parameter identification, (b) Output voltage at 0.8 g.

Full size image

First, the BEVA system is analyzed for frequency response, as shown in Fig. 3(a). In doing so, the waveform generator (Agilent 33500B) outputs a harmonic signal which is passed through a power amplifier (YMC LA-200) to the shaker (YMC VT-200). The excitation signal, monitored by the accelerometer (LC0103TA), is simultaneously acquired with the load voltage using the acquisition device at a sampling rate of 10 kHz. The Runge–Kutta method is used to solve ODEs. The step size is 0.0001 s, corresponding to the experimental sampling rate. Figure 3(b) shows the BEVA output voltage simulation results at 0.8 g, which agrees very well with the experiment. The BEVA can produce a relatively high-level voltage in the frequency range of 10.5–15 Hz because of the periodic inter-well oscillations. In the frequency range of 15.5–18.5 Hz, the BEVA performs chaotic oscillations [28], at which point fluctuations in output voltage are acceptable. The dry friction of the BEVA is identified through the genetic algorithm as 0.0042N.

Fig. 4.
figure 4

Experimental system for simultaneous vibration absorption and energy harvesting.

Full size image
Fig. 5.
figure 5

The experimental measured excitation acceleration.

Full size image

Second, the primary structure damping is experimentally obtained. The experimental system is shown in Fig. 4. Here, the waveform generator generates a triangular pulse signal. The laser (KEYENCE LK-H050) acquires the displacement response of the cantilever beam. Figure 5 shows the experimentally measured acceleration signal with a maximum amplitude of 2.7 g and a minimum amplitude of −3.6 g. This acceleration data was substituted into Eq. (14) for simulation. It should be mentioned that only the first-order mode (n = 1) is considered in Galerkin’s series. Accordingly, only the damping ratio of the first-order mode needs to be identified. For simplicity, the cantilever beam attached to the BEVA external body (without a levitating magnet) at the free-end is called the ‘linear oscillator (LO) without BEVA’. When the levitating magnet is placed in BEVA external body, the coupling system is named the ‘linear oscillator (LO) with BEVA’. Figure 6(a) shows the displacement response of the LO without BEVA. The damping ratio of the first dominant mode can be easily find by log-decrement and the value is 0.004. The other relevant parameters of the system are listed in Table 2. As shown in Fig. 6, the simulation and experimental time-domain and frequency-domain responses are consistent.

Fig. 6.
figure 6

The transient response of the LO without BEVA. (a) Displacement, (b) Amplitude Spectrum.

Full size image

Finally, the developed electromechanical equations of motion for the coupled system are experimentally validated. Figure 7 shows the transient response of the LO with BEVA. In Fig. 7(a), the simulation and experimental displacements coincide almost precisely in the 0–2 s. After 2 s, the displacements appear to be inconsistent, which is acceptable. In addition, the voltage response shows a high agreement between simulation and experimental results within 0–0.5 s. After a while, the agreement between experimental and simulation results decreases, possibly due to manufacturing errors in the device. This discrepancy is acceptable, and there is no doubt that the equivalent model of the cantilever beam attached absorber proposed in this paper is correct.

Fig. 7.
figure 7

The transient response of the LO with BEVA. (a) Displacement, (b) Load voltage.

Full size image
Table 2. Properties of the cantilever beam with BEVA.
Full size table

Transient vibration absorption and energy harvesting mechanism.

In this section, the mechanism of the BEVA in vibration absorption and energy harvesting under an initial excitation is investigated. The initial excitation can be in the form of initial displacement (\({q}_{1}(0)\ne 0\)) or initial velocity ( \({\dot{q}}_{1}(0)\ne 0\)). In this paper, the initial velocity (such as 0.05 m/s, 0.1 m/s) is chosen as the initial excitation. The energy dissipation of the system is considered as follows:

System I: LO without BEVA:

$${E}_{I-in}=\frac{1}{2}{\left({\dot{q}}_{1}\left(0\right)\right)}^{2}, {E}_{I-out}={\int }_{0}^{t}2\zeta \omega {\left({\dot{q}}_{1}\left(t\right)\right)}^{2}dt$$
(16)

where the subscript ‘in’ indicates energy input and the subscript ‘out’ indicates energy dissipation.

System II: LO with BEVA:

$$ \begin{gathered} E_{II - in} = \frac{1}{2}\left( {1 + A_{11} } \right)\left( {\dot{q}_{1} \left( 0 \right)} \right)^{2} , E_{II - out1} = \mathop \smallint \limits_{0}^{t} 2\zeta \omega \left( {\dot{q}_{1} \left( t \right)} \right)^{2} dt \hfill \\ E_{II - out2} = \mathop \smallint \limits_{0}^{t} \frac{{\left( {U_{v} \left( t \right)} \right)^{2} }}{{R_{l} + R_{c} }}dt, E_{II - out3} = \mathop \smallint \limits_{0}^{t} F_{fric} \left| {\dot{y}_{m} \left( t \right)} \right|dt \hfill \\ \end{gathered} $$
(17)

here, \({E}_{II-out1}\) is the mechanical damping dissipation energy, \({E}_{II-out2}\) is the BEVA electromagnetic damping dissipation energy and \({E}_{II-out3}\) is the BEVA dry friction dissipation energy. The total energy of the system in real-time can be obtained as \({E}_{total}\left(t\right)={E}_{in}-{E}_{out}\).

$$ \left( 1 \right)\,\dot{q}_{1} \left( 0 \right) = 0.05\,{\text{m}}/{\text{s}} $$
Fig. 8.
figure 8

Transient responses of the system I and II when \({\dot{q}}_{1}\left(0\right)=0.05\;{\text{m}}/{\text{s}}\). (a) Displacement (cantilever beam), (b) Displacement (the levitating magnet), (c) Total energy, (d) Load voltage.

Full size image

Firstly, the initial velocity of the cantilever beam is set as \({\dot{q}}_{1}\left(0\right)=0.05\;{\text{m}}/{\text{s}}\). The responses of the system are shown in Fig. 8. It can be seen from Fig. 8(a) that the vibration of the cantilever beam with BEVA is suppressed. In this case, the levitating magnet oscillates in a single potential well (Fig. 8(b)), corresponding to a small output voltage (Fig. 8(d)). The attachment of BEVA accelerates the energy dissipation of the system (Fig. 8(c)). For system I, the time required to dissipate 97.5% of the initial energy is 10.4 s. With the BEVA attached, this time is reduced to 4.9 s. Figure 9 shows the different forms of energy dissipation in System II. The result indicates that the BEVA relies mainly on dry friction for energy dissipation under low excitation.

$$ \left( 2 \right)\,\dot{q}_{1} \left( 0 \right) = 0.1\,{\text{m}}/{\text{s}} $$
Fig. 9.
figure 9

Energy dissipation in the system II (LO with BEVA) when \({\dot{q}}_{1}\left(0\right)=0.05\;{\text{m}}/{\text{s}}\).

Full size image
Fig. 10.
figure 10

Transient responses of the system I and II when \({\dot{q}}_{1}\left(0\right)=0.1\;{\text{m}}/{\text{s}}\). (a) Displacement (cantilever beam), (b) Displacement (the levitating magnet), (c) Total energy, (d) Load voltage.

Full size image

When the initial condition of \({\dot{q}}_{1}\left(0\right)=0.1\;{\text{m}}/{\text{s}}\), the time responses of the system I and II are shown in Fig. 10. Figure 10(a) shows that the displacement of the cantilever beam in system II decays rapidly within 0–2 s, which is caused by the levitating magnet performing inter-well oscillation (Fig. 10(b)). For system I, the cantilever beam performs free-vibration, so the time required to dissipate 97.5% of the initial energy is still 10.4s (Fig. 10(c)). However, for System II, the inter-well oscillation significantly increases the energy dissipation speed, taking only 2.2 s to achieve 97.5% energy dissipation. The large-amplitude vibration of the levitating magnet also corresponds to an increase in output voltage, as shown in Fig. 10(d), with a peak load voltage of 2.5 V. An attractive phenomenon emerges in Fig. 11, where the energy dissipated by the friction is the primary part of the energy dissipated in System II. At the same time, the electromagnetic damping energy dissipation also shows an increase.

Fig. 11.
figure 11

Energy dissipation in the system II (LO with BEVA) when \({\dot{q}}_{1}\left(0\right)=0.1\;{\text{m}}/{\text{s}}\).

Full size image

4 Conclusions

In this research, a bi-stable electromagnetic vibration absorber (BEVA) is utilized for simultaneous vibration absorbing and energy harvesting. The vibration absorber employs a tri-magnet levitation structure, where the bistable characteristic is achieved by the magnetic mechanism between the cylindrical and ring magnets. The proposed absorber is connected to a cantilever beam subjected to transient excitation to suppress vibrations in the vertical direction and harvest electrical energy. Firstly, the continuous magneto-mechanical control equations are derived using Hamilton’s principle, while the magnetic forces are derived based on the equivalent magnetic charge method. The parameters of the coupled system are identified using experimental data. Next, numerical simulations are carried out to reveal the vibration absorption and energy harvesting mechanism of the BEVA based on the validated system model. The results show that large-amplitude inter-well oscillation contributes to faster energy dissipation while generating high output load voltage. The analysis of the energy dissipation ratio of each component shows that at low excitation, the BEVA dissipates energy mainly through dry friction. As the energy input increases, the proportion of energy dissipated by electromagnetic damping increases.