A Mathematical Model for COVID-19 in Italy with Possible Control Strategies

Abstract

Italy faced the COVID-19 crisis in the early stages of the pandemic. In the present study, a SEIR compartment mathematical model has been proposed. The model considers four stages of infection: susceptible(S), exposed (E), infected (I) and recovered (R). Basic reproduction number $R_0$ which estimates the transmission potential of a disease has been calculated by the next-generation matrix technique. We have estimated the model parameters using real data for the Coronavirus transmission. To get a dipper insight into the transmission dynamics, we have also studied four of the most pandemic affected regions of Italy. Basic reproduction number stood differently for different regions of Italy i.e. Lombardia (2.1382), Veneto (1.7512), Emilia Romagna (1.6331), Piemonte (1.9099) and for Italy at 2.0683. The sensitivity of $R_0$ corresponding to various disease transmission parameters has also been demonstrated via numerical simulations. Besides, it has been demonstrated with the help of simulations that earlier lockdown and rapid isolation of infective individuals would have been helpful in a dual way; by substantially reducing the number of susceptible people on one hand and preponing the end of the pandemic on the other. This paper also includes complete theoretical analysis of the proposed model including the epidemic feasibility of the model and existence of endemic equilibrium point. We have also derived the conditions under which the disease became endemic. Since the existence of an endemic equilibrium point refers to the possibility of backward bifurcation, we have given a detailed analysis regarding the same. All the theoretical analysis is supported by detailed numerical simulations to understand the transmission dynamics of COVID-19 While analyzing different regions of Italy it was found that Lombardia was the hardest hit and had the highest number of infectives. We have also forecasted the future scenario of the pandemic in Italy. The model predicts that the COVID-19 epidemic shall die out from the worst affected Lombardia region by approximately by November 2020.

Introduction

Epidemics and pandemics have shaped human history since long. It has been proposed that a majority of human Coronovirus have been derived from bat reservoir [1]. At the initial stage it was believed that transmission of disease took place through animal to human mode but later it has been established that direct transmission of the disease is also possible and is the primary reason for transmission to various countries [2,3,4]. Hospital related transmission is also suspected in 41 percent of the patients [3].

Along with high transmission efficiency, global travel has also contributed to SARS-CoV-2 spread across the globe [5]. On 30 January 2020, the WHO initially declared COVID-19 a public health emergency of international concern and later a pandemic on 11 March 2020 [6]. Interestingly African region has lowest reported cases of COVID-19 which is otherwise host to many infectious diseases. Italy recorded its first case of COVID-19 on February 20, 2020, at Lodi40 (Lombardy) [7]. In the next 24 h, the infected cases increased to 36 [7].

In the begning, Italian data followed similar trend observed in Hubei Province, China. Till date, Italy is one of the countries that have faced grievous consequences of COVID-19. Till 20th May 2020, Italy has 2,27,364 recorded cases and 32,330 deaths due to COVID-19. In terms of reported cases, it is the sixth highest while it is third when it comes to the number of deaths across the globe. 42.2% of the patients who died were 80–89 years old, 32.4% were 70–79 years, 8.448% were 60–69 years, and 2.8% were 50–59 years old. The male to female ratio is 80–20% with older median age for women (83.4 years for women vs 79.9 years for men) [8]. Moreover, the estimated mean age of those who lost their lives in Italy was 81 years [8]. The COVID-19 outbreak completely disturbed the economic condition of Italy. Several family owned small sectors are suering [9]. The condition of Italy surprised the research fraternity because Italy stands in the top ve countries in terms of medical facilities. The ongoing dismal scenario in Italy has forced the government to admit that they do not have any control over the spread of the disease as well as do not know when the ongoing web of COVID-19 will stop.

Besides, the situation is so grim that Italian College of Anaesthesia, Analgesia, Resuscitation and Intensive Care has published guidelines that said resources that could be every scarce are reserved for those who have the greatest chances of survival first and secondly to those who have more years of life to be saved, with a view to maximizing the benefits for the most number of people. Due to the catastrophic impacts of the COVID-19 outbreak, efforts have been made to analyze the trend of the disease and predict the future of the epidemic [8, 10]. The work carried out in [8] predicts that in the absence of timely implementation of available medical resources, the authorities will not be able to control the outbreak of the disease. The study further concludes that together with the medical facilities people’s movement and social activities should be restricted immediately in order to curtail the burden of the COVID-19. The work carried out in [8], collected the day to day data and measured the possible similarity between Italy and Hubei Province (China). Further, the study also shows that the number of deaths increased almost five times as the available treatment facilities reached the limit. As of now, there is no vaccination available for COVID-19.

There are many models for infectious diseases and in the class of compartmental models, they may range from very classical SIR to more complex ones. In the current work, we have developed a compartmental model to examine the case of Italy. The proposed model incorporates four different compartments namely—Susceptible, Exposed, Infected and Recovered population. The present COVID-19 has an latency period which ranges up to 14 days. Therefore, to make our model realistic, we include the exposed population along with the infected population, which certainly results in improved prediction. We collected the data of Italy for COVID-19 available on the Worldometers website [11]. Further we trained the proposed mathematical model using the data available till 20th May 2020. Using this enhanced model we analyze the effect of lock down on the spread of COVID-19 in Italy. Also, we predict the possible end of the current outbreak of COVID-19 in Italy. Moreover, to make our predictions more realistic, we have trained and validated our model with COVID-19 data of some the highly affected regions of Italy.

The Mathematical Model

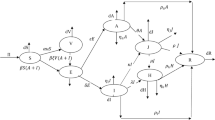
The proposed model describes the transmission mechanism of COVID-19. In the modelling process, we have divided the human population into four mutually exclusive compartments, namely, susceptible (S), exposed (E) infected but asymptomatic, infected (I) symptomatic and infectious and recovered (R). The flow chart of the model is presented in Fig. 6.1.

Fig. 6.1

Flow chart for the COVID-19 Italy model

Based on the above assumptions, the model is governed by the following system of equations:-

$$\begin{aligned} \begin{array}{l} \frac{\text {d}S}{\text {d}t}=A-\beta S \frac{I}{N}-\beta _0 S\frac{E}{N}- \mu S \\ \frac{\text {d}E}{\text {d}t}=\beta S \frac{I}{N}+\beta _0 S\frac{E}{N}-\alpha E-\alpha _1 E-\mu E \\ \frac{\text {d}I}{\text {d}t}=\alpha E -\theta I-\alpha _2 I -\mu I \\ \frac{\text {d}R}{\text {d}t}=\alpha _1 E+\alpha _2 I-\mu R \end{array} \end{aligned}$$

(6.1)

In the above model, N represents the total population. We assume that all the new recruiters joined the susceptible class at a constant rate A. $\beta$ is the disease transmission rate from the infected individuals to susceptible individuals. We further assume that susceptible individuals once come into the contact of infected individual will not directly join the infected class. They first join the exposed class (E) and after certain period of time shows visible symptoms of the disease and enters into the infected class (I). Exposed class individuals are assumed to be less infectious as compared to the infected class individuals. Therefore, $\beta _0$ represents the disease transmission rate for exposed individuals. Clearly, $\beta _0 \le \beta$. Here, $\alpha$ is the rate by which exposed population moves to infected compartment. $\alpha _1$ is the recovery rate of exposed individuals and $\alpha _2$ is the recovery rate of infected individuals. $\theta$ is the disease induced death rate. $\mu$ is the natural death rate.

Our proposed model system involves human population. Hence for the initial state, all the compartmental values are assumed to be non-negative. The model will be studied under the following initial conditions:

$$\begin{aligned} S(0)\ge 0, E(0)\ge 0, I(0)\ge 0, R(0)\ge 0 \end{aligned}$$

(6.2)

Basic Properties

In this section, we check the mathematical feasibility of the proposed model. For this purpose, we check whether all the solutions of the proposed model will remain positive and bounded or not.

Non-negativity of the Solution

To show the epidemiological feasibility of the proposed model system (6.1), it is required that all the solutions remain non-negative. Hence, in the following theorem we verify that all the solutions with non-negative initial condition will remain non-negative.

Theorem 1

The solution $\left( S(t), E(t), I(t), R(t) \right)$ of the proposed model system is non-negative for all $t \ge 0$ with non-negative initial condition (6.2).

Proof

From the first equation of system (6.1), we have

$$\begin{aligned} \frac{\text {d}S}{\text {d}t} = A -\left( \frac{\beta I}{N}+\frac{\beta _0 E}{N}+\mu \right) S \end{aligned}$$

From this equation, we can deduce that

$$\begin{aligned} \begin{array}{ll} \frac{\text {d}}{\text {d}t}\left[ S(t) \exp \left\{ \int \limits _0^t\left( \frac{\beta I(v)}{N}+\frac{\beta _0 E(v)}{N}\right) . \text {d}v+\mu t\right\} \right] \\ = A\exp \left\{ \int \limits _0^t\left( \frac{\beta I(v)}{N}+\frac{\beta _0 E(v)}{N} \right) .\text {d}v +\mu t\right\} \end{array} \end{aligned}$$

Now, integrating the equation on both sides

$$\begin{aligned} \begin{array}{l} S(t_1) \exp \left\{ \int \limits _0^{t_1}\left( \frac{\beta I(v)}{N}+\frac{\beta _0 E(v)}{N}\right) .\text {d}v+\mu t_1\right\} -S(0) = \\ \int \limits _0^{t_1} \frac{A}{2}\exp \left\{ \int \limits _0^u\left( \frac{\beta I(v)}{N}+\frac{\beta _0 E(v)}{N}\right) .\text {d}v+\mu t\right\} .\text {d}u \end{array} \end{aligned}$$

On simplification we have,

$$\begin{aligned} \begin{array}{c} S(t_1) = S(0) \exp \left\{ -\left( \int \limits _0^{t_1}\left( \frac{\beta I(v)}{N}+\frac{\beta _0 E(v)}{N}\right) .\text {d}v+\mu t_1 \right) \right\} \\ +\exp \left\{ -\left( \int \limits _0^{t_1}\left( \frac{\beta I(v)}{N}+\frac{\beta _0 E(v)}{N}\right) .\text {d}v+\mu t_1 \right) \right\} \times \\ \int \limits _0^{t_1} \frac{A}{2}\exp \left\{ \int \limits _0^u\left( \frac{\beta I(v)}{N}+\frac{\beta _0 E(v)}{N}\right) .\text {d}v+\mu t\right\} .\text {d}u \end{array} \end{aligned}$$

This gives

$$\begin{aligned} S(t_1) \ge 0 \end{aligned}$$

where $t_1 \ge 0$ is arbitrary. Similarly we can show the non-negativity for compartments E, I and R.

Hence, the solution $\left( S(t), E(t), I(t), R(t) \right)$ will remain positive for non-negative initial condition.

Boundedness of the Solution

In order to accurately predict the epidemic, the solutions of the mathematical model should be bounded.

Theorem 2

All solutions of the proposed model are bounded.

Proof

We need to show that $\left( S(t), E(t), I(t), R(t) \right)$ is bounded for each value of $t \ge 0$. From our model system (6.1) we obtain:

$$\begin{aligned} {\left( S+E+I+R\right) }'= A-\mu \left( S+E+I+R\right) -\theta I \le A-\mu \left( S+E+I+R\right) \end{aligned}$$

which gives us

$$\begin{aligned} \lim _{t \rightarrow \infty }\text {Sup}\left( S+E+I+R\right) \le \frac{A}{\mu } \end{aligned}$$

which implies that each individual component is also bounded.

Disease Free Equilibrium and Basic Reproduction Number

The basic reproduction number is one of the critical parameters to examine the long term behaviour of an epidemic. It can be defined as the expected number of cases directly generated by one case in a population where all individuals are susceptible to infection. We have used next-generation matrix technique explained in [12], to obtain the expression of reproduction number $R_0$.

In order to reduce the number of parameter in proposed model system (6.1), we normalize the model by considering $X_1= \frac{S}{N}$, $X_2=\frac{E}{N}$, $X_3=\frac{I}{N}$, $X_4=\frac{R}{N}$ and $A = \mu N$. For convenience, we represent the variables $X_1$, $X_2$, $X_3$ and $X_4$ by the same variables as S, E, I and R. The proposed model takes the following form:

$$\begin{aligned} \begin{array}{l} \frac{\text {d}S}{\text {d}t}=\mu -\beta S I-\beta _0 SE- \mu S \\ \frac{\text {d}E}{\text {d}t}=\beta S I+\beta _0 SE-\alpha E -\alpha _1 E-\mu E \\ \frac{\text {d}I}{\text {d}t}=\alpha E -\theta I-\alpha _2 I -\mu I \\ \frac{\text {d}R}{\text {d}t}=\alpha _1 E+\alpha _2 I-\mu R \end{array} \end{aligned}$$

(6.3)

The disease fee equilibrium (DFE)of the model system (6.3) can be given as:

$$\begin{aligned} E^0=\lbrace 1,0,0,0 \rbrace \end{aligned}$$

The infection states of the model are E and I. The progression from E to I is not considered as new infection but rather a progression of infection through compartment. Therefore,

$$ F = \left( \begin{array}{l} \beta _0 S E+ \beta SI\\ 0\\ \end{array}\right) \text { and } V = \left( \begin{array}{l} - \alpha E-\alpha _1 E-\mu E\\ \alpha E - \alpha _2 I+\theta I+\mu I \\ \end{array}\right) $$

At DFE $E^0$ the transmission matrix $\mathcal {F}$ and the transition matrix $\mathcal {V}$ are given as:

$$ \mathcal {F}= \begin{pmatrix} \beta _0 &{} \beta \\ 0&{} 0\\ \end{pmatrix} \text { and } \mathcal {V}= \begin{pmatrix} \alpha +\alpha _1+\mu &{} 0\\ -\alpha &{} \alpha _2+\theta +\mu \\ \end{pmatrix}$$

Which gives,

$$\begin{aligned} \begin{array}{l} \mathcal {F} {\mathcal {V}}^{-1}= \frac{1}{\left( \alpha +\alpha _1+\mu \right) \left( \alpha _2+\theta =\mu \right) }\begin{pmatrix} \left( \beta _0 \left( \alpha _2+\theta +\mu \right) + \beta \alpha \right) &{} \beta \left( \alpha +\alpha _1 + \mu \right) \\ 0 &{} 0 \\ \end{pmatrix} \end{array} \end{aligned}$$

Hence, the $R_0$ takes the following expression

$$\begin{aligned} R_0= \rho \left( \mathcal {F}{\mathcal {V}}^{-1} \right) = \frac{\beta _0\left( \alpha _2+\theta +\mu \right) +\beta \alpha }{\left( \alpha +\alpha _1+\mu \right) \left( \alpha _2+\theta +\mu \right) } \end{aligned}$$

We will analyse the variation in $R_0$ for different values of the parameters involved in the model system. Figure 6.2 illustrates the simultaneous variation in the basic reproduction number for different values of corresponding parameters. The parameter values used are given in Tables 6.1 and 6.2.

Fig. 6.2

Variation in the basic reproduction number $R_0$ for different values of sensitive parameters. a Effect of $\alpha$ and $\theta$ on $R_0$. b Effect of $\alpha _1$ and $\alpha _2$ on $R_0$. c Effect of $\beta$ and $\alpha$ on $R_0$. d Effect of $\beta$ and $\beta _0$ on $R_0$

Table 6.1 Parameter values used for the model

Table 6.2 Estimated parameter values of the model for Lombardia, Veneto, Emilia Romagna, Piemonte and Italy

Existence of Endemic Equilibrium

The endemic equilibrium state is the state when the disease can not be completely eradicated but remains in the population. For the disease to persist in the population; the exposed class and infected class must not be zero at the equilibrium state.

Let $E^*=\left( S^*,E^*,I^*,R^*\right)$ be the endemic equilibria. Now, $E^*$ can be achieved by solving the equations below:

$$\begin{aligned} \begin{array}{l} \mu -\beta S^* I^*-\beta _0 S^* E^*-\mu S^*=0 \\ \beta S^* I^*+\beta _0S^*E^*-\left( \alpha +\alpha _1+\mu \right) E^*=0 \\ \alpha E^*-\left( \theta +\alpha _2+\mu \right) I^*=0 \\ \alpha _1E^*+\alpha _2I^*-\mu R^*=0 \end{array} \end{aligned}$$

(6.4)

From the third equation, we have

$$\begin{aligned} E^*=\frac{\theta +\alpha _2+\mu }{\alpha } I^* \end{aligned}$$

Also, from fourth equation, we have

$$\begin{aligned} R^*=\frac{\alpha _1 E^*+\alpha _2 I}{\mu } = \left( \frac{\alpha _1\left( \theta +\alpha _2+\mu \right) +\alpha \alpha _2}{\alpha \mu }\right) I^* \end{aligned}$$

Now, using the values of $E^*$ and $R^*$ in second equation we will have

$$\begin{aligned} S^*=\frac{\left( \alpha +\alpha _1+\mu \right) E^*}{\beta I^*+\beta _0 E^*}=\frac{\left( \alpha +\alpha _1 +\mu \right) \left( \theta +\alpha _2+\mu \right) }{\alpha \beta +\beta _0\left( \theta +\alpha _2+\mu \right) } \end{aligned}$$

Now using the values of $E^*,R^*$ and $S^*$, first equation implies

$$\begin{aligned} I^*=\frac{\mu -\mu S^*}{\left( \beta + \frac{\beta _0\left( \theta +\alpha _2+\mu \right) }{\alpha }\right) S^*} \end{aligned}$$

On simplification, we have

$$\begin{aligned} \begin{array}{l} S^* = \frac{\varLambda \varUpsilon }{\psi } \\ E^* = \frac{\mu \left[ \alpha \beta {\;+\;}\varUpsilon \left( \beta _0{\;-\;}\alpha {\;-\;}\alpha _1{\;-\;}\mu \right) \right] }{\varLambda \psi } \\ I^* = \frac{\alpha \mu \left[ \alpha \beta {\;+\;}\varUpsilon \left( \beta _0{\;-\;}\alpha {\;-\;}\alpha _1{\;-\;}\mu \right) \right] }{\psi \varLambda \varUpsilon } \\ R^*= \frac{\left[ \alpha \beta {\;+\;}\varUpsilon \left( \beta _0{\;-\;}\alpha {\;-\;}\alpha _1{\;-\;}\mu \right) \right] \left( \alpha _1\varUpsilon {\;+\;}\alpha \alpha _2\right) }{\psi \varLambda \varUpsilon } \end{array} \end{aligned}$$

(6.5)

where,

$$\begin{aligned} \begin{array}{l} \psi = \alpha \beta +\beta _0\left( \theta +\alpha _2+\mu \right) \\ \varLambda = \alpha +\alpha _1+\mu \\ \varUpsilon = \theta +\alpha _2+\mu \end{array} \end{aligned}$$

(6.6)

Hence, there exist a unique endemic equilibrium point for our proposed model system 6.3.

Backward Bifurcation

The analysis conducted in the previous section on the occurrence of endemic equilibrium $E^*$ suggests the probability of backward bifurcation. We have used the resuts based on the center manifold theorem (theorem 4.1) given in [13], to check the occurrence of backward bifurcation. From the expression of $R_0$ it is clear that $R_0$ is directly related to $\beta$ as well as $\beta _0$. Therefore we will consider two separate cases one for each $\beta$ and $\beta _0$.

• Case 1: If we select $\beta$ as the bifurcation parameter. Moreover, $R_0=1$ implies

  $$\begin{aligned} \beta ^* =\frac{\left( \alpha _2+\theta +\mu \right) \left( \alpha +\alpha _1+\mu -\beta _0\right) }{\alpha } \end{aligned}$$

  Now,

  $$\begin{aligned} J_0(E_0,\beta ^*)=D_xf(E_0,\beta ^*) =\begin{pmatrix} -\mu &{} -\beta _0&{} -\beta ^*&{} 0\\ 0&{} \beta _0-\left( \alpha +\alpha _1+\mu \right) &{} \beta ^* &{}0\\ 0&{} \alpha &{}-\left( \theta +\alpha _2+\mu \right) &{}0\\ 0 &{}\alpha _1&{} \alpha _2&{} -\mu \\ \end{pmatrix} \end{aligned}$$

  It is clear that 0 is a simple eigenvalue of $J_0$. Let $w=\left( w_1,w_2,w_3,w_4\right)$ be the associated right eigenvector, then

  $$\begin{aligned} \begin{array}{l} -\mu w_1-\beta _0 w_2-\beta ^* w_3=0 \\ \left( \beta _0-\left( \alpha +\alpha _1+\mu \right) \right) w_2+\beta ^* w_3=0 \\ \alpha w_2-\left( \theta +\alpha _2+\mu \right) w_3=0 \\ \alpha _1 w_2+\alpha _2 w_3 -\mu w_4 =0 \end{array} \end{aligned}$$

  On solving the above system of equation and substituting the value of $\beta ^*$, we obtain

  $$\begin{aligned} \begin{array}{l} \left( w_1,w_2,w_3,w_4\right) = \left( -\frac{\left( \theta +\alpha _2+\mu \right) \left( \alpha +\alpha _1+\mu \right) }{\alpha \mu }, \frac{\theta +\alpha _2+\mu }{\alpha }, 1, \frac{\alpha _1\left( \theta +\alpha _2+\mu \right) +\alpha \alpha _2}{\alpha \mu } \right) \end{array} \end{aligned}$$

  Similarly, Let $v=\left( v_1,v_2,v_3,v_4\right)$ be the corresponding left eigenvector satisfying $w.v=1$. After evaluation, we have

  $$\begin{aligned} \begin{array}{l} \left( v_1, v_2, v_3, v_4\right) =\left( 0, \frac{\alpha }{\left( \theta +\alpha _2+\mu \right) +\left( \alpha +\alpha _1+\mu -\beta _0\right) }, \frac{\alpha +\alpha _1+\mu -\beta _0}{\left( \theta +\alpha _2+\mu \right) +\left( \alpha +\alpha _1+\mu -\beta _0\right) }, 0\right) \end{array} \end{aligned}$$

  As discussed in Theorem 4.1 [13], the coefficients ‘a’and ‘b’can be computed as:

  $$a=\sum _{k,i,j=1}^{4} v_k w_i w_j \frac{\text {d}^2f_k}{\text {d}x_i\text {d}x_j}\left( E_0,\beta ^*\right) $$
  $$b=\sum _{k,i=1}^4 v_k w_i \frac{d^2f_k}{\text {d}x_i\text {d}\beta }\left( E_0,\beta ^*\right) $$

  Algebraic calculations shows that

  $$\begin{aligned} \frac{\text {d}^2f_2}{\text {d}x_1\text {d}x_2}=\beta _0=\frac{\text {d}^2f_2}{\text {d}x_2\text {d}x_1}, \quad \frac{\text {d}^2f_2}{\text {d}x_1\text {d}x_3}=\beta ^*=\frac{\text {d}^2f_2}{\text {d}x_3\text {d}x_1} \end{aligned}$$
  $$\begin{aligned} \frac{\text {d}2f_2}{\text {d}x_3\text {d}\beta }=S^0=1 \end{aligned}$$

  The rest of the second derivatives appearing in the formula for ‘a’ and ‘b’ are all zero. Hence,

  $$\begin{aligned} a= v_2 \left( w_1 w_2 \beta _0+w_1 w_3 \beta ^*+w_2 w_1 \beta _0+w_3 w_1 \beta ^*\right) \end{aligned}$$

  After simplifying and substituting the value of $\beta ^*$, we have

  $$\begin{aligned} a= -\frac{2\left( \alpha _2+\theta +\mu \right) ^2 \left( \alpha +\alpha _1+\mu \right) ^2}{\alpha \left[ \left( \alpha +\alpha _1+\mu -\beta _0\right) +\left( \theta +\alpha _2+\mu \right) \right] } \end{aligned}$$

  Similarly, we have

  $$\begin{aligned} b = \frac{\alpha }{(\theta +\alpha _2+\mu )+(\alpha +\alpha _1+\mu -\beta _0)} \end{aligned}$$

  Now, from the above two expressions it is clear that:

  $$\begin{aligned} \begin{array}{l} a> 0 \quad if \quad \beta _0> \alpha +\alpha _1+\alpha _2+\theta +2\mu \\ b > 0 \quad if \quad \beta _0 < \alpha +\alpha _1+\alpha _2+\theta +2\mu \end{array} \end{aligned}$$

  Now, from the above two conditions it is clear that the coefficients ‘a’ and ‘b’ can not be positive simultaneously. Hence, backward bifurcation is not possible at $R_0 = 1$ for this particular case.

• Case 2: In this case, we will consider ‘$\beta _0$’ as our the bifurcation parameter. Now $R_0 = 1$ implies:

  $$\begin{aligned} \beta _0^* = \frac{(\alpha +\alpha _1+\mu )(\alpha _2+\theta +\mu )-\beta \alpha }{(\alpha _2+\theta +\mu )} \end{aligned}$$

  On following the same procedure as in “case 1", the associated right eigenvector $w = (w_1, w_2, w_3, w_4)$ can be given as:

  $$\begin{aligned} \begin{array}{l} \left( w_1,w_2,w_3,w_4\right) = \left( -\frac{\left( \alpha +\alpha _1+\mu \right) \left( \alpha _2+\theta +\mu \right) }{\alpha \mu }, \frac{\theta +\alpha _2+\mu }{\alpha }, 1, \frac{\alpha _1\left( \theta +\alpha _2+\mu \right) +\alpha \alpha _2}{\alpha \mu } \right) \end{array} \end{aligned}$$

  and the corresponding left eigenvector $v = (v_1, v_2,v_3, v_4)$ can be given as:

  $$\begin{aligned} \left( v_1, v_2, v_3, v_4\right) =\left( 0, \frac{\theta +\alpha _2+\mu }{\theta +\alpha _2+\mu +\beta }, \frac{\beta }{\theta +\alpha _2+\mu +\beta }, 0\right) \end{aligned}$$

  Further calculations gives as the values of the coefficients ‘a’ and ‘b, as:

  $$\begin{aligned} a =\frac{-2}{\alpha ^2 \mu } \frac{(\theta +\alpha _2+\mu )^3(\alpha +\alpha _1+\mu )^2}{(\theta +\alpha _2+\mu +\beta )} \end{aligned}$$
  $$\begin{aligned} b = \frac{\theta +\alpha _2+\mu }{\theta \alpha _2+\mu +\beta } \end{aligned}$$

  Hence it is clear that ‘a’ is always negative and ‘b’ is always positive. Hence, for this case also there does not exist backward bifurcation at $R_0 = 1$.

Therefore, from case 1 and case 2, we can conclude that there does not exist backward bifurcation at $R_0 = 1$. Only bifurcation which occur at $R_0 = 1$ will be forward in nature.

Stability Analysis

Local Stability of Disease Free Equilibrium

Theorem 3

The disease free equilibrium of the proposed model system is locally asymptotically stable when $R_0 < 1$ and unstable for $R_0 >1$.

Proof

The Jacobian matrix corresponding to the disease free equilibrium is

$$\begin{aligned} M = \begin{pmatrix} -\mu &{}-\beta _0&{} -\beta &{}0\\ 0&{} \left( \beta _0-\alpha -\alpha _1-\mu \right) &{} \beta &{} 0\\ 0 &{}\alpha &{}-(\theta +\alpha _2+\mu )&{} 0\\ 0&{}\alpha _1&{}\alpha _2&{}-\mu \end{pmatrix} \end{aligned}$$

The characteristic equation of M is

$$\begin{aligned} (-\mu -\varSigma )(-\mu -\varSigma )\left( -\left( \beta _0-\alpha -\alpha _1-\mu -\varSigma \right) \left( \theta +\alpha _2+\mu +\varSigma \right) -\beta \alpha \right) =0 \end{aligned}$$

The first two eigenvalues can be given as $\varSigma =-\mu ,-\mu$.

In order to find the other two eigenvalues we will simplify

$$\begin{aligned} \left( -\left( \beta _0-\alpha -\alpha _1-\mu -\varSigma \right) \left( \theta +\alpha _2+\mu +\varSigma \right) -\beta \alpha \right) =0 \end{aligned}$$

The above equation can be written as

$$\begin{aligned} \left( \beta _0-D_1-\varSigma \right) \left( D_2+\varSigma \right) +\alpha \beta =0 \end{aligned}$$

Here, $D_1=\alpha +\alpha _1+\mu$ and $D_2=\theta +\alpha _2+\mu$. On simplification, the above equation will be reduced to

$$\begin{aligned} \varSigma ^2+\left( D_1+D_2-\beta _0\right) \varSigma +D_1D_2-\beta _0D_2-\alpha \beta =0 \end{aligned}$$

(6.7)

The basic reproduction number in terms of $D_1$ and $D_2$ is

$$\begin{aligned} R_0=\frac{\beta _0D_2+\beta \alpha }{D_1D_2} \end{aligned}$$

Now, $R_0 <1$ implies

$$\begin{aligned} \begin{array}{l} D_1D_2-\beta _0D_2-\alpha \beta>0 \\ D_1+D_2-\beta _0 >0 \end{array} \end{aligned}$$

The positivity of these two values and Eq. 6.7 implies that the other two eigenvalues of Jacobian matrix M are negative.

Hence, the disease free equilibrium $E_0$ of the model system (6.1) is locally asymptotically stable if $R_0 \le 1$ and unstable for $R_0 >1$.

Global Stability of Disease Free Equilibrium

In order to obtain the conditions for the global stability for $E_0$, we have used the approach set out in [14], which states that if the model system can be written in the following form

$$\begin{aligned} \begin{array}{l} \frac{dX}{dt}=F(X,Z) \\ \frac{dZ}{dt}=G(X,Z), G(X,0)=0 \end{array} \end{aligned}$$

(6.8)

here $X \in R^n$ are the uninfected individuals and $Z\in R^m$ describes the infected individuals. According to this notation, the disease free equilibrium is given by $Q_0=(X_0,0)$.

K1::

For $\frac{dX}{dt}=F(X,0)$, $X_0$ is globally asymptotically stable.

K2::

$G(X,Z)=BZ-\hat{G}(X,Z)$ where $\hat{G}(X,Z)\ge 0$ for $X,Z \in \varOmega$.

here $B=D_zG(X_0,0)$ is a M-matrix (matrix whose non-diagonal elements belongs to $R^+ \cup 0$) and $\varOmega$ is the feasible of the model. Now, the following theorem establishes the global stability of the disease free equilibrium $E_0$ for our proposed model system.

Theorem 4

The disease free equilibrium point is globally asymptotically stable provided $R_0\le 1$.

Proof

First we will prove $K_1$ as

$$\begin{aligned} F(X,0)=\begin{bmatrix} \mu -\mu S\\ -\mu R \end{bmatrix} \end{aligned}$$

The characteristic polynomial of system is given by

$$\begin{aligned} (-\mu -\varGamma )(-\mu -\varGamma )=0 \end{aligned}$$

Hence, there are two negative roots $\varGamma =-\mu ,-\mu$. Hence, $X=X_0$ is globally asymptotically stable.

Now, we have $G(X,Z)=BZ-\hat{G}(X,Z)$

$$\begin{aligned} =\begin{bmatrix} \beta _0 S_0-\left( \alpha +\alpha _1+\mu \right) &{} \beta S_0 \\ \alpha &{} -\left( \theta +\alpha _2+\mu \right) \end{bmatrix} \begin{bmatrix} E\\ I \end{bmatrix} -\begin{bmatrix} \beta (S_0-S)I+\beta _0(S_0-S)E\\ 0 \end{bmatrix} \end{aligned}$$

Here, $B=\begin{bmatrix} \beta _0 S_0-\left( \alpha +\alpha _1+\mu \right) &{} \beta S_0 \\ \alpha &{} -\left( \theta +\alpha _2+\mu \right) \end{bmatrix}$ is an M matrix.

Also, $\hat{G}(X,Z)=\begin{bmatrix} \beta (S_0-S)I+\beta _0(S_0-S)E\\ 0 \end{bmatrix} \ge 0 \,\,; \quad \forall (X,Z) \in \varOmega$.

Hence $K_1$ and $K_2$ are satisfied, which proves our theorem.

Local Stability of Endemic Equilibrium

Theorem 5

When $R_0>1$ the endemic equilibrium $E^*$ is locally asymptotically stable under the condition $A_j >0 \,\,; \,\, \forall \,\, j=1,2,3$ and 4 and

$$\begin{aligned} A_1A_2A_3> A_3^2+A_1^2A_4 \,\, ,\,\, A_1A_2>A_3 \end{aligned}$$

expression of $A_1,A_2, A_3$ and $A_4$ are given in the proof.

Proof

The Jacobian matrix about $E^*$ is given as

$$\begin{aligned} J_0=\begin{bmatrix} a_{11} &{} a_{12} &{} a_{13}&{} 0\\ a_{21} &{}a_{22} &{}a_{23} &{}0\\ 0&{} a_{32} &{} a_{33} &{}0\\ 0&{} a_{42} &{}a_{43} &{} a_{44} \end{bmatrix} \end{aligned}$$

Here,

$$\begin{aligned} \begin{array}{c} a_{11}=-\beta I^*-\beta _0E^*-\mu \,\, a_{12}=-\beta _0S^* \,\, a_{13}=-\beta S^* \,\, a_{21}=\beta I^*+\beta _0 E^* \\ a_{22}=\beta _0 S^*-\left( \alpha +\alpha _1+\mu \right) \,\, a_{23}=\beta S^* \,\, a_{32}=\alpha \,\, a_{33}=-(\theta +\alpha _2+\mu ) \\ a_{42}=\alpha _1 \quad a_{43}=\alpha _2 \quad a_{44}=-\mu \end{array} \end{aligned}$$

The characteristic equation of $J_0$ is

$$\begin{aligned} \varGamma ^4+A_1\varGamma ^3+A_2\varGamma ^2+A_3\varGamma +A_4=0 \end{aligned}$$

Here,

$$\begin{aligned} \begin{array}{l} A_1=-(a_{11}+a_{22}+a_{33}+a_{44})\\ A_2 = (a_{11}a_{22}-a_{12}a_{21}+a_{11}a_{33}+a_{11}a_{44}+a_{22}a_{33}-a_{23}a_{32}+a_{22}a_{44} \\ \quad \quad +a_{33}a_{44}) \\ A_3=(-a_{11}a_{22}a_{33}+a_{11}a_{23}a_{32}+a_{12}a_{21}a_{33}-a_{13}a_{21}a_{32}-a_{11}a_{22}a_{44}\\ \quad \quad +a_{12}a_{21}a_{44}-a_{11}a_{33}a_{44}-a_{22}a_{33}a_{44}+a_{23}a_{32}a_{44})\\ A_4=\left( a_{11}a_{22}a_{33}a_{44}-a_{11}a_{23}a_{32}a_{44}-a_{12}a_{21}a_{33}a_{44}+a_{13}a_{21}a_{32}a_{44}\right) \end{array} \end{aligned}$$

Thus, under the conditions stated in the theorem, the local stability of the endemic equilibrium is guaranteed by the Routh-Hurwitz criterion.

Numerical Simulation and Model Fitting

According to the data collected from [11], the total number of COVID-19 cases has crossed 227364 as of May 20. There has been more than 17669 deaths in the country due to this epidemic. A study is needed to observe that what will be the situation in the near future in terms of daily active cases. Therefore, the aim of the proposed model is to predict the future scenario of daily active cases of the COVID-19 epidemic in Italy by analyzing its present state in the country. In this section, we perform rigorous numerical simulations to get an insight into the pandemic in Italy (Fig. 6.3).

Fig. 6.3

Current status of COVID-19 in various regions on Italy. (as on 20th May, 2020)

We calibrated the model (6.1) for daily active cases of COVID-19 in Italy and its four province namely Lombardia, Veneto, Emilia Romagna and Piemonte. For simulation, data for daily active cases has been taken from [15] for the period of 68 days (March 14 to May 20, 2020). We fit the model system (6.1) with daily active cases for the whole country as well as for the four provinces. We use in-built function lsqcurvefit in MATLAB (Mathworks, R2017a) to fit the model. The parameters $A, \beta , \beta _0, \alpha , \alpha _1$ (see Table 6.2) and initial conditions of the human population $\left( S(0), E(0), I(0), R(0)\right)$ are estimated. Other parameters, involved in the model system (6.1) are taken from the literature (Table 6.3).

Table 6.3 Estimated initial conditions of human population for Lombardia, Veneto, Emilia Romagna, Piemonte and Italy

According to the situation report-11 available on the official website of WHO [17], the first two COVID-19 positive cases in Italy were reported on January 31. Both the infected individuals had a travel history to the city of Wuhan, China. This was the initial phase of the epidemic in the country. Due to delayed imposition of lockdown, the epidemic started to grow slowly but significantly. By the end of February, the number of cases reached 1000 [11]. We fitted the proposed model system (6.1) for Italy and its four provinces with the official data available on [15] for the month of March, April and May. It is observed that the proposed model is able to predict the epidemic closely (see Figs. 6.6, 6.7, 6.8, 6.9 and 6.10). Also, the corresponding residual is also given in Fig. 6.5, which shows the efficiency of our model with the real data (Fig. 6.4).

Fig. 6.4

Fitted model to daily active cases data of Italy for the period of March 14 to May 20, 2020

Fig. 6.5

Residuals for the data fitting of Italy

Fig. 6.6

Prediction of the model for Italy

Using the parameters given in Tables 6.1 and 6.2, we evaluated basic reproduction number ($R_0$) for Lombardia, Veneto, Emilia Romagna, Piemonte and Italy (see Table 6.4). As the Lombardia was worst affected province of Italy and thus recorded highest value of $R_0$ among others. The fitting of model to daily active cases data is represented in Figs. 6.7a and 6.10a for Lombardia, Veneto, Emilia Romagna, Piemonte and Italy, respectively. The corresponding residuals for these regions are given in Figs. 6.7b and 6.10b. Further, we tried to predict the situation of daily active cases of COVID-19 in near future. Graphs of prediction are shown in Figs. 6.7c and 6.10c for Lombardia, Veneto, Emilia Romagna, Piemonte and Italy, respectively.

Table 6.4 Total population (N) and evaluated basic reproduction number ($R_0$) for Lombardia, Veneto, Emilia Romagna, Piemonte and Italy.

Fig. 6.7

Fitted model to daily active cases data of Lombardia for the period of March 14 to May 20, 2020

Fig. 6.8

Fitted model to daily active cases data of Veneto for the period of March 14 to May 20, 2020. b Residual c Model prediction

Fig. 6.9

Fitted model to daily active cases data of Emilia Romagna for the period of March 14 to May 20, 2020. b Residual c Model prediction

Fig. 6.10

Fitted model to daily active cases data of Piemonte for the period of March 14 to May 20, 2020. b Residual c Model prediction

It can be seen from Figures that the proposed model is fitted well with the actual active cases of COVID-19 for all provinces Lombardia, Veneto, Emilia Romagna, Piemonte, and Italy. In each case, first, we fit the model to the actual data from March 14 to May 20, and estimated parameter values. After that, we used these parameter values for prediction of the daily active cases for all regions considered in the present work. The prediction of the active cases for Lombardia is shown in Fig. 6.7c. From the Figure, it can be concluded that the epidemic will be over approximately by November 19, 2020 (250 days from 14 March). Next, the model fitting for Veneto and Emilia Romagna is performed and plotted in Figs. 6.8 and 6.9 and prediction for these regions is given in Figs. 6.8c and 6.9c, respectively. From the Figures, we conclude that the active cases will near to be eliminated in approximately 200 days (near about September 30, 2020). In continuation of this, Figs. 6.10 and 6.6 depicts model fitting and prediction of daily active cases of COVID-19 for Piemonte and whole country Italy, respectively. Again, it is observed that both the regions model show a good fit with actual daily active cases. One can see the model prediction in Figs. 6.10c and 6.6 for Piemonte and whole country Italy, respectively that the daily active cases will be annihilated in approximately 225 days (near about October 25, 2020).

Why Lombardia is epicenter of COVID-19 in Italy? Our model has shown that it has the highest infectives in Italy (Fig. 6.7). Besides, there may be other reasons as well; the initial case was found here and he had travel history to Wuhan and in Wuhan L and S type of strains have been documented [18]. It has also been proposed by some researchers that L type is more deadly. It has one-sixth of Italy’s 60 million population and is a region with one of the most high density of population. It also has more people over 65 years of age than any other region. In an interesting study, high association with pollution in this region has also been pointed out as one of the reasons in Lombardia [19].

Game Changers

In this section, we will discuss the factors which can significantly control the spread of pandemic. The two major factors discussed here are (a) Early Lock down and (b) Rapid Isolation.

Impact of Early Lock Down

On 9th March 2020, in response to the increasing COVID-19 pandemic in the region, the Government of Italy enforced a national quarantine restricting population movement, with the exception of necessity, work and health circumstances. In this section, we will investigate the effect of early lock down on the spread of pandemic in Italy.

Fig. 6.11

Various possible cases of Italy corresponding to different lock down efficiency rate.

It is clear from Fig. 6.11 that the epidemic could have been controlled at a very early stage if the lockdown had been imposed early in Italy. Figure 6.11 shows three different scenarios of the epidemic in Italy

Figure 6.11a shows the current scenario of Italy. However, if lock down would have been imposed prior to 9th March 2020, the number of susceptible would have been significantly low. In Fig. 6.11b, we have considered a case of lock-down with 50% efficiency. It can be seen from the plot that, it has not only significantly reduce the number of infections, but also caused the overall death of pandemic by 31st August, 2020. Also, Fig. 6.11c indicate that the epidemic could have been eliminated even more earlier if the the efficiency of lock-down would have been 80%.

Impact of Rapid Isolation on Infected Individuals

COVID-19 is a pandemic which is spreading all across the globe. Early research shows that the disease transmission rate from an infected individual to a susceptible is very high [20]. The transmission rate can be reduced by isolating the infected individuals as quickly as possible. In this subsection, with the help of numerical simulations we will show the variations in infected population for different values of $\beta$, disease transmission rate from infected individual to susceptible individuals.

Fig. 6.12

Variation in infected population for different isolation of infected population.

Figure 6.12 shows various scenarios of the epidemic in Italy in case disease transmission rate would have been timely controlled. A rapid isolation of infected population will lead to reduce the disease transmission rate, $\beta$. From Fig. 6.12, we see that as disease transmission rate, $\beta$ is reduced by 75%, it not only decrease the active number of infections from 1.5 lacks to 35000, but also the overall lifespan of pandemic reduced from November 30th to July 15, 2020.

Conclusion

A SEIR type compartmental model is proposed to study the current scenario of COVID-19 in Italy. Our proposed model accurately fits the officially available data of the pandemic in Italy. Also, we have discussed how the lock down that was imposed on 9th March, 2020 was a good but a delayed decision of the government of Italy. Through simulations, we have shown that a rapid isolation of the infective individuals and early lock down in the country are two of the most efficient procedures to terminate the spread of COVID-19. Our simulations shows that the pandemic in Italy will last till November, 2020. As of now, the vaccination of COVID-19 have not been discovered. Hence, this research can also be beneficial for the countries which are in the initial stage of the pandemic, as our research describes two of the most effective procedures to counter the spread of the pandemic and its long term impact on the spread of disease.

We have also estimated the basic reproduction number $R_0$ for the disease. As our proposed model involves several parameters, we have shown the sensitivity of these parameters via numerical simulations. It is clear from the simulations (see Fig. 6.2) that the transmission rates, $\beta$ and $\beta _0$ are the most sensitive parameters. The reproduction number can be minimized if we can reduce these two parameters. Also, we have derived the value of the basic reproduction number for Italy and some of its highly effected regions. This research can be extended in various ways. One can refine the model by introducing new compartments in order to examine the epidemic more precisely. There are certain assumptions which we have made while constructing this model because of the limited data and short onset time. As more data will be available in the future, this model can be trained with more real data to increase its efficiency. Useful future directions have been proposed Ndairou et al. (2020) in their compartment model on Wuhan, China. Besides, future mathematical models may take virus strains prevailing in a region also in account.