Probability-Based Time-Optimal Motion Planning of Multi-robots Along Specified Paths

Abstract

In this paper, we study the time-optimal motion planning problem for multi-robots under their kinodynamic constraints along specified paths. Unlike previous approaches that coordinate their motions only at a road intersection and without considering noise influence, we for the first time use the probabilistic motion model caused by the noise when planning robot motion. By deriving the conflict probability, we design a scheme to sufficiently guarantee conflict probability below our expectation. In particular, we map the potential conflict to the infeasible rectangle region in robot’s path-time coordinate plane, which enables us to apply velocity interval propagation to find a time-optimal motion for each robot. Then we integrate our approach into two popular multi-robot motion planners, i.e., conflict-based search and prioritized planning approach. Experimental results demonstrate that, conflict-based search needs more computation time to achieve less motion time than prioritized motion planner.

This work was supported in part by the National Natural Science Foundation of China under Grant 91848103, in part by the Talent Foundation of Beijing University of Chemical University under Grant buctrc201811.

1 Introduction

Recent years have witnessed the rapid growth of autonomous multi-robot deployment in many applications such as warehouse automation and manufacturing applications [1]. In multi-robot system, a central problem is how to coordinate robot motions such that they can efficiently reach their goals without collision, and in the meanwhile, their motion time should be minimized because less motion time brings more profit. Towards this aim, a vast majority of motion planning approaches have been presented (see e.g. [1]).

Previous approaches mainly focus on the problem of planning multi-robot motions without specific path constraints and without considering noise influences. Unlike them, we for the first time plan the multi-robot motions along specified paths in a dynamic environment, where the obstacle is not static and robot motions are impacted by stochastic noise. The fixed path constraints may come from scenarios such as traffic intersections or warehouses where robots need to cross multiple lanes or aisles. Along these paths, robots can only accelerate or brake to their goals. To solve the optimal motion planning of multi-robot, we have to first know how to plan an optimal motion for a single robot.

If there is not an acceleration bound, the motion planing of a single robot along a specified path can be formulated as a visibility graph in the path position/time space, as presented in [2]. Based on this formulation, a polynomial-time algorithm is presented in [3] to find an optimal solution with velocity and acceleration bounds in the absence of dynamic obstacle. The influence of dynamic obstacle has been taken into account in [4] that constructs reachable sets in the path-velocity-time space by propagating reachable velocity sets between obstacle tangent points. However, these approaches assume that robot can move strictly as our wish, which is not true in reality due to the uncertainty caused by noise.

The uncertainty of robot motion has been widely studied in the past robotic research. In the book [5], a wealth of techniques and algorithms related to the probabilistic robotics have been introduced, where the measured motion is generally given by the true motion corrupted with noise. The probabilistic motion model also needs to be taken into account when planning robot’s motion. In [6], a decentralized probabilistic framework is presented for the path planning of autonomous vehicles by deriving a relation transforming the maximum turn angle into a maximum search angle. In [7], a particle filter framework is proposed to treat the uncertainty in motion planning by updating trajectory candidates, perception measurement, trajectory selection and resampling motion goal. Via assigning probabilities to the generated trajectories according to their likelihood of obeying the driving requirements, particle filtering approach is also used in [8] that formulates the motion planning as a nonlinear non-Gaussian estimation problem. In the same line with them, this paper also builds the motion corrupted with noise as a probabilistic motion model.

For multi-robot systems, the optimal coordination is a well-known NP-hard problem [9], even in static environment. There are already some optimal approaches that solve this problem in a graph-based map. Many of them, such as [10,11,12], first plan optimal path individually for each robot and then coordinate them when necessary. Analogously, the robot motion coordination with specified paths also relies on the individually optimal motion. For example, the approach in [13] first finds out the minimum and maximum traversal times for each path segment of each robot, then formulates their coordination as a mixed integer nonlinear programming problem that combines collision avoidance constraints for pairs of robots. To handle the non-convex challenge in this formulation, another more advanced approach in [14] successfully transforms it into two linear subproblems by introducing some additional constraints. As a result, the general-purpose solver such as mixed integer linear programming can be applied to find out an approximated optimal solution in a reasonable time. However, all these approaches assume that robot’s motion is deterministic. It is true in video game or computer simulation, but not in practical implementation.

In this paper, we study how to optimally coordinate multi-robot motion with uncertain noise influence and under kinodynamic constraints along specified paths. The motion uncertainty brings the difficulty in conflict detection. For this problem, we develop a conflict detection scheme based on the probability analysis that can ensure the conflict probability below our expectation at any time. In order to plan motion in the path-time coordinate plane, we simplify dynamic obstacle or robot obstacle to rectangle and then apply the velocity interval propagation to plan the time-optimal motion of individual robot. Then, inspired by the conflict-based scheme proposed in [15], we apply a two-level scheme to resolve conflicts. In particular, a conflict tree is constructed to store all coordination options at the high-level algorithm, and optimal solution is individually found out for each coordination option. After enumerating all possible options, the final optimal motion coordination can be established. As a comparison, we also integrate our probabilistic conflict analysis into a lightweight heuristic planner, i.e., prioritized motion planning, to reduce its computation time.

The structure of this paper is as follows: in next section we present the problem formulation. In Sect. 3, we present how to plan an optimal motion for a single robot based on the probabilistic motion model. Section 4 presents the optimal multi-robot coordination scheme. In Sect. 5, experimental results are demonstrated that compare the effectiveness of our proposed probabilistic conflict-based search with prioritized path planning. Section 6 provides the conclusion of this paper.

2 Problem Formulation

We start by formally formulating the multi-robot path planning problem. Suppose there are n robots denoted as $r_1,\,r_2,\,..,\,r_n$ that need to operate in a region $\mathcal {W}$ of 2-d Euclidean space. Each robot $r_i$ is assigned a path to move from its start point $s_i$ to its goal point $g_i$ where $s_i\in \mathcal {W},\,g_i\in \mathcal {W}$, where its path can be represented as an arc-length function $q_i(p):[0,\,p_i^{\max }]\mapsto \mathcal {W}$. Our aim is to determine $\pi _i=(p_i,\,v_i,\,t_i),\,\forall i \le n$ in the path-velocity-time (PVT) state space. We assume that robot $r_i$ starts its movement at time 0 and ends at time $t_i^{\max }$. Then we have $\pi _i(0) = s_i,~\pi _i(t_i^{\max }) = g_i$, and $\pi _i(t) \in \mathcal {W}\,(0\le t \le t_i^{\max }$). The robot dynamics must be under its velocity and acceleration bounds [1]:

$$\begin{aligned} \begin{aligned} \forall 0 \le i \le n,~~&\dot{p}_i = v_i + \delta _i\\&v_i \in [\underline{v}_i,~\overline{v}_i] \\&\dot{v}_i \in [\underline{a}_i,~\overline{a}_i] \end{aligned} \end{aligned}$$

(1)

where $\delta _i$ is a noise that follows a normal distribution $N(0,\,\sigma _i^2)$, and $\underline{v}_i \ge 0$ and $\underline{a}_i<0 <\overline{a}_i$. The robot trajectory with respect to space-time is denoted as $\pi _i$, i.e., $\pi _i(t_i)=(p_i(t_i),\,v_i(t_i),\,t_i)$. Note that a robot path $q_i(p)$ has been determined and the remained problem is to decide the one-to-one correspondence between its path position $p_i(t)$ and time t. Besides, we denote that $\varPi (\pi _i,\,\pi _j)$ stands for the trajectory collision part between $\pi _i$ and $\pi _j$. Then, a feasible solution should satisfy that $\varPi (\pi _i,\,\pi _j) = \emptyset , \forall i \ne j$, which means no collision between any two robots. We further denote $T^{\max } = \max \{t_i^{\max },\,i=1..n\}$. Then we can formally define our problem as

$$\begin{aligned} \begin{aligned}&\min ~T^{\max } \\ \mathrm {subject~to}&\\&(1), \\ \mathrm {and}~&\pi _i(0) = s_i,~\pi _i(t_i^{\max }) = g_i,~i=1..n, ~~~~~~~~~~~~~~~~\\ \mathrm {and}~&\forall i\ne j,~\varPi (\pi _i,\,\pi _j) = \emptyset . \end{aligned} \end{aligned}$$

(2)

Fig. 1.

An eight-robot system, where the path of each robot has been marked out with arrow.

An example of this problem is shown in Fig. 1, where 8 robots need to move in the arrow direction. We assume that the path for each robot has been decided, but their positions with respect to time are unknown. Our goal is to decide the relationship between their positions and time such that their motions are strictly under the velocity and acceleration bounds, and they do not collide with each other, and the makespan of completing all motions is minimized.

3 Time-Optimal Motion for a Single Robot

We start by building the time-optimal motion for a single robot in a dynamic environment. This problem has been partly addressed in paper [4] that relies on the deterministic motion model to find the optimal bounded-acceleration trajectory for a single robot moving along a fixed, given path with dynamic obstacles. In this paper, we extend this approach to handle probabilistic motion model.

3.1 Velocity Interval Propagation

Velocity interval propagation(VIP) is the backbone of the single robot’s planner. In the path-time coordinate plane, dynamic obstacles can be formulated as a list of rectangles $O_i=[\underline{p}_{o_j},\overline{p}_{o_j}]\times [\underline{t}_{o_j},\overline{t}_{o_j}],j=1,...,m$, as shown in Fig. 2. The robot’s initial state is $(p_i(0),v_i(0),0)$, where $v_i(0) \in [\underline{v}_i,\overline{v}_i]$ and the terminal condition is $(p_i(t_i^{\max }),v_i(t_i^{\max }),t_i^{\max })$, where $v_i(t_i^{\max }) \in [\underline{v}_i,\overline{v}_i]$. Besides, the acceleration $a_i\in [\underline{a}_i,\overline{a}_i]$. The planner’s task is to find a set of collision-free trajectory $\pi _i$ over above conditions in the path-velocity-time state space.

Fig. 2.

An exemplified diagram of velocity interval propagation.

Ignoring obstacle’s influence and assuming the initial velocity $v_i(0)$ is $v_i^1(0)$, the robot’s reachable set $R(t:(p_i(0),v_i(0),0))$ of velocities at time t is proved to be a convex region in the path-velocity plane, where $(p_i(0),v_i^1(0),0)$ is the initial state of the robot. The set of velocities $V(t_i^{\max })$ attainable a target point $(p(t_i^{\max }),t(t_i^{\max }))$ is the intersection $R(t_i^{\max }:(p_i(0),v_i(0),0))\cap \{(p_i,v_i)|p_i=p_i(t_i^{\max }),v_i\in [\underline{v}_i,\overline{v}_i]\}$.

On the basis of the above, VIP computes the minimum and maximum starting velocity $\underline{v}_i$ and $\overline{v}_i$’s terminal velocity intervals $V_1$ and $V_2$, respectively. Then VIP minimizes and maximizes the terminal velocity without input terminal velocity constraint, and generates terminal intervals $V_1$ and $V_2$ by constructing a parabolic trajectory with acceleration $\underline{a}_i$ and $\overline{a}_i$ that interpolates $(p_i(0),0)$ and $(p_i(t_i^{\max }),t_i^{\max })$. The final terminal velocity intervals $[\underline{v}_i,\overline{v}_i]$ is the smallest interval containing $V_1,V_2,V_3,V_4$.

Meanwhile, there are only two cases of collision free trajectory. The first one connects directly to the goal and the next pass tangentially along either the upper-left or lower-right vertex of one or more path-time obstacles. So the planner is designed to find the collision-free trajectories that pass through combinations of upper-left and lower-right obstacle vertices. When there is only one obstacle O, according to the obstacle’s location in path-time coordinate plane, we just have to combine O and the interval $[\underline{v}_i,\overline{v}_i]$ to calculate the collision-free trajectory $\pi _i$, as shown in an example of Fig. 2. By connecting multiple obstacles’ upper-left and lower-right obstacle vertices, the algorithm can be easily extended to multiple obstacle environments.

Then the time-optimal motion planning approach for a single robot with dynamic obstacles can be developed as Algorithm 1. In the first step, we sort the upper left and lower right obstacle vertices in the ascending order of their time into the list $(p_1,\,t_1),...,(p_{2n}, t_{2n})$. Besides, we use a set $S_i$ to store velocity interval and singleton velocity for each element in this list. Note that we only highlight its main part and ignore details, because you can read [4] for its complete information.

3.2 Probability-Based Motion Planning

The approach of velocity interval propagation assumes that the robot strictly moves as planned. However, due to the noise influence, there may be some deviations with the planned motion, which may lead to the robot collision in reality. We thus have to take these deviations into account in order to plan a safe motion.

Suppose that robot $r_i$ starts at $t=0$ and moves as planned for $\varDelta t$. Then the robot position is:

$$\begin{aligned} \begin{aligned} p_i(\varDelta t)&= \int _{0}^{\varDelta t} v_i(t)\,dt + \int _{0}^{\varDelta t} \delta _i\,dt = p'_i(\varDelta t) + p''_i(\varDelta t), \end{aligned} \end{aligned}$$

(3)

where $p'_i(\varDelta t)$ is the part that moves exactly as our plan, and $p''_i(\varDelta t)$ is the deviation part caused by the noise. Because the noise $\delta _i$ is an independent input that follows normal distribution $N(0,\sigma _i^2)$, we can conclude that $p''_i(\varDelta t)$ follows $N(0,\varDelta t\cdot \sigma _i^2)$. As shown in Fig. 3, the red curve represents the planned motion. At time $\varDelta t$, the robot is planned to move to $p'_i(\varDelta t)$. The deviation at this moment is represented as $p''_i(\varDelta t)$, from which we find that the small overlapping white area between dynamic obstacle and normal distribution represents the probability that robot collide with dynamic obstacle. This probability can be calculated by

$$\begin{aligned} \begin{aligned} \mathcal {P}_i(\varDelta t)&= \int _{-z-l_d}^{-z} \frac{1}{\sqrt{2\pi \varDelta t}\sigma _i}e^{-\frac{x^2}{2\varDelta t\sigma _i^2}}\,dx. \end{aligned} \end{aligned}$$

(4)

If this probability is small enough, it can be inferred that the planned path is safe. We use $\mathcal {P}_{\epsilon }$ as the probability threshold, i.e., a safe path should meet $\mathcal {P}_i(\varDelta t) \le \mathcal {P}_{\epsilon }$. By this means, we can get the minimum $z^*(\varDelta t)$ that meets this condition:

$$\begin{aligned} \begin{aligned} z^*(\varDelta t) = \min \Big \{z| \mathcal {P}_i(\varDelta t) \le \mathcal {P}_{\epsilon } \Big \}. \end{aligned} \end{aligned}$$

(5)

Since $\mathcal {P}_i(\varDelta t)$ is a monotonously decreasing function with z, $z^*(\varDelta t)$ can be easily found out by solving

$$\begin{aligned} \begin{aligned} \mathcal {P}_i(\varDelta t) = \int _{-z-l_d}^{-z} \frac{1}{\sqrt{2\pi \varDelta t}\sigma _i}e^{-\frac{x^2}{2\varDelta t\sigma _i^2}}\,dx = \mathcal {P}_{\epsilon }. \end{aligned} \end{aligned}$$

(6)

Fig. 3.

An illustration of robot position influenced by noise.

Suppose that this dynamic obstacle obstructs the path from $t_1$ to $t_2$. Then for $\varDelta t \in [t_1,\,t_2]$, its corresponding $z^*(\varDelta t)$ can be determined. As shown in Fig. 4, $z^*(\varDelta t)$ forms two curves $z_l^*(\varDelta t)$ and $z_r^*(\varDelta t)$, which are at the left and right side of dynamic obstacle, respectively. It is easy to prove that the extended dynamic obstacle is centerline symmetry because

$$\begin{aligned} \mathcal {P}_i(\varDelta t)&= \int _{-z-l_d}^{-z} \frac{1}{\sqrt{2\pi \varDelta t}\sigma _i}e^{-\frac{x^2}{2\varDelta t\sigma _i^2}}\,dx \end{aligned}$$

(7)

$$\begin{aligned}&= \int _{z}^{z+l_d} \frac{1}{\sqrt{2\pi \varDelta t}\sigma _i}e^{-\frac{x^2}{2\varDelta t\sigma _i^2}}\,dx = \mathcal {P}_{\epsilon }, \end{aligned}$$

(8)

where (7) denotes the right-side curve and (8) denotes the left-side curve. With the extended dynamic obstacle, a feasible path is the one that does not cross over it. In this way, we can apply the approach of velocity interval propagation to find the time-optimal path, only if it takes the extended dynamic obstacle into account.

Fig. 4.

The extension of dynamic obstacle for collision avoidance.

4 Time-Optimal Motion for Multiple Robots

It is difficult to plan time-optimal motions for multi-robots because each robot has numerous motion options to reach their goals. The time-optimal motion planner should take all potential options into account and find out the best one from them. We have already proposed an approach to plan the time-optimal motion for a single robot in dynamic environment. To coordinate the multi-robot motions, we can either apply a conflict-based search scheme to spot all conflicts and resolve them by constructing a conflict tree, or prioritize the motion order of all robots and plan their motions successively according to this order.

4.1 Conflict Probability Between Robots

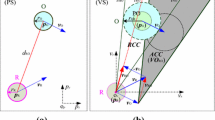
We have derived how to get the conflict probability between a robot and a dynamic obstacle. Analogously, we can derive the conflict probability between robots, by replacing deterministic moving obstacle with non-deterministic moving robot. Suppose that there are two robots $r_1$ and $r_2$ whose paths and motion have been given. Their paths intersect at point v, as shown in Fig. 5(a). The conflict is defined to happen when both robots are very near v simultaneously.

To quantitatively provide the conflict probability, we define that the intersection point v is located at $p_1^v$ of $r_1$’s path and $p_2^v$ of $r_2$’s path. The collision happens when $r_1$ stays within the region $[p_1^v-d_{\epsilon }, p_1^v+d_{\epsilon }]$ and $r_2$ within $[p_2^v-d_{\epsilon }, p_2^v+d_{\epsilon }]$ at the same time, where $d_{\epsilon }$ denotes a small path segment. We have derived that $p_1(\varDelta t) = p'_1(\varDelta t) + p''_1(\varDelta t)$ in (3) where $p'_1(\varDelta t)$ is given and $p''_1(\varDelta t)$ follows normal distribution $N(0,\varDelta t \cdot \sigma _1^2)$. Thus, $p_1(\varDelta t)$ follows $N\big (p'_1(\varDelta t),~\varDelta t \cdot \sigma _1^2\big )$. In a similar way, we know that $p_2(\varDelta t)$ follows $N\big (p'_2(\varDelta t),~\varDelta t \cdot \sigma _2^2\big )$. We can further get the probability of robot $r_1$ and $r_2$ staying within the region $[p_1^v-d_{\epsilon }, p_1^v+d_{\epsilon }]$ and $[p_2^v-d_{\epsilon }, p_2^v+d_{\epsilon }]$ at time $t=\varDelta t$,

$$\begin{aligned} \mathcal {P}_1^v(\varDelta t)&= \int _{p_1^v-d_{\epsilon }}^{p_1^v+d_{\epsilon }} \frac{1}{\sqrt{2\pi \varDelta t}\sigma _1}e^{-\frac{\big (x-p'_1(\varDelta t)\big )^2}{2\varDelta t\sigma _1^2}}\,dx, \end{aligned}$$

(9)

$$\begin{aligned} \mathcal {P}_2^v(\varDelta t)&= \int _{p_2^v-d_{\epsilon }}^{p_2^v+d_{\epsilon }} \frac{1}{\sqrt{2\pi \varDelta t}\sigma _2}e^{-\frac{\big (x-p'_2(\varDelta t)\big )^2}{2\varDelta t\sigma _2^2}}\,dx. \end{aligned}$$

(10)

So the conflict probability at $\varDelta t$ between $r_1$ and $r_2$ is $\mathcal {P}_{1,2}^v(\varDelta ) = \mathcal {P}_1^v(\varDelta t) \cdot \mathcal {P}_2^v(\varDelta t)$. Our aim is to let

$$\begin{aligned} \begin{aligned} \forall \varDelta t > 0,~\mathcal {P}_{1,2}^v(\varDelta t) \le \mathcal {P}_{\epsilon }. \end{aligned} \end{aligned}$$

(11)

4.2 Conflict Resolution

To coordinate the motion of $r_1$ and $r_2$ at v, we can let one of them move freely, and the other one considers it as a dynamic obstacle. Suppose that $r_1$ has the time-optimal motion without considering $r_2$’s motion. Its motion will be considered as a dynamic obstacle by $r_2$, as presented in Fig. 5(b). To apply VIP to find $r_2$’s time-optimal motion, we should get the feasible area in its path-time coordinate plane. Because $r_1$’s motion is given, $\mathcal {P}_1^v(\varDelta t)$ is known, and we can find probability requirement on $r_2$ passing $[p_2^v-d_{\epsilon }, p_2^v+d_{\epsilon }]$ by solving

$$\begin{aligned} \begin{aligned} \mathcal {P}_2^v(\varDelta t) = \int _{p_2^v-d_{\epsilon }}^{p_2^v+d_{\epsilon }} \frac{1}{\sqrt{2\pi \varDelta t}\sigma _2}e^{-\frac{\big (x-p'_2(\varDelta t)\big )^2}{2\varDelta t\sigma _2^2}}\,dx < \frac{ \mathcal {P}_{\epsilon }}{\mathcal {P}_1^v(\varDelta t)}, \end{aligned} \end{aligned}$$

(12)

as shown in Fig. 5(c). Then we can get $r_2$’s conflict region in its path-time coordinate plane. As shown in Fig. 5(d), we use $C^v_{r_1,r_2}$ to denote it. On the contrary, when $r_2$ moves freely, $C^v_{r_2,r_1}$ denotes the conflict region that $r_1$ needs to avoid.

Fig. 5.

A two-robot motion coordination, (a) $r_1$ and $r_2$ intersects at v, and red lines represent conflict segment, (b) $r_1$’s optimal motion is given, (c) $r_1$’s probability at conflict segment and probability requirement on $r_2$, both with respect to time, (d) the infeasible region on $r_2$’s path-time coordinate plane. (Colour figure online)

4.3 Obstacle Simplification

It should be noted that VIP can only handle the dynamic obstacle whose shape is rectangle in the path-time coordinate plane, while the shape of our obstacle based on probability is not. In order to apply VIP to solve our problem, we have to simplify the shape of our obstacle to rectangle. We discuss the simplification scheme of dynamic obstacle and robot obstacle, respectively.

Dynamic Obstacle Simplification. We suppose that the exact region of its original dynamic obstacle is known, as shown in gray part of Fig. 6(a). The extension part can be obtained by applying (7) and (8) for $\varDelta t \in (t_1,\,t_2)$, as shown in the dark area of Fig. 6(a), where $z^{\max }$ denotes its maximum path length. Then we can use a rectangle with length $l^d+2z^{\max }$ and width $t_2-t_1$ to cover it, and this rectangle can be applied for calling VIP to obtain the optimal motion.

Robot Obstacle Simplification. For the robot obstacle, we suppose that it is covered by a rectangle with a top left vertex $(t_u,\,p_u)$ and bottom right vertex $(t_d,\,p_d)$. Our job is to decide the two vertexes. From (12), we know that if $\mathcal {P}_1^v(\varDelta t)$ is smaller than $\mathcal {P}_{\epsilon }$, the required probability of $\mathcal {P}_2^v(\varDelta t)$ is less than 1. In this case there is no limitation on robot path. However, when $\mathcal {P}_1^v(\varDelta t)$ is equal to $\mathcal {P}_{\epsilon }$, the limitation comes. Thus, we can conclude that the robot obstacle comes into being when $\mathcal {P}_1^v(\varDelta t) = \mathcal {P}_{\epsilon }$. Then we can get two $\varDelta t$ to meet this condition, where the large one is $t_u$ and the small one is $t_d$, i.e.,

$$\begin{aligned} \begin{aligned} \mathcal {P}_1^v(t_u) = \mathcal {P}_1^v(t_d) =\mathcal {P}_{\epsilon } \end{aligned} \end{aligned}$$

(13)

Next, we need to decide the width of this rectangle. It can be found that the width of robot obstacle is negatively proportional to the required probability. The smaller required probability is, the larger obstacle width should be. According to (12), we can infer that the smallest required probability corresponds to the largest $\mathcal {P}_1^v(\varDelta t)$, i.e.,

$$\begin{aligned} \begin{aligned}&\mathcal {P}_{1,\max }^v = \mathcal {P}_1^v(\varDelta t_{\max }) =\max \Big \{\mathcal {P}_1^v(\varDelta t), \forall \varDelta t >0 \Big \}, \\&\mathcal {P}_{2,\min }^v = \frac{\mathcal {P}_{\epsilon }}{\mathcal {P}_{1,\max }^v}, \end{aligned} \end{aligned}$$

(14)

where $\varDelta t_{\max }$ denotes the moment of maximizing $\mathcal {P}_1^v$. Then, we can also get two $p'_2(\varDelta t)$ to meet (14), where the small one is $p_u$ and the large one is $p_d$, i.e.,

$$\begin{aligned} \begin{aligned} \mathcal {P}_{2,\min }^v&= \int _{p_2^v-d_{\epsilon }}^{p_2^v+d_{\epsilon }} \frac{1}{\sqrt{2\pi \varDelta t_{\max }}\sigma _2}e^{-\frac{\big (x-p_u\big )^2}{2\varDelta t_{\max }\sigma _2^2}}\,dx, \\&= \int _{p_2^v-d_{\epsilon }}^{p_2^v+d_{\epsilon }} \frac{1}{\sqrt{2\pi \varDelta t_{\max }}\sigma _2}e^{-\frac{\big (x-p_v\big )^2}{2\varDelta t_{\max }\sigma _2^2}}\,dx. \end{aligned} \end{aligned}$$

(15)

Hence, to find the rectangle that can cover robot obstacle, it is not necessary to compute all parts of robot obstacle. By simply calling (13), (14) and (15), the simplified rectangle can be built.

Fig. 6.

Obstacle simplification illustration, (a) gray part is the original dynamic obstacle, dark part is the extension, and rectangle is its simplified form, (b) gray part is the robot obstacle, and rectangle is its simplified form.

4.4 Probabilistic Conflict-Based Search Scheme

The conflict-based search (CBS) is originally presented to minimize the sum of all robots’ cost in an undirected graph whose edges have been assigned specific cost. In this section we extend it to find the time-optimal motion for multi-robots with specific paths. CBS works at two levels, where at the low level a time-optimal motion is planned for each individual robot under dynamic obstacles and high-level constraints, and at the high level conflicts are spotted and resolved at their earliest start time. Conflict is resolved by adding two successor nodes in the conflict tree. Each robot involved by this conflict is assigned an additional constraint at the low level.

We have presented how to plan time-optimal motion for a single robot with dynamic obstacle, as presented as Algorithm 1. This acts as the low-level algorithm in the probabilistic conflict-based search (P-CBS) scheme. We extend the high-level search to incorporate the conflict based on probability, as presented in Algorithm 2. At the beginning, all robots are given their time-optimal motions by solely considering dynamic obstacles. Then, the first conflict between two robots is spotted, as shown in line 12, where the two robots are denoted as $r_i$ and $r_j$. For each of them, a new node is added to the conflict tree, and a new solution is found. This procedure continues until all conflicts have been resolved.

Similar to CBS, P-CBS is also a complete and optimal algorithm with respect to the motion time, because the search of P-CBS has enumerated all possible situations for the time-optimal solution.

4.5 Prioritized Motion Planning

Intuitively, priority-based approach assigns each robot an unique priority, and robots’ motion is planned in the descending order of their priorities [16, 17]. The collision can thus be avoided with this scheme because low-priority robot consider high-priority robot as dynamic obstacle. In this approach, priority assignment plays a significant role in its performance. We assign the priority to robots according to their Euclid distance of start points and goal points, with a long Euclid distance leading to a high priority, because robots with long distance should avoid interference as much as possible to shorten the maximum of motion time. Its basic procedures are presented in Algorithm 3.

5 Experiments and Results

5.1 Environments and Metrics

The experimental environments are set up like Fig. 1, where there are $n \times n$ robots moving in horizontal and vertical directions with path length = 70 m. Thus, there are 2n robots in total. Here we evaluate the performance of motion planning approaches in three configurations, which are $n=2,\,4,\,6$. A robot is configured to be with width = 1 m and length = 2 m. Its velocity and acceleration bound is set to $\underline{v}_i=0,~\overline{v}_i=3$ and $\underline{a}_i=-3,~\overline{a}_i=2$, respectively.

In general, we investigate the influence of noise intensity and safety requirement on their performance. The noise intensity is represented by its standard variance, i.e., $\sigma _i$, and safety requirement means the conflict probability threshold, i.e., $\mathcal {P}_{\epsilon }$. Here we vary $\sigma _i$ from 0.1 to 0.9 and vary $\mathcal {P}_{\epsilon }$ from $10^{-4}$ to $10^{-1}$, respectively. We set the maximum of their motion time as our optimized goals. In addition, we compare the computation time of compared approaches to evaluate their computation complexity.

5.2 Results

First, we investigate the influence of noise intensity on the performance of compared approaches by fixing conflict probability threshold to 0.01. The maximum of motion time of all robots and computation time in finding solution are presented in Fig. 7, where PRIOR denotes the prioritized motion planning and P-CBS denotes the probabilistic conflict-based search. From Fig. 7(a), we find that, with the increase of noise intensity, the maximum of motion time also increases for both approaches, because an intensive noise brings more uncertainty and forces robots to take more conservative actions to keep safety. It can also be observed that P-CBS achieved a lower motion time compared to PRIOR, especially for a large number of robots. From Fig. 7(b), we observe that the noise intensity has a minor impact on the computation time when robot count is small, but clearly increases it when robot count is large, such as $n=6$. Besides, P-CBS needs more computation time than PRIOR in general because P-CBS needs to check more motion options, while there is only one option for PRIOR. Last, Fig. 7 does not show the results of 6 robots when noise intensity is large, because there is not a feasible solution in these cases. This tells us that a large number of robot or an intensive noise may result in the failure of P-CBS and PRIOR.

Fig. 7.

Performance of compared approaches w.r.t. noise intensity, where (a) is the maximum of motion time, (b) is the computation time, and the conflict probability threshold $\mathcal {P}_{\epsilon }=0.01$

Fig. 8.

Performance of compared approaches w.r.t. conflict probability threshold, where (a) is the maximum of motion time, (b) is the computation time, and the noise intensity $\sigma _i=0.3$

Second, we investigate the influence of conflict probability threshold on the performance of compared approaches by fixing noise intensity to 0.3. The results of motion time and computation time are presented in Fig. 8. We find that the motion time decreases with the increase of conflict probability threshold, because a large conflict probability threshold relieves safety requirement and provides a large freedom in motion planning. Regarding to its influence on the computation time, the planner needs more computation time when conflict probability threshold is small. Last, Fig. 8 also demonstrates that P-CBS achieves smaller motion time and needs more computation time than the prioritized motion planning approach.

6 Conclusions

In this paper, we study the problem how to plan time-optimal motion for multi-robots moving along specified paths. Unlike previous approaches that plan robots’ motion without considering their stochastic noise, we build our approach on the probabilistic motion robot. Towards the aim of minimizing the motion time, we present the conflict probability analysis to ensure the robot’s safety. Because the shape of dynamic obstacle and robot obstacle is irregular in the path-time coordinate plane, we present a simplification scheme to transform them to rectangle, such that the velocity interval propagation can be used to find the time-optimal motion of each individual robot. In the end, we integrate our probability analysis with two popular multi-robot planners, i.e., conflict-based search and prioritized planning, and compare their performance in solution quality and computation time. Experimental results show that conflict-based search can find better solution, while incurring more computation time than prioritized planning.

In the future, we are going to relax the constraint of specified path. For example, in a free space, there can be many paths for a robot walking from a start position to the goal position. The motion planning becomes more complicated because robots need to first decide their paths and then their motions. In addition, P-CBS demands long computation to find an excellent solution. It would be useful to develop a simplified but efficient algorithm that can find a competent solution in a short time.