Keywords

1 Introduction

Suspension system is one of the critical subsystems of a vehicle, which ensures not only the ride comfort but also the passenger safety. Many researchers devoted for improving the design of suspension systems. There are two types of suspension systems, namely active and passive. The active suspension system needs controlled input excitation power to reduce the effects of undesired oscillations due to road profile, and such type of suspension is used only in high-end vehicles due to their complexity and cost. Most of the vehicles use the passive suspension systems; in the present work, we focus on the dynamic analysis of the passive suspension system.

It is important to design the passive suspension system with optimum values of the elements such as spring stiffness and damping coefficient. In the existing literature, many works on the suspension system design have been found, which are detailed as follows. Lee [1] in his study tuned the damper by using the genetic algorithm and evaluated the optimized design parameters for damping force which resulted in the reduction in the acceleration of the sprung mass for the assumed vehicle suspension system. Mitra et al. [2] in their study used the genetic algorithm optimization technique to model a quarter car comprising of driver seat with driver body and found increase in the ride comfort by optimizing the suspension parameters like spring stiffness, tire stiffness, damping coefficient, and sprung mass acceleration.

Nagarkar et al. [3] presented a seat driver nonlinear quarter car model and determined the improvement in the ride comfort and health criterions using the non-dominated sort genetic algorithm (NSGA-II) technique. Chen et al. [4] presented the more accurate improved ride comfort model by introducing nonlinear damper, verified it with experiments and performed a bivariate analysis for finding out the sensitivity of suspension parameters to ride comfort. Puneet et al. [5] in their work determined the damping coefficient from the damper of the light motor vehicle and use those values in quarter car analysis to evaluate the ride comfort and road holding parameters using design of experiments.

Florea et al. [6] in their study optimized the suspension stiffness and damping coefficients by minimizing the sprung mass accelerations and displacements arising from kinematic factors. They excited the quarter car model of 2 D.O.F. by random road profiles having different road roughnesses and used genetic algorithm to obtain the required optimized results. Nagarkar et al. [7] implemented the genetic algorithm in the Mac person strut passive suspension system to minimize the vibration dose values (VDV), suspension space and sprung mass acceleration and displacement for better ride comfort. Maher et al. [8] in their study carried out the linear quarter car simulations and compared those results with the experimental results of passive suspensions which had shown reasonable unsprung mass amplitude frequency range for sinusoidal excitation.

Several researches had been performed in optimizing the parameters in quarter car suspensions using the genetic algorithm technique. Most of the previous researches are focused on optimizing the suspension system parameters having linear and nonlinear damper for providing the better ride comfort and road holding. Our present work focuses on the quadratic nonlinear damper in the passive suspension for optimizing the suspension parameters by utilizing the genetic algorithm technique. The quadratic nonlinear damper used in this study along with the genetic algorithm optimization technique has never used before in the previous researches of the quarter car suspension systems. The contribution of this work is that the optimized parameters can be considered in the automobile vehicle suspension systems for providing the improved ride comfort to the passengers and the driver.

The rest of the paper is organized in the following sections. The modeling of the quarter car model is presented in Sect. 2. Simulation results are discussed in Sect. 3. The paper is concluded in Sect. 4 with some future works.

2 Modeling

2.1 Suspension Parameters

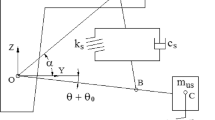
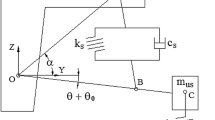
In this work, a quarter car model is developed in order to analyze the performance of the suspension. The schematic diagram of the quarter car model is shown in Fig. 1. The quadratic nonlinear damping effect on the performance of suspension is studied using the quarter car model as shown in Fig. 1. The sprung mass is labeled as ms and is suspended on the suspension spring labeled as ks representing spring stiffness. The damper is labeled in Fig. 1 as cs representing damping coefficient of suspension. The mass of wheel, wheel hub, and the adjoining suspension parts is lumped together as unsprung mass, labeled in Fig. 1 as mu. This unsprung mass rests on the tire whose spring stiffness and damping coefficient are labeled in the figure as ku and cu, respectively. zr is the vertical height from the road surface. zs and zu are the sprung mass and unsprung mass displacements, respectively.

Fig. 1
figure 1

Schematic diagram of the quarter car model

Full size image

The equations of motion for the quarter car model can be derived using Newton’s second law of motion, and the second-order differential equations are given by:

$$ \ddot{z}_{s} = - \frac{{k_{s} }}{{m_{s} }}(z_{s} - z_{u} ) - \frac{{c_{s} }}{{m_{s} }}{\text{Sgn}}(\dot{z}_{s} - \dot{z}_{u} )(\dot{z}_{s} - \dot{z}_{u} )^{2} - g $$
(1)
$$ \begin{gathered} \ddot{z}_{u} = \frac{{k_{s} }}{{m_{u} }}(z_{s} - z_{u} ) + \frac{{c_{s} }}{{m_{u} }}{\text{Sgn}}(\dot{z}_{s} - \dot{z}_{u} )(\dot{z}_{s} - \dot{z}_{u} )^{2} - \frac{{k_{u} }}{{m_{u} }}(z_{u} - z_{r} ) \hfill \\ \, - \frac{{c_{u} }}{{m_{u} }}(\dot{z}_{u} - \dot{z}_{r} ) - g \hfill \\ \end{gathered} $$
(2)

where first and second derivatives zs, zu, and zr represent their velocities and accelerations, respectively. Sgn is the signum function. The numerical values of the parameters used in the study are given in Table 1.

Table 1 Numerical values for the various parameters of the quarter car model
Full size table

2.2 Optimization

Genetic algorithm (GA) is an advanced tool for finding best solution in optimization of desired variables of an objective function. GAs are based on the procedure for searching of natural genetics and natural selection. This way of GA has struck several researches in natural science and engineering. Robustness of solution is the main objective of GA with the help of balance between efficiency and effectiveness of the solution. Goldberg [9] stated the principle and application of GA in engineering field. GA starts from initial population of possible outcomes, i.e., first generations. Reproduction (selection), crossover, and mutation are main operators for optimization of objective function of GA. However, there exist many other optimization techniques, but in this study, GA has been selected due to its ability of global search and easy implementation with good results [10]. GAs have been applied in the vehicle dynamic systems [11] including suspension system [12].

In the suspension system of the quarter car model, we are interested in improving the ride comfort, which can be realized by minimizing the acceleration of the sprung mass. Therefore, the optimization problem can be defined as follows:

$$ \begin{gathered} \mathop {\min }\limits_{{k_{s} ,c_{s} }} \ddot{z}_{s} = f(z_{s} ,z_{u} ,z_{r} ,\dot{z}_{s} ,\dot{z}_{u} ,k_{s} ,c_{s} ) \hfill \\ {\text{subjected to:}} \hfill \\ k_{s\min } \le k_{s} \le k_{s\max } \hfill \\ c_{s\min } \le c_{s} \le c_{s\max } \hfill \\ \end{gathered} $$
(3)

The fitness function for GA is based on the integral time absolute error (ITAE), where the absolute value of the sprung mass acceleration is multiplied by time, and its integration is performed for obtaining the ITAE value.

3 Simulation

The quarter car model is implemented in MATLAB/Simulink for analyzing the dynamic behavior over a road bump. The road bump profile is shown in Fig. 2a and the displacements of the sprung (zs) and unsprung (zu) masses are shown in Fig. 2b. In these results, the values of ks and cs are not optimized and taken as given in Table 1. From these results, it can be observed that initially there is no displacement for two masses, but as the tire strikes the bump at 5 s, there are peaks for zs and zu. The sprung and unsprung masses start oscillating due to the effect of road bump, which leads to reduce in comfort for the driver and passengers. Therefore, it is necessary to reduce the amplitude of oscillations using suitable values of the parameters. Since drive comfort mainly depends on the sprung mass acceleration, hence, it is minimized by optimizing the values of suspension parameters, viz. ks and cs.

Fig. 2
figure 2

a Road excitation and b displacements of the sprung and unsprung masses

Full size image

The values of ks and cs have been optimized using GA, and the population size and the number of generations take 50. The upper and lower bounds for ks and cs are taken as follows: ks = [10,000 30,000] and cs = [1000 3000]. From the GA, the obtained optimized values are ks = 21,960 N/m and cs = 1382 N s/m. The results are shown in Fig. 3, where non-optimized and optimized results are compared.

Fig. 3
figure 3

Simulation results before and after the optimization a absolute acceleration of the sprung mass, b acceleration of the sprung mass, c displacement of the sprung mass, and d relative displacement between the unsprung mass and road height

Full size image

From the simulation results in Fig. 3a, b, it can be observed that after applying the optimized values of ks and cs, amplitude of the sprung mass acceleration reduces which leads to improved ride comfort. In Fig. 3c, the amplitude of oscillations for sprung mass displacement is also reduced after optimization. Moreover, in Fig. 3d, the relative displacement between the unsprung mass and the road excitation is also reduced after optimization, which ensures better road holding capability.

4 Conclusion

The suspension dynamics of a vehicle is analyzed considering the nonlinear quarter car model. The suspension of the quarter car is modeled using a quadratic nonlinear damper. The performance of this nonlinear model is analyzed over a bumpy road. The optimization of the suspension parameters is performed using the genetic algorithm. From the simulation results, it can be concluded that the amplitudes of peaks are reduced for (i) sprung mass acceleration, (ii) sprung mass displacement, and (iii) relative displacement between the unsprung mass and road height, after incorporating the optimized values of ks and cs. Therefore, the optimized values of the suspension parameters resulted in improved ride comfort and road holding capability. For future work, it is interesting to analyze the performance of the suspension system over real road data.