9.1 Introduction

The measurement of several observables in B meson decays do not agree with their Standard Model (SM) predictions. These observables include the measurement of \(R_{K^{(*)}}\), angular observables in \(B \rightarrow K^* \mu ^+ \mu ^-\) (in particular \(P_5^{'}\)), \({\mathscr {B}}(B_s \rightarrow \phi \mu ^+ \mu ^-)\) in the neutral current sector and \(R_{D^{(*)}, J/\psi }\) in the charged current sector. These measurements can be considered as hints of physics beyond the SM.

Apart from the decays of B meson, the top quark decays are particularly important for hunting physics beyond the SM. As it is the heaviest of all the SM particles, it is expected to feel the effect of new physics (NP) most. Also, LHC is primarily a top factory producing abundant top quark events. Hence one expects the observation of possible anomalous couplings in the top sector at the LHC. The SM predictions for the branching ratios of the flavor changing neutral current (FCNC) top quark decays, such as \(t \rightarrow uZ\) and \(t \rightarrow cZ\) decays are \({\sim }10^{-17}\) and \(10^{-14}\), respectively [1, 2], and are probably immeasurable at the LHC until NP enhances their branching ratios up to the detection level of LHC.

In this work, we study the effects of anomalous tcZ couplings on rare B and K meson decays. Using these decays, we obtain constraints on anomalous \(t\rightarrow cZ\) coupling. We then look for flavor signatures of anomalous tcZ coupling. In particular, we examine \({\mathscr {B}}(K_L\rightarrow \pi \, \nu \, \bar{\nu }) \) and various CP violating angular observables in \({B} \rightarrow {K}^* \, \mu ^+\, \mu ^-\). We find that the complex tcZ coupling can give rise to large new physics effects in these CP violating observables.

9.2 Effect of Anomalous \(t\rightarrow cZ\) Couplings on Rare B and K Decays

The effective tcZ Lagrangian can be written as [3]

$$\begin{aligned} {\mathscr {L}}_{tcZ}&= \frac{g}{2 \cos \theta _W} \bar{c}\gamma ^{\mu } \left( g^L_{ct} P_L + g^R_{ct} P_R\right) tZ_{\mu } \nonumber \\&\quad +\frac{g}{2 \cos \theta _W} \bar{c}\frac{i\sigma ^{\mu \nu }p_{\nu }}{M_Z} \left( \kappa ^L_{ct} P_L + \kappa ^R_{ct} P_R\right) tZ_{\mu } + \mathrm{h.c.}, \end{aligned}$$
(9.1)

where \(P_{L,R}\equiv (1\mp \gamma _5)/2\) and \(g^{L,R}_{ct}\) and \(\kappa ^{L,R}_{ct}\) are NP couplings. The anomalous tcZ couplings can provide additional contributions to \(b \rightarrow s\, l^+\, l^-\), \(b \rightarrow d\, l^+\, l^-\) and \(s \rightarrow d \nu \bar{\nu }\) decays via Z penguin diagrams and hence have the potential to affect the decays of several B and K mesons.

Let us now consider the contribution of anomalous tcZ couplings to the rare B decays induced by the quark-level transition \(b \rightarrow s\, \mu ^+\, \mu ^-\). The effective Hamiltonian for the quark-level transition \(b \rightarrow s\, \mu ^+\, \mu ^- \) in the SM can be written as

$$\begin{aligned} {\mathscr {H}}_{\textit{eff}} = - \frac{4 G_F}{\sqrt{2}} V^*_{ts}V_{tb} \sum _{i=1}^{10} C_i(\mu ) \, O_i(\mu )\;, \end{aligned}$$
(9.2)

where the form of the operators \(O_i\) are given in [4]. The effective tcZ vertices, given in (9.1), affect \(b \rightarrow s\, \mu ^+\, \mu ^-\) transition. This contribution modifies the Wilson coefficients (WCs) \(C_{9}\) and \(C_{10}\). The NP contributions to these WCs are [5]

$$\begin{aligned} {C}_9^{s, NP} = - {C}_{10}^{s, NP} = - \frac{1}{8 \sin ^2 \theta _W} \frac{V^*_{cs}}{V^*_{ts}} \Bigg [\left( -x_t \ln \frac{M^2_W}{\mu ^2}+\frac{3}{2}+x_t-x_t\ln x_t\right) g^L_{ct}\Bigg ], \end{aligned}$$
(9.3)

with \(x_t =\bar{m}^2_t/M^2_W\). Here the right-handed coupling, \(g^R_{ct}\), is neglected as it is suppressed by a factor of \(\bar{m_c}/M_W\). Here we have also neglected the contributions from CKM suppressed Feynman diagrams. The NP contributions to \(C_{9,\,10}\) have been calculated in the unitary gauge with the modified minimal subtraction (\( \overline{\text {MS}}\)) scheme [5]. The effective Hamiltonian and the NP contributions to the WCs \(C_{9}\) and \(C_{10}\) for the process \(b \rightarrow d\, \mu ^+\, \mu ^-\) can be obtained from (9.2) to (9.3), respectively, by replacing s by d.

We now consider NP contribution to \(s \rightarrow d \, \nu \bar{\nu }\) transition. The \(K^+ \rightarrow \pi ^+ \, \nu \bar{\nu }\) decay is the only observed decay in this sector. The effective Hamiltonian for \(K^+ \rightarrow \pi ^+ \, \nu \bar{\nu }\) in the SM can be written as

$$\begin{aligned} {\mathscr {H}}_{\textit{eff}} = \frac{G_F}{\sqrt{2}}\frac{\alpha }{2 \pi \sin ^2 \theta _W} \sum _{l=e,\mu ,\tau } \left[ V^*_{cs}V_{cd} X^l_{NL} + V^*_{ts}V_{td} X(x_t) \right] \times (\bar{s}d)_{V-A}(\bar{\nu }_l\nu _l)_{V-A}\,, \end{aligned}$$
(9.4)

where \(X^l_{NL}\) and \(X(x_t)\) are the structure functions corresponding to charm and top sector, respectively [4, 6, 7]. The contribution of anomalous tcZ coupling to \(\bar{s} \rightarrow \bar{d} \, \nu \bar{\nu }\) transition then modifies the structure function \(X(x_t)\) in the following way:

$$\begin{aligned} X(x_t) \rightarrow X^\mathrm{tot}(x_t) = X(x_t) + X^{NP}, \end{aligned}$$
(9.5)

where

$$\begin{aligned} X(x_t)= & {} \eta _X \frac{x_t}{8}\left[ \frac{2+x_t}{x_t-1}+\frac{3x_t-6}{(1-x_t)^2}\ln x_t\right] ,\end{aligned}$$
(9.6)
$$\begin{aligned} X^{NP}= & {} -\frac{1}{8} \left( \frac{V_{cd}V^*_{ts}+V_{td}V^*_{cs}}{V_{td}V^*_{ts}}\right) \left( -x_t \ln \frac{M^2_W}{\mu ^2}+\frac{3}{2}+x_t-x_t\ln x_t\right) (g^{L}_{ct})^*\,.\qquad \end{aligned}$$
(9.7)

Here \(\eta _x=0.994\) is the NLO QCD correction factor.

9.3 Constraints on the Anomalous tcZ Couplings

In order to obtain the constraints on the anomalous tcZ coupling \(g^L_{ct}\), we perform a \(\chi ^2\) fit using all measured observables in B and K sectors. The total \(\chi ^2\) is written as a function of two parameters: \(\mathrm{Re} (g^L_{ct})\) and \(\mathrm{Im} (g^L_{ct})\). The \(\chi ^2\) function is defined as

$$\begin{aligned} \chi ^2_\mathrm{total} = \chi ^2_{b \rightarrow s\, \mu ^+ \,\mu ^-} +\chi ^2_{b \rightarrow d\, \mu ^+ \,\mu ^-} + \chi ^2_{s \rightarrow d \nu \bar{\nu }}~. \end{aligned}$$
(9.8)

In our analysis, we include all recent CP conserving data from \(b \rightarrow s \mu ^+ \mu ^-\) to obtain constraints on \({C}_{9,10}^{s, NP}\). Assuming the WCs \(C_i\) to be real, we obtain \(C^{NP}_9=-C^{NP}_{10}=-0.51\pm 0.09\) [8]. This is consistent with several global fit results such as [9,10,11]. For complex WCs, we get \(C^{NP}_9=-C^{NP}_{10}= (-0.56\pm 0.26) + i (0.55\pm 1.36)\). The fit values thus obtained can be used to constrain \(g^L_{ct}\). For real \(g^L_{ct}\) coupling, we have

$$\begin{aligned} \chi ^2_{b \rightarrow s \mu ^+ \mu ^-} = \bigg (\frac{{C}_9^{s, NP} +0.51}{0.09} \bigg )^2. \end{aligned}$$
(9.9)

For complex \(g^L_{ct}\) couplings, the \(\chi ^2\) function can be written as

$$\begin{aligned} \chi ^2_{b \rightarrow s \mu ^+ \mu ^-} = \bigg (\frac{Re({C}_9^{s, NP}) + 0.56}{0.26} \bigg )^2 +\bigg (\frac{Im({C}_9^{s, NP}) -0.55}{1.36} \bigg )^2. \end{aligned}$$
(9.10)

From \(b \rightarrow d \mu ^+ \mu ^-\) sector the branching ratio of \(B^+ \rightarrow \pi ^+\, \mu ^+\, \mu ^-\) and \(B_d \rightarrow \mu ^+ \mu ^-\) decay are included in our analysis:

$$\begin{aligned} \chi ^2_{b \rightarrow d\, \mu ^+\, \mu ^-} = \chi ^2_{B^+ \rightarrow \pi ^+\, \mu ^+\, \mu ^-} + \chi ^2_{B_d \rightarrow \mu ^+ \mu ^-}. \end{aligned}$$
(9.11)

For \(B^+ \rightarrow \pi ^+\, \mu ^+\, \mu ^-\) decay,

$$\begin{aligned} \chi ^2_{B^+ \rightarrow \pi ^+\, \mu ^+\, \mu ^-} =\bigg ( \frac{{\mathscr {B}}(B^+ \rightarrow \pi ^+\, \mu ^+\, \mu ^-) - 2.3\times 10^{-8}}{0.66\times 10^{-8}} \bigg )^2, \end{aligned}$$
(9.12)

where, following [12], a theoretical error of \(15\%\) is included in \({\mathscr {B}}(B^+ \rightarrow \pi ^+\, \mu ^+\, \mu ^-)\). For \({\mathscr {B}}(B_d \rightarrow \mu ^+ \mu ^-)\) decay,

$$\begin{aligned} \chi ^2_{B_d \rightarrow \mu ^+ \,\mu ^-} =\bigg ( \frac{{\mathscr {B}}(B_d \rightarrow \mu ^+ \,\mu ^-) - 3.9\times 10^{-10}}{1.6\times 10^{-10}} \bigg )^2. \end{aligned}$$
(9.13)

The branching ratio of \(B_d \rightarrow \mu ^+ \,\mu ^-\) in the presence of anomalous tcZ coupling is given by

$$\begin{aligned} {\mathscr {B}}(B_d \rightarrow \mu ^+ \,\mu ^-) = \frac{G^2_F \alpha ^2 M_{B_d} m_\mu ^2 f_{B_d}^2 \tau _{B_d}}{16 \pi ^3} |V_{td}V^*_{tb}|^2 \sqrt{1-4 (m_\mu ^2/M_{B_d}^2)} \left| {C}_{10} + C^{d,NP}_{10} \right| ^2. \end{aligned}$$
(9.14)

The branching ratio of \(K^+ \rightarrow \pi ^+ \nu {\bar{\nu }}\), the only measurement in \(s \rightarrow d\, \nu {\bar{\nu }}\) sector, in the presence of anomalous tcZ coupling is given by

$$\begin{aligned} \frac{{\mathscr {B}}(K^+ \rightarrow \pi ^+ \nu {\bar{\nu }})}{\kappa _{+}}&= \left( \frac{\mathrm{Re}(V_{cd}V^*_{cs})}{\lambda } P_c(X) +\frac{\mathrm{Re}(V_{td}V^*_{ts})}{\lambda ^5}X^\mathrm{tot}(x_t) \right) ^2 \nonumber \\&\quad +\, \left( \frac{\mathrm{Im}(V_{td}V^*_{ts})}{\lambda ^5} X^\mathrm{tot}(x_t)\right) ^2, \end{aligned}$$
(9.15)

where \(P_c(X)=0.38\pm 0.04\) [13] is the NNLO QCD-corrected structure function in the charm sector and

$$\begin{aligned} \kappa _+ = r_{K^+} \frac{3 \alpha ^2 {\mathscr {B}}(K^+\rightarrow \pi ^0 e^+ \nu )}{2 \pi ^2 \sin ^4 \theta _W} \lambda ^8 ~. \end{aligned}$$
(9.16)

Using \(r_{K^+}=0.901\), we estimate

$$\begin{aligned} \frac{{\mathscr {B}}(K^+\rightarrow \pi ^+\nu \bar{\nu })}{\kappa _+} = 3.17 \pm 2.05. \end{aligned}$$
(9.17)

In order to include \({\mathscr {B}}(K^+\rightarrow \pi ^+\nu \bar{\nu })\) in the fit, we define

$$\begin{aligned} \chi ^2_{K^+\rightarrow \pi ^+\nu \bar{\nu }} =\bigg ( \frac{{\mathscr {B}}(K^+\rightarrow \pi ^+\nu \bar{\nu })/\kappa _{+} - 3.17}{2.05} \bigg )^2 +\bigg ( \frac{P_c(X) - 0.38}{0.04} \bigg )^2. \end{aligned}$$
(9.18)

Thus, the error on \(P_c(X)\) has been taken into account by considering it to be a parameter and adding a contribution to \(\chi ^2_\mathrm{total}\).

Table 9.1 Values of anomalous tcZ couplings
Full size table

The \({\mathscr {B}}(t \rightarrow c Z)\) in the presence of tcZ coupling is given as [14,15,16]

$$\begin{aligned} {\mathscr {B}}(t\rightarrow c\, Z)= \frac{\beta ^4_Z (3-2\beta ^2_Z)}{2\beta ^4_W (3-2\beta ^2_W)} \frac{\vert g_{ct}^L\vert ^2 + \vert g_{ct}^R\vert ^2}{\vert V_{tb}\vert ^2}, \end{aligned}$$
(9.19)

with \(\beta _x = (1-m^2_x/m^2_t)^{1/2}\), being the velocity of the \(x=W,Z\) boson in the top quark rest frame.

The fit results for real and complex tcZ couplings are presented in Table 9.1. Using the fit results, we find that for real tcZ coupling, \({\mathscr {B}}(t \rightarrow c \, Z)= (0.90 \pm 0.33) \times 10^{-5}\). For complex tcZ coupling, 2\(\sigma \) upper bound on the branching ratio is \(2.14 \times 10^{-4}\). Hence, any future measurement of this branching ratio at the level of \(10^{-4}\) would imply the coupling to be complex.

9.4 Predictions for Various CP Violating Observables

We now see whether large deviation is possible in some of the flavor physics observables due to the anomalous tcZ coupling.

\(\mathbf {{\mathscr {B}}(K_L\rightarrow \pi ^0 \, \nu }\) \(\bar{\nu }\)): The preset upper bound on \({\mathscr {B}}(K_L\rightarrow \pi ^0 \, \nu \, \bar{\nu })\) is \(2.6\times 10^{-8}\) [17] at \(90\%\) C.L. which is about three orders of magnitude above the SM prediction. The branching ratio of \(K_L\rightarrow \pi ^0 \, \nu \, \bar{\nu }\) is a purely CP violating quantity.The branching ratio of \(K_L \rightarrow \pi ^0 \, \nu \, \bar{\nu }\) in the presence of tcZ coupling is given by

$$\begin{aligned} {\mathscr {B}}(K_L\rightarrow \pi ^0 \, \nu \, \bar{\nu }) = \kappa _L \left[ \frac{\mathrm{Im}\left( V_{ts}^* V_{td} X^\mathrm{tot}(x_t)\right) }{\lambda ^5}\right] ^2, \end{aligned}$$
(9.20)

where \(X^\mathrm{tot}(x_t)\) is given in (9.5).

Using fit result for the complex tcZ coupling, we get \(Br(K_L \rightarrow \pi ^0 \nu \bar{\nu })=(9.88 \pm 5.96) \times 10^{-11}\). The 2\(\sigma \) upper bound on \({\mathscr {B}}(K_L\rightarrow \pi ^0 \, \nu \, \bar{\nu })\) is obtained to be \(\le 2.18\times 10^{-10}\), an order of magnitude higher than its SM prediction.

Fig. 9.1
figure 1

(Color Online) The plots depicts various CP violating observables in \(B \rightarrow K^*\, \mu ^+ \,\mu ^-\) decays

Full size image

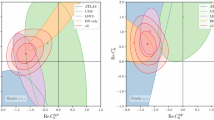
\(\mathbf {CP}\) violating observables in \(\mathbf {B \rightarrow K^*\, \mu ^+ \,\mu ^-}\): We study various CP violating observables in \(B \rightarrow K^*\, \mu ^+ \,\mu ^-\) decays in the presence of complex anomalous tcZ couplings.The CP-violating observables for these decays are defined as [18]

$$\begin{aligned} A_i = \frac{I_i - \bar{I_i}}{d(\varGamma + \bar{\varGamma })/dq^2}, \end{aligned}$$
(9.21)

where \( I_is\) are given in [18]. These asymmetries are largely suppressed in SM because of the small weak phase of CKM and hence they are sensitive to complex NP couplings. These symmetries can get significant contribution from the NP in the presence of CP-violating phase [19,20,21].

The predictions for CP-violating asymmetries \(A_7\) and \(A_8\) in the presence of complex anomalous tcZ couplings are shown in Fig. 9.1. It can be seen from our results that the asymmetry \(A_7\) can be enhanced up to \(~20\%\) whereas enhancement in \(A_8\) can be up to \(~10\%\) in the low-\(q^2\) region. For all other asymmetries, large enhancement is not possible.