Keywords

13.1 Introduction

Semileptonic decays of charmed meson provide the key window to understand the decay of heavy quark dynamics because of the involvement of strong as well as weak interaction. The CKM matrix elements \(|V_{cd}|\) and \(|V_{cs}|\) can be extracted from semileptonic decays of \(D_{(s)}\) mesons as they are parameterized by the form factor calculations. Experimentally, the data on form factors and branching fractions are reported by BESIII [1,2,3,4], BABAR [5], Belle [6], and CLEO collaborations [7]. The form factors for the channels \(D \rightarrow (K, \pi )\) have also been reported using lattice quantum charmodynamics (LQCD) by ETM Collaborations [8, 9] and light cone sum rules (LCSR) [10]. The form factors and branching fractions are also computed using light front quark model [11], heavy meson chiral theory [12], constituent quark model [13], and chiral unitary approach [14]. The charmed meson decay properties are also studied in the potential model formalism [15,16,17,18].

In this article, we employ the Covariant Confined Quark Model for computation of semileptonic transition form factors and branching fractions of D mesons. We compare our findings with the experimental data from the BESIII, BABAR, CLEO, and Belle collaborations.

13.2 Form Factors and Branching Fractions in Covariant Confined Quark Model

The Covariant Confined Quark Model (CCQM), developed by Efimov and Ivanov [19,20,21,22] is a quantum field theoretical approach for hadronic interaction with the constituent quark via exchange of quark only. The effective interaction Lagrangian for meson \(M(q_1,\bar{q}_2)\) corresponding to the constituent quarks \(q_1\) and \(\bar{q}_2\) is given by

$$\begin{aligned} L_{\text {int}} = g_M M(x) \int dx_1 \int dx_2 F_M(x;x_1,x_2) \cdot \bar{q}_{f_1}^a (x_1) \varGamma _{M} q_{f_2}^a (x_2) + H.c. \end{aligned}$$
(13.1)

with \(F_M(x;x_1,x_2)\) as the vertex function that characterizes the quark distribution within the mesons. For simplicity, we choose the vertex function to be of the Gaussian form. Here, \(\varGamma _M\) is the Dirac matrix corresponding to spin of the respective mesonic field M(x) and \(g_M\) is the meson coupling constant computed from the meson self-energy diagram. The model parameters, namely quark masses and size parameters are given in Tab. 13.1.

Table 13.1 Constituent quark masses and size parameters (in GeV)
Full size table

For computation of semileptonic branching fractions, the invariant matrix element can be written as

$$\begin{aligned} M(D \rightarrow (P,V) \ell ^+ \nu _{\ell }) = \frac{G_F}{\sqrt{2}} V_{cq} \langle P,V | \bar{q} \gamma ^\mu (1-\gamma _5) c | D \rangle \ \ell ^+ \gamma ^\mu (1-\gamma _5) \nu _{\ell },\qquad \end{aligned}$$
(13.2)

where \(G_F\) is the Fermi coupling constant, P, V correspond to the pseudoscalar or vector mesons in the final state, respectively. The matrix element for the semileptonic decays can be written in terms of transition form factors as

$$\begin{aligned} \langle P (p_2) | \bar{s}O^\mu c | D (p_1) \rangle= & {} F_+(q^2) P^{\mu } + F_-(q^2) q^{\mu } \end{aligned}$$
(13.3)
$$\begin{aligned} \langle V (p_2,\epsilon _{\nu }) | \bar{s}O^\mu c | D (p_1) \rangle= & {} \frac{\epsilon _{\nu }^{\dag }}{m_1 + m_2} \left[ -g^{\mu \nu } P\cdot q A_0(q^2) + P^{\mu } P^{\nu } A_+(q^2) \right. \\&\left. + q^{\mu } P^{\nu } A_-(q^2) + i\varepsilon ^{\mu \nu \alpha \beta } P_{\alpha } q_{\beta }V(q^2) \right] , \end{aligned}$$
(13.4)

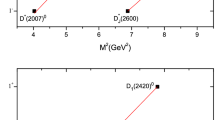
where \(P = p_1 + p_2\), \(q = p_1-p_2\) and \(p_1\), \(p_2\) are the momenta of parent and daughter mesons, respectively. We present our form factors in Fig. 13.1. The form factors in the double pole approximation are given as

$$\begin{aligned} F(q^2) = \frac{F(0)}{1 - a \frac{q^2}{m_1^2}+ b (\frac{q^2}{m_1^2})^2}. \end{aligned}$$
(13.5)

The form factors and associated double pole parameters are given in Table 13.2.

Fig. 13.1
figure 1

Form factors

Full size image
Table 13.2 Double pole parameters
Full size table

After defining the form factors, we compute the semileptonic branching fractions using the relations [23, 24]

$$\begin{aligned} \frac{d\varGamma (D \rightarrow (P,V) \ell ^+ \nu _\ell )}{dq^2}= & {} \frac{G_F^2 |V_{cq}|^2 |\mathbf{p_2}| q^2}{12 (2\pi )^3m_{D}^2} \left( 1 - \frac{m_\ell ^2}{q^2}\right) ^2 \\&\times \left[ \left( 1+\frac{m_\ell ^2}{2q^2}\right) \sum _{n=0,+,-} |H_n|^2 + \frac{3m_\ell ^2}{2q^2} |H_t|^2\right] .\qquad \qquad \end{aligned}$$
(13.6)

Here \(|\mathbf{p_2}| =\lambda ^2 (m_D^2, m_{P/V}^2, q^2)/2 m_D^2\) is the momentum of daughter meson in the rest frame of the D meson with \(\lambda \) is the Källen function. \(H_\pm \), \(H_0\), and \(H_t\) are the helicity amplitudes expressed as

For \(D \rightarrow P\) channel:

$$\begin{aligned} \nonumber H_t= & {} \frac{1}{\sqrt{q^2}} (Pq F_+ + q^2 F_-),\\ H_\pm= & {} 0 \ \ \ {\text {and}} \ \ \ H_0 = \frac{2 m_1 |\mathbf {p_2}|}{\sqrt{q^2}} F_+ \end{aligned}$$
(13.7)

For \(D \rightarrow V\) channel:

$$\begin{aligned} \nonumber H_t= & {} \frac{1}{m_1+m_2} \frac{m_1 |\mathbf{p_2}|}{m_2\sqrt{q^2}} \left( (m_1^2 - m_2^2) (A_+ - A_-) + q^2 A_-\right) \\ H_\pm= & {} \frac{1}{m_1+m_2} (-(m_1^2 - m_2^2)A_0 \pm 2 m_1 |\mathbf{p_2}| V) \nonumber \\ H_0= & {} \frac{1}{m_1+m_2} \frac{1}{2m_2\sqrt{q^2}} (-(m_1^2 - m_2^2)(m_1^2 - m_2^2-q^2)A_0 + 4m_1^2 |\mathbf{p_2}|^2A_+). \end{aligned}$$
(13.8)

The computed semileptonic branching fractions for \(D^+\) meson are given in Table 13.3 in comparison with experimental observations.

Table 13.3 Charmed semileptonic branching fractions (in %)
Full size table

13.3 Results and Discussion

Having defined the model parameters and form factors, we compute the semileptonic branching fractions within the framework of the Covariant Confined Quark Model. The numerical results of semileptonic branching fractions are tabulated in Table 13.3. Our results for \(D^+ \rightarrow \pi ^0 e^+ \nu _e\) are found to be nearer to the BESIII data and for muon channel the experimental results are still not available. For \(D^+ \rightarrow \bar{K}^0 \ell ^+ \nu _\ell \) channel, our results are in good agreement with the CLEO and BESIII data. For \(D^+ \rightarrow \bar{K}^*(892)^0 \ell ^+ \nu _\ell \) channel our results overestimate the experimental data. For detailed description of the model and computation technique we suggest the readers to refer our papers [25,26,27] as well as our recent review article [28]. In these papers, we have extensively studied the leptonic and semileptonic decay of D and \(D_s\) mesons. We study \(D^{+(0)} \rightarrow (K, K^*(892), \pi , \rho , \omega , \eta , \eta ^\prime , D^0) \ell ^+ \nu _\ell \), \(D_s^+ \rightarrow (K, K^*(892)^0, \phi , \eta , \eta ^\prime , D^0) \ell ^+ \nu _\ell \). We also study the other physical observables such as forward-backward asymmetry, longitudinal and transverse polarizations, lepton-side, and hadron-side convexity parameters.

The study of hadronic properties in Covariant Confined Quark Model is very general and this formalism is applicable to any number of quarks with any number of loops. In the last few years this formalism is successfully employed for computation of decay properties of \(B_{(s)}\) mesons [32,33,34,35,36,37,38], \(B_{c}\) mesons [39,40,41], charmed and beauty baryons [42,43,44,45,46] and exotic states [47,48,49].