Entropy Based Cluster Selection

Abstract

Clustering has emerged as a method of unsupervised partitioning of a given set of data instances into a number of groups (called clusters) so that instances in the same group are more similar among each other with respect to instances in other groups. But there does not exist a universal clustering algorithm that can yield satisfactory result for any dataset. In this work we consider an ensemble (collection) of clusterings (partitions) of a dataset obtained in different ways and devise two methods that judiciously select clusters from different clusterings in the ensemble to construct a robust clustering. The superior performances of the proposed methods over well-known existing clustering algorithms on several benchmark datasets are empirically reported.

1 Introduction

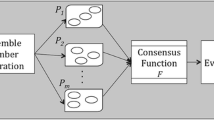
Cluster analysis or clustering [1] is a machine learning technique that unsupervisely recognizes groups (clusters) of similar data instances collected from fields such as marketing, social network, bio-medical etc. [2]. In the literature numerous clustering algorithms [3] have been proposed that conceptually differ among themselves for clustering datasets having a different distribution of instances. But since there does not exist a universal clustering algorithm that can provide an acceptable result for any dataset [4], clustering ensemble (also referred to as consensus clustering) [5] techniques have been proposed in the literature that optimally combine the results of different clusterings to yield a qualitatively better and robust clustering solution. But since finding a consensus clustering in the space of clusterings is an NP-hard problem, several heuristics are being proposed to find an acceptable consensus, which can be broadly categorized into hyper-graph based, information theory based, mixture model (EM) based, voting based and co-association based methods.

In this work, we propose a new way of arriving at a consensus clustering from an ensemble of clusterings with a true number of clusters. We present a concept of consensus clustering that can be formed by selecting clusters from the existing clusterings in the ensemble. Every cluster in the ensemble can be assigned with an entropy measure representing its reliability in the ensemble. A cluster having lower entropy can be considered being of higher priority in forming a consensus. Hence selection of clusters and overlapping problem (if any) of selected clusters can be resolved by prioritizing clusters having lower entropy values to form the final consensus clustering. In a second approach we propose to select a cluster having the lowest entropy from an ensemble of clusterings and iteratively the process is repeated after removing the data instances of the selected clusters to construct the final clustering. In the empirical section, we explain the significance of our proposed methods and show their superiority over well-known existing clustering methods on several benchmark datasets.

The outline of the rest of this paper is as follows. The related work is written in Sect. 2. Section 3 presents the problem statement and the proposed methods are described in Sect. 4. Section 5 empirically demonstrates the performance of the proposed algorithms and Sect. 6 concludes the paper.

2 Related Work

In recent years a significant number of research papers have been published on new algorithms of consensus clustering [7]. We give a brief overview of the well-known clustering ensemble algorithms in this section.

Fred et al. [5] combined ensemble of clusterings produced in different ways into a co-association matrix (also called similarity matrix) and the final consensus clustering was obtained by applying hierarchical single-link algorithm on the co-association matrix. The method was referred to as Evidence Accumulation (EAC) method. Huang et al. [8] applied average-linked agglomerative clustering technique on a cluster-level weighted co-association matrix to derive a consensus clustering. The proposed method was referred by them as Locally Weighted Ensemble Accumulation(LWEA) method, in which the said cluster-level weight depended on a user defined parameter, and the best result was reported in the experiment. Strehl et al. [6] represented the problem of clustering ensemble as a combinatorial optimization problem in terms of shared mutual information and tried to solve the problem by representing the clustering ensemble as a hyper-graph, where each clustering is an hyper-edge. They proposed three different algorithms, namely Cluster-based Similarity Partitioning (CSPA), Hyper Graph Partitioning (HGPA), and Meta-Clustering (MCLA). Huang et al. [10] implemented Crowd Agreement Estimation and Multigranularity Link Analysis to solve the clustering ensemble problem. They proposed two algorithms namely, weighted evidence accumulation clustering (WEAC) and graph partitioning with multi-granularity link analysis (GP-MGLA). Huang et al. [10] computed Probability Trajectory based Similarity between clusters in the clusterings and proposed two algorithms namely, Probability Trajectory Accumulation(PTA) and Probability Trajectory Based Graph Partitioning(PTGP). PTA was an agglomerative clustering algorithm that depended on two user-defined parameters. In our experimental comparison the best result of the method is reported. Nguyen et al. [12] presented iterative voting techniques to find a clustering ensemble in which the principal operation was to learn the closest cluster from each data instance in every iteration. On this basis they proposed their algorithms, namely Iterative Voting Consensus (IVC), Iterative Pairwise Consensus (IPC) and Iterative Probabilistic Voting Consensus (IPVC). Fern et al. [9] proposed Cluster and select(CAS) method that used NMI [6] measure to group similar clusterings from the initial ensemble. The final ensemble was created by selecting a representative from each group of clusterings. Finally, CSPA was used as the clustering ensemble method on the final ensemble. The size of the final ensemble was a user-defined parameter, and the best result was reported in the experiment.

3 Problem Statement

Let D be the set of N data instances $D = \{d_1, d_2, \ldots , d_N \}$. We are given with an ensemble of M clusterings, $E = \{P_1, P_2, \ldots , P_M\}$ of D, where a clustering $P_t$ $(t=1,2, \ldots , M)$ on D is defined as a set of clusters $P_t = \{C^t_1, C^t_2, \ldots , C^t_{K}\}$ such that $C^t_i \subseteq D$, $C^t_i \cap C^t_j = \phi$,($i\ne j$) and $\bigcup \nolimits _{i=1}^{K} C_i^t = D, (i,j=1,2, \ldots K)$. The goal of clustering ensemble is is to find a clustering $P^* = \{C^*_1, C^*_2, \ldots , C^*_k\}$ that is a sort of median of the given ensemble of clusterings $P_1, P_2, \ldots$ and $P_M$. $P^*$ is called the consensus clustering.

In this work we approach the problem of consensus clustering by assigning an entropy value to individual cluster in the ensemble. To do that let us define the joint probability $p(C^t_i,C_j^s)$ that signifies the level of agreement cluster $C^t_i$ ( in clustering $P_t$ ) has with cluster $C^s_j$ (in clustering $P_s$). By level of agreement we mean the number of elements both clusters have in common. Then,

$$\begin{aligned} p(C^t_i,C_j^s)=\frac{|C^t_i\cap C_j^s|}{|C^t_i|} \end{aligned}$$

(1)

Let the entropy measure $\text {Ent}(C^t_i,C_j^s)$ represents the entropy of a cluster $C^t_i$ w.r.t. $C^s_j$ (and vice versa) and is computed as in Huang et al. [8] (it is to note that, our proposed methods do not depend on a specific surprisal measure),

$$\begin{aligned} \text {Ent}(C^t_i,C_j^s)= -p(C^t_i,C_j^s) \cdot \log _2 p(C^t_i,C_j^s) \end{aligned}$$

(2)

Then the total entropy of the cluster $C^t_i$ w.r.t all clusters in the ensemble E is

$$\begin{aligned} \text {Ent}(C^t_i)=- \sum _{\begin{array}{c} s=1\\ s\ne t \end{array}}^M\sum _{j=1}^K p(C^t_i,C_j^s) \cdot \log _2 p(C^t_i,C_j^s) \end{aligned}$$

(3)

Less the total entropy of a cluster more it agrees with other intersecting clusters in the ensemble. Hence a clustering, containing clusters having minimum possible entropy values, is a sort of median of the entire ensemble which approximates the consensus clustering $P^*$. In our work we propose two heuristics to achieve the said goal. It is also to note that, Eq. 3 tends to allot lower entropy to finer clusters than that of coarser clusters. In a trivial case, a cluster having a single data instance has an entropy value of zero.

4 Proposed Methods

In our first approach we put all the clusters of each clustering in the ensemble into a set say C. Since each clustering contains K clusters and there are total M number of clusterings in the ensemble E, there will be $K \cdot M$ number of clusters in C. We consider a collection, say S, of all possible subsets of C, where each set consists of K clusters and covers all the data instances in D. Cluster overlapping may happen in a set if all the K clusters are not mutually exclusive. Out of all the sets in S we consider the set, say $\overline{C}^*$, in which the sum of entropy values of all the constituent clusters is minimum. If all the K clusters in $\overline{C}^*$ are mutually exclusive, then $\overline{C}^*$ is the desired consensus clustering $P^*$. Else the cluster overlapping problem is solved by prioritizing clusters having lower entropy value. More precisely, if two clusters are not disjoint, the cluster having less Entropy value will be retained, whereas the intersection part of the said two clusters is removed from the other cluster. It is to note that, reduction of a cluster reduces its degree of disagreement with other clusters in the ensemble; as a result the reduced cluster tends to have a lower entropy value than that of its previous version. The final set, without overlapping clusters, is the desired consensus clustering $P^*$. The proposed solution of the overlapping problem can actually decrease the entropy of the clustering (which is the sum of the total entropy values of its constituent clusters), hence resulting in a better consensus. We write down the said heuristics in form of an algorithm and we call it Entropy based Cluster Selection (ECS) Consensus Clustering. The output of the algorithm cannot be empty, as the existing clustering with the lowest entropy in the ensemble is also a possible output. Such output can occur only when the selected clusters are non-overlapping. The time complexity of the proposed algorithm can be reduced by solving it using dynamic programming.

We propose an alternative approach in generating a robust and good quality clustering from an ensemble of clusterings. In our second approach we follow the following steps to come up with the final clustering.

• 1. Consider the set of all clusters C in an ensemble of clusterings each having K number of clusters.

• 2. Select the cluster in C having the lowest entropy value.

• 3. Remove the data instances contained in the selected cluster from the dataset D.

• 4. Generate a new ensemble of clusterings each having $K=K-1$ number of clusters.

• 5. Repeat steps 1–4 until the remaining data instances in D is grouped into a single cluster.

The above method cannot be categorized as a traditional consensus clustering method. It iteratively generates the final clustering from a sequence of an ensemble of clusterings with a reducing number of clusters. In this method the quality of the final clustering depends more on the ensemble generation process than ECS. We write down this method in form of an algorithm and we call it Maximum Entropy Cluster Selection (MECS) Clustering.

5 Experimental Result

In this section, we empirically show the efficiency of our proposed methods over other existing well-known clustering ensemble algorithms. First, we discuss the data sets and the basic settings of our experiments used in the evaluation process.

5.1 Datasets

In our experiments, we use nine well known real-world labeled datasets, namely, Iris, Wine, Glass, Image Segmentation (IS),Ecoli and Steel Plates Faults (SPF). Table 1 displays the details of the datasets. All the datasets are taken from the UCI machine learning repository [11].

Table 1 Description of datasets

Table 2 Comparison of performance with NMI

5.2 Ensemble Generation

The clusterings in the ensemble are generated by applying the K-means algorithm [1] with different random initializations. The K-means method is considered here as it is widely used in the clustering ensemble studies in the literature. We generate an ensemble of 100 clusterings for all datasets in which clusterings may repeat. We denote E as the entire ensemble, E/x as the ensemble formed by randomly selected x percentage of clusterings from E, $E_d$ as the distinct partitions in E, and $E_d/x$ would mean a randomly selected x percentage clusterings from $E_d$. We perform tests on three types of ensembles E/20, $E_d/10$ and $E_d/5$. We run all the clustering ensemble algorithms, discussed in Sect. 2, ten times for each dataset and report the average performance. The performances (validity) of the methods are measured with the help of Normalized Mutual Information (NMI) [6], by comparing their result with the ground truth information available with each dataset. The range of NMI is between 0 and 1 and a larger value indicates better quality clustering w.r.t ground-truth information. Let $P^*$ be the consensus clustering and G is the ground-truth clustering. The NMI score of $P^*$ given G is defined as follows:

$$\begin{aligned} \text {NMI}(P^*, G)=\frac{\sum _{i=1}^{K}\sum _{j=1}^{K}N_{ij}\log \frac{N_{ij}N}{N_i^{P^*}N_j^G}}{\sqrt{\sum _{i=1}^{K}N_i^{P^*}\log \frac{N_i^{P^*}}{N}\sum _{j=1}^{K}N_j^G\log \frac{N_j^G}{N}}}, \end{aligned}$$

(4)

where $P^*$ and G have K (true) number of clusters and N is the total number of instances in the data set. $N_i^{P^*}$, $N_j^G$ and $N_{ij}$ are the numbers of data instances in the ith cluster of $P^*$, jth cluster of G and in both ith cluster in $P^*$ and jth cluster in G, respectively.

5.3 Evaluation

We report the experimental outcomes in Table 2. The proposed ECS achieves highest NMI scores on the Iris, Wine and Ecoli datasets. It performs second best and third best in the case of Glass and IS datasets, respectively. The performance of the proposed MECS is inferior to that of ECS, but superior to most of the well-known methods.

6 Conclusion

In this work, we introduce the concept of cluster selection based consensus clustering technique. We demonstrate that judiciously selecting a set of clusters from the ensemble can result in a better consensus. Evaluations on different datasets show the proposed approaches are efficient and effective in improving the quality of consensus as compared to the existing approaches when the true number of clusters is considered. In the future, we would like to explore other possibilities towards consensus using our proposed concept of cluster selection.