Keywords

1 Introduction

The hydraulic conductivity of porous media is often predicted either based on empirical relationships or hydraulic radius theories, or using capillary models or statistical models, and, more recently, network or fractal models. A great deal of experimental work has been performed by several investigators [1–8], in an effort to reflect the complexity of permeability in models with general applicability. These widely used models represent simplified macroscopic approaches in which the porous medium is treated as an easy-to-use continuum. However, the continuum approach suffers from a major limitation, which is to disregard the physics of flow at pore level, because all its complexities and fine details at the pore scale are hidden in bulk terms, such as empirical coefficients [2], shape coefficients, permeability, tortuosity, etc. In fact, although these investigations give us a clearer understanding of some of the factors that control permeability, a universal relationship between permeability and all these factors seems to be an illusion.

1.1 Permeability Models

To model the flow rate through a porous medium, we need to know the parameters of the pore structure, such as the pore sizes throughout the medium, the connectivity of the pore channels, and the tortuosity of these channels (morphology and topology). An accurate description of the pore space is a crucial, and rich, source of information about the porous medium. This information is required to investigate the velocity, pressure, and distribution of the fluid flow. Modeling flow rate is an indispensable task, as it is vital to know what occurs inside the porous medium, which is a complex structure consisting of a solid skeleton and pores through which the flow occurs. However, this task is a difficult one. Numerous studies have been carried out to link the microscopic structural quantities to macroscopic properties. One of the most widely accepted relationships between permeability and the properties of pores was proposed by Kozeny and later modified by Carman. The well-known semi-empirical Kozeny-Carman model [2, 9] relates permeability to porosity, specific surface, tortuosity, and the shape factor. This model was developed based on Poiseuille flow through bundled parallel tubes of equal length and constant cross-section for which the Navier-Stokes equation can be solved. However, this model does not work accurately for all types of porous medium, and it gives very poor predictions for complex porous media. Many empirical models have been proposed [1, 4, 6–8, 10–12], but their correlations all have a significant drawback, which is that fully empirical models are technically valid only for the samples for which the results have been collected. A reasonable prediction can be generated by semi-empirical models of permeability, and are an alternative to permeability tests for granular soils. These models relate permeability to parameters like porosity, specific surface area, tortuosity, the shape factor, and particle size distribution. However, not only do they have limitations, they also lack accuracy.

1.2 Tortuosity

Because the shape of the pore space is highly chaotic, the concept of tortuosity has been introduced to represent the complex structure of porous media. Tortuosity is an important feature of the flow through such media, and serves as an adjustable parameter for matching experimental results to those predicted by bundled parallel tubes. It is governed mainly by the topology of the pore network, and defined as the ratio of the length of the fluid streamlines to the shortest path in the direction of the flow. To date, it has not been possible to measure tortuosity directly. Several attempts have been made, among them the development of models of fluid movement in soils which idealize the intricate structures of soil in the form of fractals [13] or networks [14]. These models represent void space in a regular two- or three-dimensional lattice of pores connected by throats. However, in a three-dimensional model, the shape of every pore or throat is generally simplified to either a sphere or cylinder, while natural systems have a random topology.

Frequently, tortuosity has been assumed to be responsible for discrepancies between predictions and observed behavior in various porous systems, and, as such, tends to have been used largely as a fitting parameter. In contrast, the use of the Kozeny–Carman equation involves a key factor which gathers together all the geometrical features, such as pore shape and pore size distribution, particle shape, tortuosity, pore throat, pore interconnectivity, etc. The literature dealing with tortuosity is very broad. Although the concept of tortuosity is used in various areas of science, it is not yet well understood, mainly because the theoretical research includes simplifications that do not reflect the complex reality encountered in porous media. An examination of this research reveals that no consensus has yet been reached.

1.3 Inaccuracy of Experimental Tests

The accuracy of laboratory permeability tests involving coarse-grained materials is often open to discussion, as there are many factors that affect the measurement of hydraulic conductivity. Chapuis and Aubertin [15] note that the experimental hydraulic conductivity values obtained from just three replicate tests may vary broadly. This lack of precision partially depends on the test equipment and procedures applied, in addition to the natural variability of the material tested. Dunn and Mitchell [16] point out in a practice review of hydraulic conductivity measurements that, in addition to test apparatus and procedural errors, such as head and flow measurement errors, temperature variations, and non-uniform specimen sizes, there are many other factors that contribute to hydraulic conductivity estimation inaccuracy, such as (1) the influence of specimen preparation methods; (2) water quality; (3) consolidation during the test; (4) the influence of hydraulic gradient; and (5) methods of specimen saturation and verification of the degree of saturation. The wall effect is another source of errors. Strizhov and Khalilov [17] demonstrate that the non-curvature of a smooth wall causes a decrease in resistance in its vicinity and an increase in flow velocity (by a factor of 1.5–2, in the case of gas flows), which leads to the wall effect. In addition, the use of small samples with a diameter of less than 15 cm would lead to an underestimation of the in situ hydraulic conductivity by a factor of 10–10,000 [18].

An additional source of error is the laboratory test procedure itself, which forces the flow in a prescribed direction that probably does not represent the actual direction of the flow encountered in the field. This is because the laboratory test usually checks the vertical hydraulic conductivity, whereas the soil is anisotropic.

2 3D Virtual Laboratory: Simsols

Until the late of 1970s, when computer processing power increased dramatically, the pore-scale modeling of porous medium processes was considered a fruitless undertaking. To overcome the difficulties associated with the inherent complexity of porous media, a three-dimensional virtual laboratory, called SIMSOLS, was developed by IREQ to simulate the flow through porous media at a micro level. The pore sizes throughout the medium, the connectivity of the pore channels, and the tortuosity of these channels were generated using the virtual laboratory, creating a virtual porous medium made up of idealized particles. This approach can provide a high level of detail, which would be impossible to acquire in any other way. Subsequently, a more accurate representation of the flow through porous media was realized using the full Navier–Stokes equations, involving inertial terms that are significant in high speed flows.

The primary purpose of this study is to demonstrate the ability of the virtual laboratory to mimic reality, and then to achieve a better understanding of the tortuosity of streamlines through a porous medium made up of multisized glass beads. This paper addresses the following topics: (1) the discrete element method used to model the motion of glass beads during generation of the porous medium; (2) the sample generation process; (3) the Navier–Stokes equations solved by the Marker and Cell method; (4) the representative elementary volume; and (5) the results obtained and a discussion.

2.1 Discrete Element Method

The three-dimensional Discrete Element Method (3D DEM), a common approach to the numerical modeling of non cohesive granular materials, is used in this study. In this approach, which was first introduced by Cundall and Strack [19], every particle in the system is modeled as a rigid body subject to various body and surface forces. The method is presented in detail in [20]. However, combining the DEM approach for granular materials with pore network methods remains a difficult task. Although the investigations carried out by various researchers have been limited mostly to 2D models, with a few involving 3D models with an idealized pore space, these models may not reflect the random nature of a real porous space. The main drawback of the DEM approach is its high computational cost. To address this drawback, we parallelized the model using GPU (Graphics Processing Units), and, for portability, we used the OpenCL (Open Computing Language) framework, which provides an abstract view of the parallel architecture. This allowed us to use CPU (Central Processing Units) with a GPU backend.

2.2 Sample Generation Process

The samples, consisting of spherical particles, were virtually generated layer by layer according to the particle size distribution shown in Fig. 1. This procedure was conducted randomly to ensure homogeneity. Each layer of particles (Fig. 2a) was generated so that the sample surface would be as flat as possible, but in such a way as to fill the gaps in the vicinity of the edges of the sample. To accomplish this, each layer was generated with a rotation of 90º in the horizontal plane with respect to the previous layer. In the first step, the sample was generated with a minimum density (e max). At this stage, before a layer is subjected to gravity, it is important to confirm that the particles in the previous layer are all steady (Fig. 2b). The loosest possible packing is then achieved by carefully pouring the glass beads into a container, avoiding any disturbance, which gives e max. This procedure avoids the possibility of segregation. From Fig. 2c, we can see that there was no segregation. Once the sample had been completely generated, it was vibrated until the maximum density (e min) was achieved. A constant surcharge (dead weight) of 14 kPa was maintained at the surface during vibration, with a predominant frequency of 60 Hz and a double amplitude of 0.33 mm, based on the test procedures found in ASTM D 4253. To ensure total densification of the sample, the sample height was calculated at different time intervals during the vibration process. Figure 3 shows the evolution of the sample height with the time of vibration, and reveals that the height of the sample decreases throughout the process of vibration and stabilizes after 15 s. When vibration is complete (after 20 s), the height of the sample suddenly decreases by 0.1 mm, as shown in Fig. 3.

Fig. 1
figure 1

Particle size distribution curve

Full size image
Fig. 2
figure 2

Generation of porous media with different colors representing: a successive layers, b velocity, and c particle size

Full size image
Fig. 3
figure 3

Sample height variation during and after vibration

Full size image

2.3 Marker and Cell Method

The water flow through a pore channel is described by the Navier-Stokes equations for a viscous-incompressible fluid. One of the more successful methods for solving the Navier–Stokes equations in physical variables is the Marker and Cell (MAC) method, developed at the Los Alamos Laboratory in 1965 [21]. This method uses a staggered grid. Since its initial success, many modified schemas have been introduced. SIMSOLS uses the schema based on the splitting of physical parameters [22, 23], and is described in detail in [24].

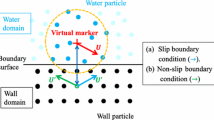
The boundary conditions for the solid cylindrical walls and the particle boundaries are nonslip and non penetration, as proposed in [25]. In the simplest case, all liquid grid velocities located ‘inside’ the particles are forced to equal the particle velocity, or zero in the case of fixed obstacles, prior to evaluation of the temporary velocity, while all other points retain the old values. The ‘interior’ points are updated once the pressure has been determined in the same way as for all the other points, in order to ensure incompressibility.

To arrive at the proper particle–liquid interaction, the fluid stress tensor is integrated over the particle surface.

With the aim of verifying and validating this model, many experimental tests have been conducted in the 3D configuration [26]. Examples of an experiment and the corresponding numerical simulation of spherical particle–particle collision and rebound in a Newtonian fluid are shown in Fig. 4. The experimental and numerical results obtained are compared in Fig. 5. These results demonstrate the validity of our approach.

Fig. 4
figure 4

Close view of the experimental and numerical tests

Full size image
Fig. 5
figure 5

Comparison of the experimental and numerical results as a function of time: a elevation; and b velocity

Full size image

2.4 Representative Elementary Volume

To ensure the representativeness of the sample in terms of size, and then to set the volume as a representative parameter, simulations were performed on samples of different dimensions (height and diameter) to obtain the Representative Elementary Volume (REV). The REV that represents the continuous scale for which the macroscopic properties of a porous medium are reached when the parameter studied did not change with a further increase in sample size [27]. The REV must be sufficiently large to contain enough elements of the microstructure, and the effects of boundary conditions (wall effect) must be not significant. This approach, which has been applied for void ratio, particle size distribution, and permeability, as suggested by many authors [28–34], allows us to reduce the dimensions of the sample by reducing the number of particles involved. The handling of a large number of particles tends to compromise the computation times.

The sample diameter was determined through simulation for different ratios of the sample diameter to the smallest particle diameter (Fig. 6). A view of the sample we generated is shown in Fig. 7. The smallest particles, with a 623 micron diameter, are in blue. The sample height was determined by calculating the void radio, defined as the ratio of the volume of the pores to the volume of the solids, for 20 slices 2 mm in height along the sample, starting from the bottom, as shown in Fig. 8. Using this procedure, we can see the evolution of the void ratio as a function of height, and so define the minimum height of the sample. This exercise was carried out with two increments of height (2 and 4 mm) to make sure that all the information along the sample was captured and that identical results would be produced. The sample is 25 mm in diameter and 16.7 mm in height. Note that the sample height is more than 25 times the diameter of the smallest particle. The smallest particles are considered to affect tortuosity the most, since they can occupy the most space between the larger particles.

Fig. 6
figure 6

The dependency of the maximum void ratio on the ratio of the sample diameter to the diameter of the smallest particle

Full size image
Fig. 7
figure 7

View of the sample generated, consisting of spherical particles

Full size image
Fig. 8
figure 8

Variation in void ratio along the sample height

Full size image

The void ratio of the sample is 0.61, when the voids created in the upper and lower parts of the sample are considered, and 0.56 if the sections at the top and bottom of the sample are not taken into account. To simulate the real behavior in the laboratory, the upper and lower parts of the sample were not removed in the current analysis.

3 Results and Perspectives

Our achievement is the direct measurement of the flow path length in porous media. Figure 9 shows an example of a three-dimensional view of the streamline patterns obtained by numerical simulations. A streamline is a path traced by a massless particle as it moves with the flow. Figure 10a, b show a projection of the streamlines of the loosest sample onto the XY and YZ planes respectively. Figure 11a, b present similar views for the densest sample.

Fig. 9
figure 9

Front view of the streamlines in the sample with the loosest packing

Full size image
Fig. 10
figure 10

The middle range of the projection of streamlines onto the: a XY; and b YZ planes for the loosest packing

Full size image
Fig. 11
figure 11

The middle range of the projection of streamlines onto the: a XY; and b YZ planes for the densest packing

Full size image

In order to analyze the data obtained from images, the tortuosity values were subdivided into 30 ranges. Figure 12 presents the distribution of more than 30,000 tortuosity values. The tortuosity values before and after compaction show that the tortuosity does not vary significantly. The results given in Table 1 show that there is no significant difference between the tortuosity evaluated in the projections onto the XY and ZY planes. The hydraulic conductivity (m/s) is calculated as follows [35]:

$$ K = \frac{ - \left\langle v \right\rangle s\rho g}{{\Delta p}} $$
(1)

where \( \left\langle v \right\rangle \) is the average velocity in the soil (m/s), s is the length of the sample in the direction of flow (m), \( \Delta p \) is the pressure drop (Pa), g is the acceleration due to gravity, and ρ is the fluid density.

Fig. 12
figure 12

Streamline distribution as a function of tortuosity

Full size image
Table 1 Numerical results for both loose (e max) and dense (e min) samples
Full size table

From these results, it is clear that the flow path does not take any preferential direction, and therefore is isotropic in nature. Naturally, the fluid flow will follow the path of least resistance, where the lowest amount of energy is required to produce the motion of the fluid particle. However, the hydraulic conductivity values obtained, which were computed for e min and e max, are not consistent with those presented in the literature in which hydraulic conductivity is related as a power-law of porosity (or void ratio). However, it should be noted that, to our knowledge, no pore-scale studies have been conducted for calculating the permeability of a granular medium in both loose and dense state to confirm our results.

It must be noted that the computed tortuosity does not depend only on spatial discretization, but also on the number of streamlines in each pore channel. In this work, we assume that the streamlines have been uniformly seeded over the inlet plane, and that the starting positions of each streamline were centered in the cell of that plane. There are still many improvements to be made in this area, such as refinement in both space and time, which will result in greater precision in evaluating tortuosity.

The results indicate that compaction of the multisized porous media leads to less tortuous pore channels. However, the influence of particle size distribution needs further investigation.

At the same time, considering the particle size distribution chosen, we may be able to conclude that the difference between the total streamline length and the streamline lengths computed on the plane projections is small. If confirmed, the flow in porous media can be investigated in two-dimensional simulations with confidence.

4 Conclusion

In this preliminary part of a research project currently under way, we presented a simulation tool, called SIMSOLS, which can generate a granular medium by means of the discrete element method, consisting of polydispersed spherical particles. This tool also simulates the flow of a fluid, in order to define its permeability, but other properties as well, such as tortuosity. The medium is generated according to the principle of gravitational deposition. The samples are initially generated in their loosest state, and then densified by means of vibration, as in laboratory tests.

This simulation tool enables us to extract the streamlines in three dimensions. However, the results obtained do not correspond to those already widely published, in which hydraulic conductivity can be approximated by a power-law function of the porosity. Refinement, in the form of simulations associated with laboratory tests performed on porous media with different size distributions, will allow us to better understand the various aspects of flow through a porous medium and the contradictions noted. We have no doubt that the work presented here is a realistic approach to mimicking reality, and that our approach will better quantify the effect of the parameters involved in flow in porous media. The use of three-dimensional simulations of the phenomena of fluid flowing directly into the pore spaces will relax a number of the simplifications inherent in network modeling, and is a promising avenue for the use of the complex morphology of pore spaces.

SIMSOLS seems to be the most realistic numerical tool available for generating granular media and modeling flow through these media, even though it is not yet able to account for all complexities involved and to make accurate predictions. Despite the fact that the results are controversial, we hope that this work will motivate further research exploring more types of granular media. Three-dimensional visualization through the virtual laboratory appears to be a promising approach.