Adaptive Observer for Capacitor Voltages in Multilevel STATCOMs

Abstract

Control of multilevel STATCOMs is complex mainly due to the internal converter control, where several capacitors are used as a fundamental component of multilevel converters. The capacitor voltage must be regulated to ensure the multilevel output voltage waveform, and to equally distribute the high input voltage among the power semiconductors. Regulation of the capacitor voltages needs the knowledge of the capacitor voltages. In this chapter, a nonlinear adaptive observer for DC capacitor voltages estimation is proposed for a class of multilevel converters. The observation scheme estimates simultaneously the state of the system and the system parameters, adding robustness and improving the state estimation when system parameters are uncertain. The observation scheme is developed using an instantaneous model of the system. The original system model is an n-dimensional system which is not observable. The original model is split into a suitable set of n-interconnected subsystems. This new representation allows overcoming the unobservable condition of the original system, which enables the design of an observation scheme for the capacitor voltages and system parameters. Hence, the observer for the whole system is approached by designing a separate exponential observer for each individual subsystem. As a result, the whole system state is reconstructed from the individual exponential observer designed for each subsystem. Thus, the interconnected system, which is constituted by the interconnected exponential observers, is an observer for the original system.

9.1 Introduction

The power electronics-based converters are nowadays an essential technology to control and conditioning electrical power. Advancements in areas as power semiconductors, control electronics or control theory, have enabled new applications and new power converter topologies have been created. Thus, in medium or high voltage applications the classical 2-level inverter topology can be replaced by a new breed of power converters called multilevel converters [1–5]. Thereby multilevel converters are very attractive for STATCOMs used in electrical network compensation [6–10].

One common characteristic of multilevel power converters is the use of several capacitors in their power structure. Proper and safe operation of multilevel power converters requires the regulation of the voltage across the capacitors. Capacitor voltage regulation can be obtained by a feedback control loop using voltage sensors. In one hand, using voltage sensors to measure the capacitor voltages is a relative straightforward approach. In the other hand, as the number levels increases it will be necessary to increase the number of voltage sensors and its associated conditioning electronics, resulting in an increased hardware complexity, which impact negatively the system reliability. As an alternative to the physical voltage sensors are the software based sensors. The last ones are known as observers. Observers are computational algorithms that take advantage of the mathematical model of the system to reconstruct the system states from the inputs and some measured outputs [11–14]. Using observers to measure the capacitor voltages will reduce the number of physical sensors reducing the system costs and increasing the system reliability. The use of observers to estimate system states or system parameters have recently been proposed in several applications related to electromechanical and electrical power conversion systems [15–19]. Moreover, observer are becoming standard in applications such as high performance motor drives, as its use have proved to enhance drive performance and reliability [20, 21]. Even though the aforementioned applications of observers are all related or linked to the use of power converters, their main objective is not the observation of the converter states by itself but the observation of variables related to global system performance. As the complexity of power converters has evolved, new requirements in terms of the converter itself have emerged. In the case of multilevel converters, it is required to control and to monitor some of the converter internal states, and specifically the voltages across the capacitors which are used in the multilevel power structure. Recently, some proposals regarding those problems have being presented [22, 23].

9.2 System Description and Modeling

In this section, two known multilevel power converters are modeled. The cascaded H-bridge and the Flying capacitor multilevel converters are modeled as n interconnected subsystems, which allows to design an exponential observer for each subsystem.

9.2.1 Modeling of Cascaded H-Bridge Multilevel Converters

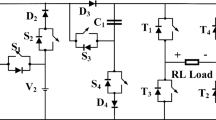
Cascaded H-bridge multilevel inverters are based on serial connection of single phase inverters bridges. A single phase-leg is shown in Fig. 9.1. As shown, each inverter bridge is supplied by a separate and isolated DC power supply. When the inverter is used to compensate reactive power and harmonics in electrical networks, a charged capacitor provides the needed voltage in the DC side of each H-bridge.

Fig. 9.1

One leg of a three-phase cascaded H-bridge multilevel structure

The output voltage of a cascaded H-bridge inverter-leg is obtained by adding the single H-bridge output voltages as follows:

$$v_{o} (t) = \sum\limits_{j = 1}^{n} {v_{oj} } (t)$$

(9.1)

where $n$ is the number of cascaded H-bridges. If the DC side of each H-bridge has a value of $V_{dc}$ volts, then the output voltage of each individual H-bridge can take 3 different values: $- V_{dc} ,0\,{\text{or}} + V_{dc}$, as a function of the switching states. Taking into account that each H-bridge inverter-leg is composed of a series connected pair of switches, $(T_{1j} ,T_{2j} )$ and $(T_{3j} ,T_{4j} )$, which are commanded in a complementary way, then, it is possible to define a switching function, $S_{j}$, to describe the output voltage of each jth H-bridge. This switching function is defined by the switching state and can take 3 different values: −1, 0 or 1. In Table 9.1, the switching function, $S_{j}$, is defined as a function of the switching states.

Table 9.1 Switching function

Introducing the switching function in (9.1), then:

$$v_{o} (t) = \sum\limits_{j = 1}^{n} {V_{dc} } S_{j}$$

(9.2)

If a capacitor is used at the DC side of each H-bridge, as shown in Fig. 9.2, then the capacitor voltage for the jth bridge, $v_{{c_{j} }}$, is be described by:

$$\frac{d}{dt}v_{{c_{j} }} = \frac{1}{{C_{j} }}i(t)S_{j}$$

(9.3)

where $C_{j}$ is the capacitance associated to the jth H-bridge.

Fig. 9.2

Single-phase H-bridge

Using the capacitor voltages, the inverter phase voltage $v_{o} (t)$ can be expressed as:

$$v_{o} (t) = \sum\limits_{j = 1}^{n} {v_{{c_{j} }} } (t)S_{j}$$

(9.4)

Now, if the multilevel inverter is connected to the electrical power system, the equivalent circuit is shown in Fig. 9.3, where the phase current $i(t)$ is given by:

$$\frac{d}{dt}i(t) = - \frac{1}{{l_{c} }}\left[ {v_{o} (t) - v_{net} (t)} \right] - \frac{{r_{c} }}{{l_{c} }}i(t)$$

(9.5)

where $v_{net} (t)$ is the network phase voltage, $l_{c}$ and $r_{c}$ are respectively the equivalent inductance and the resistance of the linker transformer or reactor.

Fig. 9.3

Equivalent circuit of the multilevel converter connected to an electrical power system

Now, using (9.3), (9.4) and (9.5), the dynamical model describing the whole system is given by:

$$\sum\nolimits_{NH} {:}\;{\left\{ {\begin{array}{*{20}l} {\frac{d}{dt}i(t)} \hfill & = \hfill & { - \frac{1}{{l_{c} }}\sum\nolimits_{j = 1}^{n} {v_{cj} (t)S_{j} + \frac{1}{{l_{c} }}v_{net} - \frac{{r_{c} }}{{l_{c} }}i(t)} } \hfill \\ {\frac{d}{dt}v_{{c_{1} }} (t)} \hfill & = \hfill & {\frac{1}{{C_{1} }}i(t)S_{1} } \hfill \\ {\frac{d}{dt}v_{{c_{2} }} (t)} \hfill & = \hfill & {\frac{1}{{C_{2} }}i(t)S_{2} } \hfill \\ \vdots \hfill & \vdots \hfill & \vdots \hfill \\ {\frac{d}{dt}v_{{c_{n} }} (t)} \hfill & = \hfill & {\frac{1}{{C_{n} }}i(t)S_{n} } \hfill \\ y \hfill & = \hfill & {i(t)} \hfill \\ \end{array} } \right.}$$

(9.6)

It is important to remark that the capacitance value $C_{j}$ for the jth capacitor and the equivalent impedance $(l_{c} ,r_{c} )$ could be uncertain or unknown. The resulting system is an (n + 1)-dimensional nonlinear system where the output is given by $y(t) = i(t)$, and $S_{j}$, for $j = 1, \ldots ,n$; are the inputs of the system. Assuming that the current $i(t)$ is the only measurable variable of the system (9.6), from the observability rank condition, it is clear that the system is not observable because the observation space is not of full rank.

9.2.2 Modeling of Flying Capacitor Multilevel Converter

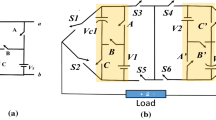
Flying capacitor multilevel converters are based on an imbricated structure of commutation cells, as shown in Fig. 9.4. Each commutation cell is composed of a DC source, assured by charged capacitor, and a pair of switches (i.e. $T_{x} ,T_{x}^{\prime }$) which are commanded in a complementary way.

Fig. 9.4

Five-level flying capacitor converter

The output voltage of an N-cell converter can be described as a linear combination of DC voltages, given by

$$v_{o} (t) = - \sum\limits_{j = 1}^{N} {v_{dcj} } (t)S_{j}$$

(9.7)

where $v_{{dc_{j} }}$ represents the jth DC power supply voltage, and $S_{j}$ is the switching function linking the jth DC power supply to the output voltage. $S_{j}$ is defined by the control signals, $u_{j}$, applied to the converter switches as

$$S_{j} = u_{j + 1} - u_{j}$$

(9.8)

where $u_{j}$ is the control signal applied to the jth switch, $T_{j}$. Considering that each internal DC power supply is defined by the voltage across a flying capacitor, then the DC voltage dynamics for the jth cell is given by

$$\frac{d}{dt}v_{cj} = \frac{1}{{C_{j} }}i(t)S_{j}$$

(9.9)

where $C_{j}$ is the capacitance. The voltage of the Nth cell is given by $v_{{c_{N} }} = E$.

Furthermore, the output current, $i(t)$, is given by

$$\frac{d}{dt}i(t) = - \frac{1}{{l_{c} }}v_{o} (t) - \frac{{r_{c} }}{{l_{c} }}i(t)$$

(9.10)

Then, the whole dynamics system is described by

$$\sum\nolimits_{NF}{:}\;{\left\{ {\begin{array}{*{20}l} {\frac{d}{dt}i(t)} \hfill & = \hfill & { - \frac{1}{{l_{c} }}\sum\nolimits_{j = 1}^{N - 1} {v_{cj} (t)S_{j} + \frac{E}{{l_{c} }}S_{N} - \frac{{r_{c} }}{{l_{c} }}i(t)} } \hfill \\ {\frac{d}{dt}v_{{c_{1} }} (t)} \hfill & = \hfill & {\frac{1}{{C_{1} }}i(t)S_{1} } \hfill \\ {\frac{d}{dt}v_{{c_{2} }} (t)} \hfill & = \hfill & {\frac{1}{{C_{2} }}i(t)S_{2} } \hfill \\ \vdots \hfill & \vdots \hfill & \vdots \hfill \\ {\frac{d}{dt}v_{{c_{N - 1} }} (t)} \hfill & = \hfill & {\frac{1}{{C_{N - 1} }}i(t)S_{N - 1} } \hfill \\ y \hfill & = \hfill & {i(t)} \hfill \\ \end{array} } \right.}$$

(9.11)

The resulting system is an n-dimensional nonlinear system, where the output is defined by $y = i(t)$ and $S_{j}$, for $j = 1, \ldots ,N - 1$, are the $N - 1$ inputs of the system. It is important to remark that the capacitance value $C_{j}$ for the jth capacitor and the equivalent impedance $(l_{c} ,r_{c} )$ could be uncertain or unknown.

Again as in the cascaded H-bridge converter model (9.6), note that $i(t)$ is the only measurable variable of the system (9.11) and, from the observability rank conditions, it is clear that the system (9.11) is not observable, i.e. the space of differentiable elements of the observation space is not of full rank.

9.3 Observer Design

In this section an alternative representation of models (9.6) and (9.11) will be considered, i.e. the original model will be split into a suitable set of n subsystems for which it will be possible to design an observer to estimate the capacitor voltages.

In order to unify the representation of both converter models we define (without loss of generality) $V = v_{net}$ for the H-bridge and $V = - S_{n + 1} E$ for the flying capacitors. Note that in both cases V is known.

Equations (9.6) and (9.11) can be split into $n$ subsystems of the form:

$$\begin{aligned} & \sum\nolimits_{1} {:}\;{\left\{ {\begin{array}{*{20}l} {\frac{d}{dt}i(t) = - \frac{{r_{c} }}{{l_{c} }}i(t) - \frac{1}{{l_{c} }}S_{1} v_{{c_{1} }} + \frac{V}{{l_{c} }}\underbrace {{ - \frac{1}{{l_{c} }}(S_{2} v_{{c_{2} }} + \cdots + S_{n} v_{{c_{n} }} )}}_{{\Gamma _{1} }}} \hfill \\ {\frac{d}{dt}v_{c1} = \frac{1}{{C_{1} }}S_{1} i(t)} \hfill \\ {y = i(t)} \hfill \\ \end{array} } \right.} \\ & \sum\nolimits_{2} {:}\;{\left\{ {\begin{array}{*{20}l} {\frac{d}{dt}i(t) = - \frac{{r_{c} }}{{l_{c} }}i(t) - \frac{1}{{l_{c} }}S_{2} v_{{c_{2} }} + \frac{V}{{l_{c} }}\underbrace {{ - \frac{1}{{l_{c} }}(S_{1} v_{c1} + \cdots + S_{n} v_{{c_{n} }} )}}_{{\Gamma _{2} }}} \hfill \\ {\frac{d}{dt}v_{c2} = \frac{1}{{C_{2} }}S_{2} i(t)} \hfill \\ {y = i(t)} \hfill \\ \end{array} } \right.} \\ & \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \begin{array}{*{20}c} \vdots & \vdots & \vdots \\ \end{array} \\ & \sum\nolimits_{n} {:}\;{\left\{ {\begin{array}{*{20}l} {\frac{d}{dt}i(t) = - \frac{{r_{c} }}{{l_{c} }}i(t) - \frac{1}{{l_{c} }}S_{n} v_{{c_{n} }} + \frac{V}{{l_{c} }}\underbrace {{ - \frac{1}{{l_{c} }}(S_{1} v_{{c_{1} }} + \cdots + S_{n - 1} v_{{c_{n - 1} }} )}}_{{\Gamma _{n} }}} \hfill \\ {\frac{d}{dt}v_{{c_{n} }} = \frac{1}{{C_{n} }}S_{n} i(t)} \hfill \\ {y = i(t)} \hfill \\ \end{array} } \right.} \\ \end{aligned}$$

Each subsystem can be written in a state affine form as:

$$\sum\nolimits_{j} {:}\;{\left\{ {\begin{array}{*{20}l} {\dot{\chi }_{j} = A(S_{j} ,i)\chi_{j} +\Phi (S_{j} ,i)\tau +\Psi (S_{j} ,i) +\Gamma _{j} (\bar{S}_{j} ,\bar{\chi }_{j} )} \hfill \\ {y = {\mathcal{C}}\chi_{j} } \hfill \\ \end{array} } \right.}$$

(9.12)

for $j = 1, \ldots ,n$, where $\tau$ stands for an uncertain parameter; $\chi_{j}$ represents the state of the jth subsystem, $S_{j}$ are the instantaneous inputs applied to the system and y = i(t) is the measurable output. The matrices $A(S_{j} ,i)$, $\Psi (S_{j} ,i)$ and $\Phi (S_{j} ,i)$ are known and defined by the system parameters and measured input and outputs. The output matrix is

$${\mathcal{C}} = \left( {\begin{array}{*{20}c} 0 & 1 \\ \end{array} } \right)$$

and the interconnection

$$\Gamma _{j} (\bar{S}_{j} ,\bar{\chi }_{j} ) = B\varphi (\bar{S}_{j} ,\bar{\chi }_{j} )$$

with

$$B = \left( {\begin{array}{*{20}c} 1 \\ 0 \\ \end{array} } \right)$$

and

$$\varphi (\bar{S}_{j} ,\bar{\chi }_{j} ) = - \frac{1}{{l_{c} }}\sum\limits_{{\begin{array}{*{20}c} {m = 1} \\ {m \ne j} \\ \end{array} }}^{n} {v_{{c_{m} }} } S_{m}$$

where $\bar{S}_{j} = (S_{1} , \ldots ,S_{j - 1} ,S_{j + 1} , \ldots ,S_{n - 1} )$ and $\bar{\chi }_{j} = (v_{{c_{1} }} , \ldots ,v_{{c_{j - 1} }} ,v_{{c_{j + 1} }} , \ldots ,v_{{c_{n} }} )$.

The function $\varphi (\bar{S}_{j} ,\bar{\chi }_{j} )$ is the interconnection term which depends on the inputs and state of each subsystem. Notice that the output is the current $i(t)$ and is the same for each subsystem as shown in Fig. 9.5.

Fig. 9.5

Interconnected observer block diagram

The new set of subsystems will be used to design an observer ${\mathcal{O}}$ for the $n$ capacitor voltages. It is clear that the observability of the system depends on the applied input. Then, the convergence of this observer can be proved assuming that the inputs $S_{j}$ are regularly persistent, i.e. it is a class of admissible inputs that allows to observe the system (for more details see [11, 12]).

Now, a further result based on regular persistence is introduced [24, 25].

Lemma

Assume that the input $S_{j}$ is regularly persistent for system (9.12) and consider the following Lyapunov differential equation:

$$\dot{P}_{j} = - \theta_{j} P_{j} - A^{T} (S_{j} ,i)P_{j} - P_{j} A(S_{j} ,i) + {\mathcal{C}}^{T} {\mathcal{C}}$$

with $P_{j} (0) > 0$ . Then, $\exists \theta_{{j_{0} }} > 0$ such that for any symmetric positive definite matrix $P_{j} (0),\,\exists \theta_{j} \ge \theta_{{j_{0} }} ,\,\exists \alpha_{j} ,\beta_{j} > 0,t_{0} > 0:\forall t > t_{0} ,$

$$\alpha_{j} I < P_{j} (t) < \beta_{j} I,$$

where $I$ is the identity matrix.

This guarantees the matrix $P_{j}$ is non-singular, and the observer works properly.

Remark

The proposed observer ${\mathcal{O}}$ works for inputs satisfying the regularly persistent condition, which is equivalent to each subsystem $\Sigma _{j}$ being observable, and hence, observer ${\mathcal{O}}_{j}$ works at the same time while the other subsystems become observable when their corresponding input satisfies the regularly persistent condition.

Now, we will give the sufficient conditions which ensure the convergence of the interconnected observer ${\mathcal{O}}$. For that, we introduce the following assumptions:

Assumption

Assume that the input $S_{j}$ is a regularly persistent input for subsystem $\Sigma _{j}$ and admits an exponential observer ${\mathcal{O}}_{j}$ for $j = 1, \ldots ,n$. In this case, an observer of the proposed form can be designed and the estimation error will be bounded.

Assumption

The term $\Gamma _{j} (\bar{S}_{j} ,\bar{\chi }_{j} )$ does not destroy the observability property of subsystem $\Sigma _{j}$ under the action of the regularly persistent input $S_{j}$. Moreover, $\Gamma _{j} (\bar{S}_{j} ,\bar{\chi }_{j} )$ is Lipschitz with respect to $\bar{\chi }_{j}$ and uniformly with respect to $S_{j}$ for $j = 1, \ldots ,n$.

This technique will be used to design three different observer schemes: an interconnected observer, an adaptive interconnected observer and an extended adaptive interconnected observer. We consider all the assumptions hold for the proposed systems.

9.3.1 Interconnected Observer for the Cascaded H-Bridge Multilevel Converter

In this case we assume that the system parameters are known. The objective of the observer is to reconstruct the capacitor voltages $v_{{c_{j} }}$ and the output current $i(t)$. The state is defined as: $\chi_{j} = (i,v_{{c_{j} }} )^{T}$ with:

$$A(S_{j} ,i) = \left( {\begin{array}{*{20}c} { - \frac{{r_{c} }}{{l_{c} }}} & { - \frac{1}{{l_{c} }}S_{j} } \\ {\frac{1}{{C_{j} }}S_{j} } & 0 \\ \end{array} } \right)\quad\Phi (S_{j} ,i) = 0\quad\Psi (S_{j} ,i) = \left( {\begin{array}{*{20}c} {\frac{{v_{net} }}{{l_{c} }}} \\ 0 \\ \end{array} } \right)$$

Each subsystem can be written in a particular form as:

$$\sum\nolimits_{j} {:}\;{\left\{ {\begin{array}{*{20}l} {\dot{\chi }_{j} = A(S_{j} ,i)\chi_{j} +\Psi (S_{j} ,i) +\Gamma _{j} (\bar{S}_{j} ,\bar{\chi }_{j} )} \hfill \\ {y = {\mathcal{C}}\chi_{j} \quad j = 1, \ldots ,n} \hfill \\ \end{array} } \right.}$$

(9.13)

Note that the term $\Phi (S_{j} ,i)$ is inexistent because we assume that the all parameters are known.

Then, the following system

$${\mathcal{O}}_{j} {:}\;\left\{ {\begin{array}{*{20}l} {\dot{Z}_{j} = A(S_{j} ,i)Z_{j} +\Psi (S_{j} ,i) +\Gamma _{j} (\bar{S}_{j} ,\bar{Z}_{j} ) + P_{j}^{ - 1} {\mathcal{C}}^{T} (y - {\mathcal{C}}Z_{j} )} \hfill \\ {\dot{P}_{j} = - \theta_{j} P_{j} - A^{T} (S_{j} ,i)P_{j} - P_{j} A(S_{j} ,i) + {\mathcal{C}}^{T} {\mathcal{C} }} \hfill \\ \end{array} } \right.$$

(9.14)

is an observer for the system (9.13) for $j = 1, \ldots ,n$ where $P_{j}^{ - 1} {\mathcal{C}}^{T}$ is the gain of the observer which depends on the solution of the Riccati Equation (9.14) for each subsystem and, $\bar{Z}_{j} = (\hat{v}_{{c_{1} }} , \ldots ,\hat{v}_{{c_{j - 1} }} ,\hat{v}_{{c_{j + 1} }} , \ldots ,\hat{v}_{{c_{n} }} )$. Furthermore, if the inputs $S_{j}$ are regularly persistent, the estimation error $\varepsilon_{j} = Z_{j} - \chi_{j}$ converges to zero as $t$ tends to infinite [26]. The parameter $\theta_{j} > 0$ is called the forgetting factor and it determines the convergence rate of the observer.

Now, consider that the system can be represented as a set of the interconnected subsystems as follows:

$$\sum {:}\;{\left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\dot{\chi }_{1} } \\ {\dot{\chi }_{2} } \\ \vdots \\ {\dot{\chi }_{n} } \\ \end{array} } & {\begin{array}{*{20}c} = \\ = \\ \vdots \\ = \\ \end{array} } & {\begin{array}{*{20}c} {A(S_{j} ,i)\chi_{1} +\Psi (S_{1} ,i) +\Gamma _{1} (\bar{S}_{1} ,\bar{\chi }_{1} )} \\ {A(S_{j} ,i)\chi_{2} +\Psi (S_{2} ,i) +\Gamma _{2} (\bar{S}_{2} ,\bar{\chi }_{2} )} \\ \vdots \\ {A(S_{j} ,i)\chi_{n} +\Psi (S_{n} ,i) +\Gamma _{n} (\bar{S}_{n} ,\bar{\chi }_{n} )} \\ \end{array} } \\ \end{array} } \right.}$$

Notice that the output is the current $i(t)$ and it is the same for each subsystem.

The main idea of this technique is to construct an observer for the whole system $\Sigma$, from the separate observer design of each subsystem $\Sigma _{j}$.

In general, if each ${\mathcal{O}}_{j}$ is an exponential observer for $\Sigma _{j}$ for $j = 1, \ldots ,n$, then the following interconnected system ${\mathcal{O}}$

$${\mathcal{O}}{:}\;\left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}l} {\dot{Z}_{1} } \hfill \\ {\dot{Z}_{2} } \hfill \\ \vdots \hfill \\ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\dot{Z}_{n} } \\ {\dot{P}_{1} } \\ \end{array} } \\ {\dot{P}_{2} } \\ \vdots \\ {\dot{P}_{n} } \\ \end{array} } \hfill \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} = \\ = \\ \end{array} } \\ \vdots \\ = \\ = \\ \end{array} } \\ = \\ \vdots \\ = \\ \end{array} } & {\begin{array}{*{20}l} {\begin{array}{*{20}l} {\begin{array}{*{20}l} {A(S_{1} ,i)Z_{1} +\Psi (S_{1} ,i) +\Gamma _{1} (\bar{S}_{1} ,\bar{Z}_{1} ) + P_{1}^{ - 1} {\mathcal{C}}^{T} (y - {\mathcal{C}}Z_{1} )} \hfill \\ {A(S_{2} ,i)Z_{2} +\Psi (S_{2} ,i) +\Gamma _{2} (\bar{S}_{2} ,\bar{Z}_{2} ) + P_{2}^{ - 1} {\mathcal{C}}^{T} (y - {\mathcal{C}}Z_{2} )} \hfill \\ \end{array} } \hfill \\ \vdots \hfill \\ {A(S_{n} ,i)Z_{n} +\Psi (S_{n} ,i) +\Gamma _{n} (\bar{S}_{n} ,\bar{Z}_{n} ) + P_{n}^{ - 1} {\mathcal{C}}^{T} (y - {\mathcal{C}}Z_{n} )} \hfill \\ { - \theta_{1} P_{1} - A^{T} (S_{1} ,i)P_{1} - P_{1} A(S_{1} ,i) + {\mathcal{C}}^{T} {\mathcal{C}}} \hfill \\ \end{array} } \hfill \\ { - \theta_{2} P_{2} - A^{T} (S_{2} ,i)P_{2} - P_{2} A(S_{2} ,i) + {\mathcal{C}}^{T} {\mathcal{C}}} \hfill \\ \vdots \hfill \\ { - \theta_{n} P_{n} - A^{T} (S_{n} ,i)P_{n} - P_{n} A(S_{n} ,i) + {\mathcal{C}}^{T} {\mathcal{C}}} \hfill \\ \end{array} } \\ \end{array} } \right.$$

is an observer for the interconnected system $\Sigma$.

9.3.2 Adaptive Interconnected Observer for a Flying Capacitor Multilevel Converter

In this subsection an observer is designed for estimating the capacitor voltages $v_{{c_{j} }}$ for $j = 1, \ldots ,n$ and the resistance value $r_{c}$ for the flying capacitor multilevel converter (shown in Fig. 9.4). The resistance value is considered uncertain and all the other parameters are supposed constant and known. In order to estimate the resistance, we will define $\tau$ as ${{r_{c} } \mathord{\left/ {\vphantom {{r_{c} } {l_{c} }}} \right. \kern-0pt} {l_{c} }}$ which is uncertain because it is not known, $\chi_{j} = (i,v_{{c_{j} }} )^{T}$ represents the state of the jth subsystem; with

$$A(S_{j} ,i) = \left( {\begin{array}{*{20}c} 0 & { - \frac{1}{{l_{c} }}S_{j} } \\ {\frac{1}{{C_{j} }}S_{j} } & 0 \\ \end{array} } \right)\quad\Phi (S_{j} ,i) = \left( {\begin{array}{*{20}c} { - i} \\ 0 \\ \end{array} } \right)\quad\Psi (S_{j} ,i) = \left( {\begin{array}{*{20}c} { - \frac{E}{{l_{c} }}S_{j} } \\ 0 \\ \end{array} } \right)$$

Recalling that each subsystem can be written in a particular state affine form as:

$$\Sigma _{j} {:}\;\left\{ {\begin{array}{*{20}l} {\dot{\chi }_{j} = A(S_{j} ,i)\chi_{j} +\Psi (S_{j} ,i) +\Phi (S_{j} ,i)\tau +\Gamma _{j} (\bar{S}_{j} ,\bar{\chi }_{j} )} \hfill \\ {y = {\mathcal{C}}\chi_{j} \quad j = 1, \ldots ,n} \hfill \\ \end{array} } \right.$$

(9.15)

Then, the following system

$$\mathcal{O}_{j} {:}\;\left\{ {\begin{aligned} \dot{Z}_{j} &= A(S_{j} ,i)Z_{j} + {\varPsi }(S_{j} ,i) + {\varPhi }(S_{j} ,i)\hat{\tau }_{j} + {\varGamma }_{j} (\bar{S}_{j} ,\bar{Z}_{j} ) \\&\quad+ \{ {\varLambda }_{j} R_{j}^{ - 1} {\varLambda }_{j}^{T} {\mathcal{C}}^{T} + P_{j}^{ - 1} {\mathcal{C}}^{T} \} (y - {\mathcal{C}}Z_{j} ) \\ \dot{P}_{j} &= - \theta_{j} P_{j} - A^{T} (S_{j} ,i)P_{j} - P_{j} A(S_{j} ,i) + {\mathcal{C}}^{T} {\mathcal{C}} \\ \dot{\hat{\tau }}_{j} &= R_{j}^{ - 1} {\varLambda}_{j}^{T} {\mathcal{C}}^{T} (y - {\mathcal{C}}Z_{j} ) \\ {\dot{\varLambda }}_{j} &= \{ A^{T} (S_{j} ,i) - P_{j}^{ - 1} {\mathcal{C}}^{T} {\mathcal{C}}\} {\varLambda }_{j} + {\varPhi }(S_{j} ,i) \\ \dot{R}_{j} &= - \rho_{j} R_{j} + {\varLambda }_{j}^{T} {\mathcal{C}}^{T} {\mathcal{C}\varLambda }_{j} \end{aligned} } \right.$$

(9.16)

is an adaptive observer for the system (9.15) for $j = 1, \ldots ,n$ where $\Lambda _{j} R_{j}^{ - 1}\Lambda _{j}^{T} {\mathcal{C}}^{T} + P_{j}^{ - 1} {\mathcal{C}}^{T}$ is the gain of the observer which depends on the solution of the Riccati Equation (9.16) and the adaptation dynamics for each subsystem, $Z_{j} = (\hat{i},\hat{v}_{{c_{j} }} )$, and, $\bar{Z}_{j} = (\hat{v}_{{c_{1} }} , \ldots ,\hat{v}_{{c_{j - 1} }} ,\hat{v}_{{c_{j + 1} }} , \ldots ,\hat{v}_{{c_{n} }} )$. Furthermore, if the inputs $S_{j}$ are regularly persistent the observer gain is well defined and the estimation error $\varepsilon_{j} = Z_{j} - \chi_{j}$ converges to zero as $t$ tends to infinite [27]. The parameter $\theta_{j} > 0$ is called the forgetting factor determining the convergence rate of the observer, and $\rho_{j} > 0$ is the adaptation gain.

Now, consider that the system can be represented as a set of the interconnected subsystems as follows:

$$\Sigma {:}\;\left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\dot{\chi }_{1} } \\ {\dot{\chi }_{2} } \\ \vdots \\ {\dot{\chi }_{n} } \\ \end{array} } & {\begin{array}{*{20}c} = \\ = \\ \vdots \\ = \\ \end{array} } & {\begin{array}{*{20}c} {A(S_{1} ,i)\chi_{1} +\Psi (S_{1} ,i) +\Phi (S_{1} ,i)\tau +\Gamma _{1} (\bar{S}_{1} ,\bar{\chi }_{1} )} \\ {A(S_{2} ,i)\chi_{2} +\Psi (S_{2} ,i) +\Phi (S_{2} ,i)\tau +\Gamma _{2} (\bar{S}_{2} ,\bar{\chi }_{2} )} \\ \vdots \\ {A(S_{n} ,i)\chi_{n} +\Psi (S_{n} ,i) +\Phi (S_{n} ,i)\tau +\Gamma _{n} (\bar{S}_{n} ,\bar{\chi }_{n} )} \\ \end{array} } \\ \end{array} } \right.$$

(9.17)

Again, the main idea is to construct an observer for the whole system $\Sigma$, given by (9.17), from the individual observer design of each subsystem $\Sigma _{j}$, given that ${\mathcal{O}}_{j}$ is an exponential observer for $\Sigma _{j}$, for $j = 1, \ldots ,n$. Then, the interconnected system ${\mathcal{O}}$, which is constituted by the $n$ adaptive interconnected exponential observers ${\mathcal{O}}_{j}$, is an adaptive observer for the interconnected system $\Sigma$ (see Fig. 9.5).

In general, if each ${\mathcal{O}}_{j}$ is an exponential observer for $\Sigma _{j}$ for $j = 1, \ldots ,n$, then the following interconnected system ${\mathcal{O}}$

$${\mathcal{O}}{:}\; \left\{ {\begin{array}{*{20}l} {\dot{Z}_{1} } & = & A(S_{1} ,i)Z_{1} + \Psi (S_{1} ,i) + \Phi (S_{1} ,i)\hat{\tau }_{1} + \Gamma_{1} (\bar{S}_{1} ,\bar{Z}_{1} ) \\ & &+ \{ \Lambda_{1} R_{1}^{ - 1} \Lambda_{1}^{T} {\mathcal{C}}^{T} + P_{1}^{ - 1} {\mathcal{C}}^{T} \} (y - {\mathcal{C}}Z_{1} ) \\ \vdots & \vdots & \vdots \\ {\dot{Z}_{n} } & = & A(S_{n} ,i)Z_{n} + \Psi (S_{n} ,i) + \Phi (S_{n} ,i)\hat{\tau }_{n} + \Gamma_{n} (\bar{S}_{n} ,\bar{Z}_{n} ) \\ & &+ \{ \Lambda_{n} R_{n}^{ - 1} \Lambda_{n}^{T} {\mathcal{C}}^{T} + P_{n}^{ - 1} {\mathcal{C}}^{T} \} (y - {\mathcal{C}}Z_{n} ) \\ {\dot{P}_{1} } & = & { - \theta_{1} P_{1} - A^{T} (S_{1} ,i)P_{1} - P_{1} A(S_{1} ,i) + {\mathcal{C}}^{T} {\mathcal{C}}} \\ \vdots & \vdots & \vdots\\ {\dot{P}_{n} } & = & { - \theta_{n} P_{n} - A^{T} (S_{n} ,i)P_{n} - P_{n} A(S_{n} ,i) + {\mathcal{C}}^{T} {\mathcal{C}}} \\ {\dot{\hat{\tau }}_{1} } & = & {R_{1}^{ - 1} \Lambda_{1}^{T} {\mathcal{C}}^{T} (y - {\mathcal{C}}Z_{1} )} \\ \vdots & \vdots& \vdots \\ {\dot{\hat{\tau }}_{n} } & = & {R_{n}^{ - 1} \Lambda_{n}^{T} {\mathcal{C}}^{T} (y - {\mathcal{C}}Z_{n} )} \\ {\dot{\Lambda }_{1} } & = & {\{ A^{T} (S_{1} ,i) - P_{1}^{ - 1} {\mathcal{C}}^{T} {\mathcal{C}}\} \Lambda_{1} + \Phi (S_{1} ,i)} \\ \vdots & \vdots & \vdots \\ {\dot{\Lambda }_{n} } & = & {\{ A^{T} (S_{n} ,i) - P_{n}^{ - 1} {\mathcal{C}}^{T} {\mathcal{C}}\} \Lambda_{n} + \Phi (S_{n} ,i)} \\ {\dot{R}_{1} } & = & { - \rho_{1} R_{1} + \Lambda_{1}^{T} {\mathcal{C}}^{T} {\mathcal{C}}\Lambda_{1} } \\ \vdots & \vdots & \vdots \\ {\dot{R}_{n} } & = & { - \rho_{n} R_{n} + \Lambda_{n}^{T} {\mathcal{C}}^{T} {\mathcal{C}}\Lambda_{n} } \\ \end{array} } \right.$$

is an adaptive observer for the interconnected system $\Sigma$ (see Fig. 9.5). The proof can be found in [28].

9.3.3 Extended Adaptive Interconnected Observer for a Cascaded H-Bridge Multilevel Converter

In this subsection an alternative representation of model (9.6) will be considered, i.e. the original model will be split into a suitable set of $n$ subsystems for which it is possible to design an observer for estimating also the capacitance values $C_{j}$ for $j = 1, \ldots ,n$. In order to estimate the capacitance values the state vector can be extended by the vector of constant parameters $dC_{j} /dt = 0$, introducing the capacitance dynamics, and preserving the state affine form:

$$\sum\nolimits_{E} {:}\;{\left\{ {\begin{array}{*{20}l} {\frac{d}{dt}i(t)} \hfill & = \hfill & { - \frac{1}{{l_{c} }}\sum\nolimits_{j = 1}^{n} {v_{cj} (t)S_{j} + \frac{1}{{l_{c} }}v_{net} - \frac{{r_{c} }}{{l_{c} }}i(t)} } \hfill \\ {\frac{d}{dt}v_{{c_{1} }} (t)} \hfill & = \hfill & {\frac{1}{{C_{1} }}i(t)S_{1} } \hfill \\ {\frac{d}{dt}C_{1}^{ - 1} } \hfill & = \hfill & 0 \hfill \\ \vdots \hfill & \vdots \hfill & \vdots \hfill \\ {\frac{d}{dt}v_{{c_{n} }} (t)} \hfill & = \hfill & {\frac{1}{{C_{n} }}i(t)S_{n} } \hfill \\ {\frac{d}{dt}C_{n}^{ - 1} } \hfill & = \hfill & 0 \hfill \\ y \hfill & = \hfill & {i(t)} \hfill \\ \end{array} } \right.}$$

(9.18)

Then, the system (9.18) can be split in n subsystems of the form:

$$\sum\nolimits_{j} {:}\;{\left\{ {\begin{aligned} \frac{d}{dt}i(t) & = - \frac{{r_{c} }}{{l_{c} }}i(t) - \frac{1}{{l_{c} }}S_{j} v_{cj} + \frac{{v_{net} }}{{l_{c} }} \\ &\quad \underbrace { - \frac{1}{{l_{c} }}(S_{1} v_{c1} + \cdots + S_{j - 1} v_{j - 1} + S_{j + 1} v_{j + 1} + \cdots + S_{n} v_{{c_{n} }} )}_{{\Gamma _{j} }} \\ \frac{d}{dt}v_{{c_{j} }} & = \frac{1}{{C_{j} }}S_{j} i(t) \\ \frac{d}{dt}C_{j}^{ - 1} & = 0 \hfill \\ y & = i(t) \\ \end{aligned} } \right.}$$

for $j = 1, \ldots ,n$. Note that each subsystem can be written in a state affine form as:

$$\sum\nolimits_{j} {:}\;{\left\{ {\begin{array}{*{20}l} {\dot{\chi }_{j} = A(S_{j} ,i)\chi_{j} +\Psi (S_{j} ,i) +\Phi (S_{j} ,i)\tau +\Gamma _{j} (\bar{S}_{j} ,\bar{\chi }_{j} )} \hfill \\ {y = {\mathcal{C}}\chi_{j} \quad j = 1, \ldots ,n} \hfill \\ \end{array} } \right.}$$

(9.19)

where $\tau$ stands for ${{r_{c} } \mathord{\left/ {\vphantom {{r_{c} } {l_{c} }}} \right. \kern-0pt} {l_{c} }}$ which is uncertain; $\chi_{j} = (i,v_{{c_{j} }} ,\text{C}_{j}^{ - 1} )^{T}$ represents the extended state of the jth subsystem; with

$$A(S_{j} ,i) = \left( {\begin{array}{*{20}c} 0 & {{{ - S_{j} } \mathord{\left/ {\vphantom {{ - S_{j} } {l_{c} }}} \right. \kern-0pt} {l_{c} }}} & 0 \\ 0 & 0 & {S_{j} i} \\ 0 & 0 & 0 \\ \end{array} } \right)\quad\Phi (S_{j} ,i) = \left( {\begin{array}{*{20}c} { - i} \\ 0 \\ 0 \\ \end{array} } \right)\quad\Psi (S_{j} ,i) = \left( {\begin{array}{*{20}c} {\frac{{v_{net} }}{{l_{c} }}} \\ 0 \\ 0 \\ \end{array} } \right)$$

The new set of subsystems will be used to design an observer for the n capacitor voltages and capacitance values, obtaining simultaneously the $r_{c}$ value.

Then, the following system [identical to the adaptive observer (9.16)]

$${\mathcal{O}}_{j} {:}\;\left\{ {\begin{array}{*{20}l} {\dot{Z}_{j} } = A(S_{j} ,i)Z_{j} + \Uppsi (S_{j} ,i) + \Upphi (S_{j} ,i)\hat{\tau }_{j} + \Upgamma_{j} (\bar{S}_{j} ,\bar{Z}_{j} ) \\ \quad \quad + \{ \Uplambda_{j} R_{j}^{ - 1} \Uplambda_{j}^{T} {\mathcal{C}}^{T} + P_{j}^{ - 1} {\mathcal{C}}^{T} \} (y - {\mathcal{C}}Z_{j} ) \hfill \\ {\dot{P}_{j} } = { - \theta_{j} P_{j} - A^{T} (S_{j} ,i)P_{j} - P_{j} A(S_{j} ,i) + {\mathcal{C}}^{T} {\mathcal{C}}} \hfill \\ {\dot{\hat{\tau }}_{j} } = {R_{j}^{ - 1} \Uplambda_{j}^{T} {\mathcal{C}}^{T} (y - {\mathcal{C}}Z_{j} )} \hfill \\ {\dot{\Uplambda }_{j} } = {\{ A^{T} (S_{j} ,i) - P_{j}^{ - 1} {\mathcal{C}}^{T} {\mathcal{C}}\} \Uplambda_{j} + \Upphi (S_{j} ,i)} \hfill \\ {\dot{R}_{j} } = { - \rho_{j} R_{j} + \Uplambda_{j}^{T} {\mathcal{C}}^{T} {\mathcal{C}}\Uplambda_{j} } \hfill \\ \end{array} } \right.$$

(9.20)

is an adaptive observer for the system (9.19) for $j = 1, \ldots ,n$ where $\Lambda _{j} R_{j}^{ - 1}\Lambda _{j}^{T} {\mathcal{C}}^{T} + P_{j}^{ - 1} {\mathcal{C}}^{T}$ is the gain of the observer which depends on the solution of the Riccati Equation (9.20) and the adaptation dynamics for each subsystem, $Z_{j} = (\hat{i},\hat{v}_{{c_{j} }} ,{\hat{C}}_{j}^{ - 1} )$, and, $\bar{Z}_{j} = (\hat{v}_{{c_{1} }} , \ldots ,\hat{v}_{{c_{j - 1} }} ,\hat{v}_{{c_{j + 1} }} , \ldots ,\hat{v}_{{c_{n} }} ,{\hat{\rm C}}_{1}^{- 1} , \ldots ,{\hat{\rm C}}_{j - 1}^{- 1} ,{\hat{\rm C}}_{j + 1}^{- 1} , \ldots ,{\hat{\rm C}}_{n}^{- 1})$. Furthermore, if the inputs $S_{j}$ are regularly persistent and the gain is well defined, the estimation error $\varepsilon_{j} = Z_{j} - \chi_{j}$ converges to zero as $t$ tends to infinite [29]. The parameter $\theta_{j} > 0$ is called the forgetting factor determining the convergence rate of the observer, and $\rho_{j} > 0$ is the adaptation gain.

Now consider that the system can be represented as a set of the interconnected subsystems as follows:

$$\sum {:}\;{\left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\dot{\chi }_{1} } \\ {\dot{\chi }_{2} } \\ \vdots \\ {\dot{\chi }_{n} } \\ \end{array} } & {\begin{array}{*{20}c} = \\ = \\ \vdots \\ = \\ \end{array} } & {\begin{array}{*{20}c} {A(S_{1} ,i)\chi_{1} +\Psi (S_{1} ,i) +\Phi (S_{1} ,i)\tau +\Gamma _{1} (\bar{S}_{1} ,\bar{\chi }_{1} )} \\ {A(S_{2} ,i)\chi_{2} +\Psi (S_{2} ,i) +\Phi (S_{2} ,i)\tau +\Gamma _{2} (\bar{S}_{2} ,\bar{\chi }_{2} )} \\ \vdots \\ {A(S_{n} ,i)\chi_{n} +\Psi (S_{n} ,i) +\Phi (S_{n} ,i)\tau +\Gamma _{n} (\bar{S}_{n} ,\bar{\chi }_{n} )} \\ \end{array} } \\ \end{array} } \right.}$$

In general, if each ${\mathcal{O}}_{j}$ is an exponential observer for $\Sigma _{j}$ for $j = 1, \ldots ,n$. Then the interconnected system ${\mathcal{O}}$ which is constituted by interconnected exponential observers ${\mathcal{O}}_{j}$ is an adaptive observer for the interconnected system $\Sigma$ (see Fig. 9.5).

9.4 Simulation and Experimental Results

In this section the presented observer schema are validated through simulation and experimental data which is incorporated into the simulation.

9.4.1 Validation of the Interconnected Observer Using Simulation Experiments

The interconnected observer presented in Sect. 9.3.1 is validated in a system in which the cascaded H-bridge multilevel converter is used to compensate for reactive power and harmonic currents in a power system [27].

The general block diagram is shown in Fig. 9.6. Each multilevel inverter leg has 4 H-bridges per phase (Block 1). A capacitor C _nom  = 50 mF (nominal value) per bridge was used. The capacitors were pre-charged at 50 V. The compensator is coupled to a 100 V utility network through a 0.5 mH inductor and 0.1 Ω resistor (Block 2). Simulated load is a combination of linear and nonlinear elements (Block 3), with four linear and two nonlinear three-phase symmetrical loads. Load parameters are as follows: Linear loads 1 and 2: R = 10 Ω, L = 5 mH. Linear loads 3 and 4: R = 1 Ω, L = 25 mH. Nonlinear load consists of two three-phase diode rectifiers with the following parameters: Nonlinear load 1: AC input impedance: R = 0.1 Ω, L = 5 mH, DC side: L = 1 mH, C = 2 mF and R _load1 = 30 Ω. Nonlinear load 2: AC input impedance: R = 0.1 Ω, L = 0.1 mH, DC side: L = 50 mH, C = 20 µF and R _load2 = 5 Ω. The modulation switching frequency is 5 kHz. Simulations were carried out using PSIM from Powersim and MATLAB/SIMULINK from Mathworks, working in co-simulation mode.

Fig. 9.6

Block diagram of a cascaded H-bridge multilevel-inverter-based compensator and interconnected observer

Compensation currents are calculated in Block 4 using the instantaneous power concepts [30]. Basically it calculates compensation currents in such a way that reactive power and oscillating power will be supplied by the multilevel compensator. Then compensation currents are controlled using Proportional-Integral (PI) controllers, the PI gains are k _P  = 0.05, k _I  = 1 (Block 5) in a synchronous reference frame. The proportional-integral current controllers generate the voltage references to command the multilevel inverter. The control signals for the multilevel inverter H-bridges are generated by a Carrier based multilevel Pulse Width Modulation (CPWM) controller shown in Block 6. The modulation voltages, v_cm1, v_cm2 and v_cm3, calculated by the PI current controllers are fed into the CPWM in order to generate the H-bridge control signals.

Also, in Block 6, the switching function, S _j , is generated as defined in Table 9.1. S _j is used in the interconnected observer, Block 7, to estimate the H-bridges capacitor voltages according to (9.14) where the observer gain θ _j  = 10,000 for j = 1, …,3.

During simulation, the loads are connected at different times to study the observer behavior. Nonlinear load 1 is connected at t = 0.01 s, then at t = 0.15 s nonlinear load 2 and linear load 1 are connected and finally at t = 3.5 s linear loads 2, 3 and 4 are connected.

Figure 9.7 shows the real and estimated capacitor voltages for one phase and their corresponding estimation errors. As shown, the interconnected observer follows the real capacitor voltages accurately. From 1.5 to 1.75 s, direct axis current was commanded to absorb active power from the electrical network and thus, forcing the capacitor voltages to increase. Then, at 3.5 s an increase in reactive current is causing a decrease in the capacitor voltages. In any condition, the observer is able to follow the real capacitor voltages accurately. Once the observer transient is over, the estimated voltages are always close to their real values.

Fig. 9.7

Capacitor voltages and their estimations. a Real and estimated capacitor voltages. b Estimation errors (considering nominal capacitance values C₁ = C₂ = C₃ = C₄ = 50 mF)

Finally, as the model parameters are always a concern, a simulation with uncertain capacitance values was conducted. The capacitance values at each H-bridge are changed from their nominal values, C _nom  = 50 mF, as follows: C ₁ = 1.2 C _nom , C ₂ = 0.8 C _nom , C ₃ = 1.1 C _nom , C ₄ = 0.8 C _nom . Figure 9.8 shows the real and estimated capacitor voltages and their corresponding estimation errors when non-nominal capacitance values are used. As shown, the observer keeps tracking of the real capacitor voltages, but its convergence time is increased. Also, notice that when a capacitor voltage is changing rapidly, when real power is being absorbed from the network (from 1.5 to 1.75 s), the estimation error is increased, but it converges to the real value when the transient at the capacitor voltages is over. That behavior justifies the use of an adaptive observer scheme [27].

Fig. 9.8

Capacitor voltages and their estimation errors under non-nominal capacitances. a Real and estimated capacitor voltages. b Estimation errors (considering non-nominal capacitances values: C₁ = 1.2 C_nom, C₂ = 0.8 C_nom, C₃ = 1.1 C_nom, C₄ = 0.8 C_nom, C_nom = 50 mF)

9.4.2 Validation of the Extended Adaptive Interconnected Observer for a Flying Capacitor Converter Using Experimental Data

The proposed observation scheme introduced in (9.3.3) is validated using experimental data from a 5-level flying capacitor converter. The block diagram of the experimental setup is shown in Fig. 9.9, and the laboratory prototype photo is shown in Fig. 9.10.

Fig. 9.9

Experimental setup block diagram

Fig. 9.10

Experimental laboratory prototype

The converter prototype has 4 commutation cells, and it is commanded by a dSPACE 1104 system and an Actel ProAsic FPGA board. The capacitors assuring the floating DC sources are 390 µF each. An R-L charge is connected at the output. During the test, resistive part, r _c , is changed from 12.6 to 21.6 Ω, while the inductance, l _c , has a constant nominal value of 2.3 mH. The converter modulation scheme is based on a 1 kHz phase-shifted carrier PWM strategy [31], which is implemented in the dSPACE system. Then, the control signals are sent to the FPGA board, where a dead time of 2 µs is introduced to the control signals. The observer scheme needs the input voltage, output current and control signals, which are recorded by a data acquisition system (Agilent U2541A), and then used to evaluate the performance of the proposed estimation scheme. The observer gains were chosen as: θ _j  = 1, and ρ _j  = 5 for j = 1, …, 3. Experiment is as follows. The converter is commanded through the dSPACE board.The modulation algorithm is executed each 50 μs, while the observer input data is collected each 4 μs.

The test was run for 8 s. The input voltage source, E, is set to a constant value of 58 V. During the test, input voltage, control signals and output current are sampled each 4 µs and recorded by a data acquisition system. Then, collected data is fed to the estimation algorithm to get the capacitor voltage estimates.

Following, we present the results obtained with the observation scheme. Initial estimated voltages are set to zero and initial value for r _c is set to 4 Ω. Figure 9.11a shows estimated and measured voltages, and Fig. 9.11b shows estimation errors, which demonstrates that estimated values are close to real values, with estimation error being less than 1.5 V once the transient period is over. Note that the transient error is high because initial estimated values start from zero, while the real values are, in this case, at their nominal values. If the initial estimated values are close to the real values then the transient errors and convergence time will be reduced.

Fig. 9.11

Adaptive observer estimation results. a Real (black traces) and estimated (blue traces) capacitor voltages. b Estimation errors

The adaptation properties improve the state estimation with respect to the traditional observer scheme, where adaptation correction is zero (Λ _j  = 0). Experiments were carried out to compare both schemes, where the resistive part r _c is changed from 12.6 to 21.6 Ω. For both observer schemes the nominal value of τ is used. Figure 9.12a shows measured voltages and estimated voltages for both adaptive and non-adaptive schemes, and Fig. 9.12b shows estimation errors, which demonstrates that estimated values are better when using the adaptive scheme. The non-adaptive scheme presents errors 300 % larger than the adaptive observer.

Fig. 9.12

Estimation results for adaptive and non-adaptive schemes. a Capacitor voltages: real (black traces), adaptive estimation (blue traces) and non-adaptive estimation (magenta traces). b Adaptive estimation errors (blue traces) and non-adaptive estimation errors (magenta traces)

Finally, we run a test to evaluate the observer performance when inductance value is uncertain. Figure 9.13a shows measured voltages and estimated voltages for nominal inductance value l _c , and with uncertainties of ±20 %, and Fig. 9.13b shows the estimation error, which shows that estimated voltages are close to the real voltages in spite of the introduced uncertainties.

Fig. 9.13

Observer responses under uncertain inductance value. a Estimated capacitor voltages: Real (black traces), nominal inductance (blue traces), 120 % nominal inductance (magenta traces), 80 % nominal inductance (green traces). b Estimation errors nominal inductance (blue traces), 120 % nominal inductance (magenta traces), 80 % nominal inductance (green traces)