Keywords

Introduction

In current retail business market, the incidence of partial stock-outs in the types of usually purchasing products is a very common phenomenon. In certain situations, it is regular for purchasers who are looking to purchase a particular product to buy a similar product in order to save time, rather of traveling to another supermarket/retail shop to find the first product. A product is replacement for other product only if it can be used in just the same way and follows the same requirements. In the case of alternatives, an increment in the cost of one of the products rises the substitute demand. Anupindi et al. [1] presented a study result in which he observed that 82–88% of the customer would be interested to purchase substitute goods if the requested goods are out of stock. In retail shops, substitution is a regular happening event for example between different brand of toothpaste, Coke and Pepsi, milk, etc. The effect of deterioration is very common in products, which play crucial role in the decision of ordering quantity. Hence, it would be beneficial for retailers to consider the effect of deterioration with substitution into account, when making inventory policies. To avoid extra transportation cost (ordering cost), and supplier cost, several organizations try to refill products jointly to take profit of joint ordering. In this research work, we present an inventory model having two non-instantaneous substitutable decaying products under joint ordering policy for a retailer perspective.

There is large number of literature available on product substitution, deterioration with joint replenishment separately. McGillivray and Silver [2] was the earliest researcher to establish an inventory model with similar cost of substitute product and shortage cost. Drezner et al. [3] presented an economic order quantity (EOQ) model with substitution and compared the output with no substitution. Salameh et al. [4] developed an inventory strategy by considering substitute product with joint ordering policy and show that substitution between items can be saved in a fixed order price, which is free from the quantity of items involved in the order. Krommyda et al. [5] expanded the previous model by incorporating a joint ordering strategy and a substitution rate ranging from 0 to 1. Many researchers categorized substitution into different parts. Tang and Yin [6] divided substitution into some categories: stock-out, price, and assortment-based substitution. They investigate how under variable and fixed pricing policies, the order size and selling price of two substitute products could be jointly determined by the retailer. A brief literature review on substitutable products in the inventory is given by [7,8,9,10,11].

Whitin [12] first investigated the inventory problem of deteriorating products, considering fashion products deteriorating at the end of storage interval. [13,14,15,16,17,18] presented extensive literature on decaying/deteriorating items in inventory system. Mishra [19] generalized Salameh et al. [4] model by taking deterioration of product into account. Tiwari et al. [20] developed an ordering policy inventory model for non-instantaneous deteriorating item with different realistic situation.

Based on the above literature review and our knowledge, no study has considered the effect of non-instantaneous deterioration for substitutable products. To fill this literature gap, authors have considered two mutually substitutable products considering non-instantaneous decay and the cost of substitution. The cost of substitution includes the promotional effects like (cost comes from advertisements and sales promotions). The objective of this study is to obtain the optimal ordering quantities to minimize the overall costs. A comparative study has been done in the with substitution and without substitution cases. A solution methodology is developed to determine the optimal values of decision parameters. The nature of the overall cost function is also discussed. The comparative study and gap analysis of the relevant paper are presented in Table 5.1.

Table 5.1 Comparative study and gap analysis
Full size table

The remaining part of this article is ordered as follows: The assumptions and notations of the study, model description and formulation, solution method, numerical application, and sensitivity of key variables are given in section-wise, respectively. The last section represents the conclusion of the research.

Assumptions and Notations

Assumptions

  1. i.

    Lead time is assumed to be zero.

  2. ii.

    Two substitutable products are taken, and each are ordered jointly in every cycle.

  3. iii.

    Deterioration and demand rates are constant, and each product has distinct deterioration rates.

  4. iv.

    Both products are partially substitutable, if one of them is out of stock, then the other can be a substitute for that product.

  5. v.

    Substitution cost includes promotional effects like (cost comes from advertisements and sales promotions) are considered.

Notations

Symbol

Description

\(D_{1} , D_{2}\)

Demand rate of product 1 and product 2

\(C_{1 } ,C_{2 }\)

Unit purchase cost of product 1 and product 2

\(\theta_{1 } , \theta_{1 }\)

Deterioration rate of product 1 and product 2

\(A_{1 } ,A_{2 }\)

Setup cost for product 1 and product 2

\(Q_{i } ,i = 1, 2\)

Stock level of product 1 and product 2

h

Holding cost of each product

\(\alpha_{i } , i = 1, 2\)

Substitution rate for product 1 and product 2

\(\pi_{i} , i = 1, 2\)

Unit lost sale cost of product 1 and product 2

\({\text{CS}}_{12}\), \({\text{CS}}_{21}\)

Unit substitution cost for product 1 and product 2

l

Stock level of product when other product is completely depleted

s

Part of period when substitution occur

\(I_{i}^{1}\) (t)\(, i = 1,2\)

Stock level of product i when first product finishes before second

\(I_{3}^{1}\) (t)

Stock level of product 2 when first product finishes before second and substitution takes place

\({\text{TC}}i\left( {Q_{1} ,Q_{2} } \right)\), i = 1, 2

Average total cost for case 1 and case 2

\({\text{TC}}_{{{\text{NS}}}} \left( {Q_{1} ,Q_{2} } \right)\)

Average total cost for case 3

Model Description and Formulation

Based on assumptions, we assume two substitutable non-instantaneous decaying products. At starting, the retailer’s orders \(Q_{1}\) and \(Q_{2}\) quantity (unit) of product 1 and 2 jointly. The stock level of each product consumes due to demand in time period [0, \({ }t_{1}\)] and deplete due to deterioration and demand in period [\(t_{1} ,t_{2}\)] and after that substitution occurs. Both products replenish jointly after consumption to acquire the benefits of joint ordering. At \(t = t_{2}\), three possibilities arise as follows.

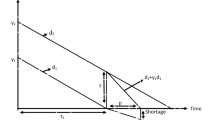
Case 1: Product 1 fully consumes before product 2, i.e., if product 1 is out of stock at time \(t_{2}\), as seen in Fig. 5.1, then requirement of product 1 is partially satisfied by product 2 with substitution rate \(\alpha_{1} { }\) and rest demand for product 1 is lost with rate of (1 \(- { }\alpha_{1}\)). The stock level of products is depicted by the given below differential equation, as seen in Fig. 5.1.

$$\frac{{{\text{d}}I_{1}^{1} \left( t \right)}}{{{\text{d}}t}} = - D_{1} ;\quad 0 \le t \le t_{1}$$
(5.1)
$$\frac{{{\text{d}}I_{1}^{1} \left( t \right)}}{{{\text{d}}t}} + \theta_{1} I_{1}^{1} \left( t \right) = - D_{1} ;\quad t_{1} \le t \le t_{2}$$
(5.2)
Fig. 5.1
figure 1

Stock size for case 1 at time t

Full size image

With \(I_{1}^{1} \left( 0 \right) = Q_{1} ,{ }I_{1}^{1} \left( {t_{2} } \right) = 0\).

$$\frac{{{\text{d}}I_{2}^{1} \left( t \right)}}{{{\text{d}}t}} = - D_{2} ;\quad 0 \le t \le t_{1}$$
(5.3)
$$\frac{{{\text{d}}I_{2}^{1} \left( t \right)}}{{{\text{d}}t}} + \theta_{2} I_{2}^{1} \left( t \right) = - D_{2} ;\quad t_{1} \le t \le t_{2}$$
(5.4)

With \(I_{2}^{1} \left( 0 \right) = Q_{2} ,{ }I_{2}^{1} \left( {t_{1} } \right) = Q_{2} - D_{2} t_{1} { },I_{2}^{1} \left( {t_{2} } \right) = l\).

$$\frac{{{\text{d}}I_{3}^{1} \left( t \right)}}{{{\text{d}}t}} + \theta_{2} I_{3}^{1} \left( t \right) = - \left( {D_{2} + \alpha_{1} D_{1} } \right);\quad t_{2} \le t \le t_{2} + s$$
(5.5)

With \(I_{3}^{1} \left( {t_{2} } \right) = l,{ }I_{3}^{1} \left( {t_{2} + s} \right) = 0\).

The result of Eqs. (5.1–5.5) are

$$I_{1}^{1} \left( t \right) = Q_{1} - D_{1} t;\quad 0 \le t \le t_{1} { }$$
(5.6)
$$I_{1}^{1} \left( t \right) = \frac{{D_{1} }}{{\theta_{1} }}\left( {e^{{\theta_{1} \left( {t_{2} - t} \right)}} - 1} \right);\quad t_{1} \le t \le t_{2}$$
(5.7)
$$I_{2}^{1} \left( t \right) = Q_{2} - D_{2} t;\quad 0 \le t \le t_{1} { }$$
(5.8)
$$I_{2}^{1} \left( t \right) = - \frac{{D_{2} }}{{\theta_{2} }} + e^{{\theta_{2} \left( {t_{1} - t} \right)}} \left( {Q_{2} - D_{2} t_{1} + \frac{{D_{2} }}{{\theta_{2} }}} \right);\quad t_{1} \le t \le t_{2}$$
(5.9)
$$I_{3}^{1} \left( t \right) = \frac{{D_{2} + \alpha_{1} D_{1} }}{{\theta_{2} }}\left( {e^{{\theta_{2} \left( {t_{2} + s - t} \right)}} - 1} \right);\quad t_{2} \le t \le t_{2} + s$$
(5.10)

Total cost of product 1 and product 2 during each cycle consists purchase, setup, and holding cost with their emissions cost and can be symbolized as

$${\text{TC}}11\left( {Q_{1} ,Q_{2} } \right) = A_{1} + C_{1} Q_{1} + h\left( {Q_{1} t_{1} + \frac{{D_{1} }}{{\theta_{1} }}\left( {t_{1} - t_{2} } \right) + \frac{{D_{1} }}{{\theta_{1}^{2} }}\left( {e^{{\theta_{1} \left( {t_{2} - t_{1} } \right)}} - 1} \right) - \frac{{D_{1} t_{1}^{2} }}{2}} \right)$$
(5.11)
$$\begin{aligned} TC12\left( {Q_{1} ,Q_{2} } \right) & = A_{2} + C_{2} Q_{2} + \left( h \right)\left( {Q_{2} t_{1} + \frac{{D_{2} }}{{\theta_{2} }}\left( {t_{1} - t_{2} } \right)} \right. \\ & \quad + \frac{{\left( {Q_{2} \theta_{2} - D_{2} t_{1} \theta_{2} + D_{2} } \right)}}{{\theta_{2}^{2} }}\left. {\left( {1 - e^{{\theta_{2} \left( {t_{1} - t_{2} } \right)}} } \right) - \frac{{D_{2} t_{1}^{2} }}{2}} \right) \\ \end{aligned}$$
(5.12)

The lost sale costs of product 1 per length cycle

$$= \pi_{1} { }\left( {1 - \alpha_{1} } \right)D_{1} \frac{{\ln \left( {\frac{{\left( {\left( { - D_{2} t_{1} + Q_{2} } \right)\theta_{2} + D_{2} } \right)e^{{\theta_{2} \left( {t_{1} - t_{2} } \right)}} + \alpha_{1} D_{1} }}{{D_{2} + \alpha_{1} D_{1} }}} \right)}}{{\theta_{2} }}$$
(5.13)

Substitution cost due to product 1 partially replaced by product 2 per length cycle

$$= {\text{CS}}_{12} \alpha_{1} D_{1} { }\frac{{\ln \left( {\frac{{\left( {\left( { - D_{2} t_{1} + Q_{2} } \right)\theta_{2} + D_{2} } \right)e^{{\theta_{2} \left( {t_{1} - t_{2} } \right)}} + \alpha_{1} D_{1} }}{{D_{2} + \alpha_{1} D_{1} }}} \right)}}{{\theta_{2} }}$$
(5.14)

Thus, the average total costs \({\text{TC}}\left( {Q_{1} ,Q_{2} } \right)\) for case 1 per unit time

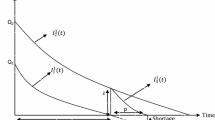
$$\begin{aligned} {\text{TC}}1\left( {Q_{1} ,Q_{2} } \right) = & \frac{1}{{t_{1} + t_{2} + s}}\left[ {A_{1} + A_{2} + C_{1} Q_{1} + C_{2} Q_{2} + h\left\{ {Q_{1} t_{1} + \frac{{D_{1} }}{{\theta_{1} }}\left( {t_{1} - t_{2} } \right)} \right.} \right. \\ & + \frac{{D_{1} }}{{\theta _{1}^{2} }}\left( {e^{{\theta _{1} \left( {t_{2} - t_{1} } \right)}} - 1} \right) - \frac{{D_{1} t_{1}^{2} }}{2} + Q_{2} t_{1} + \frac{{D_{2} }}{{\theta _{2} }}\left( {t_{1} - t_{2} } \right) \\ & + \frac{{\left( {Q_{2} \theta _{2} - D_{2} t_{1} \theta _{2} + D_{2} } \right)}}{{\theta _{2}^{2} }}\left( {1 - e^{{\theta _{2} \left( {t_{1} - t_{2} } \right)}} } \right) - \frac{{D_{2} t_{1}^{2} }}{2} \\ & \left. { +\, \frac{{\left( {D_{2} + \alpha _{1} D_{1} } \right)}}{{\theta _{2}^{2} }}\left( {e^{{\theta _{2} s}} - 1 - \theta _{2} s} \right)} \right\} \\ & + \pi _{1} \left( 1 -\, \alpha _{1} \right)D_{1} \frac{{\ln \left( {\frac{{\left( {\left( { - D_{2} t_{1} + Q_{2} } \right)\theta _{2} + D_{2} } \right)e^{{\theta _{2} \left( {t_{1} - t_{2} } \right)}} + \alpha _{1} D_{1} }}{{D_{2} + \alpha _{1} D_{1} }}} \right)}}{{\theta _{2} }} \\ & \left. { +\, {\text{CS}}_{{12}} \alpha _{1} D_{1} \frac{{\ln \left( {\frac{{\left( {\left( { - D_{2} t_{1} + Q_{2} } \right)\theta _{2} + D_{2} } \right)e^{{\theta _{2} \left( {t_{1} - t_{2} } \right)}} + \alpha _{1} D_{1} }}{{D_{2} + \alpha _{1} D_{1} }}} \right)}}{{\theta _{2} }}} \right] \\ \end{aligned}$$
(5.15)

Case 2: Product 2 fully consumes before product 1, that means, if product 2 is out of stock at time \(t_{2}\), as seen in Fig. 5.2, then requirement of product 2 is partially met by product 1 with substitution rate \(\alpha_{2}\) and rest demand for product 2 is lost with rate (1 \(- \alpha_{2}\)). The mathematical formation of case 2 is identical to case 1. The models are depicted in Fig. 5.2.

Fig. 5.2
figure 2

Stock size for case 2 at time t

Full size image

Therefore, the average total costs \({\text{TC}}2\left( {Q_{1} ,Q_{2} } \right)\) of case 2 is

$$\begin{aligned} {\text{TC2}}\left( {Q_{1} ,Q_{2} } \right) = & \frac{1}{{t_{1} + t_{2} + s}}\left[ {A_{1} + A_{2} + C_{1} Q_{1} + C_{2} Q_{2} + h\left\{ {Q_{1} t_{1} + \frac{{D_{1} }}{{\theta_{1} }}\left( {t_{1} - t_{2} } \right)} \right.} \right. \\ & + \frac{{D_{2} }}{{\theta _{2}^{2} }}\left( {e^{{\theta _{2} \left( {t_{2} - t_{1} } \right)}} - 1} \right) - \frac{{D_{1} t_{1}^{2} }}{2} + Q_{2} t_{1} + \frac{{D_{2} }}{{\theta _{2} }}\left( {t_{1} - t_{2} } \right) \\ & + \,\frac{{\left( {Q_{1} \theta _{1} - D_{1} t_{1} \theta _{1} + D_{1} } \right)}}{{\theta _{1}^{2} }}\left( {1 - e^{{\theta _{1} \left( {t_{1} - t_{2} } \right)}} } \right) - \frac{{D_{2} t_{1}^{2} }}{2} \\ & \left. { +\, \frac{{\left( {D_{1} + \alpha _{2} D_{2} } \right)}}{{\theta _{1}^{2} }}\left( {e^{{\theta _{1} s}} - 1 - \theta _{1} s} \right)} \right\} + \pi _{2} \left( 1 \right. \\ & \left. { -\, \alpha _{2} } \right)D_{2} \frac{{\ln \left( {\frac{{\left( {\left( { - D_{1} t_{1} + Q_{1} } \right)\theta _{1} + D_{1} } \right)e^{{\theta _{1} \left( {t_{1} - t_{2} } \right)}} + \alpha _{2} D_{2} }}{{D_{1} + \alpha _{2} D_{2} }}} \right)}}{{\theta _{1} }} \\ & \left. { + \,{\text{CS}}_{{21}} \alpha _{2} D_{2} \frac{{\ln \left( {\frac{{\left( {\left( { - D_{1} t_{1} + Q_{1} } \right)\theta _{1} + D_{1} } \right)e^{{\theta _{1} \left( {t_{1} - t_{2} } \right)}} + \alpha _{2} D_{2} }}{{D_{1} + \alpha _{2} D_{2} }}} \right)}}{{\theta _{1} }}} \right] \\ \end{aligned}$$
(5.16)

Case 3 (without substitution): The stock level of each product is totally consumed at \(t_{2,}\) i.e., no substitution happens, as shown in Fig. 5.3. The stock level of each product is depleted at \(t_{2} = t_{3,}\) i.e., \(Q_{1} /D_{1}\) = \(Q_{2} /D_{2}\) as displayed in Fig. 5.3.

Fig. 5.3
figure 3

Stock size for case 3 at time t

Full size image

Therefore, the average total costs \({\text{TC}}_{{{\text{NS}}}} \left( {Q_{1} ,Q_{2} } \right)\) for case 3 is

$$\begin{aligned} {\text{TC}}_{{{\text{NS}}}} \left( {Q_{1} ,Q_{2} } \right) = & \frac{1}{{t_{1} + t_{2} }}\left[ {A_{1} + A_{2} + \left( {C_{1} } \right)Q_{1} + \left( {C_{2} } \right)Q_{2} + \left( h \right)} \right.\left( {\left( {Q_{1} + Q_{2} } \right)t_{1} } \right. \\ & + \left( {\frac{{D_{1} }}{{\theta _{1} }} + \frac{{D_{2} }}{{\theta _{2} }}} \right)\left( {t_{1} - t_{2} } \right) - \left( {D_{1} + D_{2} } \right)\frac{{t_{1}^{2} }}{2} + \frac{{D_{1} }}{{\theta _{1}^{2} }}\left( {e^{{\theta _{1} \left( {t_{2} - t_{1} } \right)}} - 1} \right) \\ & \left. {\left. { +\, \frac{{D_{2} }}{{\theta _{2}^{2} }}\left( {e^{{\theta _{2} \left( {t_{2} - t_{1} } \right)}} - 1} \right)} \right)} \right] \\ \end{aligned}$$
(5.17)

Solution Procedure

To obtain most desirable ordering quantity from overall cost function in the subsequent phase due to highly nonlinear function, we have graphically shown that the nature of overall cost expression is strictly convex nature. We develop an algorithm to achieve the most desirable ordering quantity.

Algorithm to achieve the optimal overall cost and ordering quantity.

  1. Step 1:

    Solve the constraint-based problem

    $$\mathop {\min }\limits_{{Q_{1} ,Q_{2} }} {\text{TC}}1\left( {Q_{1} ,Q_{2} } \right){\text{ Subject to}},\frac{{Q_{1} }}{{D_{1} }} \le \frac{{Q_{2} }}{{D_{2} }}$$
  2. Step 2:

    Solve the constraint-based problem

    $$\mathop {\min }\limits_{{Q_{1} ,Q_{2} }} {\text{TC}}2\left( {Q_{1} ,Q_{2} } \right){\text{ Subject to}},\frac{{Q_{1} }}{{D_{1} }} \ge \frac{{Q_{2} }}{{D_{2} }}$$
  3. Step 3:

    To get optimum value, choose minimum between above two steps, i.e.,

    $$\min \left[ {{\text{TC}}1\left( {Q_{1} ,Q_{2} } \right){ },{\text{ TC}}2\left( {Q_{1} ,Q_{2} } \right)} \right].$$

Numerical Example and Sensitivity Analysis

In this section, we first establish numerical experiment that demonstrates the implementation of proposed inventory model. The value of parameter of the numerical example is \(C_{1} = 3\), \(C_{2} = 2.5,{ }A_{1} = 300,{ }A_{2} = 250\), h = 2, \(t_{1} = 0.20\), \(\theta_{1} = 0.50\), \(\theta_{2} = { }\) 0.55, \(D_{1} = 200\), \(D_{2} = { }\) 40, \(\alpha_{1} = 0.2\), \(\pi_{1} = 0.4\), and \(CS_{12} = 2\). We solve the above optimization problem with the above-developed algorithm and software maple. The outcomes of step 1 are \({\text{TC}}1\left( {Q_{1} ,Q_{2} } \right) = 1288.56\), \(Q_{1} = 92.41\), and \(Q_{2} = 91.07,\) and the outcomes of step 2 are \({\text{TC}}2\left( {Q_{1} ,Q_{2} } \right) = 1350.79\), \(Q_{1} = 171.21\), and \(Q_{2} = 27.27\). On comparing both of outcomes in step 3 of the algorithm, step 1 outcomes dominance to the optimal values. Hence, the optimal total costs for with substitution is 1288.56 and optimal ordering quantities is \(\left( {Q_{1}^{*} ,Q_{2}^{*} } \right) = \left( {92.41,{ }91.07} \right)\). The optimal ordering quantities and overall cost for without substitution case is \(\left( {Q_{1} ,Q_{2} } \right) = \left( {163.29,{ }32.65} \right)\) and \({\text{TC}}_{{{\text{NS}}}} \left( {Q_{1} ,Q_{2} } \right) = 1358.39\).

Comparing the outcomes of with substitution and without substitution, the beneficial difference in optimal total cost is 69.83 and the benefits of substitution over without substitution in percentage is 5.14%.

To investigate the essence of the total cost, we draw the overall cost function for product 1 and product 2 with different order quantities. Figure 5.4 shows the optimal total cost expression is strictly convex nature. Decision-making situations rarely remain fixed in the real world; thus, the parameters of the model change so, we perform sensitivity analysis numerically by varying the value of fixed parameter. Table 5.2 shows the numerical output of sensitivity analysis. The results of changes in parameters and percentage change are illustrate in Figs. 5.5, 5.6, 5.7 and 5.8.

Fig. 5.4
figure 4

Optimal overall cost versus optimal total quantities (Q1*, Q2*)

Full size image
Table 5.2 Sensitivity analysis when key parameters change
Full size table
Fig. 5.5
figure 5

Sensitivity analysis with variation in ordering cost (\(A_{1}\)) and holding cost (h)

Full size image
Fig. 5.6
figure 6

Sensitivity analysis with variation in purchase cost (\(C_{1} { },{ }C_{2}\))

Full size image
Fig. 5.7
figure 7

Sensitivity analysis with variation in substitution cost \(\left( {CS_{12} } \right)\) and lost sale cost \(\left( {\pi_{1} } \right)\)

Full size image
Fig. 5.8
figure 8

Sensitivity analysis with variation in substitution rate (\(\alpha_{1}\)) and non-decaying period (\(t_{1}\))

Full size image

Conclusion

This study presents an inventory management model for two non-instantaneous decaying substitute products under joint ordering policy in each ordering cycle. At any time, if one of product is out of stock, a fraction of its demand may be met using the stock of the other product and other undesirable demand goes to loss. The suggested resulting model and solution method for determining the optimal ordering strategy is easy to understand and enforce. We first derive the overall cost expressions and illustrate graphically that they are convex. The numerical example demonstrates the application of the model, and the numerical output provides the percentage profitable improvement in overall cost, comparing with substitution and without substitution. This suggested that the impact of substitution with joint replenishment is a significant consideration that a retailer should consider into account, when picking inventory selections.

As the present model is restricted with two products which can be extended for multi-products. Another expansion of this study may be the consideration of trade credit systems and coordination between manufacturers and retailers. This study can also be extended for fuzzy stochastic environment, screening process, quality discounts, promotional effect, trade credit policies, and several other practical situations [22, 23].