Robust Flutter Analysis Considering Control Surface Aerodynamic Uncertainty

Abstract

To reduce the conservation of robust flutter analysis results, only the uncertainty of control surface unsteady aerodynamic was modeled. The $\mu - k$ approach was used to compute the robust flutter speed. The results indicate that robust flutter speed considering only the control surfaces unsteady aerodynamic is 716% less than entire surface case, also show that the approach for robust flutter analysis is applicable to multiple flutter modes in engineering practice.

1 Introduction

Traditional aeroelastic system stability can be modeled as linear system stability, flutter boundary is defined by solving system matrix single value. Lind firstly applied robust control theory to flutter problem which take uncertainty into account [1]. Structural singular value became the criteria of stability for robust flutter. From system equation point of view, the uncertainty sources including mass, stiffness, damping, and aerodynamic.

For stiffness uncertainty, Gu Yingsong proposed robust flutter margin is calculated for an airfoil with flap freeplay uncertainty with uncertain nonlinear operator method [2]. Sebastian Heinze proposed two useful methods for taking mode shape variation one is increasing the modal base by adding additional vectors, the other is a iterative approach to capture mode shape variations without the need of mode shape derivatives [3]. Dai Yuting using robust flutter analysis considered the mode shape variations that result due to variations of structural properties [4]. For mass uncertainty, Sebastian Heinze presented an approach to assess critical fuel configurations using robust flutter analysis, the worst-case flutter speed and the corresponding worst-case fuel configuration is found [5]. For aerodynamic uncertainty, general modeling method is introduced [6] but more useful description of uncertainty to engineering practice is limited. In this study, only aerodynamic uncertainty of concerned area is considered to reduce robust flutter conservation, μ-k approach [7] is applied to an aircraft vertical fin with control surface aerodynamic uncertainty.

2 Uncertainty Modeling

There are two possible sourcex of the control surface aerodynamic uncertainty, one is from the error or assumption in mathematical modeling process, the other is physically existed but not considered or modeled accurately. For example, traditional flutter model use Doublet Lattice Method (DLM) which is based on linear assumption, the aerodynamic interpolation spline can be source of uncertainty. Physically it can be complex local aeroflow condition, flight condition uncertainty etc. Aeroflow separation normal starts form trailing edge, which can cause control surface aerodynamic uncertainty, analysis shows that uncertainty at trailing edge is significantly high than leading edge [8]. Besides, for aircraft flutter boundary in transonic regime, nonlinear phenomenon such as shock wave is difficulty to accurate modeled [9].

Flutter equation in Laplace domain can be written in the non-dimensional form [3]:

$$ [Mp^2 + (L/V)Dp + (L^2 /V^2 )K - (\rho L^2 /2)Q(p,m)]\eta (p) = 0 $$

(1)

where $M,D,K$ and $Q(p,m)$ are the mass, damping, stiffness and the aerodynamic transfer matrix, these matrices are $f \times f$, where $f$ is the number of modes used in the modal basis. $\eta (p)$ is the vector of modal coordinates. Further, $V$ is the airspeed, $L$ is the aerodynamic reference length, $\rho$ is the air density and $M$ is the Mach number. The non-dimensional Laplace variable is denoted $p = g + ik$, where g is the damping and k is the reduced frequency, to compute the critical flutter boundary let g = 0.

To define the aerodynamic uncertainty model, it is necessary to partition the aerodynamic matrix [10]:

$$ Q_{0} (ik,m) = R_{0} S_{0} (ik,m) $$

(2)

where the $S_{0} (ik,m)$ defines the mapping from modal coordinates to lifting surface pressure coefficients, and $R_{0}$ defines the mapping from lifting surface-pressure coefficients to generalized forces. Note that $R_{0}$ is independent of the reduced frequency and the Mach number because it is made up of information from the spline interface between structural and aerodynamic models and modal eigenvector information.

Then the uncertainty aerodynamic transfer function can be written:

$$ \begin{aligned} Q(ik,m) & = R_{0} (I + w_{j} \delta _{j} E_{j} )S_{0} (ik,m). \\ & = Q_{0} (ik,m) + w_{j} \delta _{j} Q_{j} (ik + m) \\ \end{aligned} $$

(3)

where, $w_{j}$ defines uncertainty bound i.e. 0.1 means 10% uncertainty is assigned to the specified boxes in aerodynamic model, uncertainty parameter $\delta_{j}$ meets $\left| {\delta_{j} } \right| \le 1$, $E_{j}$ is the matrix with $e_{jj} = 1$.

$$ Q_{j} (ik,m){ = }R_{0} E_{j} S_{0} (ik,m) $$

(4)

Generalized description can be written as:

$$ Q(ik,m){ = }Q_{0} (ik,m){ + }\sum\limits_{j = 1}^{n} {w_{j} \delta_{j} Q_{j} } (ik,m) $$

(5)

where n is the total pressure coefficient number, rewrite as:

$$ Q(ik,m){ = }Q_{0} (ik,m){ + }V_{Q} (ik,m)\Delta_{Q} W_{Q} $$

(6)

where, $V_{Q} = [Q_{1} Q_{2} \ldots Q_{n} ]$

$$ \Delta _{Q} = diag(\delta _{1} I_{{f \times f}} ,\delta _{2} I_{{f \times f}} , \ldots ,\delta _{n} I_{{f \times f}} ) $$

$$ W_{Q} = \left[ {\begin{array}{*{20}c} {w_{1} I_{{f \times f}} } \\ {w_{2} I_{{f \times f}} } \\ \vdots \\ {w_{n} I_{{f \times f}} } \\ \end{array} } \right] $$

3 Nominal Flutter Analysis

An aircraft vertical fin-rudder model was used for analysis, the NASTRAN structural model as shown in Fig. 1, ZAERO aerodynamic model as shown in Fig. 2, in which the dash blue line indicates the rudder area.

Nominal flutter speed was determined using ZAERO, results indicates two flutter modes with difference frequency, the lower frequency mode is the critical mode which was due to coupling between first bending and rudder rotating, flutter speed is 355kn, flutter frequency is 16 Hz, i.e. the low frequency mode. The other is coupling among first torsional, rudder rotating and second bending, flutter speed 438 kn and frequency 32 Hz i.e. the high frequency mode. The V-g and V-f plot of flutter results is shown in Figs. 3 and 4.

For robust flutter analysis, the matrix in flutter equation were generated with OUTPUT function of ZAERO [11].

Fig. 1.

Structure model.

Fig. 2.

Aerodynamic model.

Fig. 3.

V-g curve

Fig. 4.

V-f curve.

4 Robust Flutter Analysis

4.1 Robust Flutter Equation

Combing Eqs. (6) and (1) and uncertainty:

$$ F_{0} (p,q,m)\eta = V(p,q,m)w $$

(7)

where,$F_{0} (p,q,m) = [Mp^{2} + (L/V)Dp + (L^{2} /V^{2} )K - (\rho L^{2} /2)Q_{0} ]$, $V(p,q,m) = (\rho L^{2} /2)V_{Q} (p,m)$

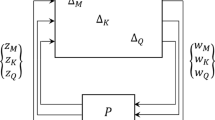
The uncertainty flutter equation feedback structure model as shown in Fig. 5:

Fig. 5.

Feedback model of uncertainty flutter equation

where, the input and output of uncertainty matrix being defined as:

$$ z = W\eta $$

(8)

$$ W = \Delta z $$

(9)

The transfer function F between input $W$ and output z:

$$ F(p,q,m) = WF_{0}^{ - 1} (p,q,m)V(p,q,m) $$

(10)

Rewrite using general aerodynamic force input ξ and general vector $\eta$ in the modal base:

$$ F_{0} (p,q,m)\eta = V(p,q,m)w + \xi $$

(11)

Transfer function between input $\xi$ and output $\eta$ which presents as Linear Fraction structure of uncertainty system as shown in Fig. 6:

Fig. 6.

Linear Fraction structure of uncertainty system

Then the uncertainty state space equation is as follow:

$$ \left[ \begin{gathered} z \hfill \\ \eta \hfill \\ \end{gathered} \right]{ = }\left[ {\begin{array}{*{20}c} {P_{11} } & {P_{12} } \\ {P_{21} } & {P_{22} } \\ \end{array} } \right]\left[ \begin{gathered} w \hfill \\ \xi \hfill \\ \end{gathered} \right]{ = }\left[ {\begin{array}{*{20}c} {WF_{0}^{ - 1} V} & {WF_{0}^{ - 1} } \\ {F_{0}^{ - 1} V} & {F_{0}^{ - 1} } \\ \end{array} } \right]\left[ \begin{gathered} w \hfill \\ \xi \hfill \\ \end{gathered} \right] $$

(12)

Transfer function matrix between $\xi$ and $\eta$:

$$ \eta { = }f_{u} {\text{(P,}}\Delta {)}\xi = [P_{22} + P_{21} \Delta (1 - P_{11} \Delta )^{ - 1} P_{12} ]\xi $$

(13)

where $f_{u} (P,\Delta )$ is the linear fractional transformation, if system is nominal stable, the only instability term is $f_{u} (1 - P_{11} \Delta )^{ - 1}$ which is equivalent to $P_{11} - \Delta$ stability,with $\left\| \Delta \right\| \le 1$ and $P_{11}$ is the flutter transfer function $WF_{0}^{ - 1} V$. The stability of input-output system is equivalent to flutter feedback stability.

The transfer function of flutter feedback system is:

$$ F(p,q,m) = P_{11} (p,q,m) $$

(14)

4.2 $\eta - k$ Curve

If the system is stable at specified flight condition, and structural singular value meet:

$$ \mu (k,q,m) = \mu \left[ {F(ik,q,m)} \right] < 1 $$

(15)

Then the system is robust stable at specified condition. If all the structural singular value $\mu (k_{j} ,q,m) < 1$, then system is robust stable. The critical robust flutter dynamic is determined at $\mu (k,q,m) < 1$, which is solved using μ toolbox of MATLAB [12]. A 10% aerodynamic uncertainty is used for all patches in control surface only, as the results shown in Figs. 7 and 8 is the result of whole fin 10% aerodynamic uncertainty case. Both shown two peak of μ which corresponding to the two flutter mode of nominal model. The robust flutter speed is shown in Table 1. Compare to nominal model, with only control surface 10% uncertainty, the low frequency robust flutter speed decreased by 10.6%, while high frequency mode decreased by 3.9%, which indicates low frequency flutter is more sensitive to control surface aerodynamic uncertainty, this also consists with the flutter mode tracking result of ZAERO. For the whole fin 10% aerodynamic uncertainty case, both low and high frequency robust flutter speed decreased by approximately 16%, which is obviously high than rudder case.

Fig. 7.

$\mu - k$curve of control surface 10% aerodynamic uncertainty

Fig. 8.

$\mu - k$ curve of fin 10% aerodynamic uncertainty

Table 1. Robust flutter results

5 Conclusion

For flutter problem with the control surface, the local aerodynamic uncertainty modeling of the control surface can effectively reduce the conservatism of robust flutter calculation results. At the same time, the calculation shows that the robust flutter analysis based on the approach is applicable to the presence of multiple flutter modes, which is of value for aircraft flutter design and flutter optimization in engineering practice.