1 Introduction

The accurate estimation of flutter boundary of civil/military aircraft is very important during design, certification and initial flight tests. Sometimes, many military aircraft require flight tests throughout their life as their operational demands change due to induction of new external stores. Hence, an accurate and reliable flutter boundary estimation will give more confidence in decision making during design, certification and testing of aircraft. Traditionally, the most widely used methods to perform flutter analysis of aircraft are the p–k method, k method or g method considering linear structural dynamics and linear unsteady aerodynamics based on panel method. Since, these methods depend on various assumptions, there exists significant difference in the flutter boundary obtained from the numerical model and the actual flight vehicle. Further, in reality, uncertainties are present in the various structural and aerodynamic parameters of aeroelastic systems which can influence the flutter boundary significantly. Hence, the assumption of complete determinacy in the various parameters of aeroelastic systems results in inaccurate flutter boundary. The uncertainties present in aeroelastic systems can be in the physical parameter level of structural and aerodynamic subsystems. In structural subsystem, dispersion in elastic modulus and density, uncertainty in stiffness and damping coefficients, uncertainty in store mass as well as its location, and variations in modal parameters can influence the aeroelastic stability boundary. In aerodynamic subsystem, aerodynamic influence coefficients, generalized aerodynamic forces and unsteady aerodynamic pressure can influence the aeroelastic behavior. There are two main techniques to quantify the propagation of uncertainty in aeroelastic systems: probabilistic and non-probabilistic methods [1,2,3]. The most common probabilistic approaches used to study the influence of uncertain parameters on aeroelastic stability are: the stochastic finite element method, the polynomial chaos expansion, the stochastic collocation and Monte Carlo Simulation (MCS) [4,5,6]. In the probabilistic methods, the uncertain parameters are described as probabilistic variables and distribution characteristics of the aeroelastic stability boundary are studied. Xiaowen et al. [7] developed a framework for probabilistic flutter analysis of a bridge deck including uncertainties in the structural and aerodynamic parameters. Here, critical wind speed and modal damping ratio were reformulated with the generalized flutter analysis, and their moments were evaluated using point estimation method. The developed framework was also validated with experimental data. Mannini and Bartoli [8] presented a method for flutter instability of a bridge deck by calculating the probability distribution of the flutter wind speed. The statistical properties of experimental aeroelastic coefficients were also calculated with wind tunnel tests performed on the bridge deck model. Cheng and Xiao [9] studied the probabilistic free vibration and flutter characteristics of suspension bridges considering uncertainties in the structural parameters using a stochastic finite-element-based algorithm. The proposed algorithm was based on combination of the response surface method, finite element method and MCS. The accuracy and efficiency of the proposed algorithm were also investigated by comparing results with MCS. Wu and Livne [10] developed an MCS based technique to predict flutter statistics of uncertain aeroelastic systems considering structural and aerodynamic uncertainties. Two different schemes, namely, AIC-based aerodynamic uncertainty scheme and a Roger approximation-based uncertainty scheme were considered. A comparative study was also made to see the effects of different structural and aerodynamic uncertainty sources on the flutter statistics of the AGARD wing. Kumar et al. [11, 12] developed a stochastic finite element method (SFEM) based on first order perturbation approach to investigate the probabilistic flutter boundary of an airfoil and a cantilever wing considering structural and aerodynamic uncertainties. The probability density functions (pdfs) of damping ratio and frequency obtained from SFEM were also compared with MCS at various free stream velocities. Further, the flutter probability in terms of Cumulative Distribution Function (CDF) was studied by defining implicit limit state function in conditional sense on flow velocity for the flutter mode using the first order second moment (FOSM), first order reliability method (FORM) and MCS.

The main disadvantage of the probabilistic methods is their dependency on a large amount of experimental data for generating uncertainties information, which is usually difficult to obtain. Instead, it is much easier to define the upper and lower bounds of uncertain variables as compared to the distribution information. The most commonly used non-probabilistic approaches for robust aeroelastic studies are based on the structured singular value (μ) method and the interval theory. In these approaches, the uncertain parameters are defined as bounded variables and the “worst case” stability boundary is studied for a given set of uncertainties. Zheng and Qiu [13] proposed a method for flutter stability of aeroelastic systems in the presence of structural and aerodynamic uncertainties. An interval form of the aeroelastic equation was developed by introducing interval variables into a deterministic aeroelastic system. Bernstein polynomial based uncertain propagation method was proposed to analyse flutter stability in terms of interval bounds on eigenvalues. The results obtained from the present approach were also compared with perturbation-based uncertainty propagation method and MCS. Lokatt [14] presented an efficient method for flutter stability of aeroelastic systems considering uncertainties in the structural and aerodynamic parameters. The variations in eigenvalue due to combined structural and aerodynamic uncertainties were calculated using eigenvalue differentials and Minkowski sums approaches. The method was demonstrated to study the flutter characteristics of a delta wing and it was found that the damping trends of the flutter mode was significantly influenced by the presence of both structural and aerodynamic uncertainties. Haiwei et al. [15] studied robust stability of a 2-D nonlinear aeroelastic system using the μ-method and the value set approach considering uncertainties in the structural and aerodynamic parameters. The aeroelastic system was made of a nonlinear spring in the pitch degree-of-freedom and a nonlinear aerodynamic model. In this study, both vanishing and nonvanishing perturbation types of uncertainty were investigated. The lower and upper bounds of robust flutter speeds were determined from the V – μ graph for a set of flow velocities. Lind and Brenner [16] developed an approach based on structured singular value to study robust stability of aeroelastic systems with dynamic pressure perturbations. The aeroelastic equations were represented in state space form considering the frequency domain unsteady aerodynamics transformed to the time domain using rational function approximations. Lind [17] introduced a model formulation for computing match point solutions using μ analysis. In this formulation, perturbation to airspeed was introduced and a function was constructed in terms of airspeed to approximate freestream density at a fixed Mach number. Borglund [18] developed a robust flutter technique in frequency domain which could handle aerodynamic uncertainties in its original form and find the worst-case flutter condition. However, this method focused only on calculating the worst-case flutter boundary for a given set of uncertainties. Later, Borglund [19] extended this technique to investigate robust stability of aeroelastic systems in subcritical conditions by representing aeroelastic equations in the Laplace domain. The estimation of uncertainty magnitude present in the aerodynamic model were also discussed using different model validation techniques. However, this technique focused on estimating the worst-case flutter boundary for a given flow condition. Bueno et al. [20] presented an approach to conduct flutter analysis of a swept back wing by modelling uncertainties in natural frequencies and damping ratios. The main aim of this work was to demonstrate the nominal system’s stability by incorporating variations in the modal parameters for a given range. An affine parameter model was used to represent the aeroelastic system and robust stability was studied by solving a Lyapunov function through linear matrix inequalities and convex optimization. Danowsky et al. [2] presented a linear reduced-order model from a high-fidelity nonlinear aeroelastic model for uncertainty analysis using various methods. Using reduced-order models, the design of experiment (DOE)/response surface method (RSM), and μ analysis method were compared with traditional Monte Carlo-based stochastic simulation. The advantages and drawbacks of all these approaches to uncertainty analysis were discussed. Huang et al. [21] presented a novel nonlinear reduced-order modelling approach for multi-input/multi-output aerodynamic systems based on a finite sum of Wiener-type cascade models. The unsteady transonic compressible flow over a 2-DOF NACA 64A010 airfoil system was considered to demonstrate the performance of the proposed approach. The nonlinear reduced-order model was also applied to transonic flutter analysis of the Isogai wing model and the flutter boundary was compared with CFD and linear reduced order model. Xiong et al. [22] proposed an iterative dimension-by-dimension method (IDDM) for the structural interval response prediction with multidimensional uncertain variables. Both the vertex method (VM) and Chebyshev interval method (CIM) were improved through iterative dimension-by-dimension approach to increase the efficiency of structural interval uncertainty analysis. Iannelli et al. [23] proposed a new Linear Fractional Transformation-Fluid Stricture Interaction (LFT-FSI) framework for robust flutter analysis of high-order aeroelastic systems. The co-modeling framework was developed by coupling fluid–structure interaction solvers with robust control-based methods and applied on an unconventional aircraft configuration for robust flutter studies. Chen et al. [24] developed a concept of CFD-based model reduction technique based on system identification theory to estimate bounded uncertainties associated with CFD simulation for aerodynamic subsystems. Here, the first-order interval perturbation method was used to estimate interval uncertainty in the identified coefficients of the uncertain reduced-order model. Further, the robust flutter boundary of uncertain aeroelastic system was predicted by defining stability criterion for the interval aeroelastic state matrix. Both Isogai wing and AGARD wing models were investigated to assess the capability of the proposed approach.

From the above literature, it can be observed that both probabilistic and non-probabilistic approaches have been extensively applied to study the stability boundary of aeroelastic systems in the presence of uncertainties. In addition, few studies have also focused on the estimation of aeroelastic stability (worst-case flutter boundary) in the presence of uncertainties for a given flow condition. In transonic regime, there can be abrupt occurrence of flutter due to sudden decrease in damping of a particular mode. Since it is difficult to predict the flight conditions which can induce such flutter condition, wind tunnel test and flight flutter test programs are extensively conducted to ensure that the flutter point is approached gradually. Hence, in order to predict such flutter point a priori and improve the overall efficiency of wind tunnel and flight flutter tests (decrease time and cost by reducing number of tests), methods for transonic flutter prediction of aeroelastic systems in the presence of uncertainties should be further studied.

In this work, a successive robust flutter prediction technique is proposed by coupling nominal analysis, ground vibration test (GVT), wind tunnel (WT) test, uncertainty model updation and robust analysis using the structured singular value (μ) method to accurately predict the robust flutter boundary of a swept back wing in transonic regime. To the author’s best knowledge this technique has not been attempted by the researchers to predict the flutter boundary of aeroelastic systems at various Mach numbers in transonic regime. In this technique, nominal flutter analysis of the wing is performed using the standard p–k method. Here, uncertainties in both structural and unsteady aerodynamics parameters of aeroelastic systems are considered in the generalized coordinates. These uncertainties are introduced in the nominal aeroelastic system in a Linear Fractional Transformation (LFT) framework. The magnitudes of structural uncertainties are estimated based on the difference in structural frequencies between ground vibration test (GVT) and nominal analysis. The magnitudes of aerodynamic uncertainties are estimated using a model updation technique based on the μ method considering the difference in damping values between wind tunnel and nominal analysis. Finally, a successive robust flutter prediction approach is developed by closely combining nominal analysis, GVT, wind tunnel testing, uncertainty model updation and robust analysis. The applicability of the present approach is demonstrated by predicting the robust flutter boundary of a swept back wing in transonic regime. The transonic flutter boundary (transonic dip) predicted using the present approach is also compared with the wind tunnel data. The proposed robust flutter prediction framework will be useful from practical application point of view as it can predict a worst-case flutter boundary of aircraft a priori for a range of transonic Mach number using subcritical (lower Mach) test data obtained from wind tunnel/flight flutter tests.

2 Uncertain flutter equation

The governing equation of aeroelastic system with uncertainty in the Laplace domain can be expressed as:

$$\left[ {M\left( \delta \right)p^{2} + \frac{L}{U}C\left( \delta \right)p + \frac{{L^{2} }}{{U^{2} }}K\left( \delta \right) - \frac{{\rho L^{2} }}{2}Q\left( {p,\delta } \right)} \right]\eta = 0$$
(1)

where \(M\left( \delta \right)\), \(C\left( \delta \right)\), \(K\left( \delta \right)\) and \(Q\left( {p,\delta } \right)\) are the generalized mass, damping, stiffness and aerodynamic force matrices respectively. L, U and \(\rho\) are the reference length, freestream velocity and density respectively. \(\eta\) is the vector of modal coordinates and p is the non-dimensional Laplace variable defined by \(p = g + ik\), where \(g\) and \(k~\left( { = \frac{{\omega L}}{U}} \right)\) are the damping and reduced frequency respectively.

In general, the sources of uncertainty are difficult to be defined due to complex nature of aeroelastic systems. Usually, the sources and structures of uncertainties are described by the properties of the actual system or by the engineering experiences. The uncertainties of mass, damping, stiffness and unsteady aerodynamic force are the common sources of uncertainty for aeroelastic systems. In the present study, the parametric uncertainties of generalized mass, stiffness, and unsteady aerodynamic forces are considered which can be expressed as:

$$\begin{array}{*{20}l} {M\left( \delta \right) = M_{0} + V_{M} {{\Delta }}_{M} W_{M} } \\ {K\left( \delta \right) = K_{0} + V_{K} {{\Delta }}_{K} W_{K} } \\ {Q\left( {p,\delta } \right) = Q_{0}\left( {p} \right) + V_{Q} {{\Delta }}_{Q} W_{Q} } \\ \end{array}$$
(2)

where the subscript ‘0’ represents the nominal value of the system parameters. \(V\)’s and \(W\)’s are the perturbation and weighing matrices respectively for each uncertain parameter. Here, \({{\Delta }}\)’s are the block-structured uncertainty matrices for each uncertain parameter such that \(\delta \in D\) where the set \(D = \left\{ {\delta ~:~\parallel \delta \parallel _{\infty } \le 1} \right\}\). In this study, the frequency domain aerodynamic matrix is obtained by linear aerodynamic theory based on unsteady Doublet–Lattice Method (DLM) and ZONA51 [26]. Since, various assumptions are made in these theoretical aerodynamic models, this may lead to inaccuracy in capturing wing surface aerodynamics in transonic regime due to the presence of flow nonlinearity. Here, uncertainties in the unsteady aerodynamics may be the most significant source and may have a strong influence on the aeroelastic behavior of the system as compared to other uncertainties.

The uncertain aeroelastic equation can be rewritten by introducing the above uncertainties into Eq. (1) as:

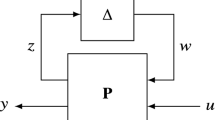
$$\left[ {M_{0} p^{2} + \frac{L}{U}C_{0} p + \frac{{L^{2} }}{{U^{2} }}K_{0} - \frac{{\rho L^{2} }}{2}Q_{0} } \right]\eta + \left[ {V_{M} {{\Delta }}_{M} W_{M} p^{2} + \frac{{L^{2} }}{{U^{2} }}V_{K} {{\Delta }}_{K} W_{K} - \frac{{\rho L^{2} }}{2}V_{Q} {{\Delta }}_{Q} W_{Q} } \right]\eta = 0$$
(3)

To find robust stability of aeroelastic systems using the structures singular value (µ) method, the above uncertain flutter equation is represented in an LFT form. This can be performed by separating uncertainties from the nominal system and then introduce them into the system matrix in a feedback manner as shown in Fig. 1. To explain this, let the input signals to the total uncertainty matrix \({{\Delta }}\) be defined as:

$$z = W\eta$$
(4)

where the total weighing matrix is represented as \(W = \left[ {\begin{array}{*{20}c} {W_{M} } \\ {W_{K} } \\ {W_{Q} } \\ \end{array} } \right]\).

Fig. 1
figure 1

LFT representation of uncertain aeroelastic equation

Full size image

Further, the output signals from the total uncertainty matrix can be defined as:

$$w = {{\Delta }}z$$
(5)

where the total uncertainty matrix \({{\Delta }}\) is represented as:

$${{\Delta }} = diag~\left( {{{\Delta }}_{M} ,~~{{\Delta }}_{K} ,~~{{\Delta }}_{Q} } \right)$$
(6)

By introducing Eqs. (4) and (5) into Eq. (3), the linear fractional transformation of uncertain aeroelastic system can be expressed as:

$$P_{0} \eta = Vw$$
(7)

where \(P_{0}\) and \(V\) are the nominal flutter matrix and total perturbation transfer function matrix respectively defined as:

$$P_{0} = \left[ M_{0} p^{2} + \frac{L}{U}C_{0} p + \frac{{L^{2} }}{{U^{2} }}K_{0} - \frac{{\rho L^{2} }}{2}Q_{0} \right]$$
(8)
$$V = \left[ { - V_{M} p^{2} \quad - \frac{{L^{2} }}{{U^{2} }}V_{K} \quad \frac{{\rho L^{2} }}{2}V_{Q} ~} \right]$$
(9)

Figure 1 shows the upper linear fractional transformation of uncertain aeroelastic equation in a feedback form. Using Eqs. (4) and (7), the transfer function matrix \(P\left( p \right)\) which connects the input (\(w\)) and output signals (\(z\)) can be defined as:

$$z = WP_{0}^{{ - 1}} Vw = P\left( p \right)w$$
(10)

Further, using Eqs. (5) and (10), the feedback loop between \(w\) and \(z\) can be expressed as:

$$\left[ {I - P\left( p \right){{\Delta }}} \right]z = 0$$
(11)

where \(P\left( p \right) = WP_{0}^{{ - 1}} V\).

Here, \(P\left( p \right)\) represents the system matrix which contains the components of the nominal flutter matrix (\(P_{0}\)) and the scaling matrices (\(V\) and \(W\)). Then, structured singular value (µ) analysis is performed to find all feasible eigenvalues of the uncertain aeroelastic equation [27]. The structured singular value (\(\mu\)) of the system matrix \(P\left( p \right)\) is expressed as the reciprocal of the minimum norm of a structured \({{\Delta }}\) such that \(det\left[ {I - P\left( p \right){{\Delta }}} \right]\) becomes zero:

$$\mu \left[ {P\left( p \right)} \right] = \frac{1}{{{}_{{{\Delta }}}^{{min}} ~\left\{ {\bar{\sigma }\left( {{\Delta }} \right)~~:~\det \left( {I - P\left( p \right){{\Delta }}} \right) = 0{{~}}\;{\text{for}}\;{\text{structured~}}\;{{\Delta }}} \right\}}}$$
(12)

If there is no such structured \({{\Delta }}\) which makes \(\det \left( {I - P\left( p \right){{\Delta }}} \right) = 0\), then \(\mu \left[ {P\left( p \right)} \right] = 0\). Thus, if \(\mu \left[ {P\left( p \right)} \right] = \mu \left( p \right) \ge 1\) then p is a feasible solution of Eq. (7) for some \({{\Delta }} \in B\), where \(B = \left\{ {{{\Delta }}~:~{{\Delta\,\text{structured}\,\text{and}\,}}\bar{\sigma }\left( {{\Delta }} \right) \le 1} \right\}\), and \(\bar{\sigma }\left( ~ \right)\) is the maximum singular value. Further, p is not a solution if \(\mu \left( p \right) < 1\). Hence, based on a single evaluation of µ, it is possible to find whether a given eigenvalue p is a possible solution of the uncertain aeroelastic equation. It is possible to find the regions of all feasible eigenvalues using search algorithms in the complex plane. The extreme eigenvalues with the minimum and maximum real parts (denoted by p- and p+ respectively) can also be found within the feasible regions such that \(\mu \left( p \right) = 1\). Here, these extreme eignevalues are calculated for each aeroelastic mode at various flow conditions representing damping bounds of the aeroelastic mode. The criteria for the aeroelastic system to be robustly stable is that p+ should be negative for all modes at a given flow condition. Thus, the robust flutter boundary of aeroelastic systems can be estimated by checking the sign of p+ for each mode at various flow conditions. The following sections discuss about the initial and successive robust flutter prediction techniques for aeroelastic systems using the structured singular value method.

3 Initial robust flutter prediction technique

The concept of initial robust flutter prediction approach is to estimate the possible variations in flutter boundary due to the applied uncertainty in aeroelastic systems at different transonic flow conditions before WT tests and model updation procedure. The method includes nominal aeroelastic model development, uncertainty modeling and robust flutter analysis as discussed in the previous section. Here, the structures of uncertainty are assumed based on engineering experiences and provide the representation of uncertain parameters in the aeroelastic model. However, it is difficult to estimate the magnitudes of uncertainty in various parameters. In the initial flutter prediction approach, robust aeroelastic analysis is performed using the uncertainty information available before the first WT test. In this analysis, uncertainties in both structural and aerodynamic parameters are considered. The estimation of structural uncertainty magnitude is based on the difference in natural frequencies between nominal analysis and ground vibration test (GVT). This uncertainty is introduced as real, parametric uncertainty in the generalized stiffness matrix. For the aerodynamic uncertainties, the generalized aerodynamic force matrix is considered with assumed uncertainty magnitude in all modes. This uncertainty is introduced as complex, parametric uncertainty in the generalized aerodynamic force matrix. Then, initial robust flutter prediction analysis is performed to estimate the possible variations in frequency and damping due to the applied uncertainty at different flow conditions. Since the aerodynamic uncertainty magnitude is based on assumption, it can be useful to study how much influence the magnitude has on the flutter boundary of aeroelastic systems in transonic regime.

4 Successive robust flutter prediction technique

In this section, a successive robust flutter prediction technique by coupling nominal analysis, ground vibration test, wind tunnel test, uncertainty model updation and robust analysis using the structured singular value method is discussed. Figure 2 shows the flowchart of successive robust flutter prediction approach applied in this study. Here, the approach begins with nominal flutter analysis, uncertainty modeling, followed by initial robust flutter analysis as discussed in the preceding sections. Then, a plan of WT tests is proposed based on the initial estimate of robust flutter boundary. Once WT tests start, then a closely coupled successive robust flutter prediction approach is applied, where the magnitude of uncertainty is continuously updated based on validation of robust eigenvalue/damping with WT test data. Here, wind tunnel tests are divided into a number of sets where each set include a number of test conditions and Mach number is gradually increased between each set. After completion of WT tests for each set, the measured damping and frequency of each aeroelastic mode are compared with nominal analysis. If some of the damping values are less than the nominal damping, then an aerodynamic uncertainty validation is performed using the most deviating damping value within the set and the minimum uncertainty magnitude is computed. The aerodynamic uncertainty model is then updated with the new uncertainty magnitude, and a new robust analysis is performed using the updated model. This procedure is applied independently for all aeroelastic modes. The whole process makes it possible to capture aerodynamic uncertainty and predict the robust flutter boundary more accurately at various transonic Mach numbers by continuously updating the uncertainty magnitudes based on modal updation using WT test data. This type of successive robust flutter study will be useful in predicting  any instability a priori in aeroelastic systems caused by uncertainties within the flight envelope. Hence, this study will help to become more cautious when performing flight flutter testing in this region (e.g., use smaller steps when increasing the speed). The model updation techniques implemented in the present successive flutter prediction technique are discussed next.

Fig. 2
figure 2

Flowchart of successive robust flutter prediction process

Full size image

4.1 Uncertainty model updation

It becomes very important to estimate the magnitude of aerodynamic uncertainty particularly in transonic regime where the flow behaves nonlinearly. A small magnitude of uncertainty in parameters may not be able to capture the worst case flutter boundary from robust analysis, whereas a large magnitude of uncertainty in parameters will result in an over conservative estimation of the robust flutter boundary. The main idea of model updation is to estimate the uncertainty magnitude to a suitable level such that the predicted robust flutter boundary match close to experimental data in terms of frequency and damping of aeroelastic systems. Next, uncertainty model updation based on p- and g- updation methods are discussed.

4.1.1 \(\varvec{p}\)-updation method

Let \(p_{{WT}} = g_{{WT}} + ik_{{WT}}\) represents an eigenvalue of a certain aeroelastic mode of aeroelastic system obtained in wind tunnel test at some flow condition. The minimum aerodynamic uncertainty magnitude (\(\bar{\sigma }_{p}\)) is estimated such that the uncertain aeroelastic equation has an eigenvalue \(p_{{WT}}\) as:

$$\bar{\sigma }_{p} = \frac{1}{{\mu \left( {p_{{WT}} } \right)}}$$
(13)

where \(\mu \left( {p_{{WT}} } \right)\) is calculated in wind tunnel at the same flow condition. It can be noted from the singular value expression \(\mu \left( p \right)\) given in Eq. (12) that, the region of eigenvalue of the particular mode is expanded such that eigenvalue (\(p_{{WT}}\)) obtained in wind tunnel falls within the region. Note that, the magnitudes of uncertainty of all aerodynamic parameters are adjusted uniformly to update the model.

4.1.2 \(\varvec{g}\)-updation method

Sometimes, it is useful to update the model with respect to aeroelastic damping \(g_{{WT}}\) only instead of eigenvalue \(p_{{WT}}\) obtained in wind tunnel testing to avoid large uncertainty bound. This is important when a discrepancy in frequency cannot be captured by the uncertainty description. This type of updation is called as \(g\)-updation method where the model is updated against the aeroelastic damping, which is the critical parameter for aeroelastic stability. Here, the minimum magnitude of aerodynamic uncertainty (\(\bar{\sigma }_{g}\)) is estimated such that the uncertain aeroelastic equation has an eigenvalue with the real part \(g_{{WT}}\) as:

$$\bar{\sigma }_{g} = \frac{1}{{\mu _{k} \left( {g_{{WT}} } \right)}}$$
(14)

where the function \(\mu _{k} \left( g \right) = \mathop {\max }\limits_{k} \mu \left( {g + ik} \right)\). Here, the region of eigenvalue of the particular mode is expanded such that that the real part of eigenvalue (\(g_{{WT}}\)) obtained in wind tunnel falls within the region i.e. \(g = g_{{WT}}\). In this updation technique, the uncertain aeroelastic equation has eigenvalue \(p = g_{{WT}} + i\bar{k}\), where \(\bar{k}\) is the frequency that maximizes \(\mu \left( {g_{{WT}} + ik} \right)\).

Note that, the above model updation is performed for each mode, i.e. an individual uncertainty magnitude is estimated for each mode of interest. Here, the critical flutter mechanism is isolated in the model updation, which reduces the potential conservatism of robust analysis.

5 Numerical results

In this section, the robust flutter prediction techniques discussed in the preceding sections are employed to demonstrate robust stability of aeroelastic systems. First, the present structured singular value method (µ) is validated by studying robust stability of the Aerostructures Test Wing (ATW) model. Then, the applicability of the present successive robust flutter prediction technique is demonstrated by studying robust stability of the AGARD wing in transonic regime. The robust flutter boundary obtained from the present approach is also compared with the available WT data in transonic regime.

5.1 Aerostructure test wing model

In this section, the Aerostructures Test Wing (ATW) model [17] is considered to validate the present structured singular value (µ) method. The ATW is a wing and boom assembly with NACA 65A004 airfoil cross section. The root and tip chord lengths of the wing are 13.2 inch and 8.7 inch respectively with a span length of 18.0 inch. The wing is mounted with hollow boom at wing tip with length of 21.5 inch and diameter of 1 inch. The generalized structural matrices (mass, damping, stiffness) and generalized unsteady aerodynamic force matrix of the ATW model considered in this study are taken from Lind [17]. The structural matrices of the wing were computed from the structural dynamic model formulated by combining a theoretical mass distribution matrix with frequencies and modes shapes obtained from GVT. The generalized mass, damping and stiffness matrices describing the first three primary modes of the ATW model are given as [17]:

$$ \begin{aligned} M & = \left[ {\begin{array}{*{20}l} {0.0158} & 0 & 0 \\ 0 & {0.008} & 0 \\ 0 & 0 & {0.0003} \\ \end{array} } \right]\quad C = \left[ {\begin{array}{*{20}c} {0.0068} & 0 & 0 \\ 0 & {0.0079} & 0 \\ 0 & 0 & {0.001} \\ \end{array} } \right] \\ K & = \left[ {\begin{array}{*{20}c} {117.1808} & 0 & 0 \\ 0 & {150.4427} & 0 \\ 0 & 0 & {67.9218} \\ \end{array} } \right] \\ \end{aligned} $$

Since, Lind [17] used the state space model to represent uncertain aeroelastic equations, the generalized unsteady aerodynamics force matrix was expressed in the time domain using the Roger’s rational function approximation as:

$$Q\left( {ik} \right) = \left[ {\mathop \sum \limits_{{j = 0}}^{2} A_{j} \left( {ik} \right)^{j} + \mathop \sum \limits_{{j = 1}}^{2} A_{{j + 2}} \left( {\frac{{ik}}{{ik + \beta _{j} }}} \right)} \right]$$

where \(A_{0}\), \(A_{1}\) and \(A_{2}\) are the quasi-steady aerodynamic forces representing equivalent aerodynamic stiffness, aerodynamic damping and aerodynamic inertia forces respectively. \(A_{3}\) and \(A_{4}\) are unsteady aerodynamic forces consists of purely unsteady aerodynamic lags represented by Padé approximates. \(\beta _{j}\) and k denote the lag terms and reduced frequency respectively.

The aerodynamic force coefficient matrices for the ATW model at \(M = 0.8\) are given with respect to reference length L = 0.55 ft and the lag terms β1 = 0.1, β2 = 0.5 as [17]:

$$\begin{aligned} A_{0} & = \left[ {\begin{array}{*{20}l} {0.1562} & {0.4833} & { - 0.0912} \\ { - 0.0027} & {0.0504} & { - 0.0076} \\ { - 0.0499} & { - 0.1302} & {0.0357} \\ \end{array} } \right]\quad A_{1} = \left[ {\begin{array}{*{20}l} {0.6295} & {0.6959} & { - 0.1671} \\ {0.1605} & {0.3509} & { - 0.0507} \\ { - 0.1527} & { - 0.1397} & {0.0604} \\ \end{array} } \right] \\ A_{2} & = \left[ {\begin{array}{*{20}l} {0.2837} & {0.012} & { - 0.0418} \\ {0.1743} & {0.0437} & { - 0.0282} \\ { - 0.0427} & {0.009} & {0.0139} \\ \end{array} } \right]\quad A_{3} = \left[ {\begin{array}{*{20}l} {0.0007} & { - 0.0055} & {0.0013} \\ { - 0.0002} & {0.0018} & { - 0.0004} \\ { - 0.0003} & {0.0021} & { - 0.0005} \\ \end{array} } \right] \\ A_{4} & = \left[ {\begin{array}{*{20}l} { - 0.0366} & { - 0.0986} & {0.0284} \\ { - 0.004} & { - 0.0107} & {0.0031} \\ {0.0086} & {0.0231} & { - 0.0067} \\ \end{array} } \right] \\ \end{aligned}$$

Further, the expression for air density as a function of freestream velocity is given as [17]:

$$\rho = - 0.1287 + \left( {4.839 \times 10^{{ - 4}} } \right)U - \left( {6.1575 \times 10^{{ - 7}} } \right)U^{2} + \left( {2.6675 \times 10^{{ - 10}} } \right)U^{3}$$

This density model is valid for \(M = 0.8\) between the range of airspeeds 830 ft/s and 1050 ft/s.

First, the nominal flutter speed of the ATW model is studied using the standard p-k method at M = 0.8. Figure 3 shows the variation of nominal damping (\(2g/k\)) and frequency ratio (\(\omega /\omega _{\alpha }\)) for the first two aeroelastic modes at various flow velocities. Here, \(\omega _{\alpha }\) represents the first torsional frequency (Mode 2) of the ATW model. From the results, it can be observed that the aeroelastic mode 1 is the most critical, showing the lowest nominal damping with a decreasing trend. Here, the nominal flutter velocity of the wing is found to be 861.3 ft/s which is very close those obtained by Lind [17].

Fig. 3
figure 3

Variation of nominal damping (\(2g/k\)) and frequency ratio (\(\omega /\omega _{\alpha }\)) with flow velocity for the ATW model at M = 0.8

Full size image

In order to demonstrate the robust flutter speed of the ATW model, parametric uncertainty is introduced in the nominal aeroelastic equation. Here, the uncertainty is considered in the stiffness matrix only. In particular, 5% variation in the first bending mode (\(K_{{11}}\)), 10% variation in the first torsion mode (\(K_{{22}}\)), and 20% variation in the second bending mode (\(K_{{33}}\)) are considered [17]. Then, structured singular value (µ) analysis is conducted to estimate the robust flutter speed of the ATW model. Figure 4 shows the variation of robust damping (\(2g/k\)) (corresponding to p+) and frequency ratio (\(\omega /\omega _{\alpha }\)) of the first aeroelastic mode (flutter mode) at various flow velocities. From the results, it can be observed that the robust damping changes its sign (becomes positive) at much lower speed as compared to the nominal damping due to the presence of uncertainties. Here, the robust flutter speed of the ATW model is found to be 837.8 ft/s which matches well with the speed (838 ft/s) predicted by Lind [17].

Fig. 4
figure 4

Variation of robust damping (\(2g/k\)) and frequency ratio (\(\omega /\omega _{\alpha }\)) of Mode 1 (flutter mode) with flow velocity for the ATW model at M = 0.8

Full size image

5.2 AGARD wing model

In this section, the AGARD 444.6 wing model [25] is considered to demonstrate the applicability of the present successive robust flutter prediction technique in transonic flow regime. The geometric properties of the AGARD 445.6 wing is shown in Fig. 5. The wing has a NACA 65A004 airfoil cross section with aspect ratio 1.65, taper ratio 0.66 and quarter chord sweep angle of 45°. The orthotropic material properties of the wing used in the present analysis are taken as [25]:

$$\begin{aligned} E_{{xx}} ~ & = {{ 3}}.{\text{1511}}\;{\text{GPa}},\;E_{{yy}} = E_{{zz}} = {\text{ }}0.{\text{4162}}\;{\text{GPa}}, \\ \nu _{{xy}} & = \nu _{{yz}} = \nu _{{zx}} = 0.31\; \\ G_{{xy}} & = G_{{yz}} = G_{{zx}} = 0.{{4392}}\;{\text{GPa}},\;{\text{and}}\;\rho _{s} = {{381}}.{{98}}\;{\text{kg}}/{\text{m}}^{3} \\ \end{aligned}$$
Fig. 5
figure 5

Geometric properties of the AGARD 445.6 wing

Full size image

Various wind tunnel test models of the AGARD wing are given in [25]. In this study, a weakened wing model is considered to study the robust flutter boundary at different test conditions mentioned in Table 1.

Table 1 Test conditions
Full size table

5.2.1 Nominal flutter analysis

First, the nominal flutter boundary of the AGARD wing is investigated using the standard p–k method [26] at various flow conditions. Here, the nominal finite element structural model is based on a single layer orthotropic material consisting of three dimensional 20-node hexahedral and 15-node wedge elements. The nominal aerodynamic model of the wing is based on unsteady doublet-lattice method/ZONA51 with 15 aerodynamic boxes in spawise direction and 10 aerodynamic boxes in chordwise direction. The structural FE mesh (top view) and aerodynamic mesh used for the AGARD wing are shown in Fig. 6. The generalized aerodynamic force matrices are calculated for a set of reduced frequencies (k = 0.001, 0.05, 0.1, 0.2, 0.3, 0.5, 0.6, 0.8, 0.9, 1.0) at each Mach number. The nominal flutter boundary of the wing is calculated considering the first five fundamental structural modes. In this study, structural damping is not considered.

Fig. 6
figure 6

a Finite element structural mesh and b Aerodynamic mesh of the AGARD wing

Full size image

Figure 7 shows the variation of nominal damping (\(2g/k\)) and frequency ratio (\(\omega /\omega _{\alpha }\)) with flutter index (FI) for the first two aeroelastic modes at various Mach numbers. Here, flutter index (FI) is the non-dimensional flow velocity defined as \(FI = U/L\omega _{\alpha } \sqrt m\), where \(\omega _{\alpha }\) and \(m\) are the first torsional frequency (Mode 2) and mass ratio respectively. From the results, it can be observed that the aeroelastic mode 1 is found to be the most critical, showing the lowest damping with a decreasing trend at all Mach numbers.

Fig. 7
figure 7

Variation of nominal damping (\(2g/k\)) and frequency ratio (\(\omega /\omega _{\alpha }\)) with flutter index for the AGARD wing at various Mach numbers (a) M = 0.678, (b) M = 0.901, (c) M = 0.954 and (d) M = 1.141

Full size image

Figure 8 shows the comparison of nominal flutter index and flutter frequency ratio of the AGARD wing with experimental (WT) data at various Mach numbers. From the figure, it can be observed that nominal analysis shows higher flutter index as compared to the WT data. Here, the difference in flutter index is found to be 8% at M = 0.678 as compared to 17% and 28% at M = 0.954 and 1.072 respectively. It can also be noted that the nominal flutter index is non-conservative in comparison with the experimental data at all Mach numbers.

Fig. 8
figure 8

Comparison of nominal flutter index and flutter frequency ratio of the AGARD wing with WT data at various Mach numbers

Full size image

5.2.2 Initial robust flutter analysis

In this section, initial robust flutter analysis of the AGARD wing is carried out using the structured singular value (µ) method at various Mach numbers before WT tests and model updation procedure. Here, frequency domain based uncertainties are considered in both structural and aerodynamic parameters of the AGARD wing. For the estimation of structural uncertainty magnitude, the difference in natural frequencies between nominal analysis and GVT [25] is considered as shown in Table 2. This uncertainty is introduced as real, parametric uncertainty in the generalized stiffness matrix. For aerodynamic uncertainties, the generalized aerodynamic force matrix is considered and it is assumed to have 5% complex parametric uncertainty in all modes. Then, robust flutter analysis of the AGARD wing is conducted by considering two different uncertainties sets (1) uncertainty in structural parameters and (2) uncertainty in both structural and aerodynamic parameters.

Table 2 Comparison of natural frequencies between GVT and nominal analysis
Full size table

Figure 9 shows the robust flutter index (worst-case) and flutter frequency ratio of the AGARD wing at various Mach numbers considering structural uncertainties. The comparison of robust flutter boundary with nominal as well as experimental (WT) data at various Mach numbers is also shown in the figure. It can be observed that, due to structural uncertainties, the robust flutter indices have slightly moved towards the experimental flutter results for Mach numbers upto 0.9. However, the difference between the present robust flutter index and WT data remains high for Mach numbers greater than 0.9. This indicates that the structural uncertainties have no much influence on the robust flutter index for Mach numbers greater than 0.9. It can also be observed that the present robust flutter boundary is non-conservative with respect to the WT data at all Mach numbers.

Fig. 9
figure 9

Comparison of robust flutter index and flutter frequency ratio of the AGARD wing with WT data considering structural uncertainties

Full size image

Next, the robust flutter boundary of the AGARD wing is studied by introducing 5% aerodynamic uncertainty (initial assumption) in the generalized aerodynamic force matrix along with structural uncertainties. Figure 10 shows the comparison of robust flutter index (worst-case) and flutter frequency ratio with nominal as well as experimental (WT) data at various Mach numbers. It can be observed that by introducing aerodynamic uncertainty, the robust flutter indices have moved slightly lower than the WT flutter indices. Hence, the flutter boundary with both uncertainty levels indicates that the present results are conservative with respect to the WT data. This type of initial robust flutter analysis may be important when planning for flight flutter tests. Suppose, if the initial analysis indicates that some region of the flight envelope is not safe (from flutter) due to the presence of uncertainties, then testing in this region should be performed more cautiously. In the next section, an appropriate estimation of aerodynamic uncertainty magnitude based on comparison of eigenvalue/damping with WT data is discussed to predict accurate robust flutter boundary at different test conditions.

Fig. 10
figure 10

Comparison of robust flutter index and flutter frequency ratio of the AGARD wing with WT data considering structural and aerodynamic uncertainties

Full size image

5.2.3 Aerodynamic uncertainty model updation

In this study, the generalized aerodynamic force matrix is considered for modeling aerodynamic uncertainty. Here, the magnitude of aerodynamic uncertainty is estimated using the model updation technique based on g-updation method. First, at each test condition, the measured damping obtained from WT test is compared with nominal analysis for each aeroelastic mode. If the measured damping value is lower than the nominal damping value, a g-updation method is conducted to estimate the minimum magnitude of aerodynamic uncertainty required to match the nominal damping value with WT data. Here, the various WT tests given in Table 1 are divided into three sets. Set number 1 contains one test condition with Mach number 0.678, set number 2 contains two test conditions with Mach numbers 0.901, 0.954, and set number 3 contains two test conditions with Mach numbers 1.072, 1.141. Table 3 shows the minimum aerodynamic uncertainty magnitudes (\(\bar{\sigma }_{g}\)) estimated for mode 1 (flutter mode) using the g-updation method for each set of WT tests. This uncertainty is introduced as complex, parametric uncertainty in the generalized aerodynamic force matrix for successive robust flutter studies of the AGARD wing in transonic regime.

Table 3 Estimation of aerodynamic uncertainty magnitudes for the AGARD wing for different set of wind tunnel tests
Full size table

5.2.4 Successive robust flutter prediction analysis

The successive robust flutter prediction approach discussed in Sect. 4 is applied to study the robust flutter boundary of the AGARD wing at various test conditions in transonic regime. Here, the aerodynamic uncertainty model is successively updated with the uncertainty magnitudes given in Table 3, and updated robust flutter analyses are performed. Figure 11 shows the robust flutter index (worst-case) and flutter frequency ratio of the AGARD wing predicted using the present successive robust flutter prediction approach. In the figure, the robust flutter boundary predicted using the updated aerodynamic uncertainty magnitude w.r.to set number 1 (M = 0.678) is denoted by “Robust 1”. From the results, it can be observed that the predicted robust flutter boundary (Robust 1) w.r.to set number 1 is slightly lower than the WT flutter boundary at all Mach numbers. This indicates that “Robust 1” is conservative w.r.to the WT flutter boundary. The updated analysis also indicates that the wing is robustly stable for set number 2 and the next set of WT tests can be continued. Next, successive robust flutter analysis of the wing is conducted using the updated aerodynamic uncertainty magnitude w.r.to set number 2 and the corresponding robust flutter boundary is denoted by “Robust 2”. The updated analysis indicates that the predicted robust flutter boundary (Robust 2) is very close to the WT flutter boundary and conservative in nature. The analysis also indicates that the wing is robustly stable for set number 3 and the next set of WT tests can be conducted. Finally, successive robust flutter analysis of the wing is conducted using the updated aerodynamic uncertainty magnitude w.r.to set number 3 and the corresponding robust flutter boundary is denoted by “Robust 3”. The predicted robust flutter boundary (Robust 3) is found to be very close to the WT flutter boundary. Hence, the present successive approach gives a good estimation of transonic flutter boundary (transonic dip) a priori using the previous test data which can be extremely useful in deciding whether the next test should be conducted or it should be modified with respect to flow conditions. In the case of real aircraft, the flight envelope needs to be cleared through flight flutter test without reaching the flutter condition, and the above approach will be helpful in improving flight test efficiency with reduced number of flight test points, saving time and costs of flight flutter tests.

Fig. 11
figure 11

Estimation of robust flutter index and flutter frequency ratio of the AGARD wing considering structural and aerodynamic uncertainties

Full size image

6 Conclusions

In this work, a successive robust flutter prediction technique is developed by coupling nominal analysis, ground vibration test, wind tunnel test, uncertainty model updation and robust analysis using the structured singular value (µ) method to predict the worst flutter boundary of a swept back wing in transonic flow regime. Here, uncertainties in both structural parameters and unsteady aerodynamics are modelled in a LFT framework. The magnitudes of structural uncertainties are estimated based on the difference in natural frequencies between experiment (GVT) and nominal analysis. Further, the magnitudes of aerodynamic uncertainties are estimated using a model updation technique based on the μ method considering the difference in damping values between WT and nominal analysis. Finally, successive robust flutter analyses are performed to predict the robust flutter boundary of the swept back wing based on the obtained model validating aerodynamic uncertainty magnitudes. From the results, it can be observed that the model updation technique estimates a reasonable uncertainty magnitude for robust flutter analysis. Further, the successive robust flutter prediction approach gives a good estimate of transonic flutter boundary a priori using the updated aerodynamic uncertainty magnitude based on the previous test data. It can also be observed that the transonic dip predicted using the present approach is very close to the WT data. This indicates that the present successive flutter prediction technique will be useful when planning for flight flutter tests as it will help to clear flight envelope using subcritical (low speed) flight test data without reaching the flutter condition.