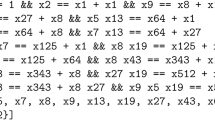Keywords

1 Introduction

A magic cube (or additive magic cube (AMC)) of order n is a three-dimensional array of \( n^{3} \) numbers in which the sum of n elements of each row, each column, each pillar, and each of the four space diagonals is the same [3]. The fixed sum is known as magic sum and is given by \( \frac{n(n^{3}+1)}{2} \). For instance, the first, second, and third layer of a third-order magic cube are, respectively, given below

$$ \left[ {\begin{array}{ccc} 10 &{} 26 &{} 6 \\ 24 &{} 1 &{} 17\\ 8 &{} 15 &{} 19 \\ \end{array} } \right] \;\;\;\;\; \left[ {\begin{array}{ccc} 23 &{} 3 &{} 16 \\ 7 &{} 14 &{} 21 \\ 12 &{} 25 &{} 5 \\ \end{array} } \right] \;\;\; \;\;\; \left[ {\begin{array}{ccc} 9 &{} 13 &{} 20 \\ 11 &{} 27 &{} 4 \\ 22 &{} 2 &{} 18 \\ \end{array} } \right] $$

A multiplicative magic cube (MMC) of order n is a three-dimensional array of \( n^{3} \) numbers with the property that the product of n elements along each row, column, pillar, and each space diagonal is the same [1]. The generation of multiplicative magic cubes opens a new direction to the application areas concerning image processing, cryptography, stenography, game theory, etc., which motivate the researchers for their study and utilization. Trenkler [4] has introduced the formula for the construction of an additive magic cube of odd, singly even, and doubly even order separately. Uko and Barron [2] has generalized the Trenkler’s formula for the magic cubes and derive sufficient conditions to generate regular magic cubes. They illustrate three new formulas for the construction of odd order magic cubes that differ from each other and from the magic cubes generated with Trenkler’s rule. Trenkler [5] has demonstrated several ways to construct additive and multiplicative magic cubes and provide the formula for the construction of multiplicative magic cubes from the existing additive magic cubes. He has also given an algorithm for constructing magic cubes [6]. In this paper, the various ways of constructing multiplicative magic cubes from the existing additive magic cubes of order n (\( n\ne 2 \)) have been introduced. Also, the Trenkler’s rules for constructing odd and doubly even order magic cubes have been modified.

2 Ways of Constructing Multiplicative Magic Cubes of Odd and Doubly Even Order

2.1 Power Method

Let \( A_{n}= \bigg \lbrace a_{n}(i,j,k)\; \bigg \vert \;\; 1\le i,j,k \le n \bigg \rbrace \) be an additive magic cube (AMC) and \( M_{n} \) be a multiplicative magic cube (MMC) of order n. Then the first formula for constructing magic cubes of order n with magic constant \( \sigma (M_{n})=2^{\frac{n(n^{3}+1)}{2}} \) is given as

$$ M_{n}= \bigg \lbrace m_{n}(i,j,k)=2^{a_{n}(i,j,k)}\; \bigg \vert \;\; 1\le i,j,k \le n \bigg \rbrace $$

By using this formula, one can obtain a multiplicative magic cube of smallest magic constant. But if there is no problem with the larger magic constant, then the above formula is generalized as below

$$ M_{n}= \bigg \lbrace m_{n}(i,j,k)=r^{a_{n}(i,j,k)}\; \bigg \vert \;\; 1\le i,j,k \le n \bigg \rbrace $$

where r is any real (or complex) number. It is a multiplicative magic cube with magic constant depicted below

$$ \sigma (M_{n})=r^{\frac{n(n^{3}+1)}{2}} =r^{\sigma (A_{n})} $$

The following table shows the effect of the elements of a multiplicative magic cube on changing the values of variable r:-

S.no.

Value of r

Effect on the elements of MMC

1

r is even number

All entries of the required MMC are even

2

r is odd number

All entries of the required MMC are odd

3

r is mixed type number

All the elements of the resulting MMC are mixed numbers

Example depicting the above formula is as below

Let \( A_{n} \) be the following AMC of order three with magic constant 42.

$$ \left[ {\begin{array}{ccc} 8 &{} 15 &{} 19 \\ 24 &{} 1 &{} 17\\ 10 &{} 26 &{} 6 \\ \end{array} } \right] \;\;\;\;\; \left[ {\begin{array}{ccc} 12 &{} 25 &{} 5\\ 7 &{} 14 &{} 21 \\ 23 &{} 3 &{} 16 \\ \end{array} } \right] \;\;\; \;\; \left[ {\begin{array}{ccc} 22 &{} 2 &{} 18 \\ 11 &{} 27 &{} 4 \\ 9 &{} 13 &{} 20 \\ \end{array} } \right] $$

                     Layer 1          Layer 2           Layer 3

Then the required MMC for \(r=3\) with magic sum \( 3^{42} \) is given by

$$ \left[ {\begin{array}{ccc} 3^{8} &{} 3^{15} &{} 3^{19} \\ 3^{24} &{} 3^{1} &{} 3^{17} \\ 3^{10} &{} 3^{26} &{} 3^{6} \\ \end{array} } \right] \;\;\;\;\; \left[ {\begin{array}{ccc} 3^{12} &{} 3^{25} &{} 3^{5} \\ 3^{7} &{} 3^{14} &{} 3^{21} \\ 3^{23} &{} 3^{3} &{} 3^{16} \\ \end{array} } \right] \;\;\; \;\; \left[ {\begin{array}{ccc} 3^{22} &{} 3^{2} &{} 3^{18} \\ 3^{11} &{} 3^{27} &{} 3^{4} \\ 3^{9} &{} 3^{13} &{} 3^{20} \\ \end{array} } \right] $$

                   Layer 1            Layer 2             Layer 3

The above formula can be modified by adding or subtracting 1,2,3,...,\( \sigma (A_{n}) \) from the powers of each entry of a MMC.

Thereby, \( M_{n}= \bigg \lbrace m_{n}(i,j,k)=r^{a_{n}(i,j,k)-\sigma (A_{n})}\; \bigg \vert \;\; 1\le i,j,k \le n \bigg \rbrace \) where r and \( \sigma (A_{n}) \) are any real number and magic sum of the additive magic cube \( A_{n} \) respectively. The addition of \(1,2,3,\ldots ,\sigma (A_{n})\) in the powers makes the magic constant larger whereas the subtraction decreases the value of the multiplicative magic constant.

2.2 Modified Trenkler’s Formula for MMC

Trenkler [5] has introduced formula for the construction of MMC of odd, singly even, and doubly even order by using his formulas for AMC. The formula for odd order MMC is represented as below

Let \( M_{n}= \bigg \lbrace m_{n}(i,j,k)=\alpha n^{2}+\beta n+\gamma +1 \; \bigg \vert \;\; 1\le i,j,k \le n \bigg \rbrace \) be an AMC of order n, for \( \alpha =(i-j+k-1)\;(mod\; n),\;\; \beta = (i-j-k)\;(mod\;n)\) and \( \gamma =(i+j+k-2)\;(mod\;n).\) Then, \( Q_{n}= \bigg \lbrace q_{n}(i,j,k)=2^{\alpha }\cdot 3^{\beta }\cdot 5^{\gamma }\; \bigg \vert \;\; 1\le i,j,k \le n \bigg \rbrace \) is the required MMC. If in the above formula 3 is replaced by \((2\beta +1)\) for \( \beta =1,2,...,n-1 \) and 5 by the numbers (\( 2n+2\gamma -1 \)) for \( \gamma =1,2,...,n-1 \) uniquely, then the MMC with smaller magic constant has been obtained.

Modification in the formula: By studying the above formula, we have analyzed that the expressions used for replacing 3 and 5 are not the fixed one and there is no restriction of such kind needed if we should not confine to the construction of normal magic cubes. So, it is possible to construct the multiplicative magic cube by using the formula

$$\begin{aligned} P_{n}= \bigg \lbrace p_{n}(i,j,k)=a^{u}\cdot b^{v}\cdot c^{w}\; \bigg \vert \;\; 1\le i,j,k \le n \bigg \rbrace \end{aligned}$$
(1)

where \( u=(i-j+k-1)\;(mod\; n),\;\; v= (i-j-k)\;(mod\;n)\), \( w=(i+j+k-2)\;(mod\;n) \) and a, b, c are any three distinct real numbers. By using this formula, the construction of a MMC of any order n (\( n\ne 2 \)) with magic constant \( \sigma (P_{n})=a^{\kappa }b^{\kappa }c^{\kappa }=(abc)^{\kappa }=(abc)^{\frac{n(n-1)}{2}} \) has been instigated, where \(\kappa \) is the sum of numbers \( 0,1,2,3,...,n-1 .\)

Example of the 4th order MMC is represented by putting \(a=2, b=4, c=6, n=4\), and \(k=6\) as under:

$$ \left[ {\begin{array}{cccc} 384 &{} 4608 &{} 3456 &{} 2 \\ 72 &{} 13824 &{} 128 &{} 96\\ 3456 &{} 2 &{} 384 &{} 4608\\ 128 &{} 96 &{} 72 &{} 13824 \\ \end{array} } \right] \;\;\; \left[ {\begin{array}{cccc} 1152 &{} 864 &{} 8 &{} 1536 \\ 55296 &{} 32 &{} 24 &{} 288 \\ 8 &{} 1536 &{} 1152 &{} 864 \\ 24 &{} 288 &{} 55296 &{} 32 \\ \end{array} } \right] $$

                        Layer 1                       Layer 2

$$ \left[ {\begin{array}{cccc} 3456 &{} 2 &{} 384 &{} 4608 \\ 128 &{} 96 &{} 72 &{} 13824 \\ 384 &{} 4608 &{} 3456 &{} 2 \\ 72 &{} 13824 &{} 128 &{} 96 \\ \end{array} } \right] \;\;\; \left[ {\begin{array}{cccc} 8 &{} 1536 &{} 1152 &{} 864 \\ 24 &{} 288 &{} 55296 &{} 32 \\ 1152 &{} 864 &{} 8 &{} 1536 \\ 55296 &{} 32 &{} 24 &{} 288 \\ \end{array} } \right] $$

                        Layer 3                       Layer 4

which is a MMC with magic constant = \( 2^{6}\cdot 4^{6}\cdot 6^{6}=12,230,590,464 \).

Moreover, in (1), if u, v, w take the values as given below then again the MMC is obtained.

$$\begin{aligned} u=\bigg \lbrace (i-j+k-1)-n\bigg [ \frac{i-j+k-1}{n} \bigg ] \bigg \rbrace \; (mod \;n) \end{aligned}$$
$$ v=\bigg \lbrace (i-j-k)-n\bigg [ \frac{i-j-k}{n} \bigg ] \bigg \rbrace \; (mod\; n)$$
$$ w=\bigg \lbrace (i+j+k-2)-n\bigg [ \frac{i+j+k-2}{n} \bigg ] \bigg \rbrace \; (mod\; n) $$

Here, [x] denotes the integer part of x and (mod n) gives the remainder after division by n. The magic cubes obtained by using this formula are not normal magic cubes. The behavior of elements of the MMC constructed above depends entirely on the value of the variables a, b, and c. This method has also been tested by taking different values of a, b, and c like \(a=2, b=3, c=4\) and \(a=3, b=4, c=7\), etc., and for MMC of various orders. See the table below for checking the different behavior of a, b, c and the entries of a MMC:

S.no.

Value of a

Value of b

Value of c

Order of MMC

Effect on magic constant

Effect on the elements of MMC

1

Even

Even

Even

Odd

Even

All \( p_{n}(i,j,k) \) are even except one entry when \( p_{n}(i,j,k)=1 \)

2

Even

Even

Even

Even

Even

All \( p_{n}(i,j,k) \) are only even

3

Odd

Odd

Odd

Odd/ Even

Odd

All \( p_{n}(i,j,k) \) are only odd

4

Even

Odd

Even

Odd

Even

All \( p_{n}(i,j,k) \) are either odd or even

5

Even

Odd

Even

Even

Even

All \( p_{n}(i,j,k) \) are only even

6

Odd

Even

Even

Odd

Even

All \( p_{n}(i,j,k) \) are either odd or even

7

Odd

Even

Even

Even

Even

All \( p_{n}(i,j,k) \) are only even

8

Even

Even

Odd

Odd

Even

All \( p_{n}(i,j,k) \) are either odd or even

9

Even

Even

Odd

Even

Even

All \( p_{n}(i,j,k) \) are only even

2.3 Modified Trenkler’s Formula for MMC of Doubly Even Order

Trenkler [5] has introduced the following formula for the construction of MMC of doubly even order, i.e., for \( n\equiv 0 \; (mod\; 4) \), from the AMC.

If \( M_{n}= \bigg \lbrace m_{n}(i,j,k) \; \bigg \vert \;\; 1\le i,j,k \le n \bigg \rbrace \) is the AMC, then its each entry \( m_{n}(i,j,k) \) is given as below

\( m_{n}(i,j,k)={\left\{ \begin{array}{ll} (i-1)n^{2}+(j-1)n+k &{}{\text {if}} \;\; \phi (i,j,k)=1 \\ (\bar{i}-1)n^{2}+(\bar{j}-1)n+\bar{k} &{}{\text {if}} \;\; \phi (i,j,k)=0 \end{array}\right. } \)

Then, its corresponding MMC, \( Q_{n}=\bigg \lbrace q_{n}(i,j,k) \; \bigg \vert \;\; 1\le i,j,k \le n \bigg \rbrace \) is defined as below

\( q_{n}(i,j,k)={\left\{ \begin{array}{ll} 2^{(i-1)}\cdot 3^{(j-1)}\cdot 5^{(k-1)} &{}{\text {if}} \;\; \phi (i,j,k)=1 \\ 2^{(\bar{i}-1)}\cdot 3^{(\bar{j}-1)}\cdot 5^{(\bar{k}-1)} &{}{\text {if}} \;\; \phi (i,j,k)=0 \end{array}\right. } \)

where \( \phi (i,j,k)=\bigg \lbrace i+\widetilde{i}+j+\widetilde{j}+k+\widetilde{k} \bigg \rbrace (mod\;2) \) and \( \bar{x}=n+1-x \)

\( \widetilde{x}={\left\{ \begin{array}{ll} 0 &{}{\text {for}} \;\; 1\le x\le \frac{n}{2} \\ 1 &{}{\text {for}} \;\; \frac{n}{2} < x\le n \end{array}\right. } \)

Modification in the formula: Let \( A_{n}=\bigg \lbrace a_{n}(i,j,k) \; \bigg \vert \;\; 1\le i,j,k \le n \bigg \rbrace \) be an AMC of order n, \( n\equiv 0\;(mod\; 4) \), where each entry is defined as

\( a_{n}(i,j,k)={\left\{ \begin{array}{ll} (k-1)n^{2}+(j-1)n+i &{}{\text {if}} \;\; f(i,j,k)=1\\ (n-k)n^{2}+(n-j)n+(n-i)+1 &{}{\text {if}} \;\; f(i,j,k)=0 \end{array}\right. } \)

$$\begin{aligned} {\text {and}} \;\; f(i,j,k)=\bigg \lbrace i+\bigg [ \frac{2(i-1)}{n} \bigg ] + j+\bigg [ \frac{2(j-1)}{n} \bigg ]+k+\bigg [ \frac{2(k-1)}{n} \bigg ] \bigg \rbrace \;(mod\;2) \end{aligned}$$
(2)

Here, [x] denotes the integer part of x. Then the resulting MMC, \( P_{n}=\bigg \lbrace p_{n}(i,j,k) \; \bigg \vert \;\; 1\le i,j,k \le n \bigg \rbrace \) of order \( n \equiv 0\;(mod\; 4)\) is demonstrated by the following formula:

\( p_{n}(i,j,k)={\left\{ \begin{array}{ll} u^{(k-1)}\cdot v^{(j-1)}\cdot w^{i} &{}{\text {if}} \;\; f(i,j,k)=1\\ u^{(n-k)}\cdot v^{(n-j)}\cdot w^{(n-i)} &{}{\text {if}} \;\; f(i,j,k)=0 \end{array}\right. } \)

and the value of the function f(i, j, k) is same as given in equation (3). Also, u, v, and w are any three distinct real numbers. If all the three variables u, v, and w are odd, then we get the MMC with only odd elements and having odd magic constant. Similarly, if u, v, and w are even, then all the entries of MMC are even including its magic constant. Moreover, if one or two of u, v and w is/ are taken to be even and the remaining as odd numbers, then the mixture of both odd as well as even numbers as the entries of MMC of order \( n\equiv 0\;(mod\; 4) .\)

Example of \( P_{4} \) on putting \(u=3,\; v=5\), and \(w=7\) with magic constant \( (3\cdot 5\cdot 7)^{6}=65,664,686,390,625 \) is as below

$$ \left[ {\begin{array}{cccc} 7 &{} 231525 &{} 46305 &{} 875 \\ 165375 &{} 245 &{} 1225 &{} 1323\\ 23625 &{} 1715 &{} 8575 &{} 189 \\ 2401 &{} 675 &{} 135 &{} 300125 \\ \end{array} } \right] \;\;\;\; \left[ {\begin{array}{cccc} 385875 &{} 105 &{} 525 &{} 3087 \\ 147 &{} 11025 &{} 2205 &{} 18375\\ 1029 &{} 1575 &{} 315 &{} 128625\\ 1125 &{} 36015 &{} 180075 &{} 9 \\ \end{array} } \right] $$

                    Layer 1                              Layer 2

$$ \left[ {\begin{array}{cccc} 128625 &{} 315 &{} 1575 &{} 1029 \\ 441 &{} 3675 &{} 735 &{} 55125\\ 3087 &{} 525 &{} 105 &{} 385875\\ 375 &{} 108045 &{} 540225 &{} 3 \\ \end{array} } \right] \;\;\;\; \left[ {\begin{array}{cccc} 189 &{} 8575 &{} 1715 &{} 23625 \\ 6125 &{} 6615 &{} 33075 &{} 49\\ 875 &{} 46305 &{} 231525 &{} 7\\ 64827 &{} 25 &{} 5 &{} 8103375 \\ \end{array} } \right] $$

Layer 3 Layer 4

2.4 Power Method for MMC of Order \( n\equiv 0\;(mod\;4) \)

In this method, the construction of MMC of order \( n\equiv 0\;(mod\;4)\) from the existing AMC of order \( n\equiv 0\;(mod\;4) \), defined by the equation (2) and (3), has been represented using the following formula:

If \( R_{n}=\bigg \lbrace r_{n}(i,j,k) \; \bigg \vert \;\; 1\le i,j,k \le n \bigg \rbrace \) is the required MMC, then its all elements \( r_{n}(i,j,k) \) are defined by

\( r_{n}(i,j,k)={\left\{ \begin{array}{ll} m^{(k-1)n^{2}+(j-1)n+i} &{}{\text {if}} \;\; g(i,j,k)=1\\ m^{(n-k)n^{2}+(n-j)n+(n-i)+1} &{}{\text {if}} \;\; g(i,j,k)=0 \end{array}\right. } \)

where g(i, j, k) is equal to the function f(i, j, k) as given by the equation (3). The magic constant of MMC is

$$ \sigma (R_{n})=m^{\frac{n(n^{3}+1)}{2}} $$

Example of \( R_{n} \) with magic constant \(2^{130}\) is depicted as below by substituting \(m=2\) in the above formula in (4),

$$ \left[ {\begin{array}{cccc} 2^{1} &{} 2^{60} &{} 2^{56} &{} 2^{13} \\ 2^{63} &{} 2^{6} &{} 2^{10} &{} 2^{51}\\ 2^{62} &{} 2^{7} &{} 2^{11} &{} 2^{50}\\ 2^{4} &{} 2^{57} &{} 2^{53} &{} 2^{16} \\ \end{array} } \right] \;\;\;\;\;\; \left[ {\begin{array}{cccc} 2^{48} &{} 2^{21} &{} 2^{25} &{} 2^{36} \\ 2^{18} &{} 2^{43} &{} 2^{39} &{} 2^{30}\\ 2^{19} &{} 2^{42} &{} 2^{38} &{} 2^{31}\\ 2^{45} &{} 2^{24} &{} 2^{28} &{} 2^{33} \\ \end{array} } \right] $$

                          Layer 1                  Layer 2

$$ \left[ {\begin{array}{cccc} 2^{32} &{} 2^{37} &{} 2^{41} &{} 2^{20} \\ 2^{34} &{} 2^{27} &{} 2^{23} &{} 2^{46}\\ 2^{35} &{} 2^{26} &{} 2^{22} &{} 2^{47}\\ 2^{29} &{} 2^{40} &{} 2^{44} &{} 2^{17}\\ \end{array} } \right] \;\;\;\;\;\; \left[ {\begin{array}{cccc} 2^{49} &{} 2^{12} &{} 2^{8} &{} 2^{61} \\ 2^{15} &{} 2^{54} &{} 2^{58} &{} 2^{3}\\ 2^{14} &{} 2^{55} &{} 2^{59} &{} 2^{2}\\ 2^{52} &{} 2^{9} &{} 2^{5} &{} 2^{64} \\ \end{array} } \right] $$

Layer 3 Layer 4

3 Conclusion

In this paper, it can be concluded that there are various ways of constructing multiplicative magic cubes of several orders from the existing additive magic cubes. It is also explained very well that the change in behavior of the elements of MMC including its magic constant on making some changes in the variables used in the construction formulas. Hence, it becomes possible to obtain a MMC consisting of either even or odd or composite numbers as its elements.

Conflict of interests The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.