Virtual Element Methods for Optimal Control Problems Governed by Elliptic Interface Problems

Abstract

A conforming Virtual Element Method along with a variational discretization concept for solving the optimization problem governed by an elliptic interface problem is presented. Elements with small edges and hanging nodes occur naturally while numerically solving interface problems. Conforming Finite Element Methods cannot handle these difficulties naturally. VEM has the attractive feature that it can tackle hanging nodes and is even robust with respect to small edges. We use these features of VEM to design a method that can tackle these difficulties naturally. The state, adjoint and control estimates have been derived in suitable norms. Numerical results verify our theoretical findings and show the robustness and flexibility of the proposed method.

1 Introduction

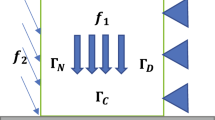
There are numerous applications of interface problems in applied sciences and engineering. For example, in material sciences, problems involve discontinuous material coefficients across the interface, such as conductivity in heat transfer, permeability in porous media flow. Optimizing these physical processes lead to optimal control problems governed by partial differential equations (PDEs) with interfaces. To numerically solve these problems, one of the standard practices is to use a finite element method (FEM) (cf. [4, 7]), which has element boundaries coincident with the interface (see [2] and references therein). These methods are categorized as fitted methods. In this group of methods, the meshing of the domain depends on the location of the interface. One faces several difficulties in generating a mesh that resolves the interface. For example, aligning the element edges coincidentally at the interface is not trivial when meshing domains on either side of the interface. The relaxation of the edge alignment condition on the mesh can naturally lead to meshes that have arbitrarily small edges. The attractive properties of VEM make it robust under small edges and allow it to handle hanging nodes; we present a conforming virtual element method (VEM) along with the variational discretization concept presented in [3] for the discretization of the continuous optimization problem governed by an elliptic problem with a polygonal interface which can tackle these difficulties naturally. Our approach allows for greater flexibility in meshing since we can use different meshes on either side of the interface (see Fig. 1). Moreover, we also show that using the same feature of VEM, we can generate background fitted meshes independent of the location of the interface (see Fig. 1). Thus, it is easier to generate meshes as compared to conforming FEM. Our numerical experiments show that the original linear VEM stabilization presented in [5] will generate small but visible oscillations in the solution (see Fig. 2). This motivates us to use the boundary stabilization presented in [6], which smoothens these oscillations at the interface (see Fig. 3). The model problem is to find the distributed control z and the associated state $y = y(z)$ satisfying

$$\begin{aligned} \min _{z \in Z_{ad}} J(y,z) := \frac{1}{2} \left\| y - y_d\right\| ^2_{0,\varOmega } + \frac{\lambda }{2} \left\| z\right\| ^2_{0,\varOmega }, \end{aligned}$$

(1)

subject to

$$\begin{aligned} - \nabla \cdot (\beta \; \nabla y) = z + f, \;\;\;\; \text{ in } \; \; \varOmega , \quad&\nonumber \\ y = 0, \;\;\;\;~~~~~ \text{ on } \;\; \partial \varOmega , \quad&\\ \left[ y\right] = 0, \left[ \beta \frac{\partial y}{\partial {\textbf {n}}}\right] = g \;\; \text{ on } \; \varGamma , \,\,&\nonumber \\ z_a \le z \le z_b\;\;\;\;\; \text{ for } \text{ a.e. }\; \text{ in }\; \varOmega .&\nonumber \end{aligned}$$

(2)

We define the jump of a function $\zeta$ across $\varGamma$ by $\left[ \zeta \right] (x) := \zeta _1({\textbf {x}}) - \zeta _2({\textbf {x}}), \; \forall \; {\textbf {x}} \in \varGamma$, where $\zeta _1$ and $\zeta _2$ are restrictions of $\zeta$ on $\varOmega _1$ and $\varOmega _2$, respectively, n denotes the unit outward normal vector to the interface. The coefficient $\beta$ is assumed to be piecewise constant and positive and is defined as $\beta _1$ in $\varOmega _1$ and $\beta _2$ in $\varOmega _2$. Let $z_a, z_b \in \mathbb {R}$ with $z_a < z_b$, $y_d \in L^2(\varOmega )$ is the desired state and $\lambda > 0$ is the regularization or the penalty parameter. The admissible set of controls is defined as follows:

$$\begin{aligned} Z_{ad} := \left\{ z \in L^2(\varOmega ) : z_a \le z \le z_b \;\; \text{ a.e. } \text{ in } \;\; \varOmega \right\} . \end{aligned}$$

Define the space $X := H^1(\varOmega ) \cap H^2(\varOmega _1) \cap H^2(\varOmega _2)$ equipped with the norm

$$\begin{aligned} \left\| \zeta \right\| _{X} = \left\| \zeta \right\| _{1,\varOmega } + \left\| \zeta \right\| _{2,\varOmega _1} + \left\| \zeta \right\| _{2,\varOmega _2}, \;\; \forall \;\; \zeta \in X. \end{aligned}$$

Sobolev embedding theorem dictates that for any $\zeta \in X$, we have $\zeta \in W^{1,p}(\varOmega )$ for all $p > 2$. The regularity of the state equation (2) is given by the following Lemma (see Theorem 2.1, [2])

Lemma 1

Assuming $f, z \in L^2(\varOmega )$ and $g \in H^{1/2}(\varGamma )$. We have that the problem (2) has a unique solution $y \in X$ which satisfies

$$\begin{aligned}\left\| y\right\| _{X} \lesssim \left\| f\right\| _{0,\varOmega } + \left\| z\right\| _{0,\varOmega } + \left\| g\right\| _{1/2,\varGamma }\end{aligned}$$

Using the standard techniques employed in PDE optimal control, we can find that the optimal control satisfies the following variational inequality also known as the first-order necessary optimality condition

$$\begin{aligned}(\lambda z + p, w - z) \ge 0, \; \forall \; w \in Z_{ad},\end{aligned}$$

where p is the adjoint variable or the co-state variable and solves the subsequent adjoint equation

$$\begin{aligned} - \nabla \cdot (\beta \; \nabla p)= & {} y - y_d, \;\;\;\;\;\;\;\qquad \text{ in } \;\; \varOmega , \nonumber \\ p= & {} 0, \;\;\;\;\;\;~~~~~~~ \qquad \text{ on } \;\; \partial \varOmega , \nonumber \\ \left[ p\right] = 0,{} & {} \;\;\; \left[ \beta \frac{\partial p}{\partial {\textbf {n}}}\right] = 0 \;\;\;\; \text{ on } \; \varGamma . \nonumber \end{aligned}$$

A unique $p \in X$ exists, which solves the adjoint equation follows from (Theorem 2.1, [2]). We can rewrite the first-order necessary optimality condition as a pointwise projection formula

$$\begin{aligned} z = \mathcal {P}_{Z_{ad}} \left( -\frac{1}{\lambda } p\right) .\end{aligned}$$

If we introduce a control-to-state map S defined as $Sz = y$, then the problem (1)–(2) reduces to

$$\begin{aligned} \min _{z \in Z_{ad}} j(z) = \min _{z \in Z_{ad}} J(Sz,z),\end{aligned}$$

then the optimal control satisfies the following coercivity condition

$$\begin{aligned} {} j''(z)(w,w) \ge \lambda \left\| w\right\| ^2_{L^2(\varOmega )}, \;\; \forall \;\; w \in Z:=L^2(\varOmega ). \end{aligned}$$

(3)

Define $a(\cdot ,\cdot ) : H^1(\varOmega ) \times H^1(\varOmega ) \longrightarrow \mathbb {R}$ such that $a(\zeta ,\eta ) := \int _{\varOmega } \beta \; \nabla \zeta \cdot \nabla \eta$. Now the optimality system corresponding to (1)–(2) is to find $(y,p,z) \in V (:= H_0^1(\varOmega )) \times V \times Z_{ad}$ such that

$$\begin{aligned} a(y,v)= & {} (z + f,v) + \langle {g,v\rangle }_{\varGamma }, \;\; \forall \;\; v \in V \end{aligned}$$

(4)

$$\begin{aligned} a(p,q)= & {} (y - y_d,q), \;\; \forall \;\; q \in V \end{aligned}$$

(5)

$$\begin{aligned} (\lambda z + p, w - z)\ge & {} 0, \;\;\;\; \forall \;\;\; w \in Z_{ad}. \end{aligned}$$

(6)

We adopt the standard Sobolev space notations. Additionally, we have the notation $a \lesssim b$, which represents that a is less than or equal to some positive constant (independent of the mesh parameter) times b. An outline of the manuscript is as follows. In Sect. 2, a VEM discretization of the continuous problem is proposed. In Sect. 3, we give the convergence analysis for the proposed scheme under suitable norms. Afterward, in Sect. 4, we conduct two numerical experiments to analyse the behaviour of the solution and verify the theoretical results proved in Sect. 3.

2 Discrete Formulation

Let $\mathcal {T}_h$ be the triangulation of $\varOmega$ into simple polygons K with discretization parameter $h := \max _{K \in \tau _h} h_K \in \left( 0,1\right]$, where $h_K$ is the diameter of K. $\varGamma$ is the polygonal interface which is resolved by $\mathcal {T}_h$. $\mathcal {T}^*_h := \left\{ K \in \tau _h : K \cap \varGamma \ne \emptyset \right\}$ is the set of interface polygons. Then $\mathcal {T}_h$ satisfies:

• (A1) $\bar{\varOmega } = \cup _{K \in \mathcal {T}_h} K$.

• (A2) If $K_1, K_2 \in \mathcal {T}_h$ are two distinct polygons, then either their intersection is empty or they share a common vertex or edge.

• (A3) Each polygon either lies in $\varOmega _1$ or $\varOmega _2$ and has at most two vertices lying on the interface.

Moreover, we introduce the following relaxed assumptions which allow small edges on any polygon $K \in \tau _h$,

• (A4) Any $K \in \mathcal {T}_h$ is star-shaped w.r.t. disc $\mathbb {B}_K \subset K$ with radius $\rho _K h_K$ where, and there exists $\rho \in (0,1)$, such that $\rho _K \ge \rho$ for all $K \in \mathcal {T}_h$.

• (A5) There exists $N \in \mathbb {Z}^+$ independent of the mesh parameter such that $|E_K| \le N$, where $E_K$ denotes the set of all edges of K.

2.1 Discretization of State and Adjoint Equations

Following [1], the linear local virtual element space $V(K) \subset H^1(K)$ is defined as follows:

$$\begin{aligned} V(K):= & {} \left\{ \zeta \in H^1(K) : \zeta |_{\partial K} \in \mathbb {P}_1(\partial K), \; - \Delta \zeta \in \mathbb {P}_1(K), \right. \nonumber \\{} & {} ~~~~~~~~~~~~~\;\;\;\;\;\;\;\;\;\;\;\;\; ~~~~~\left. (\zeta - \varPi ^{\nabla }_{1,K} \zeta , q)_K = 0 \; \forall \; q \in \mathcal {M}^*_0(K) \cup \mathcal {M}^*_1(K)\right\} . \nonumber \end{aligned}$$

where

$$\begin{aligned}\mathcal {M}^*_r(K) := \left\{ m | m = \left( \frac{x - x_K}{h_K}\right) ^{{\textbf {s}}} \; \text{ for } \; {\textbf {s}} \in \mathbb {N}^2 \; \text{ with } \; |{\textbf {s}}| = r \right\} .\end{aligned}$$

We denote by $x_K$ the centroid of K, the space of all polynomials of degree $\le 1$ is denoted by $\mathbb {P}_{1}(K)$. The degrees of freedom of V(K) consist of the values of v at the vertices of K. Ritz projection operator $\varPi ^{\nabla }_{1,K} : H^1(K) \longrightarrow \mathbb {P}_1(K)$ satisfies

$$\begin{aligned} (\!(\varPi ^{\nabla }_{1,K} \zeta , q)\!) = (\!(\zeta ,q)\!) \;\; \forall \; q \in \mathbb {P}_1(K), \end{aligned}$$

(7)

where the inner product $(\!(\zeta ,w)\!) := (\nabla \zeta , \nabla w) + (\int _{\partial K} \zeta \; ds) (\int _{\partial K} w \; ds)$. Moreover, (7) is equivalent to

$$\begin{aligned} \int _{K} \nabla (\varPi ^{\nabla }_{1,K} \zeta ) \cdot \nabla q \; dx = \int _{K} \nabla \zeta \cdot \nabla q \; dx;\int _{\partial K} \varPi ^{\nabla }_{1,K} \zeta \; ds = \int _{\partial K} \zeta \; ds. \end{aligned}$$

(8)

$\varPi ^0_{1,K}$ is the projection from $L^2(K)$ onto $\mathbb {P}_1(K)$. $\mathcal {P}_h^1$ represents the space of discontinuous piecewise polynomials of degree $\le 1$. Then the global projection operators $\varPi ^{\nabla }_{1,h} : H^1(\varOmega ) \longrightarrow \mathcal {P}^1_h, \;\; \varPi ^{0}_{1,h} : L^2(\varOmega ) \longrightarrow \mathcal {P}^1_h,$ are understood in the sense of their local counterparts as

$$\begin{aligned}(\varPi ^{\nabla }_{1,h} v)|_{K} = \varPi ^{\nabla }_{1,K} (v|_K), \;\;\;\; (\varPi ^{0}_{1,h} v)|_{K} = \varPi ^{0}_{1,K} (v|_K).\end{aligned}$$

We glue to the local virtual element spaces to write the following global virtual element space

$$\begin{aligned}V_h = \{ \zeta \in H_0^1(\varOmega ) : \zeta |_K \in V(K) \;\; \forall \; K \in \mathcal {T}_h\}. \end{aligned}$$

The mesh dependent norm is defined as $|v|_{h,1} := \left( \sum _{K \in \tau _h} |v|^2_{H^1(K)}\right) ^{\frac{1}{2}}$. We define the discrete bilinear form as follows:

$$\begin{aligned} a_h(w,v)= & {} \sum _{K \in \tau _h} a_h^K(w,v) \nonumber \\= & {} \sum _{K \in \tau _h} \left[ a^K(\varPi ^{\nabla }_{1,K} w, \varPi ^{\nabla }_{1,K} v) + S^K(w - \varPi ^{\nabla }_{1,K} w,\; v - \varPi ^{\nabla }_{1,K} v)\right] , \\ a^K(w,v)= & {} \int _{K} \beta |_K \nabla w \cdot \nabla v \; dx, \nonumber \end{aligned}$$

(9)

Note that $supp(\beta - \beta |_K) \cap K = \{0\}$ for all $K \in \tau _h$. The two choices of local stabilization bilinear forms are defined as follows:

$$\begin{aligned} S^K(\zeta ,v) = {\left\{ \begin{array}{ll} S_1^K(\zeta ,v) := \sum _{\varphi \in \mathcal {B}_{\partial K}} \zeta (\varphi ) v(\varphi ), \\ S_2^K(\zeta ,v) := h_K \left( \partial \zeta / \partial s, \partial v / \partial s \right) _{0,\partial K}. \nonumber \end{array}\right. } \end{aligned}$$

Here, $\mathcal {B}_{\partial K}$ denotes the set of nodes of K. and $\partial \zeta / \partial s$ is the tangential derivative of $\zeta$ along $\partial K$. From ((3.55) in [1]), we have for all $u \in V(K)$ the following inequality

$$\begin{aligned} |u|^2_{1,K} \lesssim |\varPi ^{\nabla }_{1,K} u|^2_{1,K} + h_K \left\| \partial (u - \varPi ^{\nabla }_{1,K} u) / \partial s\right\| ^2_{0,\partial K}, \end{aligned}$$

(10)

with a hidden constant depending on $\rho _K$ and the degree of the polynomial. Also from ((3.56) in [1]) for all $u \in V(K)$, we have

$$\begin{aligned} |u|^2_{1,K} \lesssim |\varPi ^{\nabla }_{1,K} u|^2_{1,K} + \ln \left( 1 + \tau _K \right) \left\| u-\varPi ^{\nabla }_{1,K} u\right\| ^2_{\infty ,\partial K)}, \end{aligned}$$

(11)

with the constant depending on $|E_K|$ along with $\rho _K$ and the degree of the polynomial. Here, $\tau _K := \max _{e \in E_K} h_e / \min _{e \in E_K} h_e$. On combining (10) and (11), we get the following stability estimate for $a_h(\cdot ,\cdot )$,

$$\begin{aligned} |v|^2_{H^1(\varOmega )} \lesssim \alpha _h a_h(v,v) \;\; \forall \; v \in V_h, \end{aligned}$$

(12)

where

$$\begin{aligned} \alpha _h = {\left\{ \begin{array}{ll} \ln \left( 1 + \max _{K \in \tau _h} \tau _K\right) \;\; \text{ if } \;\; S^K(\cdot ,\cdot ) = S^K_1(\cdot ,\cdot ), \\ ~~~~~~~~~~~~~1 ~~~~~~~~~~~~~~~~~~~~~~~ \text{ if } \;\; S^K(\cdot ,\cdot ) = S_2^K(\cdot ,\cdot ). \end{array}\right. } \end{aligned}$$

(13)

The source term is discretized using $\varPi ^0_{1,h}$ operator as follows

$$\begin{aligned}(\varPi ^0_{1,h} f, v) := (f, \varPi ^0_{1,h} v) = \sum _{K \in \tau _h} \int _{K} f \varPi ^0_{1,K} v_h. \end{aligned}$$

2.2 Variational Discretization

In this approach, we discretize the control variable implicitly. Thus the discrete admissible set of controls coincides with $Z_{ad}$. Following the optimize-then-discretize approach, we can write the discrete optimality system as follows: Find $(y_h,p_h,z_h) \in V_h \times V_h \times Z_{ad}$ such that

$$\begin{aligned} a_h(y_h,v_h)= & {} \left( \varPi ^0_{1,h} (f + z_h), v_h\right) + \langle {g,v_h\rangle }_{\varGamma } \;\; \forall \; v_h \in V_h \end{aligned}$$

(14)

$$\begin{aligned} a_h(p_h,q_h)= & {} \left( \varPi ^0_{1,h} (y_h - y_d), q_h\right) \;\; \forall \; q_h \in V_h \end{aligned}$$

(15)

$$\begin{aligned} \left( \lambda z_h + \varPi ^0_{1,h} p_h, \tilde{w} - z_h\right)\ge & {} 0 \;\; \forall \; \tilde{w} \in Z_{ad}. \end{aligned}$$

(16)

The discrete variational inequality (16) is rewritten as a discrete projection formula

$$\begin{aligned} u_h|_K = \mathcal {P}_{U_{ad}} \left( -\frac{1}{\lambda } (\varPi ^0_{1,h} p_h)|_K \right) \;\; \forall \; K \in \tau _h. \end{aligned}$$

(17)

The stability estimate (12) implies that the discrete state Eq. (14) and discrete adjoint Eq. (15) are well-posed.

3 Convergence Analysis

This section is dedicated to deriving the error estimates for the state, adjoint and control variable under variational discretization of control. We begin by considering the following auxiliary equations: For any arbitrary control $\tilde{z} \in L^2(\varOmega )$, let $y_h(\tilde{z}) \in V_h$ solve

$$\begin{aligned} a_h(y_h(\tilde{z}), v_h) = (\varPi ^0_{1,h}(\tilde{z} + f), v_h) + \langle { g,v_h \rangle }_{\varGamma }\;\; \forall \;\; v_h \in V_h, \end{aligned}$$

(18)

and for any arbitrary $\tilde{y} \in H^1_0(\varOmega )$, let $p_h(\tilde{y}) \in V_h$ solve

$$\begin{aligned} a_h(q_h,p_h(\tilde{y})) = (\varPi ^0_{1,h}(\tilde{y}-y_d),q_h) \;\; \forall \; q_h \in V_h. \end{aligned}$$

(19)

Let us define the following notations $y_h := y_h(z_h)$, $p_h := p_h(y_h)$. For the subsequent analysis we will need the following Lemma.

Lemma 2

For any arbitrary $\tilde{z}_i \in L^2(\varOmega )$, and $\tilde{y}_i \in H^1_0(\varOmega )$, let $y_h(\tilde{z}_i)$ and $p_h(\tilde{y}_i)$, $i = 1,2$ solve (18) and (19), respectively. Then

$$\begin{aligned} |y_h(\tilde{z}_1) - y_h(\tilde{z}_2)|_{1,\varOmega }\lesssim & {} \alpha _h \left\| \tilde{z}_1 - \tilde{z}_2\right\| _{0,\varOmega }, \nonumber \\ |p_h(\tilde{y}_1) - p_h(\tilde{y}_2)|_{1,\varOmega }\lesssim & {} \alpha _h \left\| \tilde{y}_1 - \tilde{y}_2\right\| _{0,\varOmega }, \nonumber \end{aligned}$$

where $\alpha _h$ is as defined in (13).

Proof

Test (18) with $y_h(\tilde{z}_1)$ and $y_h(\tilde{z}_2)$ to get,

$$\begin{aligned}a_h(y_h(\tilde{z}_1) - y_h(\tilde{z}_2), v_h) = (\varPi ^0_{1,h}(\tilde{z}_1 - \tilde{z}_2), v_h). \end{aligned}$$

Now using the stability estimate (12) along with $v_h = y_h(\tilde{z}_1) - y_h(\tilde{z}_2)$, the stability of $\varPi ^0_{1,K}$ operator and the consequence of Poincaré-Friedrichs inequality we have,

$$\begin{aligned} |y_h(\tilde{z}_1)-y_h(\tilde{z}_2)|^2_{1,\varOmega }\lesssim & {} \alpha _h \left\| \tilde{z}_1-\tilde{z}_2\right\| _{0,\varOmega } \left\| \varPi ^0_{1,h} (y_h(\tilde{z}_1)-y_h(\tilde{z}_2))\right\| _{0,\varOmega }, \nonumber \\\lesssim & {} \alpha _h \left\| \tilde{z}_1-\tilde{z}_2\right\| _{0,\varOmega } \sum _{K \in \tau _h} \left\| \varPi ^0_{1,K} (y_h(\tilde{z}_1)-y_h(\tilde{z}_2))\right\| _{0,K}, \nonumber \\\lesssim & {} \alpha _h \left\| \tilde{z}_1-\tilde{z}_2\right\| _{0,\varOmega } \sum _{K \in \tau _h} \left\| y_h(\tilde{z}_1)-y_h(\tilde{z}_2)\right\| _{0,K}, \nonumber \\\lesssim & {} \alpha _h \left\| \tilde{z}_1-\tilde{z}_2\right\| _{0,\varOmega } |y_h(\tilde{z}_1)-y_h(\tilde{z}_2)|_{1,\varOmega }, \nonumber \\\lesssim & {} \alpha _h \left\| \tilde{z}_1-\tilde{z}_2\right\| _{0,\varOmega }. \nonumber \end{aligned}$$

Similarly, test (19) with $p_h(\tilde{y}_1)$ and $p_h(\tilde{y}_2)$ along with $q_h = p_h(\tilde{y}_1)-p_h(\tilde{y}_2)$ and follow the same steps to get the second desired inequality. $\square$

Estimates corresponding to the auxiliary problems (18) and (19) can be proved using the techniques of [1] and [2] in the following Lemma.

Lemma 3

Let $y(\tilde{z})$ and $y_h(\tilde{z})$ be the solutions of (4) and (18), respectively. Let $p(\tilde{y})$ and $p_h(\tilde{y})$ be the solutions of (5) and (19), respectively. Let $f, y_d \in L^2(\varOmega )$ and $g \in H^{1/2}(\varGamma )$ and $\alpha _h$ is as defined in (13). Then

$$\begin{aligned} |y(\tilde{z}) - y_h(\tilde{z})|_{1,\varOmega } + |p(\tilde{y}) - p_h(\tilde{y})|_{1,\varOmega }\lesssim & {} \alpha _h \; h. \nonumber \end{aligned}$$

Additionally, if $f, y_d \in H^1(\varOmega )$ then

$$\begin{aligned} \left\| y(\tilde{z})-y_h(\tilde{z})\right\| _{0,\varOmega } + \left\| p(\tilde{y})-p_h(\tilde{y})\right\| _{0,\varOmega }\lesssim & {} \alpha _h \; h^2. \nonumber \end{aligned}$$

Moreover, for $\tilde{z} = z_h$,

$$\begin{aligned} \left\| p(z_h)-p_h(z_h)\right\| _{L^2(\varOmega )} \lesssim \alpha _h h^2. \nonumber \end{aligned}$$

Following the arguments of Lemma 2.1 in [2] and the standard approximation property of $\varPi ^0_{1,K}$ given in [1], we have

$$\begin{aligned} \left\| \zeta - \varPi ^0_{1,h} \zeta \right\| _{0,\varOmega }\lesssim & {} h^{2} \left\| \zeta \right\| _X \;\; \forall \;\; \zeta \in X. \end{aligned}$$

(20)

Now we derive the error estimates for the state, adjoint and control variables under variational discretization of control.

Theorem 1

Let (y, p, z) solve the continuous optimality system (4)–(6). Let $(y_h,p_h,z_h)$ solve the discrete optimality system (14)–(16). Then under the assumptions of Lemma 2 and Lemma 3, then following estimate holds

$$\begin{aligned} \left\| z - z_h\right\| _{L^2(\varOmega )} \lesssim \alpha _h \; h^2, \nonumber \end{aligned}$$

where $\alpha _h$ is as defined in (13).

Proof

The discrete (16) and continuous (6) variational inequalities give the following

$$\begin{aligned} (\lambda z_h + \varPi ^0_{1,h} p_h, z - z_h) \ge 0 \ge (\lambda z + p, z - z_h), \end{aligned}$$

(21)

The coercivity condition (3) for $z - z_h \in Z$ and (21) leads to

$$\begin{aligned} \lambda \left\| z - z_h\right\| ^2_{0,\varOmega }\le & {} (\lambda z + p, z-z_h) - (\lambda z_h + p(z_h),z - z_h), \nonumber \\\le & {} (\lambda z_h + \varPi ^0_{1,h} p_h, z - z_h) - (\lambda z_h + p(z_h),z - z_h) \nonumber \\= & {} (\varPi ^0_{1,h} p_h - p(z_h), z - z_h), \nonumber \\= & {} \left[ (\varPi ^0_{1,h}(p_h-p(z_h)),z-z_h) \right. \nonumber \\{} & {} \qquad \qquad \left. + (\varPi ^0_{1,h} p(z_h)-p(z_h),z-z_h) \right] \nonumber \\= & {} T_A + T_B \nonumber \end{aligned}$$

In view of the stability of $\varPi ^0_{1,K}$ operator, Lemmas 2 and 3, $T_A$ is bounded as follows:

$$\begin{aligned} T_A\le & {} \sum _{K \in \tau _h} \left\| \varPi ^0_{1,K} (p_h - p(z_h))\right\| _{0,K} \left\| z - z_h\right\| _{0,K} \nonumber \\\le & {} \sum _{K \in \tau _h} \left\| p_h - p(z_h)\right\| _{0,K} \left\| z-z_h\right\| _{0,K} \nonumber \\\le & {} \sum _{K \in \tau _h} \left( \left\| p_h-p_h(y(z_h))\right\| _{0,K} + \left\| p_h(y(z_h))-p(z_h)\right\| _{0,K}\right) \left\| z - z_h\right\| _{0,K} \nonumber \\\lesssim & {} \left( |p_h-p_h(y(z_h))|_{1,\varOmega } + \left\| p_h(y(z_h))-p(z_h)\right\| _{0,\varOmega }\right) \left\| z - z_h\right\| _{0,\varOmega } \nonumber \\\lesssim & {} \left( \alpha _h \left\| y_h(z_h)-y(z_h)\right\| _{0,\varOmega } + \left\| p_h(y(z_h))-p(z_h)\right\| _{0,\varOmega }\right) \left\| z-z_h\right\| _{0,\varOmega } \nonumber \\\lesssim & {} \alpha _h \; h^2 \; \left\| z-z_h\right\| _{0,\varOmega }. \nonumber \end{aligned}$$

The term $T_B$ is bounded using (20) as follows

$$\begin{aligned} T_B \le \sum _{K \in \tau _h} \left\| \varPi ^0_{1,K} p(z_h) - p(z_h)\right\| _{L^2(\varOmega )} \left\| z - z_h\right\| _{L^2(\varOmega )} \lesssim h^2 \left\| p(z_h)\right\| _X \left\| z-z_h\right\| _{0,\varOmega }. \nonumber \end{aligned}$$

Combining the bounds of $T_A$ and $T_B$ leads to the desired estimate. $\square$

Theorem 2

Assuming Theorem 1 holds. Then under variational discretization of control the following estimates hold

$$\begin{aligned} \left\| y-y_h\right\| _{0,\varOmega } + \left\| p-p_h\right\| _{0,\varOmega } \lesssim \alpha _h \; h^2;\; |y-y_h|_{1,\varOmega } + |p-p_h|_{1,\varOmega } \lesssim \alpha ^h \; h.\nonumber \end{aligned}$$

Proof

We split the error in state equation using $y_h(z)$ as $y-y_h = (y-y_h(z)) + (y_h(z)-y_h)$. Now we use Lemmas 2, 3 and Theorem 1 as follows:

$$\begin{aligned} \left\| y-y_h\right\| _{0,\varOmega }\le & {} \left\| y-y_h(z)\right\| _{0,\varOmega } + \left\| y_h(z)-y_h\right\| _{0,\varOmega } \nonumber \\\le & {} \left\| y-y_h(z)\right\| _{L^2(\varOmega )} + \alpha _h \left\| z - z_h\right\| _{L^2(\varOmega )} \lesssim \alpha _h \; h^2 \nonumber \\ |y-y_h|_{1,\varOmega }\le & {} |y-y_h(z)|_{1,\varOmega } + |y_h(z)-y_h|_{1,\varOmega } \nonumber \\\le & {} |y-y_h(z)|_{1,\varOmega } + \alpha _h \left\| z-z_h\right\| _{0,\varOmega } \lesssim \alpha _h \; h. \nonumber \end{aligned}$$

Following analogous steps and using the splitting $p-p_h = (p-p_h(y))+(p_h(y)-p_h)$, we can get the estimates for the adjoint variable. $\square$

4 Numerical Experiments

In this section, we present two numerical examples to study the behaviour of our scheme. In Example I, we study the behaviour of the solution at the interface in the presence of small edges under both the proposed stabilization terms $S^K_1(\cdot ,\cdot )$ and $S^K_2(\cdot ,\cdot )$. The mesh $\mathcal {T}^1_h$ (see Fig. 1) under (A1)–(A5) that we consider arises naturally, if we mesh the domain $\varOmega$ either side of the interface $\varGamma$ with different elements. The error in control, state, and adjoint variables are illustrated, and the theoretical results of Sect. 3 are corroborated. In Example II, we employ a segment interface which is independent of the background fitted mesh $\mathcal {T}^2_h$ (see Fig. 1) such that it satisfies (A1)–(A3). In Fig. 1, the red star markers on the slant interface are the intersection points of the interface with $\mathcal {T}^2_h$ and result in hanging nodes that are repurposed to generate a fitted mesh; hence the name background fitted mesh. Error in control, state, and adjoint variables under variational discretization of control is illustrated which verifies the results obtained in Sect. 3.

Fig. 1

Meshes $\mathcal {T}^1_h$ and $\mathcal {T}^2_h$, respectively

Example 1

(Vertical interface) Let $\varOmega$ be a unit square domain. Consider the problem (1)–(2). The interface $\varGamma := \{{\textbf {x}} \in \varOmega : x_1 - 0.5 = 0\}$ and the following data

$$\begin{aligned} \lambda = 0.1, \; u_a = -0.25, \; u_b = 0.25, \; \beta _1 = 1,{} & {} \beta _2 = 10, \; y({\textbf {x}}) = x_1^2 (x_1-1) x_2 (x_2-1), \nonumber \\ \; p({\textbf {x}}) = x_1 (x_1-1) x_2 (x_2-1),{} & {} z({\textbf {x}}) = \max (z_a, \min (z_b,-\frac{1}{\lambda } p({\textbf {x}}))).\nonumber \end{aligned}$$

The optimal control problem is solved using the variational variant of the projected gradient algorithm presented in [3]. In our numerical experiment, we observe that under the classical VEM stabilization choice of $S^1_K(\cdot ,\cdot )$, the solution of the state and the adjoint variable exhibits oscillations at the interface under the presence of small edges; however, the control variable is free of these oscillations under variational discretization of control (See Fig. 2). The red dotted lines in Fig. 2 represent the true solution at the interface, and the blue lines represent the approximated solution on $\mathcal {T}^2_h$.

Fig. 2

Solution profile of state, adjoint and control variables, respectively at the interface under variational discretization of control with $S_1^K(\cdot ,\cdot )$ on $\mathcal {T}^2_h$

We do the same experiment with the boundary stabilization $S^2_K(\cdot ,\cdot )$ and observe that the oscillations at the interface have smoothened (see Fig. 3).

Fig. 3

Solution profile of state, adjoint and control variables, respectively at the interface under variational discretization of control with $S_2^K(\cdot ,\cdot )$ on $\mathcal {T}^2_h$

Remark 1

It is also observed in our numerical experiments that the oscillations are sensitive to the parameter $\beta$. For example, if we consider the same numerical example with $\beta _1 = 1$ and $\beta _2 = 0.5$, the oscillations with $S^1_K(\cdot ,\cdot )$ in the state and the adjoint will be still visible but much smaller.

Now we compare the error under a sequence of meshes $\mathcal {T}^1_1$ to $\mathcal {T}^1_5$ (see Fig. 4). We compare the exact solution of the state and co-state variables with the $L^2$-projection of the discrete state and co-state variables since the virtual element solution is not known explicitly inside the element. The discrete control is computed using the discrete projection formula (17). We denote the $L^2$-error as follows

$$\begin{aligned} E_0(w) = \sum _{K \in \tau _h} \left\| w-\varPi ^0_{1,K} w_h\right\| _{0,K} \;\; \text{ for }\, w = \text{ y, } \text{ p }, \;\; E_0(z) = \sum _{K \in \tau _h} \left\| z - z_h\right\| _{0,K}. \end{aligned}$$

Similarly, we denote the error in the energy norm for the state and the co-state variable by $E_1(y)$ and $E_1(p)$, respectively with the help of $\varPi ^{\nabla }_{1,K}$ operator. We denote by $R_0(w)$ and $R_1(w)$ the order of convergence corresponding to the variable w in the $L^2$ and $H^1$ norms, respectively. The numerical errors and the corresponding rate of convergence under $\mathcal {T}^1_1$-$\mathcal {T}^1_5$ are given in Table 1 and corroborate theoretical results of Theorems 1 and 2. The solution profile on $\mathcal {T}^1_3$ is given in Fig. 5.

Fig. 4

Sequence of meshes $\mathcal {T}^1_1$, $\mathcal {T}^1_2$, $\mathcal {T}^1_3$, $\mathcal {T}^1_4$ and $\mathcal {T}^1_5$, respectively

Example 2

(Segment interface) Consider the problem (1)–(2) on a unit square domain with the interface $\varGamma := \{ {\textbf {x}} \in \varOmega : x_2 = k x_1 + b \}$, where $k = \frac{-\sqrt{3}}{3}$ and $b = \frac{(6+\sqrt{6}-2 \sqrt{3})}{6}$ and the following data

$$\begin{aligned} \lambda = 1, \; u_a = -0.2, \; u_b = 0.2, \; \beta _1 = 1, \; \beta _2 = 1/2, \; y({\textbf {x}}) = x_1^2 (x_1-1) x_2 (x_2-1), ~~~\nonumber \\ z({\textbf {x}}) = \max (z_a, \min (z_b,-\frac{1}{\lambda } p({\textbf {x}}))), \; p({\textbf {x}}) = (x_2 - k x_1 - b)^2 (x_1 (x_1 - 1) x_2 (x_2 - 1)). \nonumber \end{aligned}$$

Table 1 Error and order of convergence in y, p and u under $\mathcal {T}^1_1$-$\mathcal {T}^1_5$ and variational discretization of control in $L^2$-norm and energy norm for Example I

Fig. 5

Solution profile of state, adjoint and control variables, respectively on $\mathcal {T}^1_3$ for Example I

The numerical errors and the corresponding order of convergence under a sequence of refined meshes of the type $\mathcal {T}^2_h$ independent of the interface $\varGamma$ are given in Table 2 and confirm the theoretical results of Theorems 1 and 2.

Table 2 Error and order of convergence in y, p and u under a sequence of meshes of type $\mathcal {T}^2_h$ and variational discretization of control in energy and $L^2$ norms for Example II