Propagation of Water Waves in the Presence of a Horizontal Plate Submerged in a Two-Layer Fluid

Abstract

The interaction of surface and interface waves with a thin horizontal plate submerged in the lower layer of a two-layer fluid is studied under linearised theory of water waves. The associated boundary value problem is solved here by Fourier integral transform by reducing it to an integral equation involving the potential difference function across the plate. Application of multi-term Galerkin method to the solution of the integral equation leads to a simple, rapidly convergent numerical scheme and suitable expressions for different hydrodynamic quantities of interest. Numerical results for the reflection coefficients and the hydrodynamic force on the plate are presented to study the effect of different physical parameters. The present method is verified by recovering the published numerical results for a limiting case and through an energy balance relation.

1 Introduction

The study of water wave interaction with obstacles has sparked enormous attention for a variety of applications in coastal and marine environments. Also, obtaining a less cost-effective clean renewable energy by extracting energy from ocean waves has received considerable attention from researchers. One of the best developments in extracting wave energy is to construct a line of submerged bodies that would act like a lens and focus the diverging waves to converge waves. In Norway, they have developed many such constructions like shore-based horizontal tapered channels, oscillating water columns, phase controlled wave power buoys, etc. McIver [1] considered a horizontal flat plate moored to seabed which would act like such a lens, while Mehlum [2] considered a circular cylinder. Using Fourier integral transform together with a Galerkin method, Porter [3] investigated the oblique water wave interaction with a horizontal thin plate submerged in a single layer fluid.

In the study of the propagation of water waves in a two-layer fluid having a free upper surface in the upper layer, Lamb [4] established that for a given frequency, there exist two linear wave systems of different wavenumbers. These two wave modes mainly propagate along the free surface and the interface of the fluids. As a result, if wave fields interact with obstacles, some transformation of wave energy from one mode to another may occur. This makes the wave interaction problems in a two-layer fluid more interesting. Linton and McIver [5] developed the linear scattering theory for two-dimensional wave motion in a two-layer fluid comprised of an infinite lower layer and a finite upper layer with a free surface to investigate the problem of wave scattering by a horizontal circular cylinder with the help of multipole expansion method. Using hypersingular integral equations method, Dhillon et al. [6] and Islam and Gayen [7] investigated the scattering of water waves by a thin vertical and inclined plate in a two-layer fluid, respectively. Based on the method of eigenfunction expansion, Medina-Rodríguez and Silva [8] considered two thick horizontal plates submerged in a two-layer fluid and analysed the reflection energies of interface and surface waves.

In the present article, a thin horizontal rigid plate submerged in the lower layer of a two-layer-fluid is proposed and investigated in the context of linear potential theory. Here, both the fluids are considered to be of finite depth. The coupled boundary value problem is solved here by Fourier integral transform to obtain an integral equation involving the unknown potential difference function across the plate. Then using Galerkin method we find this potential difference function numerically and with this solution, we compute the different physical quantities. The correctness of the present analysis is established by checking the energy identity relation and by comparing the obtained numerical results for limiting case with one of the previous results available in the literature. New results are presented graphically illustrating the effects of various parameters on the hydrodynamic quantities.

Fig. 1

Schematic diagram for horizontal plate

2 Formulation of the Problem

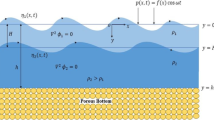
Figure 1 depicts the geometry of a horizontal plate $\varGamma$ submerged in the bottom layer of a two-layer fluid. The depths of the upper and lower layer fluids are h and H, respectively. A Cartesian coordinate system is considered in which $z=0$ represents the rest common interface of the two fluids, $z=-h$ represents the free surface, and z-axis is measured vertically downwards from the undisturbed interface. Let the plate be submerged at a depth d from the undisturbed interface of the two fluids and extends horizontally from $-b$ to b. Assuming time harmonic incident waves of angular frequency $\sigma$ making an angle $\theta$ with the positive x-axis, the motion in the upper layer fluid (of density $\rho _1$) and lower layer fluid (of density $\rho _2$) can be represented by $Re\left\{ \phi _1(x, z)e^{-\textrm{i}\sigma \tau }e^{\textrm{i}\nu y}\right\}$ and $Re\left\{ \phi _2(x,z)e^{-\textrm{i}\sigma \tau }e^{\textrm{i}\nu y}\right\}$ respectively, where $\tau$ indicates the time and $\nu$ is the wavenumber along the y direction. The functions $\phi _j(x,z)$ satisfy

$$\begin{aligned} (\nabla ^2 - \nu ^2)\phi _j(x,z)=0,\ \mathrm{in\ the\ respective\ fluid\ region.}\ \end{aligned}$$

(1)

Linearized free surface, interface and the bottom boundary conditions are

$$\begin{aligned} K\phi _1 + \phi _{1z}= & {} 0\ \textrm{on}\ z=-h,\end{aligned}$$

(2)

$$\begin{aligned} \phi _{1z}= & {} \phi _{2z}\ \textrm{on}\ z=0,\end{aligned}$$

(3)

$$\begin{aligned} s(K\phi _1+\phi _{1z})= & {} K\phi _2+\phi _{2z} \ \textrm{on}\ z=0,\end{aligned}$$

(4)

$$\begin{aligned} \phi _{2z}= & {} 0\ \textrm{on}\ z=H, \end{aligned}$$

(5)

where $s=\rho _1/\rho _2$, $K = \sigma ^2/g$ , g being the acceleration due to gravity.

The boundary condition on the horizontal plate is

$$\begin{aligned} \phi _{2z}(x,d^\pm )= & {} 0,\ \ \ \mid x\mid <b,\end{aligned}$$

(6)

$$\begin{aligned} \phi _2(x,d^+)-\phi _2(x,d^-)= & {} P(x),\ \ \ \mid x\mid <b. \end{aligned}$$

(7)

In a two-layer fluid, the progressive waves propagating at the free surface and the interface can be expressed by

$$f_1(v,z)e^{\pm \textrm{i}(v^2-\nu ^2)^{1/2}x} (-h<z<0), f_2(v,z)e^{\pm \textrm{i}(v^2-\nu ^2)^{1/2}x} (0<z<H)$$

with

$$\begin{aligned}f_1(v,z)&=\frac{\sinh {vH}}{K\cosh {vh}-v\sinh {vh}}\left[ \ v\cosh {v(h+z)}-K\sinh {v(h+z)}\right] ,\\ f_2(v,z)&=\cosh {v(H-z)} \end{aligned}$$

where v is real, positive and satisfies the dispersion equation

$$\begin{aligned} \Delta (v)\equiv (1-s)v^2 + K^2(s+\coth {vh}\coth {vH})-vK(\coth {vh}+\coth {vH})=0 . \end{aligned}$$

(8)

Equation (8) has exactly two positive real roots, m and M ($K<m<M$). Thus, there exist two wave systems with two different wavenumbers. As a result, if a wave train of mode m is obliquely incident on the horizontal plate at angle $\theta$ with the positive x-axis, the far-field behaviours of $\phi _j(j=1,2)$ are given by

$$\begin{aligned} \phi _j(x,z) \rightarrow {\left\{ \begin{array}{ll} \phi _{jm}^{I}(x,z)+r^m\phi _{jm}^{I}(-x,z)+R^m\phi _{jM}^{I}(-x,z)\ \textrm{as }\ x\rightarrow -\infty ,\\ t^m\phi _{jm}^{I}(x,z)+T^m\phi _{jM}^{I}(x,z) \ \textrm{as }\ x\rightarrow \infty , \end{array}\right. } \end{aligned}$$

(9)

where

$$\begin{aligned} \phi _{jv}^{I}(x,z)=f_j(v,z)\textrm{e}^{\textrm{i}(v^2-\nu ^2)^{1/2}x}. \end{aligned}$$

(10)

In (9), for an obliquely incident wave of mode m, the unknowns $r^m$ and $R^m$ represent the amplitudes of reflected waves associated with modes m and M respectively, while $t^m$ and $T^m$ represent the amplitude of transmitted waves associated with modes m and M respectively. Similarly, for an incident wave of mode M with incident wave angle $\theta <\sin ^{-1}( m/M )$ the far-field behaviours of $\phi _j(j=1,2)$ can be expressed as

$$\begin{aligned} \phi _j(x,z) \rightarrow {\left\{ \begin{array}{ll} \phi _{jM}^{I}(x,z)+R^M\phi _{jM}^{I}(-x,z)+r^M\phi _{jm}^{I}(-x,z)\ \textrm{as }\ x\rightarrow -\infty ,\\ T^M\phi _{jM}^{I}(x,z)+t^M\phi _{jm}^{I}(x,z) \ \textrm{as }\ x\rightarrow \infty . \end{array}\right. } \end{aligned}$$

(11)

Here, for an obliquely incident wave of mode M, the unknowns $r^M$ and $R^M$ represent the amplitudes of reflected waves associated with modes m and M respectively, while $t^M$ and $T^M$ denote the amplitudes of transmitted waves associated with modes m and M respectively.

3 Method of Solution

Let a wave train of mode m making an angle $\theta (0 \le \theta \le \pi /2)$ with the positive x-axis be incident on the plate. Then, we must have $\nu =m\sin {\theta }.$

Now, we define the Fourier transform of the scattered potential function by

$$\begin{aligned} \overline{\phi }_j(k,z)=\int _{-\infty }^{\infty }\left( \phi _j(x,z)-\phi _{jm}^{I}(x,z)\right) e^{-\textrm{i}kx} \textrm{d}x, \end{aligned}$$

(12)

with the inverse

$$\begin{aligned} \phi _j(x,z)=\phi _{jm}^{I}(x,z)+\frac{1}{2\pi }\int _{-\infty }^{\infty }\overline{\phi }_j(k,z)e^{\textrm{i}kx} \textrm{d}k, \end{aligned}$$

(13)

where the integration contour in the inverse transform will be defined later by incorporating the far-field conditions.

Then, applying (12) to (1)–(7) produces

$$\begin{aligned} (\frac{d^2}{dz^2}-\beta ^2)\overline{\phi }_j&=0, j=1,2,\end{aligned}$$

(14)

$$\begin{aligned} K\overline{\phi }_1 + \overline{\phi }_{1z}&= 0\text { on }z=-h,\end{aligned}$$

(15)

$$\begin{aligned} \overline{\phi }_{1z}&=\overline{\phi }_{2z}\text { on }z=0,\end{aligned}$$

(16)

$$\begin{aligned} s(K\overline{\phi }_1+\overline{\phi }_{1z})&=K\overline{\phi }_2+\overline{\phi }_{2z}\text { on } z=0, \end{aligned}$$

(17)

$$\begin{aligned} \overline{\phi }_{2z}&=0\text { on } z=H,\end{aligned}$$

(18)

$$\begin{aligned} \overline{\phi }_{2z}(k,d^+)&=\overline{\phi }_{2z}(k,d^-),\end{aligned}$$

(19)

$$\begin{aligned} \overline{\phi }_{2}(k,d^+)-\overline{\phi }_{2}(k,d^-)&=\int _{-b}^{b}P(x)e^{-\textrm{i}kx} dx\equiv \overline{P}(k), \end{aligned}$$

(20)

where $\beta ^2=k^2+\nu ^2$.

Solving (14) subjected to the boundary conditions (15)–(18), we get

$$\begin{aligned} \overline{\phi }_1(k,z)&=\frac{K\overline{P}(k)\sinh {\beta (H-d)}[K\sinh {\beta (h+z)}-\beta \cosh {\beta (h+z)}]}{\sinh {\beta h}\sinh {\beta H}\Delta (\beta )}, -h<z<0,\end{aligned}$$

(21)

$$\begin{aligned} \overline{\phi }_2(k,z)&= {\left\{ \begin{array}{ll} \frac{\overline{P}(k)\sinh {\beta (H-d)}[\sinh {\beta h}\cosh {\beta z}((1-s)\beta ^2+K^2s)-K\beta \cosh {\beta (h+z)}+K^2\cosh {\beta h}\sinh {\beta z}]}{\sinh {\beta h}\sinh {\beta H}\Delta (\beta )}, 0<z<d, \\ \frac{\overline{P}(k)\cosh {\beta (H-z)}[\sinh {\beta h}\cosh {\beta d}((s-1)\beta ^2-K^2s)+K\beta \sinh {\beta (h+d)}-K^2\cosh {\beta h}\cosh {\beta d}]}{\sinh {\beta h}\sinh {\beta H}\Delta (\beta )}, d<z<H. \end{array}\right. } \end{aligned}$$

(22)

Taking inverse transforms of the representations (21) in ($-h<y<0$) and (22) in $0< y < d$, we get

$$\begin{aligned} \phi _1(x,z)&=\phi _{1m}^{I}(x,z) \nonumber \\&\quad +\frac{1}{2\pi }\int _{-\infty }^{\infty }\frac{K\overline{P}(k)\sinh {\beta (H-d)}[K\sinh {\beta (h+z)}-\beta \cosh {\beta (h+z)}]}{\sinh {\beta h}\sinh {\beta H}\Delta (\beta )}e^{\text {i} kx} \text {d} k,\end{aligned}$$

(23)

$$\begin{aligned} \phi _2(x,z)&=\phi _{2m}^{I}(x,z) +\frac{1}{2\pi }\int _{-\infty }^{\infty }\overline{P}(k)\mathcal {H}(z,\beta )e^{\text {i} kx} \text {d} k, \end{aligned}$$

(24)

where

$$\begin{aligned} {\mathcal {H}}(z,\beta )=\frac{\sinh {\beta (H-d)}[\sinh {\beta h}\cosh {\beta z}((1-s)\beta ^2+K^2s)-K\beta \cosh {\beta (h+z)}+K^2\cosh {\beta h}\sinh {\beta z}]}{\sinh {\beta h}\sinh {\beta H}\Delta (\beta )}. \end{aligned}$$

(25)

In order to obtain the reflection and transmission coefficients, we find the far-field form for $\phi _1(x,z)$. There are poles on the real k-axis at $k=\pm \alpha _1$ and $k=\pm \alpha _2$ where $\alpha _1=m\cos \theta$, $\alpha _2=\sqrt{M^2-m^2\sin ^2\theta }$. Thus, in order to meet the radiation condition that $\phi _1-\phi _{1m}^{I}$ is outgoing, the contour of the integration in equation (23) is taken to pass under the poles at $k=\alpha _1,\alpha _2$ and over the poles at $k=-\alpha _1,-\alpha _2$. Thus, capturing the residues at the poles $k=\pm \alpha _1,\pm \alpha _2$, the contour can be deformed into either the upper-half or lower-half k-plane by letting $x\rightarrow \pm \infty$ in (19), and this yields

$$\begin{aligned} \phi _1(x,z)\rightarrow {\left\{ \begin{array}{ll} \phi _{1m}^{I}(x,z)-\textrm{i}m\mu _1\overline{P}(-\alpha _1)\sinh {m(H-d)} \phi _{1m}^{I}(-x,z) -\textrm{i}M\mu _2\overline{P}(-\alpha _2)\sinh {M(H-d)}\phi _{1M}^{I}(-x,z)\\ \ \textrm{as}\ x\rightarrow -\infty ,\\ \left( 1-\textrm{i}m\mu _1\overline{P}(\alpha _1)\sinh {m(H-d)}\right) \phi _{1m}^{I}(x,z) -\textrm{i}M\mu _2\overline{P}(\alpha _2)\sinh {M(H-d)}\phi _{1M}^{I}(x,z)\ \textrm{as}\ x\rightarrow \infty . \end{array}\right. } \end{aligned}$$

(26)

Comparing (26) with (9), we get

$$\begin{aligned} \begin{aligned} t^m-1&=-\textrm{i}m\mu _1\overline{P}(\alpha _1)\sinh {m(H-d)},&T^m&=-\textrm{i}M\mu _2\overline{P}(\alpha _2)\sinh {M(H-d)},\\ r^m&=-\textrm{i}m\mu _1\overline{P}(-\alpha _1)\sinh {m(H-d)},&R^m&=-\textrm{i}M\mu _2\overline{P}(-\alpha _2)\sinh {M(H-d)}, \end{aligned} \end{aligned}$$

(27)

where $\mu _1$ and $\mu _2$ are defined as

$$\mu _1=\frac{K(K\cosh {mh}-m\sinh {mh})}{\alpha _1\sinh {mh}\sinh ^2{mH}\Delta ^{'}(m)},~~\mu _2=\frac{K(K\cosh {Mh}-M\sinh {Mh})}{\alpha _2\sinh {Mh}\sinh ^2{MH}\Delta ^{'}(M)}.$$

Now with the help of the values of $t^m$, $T^m$, $r^m$ and $R^m$, we can write (24) as the sum of Cauchy principal value-integral and contributions from the four poles. Thus, $\phi _2(x,z)$ given in (24) can be expressed as

$$\begin{aligned} \phi _2(x,z)&=\frac{1}{2}(t^m+1)\phi _{2m}^{I}(x,z)+\frac{r^m}{2}\phi _{2m}^{I}(-x,z)+\frac{1}{2}[T^me^{\textrm{i}\alpha _2x}+R^me^{-\textrm{i}\alpha _2x}] \nonumber \\ {}&\quad +\frac{1}{2\pi }{\int \! \! \! \! \! \! \tiny {-}}_{-\infty }^{\infty }\mathcal {H}(z,\beta )\overline{P}(k)e^{\textrm{i}kx} \textrm{d}k. \end{aligned}$$

(28)

We note that, for $0<z<d$,

$$\begin{aligned} \mathcal {H}(z,\beta ) \rightarrow \frac{1}{2}e^{-\mid k \mid (d-z)},~~\text {as} ~\vert k\vert \rightarrow \infty . \end{aligned}$$

(29)

We also note the following identity (cf. [9]) for $d-z > 0$

$$\begin{aligned} \log \sqrt{(x-w)^2+(d-z)^2}=\frac{1}{2}\int _{-\infty }^{\infty }\frac{e^{\mid k \mid }-e^{\mid k \mid (d-z)}e^{\textrm{i}k(x-w)}}{\mid k \mid }\textrm{d}k . \end{aligned}$$

(30)

Thus, making use of the relations (20), (29) and (30), we re-write (28) as

$$\begin{aligned} \phi _2(x,z)&=\frac{1}{2}(t^m+1)\phi _{2m}^{I}(x,z)+\frac{r^m}{2}\phi _{2m}^{I}(-x,z)+ \frac{1}{2}[T^me^{\textrm{i}\alpha _2x}+R^me^{-\textrm{i}\alpha _2x}]\nonumber \\&\quad +\frac{1}{2\pi }\frac{\partial }{\partial z}\int _{-b}^{b}P(w) \log \sqrt{(x-w)^2+(d-z)^2}\textrm{d}w\nonumber \\&\quad +\frac{1}{2\pi } {\int \! \! \! \! \! \! \tiny {-}}_{-\infty }^{\infty }[\mathcal {H}(z,\beta )-\frac{1}{2}e^{-\mid k\mid (d-z)}]e^{\textrm{i}kx}\int _{-b}^{b}P(w)e^{-\textrm{i}kw}\textrm{d}w \textrm{d}k. \end{aligned}$$

(31)

Now we apply the plate condition (6) in (31) and this gives

$$\begin{aligned}&(t^m+1)f_+(x)+r^mf_-(x)+T^mg_+(x)+R^mg_-(x) =-\frac{1}{\pi }\frac{d^2}{dx^2}\int _{-b}^{b}P(w)\log \mid x-w\mid \textrm{d}w \nonumber \\&\quad +\frac{1}{2\pi }{\int \! \! \! \! \! \! \tiny {-}}_{-\infty }^{\infty } E_\nu (k)e^{\textrm{i}kx} \int _{-b}^{b}P(w)e^{-\textrm{i}kw}\textrm{d}w\textrm{d}k \end{aligned}$$

(32)

for $\mid x \mid <b$, where

$$\begin{aligned} f_{\pm }(x)=-m\sinh {m(H-d)}e^{\pm \textrm{i}\alpha _1x}\quad \textrm{and} \quad g_{\pm }(x)=-M\sinh {M(H-d)}e^{\pm \textrm{i}\alpha _2x} \end{aligned}$$

(33)

and

$$\begin{aligned} E_\nu (k)=\frac{2\beta \sinh {\beta (H-d)}[\sinh {\beta h}\sinh {\beta d}((s-1)\beta ^2-K^2s)+K\beta \sinh {\beta (h+d)}-K^2\cosh {\beta h}\cosh {\beta d}]}{\sinh {\beta h}\sinh {\beta H}\Delta (\beta )} +\vert k \vert . \end{aligned}$$

(34)

It may be noted that to obtain (32) we have used

$$\begin{aligned} \left( \ \frac{\partial ^2}{\partial x^2}+\frac{\partial ^2}{\partial z^2}\right) \ \log \sqrt{(x-w)^2+(d-z)^2}=0 \end{aligned}$$

(35)

to alter from z to x-axis before applying the plate condition on $z=d$.

Now, we define the integro-differential operator $\mathcal {K}$ by

$$\begin{aligned} (\mathcal {K} P)(x)&=-\frac{1}{\pi }\frac{\textrm{d}^2}{\textrm{d}x^2}\int \nolimits _{-b}^{b}P(w)\log \mid x-w\mid \textrm{d}w+\frac{1}{2\pi }{\int \! \! \! \! \! \! \tiny {-}}_{-\infty }^{\infty } E_\nu (k)e^{\textrm{i}kx} \nonumber \\&\qquad \int \nolimits _{-b}^{b}P(w)e^{-\textrm{i}kw}\textrm{d}w\textrm{d}k \end{aligned}$$

(36)

and let $P_\pm (x)$, $Q_\pm (x)$ satisfy

$$\begin{aligned} \left( \mathcal {K} P_\pm , \mathcal {K} Q_\pm \right) (x)=\left( f_\pm , g_\pm \right) (x), \quad \mid x\mid <b. \end{aligned}$$

(37)

Hence it follows from (32) that

$$\begin{aligned} P(x)=(t^m+1)P_+(x)+r^mP_-(x)+T^mQ_+(x)+R^mQ_-(x). \end{aligned}$$

(38)

Using (33) and the definition (20) in (27) results in

$$\begin{aligned} \begin{aligned} t^m-1&=\textrm{i}\mu _1\langle P, f_+\rangle ,&T^m&=\textrm{i}\mu _2\langle P, g_+\rangle ,\\ r^m&=\textrm{i}\mu _1\langle P, f_-\rangle ,&R^m&=\textrm{i}\mu _2\langle P, g_-\rangle , \end{aligned} \end{aligned}$$

(39)

where the operation $\langle p, q\rangle$ denotes the inner product as defined by

$$\begin{aligned} \langle p, q\rangle =\int _{-b}^{b}p(x)q^*(x)dx \end{aligned}$$

(40)

with asterisk denoting complex conjugate.

Substitution of (38) in (39) gives

$$\begin{aligned} \begin{aligned} t^m-1&=\textrm{i}\mu _1(t^m+1)S_{+,+}+i\mu _1r^mS_{-,+}+i\mu _1T^mX_{+,+}+i\mu _1R^mX_{-,+}\\ T^m&=\textrm{i}\mu _2(t^m+1)W_{+,+}+i\mu _2r^mW_{-,+}+i\mu _2T^mL_{+,+}+i\mu _2R^mL_{-,+}\\ r^m&=\textrm{i}\mu _1(t^m+1)S_{+,-}+i\mu _1r^mS_{-,+}+i\mu _1T^mX_{+,-}+i\mu _1R^mX_{-,-}\\ R^m&=\textrm{i}\mu _2(t^m+1)W_{+,-}+i\mu _2r^mW_{-,-}+i\mu _2T^mL_{+,-}+i\mu _2R^mL_{-,-} \end{aligned} \end{aligned}$$

(41)

where $W_{\pm ,\pm }=\langle P_{\pm },g_{\pm }\rangle$, $L_{\pm ,\pm }=\langle Q_{\pm },g_{\pm }\rangle$, $S_{\pm ,\pm }=\langle P_{\pm },f_{\pm }\rangle$, $X_{\pm ,\pm }=\langle Q_{\pm },f_{\pm }\rangle$ with the first ’±’s in the left-hand side corresponding to the first in the right hand side and so on.

3.1 Numerical Method

To solve the system of equations given in (41) for $R^m$, $T^m$, $r^m$ and $t^m$, we must compute the inner products; hence we need to solve for $P_{\pm }$, $Q_{\pm }$. For this, we apply the Galerkin method (cf. Porter [3]) to find the solution for (37). The method is described below.

We take

$$\begin{aligned} \left( P_{\pm }, Q_{\pm }\right) (x)=\sum _{n=0}^{\infty }\left( A_n^{\pm }, B_n^{\pm }\right) p_n(x/b), \quad \mid x\mid \le b, \end{aligned}$$

(42)

where $A_n^{\pm }$, $B_n^{\pm }$ are unknown coefficients to be determined and

$$\begin{aligned} p_n(w)=\frac{e^{in\pi /2}}{\pi (n+1)}(1-w^2)^{1/2}U_n(w), \end{aligned}$$

(43)

where $U_n$ are second kind Chebyshev polynomials of order n.

Substitution of (42) into (37), multiplication with $p_l^*(x/b)$ and integration over $-b<x<b$ results in the infinite system of equations for the unknown coefficients $A_n^{\pm }$ and $B_n^{\pm }$:

$$\begin{aligned} -\frac{1}{2\pi (l+1)} \left( A_l^{\pm }, B_l^{\pm } \right) +\sum _{n=0}^{\infty }\left( A_n^{\pm }, B_n^{\pm } \right) K_{l,n}=\left( F_{l}^{\pm }, G_{l}^{\pm } \right) ,~~~l=0,1,2,..., \end{aligned}$$

(44)

where

$$\begin{aligned} K_{l,n}=\frac{1}{2\pi }{\int \! \! \! \! \! \! \tiny {-}}_{-\infty }^{\infty }\frac{E_\nu (k)}{k^2}J_{n+1}(kb)J_{l+1}(kb)\textrm{d}k, \end{aligned}$$

(45)

and

$$\begin{aligned} F_{l}^{\pm } =- m\sinh {m(H-d)}(\pm 1)^{l}\frac{J_{l+1}(b\alpha _1)}{\alpha _1}, \quad G_{l}^{\pm }=-M\sinh {M(H-d)}(\pm 1)^{l}\frac{J_{l+1}(b\alpha _2)}{\alpha _2}. \end{aligned}$$

(46)

It is noted that $K_{l,n}=0$ if $l+n$ is odd. This indicates that we can decouple (44) into its symmetric and antisymmetric parts for $\left( A_{2n}^{\pm }, B_{2n}^{\pm } \right)$ and $\left( A_{2n+1}^{\pm }, B_{2n+1}^{\pm }\right)$. Thus, we have the following real symmetric systems of linear equations:

$$\begin{aligned}&-\frac{1}{2\pi (2l+\xi +1)} \left( A_{2l+\xi }^{\pm }, B_{2l+\xi }^{\pm }\right) +\sum _{n=0}^{\infty }\left( A_{2n+\xi }^{\pm }, B_{2n+\xi }^{\pm }\right) K_{2l+\xi ,2n+\xi }=\left( F_{2l+\xi }^{\pm }, G_{2l+\xi }^{\pm }\right) , \nonumber \\&\quad ~~ l=0,1,2,...,~~ \xi =0,1. \end{aligned}$$

(47)

Again, $F_l^+=(-1)^lF_l^-$ and $G_l^+=(-1)^lG_l^-$ imply that $A_l^+=(-1)^lA_l^-$ and $B_l^+=(-1)^lB_l^-$ and thus it is sufficient to find just the solutions of (47) for $\left( A_l^+, B_l^+\right)$.

Using (42) and (46), we have

$$\begin{aligned} W_{\pm ,\pm }=\sum _{n=0}^{\infty }A_n^{\pm }G_{n}^{\pm },~ L_{\pm ,\pm }=\sum _{n=0}^{\infty }B_n^{\pm }G_{n}^{\pm },~ S_{\pm ,\pm }=\sum _{n=0}^{\infty }A_n^{\pm }F_{n}^{\pm },~ X_{\pm ,\pm }=\sum _{n=0}^{\infty }B_n^{\pm }F_{n}^{\pm }. \end{aligned}$$

(48)

Thus, it follows that

$$\begin{aligned} W_{+,+}=W_{--}&=\sum _{n=0}^{\infty }A_{2n}^{\pm }G_{2n}^{\pm }+\sum _{n=0}^{\infty }A_{2n+1}^{\pm }G_{2n+1}^{\pm }~\text {and}~\nonumber \\ W_{+,-}=W_{-+}&=\sum _{n=0}^{\infty }A_{2n}^{\pm }G_{2n}^{\pm }-\sum _{n=0}^{\infty }A_{2n+1}^{\pm }G_{2n+1}^{\pm } \end{aligned}$$

(49)

and similarly for $L_{\pm ,\pm }$, $S_{\pm ,\pm }$ and $X_{\pm ,\pm }$.

The energy identity comprising reflection and transmission coefficients can be derived using Green’s integral theorem as

$$\begin{aligned} \vert r^m\vert ^2+\vert R^m\vert ^2+\mathcal {J}(\vert t^m\vert ^2+\vert T^m\vert ^2)=1;~~\mathcal {J}=\frac{\mathcal {J}_M}{\mathcal {J}_m}, \end{aligned}$$

(50)

with

$$\begin{aligned} \mathcal {J}_\lambda =\textrm{i}\lambda \left[ \ s\int _{-h}^{0}\{f(\lambda ,z)\}^2\textrm{d}z+\int _{0}^{H}\{\cosh {\lambda (H-z)}\}^2\textrm{d}z\right] \ ,~~\lambda =m,M. \end{aligned}$$

(51)

The vertical hydrodynamic force acting on the plate can be obtained by integrating the dynamic pressure difference across the plate and is given as

$$\begin{aligned} F_m=\textrm{i}\sigma \rho _2\int _{-b}^{b}\big (\phi _2(x,d^+)-\phi _2(x,d^-)\big )\textrm{d}x=\textrm{i}\sigma \rho _2\int _{-b}^{b}P(x)\textrm{d}x. \end{aligned}$$

(52)

Thus using (38) we have

$$\begin{aligned} F_m=\textrm{i}\sigma \rho _2\big (\ (t^m+1)S_{+,0}+r^mS_{-,0}+T^mX_{+,0}+R^mX_{-,0}\big )\ \end{aligned}$$

(53)

where $S_{\pm ,0}=\langle P_{\pm },f_0\rangle$, $X_{\pm ,0}=\langle X_{\pm },f_0\rangle$ and $f_0=1$. Since $f_0=1=U_0(x/b)$, it follows that $S_{\pm ,0}=(1/2)bA_0^+$ and $X_{\pm }=(1/2)bB_0^+$.

Thus, the dimensionless hydrodynamic force acting on the horizontal rigid thin plate is defined as

$$\begin{aligned} \hat{F_m}=\frac{F_m}{2\rho _2\sigma b\cosh {mh}}=\frac{1}{4}\left\{ ((t^m+1)+r^m)A_0^++(T^m+R^m)B_0^+\right\} . \end{aligned}$$

(54)

Following the similar mathematical analysis as described above, for a wave train of mode M obliquely incident at an angle $\theta$, the solutions for the reflection coefficients, transmission coefficients and wave load on the plate can be obtained and analysed. Thus in the present paper, we only depict the numerical results for the case of incident wave of mode m.

4 Numerical Results and Discussions

The numerical results for different hydrodynamic quantities are computed after truncating the infinite series (42) to a finite number N. After some numerical examinations, it is found that the value of $N=4$ is enough to produce sufficiently accurate numerical results.

Table 1 represents the validation of computed numerical values of the reflection and transmission coefficients against the energy balance relation. In this table, we present the variations of $r^m, R^m, t^m,T^m$ and $\vert r^m\vert ^2+\vert R^m\vert ^2+\mathcal {J}(\vert t^m\vert ^2+\vert T^m\vert ^2)$ for few values of mb with other parameters as $s=0.5, d/b=2, h/b=2, H/b=4,\theta =0^0$. It is visible from Table 1 that the reflection and the transmission coefficients satisfy the energy identity relation (50) accurately and this proves partial correctness of our numerical results.

Table 1 A numerical check on energy identity relation

Fig. 2

Comparisons between the present results and the results obtained by Gradshteyn and Ryzhik [9]

Here we note that by letting $s=1$ and $h\rightarrow 0$, we can reduce the two-layer fluid to a single layer fluid of depth H. Through Fig. 2, we validate the newly developed method by comparing the numerical results for reflection coefficient (R) with those obtained by Porter [3] where he studied water wave scattering by a horizontal rigid thin plate in a single layer fluid. Fig. 2 is generated considering $d/H=0.1,b/H=0.5,s=1,h\rightarrow 0,\theta =0^{\circ }$. This graph demonstrates that the present results agree very well with those in Porter [3], and this provides additional validation on the numerical results obtained by the current analysis.

In Fig. 3a and b, for an incident wave train of mode m, we show the variations of the reflection coefficients $\vert r^m\vert$ and $\vert R^m\vert$ against the dimensionless wavenumber mb for different values of dimensionless submergence depth $d/b(=0.5,1,1.5)$. Here the values of other fixed parameters are $s=0.5, h/b=2, H/b=4,\theta =0^{\circ }$. These two figures show that as the submergence depth increases the reflection coefficients decrease. This may illustrate the fact that as the submergence depth increases, the interface and surface waves find more regions to pass the other side of the plate. It also demonstrates that the reflection coefficients diminish to zero beyond a certain value of dimensionless wavenumber.

Fig. 3

Reflection coefficients as a function of mb for various values of d/b with $s=0.5$, $h/b=2$, $H/b=4$, $\theta =0^{\circ }$

Fig. 4

Reflection coefficients as a function of mb for various values of h/b with $s=0.5$, $H/b=4$, $d/b=2$, $\theta =0^{\circ }$

For an incident wave train of mode m, Fig. 4a and b shows the influence of the interface position on the reflection coefficients $\vert r^m\vert$ and $\vert R^m\vert$ as a function of dimensionless wavenumber mb by altering the depth of the upper layer fluid$(h/b=0.5, 1, 1.5)$ for the following fixed parameters: $s=0.5$, $H/b=4$, $d/b=2$, $\theta =0^{\circ }$. From Fig. 4a, it is visible that as the interface is moved upwards, the reflection coefficient at mode m increases, whilst opposite behaviour for the reflection coefficient at mode M can be observed in Fig. 4b.

For an incident wave train of mode m, the effects of dimensionless plate length on the values of reflection coefficients $\vert r^m\vert$ and $\vert R^m\vert$ as a function of dimensionless wavenumber md are depicted in Fig. 5a and b respectively. Here the values of other fixed parameters are chosen as $s=0.5,h/d=1.5, H/d=3,\theta =0^{\circ }$. These two graphs demonstrate the fact that as the plate length decreases, the reflection coefficients also decrease. One obvious explanation for this phenomenon is that a smaller plate obstructs less amount of waves, resulting in lower reflection.

Fig. 5

Reflection coefficients as a function of md for various values of b/d with $s=0.5$, $H/d=3$, $h/d=1.5$, $\theta =0^{\circ }$

Figs. 6 and 7 represent the dimensionless hydrodynamic force $\vert \hat{F_m}\vert$ with respect to dimensionless wavenumber mb for different values of d/b and h/b respectively. Fig. 6 is plotted by choosing the values of parameters as $s=0.5,h/b=2,H/b=3,\theta =0^{\circ }$. On the other hand, the Fig. 7 is plotted by choosing the values of parameters as $s=0.5,H/b=3,d/b=2$. The two Figs. 6 and 7 indicate that the dimensionless hydrodynamic force exerted on the plate due to a wave train of mode m decreases as the submergence depth and depth of the upper layer fluid increase. It is obvious that as the plate moves deeper into the fluid, the propagating waves experience less obstruction by the plate resulting in lower vertical force.

Fig. 6

The dimensionless hydrodynamic force $\vert \hat{F_m}\vert$ for various values of d/b with $s=0.5$, $h/b=2$, $H/b=3$

Fig. 7

The dimensionless hydrodynamic force $\vert \hat{F_m}\vert$ for various values of h/b with $s=0.5$, $H/b=3$, $d/b=2$

5 Conclusions

On the basis of two-dimensional potential theory, we have investigated the problem of oblique wave scattering by a horizontal thin plate submerged in the lower layer of a two-layer fluid, comprising of two finite layers of fluids, in which upper layer has a free surface. We have adopted the Fourier integral transform to formulate integral equation involving unknown potential difference function across the plate. Applying Galerkin method to the solution of this integral equation, we obtain simple expressions for the reflection coefficients, transmission coefficients and hydrodynamic force exerted on the plate. We have validated the results obtained for the present analysis with those in Porter [3]. Also to ensure the validity of our results, we have calculated the energy identity for an incident wave of mode m. The dependence of various hydrodynamic quantities on the various parameters are depicted through figures. The reflection coefficients and hydrodynamic force significantly depend on the submergence depth of the plate and the interface position of the fluids. Reflection coefficients at the interface mode and surface mode for the incident wave of mode m increase as the submergence depth of the plate decreases. Also, the dimensionless hydrodynamic force acting on the plate decreases as the depth of upper layer fluid increases and increases as the submergence depth of the plate decreases. As usual, here also increasing plate lengths reflect more amount of wave energy. With decreasing depth of the upper layer fluid, the effect of the plate on the surface waves becomes prominent whereas the effect of the plate on the interface waves becomes suppressed. For the normal incident wave of mode m, the horizontal plate reflects very less amount of waves incident on it even zero beyond a certain value of dimensionless wavenumber. Thus, the plate can be used to construct as a component of a lens for the purpose of wave focusing. Moreover, the present method could further be extended to study the wave interaction problem with more than one horizontal plate submerged in a two-layer fluid.